Интервалы выпуклости и вогнутости графика функции
С помощью онлайн-калькулятора можно найти точки перегиба и промежутки выпуклости графика функции с оформлением решения в Word. Является ли функция двух переменных f(x1,x2) выпуклой решается с помощью матрицы Гессе.
- Решение онлайн
- Видеоинструкция
Направление выпуклости графика функции. Точки перегиба
Определение: Кривая y=f(x) называется выпуклой вниз в промежутке (a; b), если она лежит выше касательной в любой точке этого промежутка.
Определение: Кривая y=f(x) называется выпуклой вверх в промежутке (a; b), если она лежит ниже касательной в любой точке этого промежутка.
Определение: Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции y=f(x), характеризуется знаком ее второй производной: если в некотором промежутке f’’(x) > 0, то кривая выпукла вниз на этом промежутке; если же f’’(x) < 0, то кривая выпукла вверх на этом промежутке.
Определение: Точка графика функции y=f(x), разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции y = f(x), в которых вторая производная f’’(x) обращается в нуль или терпит разрыв.
Правило нахождения точек перегиба графика функции y = f(x)
- Найти вторую производную f’’(x).
- Найти критические точки II рода функции y=f(x), т.е. точки, в которой f’’(x) обращается в нуль или терпит разрыв.
- Исследовать знак второй производной f’’(x) в промежутка, на которые найденные критические точки делят область определения функции f(x). Если при этом критическая точка x0 разделяет промежутки выпуклости противоположных направлений, то x0 является абсциссой точки перегиба графика функции.
- Вычислить значения функции в точках перегиба.
Пример 1. Найти промежутки выпуклости и точки перегиба следующей кривой: f(x) = 6x2–x3.
Решение: Находим f ‘(x) = 12x – 3x2, f ‘’(x) = 12 – 6x.
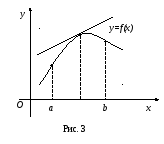
Найдем критические точки по второй производной, решив уравнение 12-6x=0. x=2.
f(2) = 6*22 – 23 = 16
Ответ: Функция выпукла вверх при x∈(2; +∞); функция выпукла вниз при x∈(-∞; 2); точка перегиба (2;16).
Пример 2. Имеет ли точки перегиба функция: f(x)=x3-6x2+2x-1
Пример 3. Найти промежутки, на которых график функции является выпуклым и выгнутым: f(x)=x3-6x2+12x+4
Содержание:
- Теоремы о выпуклости функции и точках перегиба
- Схема исследования функции на выпуклость, вогнутость
График функции $y=f(x)$, дифференцируемой на интервале
$(a ; b)$, является на этом интервале выпуклым, если график
этой функции в пределах интервала $(a ; b)$ лежит не выше любой
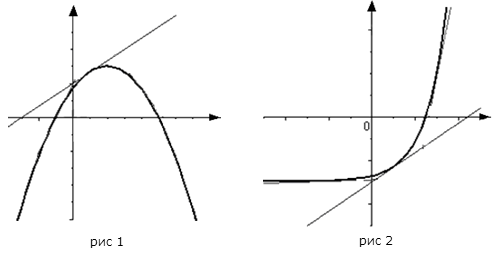
своей касательной (рис. 1).
График функции $y=f(x)$, дифференцируемой на интервале
$(a ; b)$, является на этом интервале вогнутым, если график
этой функции в пределах интервала $(a ; b)$ лежит не ниже любой
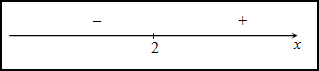
своей касательной (рис. 2).
Теоремы о выпуклости функции и точках перегиба
Теорема
(Об условиях выпуклости или вогнутости графика функции)
Пусть функция $y=f(x)$ определена на интервале
$(a ; b)$ и имеет непрерывную, не равную нулю в точке
$x_{0} in(a ; b)$ вторую производную. Тогда, если
$f^{prime prime}(x)>0$ всюду на интервале
$(a ; b)$, то функция имеет вогнутость на этом интервале,
если $f^{prime prime}(x) lt 0$, то функция имеет выпуклость.
Определение
Точкой перегиба графика функции $y=f(x)$
называется точка $Mleft(x_{1} ; fleft(x_{1}right)right)$, разделяющая промежутки выпуклости и вогнутости.
Теорема
(О необходимом условии существования точки перегиба)
Если функция $y=f(x)$ имеет перегиб в точке
$Mleft(x_{1} ; fleft(x_{1}right)right)$, то
$f^{prime prime}left(x_{1}right)=0$ или не существует.
Теорема
(О достаточном условии существования точки перегиба)
Если:
- первая производная $f^{prime}(x)$
непрерывна в окрестности точки $x_{1}$; - вторая производная $f^{prime prime}(x)=0$ или не существует в точке $x_{1}$;
- $f^{prime prime}(x)$ при переходе через точку $x_{1}$ меняет свой знак,
тогда в точке $Mleft(x_{1} ; fleft(x_{1}right)right)$ функция $y=f(x)$ имеет перегиб.
Схема исследования функции на выпуклость, вогнутость
- Найти вторую производную функции.
- Найти точки, в которых вторая производная равна нулю или не существует.
- Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.
Пример
Задание. Найти интервалы выпуклости/вогнутости функции
$y=frac{x^{3}}{6}-x^{2}+3 x+1$
Решение. Найдем вторую производную заданной функции:
$y^{prime prime}=left(frac{x^{3}}{6}-x^{2}+3 x+1right)^{prime prime}=left(frac{x^{2}}{2}-2 x+3right)^{prime}=x-2$
Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение
$y^{prime prime}(x)=0$:
$y^{prime prime}(x)=x-2=0 Rightarrow x=2$
Исследуем знак второй производной слева и справа от полученной точки:
Так как на промежутке $(-infty ; 2)$ вторая производная
$y^{prime prime}(x) lt 0$, то на этом промежутке функция
$y(x)$ выпукла; в силу того, что на промежутке
$(2 ;+infty)$ вторая производная
$y^{prime prime}(x)>0$ — функция вогнута. Так как при переходе через
точку $x=2$ вторая производная сменила знак, то
эта точка является точкой перегиба графика функции.
Ответ. Точка $x=2$ — точка перегиба графика функции.
На промежутке $(-infty ; 2)$ функция выпукла, на промежутке
$(2 ;+infty)$ функция вогнута.
Читать дальше: асимптоты графика функции.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
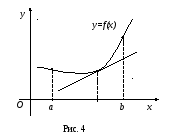
График функции
называется выпуклым в интервале
,
если он расположен ниже касательной,
проведенной в любой точке этого интервала
(рис.3).
График функции
называется вогнутым в интервале
,
если он расположен выше касательной,
проведенной в любой точке этого интервала
(рис. 4).
Достаточное
условие выпуклости (вогнутости).Пусть
функцияимеет вторую производную на интервале
.
Тогда, еслина этом интервале, то функция выпукла,
если,
то график функции вогнутый на этом
интервале.
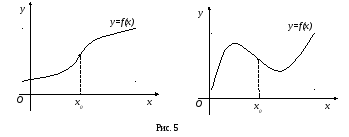
Точка графика
непрерывной функции
,
отделяющая его части выпуклости и
вогнутости, называетсяточкой перегиба(рис. 5).
Необходимое
условие точки перегиба. Если– точка перегиба функции
,
то в этой точке вторая производная
функции либо равна нулю (),
либо не существует.
Точки, в которых
вторая производная функции равна нулю
или не существует, называются критическими
точками 2 –го рода.
Точки перегиба
следует искать среди критических точек
2- го рода.
Первое достаточное
условие точки перегиба. Пусть функцияимеет первую производную в точке
и вторую производную в некоторой
окрестности этой точки (кроме, быть
может самой точки). Тогда если при
переходе через точкувторая производная меняет знак, то
— точка перегиба.
Второе достаточное
условие точки перегиба.Пусть в точкефункция
имеет производные до третьего порядка
включительно. Тогда если,
а,
то– точка перегиба этой функции.
-
Асимптоты.
П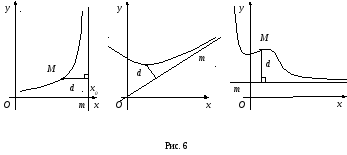
линияmназываетсяасимптотойграфика функции,
если расстояниеdот
точкиM, лежащей на
этом графике, до прямойmстремится к нулю при неограниченном
удалении этой точки по графику от начала
координат в бесконечность (Рис. 6 а),
б), в)).
б
в
а
Асимптоты бывают
трех видов: вертикальные (рис.6а), наклонные
(рис.6б) и горизонтальные (рис.6в).
Прямая
называетсявертикальной асимптотойграфика функции
,
если хотя бы один из односторонних
пределови
равен бесконечности.
Обычно вертикальными
асимптотами являются прямые в точках
разрыва 2-го рода. Поэтому для отыскания
вертикальных асимптот определяют точки
бесконечного
разрыва
функции. Тогда уравнение вертикальных
асимптот
.
Вертикальные асимптоты могут быть и на
границе области определения функции.
Например, как у функции.
Прямая
называется
наклонной асимптотойграфика
функции
при(при
),
если(соответственно,
).
Уравнение наклонной
асимптоты к графику функции
ищем
виде,
где
(*)
и
(**)
Если хотя бы один
из пределов (*) и (**) не существует или
равен бесконечности, то кривая
наклонной асимптоты не имеет. Асимптоты
графика функциипри
и
могут быть разными. Поэтому при нахождении
пределов (*) и (**) следует отдельно
рассматривать случай, когдаи когда
.
Частным случаем
наклонной асимптоты (при
)
являетсягоризонтальная асимптота.
Прямая
является горизонтальной асимптотой
графика функциипри
(при
)
тогда и только тогда, когда(соответственно,
).
-
Общая
схема исследования функции и построение
графиков функций.
При построении
графика данной функции
целесообразно пользоваться следующей
схемой:
-
найти
область определения функции; -
исследовать
функцию на четность, нечетность и
периодичность; -
найти
точки пересечения графика с осями
координат (если это возможно); -
найти
интервалы знакопостоянства функции
(промежутки, на которых
и
);
-
найти
асимптоты; -
найти
интервалы возрастания и убывания,
экстремумы функции; -
найти
интервалы выпуклости и вогнутости,
точки перегиба; -
построить
график функции.
Приведенная схема
исследования не является обязательной.
В более простых случаях достаточно
выполнить лишь несколько операций,
например 1, 3, 4, 6. Иногда бывает необходимым
вычислить несколько дополнительных
точек.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Елена Борисовна Калюжная
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Выпуклая и вогнутая функция
При исследовании заданной функции и построении ее графика встречаются понятия выпуклая и вогнутая функция.
Если функция $y=f(x)$ является дифференцируемой, тогда необходимо рассмотреть следующие определения.
Определение 1
Функция $y=f(x)$ называется выпуклой вниз на некотором интервале, если все точки графика этой функции расположены не ниже касательной, которая проведена к нему в любой точке рассматриваемого интервала.
Функция $y=f(x)$ называется выпуклой вверх на некотором интервале, если все точки графика этой функции расположены не выше касательной, которая проведена к нему в любой точке рассматриваемого интервала.
Схематическое изображение графиков выпуклой вниз (вогнутая функция) и выпуклой вверх (выпуклая) функций показано на рис.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рисунок 1. Графики выпуклой и вогнутой функции. Автор24 — интернет-биржа студенческих работ
Для нахождения интервалов выпуклости/вогнутости графика заданной функции необходимо использовать следующие теоремы.
Теорема 2
Если $f»(x)>0$ для любой точки из рассматриваемого интервала, то график заданной функции на данном интервале направлен выпуклостью вниз.
«Выпуклость и вогнутость кривой, точки перегиба» 👇
Пример 1
Найти промежутки выпуклости и вогнутости функции $y=x^{5} $:
Решение:
Первая производная: $y’=5x^{4} $; вторая производная: $y»=20x^{3} $.
Исследуя знак второй производной кривой, получаем, что $f»(x)0, , forall x>0$. Следовательно, график направлен выпуклостью вверх при $x$0$.$, ,
Правило дождя
Для облегчения запоминания данных теорем можно использовать так называемое «правило дождя» (см. рис.).
Рисунок 2. Правило дождя. Автор24 — интернет-биржа студенческих работ
«Правило дождя»:
- если $f»(x)$
- если $f»(x)>0$ (знак «+» соответствует киванию головы вверх-вниз, т.е. «да»), то лужа образуется, а значит, дождь падает во впадину (выпуклость вниз).
Отметим, что график может быть выпуклым или вогнутым на всей области определения заданной функции, а может только на отдельных промежутках. В таких случаях промежутки выпуклости и вогнутости сменяют друг друга.
Пример 2
Найти промежутки выпуклости/вогнутости графика заданной функции $y=x^{3} $.:
Решение:
$y’=3x^{2} $; вторая производная: $y»=6x$.
Изобразим на числовой оси (см. рис.).
Рисунок 3. Изображение на числовой оси. Автор24 — интернет-биржа студенческих работ
Получаем, что $f»(x)$0, , forall x>0$. Следовательно, график направлен выпуклостью вверх при $x$0$.
Определение 2
Точка перегиба — это такая точка графика выпуклой функции, которая разделяет промежутки выпуклости/вогнутости графика.
В примере 1 $x=0$ является точкой перегиба, так как при переходе через эту точку меняется поведение графика функции (в частности, с выпуклости на вогнутость).
Необходимое условие точки перегиба: В точке перегиба $(x_{0} ;y_{0} )$ вторая производная либо равна нулю, либо не существует.
Достаточное условие точки перегиба:
- $f'(x_{0} )$ непрерывна в окрестности заданной точки;
- $f»(x_{0} )=0$ или не существует в заданной точке;
- $f»(x)$ меняет знак на противоположный при переходе через заданную точку.
Учитывая все выше сказанное, составим алгоритм исследования выпуклости и вогнутости функции:
- нахождение первой производной $f'(x)$ заданной функции;
- нахождение второй производной $f»(x)$ заданной функции;
- определение точек, в которых $f»(x)$ равна нулю или не существует;
- исследование знака $f»(x)$ с помощью числовой прямой;
- определение промежутков выпуклости и вогнутости графика заданной функции;
- нахождение интервалов выпуклости и точки перегиба функции, если они существуют.
Пример 3
Найти точки перегиба графика заданной функции: $y=4x^{2} -3$.
Решение:
Первая производная: $y’=8x$; вторая производная: $y»=8$.
Изобразим на числовой оси (см. рис.).
Рисунок 4. Изображение на числовой оси. Автор24 — интернет-биржа студенческих работ
Получаем, что $f»(x)>0, , forall xin D_{y} $. Следовательно, график направлен выпуклостью вниз при любом $x$. Точек перегиба нет.
Пример 4
Найти точки перегиба графика заданной функции: $y=frac{3}{x^{2} -1} $.
Решение:
Первая производная: $y’=frac{0cdot (x^{2} -1)-3cdot 2x}{(x^{2} -1)^{2} } =-frac{6x}{(x^{2} -1)^{2} } $.
Вторая производная: $y»=-frac{6cdot (x^{2} -1)^{2} -6xcdot 2xcdot 2cdot (x^{2} -1)}{(x^{2} -1)^{4} } =-6cdot frac{x^{2} -1-4x}{(x^{2} -1)^{3} } $.
Вторая производная не существует при $x=pm 1$.
[begin{array}{l} {y»=0:-6cdot frac{x^{2} -1-4x}{(x^{2} -1)^{3} } =0Rightarrow x^{2} -4x-1=0} \ {x^{2} -4x-1=0} \ {D=16+4=20} \ {x_{1} =frac{4-sqrt{20} }{2} =2-sqrt{5} ;x_{2} =frac{4+sqrt{20} }{2} =2+sqrt{5} } end{array}]
Изобразим на числовой оси (см. рис.).
Рисунок 5. Изображение на числовой оси. Автор24 — интернет-биржа студенческих работ
Получаем, что:
- $f»(x)>0, , forall xin (-1;2-sqrt{5} ]bigcup (1;2+sqrt{5} ]$,
- $f»(x)
Следовательно, график направлен выпуклостью вверх на промежутках $(-infty ;-1)$, $[2-sqrt{5} ;1)$ и $(1;+infty )$, вниз на промежутках — $(-1;2-sqrt{5} ]$ и $(1;2+sqrt{5} ]$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
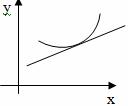
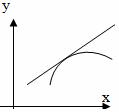
График функции y=f(x) называется выпуклым на интервале (a;
b), если он расположен ниже любой своей касательной на
этом интервале.
График функции y=f(x) называется вогнутым на интервале (a;
b), если он расположен выше любой своей касательной на
этом интервале.
На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).
Примеры.
- Полуокружность
выпукла на [–1; 1].
- Парабола y = x2 вогнута на интервале (-∞; +∞).
- График функции в одних интервалах может быть
выпуклым, а в других вогнутым. Так график функции y = sin x на
[0,2; π], выпуклый в интервале (0; π) и вогнутый в (π;
2π).
Рассмотрим достаточный признак, позволяющий установить,
будет ли график функции в данном интервале выпуклым или вогнутым.
Теорема. Пусть y=f(x) дифференцируема на (a;
b). Если во всех точках интервала (a;
b) вторая производная функции y = f(x) отрицательная, т.е. f »(x) < 0, то график функции
на этом интервале выпуклый, если же f»(x) > 0 – вогнутый.
Доказательство.
Предположим для определенности, что f»(x) < 0 и докажем, что график функции будет выпуклым.
Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.
Итак, уравнение кривой имеет вид y
= f(x). Обозначим ординату касательной,
соответствующую абсциссе x. Тогда . Следовательно, разность ординат кривой и касательной при
одном и том же значении x будет .
Разность f(x)
– f(x0) преобразуем по теореме
Лагранжа , где c между x и x0.
Таким образом,
.
К выражению, стоящему в квадратных скобках
снова применим теорему Лагранжа: , где c1 между c0 и x0. По условию теоремы f »(x) < 0. Определим знак
произведения второго и третьего сомножителей.
- Предположим, что x>x0. Тогда x0<c1<c<x,
следовательно,(x – x0)
> 0 и (c – x0) > 0. Поэтому.
- Пусть x<x0, следовательно, x < c
< c1 < x0 и (x – x0)
< 0, (c – x0) < 0. Поэтому вновь.
Таким образом, любая
точка кривой лежит ниже касательной к кривой при всех значениях x и x0 Î
(a; b), а это значит, что кривая
выпукла. Вторая часть теоремы доказывается аналогично.
Примеры.
- Установить интервалы
выпуклости и вогнутости кривой y = 2 – x2.Найдем y » и определим, где вторая
производная положительна и где отрицательна. y‘ = –2x, y» = –2 < 0 на (–∞; +∞), следовательно, функция всюду
выпукла. - y = ex. Так как y» = ex
> 0 при любых x, то кривая всюду вогнута. - y = x3. Так как y» = 6x, то y» < 0 при x
< 0 и y» > 0 при x
> 0. Следовательно, при x < 0 кривая выпукла, а
при x > 0 вогнута.
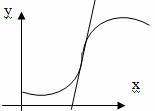
Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной
стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.
Определим достаточные
условия того, что данная точка кривой является точкой перегиба.
Теорема. Пусть кривая определяется
уравнением y = f(x). Если f »(x0) = 0 или f »(x0) не существует и при переходе
через значение x = x0 производная f »(x) меняет знак, то точка
графика функции с абсциссой x = x0 есть точка перегиба.
Доказательство. Пусть
f »(x) < 0 при x
< x0 и f
»(x) > 0 при x
> x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с
абсциссой x0 есть точка перегиба. Аналогично можно
рассматривать второй случай, когда f
»(x) > 0 при x
< x0 и f
»(x) < 0 при x
> x0.
Таким образом, точки перегиба следует искать только
среди таких точек, где вторая производная обращается в нуль или не существует.
Примеры. Найти точки перегиба и определить интервалы
выпуклости и вогнутости кривых.
Найдем производные
заданной функции до второго порядка..
. Вторая производная не существует при x =
1. Исследуем эту точку на возможный перегиб.Итак, точка
перегиба x = 1. Функция выпукла на (1; +∞), вогнута на (–∞;
1).Возможные точки
перегиба найдем, решив уравнение 2x2 – 1 = 0. Отсюда.
Точки перегиба
. Функция выпукла на
и вогнута на
.
- y = ln (1 – x2). Область определения функции D(y) = (-1; 1).
.
при всех x из
(–1; 1).Следовательно,
f(x) выпуклая на (–1; 1).
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
При исследовании функции
важно установить форму ее графика при неограниченном удалении точки графика от
начала координат.
Особый интерес
представляет случай, когда график функции при удалении его переменной точки в
бесконечность неограниченно приближается к некоторой
прямой.
Прямая называется асимптотой графика функции y = f(x), если расстояние от
переменной точки M графика до этой прямой при удалении точки M в
бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении
в бесконечность должна неограниченно приближаться к асимптоте.
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от
нее или с разных сторон, бесконечное множество раз пересекая асимптоту и
переходя с одной ее стороны на другую.
Если обозначим
через d расстояние от точки M
кривой до асимптоты, то ясно, что d стремится к нулю при
удалении точки M в бесконечность.
Будем в дальнейшем различать асимптоты вертикальные и наклонные.
ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ
Пусть при x→ x0 с какой-либо стороны функция y = f(x)неограниченно возрастает по абсолютной
величине, т.е. или
или
. Тогда из определения асимптоты следует, что прямая x = x0 является асимптотой. Очевидно и обратное,
если прямая x = x0 является асимптотой, т. о. .
Таким образом, вертикальной
асимптотой графика функции y = f(x)
называется прямая, если f(x) → ∞ хотя бы при одном из условий x→
x0 – 0 или x → x0 + 0, x = x0
Следовательно,
для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x0, при которых функция обращается в бесконечность (терпит бесконечный
разрыв). Тогда вертикальная асимптота имеет уравнение x = x0.
Примеры.
- Найти вертикальные асимптоты графика функции
.
Так как
, то прямая x =
2 является вертикальной асимптотой. .
Прямая x = 0 – вертикальная асимптота.
НАКЛОННЫЕ АСИМПТОТЫ
Поскольку
асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту,
то ее уравнение будет y = kx + b. Наша задача найти
коэффициенты k и b.
Теорема. Прямая y = kx + b служит наклонной
асимптотой при x → +∞
для графика функции y
= f(x) тогда и только тогда,
когда . Аналогичное утверждение верно и при x → –∞.
Доказательство. Пусть MP –
длина отрезка, равного расстоянию от точки M до асимптоты. По условию . Обозначим через φ угол наклона асимптоты к
оси Ox. Тогда из ΔMNP
следует, что . Так как φ постоянный угол (φ ≠ π/2), то
, но
MN = MK – NK = y — yас = f(x) — (kx+b).
Следовательно, мы можем
записать следующее равенство .
Так как x → +∞, то должно
выполняться равенство . Но при постоянных k и b
и
. Следовательно,
, т.е.
.
Если число k
уже известно, то , поэтому
.
Для
доказательства в случае x → –∞ все рассуждения аналогичны.
Докажем обратное
утверждение. Предположим, что существуют пределы, определяющие числа k и b.
Тогда несложно заметить, что выполняется равенство . Действительно
Следовательно,
прямая y = kx + b
есть асимптота. Теорема полностью доказана.
Сделаем несколько замечаний.
Замечание 1. Теорема
показывает, что для нахождения асимптот достаточно найти два указанных предела.
Причем, если хотя бы один из пределов не существует или обращается в бесконечность,
то кривая асимптот не имеет.
Замечание 2. В случае,
когда k = 0 асимптота y = b
называется горизонтальной асимптотой. Наличие горизонтальной асимптоты
означает, что существуют пределы
.
Замечание 3. Пределы для отыскания k и b могут
быть различны при x
→ +∞ и x
→ – ∞ и, следовательно, график функции может иметь две различные
асимптоты при x → +∞ и x → –∞.
Примеры. Найти асимптоты кривых.
.
- Вертикальные:
x = 0 – вертикальная асимптота.
- Наклонные:
.
При x → — ∞ получим те
же значения k и b. Следовательно, прямая
y = x + 2 является наклонной асимптотой.
- Вертикальные:
- y = e–x sin x + x.
- Функция определена и непрерывна на всей числовой прямой, следовательно,
вертикальных асимптот нет. -
а)
.
Итак, при x
→ +∞ наклонная асимптота у=
х.б)
, т. к.
, поэтому при x
→ — ∞ наклонных асимптот нет.
- Функция определена и непрерывна на всей числовой прямой, следовательно,
- y = x – 2arctg x.
- Вертикальных асимптот нет.
-
а)
.
. Наклонная асимптота y = x – π
при.
б)
при
.




















 при всех x из
при всех x из




 .
. .
. , т. к.
, т. к. , поэтому при x
, поэтому при x