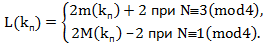Как найти инвариант числа

Хочу познакомить вас с таким интересным математическим понятием, как инвариант. Оно редко встречается при решении школьных задач, но для ребят, которые увлекаются олимпиадными задачками, должно быть знакомым.

Итак, для начала определим, что же такое инвариант. Это математическая величина или математическое свойство, которое остается постоянным, то есть не изменяется при некотором преобразовании. Например, инвариантом могут быть четность или нечетность какой-то величины, остаток при делении на число, алгебраическое выражение (сумма чисел, произведение чисел, сумма обратных величин). Попробуем решить несколько задачек, используя понятие инварианта.

Задача 1.

Леша получил двойку за контрольную работу по математике и в порыве отчаяния разорвал листок со своей работой на десять кусков. Затем один из получившихся кусков он разорвал еще на 10 кусков. Может ли по завершении релаксации оказаться 1) 2 012 кусков бумаги; 2) 2 017 кусков бумаги?

Решение.

Для начала важно определить, что в данной задаче является инвариантом. Попробуем проанализировать. Сначала у Леши был 1 листок – это один кусок. На втором шаге листков стало 10, то есть их количество увеличилось на 10 – 1 = 9 листков. На третьем шаге листков будет уже 19, и их количество, очевидно, опять увеличится на 19 – 10 = 9 листков, и так далее. Таким образом, нетрудно видеть, что инвариантом, то есть неизменной величиной на каждом шаге, в данной задаче является количество листков, на которое увеличивается общее число листков. Теперь разберемся, как нам поможет знание инварианта при решении данной задачи. Построим следующую схему.

1 шаг – 1 листок;

2 шаг – 1 + 9 листков;

3 шаг – 1 + 9 + 9 листков;

и так далее.

Из нее видно, что, если предположить, что в конечном счете может оказаться 2 012 листков, то число 2 012 – 1 = 2011 должно делиться нацело на 9. Но это неверно. Значит, 2 012 кусков в конечном итоге получиться не может.

Теперь рассмотрим случай 2. Число 2 017 – 1 = 2 016 делится на 9, так как сумма его цифр делится на 9. А, значит, второй вариант возможен.

Ответ: 1) да; 2) нет.

Задача 2.

На доске записано 10 знаков «+» и 15 знаков «–». За один ход можно стереть 2 знака и написать вместо них «+», если знаки одинаковые и «–», если знаки различные. Каким будет знак на доске после 24 ходов?

Решение.

Рассмотрим произвольный ход. Он может быть трех типов:

1) + + = + (количество плюсов уменьшилось на 1, количество минусов осталось прежним);

2) – – = + (количество плюсов увеличилось на 1, количество минусов уменьшилось на 2);

3) + – = – (количество плюсов уменьшилось на 1, количество минусов осталось прежним).

Заметим, что количество минусов за один ход или не меняется, или уменьшается на 2. То есть, мы можем утверждать, что в данной задаче инвариантом является четность количества минусов, на которое изменяется общее количество минусов при каждом последующем ходе. В начале количество минусов было 15, то есть нечетным. Значит, после 24 ходов оно также будет нечетным, так как если от нечетного числа отнимать четное, то получим опять нечетное. Значит, число минусов на доске не может стать равным, например, двум или нулю. А так как после 24 ходов на доске должен остаться ровно один знак, то это и будет «–».

В этой задаче можно было выбрать и другой инвариант. Заметим, что число плюсов на доске на каждом ходе или увеличивается на 1, или уменьшается на 1, то есть на каждом шаге меняется четность числа плюсов. Это закономерное изменение на каждом шаге и примем за инвариант. А тогда, четность числа плюсов на 24 ходе будет такая же, как и в начале (10 – четное число). Значит, число плюсов на доске не может быть 1, следовательно последний знак – «–».

Ответ: «–».

Задача 3.

2 012 шашек выставлено в ряд. За один ход любые две шашки, стоящие через одну можно, можно поменять местами. Можно ли через несколько ходов переставить шашки в обратном порядке?

Решение.

Пронумеруем все шашки по порядку, то есть первой шашке присвоим номер 1, второй – 2, третьей – 3 и так далее. Мысленно закрасим позиции, на которых стоят шашки в черный и белый цвет через одну так, чтобы на черных позициях стояли шашки с нечетными номерами, а на белых – шашки с четными номерами.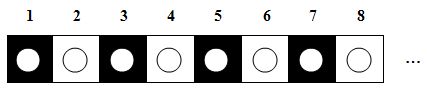
Заметим, что инвариантом в данной задаче является то, что на каждом шаге перестановки цвета позиций шашек не меняются. Цвет позиции первой шашки – черный, а последней – белый, значит, в ходе перестановки  первая шашка никак не может стать на место последней, а последняя – на место первой, ведь их цвета разные, поэтому переставить шашки в обратном порядке невозможно.

Ответ: нет.

Теперь, я думаю, очень хорошо видно, насколько понятие инварианта может оказаться полезным. Стоит только заметить некоторую закономерность, то есть свойство, повторяющееся  на каждом шаге, и задача становиться практически очевидной.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Новый инвариант числа. Исследование натурального ряда чисел (НРЧ)

          В арифметике натуральных чисел иногда возникает необходимость поиска делителей составного числа N. Простая операция, обратная умножению чисел, на сегодняшний день неизвестна. Ее отсутствие создает определенные трудности при решении некоторых практических задач, особенно, если манипулировать приходится с числами высокой и очень высокой разрядности (сотни и даже тысячи цифр, представляющих числа).

          В работе «Фундаментальные структуры натурального ряда чисел» Ваулин А.Е., Пилькевич С.В.– Интеллектуальные системы. Труды Седьмого международного симпозиума. Под ред. К.А. Пупкова.– М.: РУСАКИ, 2006. – с.384-387. Приводятся сведения об оригинальной концепции моделирования натурального ряда чисел и отдельного числа с целью установления свойств, слабо зависящих или вообще не зависящих от разрядности чисел. Дальнейшему развитию и уточнению деталей этого подхода посвящена настоящая работа.

          Независимость некоторых свойств чисел от их разрядности явилась одной из основных идейных посылок предлагаемого аналитического подхода к моделированию чисел. Наличие таких свойств у чисел подтверждает существование признаков делимости чисел. Например, какой бы величины не было заданное число, если свертка (сумма) его цифр делится на три, то и исходное число делится на три. От разрядности числа делимость на три практически не зависит. Аналогично и для других признаков делимости. Это свидетельство того, что некоторые свойства чисел могут не зависеть от их разрядности. Поиск таких свойств и разработка теории их использования в различных направлениях, в частности, при разработке алгоритмов факторизации, установлении простоты числа, и других не менее трудных задач является актуальной и важной проблемой современной математики.

          В работе описывается новый обнаруженный признак-свойство чисел. Этот признак оказывается полезным для разработки алгоритмов решения как новых, так и традиционных задач теории и практики. Приведем вначале качественные содержательные рассуждения о сущности предлагаемой работы.

          Натуральный ряд. Будем далее рассматривать натуральный ряд чисел как математический объект, имеющий сложное строение. НРЧ можно рассматривать как совокупность различных рядов с разными свойствами, например, составленным из двух арифметических прогрессий четных и нечетных чисел. Эти прогрессии имеют совпадающие разности d, равные d=2, но с разными начальными элементами: а=1 для прогрессии нечетных чисел и а=2 для прогрессии четных чисел. Загрузим все числа НРЧ в ячейки (разряды) регистра и тогда НРЧ можно представить регистром с бесконечным числом ячеек. Обратим внимание на ряд нечетных чисел.

          Рассмотрим в НРЧ три смежных последовательных числа 2n–1, 2n, 2n+1, среднее из которых четное. Возведем их в квадрат. Между квадратами крайних нечетных чисел всегда лежит четное число разрядов регистра вида 8k, которое четным квадратом разбивается на два последовательных (смежных) нечетных числа вида 4k–1 слева и 4k+1 справа. Ячейку самого четного квадрата отнесем к правому числу.

          Таким образом, любое нечетное число вида N=4k±1, k>0 – произвольное натуральное число, в НРЧ лежит всегда между квадратами чисел N=x₁²–x₀² с разной четностью. В определенных ячейках НРЧ размещаются квадраты натуральных чисел. Такому размещению соответствует ряд закономерностей. Нечетные квадраты чередуются с четными квадратами. При этом, если больший квадрат x₁² четный, то N=4k–1 и N≡3(mod4), а если больший квадрат x₁² нечетный, то N=4k+1 и N≡1(mod4).

          Представим регистр НРЧ линейкой с движком по типу логарифмической. Для заданного числа N в движке создадим окно размером в N+1 позиций (разрядов). Путем перемещения движка вдоль НРЧ-линейки будем находить и фиксировать его положения парой чисел (x₀², x₁²), которые размещены в крайних позициях окна (x₀² – левая и x₁² – правая) и оба значения будут соответствовать числовым квадратам. Разность между квадратами в крайних позициях окна, очевидно, будет совпадать с числом N=x₁²–x₀².

          Контуры НРЧ. Расстояние между квадратами двух последовательных нечетных чисел назовем контуром. Расстояние между ячейками с квадратами несмежных чисел назовем интервалом в НРЧ. Если сумма смежных нечетных чисел кратна числу 8, то она образует длину интервала, называемого контуром, а значение k является номером этого контура. Так смежные числа 11 и 13 образуют контур

(11+13=24=3•8)

с номером k=3 и длиной L(k)=24=k•8, а смежные нечетные числа 13 и 15 контур не образуют

(13+15=28≠k•8)

.

          Расстояния между нечетными квадратами-границами смежных чисел всегда образуют контуры и содержат число регистровых ячеек, равное 8k. Контуры в НРЧ образуют непрерывную последовательность с номерами k=1(1)∞, т.е. НРЧ образован заполненными числами ячейками последовательности контуров, длины которых кратны числу 8. Первый контур имеет длину

L(1)=3²–1²=1•8

, второй контур –

L(2)=5²–3²=2•8=16

, и т.д. Длины контуров образуют арифметическую прогрессию с разностью d=8 и а=8.

          Заполнение всех позиций окна числами (интервалов) в каждом из фиксированных парой чисел

(x₀², x₁²)

положений обладает закономерностью и характеризуется некоторым числовым инвариантом, устанавливаемым в работе. Так как пар

(x₀², x₁²)

может быть больше одной, то будем снабжать ее числа индексом i.

Пример 1

          Для N=105 (размер окна — 1) имеется 4 положения (4 пары квадратов разной четности), которые фиксируются. Контролировать будем положение левой границы окна. Начинаем перемещение движка от 1 вправо. Первое положение (остановка) возникает с появлением на левой границе окна числа x₀²=4, но правая граница при этом равна 109 – не квадрат, затем на левой границе окна оказывается квадрат x₀²=9, но справа число 114 – не квадрат, после прохода позиции с числом 15 в окне слева появляется число x₀²=16 – квадрат. Останавливаемся и проверяем число на правой границе окна. Там видим число x₁²=121 – тоже квадрат. Фиксируем это положение с контролем разности между квадратами:

x₁₁²–x₀₁²=11²–4²=105

.
          Продолжаем движение до прихода левого края окна в позиции 25, 36, 49 и видим, что для них правая граница на квадрат не попадает. Но когда в окне слева появляется число 64, справа видим число 169 – квадрат. Фиксируем это положение и выполняем контроль

x₁₂²–x₀₂²=13²–8²=105

.
          Следующее фиксируемое положение окна: слева число x_о²=256, а справа x₁²=361, оба квадраты. Фиксируем и выполняем контроль разности между квадратами

x₁₃²–x₀₃²=19²–16²=105

.
          И, наконец, четвертое положение окна дает разность квадратов равную

x₁₄²–x₀₄²=53²–52²=105

.
          Дальнейшее движение прекращается, так как больше не существует пары квадратов, разность между которыми равна числу N=105, разность всех пар будет больше 105. Четвертую пару x₁₄², x₀₄² назовем предельной парой.

          Полуконтуры. Место каждого четного квадрата вида (2k)² во внутренней ячейке k-го контура. Эта ячейка делит длину L(k) контура на два

m(k)=4k–1

и

М(k)=4k+1

смежных нечетных числа (левое и правое), называемых полуконтурами. Заметим, что контуры и полуконтуры – это множества ячеек, заполненных натуральными числами, а m(k) и M(k) – мощности этих множеств. Множества ячеек последовательно следующих полуконтуров формируют НРЧ. Все множество нечетных чисел образуют два класса: левые числа N≡3(mod4) и правые числа N≡1(mod4). Длины полуконтуров первого контура, левое нечетное число 4•1–1=3 и правое нечетное число 4•1+1=5, в сумме образуют длину

L(k=1)=3+5=8

контура с номером k=1.

          Границы контура. При заданном номере k контура он полностью определяется, полуконтуры с длиной

m(k)=4k–1

левый и

М(k)=4k+1

правый, границы этого контура левая

Г_л(k)=(2k–1)²

и правая

Г_п(k)=(2k+1)²

. Длина контура

L(k)=m(k)+M(k)=Г_п(k)–Г_л(k)=8k

. Четный квадрат

Г_ч(k)=(2k)²

— общая граница полуконтуров.
          Действительно, разность границ

Г_п(k)–Г_л(k)=(2k+1)²–(2k–1)²=4k²+2•2k+1–4k²+2•2k–1=8k.

          Предельный контур. Любое нечетное число N можно представить как полуконтур в некотором контуре с номером k_п. Такой контур единственный, так как контур слева от предельного имеет полуконтуры меньшие N, а справа — большие N. Число N левое или правое определяется с использованием четного квадрата предельного контура. Для левого

N=x₁²–x₀²

, и x₁ четное, для правого

N=x₁²–x₀²

и x₁ нечетное. Здесь роль границ полуконтуров играют значения x₁² и x₀². Эти границы определяются из выражений

x₁=(N+1)/2

и

x_о=(N–1)/2

. Длина предельного контура с номером k_п для числа N определяется по формуле

          Номер k_п предельного контура числа N вычисляется через длину предельного контура

k_п=L(k_п)/8

. Теперь самое время пояснить введенные понятия числовым примером. Это специально подобранный пример, очень простой, способствующий лучшему пониманию изучаемого явления.

Пример 2

          Пусть задано составное нечетное натуральное число (сннч)

N=105=3•5•7

. Для этого числа требуется найти предельный контур, его границы и определить его номер k_п. Указать все пары квадратов

(x_i1², x_i0²)

, i=1(1)… разной четности, разность между которыми равна числу N=105.

          Решение. Для лучшего усвоения содержания примера рекомендуется воспользоваться карандашом и бумагой. Известно, что сннч лежит между квадратами разной четности

N=x₁²–x₀²

. Определим левое или правое число заданного

N=105≡1(mod4)

. Число N правое, т.е. это больший полуконтур в предельном контуре. Определим границы предельного контура через значение N,

x₁=(N+1)/2=(105+1)/2=53

и

x_о=(N–1)/2=(105–1)/2=52

. Квадраты чисел 52 и 53 являются границами полуконтура.
          Длина контура

L(k_п)=2•105–2=208=8•k_п

, откуда

k_п=208/8=26

. Меньший (левый) полуконтур имеет длину

m(k_п)=L(k_п)–М(k_п)=208–105=103

, является простым числом.
          Находим через k_п границы предельного контура: левая

Г_л(k_п)=(2k_п–1)²=(2•26–1)²=51²=2601

и правая

Г_п(k_п)=(2k_п+1)²=(2•26+1)²=53²=2809

. Длина контура через его границы определяется выражением

L(k_п)=Г_п(k_п)–Г_л(k_п)=2809–2601=208=8k_п

.
          Поскольку заданное сннч N=105 является полуконтуром в предельном контуре, то будем полагать, что ему соответствует лишь половина номера предельного контура, т.е.

k_п(N)/2=26/2=13

.

          Инвариант числа. Характеристику числа N в форме k_п(N)/2 назовем инвариантом числа N, а дальше покажем, почему выбрано такое название. Инвариант может быть целым или дробным числом в зависимости от четности номера k_п предельного контура.

          Интервалы НРЧ для числа N. Далее рассмотрим возможности представления сннч N=105 разностями других пар квадратов разной четности. Число 105, как впрочем, и любое другое нечетное число можно представить суммой нечетного количества меньших смежных нечетных чисел. Полезность такого представления N следует из того, что границы всех нечетных чисел в НРЧ – квадраты, следовательно, и непрерывный интервал, представляющий N=105 из смежных нечетных чисел, будет иметь на границах квадраты. Количество слагаемых в сумме должно быть нечетным числом.

1. Допустим, что таких слагаемых будет три. Очевидно, 105:3=35 и первое слагаемое будет равно 35–2=33, второе 35, а третье 35+2=37. Числа 33, 35, 37 образуют непрерывную последовательность нечетных смежных чисел, а 35 и 37 являются полуконтурами одного контура, так как их сумма 35+37=72 кратна 8. Этот контур имеет номер k=72/8=9. Число 33 принадлежит другому предшествующему контуру с номером k=8 и в нем является правым, т.е. большим. Этому числу 33 соответствует половина номера его контура, т.е. k/2=8/2=4. Интервалу из трех примыкающих друг к другу нечетных чисел длиной в 105 ячеек в НРЧ соответствует сумма номеров контуров в виде k_п(N)/2=8/2+9=4+9=13.

   Для этого интервала определим границы. Большая граница интервала совпадает с правой границей большего контура с номером k=9, т.е.

   Г_п(k)=(2•k+1)²=(2•9+1)²=19²=x₁²=361. Меньшая граница интервала совпадает с левой границей меньшего из трех полуконтура, т.е. числа 33, находящегося в контуре с номером k=8, его граница – это четный квадрат удвоенного номера контура Г_ч(k)=Г_л(k)=(2k)²=(2•8)²=x₀²=256. Проверка: N=Г_п(9)–Г_л(8/2)=361–256=105.
   Теперь для N=105 можем записать факторы N=x₁²–x₀²=(19+16)(19–16)=35•3=105.

2. Пусть представление N имеет полуконтурами в сумме пять нечетных слагаемых. Очевидно, 105:5=21 и первое слагаемое будет равно 21–4=17, второе 21–2=19, третье 21, четвертое 21+2=23 и, наконец, пятое 21+4=25. Числа 17, 19, 21, 23, 25 образуют непрерывную последовательность нечетных смежных чисел, а 19, 21 и 23, 25 из них являются полуконтурами двух смежных контуров, так как их сумма 19+21=40=5•8 и 23+25=48=6•8 кратна 8. Эти контуры имеют номера k=40/8=5 и k=48/8=6.

   Число 17 является большим (правым) полуконтуром предшествующего контура с номером

   k=(15+17)/8=4. Этому числу соответствует половина номера меньшего контура k/2=4/2=2. Интервалу из пяти примыкающих друг к другу нечетных чисел длиной в 105 ячеек в НРЧ соответствует сумма номеров контуров k_п(N)/2=4/2+5+6=2+5+6=13.

   Для этого интервала определим границы. Большая граница интервала совпадает с правой границей большего контура с номером k=6, т.е.

   Г_п(k)=(2•k+1)²=(2•6+1)²=13²=x₁²=169. Меньшая левая граница интервала совпадает с левой границей меньшего полуконтура, т.е. числа 17, находящегося в контуре с номером k=4. Меньшая граница – это четный квадрат удвоенного номера контура Г_ч(k)=Г_л(k)=(2k)²=(2•4)²=x₀²=64.Проверка на разность квадратов: N=Г_п(6)–Г_ч(4)=169–64=105. Теперь для N=105 можем записать факторы N=x₁²–x₀²=(13+8)(13–8)=21•5=105.

3. Пусть слагаемых в представляющей число N сумме будет семь. Очевидно, 105:7=15 и первое слагаемое будет равно 15–6=9, второе 15–4=11, третье 15–2=13, четвертое 15, пятое 15+2=17, шестое 15+4=19 и, наконец, седьмое 15+6=21. Числа 9, 11, 13, 15, 17, 19, 21 образуют непрерывную последовательность нечетных смежных чисел, а 11, 13; 15, 17 и 19, 21 являются полуконтурами трех смежных контуров, так как их суммы 11+13=24=3•8; 15+17=32=4•8 и 19+21=40=5•8 кратны 8. Эти контуры имеют номера k=24/8=3, k=32/8=4 и k=40/8=5.

   Число 9 является большим (правым) полуконтуром предшествующего контура с номером

   k=(7+9)/8=2. Этому числу соответствует половина номера меньшего контура, т.е. k/2=2/2=1. Интервалу из семи примыкающих друг к другу нечетных чисел длиной в 105 ячеек в НРЧ соответствует сумма номеров контуров k_п(N)/2=2/2+3+4+5=1+3+4+5=13.

   Для этого интервала определим границы. Большая граница интервала совпадает с правой границей большего контура с номером k=5, т.е.

   Г_п(k)=(2•k+1)²=(2•5+1)²=11²=x₁²=121. Меньшая граница интервала совпадает с левой границей меньшего полуконтура, т.е. числа 9, находящегося в контуре с номером k=2, это четный квадрат удвоенного номера контура Г_ч(k)=Г_л(k)=(2k)²=(2•2)²=x₀²=16.Проверка: N=Г_п(5)–Г_ч(2)=121–16=105.
   Теперь для N=105 можем записать факторы N=x₁²–x₀²=(11+4)(11–4)=15•7=105.

          Рассмотренный пример показывает, что для числа N=105 существуют четыре пары квадратов разной четности, расстояние в НРЧ между которыми равно 105. Каждая из найденных пар квадратов позволяет решить задачу факторизации сннч N=105, исключая предельную пару – она дает тривиальное разложение на множители.

          Остается открытым очень важный вопрос, где брать, как получать для произвольного числа N пары

(x_о², x₁²)

квадратов?

          Анализ результатов примера 2 показывает, что разные пары квадратов

(x_оi², x_1i²)

, i=1(1)4, получаются при разных представлениях инварианта

k_п(N)/2=13

в виде суммы с разным числом слагаемых. Сами такие суммы можно рассматривать как разбиения числа 13 специального вида. Все слагаемые суммы представляют собой отрезок НРЧ, в котором одно из крайних слагаемых в сумму включается лишь своей половиной. Определение такого слагаемого диктуется принадлежностью числа N к классу левых или правых нечетных чисел.

Если N – левое, то половина берется от большего слагаемого:

• N=183 – левое нечетное, 183≡3(mod4), половина берется от большего слагаемого в представлении инварианта суммой k_п(183)/2=23=15+16/2; инвариант целое число;
• N=203 – левое нечетное, 203≡3(mod4), половина берется от большего слагаемого в представлении инварианта суммой k_п(203)/2=25.5=6+7+8+9/2; инвариант не целое число;

Если N – правое, то половина берется от меньшего слагаемого:

• N=213 – правое нечетное, 213≡1(mod4), половина берется от меньшего слагаемого в представлении инварианта суммой k_п(213)/2=26.5=17/2+18; инвариант не целое число;
• N=217 – правое нечетное, 217≡1(mod4), половина берется от меньшего слагаемого в представлении инварианта суммой k_п(217)/2=27=6/2+7+8+9; инвариант целое число;

Таким образом, из рассмотренных фактов следует алгоритм решения задачи факторизации чисел:

1. Для заданного сннч N найти инвариант k_n/2.
2. Инвариант представить разбиением специального вида k_n/2=a+(a+1)+(a+2)+…+(a+t-1)+k_д/2, где k_д – дополнительный номер крайнего контура, левый или правый.
3. Для крайних слагаемых вычислить границы: левую Г_л=x₀² и правую Г_п=x₁².
4. Разность границ представить произведением скобок N=x₁²–x₀²=(x₁+x₀)(x₁–x₀)=pq.

Рассмотренный материал позволяет сделать следующие выводы.

1. Модель составного нечетного натурального числа, представляемого в понятиях контуров – полуконтуров НРЧ позволяет установить инвариант такого числа, как функцию номеров представляющих число контуров. Инвариант k_п(N)/2 сохраняет значение независимо от того разностью какой пары квадратов ( при наличии нескольких пар квадратов ) представляется сннч N=x_i1²–x_i0², i=1(1)t, где t – число представляющих пар. N=105=x_i1²–x_i0²=53²–52²=19²–16²=13²–8²=11²–4²
2. Значение инварианта устанавливается элементарной обработкой заданного числа N при установлении номера предельного контура. Инвариант может быть как целым, так и дробным числом. Относительно предельного контура сформулированы и доказаны теоремы, которые в посте не приводятся, но используются.
3. Предлагаемая модель НРЧ в терминах и понятиях контуров – полуконтуров открывает возможность формулирования и исследования задачи факторизации нечетных чисел за приемлемое для практических приложений время.

«ИНВАРИАНТ – НЕОБЫЧНОЕ В ПРОСТОМ»

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение 

Начиная с 5-го класса, я занимаюсь в школьном математическом кружке. Там мы изучаем математику более углубленно, чем на уроках и решаем олимпиадные задачи. Именно там, на одном из занятий мы познакомились с понятием инвариант – это величина, неизменяемая при выполнении определенных операций. Нам объяснили, что инварианты — это довольно сложный и интересный раздел математической науки, задачи которого часто встречаются в различных конкурсах и олимпиадах. Затем мы попробовали решить несколько таких подобных заданий.

Я уже кое-что знала об инвариантах, так как в прошлом году проводила исследование по теме «Математические игры – познавательный досуг», и в моем сборнике присутствовали инвариантные игры, поэтому мне было немного проще решать задачи на кружке. Но все-таки мои знания были довольно поверхностными. Мне захотелось лучше разобраться в этой непростой теме, ведь она очень заинтересовала меня, поэтому я считаю свою тему актуальной, а исследование результативным.

Объект исследования: математические задачи, решаемые инвариантом.

Предмет исследования: инварианты в решениях.

Цель моей работы: научиться решать инвариантные задачи, создать обучающий видеоролик на соответствующую тематику.

Задачи, над которыми я работала:

1. Вспомнить точное определение термина «инвариант» составленное мною в прошлом году.

2. Попытаться классифицировать инварианты, опираясь на свой личный опыт.

3. Узнать, насколько практичны и применяемы в повседневной жизни инварианты, и чем они полезны.

4. Подумать в каких науках также применяются инварианты.

5. Понять, как находить инвариант в задачах.

6. Самостоятельно решить несколько инвариантных задач и описать их решение.

7. Обобщить полученную информацию и в качестве результата моего исследования создать обучающий видеоролик об инвариантах.

Гипотеза: предположу, что если я внимательно изучу инварианты, пойму, как найти инвариант и с его помощью решить задачу, то смогу достичь своей цели.

Новизна: раньше я никогда не рассматривала инварианты как конкретный раздел математики, поэтому вся работа с ними будет для меня новой деятельностью.

Методы исследования: размышления, поиск информации в Интернете, изучение специальной литературы, практический метод, анализ результатов.

1. Основная часть

2.1. Толкование термина «инвариант»

Итак, свое исследование я решила начать с уточнения смысла понятия инвариант. Слово инвариант не часто встретишь в повседневной жизни, и некоторым людям оно может показаться непонятным, поэтому так важно включить определение в свою работу. Для выполнения этой задачи мне пришлось вспомнить определение, которое я составила в прошлом году. Инвариант – это свойство объекта, неизменяемое в процессе определенных операций. Но не следует думать, что если компонент является чем-то неизменным, то все инварианты одинаковы. На самом деле их существует бесчисленное множество — ведь каждая математическая задача особенна и ее условие зависит от фантазии автора. И все же инварианты можно классифицировать, что я и попыталась сделать, опираясь на свой личный опыт в решении подобных задач и на дополнительную литературу. Инварианты могут сразу присутствовать в условии, а бывает так, что он надежно спрятан в решении задачи. Согласно моей классификации все инварианты делятся на 4 основные группы: четность, разбиение на пары, раскраска объекта в 2 цвета, чередование состояний. И сейчас я расскажу вам отдельно о каждой из этих групп.

1.  

   1. Классификация инвариантов

Инварианты с четностью в решениях задач могут являться четностью суммы, разности, остатка, произведения, частного и др. Эти инварианты являются четностью некоторого объекта изначально или путем простейших преобразований, таких как умножение, деление, вычитание и сложение. Четность или нечетность результата этих операций очень часто влияет на решение задачи, и, как и все инварианты имеет свои особенности решения, о которых я расскажу позже.

Инварианты с разбиением на пары чаще всеговстречаются в геометрических задачах с пересекающей стороны фигуры ломанной.

Инварианты с раскраской объектов в 2 цвета можно встретить в тех задачах, где есть предпосылки для раскраски (например, круг, поделенный на несколько секторов) или где используется шахматное поле.

Инварианты с чередованием состояний объекта часто соседствуют с инвариантами на четность. Эти инварианты характеризуют несколько состояний объекта, которые всегда сменяют друг друга в определенном порядке. Например, мяч сначала летит к стене в одном направлении, а потом отскакивает от нее и летит в руки в другом направлении.

1.  

   1. Практичность инвариантов

Итак, ознакомившись с основной информацией об инвариантах и классифицировав их, мне захотелось узнать, встречаются ли инварианты в других науках. Для этого я воспользовалась тематическими интернет-сайтами. Оказалось, что инвариант чаще встречается в информатике, физике, топологии — точных науках. Но и в сфере гуманитарных наук инвариант тоже есть. Он присутствует в фольклористике, лингвистике, экономике.

После изучения данной информации я подумала, что если инвариант присутствует в самых разных науках, то возможно и в нашей повседневной жизни тоже есть что-то неизменяемое? Поразмыслив еще немного, я нашла несколько случаев использования инвариантов в повседневной жизни. Это количество дней в месяцах, смена времен года, некоторые праздничные даты (Новый год, Рождество, Ваш день рождения). Также инвариантами являются количество часов в сутках, порядок течения дня (вечер не может наступить раньше, чем утро), режим дня и др.

Таким образом, мы можем утверждать, что в нашей жизни каждый день мы сталкиваемся с множеством инвариантов, а я могу доказать этим практичность своей темы.

1.  

   1. Полезность инвариантов

После того, как я удостоверилась в актуальности и практичности моего исследования я решила рассмотреть его влияние на умственную деятельность. Как влияет на наш мозг решение инвариантных задач? Какие качества развивает в человеке работа с инвариантами? Сейчас мы это узнаем.

Итак, обычно в условии задачи не говорится, как ее решать. Вдруг эта задача вовсе не на инвариант, а на принцип Дирихле или это вообще не задача, а игра на центральную симметрию? Поэтому в процессе выбора способа решения задачи мы развиваем свое логическое мышление. Далее, чтобы найти инвариант требуется выполнить несколько раз требуемые в условии операции. Для этого нужна усидчивость и внимательность. После этого нужно попытаться отыскать общее во всех этих решениях – тренировка абстрактного мышления, терпения и трудолюбия. Особенно терпения, ведь бывает, что нужный компонент находится не сразу. Потом, чтобы до конца решить задачу требуется умение логически мыслить и устанавливать причинно-следственные связи. Вот мы и определили качества, тренируемые решением инвариантных задач. Таких качеств довольно много, поэтому можно сказать, что решение задач данного типа полезно для мозговой деятельности.

1.  

   1. Решение инвариантных задач

После того, как я узнала немного больше об инвариантах и их видах, я решила рассмотреть решения нескольких инвариантных задач разных типов, чтобы затем сравнить их и попробовать составить алгоритм решения инвариантных задач, который будет присутствовать в моем фильме.

Итак, начнем с инварианта на четность. Рассмотрим условие классической задачи подобного типа. Задача: «На столе 6 стаканов, Из них 5 стоят правильно, а один перевернут вверх дном. Разрешается переворачивать одновременно 4 любых стакана. Можно ли все стаканы поставить правильно?». Попробуем решить данную задачу. Итак, предположим, что у нас получилось выполнить условие задачи и все стаканы стоят правильно. Тогда «правильных» стаканов будет 6, а «неправильных» будет 0. Попробуем решить задачу практическим путем – схематично изобразим стаканы и их расположения.

Мой эксперимент показан в этой таблице. Теперь нужно поискать то, что остается неизменным. Это нечетность количества «неправильных» стаканов. А так как их должно быть 0, что является четным числом, то все стаканы поставить правильно нельзя. Ответ: нельзя.

Итак, значит, чтобы решить задачу на четность надо сравнить по четности результаты эксперимента и результаты, нужные по условию задачи.

Рассмотрим другой тип задач – с разбиением на пары. Задача: «Может ли прямая пересекать (во внутренних точках) все стороны невыпуклого: а) 2007-угольника; б) 2008- угольника?»

Итак, предположим, прямая пересекает все стороны многоугольника, который обозначим как m. Рассмотрим все вершины, лежащие по одну сторону от нее. Каждой из этих вершин можно поставить в соответствие пару сторон, из нее выходящих. При этом получим разбиение всех сторон многоугольника на пары. Поэтому если прямая пересекает все стороны m-угольника, то m четно. Значит для 2008-угольника это возможно, а для 2007-угольника нет. Ответ: для 2008-угольника возможно, для 2001-угольника нельзя.

Для решения задачи с разбиением на пары, нужно попробовать разбить объекты по парам и сравнить, в каких случаях это возможно.

Попробуем решить задачу типа раскраски в 2 цвета. Задача: «Дана шахматная доска размером 5*5. Можно ли замостить доску плиточками домино размером 2*1?». Важно знать, что каждая плитка занимает одну черную и одну белую клетку, следовательно, количество белых и черных клеток должно быть равным. А так как на нашей доске размером 5*5 всего 25 клеток, значит количество черных и белых клеток неравное. Следовательно, этого сделать нельзя. Ответ: нет. И для решения подобных задач требуется «раскрасить» объекты в два цвета (обычно в чёрный и белый цвета) и сравнить количество объектов разных цветов.

И последний тип задач, который мы рассмотрим – задачи с чередованием состояний. Задача: «На плоскости лежат три шайбы А, В и С. Хоккеист бьёт по одной из шайб так, чтобы она прошла между двумя другими и остановилась в некоторой точке. Могут ли все шайбы вернуться на свои места после 25 ударов?

В этой задаче нужно понять, что после каждого удара изменяется ориентация (т.е. направление обхода) треугольника АВС. Даже если шайбы будут проходить одинаковый путь, то они не вернутся на свои первоначальные места, т.к. число 25 не делится на 3 и какие-то шайбы останутся не на своем месте. Ответ: не могут. А для решения подобных задач надо лишь найти несколько состояний объекта, и исходя из их чередования, решить задачу.

1.  

   1. Алгоритм решения инвариантных задач

После того, как я решила несколько задач разных типов и нашла особенности решения задач каждого типа, я попробовала составить алгоритм решения всех инвариантных задач, ведь алгоритм значительно упрощает решение задач. Итак, мой алгоритм:

1. Удостоверьтесь, что ваша задача – инвариантная, ведь если это не так, то мой алгоритм окажется для вас бесполезным. В инвариантных задачах всегда бывают эксперименты: переворачивать что либо, считать довольно большие суммы чисел и другие похожие задания.

2. После того, как вы удостоверились, что ваша задача инвариантная, выполните условия эксперимента. Желательно несколько раз. Это очень важно! Только эксперимент поможет вам найти инвариант. Так что не поленитесь и на практике раскрасьте клетки, переверните стаканы или раздайте пирожки детям (кстати, это можно сделать и схематично, в тетради).

3. После выполнения условий детально разложите требуемые условия для решения задачи. Например, если все стаканы должны стоять правильно, то правильных стаканов будет n, а неправильных 0.

4. Затем попытайтесь найти что-либо неизменяемое во всех ваших экспериментах. Это должно быть логичным по отношению к вашим условиям для решения.

5. Соотнесите инвариант и условия для решения. Сделайте вывод исходя из этого соотношения. Например, число неправильных стаканов всегда нечетно, а их должно быть 0 – четное количество. Значит, все стаканы не могут стоять правильно.

6. Если вашего вывода достаточно для решения задачи, то вы правильно решили задачу с помощью нахождения инварианта. Если нет, то попробуйте дальше дополнить ее логичными рассуждениями и поисками. Бывает, что после нахождения инварианта нужно еще немного додумать задачу и все получится. В противном случае попробуйте найти инвариант еще раз. Возможно, в этом и есть ваша ошибка. Желаю вам удачи!

1.  

   1. Создание обучающего видеоролика.

Финальным этапом моего исследования стало создание обучающего фильма, с помощью которого другие люди тоже смогли бы научиться решать инвариантные задачи. Такой фильм я решила создать сначала в виде презентации Microsoft Power Point, а потом с помощью какой-либо программы для записи видео с экрана монитора записать показ моей презентации. Программу для записи видео я выбрала HyperCam 4. Я выбрала именно ее, потому что эта программа имеет интуитивно-понятный интерфейс, включает в себя функцию записи видео и звука.

Для начала я скачала HyperCam 4 и установила ее на свой компьютер. Затем я настроила ее так, как мне было нужно: убрала показ курсора мыши и звук щелчка, ведь мне ни к чему посторонние шумы в фильме. Потом я отрегулировала область записи видео. Программа была настроена, и мне оставалось лишь успеть создать фильм пока не истечет срок бесплатного использования.

Далее я перешла к созданию презентации – основы для моего будущего фильма. Я создала новый файл, определила дизайн и наполнила презентацию данными из моей работы. Также я вставила в презентацию много музыки, анимации и картинок, чтобы зрителю было приятно смотреть мой фильм. К каждому слайду я с помощью микрофона и программы «Звукозапись» записала звуковое сопровождение, в котором преподносится основная информация и отредактировала громкость и формат звука. В целом, я постаралась сделать свой фильм красивым и познавательным.

После выполнения основной части работы мне осталось лишь снять показ презентации на видео с помощью HyperCam 4. Я записала показ, и у меня получился небольшой познавательный фильм. Но в нем также было записано, как я включаю презентацию и другие ненужные моменты. С помощью онлайн редактора видео я вырезала все бесполезные части фильма и сохранила на жесткий диск окончательный вариант. Затем я с помощью программы Microsoft Publisher создала буклет, в котором также были включены основные мысли моей работы. Буклет я украсила своей эмблемой и постаралась сделать ярким и познавательным.

1. Заключительная часть

3.1. Вывод

В дальнейшем, может быть, я продолжу эту работу для того, чтобы усовершенствовать свои знания об инвариантах. Я думаю, что достигла своей цели, так как научилась решать инвариантные задачи и создала обучающий видеоролик про инварианты. Работа над проектом показала мне, что инварианты не так сложно искать, как это кажется новичку, и на самом деле инварианты — один из самых занимательных разделов математики. Мне понравилось исследовать инварианты, так как это очень интересно, развивает логику, трудолюбие и практическое мышление.

1.  

   1. Медиа ресурсы

http://www.myshared.ru/slide/300605/

https://yandex.ru/images/search?p=1&text=математические%20картинки&img_url=http%3A%2F%2Freferat.znate.ru%2Fpars_docs%2Ftw_refs%2F12%2F11928%2F11928-18_1.jpg&pos=47&rpt=simage&_=1454855037230

https://yandex.ru/search/?text=инвариант%20задачи%20с%20разбиением%20на%20пары&clid=1955453-080&win=82

http://www.problems.ru/view_problem_details_new.php?id=58160

Просмотров работы: 4903

From Wikipedia, the free encyclopedia

In mathematics, an invariant is a property of a mathematical object (or a class of mathematical objects) which remains unchanged after operations or transformations of a certain type are applied to the objects.^[1][2] The particular class of objects and type of transformations are usually indicated by the context in which the term is used. For example, the area of a triangle is an invariant with respect to isometries of the Euclidean plane. The phrases «invariant under» and «invariant to» a transformation are both used. More generally, an invariant with respect to an equivalence relation is a property that is constant on each equivalence class.^[3]

Invariants are used in diverse areas of mathematics such as geometry, topology, algebra and discrete mathematics. Some important classes of transformations are defined by an invariant they leave unchanged. For example, conformal maps are defined as transformations of the plane that preserve angles. The discovery of invariants is an important step in the process of classifying mathematical objects.^[2][3]

Examples[edit]

A simple example of invariance is expressed in our ability to count. For a finite set of objects of any kind, there is a number to which we always arrive, regardless of the order in which we count the objects in the set. The quantity—a cardinal number—is associated with the set, and is invariant under the process of counting.

An identity is an equation that remains true for all values of its variables. There are also inequalities that remain true when the values of their variables change.

The distance between two points on a number line is not changed by adding the same quantity to both numbers. On the other hand, multiplication does not have this same property, as distance is not invariant under multiplication.

Angles and ratios of distances are invariant under scalings, rotations, translations and reflections. These transformations produce similar shapes, which is the basis of trigonometry. In contrast, angles and ratios are not invariant under non-uniform scaling (such as stretching). The sum of a triangle’s interior angles (180°) is invariant under all the above operations. As another example, all circles are similar: they can be transformed into each other and the ratio of the circumference to the diameter is invariant (denoted by the Greek letter π (pi)).

Some more complicated examples:

• The real part and the absolute value of a complex number are invariant under complex conjugation.
• The degree of a polynomial is invariant under a linear change of variables.
• The dimension and homology groups of a topological object are invariant under homeomorphism.^[4]
• The number of fixed points of a dynamical system is invariant under many mathematical operations.
• Euclidean distance is invariant under orthogonal transformations.
• Euclidean area is invariant under linear maps which have determinant ±1 (see Equiareal map § Linear transformations).
• Some invariants of projective transformations include collinearity of three or more points, concurrency of three or more lines, conic sections, and the cross-ratio.^[5]
• The determinant, trace, eigenvectors, and eigenvalues of a linear endomorphism are invariant under a change of basis. In other words, the spectrum of a matrix is invariant under a change of basis.
• The principal invariants of tensors do not change with rotation of the coordinate system (see Invariants of tensors).
• The singular values of a matrix are invariant under orthogonal transformations.
• Lebesgue measure is invariant under translations.
• The variance of a probability distribution is invariant under translations of the real line. Hence the variance of a random variable is unchanged after the addition of a constant.
• The fixed points of a transformation are the elements in the domain that are invariant under the transformation. They may, depending on the application, be called symmetric with respect to that transformation. For example, objects with translational symmetry are invariant under certain translations.
• The integral of the Gaussian curvature of a two-dimensional Riemannian manifold is invariant under changes of the Riemannian metric . This is the Gauss–Bonnet theorem.

MU puzzle[edit]

The MU puzzle^[6] is a good example of a logical problem where determining an invariant is of use for an impossibility proof. The puzzle asks one to start with the word MI and transform it into the word MU, using in each step one of the following transformation rules:

1. If a string ends with an I, a U may be appended (xI → xIU)
2. The string after the M may be completely duplicated (Mx → Mxx)
3. Any three consecutive I’s (III) may be replaced with a single U (xIIIy → xUy)
4. Any two consecutive U’s may be removed (xUUy → xy)

An example derivation (with superscripts indicating the applied rules) is

MI →² MII →² MIIII →³ MUI →² MUIUI →¹ MUIUIU →² MUIUIUUIUIU →⁴ MUIUIIUIU → …

In light of this, one might wonder whether it is possible to convert MI into MU, using only these four transformation rules. One could spend many hours applying these transformation rules to strings. However, it might be quicker to find a property that is invariant to all rules (i.e. that isn’t changed by any of them), and demonstrates that getting to MU is impossible. By looking at the puzzle from a logical standpoint, one might realize that the only way to get rid of any I’s is to have three consecutive I’s in the string. This makes the following invariant interesting to consider:

The number of I’s in the string is not a multiple of 3.

This is an invariant to the problem, if for each of the transformation rules the following holds: if the invariant held before applying the rule, it will also hold after applying it. Looking at the net effect of applying the rules on the number of I’s and U’s, one can see this actually is the case for all rules:

Rule	#I’s	#U’s	Effect on invariant
1	+0	+1	Number of I’s is unchanged. If the invariant held, it still does.
2	×2	×2	If n is not a multiple of 3, then 2×n isn’t either. The invariant still holds.
3	−3	+1	If n is not a multiple of 3, n−3 isn’t either. The invariant still holds.
4	+0	−2	Number of I’s is unchanged. If the invariant held, it still does.

The table above shows clearly that the invariant holds for each of the possible transformation rules, which means that whichever rule one picks, at whatever state, if the number of I’s was not a multiple of three before applying the rule, then it won’t be afterwards either.

Given that there is a single I in the starting string MI, and one that is not a multiple of three, one can then conclude that it is impossible to go from MI to MU (as the number of I’s will never be a multiple of three).

Invariant set[edit]

A subset S of the domain U of a mapping T: U → U is an invariant set under the mapping when Note that the elements of S are not fixed, even though the set S is fixed in the power set of U. (Some authors use the terminology setwise invariant,^[7] vs. pointwise invariant,^[8] to distinguish between these cases.)
For example, a circle is an invariant subset of the plane under a rotation about the circle’s center. Further, a conical surface is invariant as a set under a homothety of space.

An invariant set of an operation T is also said to be stable under T. For example, the normal subgroups that are so important in group theory are those subgroups that are stable under the inner automorphisms of the ambient group.^[9][10][11]
In linear algebra, if a linear transformation T has an eigenvector v, then the line through 0 and v is an invariant set under T, in which case the eigenvectors span an invariant subspace which is stable under T.

When T is a screw displacement, the screw axis is an invariant line, though if the pitch is non-zero, T has no fixed points.

Formal statement[edit]

The notion of invariance is formalized in three different ways in mathematics: via group actions, presentations, and deformation.

Unchanged under group action[edit]

Firstly, if one has a group G acting on a mathematical object (or set of objects) X, then one may ask which points x are unchanged, «invariant» under the group action, or under an element g of the group.

Frequently one will have a group acting on a set X, which leaves one to determine which objects in an associated set F(X) are invariant. For example, rotation in the plane about a point leaves the point about which it rotates invariant, while translation in the plane does not leave any points invariant, but does leave all lines parallel to the direction of translation invariant as lines. Formally, define the set of lines in the plane P as L(P); then a rigid motion of the plane takes lines to lines – the group of rigid motions acts on the set of lines – and one may ask which lines are unchanged by an action.

More importantly, one may define a function on a set, such as «radius of a circle in the plane», and then ask if this function is invariant under a group action, such as rigid motions.

Dual to the notion of invariants are coinvariants, also known as orbits, which formalizes the notion of congruence: objects which can be taken to each other by a group action. For example, under the group of rigid motions of the plane, the perimeter of a triangle is an invariant, while the set of triangles congruent to a given triangle is a coinvariant.

These are connected as follows: invariants are constant on coinvariants (for example, congruent triangles have the same perimeter), while two objects which agree in the value of one invariant may or may not be congruent (for example, two triangles with the same perimeter need not be congruent). In classification problems, one might seek to find a complete set of invariants, such that if two objects have the same values for this set of invariants, then they are congruent.

For example, triangles such that all three sides are equal are congruent under rigid motions, via SSS congruence, and thus the lengths of all three sides form a complete set of invariants for triangles. The three angle measures of a triangle are also invariant under rigid motions, but do not form a complete set as incongruent triangles can share the same angle measures. However, if one allows scaling in addition to rigid motions, then the AAA similarity criterion shows that this is a complete set of invariants.

Independent of presentation[edit]

Secondly, a function may be defined in terms of some presentation or decomposition of a mathematical object; for instance, the Euler characteristic of a cell complex is defined as the alternating sum of the number of cells in each dimension. One may forget the cell complex structure and look only at the underlying topological space (the manifold) – as different cell complexes give the same underlying manifold, one may ask if the function is independent of choice of presentation, in which case it is an intrinsically defined invariant. This is the case for the Euler characteristic, and a general method for defining and computing invariants is to define them for a given presentation, and then show that they are independent of the choice of presentation. Note that there is no notion of a group action in this sense.

The most common examples are:

• The presentation of a manifold in terms of coordinate charts – invariants must be unchanged under change of coordinates.
• Various manifold decompositions, as discussed for Euler characteristic.
• Invariants of a presentation of a group.

Unchanged under perturbation[edit]

Thirdly, if one is studying an object which varies in a family, as is common in algebraic geometry and differential geometry, one may ask if the property is unchanged under perturbation (for example, if an object is constant on families or invariant under change of metric).

Invariants in computer science[edit]

In computer science, an invariant is a logical assertion that is always held to be true during a certain phase of execution of a computer program. For example, a loop invariant is a condition that is true at the beginning and the end of every iteration of a loop.

Invariants are especially useful when reasoning about the correctness of a computer program. The theory of optimizing compilers, the methodology of design by contract, and formal methods for determining program correctness, all rely heavily on invariants.

Programmers often use assertions in their code to make invariants explicit. Some object oriented programming languages have a special syntax for specifying class invariants.

Automatic invariant detection in imperative programs[edit]

Abstract interpretation tools can compute simple invariants of given imperative computer programs. The kind of properties that can be found depend on the abstract domains used. Typical example properties are single integer variable ranges like 0<=x<1024, relations between several variables like 0<=i-j<2*n-1, and modulus information like y%4==0. Academic research prototypes also consider simple properties of pointer structures.^[12]

More sophisticated invariants generally have to be provided manually.
In particular, when verifying an imperative program using the Hoare calculus,^[13] a loop invariant has to be provided manually for each loop in the program, which is one of the reasons that this approach is generally impractical for most programs.

In the context of the above MU puzzle example, there is currently no general automated tool that can detect that a derivation from MI to MU is impossible using only the rules 1–4. However, once the abstraction from the string to the number of its «I»s has been made by hand, leading, for example, to the following C program, an abstract interpretation tool will be able to detect that ICount%3 can’t be 0, and hence the «while»-loop will never terminate.

void MUPuzzle(void) {
    volatile int RandomRule;
    int ICount = 1, UCount = 0;
    while (ICount % 3 != 0)                         // non-terminating loop
        switch(RandomRule) {
        case 1:                  UCount += 1;   break;
        case 2:   ICount *= 2;   UCount *= 2;   break;
        case 3:   ICount -= 3;   UCount += 1;   break;
        case 4:                  UCount -= 2;   break;
        }                                          // computed invariant: ICount % 3 == 1 || ICount % 3 == 2
}

See also[edit]

Notes[edit]

References[edit]

External links[edit]

• «Applet: Visual Invariants in Sorting Algorithms» by William Braynen in 1997

Олимпиадные задачи на инварианты можно условно
разбить на два вида: те, в которых требуется
доказать некий инвариант, т. е. он явно определен,
и те, в которых инвариант используется при
решении и сразу не очевиден. Существует также
класс задач, при решении которых используются
полуинварианты – значения точной верхней и
нижней граней для некоторой величины. Наиболее
часто они используются в задачах на
доказательство экстремума какой — либо величины.
Рассмотрим способ решения задач по методу
“Инвариант”.

В некоторых задачах по математике дается набор
преобразований исходного объекта и
спрашивается: можно ли, используя эти
преобразования, получить из одного состояния
объекта другое? Перебором вариантов часто легко
убедиться в правильности ответа “нельзя”,
однако обосновать этот ответ бывает трудно.
Методом, позволяющим во многих случаях решать
доказательную часть таких задач, является метод
инвариант. Инвариантом называется нечто, не
меняющееся в преобразованиях, например, число,
набор чисел, четность какого – либо числа и
другое. Если значение инварианта в двух
состояниях объекта различно, то одно из них
нельзя получить из другого. Придумать инвариант
должен ученик, самостоятельно решающий задачу;
обычно это вызывает у него затруднения. В
качестве инварианта чаще всего рассматриваются
четность (нечетность) чисел и остаток от деления.
Причем применение четности – одна из наиболее
встречающихся идей при решении олимпиадных
задач.

Вспомним определения четного и нечетного
числа. Особое внимание надо уделить абстрактному
понятию четности, объяснить, что такое “разная
четность”. Например, число х =2 имеет ту же
четность, что и число х (или оба четные, или оба
нечетные), а при прибавлении единицы четность
меняется. Применение идеи четности и нечетности
основано на двух важных утверждениях (леммах):

Лемма 1. Четность суммы нескольких целых
чисел совпадает с четностью количества нечетных
слагаемых.

Пример. Число 1 +2 + 3 + … + 10 – нечетное, так как в
сумме 5 нечетных слагаемых. Пример 2. Число 5 + 7 + 9 +
11 +13 + 15 – четное, так как в сумме 6 нечетных
слагаемых.

Лемма 2. Знак произведения
нескольких (отличных от 0) чисел определяется
четностью количества отрицательных
сомножителей.

Рассматриваем с учащимися несколько примеров.

Арифметика, алгебра, комбинаторика.

Пример 1. Число (-1) *(-2) *(-3) *(-4) положительно,
так как в произведении четное число
отрицательных сомножителей.
Пример 2. Число (-1) *2 * (-3) * (-4) отрицательно, так
как в произведении нечетное число отрицательных
сомножителей.

После этого разбираем подробно следующие
задачи.

Задача 1. На листе бумаги написано
число 11. Шестнадцать учеников передают листок
друг другу, и каждый прибавляет к числу или
отнимает от него единицу – как хочет. Может ли в
результате получиться число 0?

Нужно предложить выполнить эту операцию
учащимся (результат каждого хода записывается на
доске), заметить закономерность: после каждого
хода характер четности меняется: после первого
ученика число становится четным, после второго
нечетным; после третьего — четным; после
четвертого – нечетным. Тогда после
шестнадцатого число будет нечетным. Поэтому нуль
в конце получиться не может.

Задача 2. На вешалке висят 20
платков. 17 девочек по очереди подходят к вешалке
и либо снимают, либо вешают платок. Может ли после
ухода девочек остаться ровно 10 платков?

Решение. После подхода первой девочки
количество оставшихся платков либо 19, либо 21
(нечетное количество); после подхода второй
девочки – либо 18, либо 20, либо 22 (четное
количество); после подхода третьей девочки –
либо 17, либо 21, либо 23, либо 19 (нечетное
количество). После подхода 17 девочки остается
нечетное количество платков. Получается
противоречие. Значит, 10 платков остаться не
может.

В первой и во второй задачах инвариантом
является четность суммы чисел.

Задача 3. В таблице, где имеются 15
чисел (-1), можно производить следующую операцию:
одновременно изменить знак двух (не более, не
меньше) чисел в таблице. Можно ли, применяя эту
операцию конечное число раз, получить таблицу,
состоящую из (+ 1)?

Решение. Ответ: нельзя. Так как число чисел в
таблице нечетно, а после каждой операции число
чисел (+ 1) в таблице четно. На языке инвариантов
это означает: инвариантом таблицы относительно
введенной операции является произведение всех
чисел в таблице. В начальный момент это
произведение равно ( — 1), а нам нужно получить
таблицу, инвариант которой равен ( + 1).

Задача 4. Имеется набор чисел а, в,
с. Данный набор чисел меняется на тройку чисел: а +
в – с, в + с – а, а + с – в. Дан набор чисел 2000, 2002, 2003.
Можно ли из него получить набор из чисел 2001, 2002,
2003?

Решение. Ответ: нельзя. Так как (а + в + с) и (а + в —
с) +(в +с – а) +(а + с – в) равны, а сумма 2000+2002 +2003 и
сумма 2001 + 2002 +2003 различны.

Задача 5. На столе 6 стаканов, Из них
5 стоят правильно, а один перевернут вверх дном.
Разрешается переворачивать одновременно 4 любых
стакана. Можно ли все стаканы поставить
правильно?

Решение. Нет, так как в любом случае
перевернутых вверх дном стаканов будет числом
нечетным.

Задача 6. Из цифр 2, 3, 4,… 9 составили
два натуральных числа. Каждая цифра
использовалась один раз. Могло ли одно из этих
чисел оказаться вдвое больше другого?

Решение. Ответ: нет. Пусть а и b = 2а – полученные
числа, S(a) и S(b) – суммы их цифр. По признаку
делимости числа N и S(N) имеют одинаковые остатки
при делении на 3. Поскольку число a + b = 3a делится на
3, то сумма S = S(a) + S(b) должна делиться на 3, что
неверно, так как S = 2 + 3 + 4 + … + 9 = 44.

Задача 7. На доске написаны числа 1, 2,
…, 1998. За один ход разрешается стереть любое
количество чисел и вместо них записать остаток
от деления их суммы на 11. Через несколько ходов на
доске остались два числа, одно из которых – 1000.
Чему равно второе число?

Решение. Так как в конечном итоге на доске
оказались записанными два числа, то хотя бы одно
из них является остатком от деления некоторого
числа на 11, т.е. не превосходит 10.Число 1000 не может
являться остатком от деления какого-то числа на
11, поэтому искомое число не больше 10. Заметим, что
в результате выполнения указанных операций
остаток от деления суммы всех написанных чисел
не изменится, так как для любых чисел а и в (а + в)(mod
p) (a(mod p) + b(mod p))(mod
p), где р – произвольное простое число.
Первоначально 1 + 2 + … +1998 = 1997001 6 (mod 11) 1000 (mod p) + второе число. Так как 1000 10 (mod 11), то второе
число 7.

Задача 8. В некотором государстве
было 10 банков. С момента перестройки общества все
захотели стать банкирами. Но по закону открыть
банк можно только путем деления уже
существующего банка на 4 новых. Через некоторое
время министр финансов сообщил президенту, что в
стране действует 2007 банков, после чего был
немедленно уволен за некомпетентность. Что не
понравилось президенту?

Решение. Заметим, что в результате превращения
одного старого банка в четыре новых общее
количество банков увеличится на 3. Таким образом,
в любой момент времени число банков равно Б = 10 + 3 k
и остаток от деления числа банков на 3 постоянен.
(Это и есть инвариант). То есть Б . Первоначально Б ( mod 3) >, а 2007 .

Задача 9. Разместите цифры 0,1,2,3, …, 9
по кругу так, чтобы сумма всех разностей (по
модулю) между соседними числами оказалась равна
25.

Решение. Пусть заданные числа каким-то образом
проставлены по кругу и a, b, c, d – четыре соседних
числа. Поменяем местами числа a >и c. Исследуем,
как изменилась сумма рассматриваемых в задаче
разностей. Для расстановки a, b, c, d она равна , а для
расстановки a , c, b , d – , где – сумма разностей для оставшихся
чисел. Изменение общей суммы Если b >и c имеют одинаковую
четность, то
будет представлять собой сумму двух четных
чисел, а если они разной четности, то является
суммой двух нечетных чисел, но в любом случае четно.
Следовательно, мы получили инвариант – при
перестановке двух соседних чисел четность суммы
разностей не изменится. Любую расстановку
заданных чисел по кругу можно получить,
переставляя несколько раз соседние числа, тем
самым мы доказали, что для любой расстановки
заданных чисел сумма разностей имеет одну и ту же
четность. Рассмотрев произвольную расстановку
чисел (от одного до девяти), мы получим, что сумма
разностей четна, и, значит, требуемая в задаче
расстановка невозможно.

Задача 10. На доске написаны числа 1, 2,
3, …, 1998. За один ход разрешается стереть любые два
числа и вместо них записать их разность. В
результате многократного выполнения таких
действий на доске окажется записанным одно
число. Может ли оно быть нулем?

Решение. Не может. Так как вначале на доске 999
нечетных чисел. На каждом шаге их количество не
меняется, если среди выбранных чисел не более
одного нечетного числа. А если выбранные числа
оба нечетны, то количество нечетных чисел
уменьшается на два. Таким образом, инвариант
преобразования: количество нечетных чисел
нечетно. Поэтому в конце должно остаться
нечетное число. А нуль – четное число.

Задача 11. Числа 0,1,2,3, …, 9 записаны по
кругу. За один ход разрешается прибавить к двум
соседним числам одно и то же целое число. Можно ли
за несколько ходов получить десять нулей?

Решение. Нельзя. При прибавлении одинаковых
целых чисел к любым двум из имеющихся не меняет
четность общей суммы всех чисел. Первоначально
эта сумма равно 1 + 2 + 3 + … 9 = 45, следовательно,
после каждого хода общая сумма полученных чисел
должна быть нечетна, а нуль – четное число.

Задача 12. В десяти сосудах
содержится 1, 2, 3,…, 10 литров воды. Разрешается
перелить из сосуда А в сосуд В столько воды,
сколько имеется в В. Можно ли добиться, чтобы
после нескольких переливаний в 5 сосудах
оказалось 3 литра, а в остальных 6, 7, 8, 9, 10?

Решение. Нельзя. Предложенная операция
обладает полуинвариантом: при любом переливании
число нечетных сосудов (содержащих нечетное
число литров воды) не увеличивается. Количество
таких сосудов уменьшается при переливании из
нечетного сосуда в нечетный, а в остальных
случаях не изменяется. Следовательно, переход 1, 2,
… 10 —> 3, 3, 3, 3, 3, 6,…,10 невозможен, поскольку
увеличивает число нечетных сосудов.

При решении математических задач важную роль
играет анализ задач. Успех решения задачи во
многом определяется качеством анализа. Однако
владение искусством анализа дается нелегко.
Причина тому — творческий характер этого метода.
Как научить ребят сознательному владению
приемами анализа в решении математических задач?
В чем состоит его суть? Смысл анализа состоит в
извлечении из формулировки задачи полезных
сведений. Однако объём извлеченных сведений
иногда оказывается недостаточен для решения.
Тогда возникает необходимость в повторном, более
глубоком анализе. Почему в одних случаях
достигается решение, а в других – лишь некоторые
осознание проблемной ситуации? Что мешает этому
осознанию?

Одна из причин состоит в отсутствии
достаточных знаний у учащихся. Вторая причина
связана со сложностью задачи. Сложность
математической задачи зависит от многих
факторов. Один из них – формулировка задачи. Для
её решения может оказаться достаточным знание
одной единственной теоремы или же
одного-единственного её следствия. Необходимо
только отыскать подходящий критерий для
выявления этой теоремы или следствия. Рассмотрим
пример.

Задача 13. Доказать, что уравнение 3x²
– 4xy + 2y² – 21x + 12y – 3 = 0 имеет лишь конечное
число целочисленных решений.

Анализ задачи. Заданное уравнение связывает
определенными отношениями переменные x и y. Левая
её часть представляет собой довольно громоздкий
многочлен, а правая равна 0. О самих же переменных
известно, что они целые числа. Это обобщенное
понятие является и ключевым в нашей задаче. Если
рассмотреть каждое слагаемое, легко заметить,
что второе, третье, пятое из них всегда являются
четными числами, а свободный член – нечетным.
Перепишем уравнение в виде: 3x(x – 1) – 18x – 4xy + 2y²
+ 12y = 3.

Вспомнив свойство четности произведения двух
последовательных целых чисел, установим
четность первого слагаемого. Теперь мы знаем, что
каждое слагаемое левой части уравнения всегда
четно, следовательно, четна и их сумма. А в правой
части –нечетное число. Приходим к выводу о том,
что уравнение не имеет целочисленных решений. >

Задача 14. Найдите множество точек
плоскости XOY, координаты которых удовлетворяют
уравнению .

Решение. Левая часть уравнения представляет
собой сумму расстояний OM + MC, где , . Для любых трех точек имеем полуинвариант,
следующий из неравенства треугольника: . В нашем случае
.
Следовательно, точка должна лежать на отрезке .