Как найти инвариантные прямые аффинного преобразования

ISSN 1991-5497. МИР НАУКИ, КУЛЬТУРЫ, ОБРАЗОВАНИЯ. № 4 (95) 2022

УДК 514(075.8):81(075.8)

Proyaeva I.V., Cand. of Sciences (Physics, Mathematics), senior lecturer, Orenburg State Pedagogical University n.a. V.P Chkalova; senior lecturer, Plekhanov Russian University of Economics (Orenburg branch), Orenburg branch of PSUTI (Orenburg, Russia), Е-mail: docentirina@mail.ru Safarova A.D., Cand. of Sciences (Pedagogy), senior lecturer, Orenburg State Pedagogical University n.a. V.P Chkalov (Orenburg, Russia), E-mail: aliya.safarova.66@mail.ru

ON SOLVING APPLIED PROBLEMS BY MATHEMATICAL METHODS. The article discusses features of studying one of the most beautiful transformations -affine, which is practically not studied in the course of high school geometry. The authors focus on the study of special properties of affine transformation using vector algebra. Some interesting properties of affine transformations are distinguished and proved. The important and invaluable role of tasks of this nature has been confirmed by many scientific discoveries in the field of technology, science, etc. The methodology of studying this issue presented in the article is implemented in a specific educational process in the classes of the course «Geometry» [1] at the Orenburg State Pedagogical University in the preparation of future bachelors in the direction of «Pedagogical Education» and allowed to increase the efficiency of assimilation of the studied material by students. Key words: affine transformation, straight line, vector, connected vectors, sliding vectors.

И.В. Прояева, канд. физ.-мат. наук, доц., Оренбургский государственный педагогический университет имени В.П. Чкалова,

доц. Российского экономического университета имени Г.В. Плеханова (Оренбургский филиал), ПГУТИ (Оренбургский филиал), г. Оренбург,

Е-mail: docentirina@mail.ru

АД. Сафарова, канд. пед. наук, доц., Оренбургский государственный педагогический университет имени В.П. Чкалова, г. Оренбург, E-mail: aliya. safarova.66@mail.ru

ОБ ИНВАРИАНТНЫХ ПРЯМЫХ АФФИННОГО ПРЕОБРАЗОВАНИЯ

В данной статье рассмотрены особенности изучения одного из красивейших преобразований — аффинного, практически не изучаемого в курсе геометрии средней школы. Основное внимание в работе авторы акцентируют на изучении особых свойств аффинного преобразования с использованием векторной алгебры. Выделяются и доказываются отдельные интересные свойства аффинных преобразований. Важная и неоценимая роль задач такого характера подтверждена многими научными открытиями в области техники, науки и т. п. Представленная в статье методика изучения данного вопроса была реализована в конкретном учебном процессе на занятиях по курсу «Геометрия» [1] в Оренбургском государственном педагогическом университете при подготовке будущих бакалавров по направлению «Педагогическое образование» и позволила повысить эффективность усвоения изучаемого материала обучающимися.

Ключевые слова: аффинное преобразование, прямая, вектор, связные векторы.

Так как в программу по математике средней школы введены элементы векторной алгебры, то есть возможность изучать некоторые геометрические преобразования на векторной основе. Например, аппарат векторной алгебры можно использовать для вывода поворота с центром в данной точке на данный ориентированный угол, гомотетии. Рассмотрим доказательства некоторых свойств аффинных преобразований с использованием элементов векторной алгебры. Материал статьи может быть использован при проведении элективных курсов с учащимися 10-11 классов, а также для проектной работы со старшеклассниками. Согласно программе, в курсе геометрии 8 класса школьники знакомятся с понятием вектора и линейными операциями над векторами, в 9 классе — с координатами вектора и свойствами координат векторов, а также со скалярным произведением векторов и его свойствами. В старших классах изучаются элементы векторной алгебры в пространстве. Мы считаем возможным познакомить обучающихся с понятиями «связные векторы», «скользящие векторы», «свободные векторы», также следует отметить, что решение прикладных задач обладает огромным потенциалом для развития логического мышления человека, что показывает актуальность данного исследования и необходимость ее изучения. Новизна работы заключается в новом подходе к решению геометрических задач с использованием векторной алгебры. Цель исследования — рассмотреть применение математического аппарата для решения прикладных задач геометрии. Цель определила следующие задачи: 1. Показать применение векторного аппарата при решении задач теории аффинных преобразований; 2. Показать особенности и значимость точных наук в образовании обучающихся.

При изучении видов преобразований плоскости в курсе геометрии 9 класса весьма небольшое количество времени отводится на изучение нового материала. В курсе стереометрии у обучающихся возникает возможность изучить эту тему подробнее. Тем не менее времени рядовых уроков не хватает для достойного изучения этой темы, а также её взаимосвязи с практической деятельностью, которая, в свою очередь, является важнейшим смыслом изучения геометрии в целом.

Подводя обучающихся к изучению темы по геометрии, важно сначала объяснить им её практическую значимость. Всякие виды преобразований плоскости важны и имеют свою значимость в практическом применении. Аффинные преобразования не являются исключением. С их помощью создаются сложнейшие продукты компьютерной графики, требующие осмысленной кропотливой работы.

В связи с этим для общего развития обучающихся мы предлагаем провести элективный курс, в котором будет изучаться данная тема, которая играет большую роль во многих профессиях, например, программиста. Это может заинтересовать обучающихся и мотивировать их к изучению геометрии в целом. Также знакомство с данной темой обучающимися, несомненно, будет способствовать развитию их пространственно-образного и логического мышления, воображения, памяти, а также других, не менее важных для развития УУД как личностных, так и умственных качеств.

В нашей работе мы покажем предложение изучения данной темы на векторной основе. Как уже говорилось выше, это является новизной нашего исследования.

Мы будем работать со связными векторами, у которых задано начало. Будем обозначать вектор ОА череза, то есть ОА=а. В дальнейшем понадобится понятие косого произведения векторов и его основные свойства. Поэтому дадим определение косого произведения векторов и сформулируем его свойства [1].

Косым произведением векторов а* и в, расположенных в ориентированной плоскости и взятых в определенном порядке, называется число, равное произведению длин этих векторов на синус угла между ними.

Обозначение: а» в. Таким образом, а»в = |а||в| sin ¿(а, в).

Геометрический смысл косого произведения векторов: косое произведение векторов а* и в, взятых в определенном порядке, равно площади ориентированного параллелограмма, построенного на данных векторах, как на сторонах.

Свойства косого произведения.

1) Косое произведение векторов антикоммутативно, то есть а>в = -в»а.

2) Если векторы а*и в коллинеарные, то косое произведение данных векторов равно нулю.

3) Постоянный множитель можно выносить за знак косого произведения, то есть а»Яв = Я(а»в).

4) Распределительное свойство: а»(в + в) = а»в + а»с.

Следствие. а»(в + Яа) = а»в!

5) Площадь ориентированного треугольника АВС вычисляется по формуле:

5(ДАВС) = ^(а*й + в*С-а*СС

Из пятого свойства следует условие коллинеарности трех точек (условие принадлежности трех точек одной прямой) А, В, С:

а»в + в»С-а»С*= 0.

Аффинным преобразованием плоскости называется преобразование, которое каждой точке M(x,y) в аффинном репере R(O, е , e ) ставит в соответствии точку M(х,y) в аффинном репере R'(O’,е’,е’г).

1. Аффинные преобразования переводят точки в точки.

2. Аффинные преобразования переводят прямые в прямые, сохраняют принадлежность точек и прямых.

3. Аффинные преобразования сохраняют параллелизм прямых линий.

Простым отношением трёх точек A,B,C одной прямой называется число,

обозначаемое через (ABC), и удовлетворяющее условию

AC = (ABC) ■ CB

Если в репере R(O,е е2) точки A,B,C имеют координаты:

А(х1,У XВ(х2,У2),С(хз,Уз), то

ISSN 1991-5497. МИР НАУКИ, КУЛЬТУРЫ, ОБ РАЗОВАНИЯ. № 4(95) 2022

(АВС) = АС = 9в-А

СВ ККЛ — *3

у 3 — У1 .

ли 2 -Уз

дсли точка С лежит 1)«5жду тбч ками A, В, тб (ЛВС) > 0 ■ Срранедлинр и обратное собЙ(зтоо.

4. Аффинвое преоДрозововие сох|оо1Иятт простое «Бттнесэшиеэнютэ арэегх точек

РрЯМКБЙ.

Известно, что ;ос00рт1ито(т Ротобразованит плоскости одсозвачво определя-ттся тремя порами пеоивеозтиоумок почек. Пужсгт1к афОэинвок преоброзововие плоскости :ЗП^Д^•T^HEE точками А и Д/, в и 33Р С к СП.

дуитк точка М дклит АА0 о птв 01Ртвии 1 Найдкил точки N, P, которыю делятт 13В/И <р С0 П1 ТОм ЖИ ОтСОШрвии Я СООТВИТСВеввО. Выввним, CyLHTCTB^^T ли оосот зсач евие Я, крс к0т»0|С01)1 тбсисзюи IM, IN, |г лежат во о/виой прямой■ п|Я5ПпсзлEЗисхм, что такая прямая тyщ0cттн5т, и возов5п ее Я- пря^й /»nai-pnoi-c^ оффзывюго пр^обсо-зонгзви^ . Пгг условию зодочи и илеем,

АР0′!»09 м яЧЧА. Вв« 4 Щ ¡С9 4 хрЦ.

5

Рис.1Аффинноепреобразованиеплоскости

Выырозим из этих роЕвенсттв Bleквoрыl т, п, ¡д.

( У+ЯН в^Яв — i^+Яс

т 4 —- ,п 4 —_ л 4 —_ где! ± -1. (1)

лоя ‘ о+Я m j+я w

По предположив ию точки IM, IM, У лзежот во одвой прямой, поэтому, по условию колливеорвости т|зех то-ек, имеем:

тс п-иПС р-|9с р 4 о. (О )

Подставляя (1) в (О), имеем:

аВ+/н 1+Я ‘

внвяс

внияв

-с

В+Я

вн+Яс 1+Я

а нсЯа 1+Я

сн+Яс

4 0. (3)

Приведем выlрожeвиe, стоящее в левой части (3), к обще му знопевотелю, плнполкзугзмся! тр^-ич1км, четвертвю, пятым свойствомт косого произведевия и учитывая что 1 9Я 10, иод ко кli-i по «»пределе виню, получ им свысротйoe Вроивеви и следующего вида:

^(Д/ШС) -С Я (о(Д/БеС) 9 5(ДЛЛ0О) 9 5(БЛВС0) о 5(Д4ВП)) 9 S^^C0) = 0. (4)

Кожды, й коревк зсодритвого уроввевия (4) определяет — прямую. В зависимости ся количество и вида корней уроввевия (4) возможвы следующие случаи:

Библиографический список

1) Корни уравнения (4) ко мплексн ые, тогда аффи нное преобразование вмеет две м ошпых К — ггрямыых.

2) К(ы|лни уравнепия (4) действ ители>н1>1е. Тлгдо возможкы! гсллсэду/ики-Цил слу-чани рaспулуження дейггтв птнгогьныт1х -ирямиых дф^сфинн омо преоЫразования на плоскости:

а) -прямы е переее кается,

б) -прями е совпадает,

2) -прямыые параллельн ы- .

ЕК случаях а) и в) корни уравнених (4)- разлинчыlе, в слач ае б) корни квадратно го уравнения (4) — совпадыюы, случай в) не воз можен [2].

Из доказ аннога ечвер)^<дениы следует, что:

е) Точка М является инвариантной точкой данного аффинного преобразования.

2) Если прямыне ак и а2 определяе)тся соответственно кор нями Я! и Я2 квадратного уравнен ия (Ы), то птымута( делит прямуе а2 в отношении Ак, а пря-маяа2 делно пирмте ак в от ношении Я2 [3].

Если инвариантную точку М принять за це нтр связки вектотоы и рассматривать олоскость как дан^ное векторное кpoстуанству, то собственным д^вто-рами аффинного преобразования т является такие вектияы с/К, что /(МХ) = „МХ = МХ/. где чи сло ц назы1вается суfкстве нны1м числом. Пактуку вевтурыl Я -прямые) ак и а2 явлыелся субсывенныlрlи, а ч <(4ла Яг, М,2,Х/ 14 = ЯгМХ, рачныы послам, противоположны!« собственныф ннслам преобразован пя. Для ирямой ак собстзенныы числ ом является -Яи, ьрямой! а2 субствекныlк числом является -Я2.

Таким обозом:

1. Если курни уравнения (4) комплексные, то в этом случае имеем две мнимые Я прямые.

о) Если корни уравнения (4) действительные, то возможны два случая:

a. курни равные, и Я — прямые совпадает;

b. курни различные, и Я — прямые пересекается.

3. Пересекающиеся Я — прямые является инвариантными прямыми.

4. Точка пересечения Я — прямых — инвариантная точка.

5. Определяемые Я — прямыми направления есть направления собственных векторов, собственными числами является числа, противоположные корням уравнения(4).

6. Я — прямые делят всякий отрезок, соединяещий лебые две соответственные точки в отношении, равном значение корня уравнения (4), который определяет прямуе, делящуе этот отрезок.

Можно заметить, что:

1. Если рассматривать преобразование подобие как частный случай аффинного преобразования, то получаем свойство инвариантных прямых подобия второго рода: они делят лебой отрезок, соединяещий две соответственные точки, внутренним или внешним образом в отношении, равном коэффициенту подобия.

2. Полное исследование уравнения (4) по корням и коэффициентам позволяет провести классификацие аффинных преобразований плоскости.

3. Кыше не рассматривалась гомотетия плоскости, так как в этом случае точки a, N. P совпадает, и рассматриваемая задача не имеет смысла [4].

Рассмотренное в статье аффинное преобразование и его особые свойства находят применение в компьютерном моделировании и машинной графике. Этот факт делает изучение данной темы наиболее интересной для обучаю щихся.

С помощью аффинного преобразования можно совершить растяжение, сжатие, поворот осей координатной плоскости, что позволит решить новые математические и физические примеры в упрощенной форме. Тема аффинных преобразований, с одной стороны, выходит за рамки основного курса геометрии, а с другой стороны — тесно с ним переплетается. К особым ее достоинствам можно отнести, пожалуй, тот факт, что она связывает все преобразования в единое целое. А изучение аффинного преобразования на векторной основе упрощает процесс её понимания обучающимися.

1. Прояева И.В., Сафарова А.Д. Организация самостоятельной работы студентов по подготовке к ГИА курсу «Геометрия». Оренбург: Издательство ОГПУ 2016.

2. Прояева И.В., Сафарова А.Д. Об особенностях преподавания раздела геометрических преобразований в школьном курсе геометрии. Мир науки, культуры и образования. 2017; № 1(62): 150 — 152.

3. Прояева И.В. Компетентностный подход в преподавании математических дисциплин на инженерных специальностях. Материалы I Международной очно-заочной конференции. Оренбург, ПГУТИ, 2015.

4. Прояева И.В., Сафарова А.Д. Векторные уравнения некоторых простейших преобразований плоскости. Мир науки, культуры, образования. 2018; № 5 (72): 189-193.

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

References

1. ProyaevaI.V.,Safarova A.D. Organizaciyasamostoyatel’nojraboty studentovpopodgotovke kGIAkursu «Geometriya». Orenburg: Izdatel’stvo OGPU, 2016.

2. Proyaeva I.V., Safarova A.D. Ob osobennostyah prepodavaniya razdela geometricheskih preobrazovanij v shkol’nom kurse geometrii. Mir nauki, kul’tury i obrazovaniya. 2017; № 1(62):150-152.

3. Proyaeva I.V. Kompetentnostnyj podhod v prepodavanii matematicheskih disciplin na inzhenernyh special’nostyah. Materialy I Mezhdunarodnoj ochno-zaochnoj konferencii. Orenburg, PGUTI,2015.

4. Proyaeva I.V.,Safarova A.D.Vektornye uravneniya nekotoryhprostejshih preobrazovanij ploskosti. Mir nauki, kul’tury, obrazovaniya. 2018; № 5 (72): 189 — 193.

Статья поступила в редакцию 01.06.22

Задача
119.
Доказать, что линейное преобразование
плоскости тогда и только тогда будет
аффинным, когда образ каждого ненулевого
вектора будет отличен от нуля.

Задача 120
(с решением). Найти инвариантные прямые
линейного

преобразования,
заданного формулами

Образом прямой
при таком преобразовании является
прямая

или .
По условию, она должна совпасть с исходной
прямой .Две
прямые совпадут при условии
пропорциональности входящих в их
уравнения коэффициентов, т. е.

при условии ,
,
если и
условии,

если a=0.
Таким образом имеем 2 решения:
или для
первого случая и
для второго.

Задача
121.
Записать формулы, задающие произведение
и

данных аффинных преобразований (система
координат общая декартова)

1)

2)

.

Задача
122.
Записать формулы, задающие преобразование,
обратное к данному (система координат
общая декартова), если такое преобразование
существует.

1)

2)

3)

4)

Задача 123.
Доказать, что:

Если
А и В
— две
различные неподвижные точки аффинного
преобразования, то и все точки прямой
АВ неподвижны;

1. если аффинное
   преобразование f
   имеет единственную неподвижную точку,
   то все инвариантные прямые (если они
   существуют) проходят через эту точку;

2. точка пересечения
   двух инвариантных прямых аффинного
   преобразования неподвижна.

Задача 124.
Записать
формулы, задающие произведение и

данных аффинных преобразований (система
координат общая декартова)

1)

2)

.

Занятие 16 Элементы вычислительной геометрии. Триангуляция Делоне

Основные алгоритмы
вычислительной геометрии

Приведём часто
встречающиеся задачи вычислительной
геометрии и коротко обсудим их решение.

Отсечение
отрезка.

Необходимость
отсечения выводимого изображения по
границам некоторой области встречается
довольно часто. В простейших ситуациях
в качестве такой области, как правило,
выступает прямоугольник

Ниже рассматривается
достаточно простой и эффективный
алгоритм отсечения отрезков по границе
произвольного прямоугольника.

Четырьмя прямыми
вся плоскость разбивается на 9 областей
. По отношению к прямоугольнику точки
в каждой из этих областей расположены
одинаково. Определив, в какие области
попали концы рассматриваемого отрезка,
легко понять, где именно необходимо
произвести отсечение.

Классификация
точки относительно отрезка

Рассмотрим следующую
задачу: на плоскости заданы точка и
направленный отрезок. Требуется
определить положение точки относительно
этого отрезка

Расстояние от
точки до прямой

Пусть заданы точка

и прямая АВ, где ,

и требуется найти расстояние от этой
точки до прямой.

Найдем длину
отрезка АВ:
Опустим из точки С перпендикуляр на АВ.
Точку Р пересечения этого перпендикуляра
с прямой можно представить параметрически

где

Положение точки
С на этом перпендикуляре будет задаваться
параметром s, s < 0 означает, что С
находится слева от АВ, s >0, что С — справа
от АВ и s
= 0 означает, что С лежит на АВ.

Для вычисления S
воспользуемся следующей формулой:
и тогда искомое расстояние PC = sl.

Нахождение
пересечения двух отрезков

Пусть А, В, С и D —
точки на плоскости. Тогда направленные
отрезки АВ и CD
задаются следующими параметрическими
уравнениями:

Если отрезки АВ и
CD пересекаются, то
Перепишем это векторное соотношение в
координатном виде:

Эта система линейных
алгебраических уравнений при
имеет единственное решение:

Если оба получившихся
значения r
и s принадлежат отрезку [0,1], то отрезки
АВ и CD пересекаются и точка пересечения
может быть найдена из параметрических
уравнений. В случае, когда оба или одно
из полученных значений не принадлежат
отрезку [0,1], отрезки АВ и CD не пересекаются,
но пересекаются соответствующие прямые.
Равенство
означает, что отрезки АВ и CD параллельны.

Проверка
принадлежности точки многоугольнику

Для решения этой
задачи выпустим из точки А(х,у) произвольный
луч и найдем количество точек пересечения
этого луча с границей многоугольника.
Если отбросить случай, когда луч проходит
через вершину многоугольника, то решение
задачи тривиально — точка лежит внутри,
если общее количество точек пересечения
нечетнечетно, и снаружи, если четно.

Ясно, что для любого
многоугольника всегда можно построить
луч, не проходящий ни через одну из
вершин. Однако построение такого луча
связано с некоторыми трудностями и,
кроме того, проверку пересечения границы
многоугольника с произвольным лучом
провести сложнее, чем с фиксированным,
например горизонтальным.

Возьмем луч,
выходящий из произвольной точки А, и
рассмотрим, к чему может привести
прохождение луча через вершину
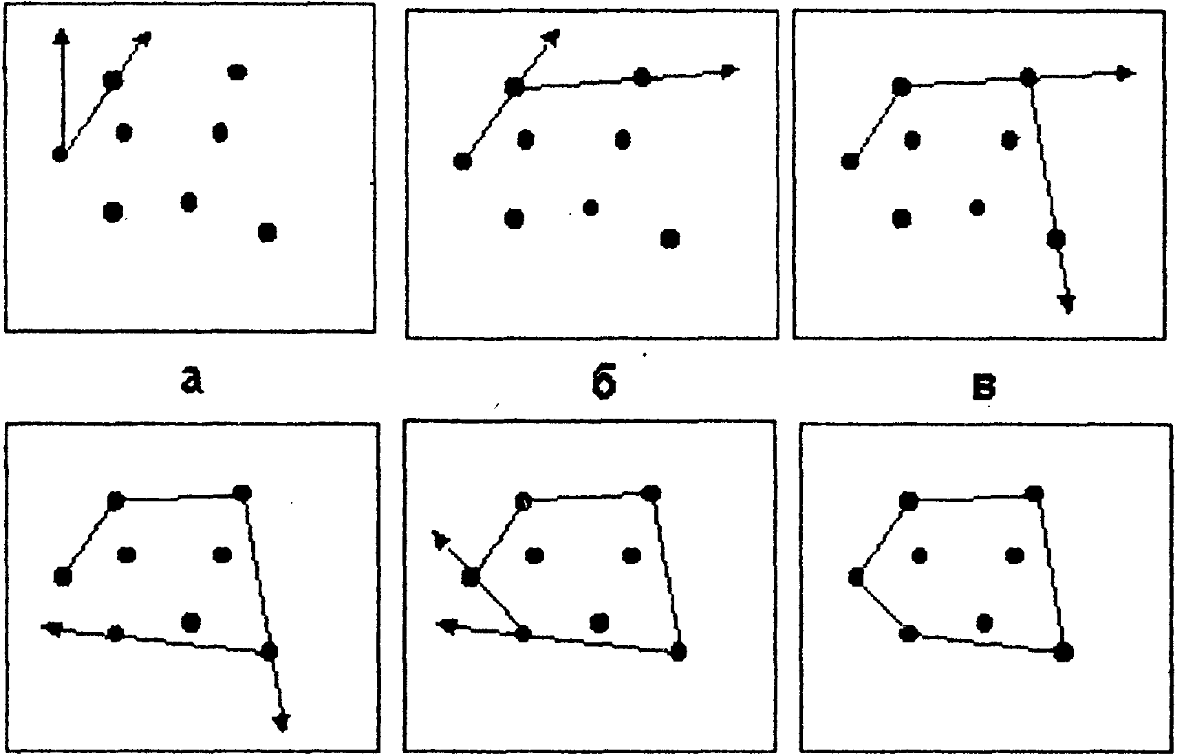
многоугольника. Основные возможные
случаи изображены на рисунке.

В случае а, когда
ребра, выходящие из соответствующей
вершины, лежат по одну сторону от луча,
четность количества пересечений не
меняется.

Случай в, когда
выходящие из вершины ребра лежат по
разные стороны от луча, четность
количества пересечений изменяется. К
случаям б и г такой подход непосредственно
неприменим. Несколько изменим его,
заметив, что в случаях а и б вершины,
лежащие на луче, являются экстремальными
значениями в тройке вершин соответствующих
отрезков. В других же случаях экстремума
нет.

Исходя из этого,
можно построить следующий алгоритм:
выпускаем из точки А горизонтальный
луч в направлении оси Ох и все ребра
многоугольника, кроме горизонтальных,
проверяем на пересечение с этим лучом.
В случае, когда луч проходит через
вершину, т.е. формально пересекает сразу
два ребра, сходящихся в этой вершине,
засчитаем это пересечение только для
тех ребер, для которых эта вершина
является верхней.

Вычисление
площади многоугольника

Для площади s(P)
многоугольника Р, образованного вершинами

справедлива следующая формула:
Эта формула дает площадь многоугольника
со знаком, зависящим от ориентации его
вершин. В случае, когда вершины упорядочены
в направлении против часовой стрелки,
s(P) < 0.

Построение
выпуклой оболочки

Пусть S — конечный
набор точек на плоскости. Выпуклой
оболочкой
набора S называется пересечение всех
выпуклых многоугольников, содержащих
S. Ясно, что
— это выпуклый многоугольник, все вершины
которого содержатся в S (заметим, что не
все точки из S являются вершинами выпуклой
оболочки).

Один из способов
построения выпуклой оболочки конечного
набора точек S на плоскости напоминает
вычерчивание при помощи карандаша и
линейки. Вначале выбирается точка
заведомо являющаяся вершиной границы
выпуклой оболочки. В качестве такой
точки можно взять самую левую точку из
набора S (если таких точек несколько,
выбираем самую нижнюю). Затем вертикальный
луч поворачивается вокруг этой точки
по направлению часовой стрелки до тех
пор, пока не наткнется на точку
Тогда отрезок
будет ребром границы выпуклой оболочки.
Для поиска следующего ребра будем
продолжать вращение луча по часовой
стрелке; на этот раз вокруг точки b до
встречи со следующей точкой
Отрезок
будет следующим ребром границы выпуклой
оболочки. Процесс повторяется до тех
пор, пока мы снова не вернемся в точку
а. Этот метод называется методом
«заворачивания подарка».

Основным шагом
алгоритма является отыскание точки,
следующей за точкой, вокруг которой
вращается луч.

Временные затраты
данного алгоритма равны
где h — число вершин в границе искомой
выпуклой оболочки. Работа данного
алгоритма проиллюстрирована на рис.

Рассмотрим еще
один алгоритм для построения выпуклой
оболочки, так называемый метод обхода
Грэхема. В этом методе выпуклая оболочка
конечного набора точек S находится в
два этапа. На первом этапе алгоритм
выбирает некоторую экстремальную точку

и сортирует все остальные точки в
соответствии с углом направленного к
ним из точки
луча. На втором этапе алгоритм выполняет
пошаговую обработку отсортированных
точек, формируя последовательность
многоугольников, которые в конце концов
и образуют искомую выпуклую оболочку

Выберем в качестве
экстремальной точки точку с минимальной
у-координатой и поменяем ее местами с

Остальные точки сортируются затем в
порядке возрастания полярного угла
относительно точки
Если две точки имеют одинаковый полярный
угол, то точка, расположенная ближе к
должна стоять в отсортированном списке
раньше, чем более дальняя точка.

Для определения
того, какая именно точка должна быть
включена в границу выпуклой оболочки
после точки
используется тот факт, что при обходе
границы выпуклой оболочки в направлении
по часовой стрелки каждая ее вершина
должна соответствовать повороту влево.
Быстродействие данного алгоритма равно

Соседние файлы в папке Архив(1 курс)

• #
• #
• #
• #
• #

Неподвижных точек действительно нет, так как система $%x=y$%; $%y=z$%; $%z=x+1$% решений не имеет.

Рассмотрим уравнение плоскости: $%ax+by+cz+d=0$%, где хотя бы одно из чисел $%a,b,c$% отлично от нуля. Если эта плоскость инвариантна, то для любой её точки после замены координат должно иметь место равенство $%ay+bz+c(x+1)+d=0$%, то есть $%cx+ay+bz+c+d=0$%. Это уравнение той же плоскости, и оно не обязательно совпадает с предыдущим, но пропорционально ему с некоторым коэффициентом $%k$%, то есть $%c=ka$%, $%a=kb$%, $%b=kc$%, $%c+d=kd$%. Легко видеть, что $%a=0Rightarrow c=0Rightarrow b=0Rightarrow a=0$%, поэтому ни одно из чисел $%a,b,c$% нулю не равно. Тогда $%abc=k^3abc$%, и после сокращения на $%abcne0$% получается $%k^3=1$%, то есть $%k=1$%. (Здесь важно, что всё происходит над полем действительных чисел, потому что в комплексной области результат был бы другим.) Теперь из равенства $%c+d=d$% получается противоречие, из которого можно сделать вывод, что инвариантных плоскостей у нас нет.

Теперь рассмотрим вопрос об инвариантных прямых. Рассмотрим на прямой две различные точки с координатами $%(x_1,y_1,z_1)$% и $%(x_2,y_2,z_2)$%. Тогда $%(x_2-x_1,y_2-y_1,z_2-z_1)$% есть направляющий вектор прямой. После замены координат он превратится в $%(y_2-y_1,z_2-z_1,x_2-x_1)$%, и этот вектор пропорционален предыдущему. Как и выше, легко проверяется, что у него нет нулевых координат (в противном случае все нулевые), а произведение координат не изменилось, поэтому коэффициент пропорциональности равен 1, и все координаты равны. Это означает, что (1,1,1) является направляющим вектором инвариантной прямой (если таковая вообще есть).

Таким образом, прямая задаётся параметрически в виде $%x=x_0+t$%, $%y=y_0+t$%, $%z=z_0+t$%. После замены, сумма координат увеличивается на 1, и это значит, что значение параметра $%t$% увеличивается на $%frac13$%. Отсюда можно сделать вывод, что $%(x_0+frac13,y_0+frac13,z_0+frac13)=(y_0,z_0,x_0+1)$%. Точку $%x_0$% можно выбрать произвольно — например, полагая $%x_0=0$%. Тогда $%y_0=frac13$%, $%z_0=frac23$%, и прямая, заданная параметрически в виде $%x=t$%, $%y=frac13+t$%, $%z=frac23+t$% оказывается инвариантной. Точка $%(y,z,x+1)$% будет принадлежать той же прямой при замене значения параметра $%t$% на $%t+frac13$%.

Можно заметить, что эта прямая является пересечением двух плоскостей: $%y=x+frac13$% и $%z=y+frac13$%.

Calling $p = (x,y),, b = (-2,0)$ we have the generic line as

$$
p = p_0 + lambda vec v
$$

then

$$
p_0 + lambda vec v = A( p_0+lambdavec v) + b
$$

or

$$
A p_0-p_0+b = lambda(vec v-Avec v),,,forall lambdain mathbb{R}
$$

so we have

$$
(A-I_2)vec v = 0\
(A-I_2)p_0 + b = 0
$$

now solving for $vec v, p_0$ we have the invariant lines.

воскресенье, 04 апреля 2010