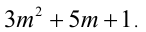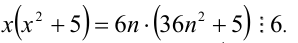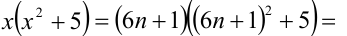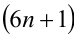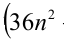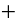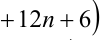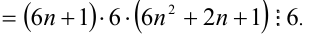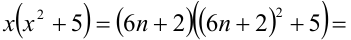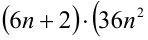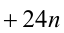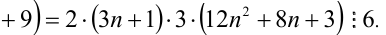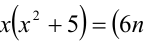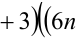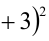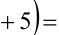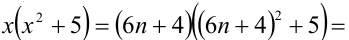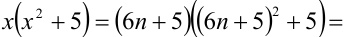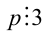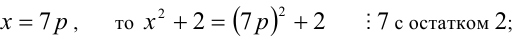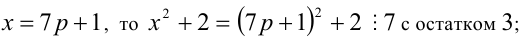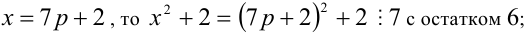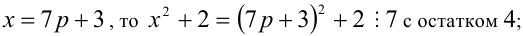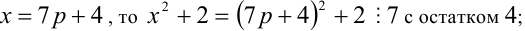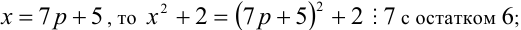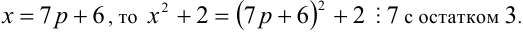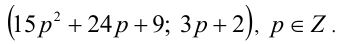Исходные остатки
Ввод исходных остатков
При помощи пункта главного меню Установка >> Исходные остатки, пользователь вызывает окно Исходные остатки (рис. 1), в котором отображён упорядоченный по коду список счетов. В каждой строке этого списка содержится код, наименование счёта и значение дебетового и/или кредитового исходного остатка по данному счёту (субсчёту).
В этом окне можно ввести и отредактировать исходные остатки и их атрибуты на момент открытия нового журнала хозяйственных операций, а также наименование единиц измерения (для счетов количественно-суммового учёта).
Рис. 1: Окно Исходные остатки
В режиме установки исходных остатков невозможно добавлять, удалять или редактировать атрибуты счетов. Эти функции доступны лишь в режиме установки плана счетов. В окне Исходные остатки можно только вводить и изменять исходные остатки по всем существующим счетам и субсчетам.
Рис. 2
В окне Исходные остатки (также как и в окне План счетов) счета, имеющие субсчета, выделены синим цветом и имеют кнопку Открыть (рис. 2).
Важно отметить, что к счетам, имеющим субсчета, невозможно ввести исходные остатки, так как они рассчитываются путём суммирования остатков на субсчетах, открытых к ним. Поэтому исходные остатки к таким счетам формируются путём последовательного ввода исходных остатков на входящие в них субсчета, то есть на счета конечного уровня.
Рис. 3: Окно ввода исходных остатков на субсчетах третьего порядка
На рисунке 3 видно окно, в котором можно вводить и редактировать исходные остатки по счетам и субсчетам, а также единицы измерения и цены (с указанием – средняя или фиксированная) для счетов, на которых ведётся количественно-суммовой учёт. Кроме того, наряду с остатком в суммовом выражении, здесь же можно вводить и количественный остаток.
Уместно напомнить, что при использовании фиксированной цены все проводки формируются только с этой ценой. При применении средней цены в проводках можно вводить произвольную цену. Расчёт средней цены осуществляется автоматически при переходе в поле Цена окна редактирования проводки. При изменении типа цены по счёту по дополнительному запросу пересчитываются проводки либо по сумме, либо по количеству.
Легко заметить, что в нижней части окна ввода исходных остатков (рис. 3) находится строка статуса (рис. 4).
Рис. 4: Фрагмент окна ввода исходных остатков. Строка статуса
В этой строке отображается информация об общем количестве счетов данного уровня и порядковом номере выбранного счёта или субсчёта, а также его код и наименование. В нашем примере выбранный субсчёт является третьим по порядку из трёх существующих в списке — 3/3, его код —
43/И-21 З — 0025, а наименование – Заказ 0025.
Как вы уже убедились, окно ввода исходных остатков удобно в применении и имеет большие возможности. Однако уместно рассказать о ещё одном его замечательном свойстве, которое очень ценят бухгалтеры.
При неравенстве суммы дебетовых и кредитовых остатков на счетах, (при превышении кредитового остатка над дебетовым или наоборот) в статусной строке появляется информация о сумме расхождения и в какую сторону (больше / меньше) это расхождение (рис. 5
Рис. 5: Фрагмент окна ввода исходных остатков. Строка статуса с информацией о расхождении
Получив такую информацию, вы быстро устраните неточности и сообщение исчезнет.
|
Примечание |
Сообщение о разнице дебетовых или кредитовых остатков выдается только при работе на уровне счетов первого порядка. |
Редактирование исходных остатков
Как вы уже знаете, исходные остатки можно вводить и редактировать только на счетах конечного уровня.
Для перехода в режим редактирования можно применить любой из уже известных вам способов:
-
на панели инструментов нажать кнопку
;
-
дважды щёлкнуть мышью по строке выбранного вами счёта;
-
нажать клавишу F7;
-
воспользоваться пунктом главного меню Правка >> Изменить.
В результате – появится окно редактирования исходных остатков. В нём можно изменить сумму остатка, а также цену, количество и единицу измерения для счетов с количественно-суммовым учётом.
Рассмотрим это на примере изменения пользователем атрибутов исходных остатков субсчёта 76/Алименты (пассивный) счета 76 (активно-пассивный, суммовой) (рис. 6).
Рис. 6: Исходные остатки активно-пассивного счета с суммовым учетом
Обратите внимание, что графы Тип цены, Ед., Цена и Количество заблокированы.
Рис. 7: Кнопки выбора
Для активно-пассивных счетов с помощью переключателя Остаток по указывается, в дебет или кредит счёта относится этот остаток. Для выбора необходимо щёлкнуть мышью по кнопке выбора перед соответствующим показателем (рис. 7). В результате кнопка выбранного пункта (по Дебету) будет отмечена точкой
.
Несколько иная ситуация отражена на рисунке Ошибка: источник перёкрестной ссылки не найден. Здесь редактируются атрибуты исходных остатков активного счета 43 с количественно-суммовым учётом. Как вы знаете, изменять исходные остатки можно только на счетах конечного уровня, поэтому в нашем примере это субсчёт третьего порядка с кодом 43/И-21 З — 0025 и наименованием — Заказ 0025.
Обратите внимание, что вы имеете возможность указать тип цены (средняя или фиксированная), а также цену за единицу, количество и единицу измерения объекта учёта. Так как этот счёт является активным, введённый остаток относится только в дебет счета, поэтому переключатель Остаток по заблокирован. После внесения необходимых изменений и окончания редактирования нажмите кнопку ОК.
Рис. 8: Исходные остатки активного счета с количественно-суммовым учетом
При вводе числовых значений удобно пользоваться встроенным калькулятором. Его можно вызвать кнопкой, расположенной справа от поля ввода числового показателя.
Бывают ситуации, когда необходимо обнулить остаток на каком-либо счёте. Для этого при помощи главного меню Установка >> Исходные остатки откройте окно Исходные остатки и установите курсор в строке обрабатываемого счета. Затем выполните одно из следующих действий:
-
на панели инструментов нажмите кнопку
;
-
нажмите клавишу F8 или Del;
-
выберите пункт главного меню Правка >> Удалить.
Программа запросит подтверждение на обнуление остатка (рис. 9).
Рис. 9: Окно с предупреждением об обнулении исходного остатка
При нажатии кнопки Да исходный остаток по выбранному счёту будет обнулён, а при нажатии кнопки Нет – операция обнуления будет отменена.
Если обнуляемый счёт имеет субсчета, то вам будет предложено подтвердить обнуление остатков всех субсчетов этого счета (рис. 10).
Рис. 10: Подтверждение обнуления исходных остатков по всем субсчетам счета
Следует подчеркнуть, что для обмена данными с внешними программами, построенными с использованием баз данных FoxPro, dBase, Clipper и др. предусмотрена возможность загрузки и сохранения плана счетов и исходных остатков в формате DBF. С
Найти число по остатку от деления
| Модуль (пробел) остаток (запятая) Модуль (пробел) остаток и т.д. |
Одна древняя китайская задача гласила:
«Найти число, которое при делении на 3 дает остаток 2, при делении на 5 дает остаток 3, а при делении на 7 дает остаток 2»
Что бы решать подобные задачи, сделаем следущее
Исходное число по исходным данным можно выразить вот так
Где k — целые числа
Выпишем ряды меняя k от 0 по возрастающей
Несложно заметить что 23, встречается во всех трех рядах.
Это и есть наш ответ, следущее число (128) встретится только через 105=3*5*7 отсчетов. Так как эти числа взаимно простые, то и берем просто их произведение.
И таким образом общий ответ нашей задачи имеет вид
Легкий алгоритм для понимания, не правда ли?
Но он не совсем неудобен, когда встречаются большие числа, и опять же, при составлении элементов ряда можно банально ошибиться.
Есть другой способ
Пусть нам дана система сравнений
где 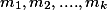
Пусть 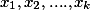
Такие уравнения мы уже можем решать Сравнения 1 степени. Теория чисел.
Узнав эти корни, мы можем вычислить наше исходное число по формуле
Для нашего примера исходные данные выглядят так
Тогда система сравнений будет иметь вид
Решая их получим
И наше решение имеет вид
Или то же самое что и
Как видите, ответ совпадает.
Наш бот решает подобные задачи используя библиотеку PHP GMP. Поэтому к точности расчетов и ограничений на длину значений, это к ним 
Хотя есть и свои материалы в частности: Расчет значения функции Эйлера, Остаток числа в степени по модулю и Диофантовое уравнение с тремя неизвестными
Важно: Логично и это надо учитывать при ввводе чисел, в паре чисел (модуль- остаток), модуль (всегда!) больше чем остаток.
Второе важное замечание. Модуль всегда(!) положительное число, остаток, может быть отрицательным, но лучше все таки привести его к положительному числу.
Как это сделать? Все ссылки на сопутствующие материалы уже приведены.
Пример
Узнать какое загадано число, если остаток при делении его на 37 равно 11, при делении на 9 равно 4, при делении на 7 равно 1, а при делении на 100 остаток равен 25.
Заметим, что модули, то есть числа (37, 9, 7, 100) на которые мы делим неизвестное число, попарно взаимно простые. То есть у нас нет ни одной пары из этих чисел, так что бы они имели общий делитель.
Раз так, то мы можем решать подобную задачу тем, методом который описан выше.Вводим в поле ввода
37 11, 9 4, 7 1, 100 25
За мгновение получим ответ
| Полученное число |
mod(233100)) |
Удачных расчетов!
В пункте меню «Установка | Исходные остатки». Вы можете задать исходные остатки по счетам и их аналитикам. При вызове этого пункта появляется таблица, состоящая из следующих колонок:
•Счет — показывает код счета и его аналитики
•Кол-во/Цена — остаток в количестве и его цена (если есть количественно-суммовые счета)
•НУ — исходный остаток по единице налогового учета. Если он равен исходному остатку по бухгалтерии, то здесь пишется = (равенство)
•Дебет — дебетовый остаток
•Кредит — кредитовый остаток
Вы можете задавать дебетовый остаток по активным счетам, кредитовый по пассивным счетам. Для активно-пассивных и забалансных счетов можно задавать остаток, как по дебету, так и по кредиту. Остаток можно задать только для счетов последнего уровня. Если счет имеет аналитику, она должна быть указана.
Здесь, в таблице исходных остатков, Вы сможете выполнять следующие функции:
Добавление исходного остатка — происходит при добавлении записи в таблицу. После чего появится диалог добавления исходного остатка. После ввода данных и нажатия <OK> новый счет добавляется в список.
Удаление исходного остатка — происходит при удалении записи из таблицы. Перед удалением появится подтверждение: Удалить исходный остаток по счету такому-то ?. Нажмите Да для удаления.
Изменить счет — происходит при редактировании записи таблицы. Появится диалог редактирования исходного остатка.
Очистить остатки — можно выбрав пункт контекстного меню Удалить все. Программа запрoсит подтверждение на удаление, после чего все остатки будут удалены.
Редактирование остатков счета происходит при редактировании записи таблицы. В появившемся диалоге укажите необходимые параметры. После нажатия <OK> изменения будут внесены.
|
|
Внимание! При неравенстве суммы дебетовых и кредитовых остатков всех счетов, например, при превышении кредитового над дебетовым остатком, справа в строке статуса внизу окна появляется сумма различия, например Дебет больше на 226.00. Надо, чтобы в строке статуса выводилась надпись «Исходные остатки занесены верно». |
См.также
Работа с таблицами
Редактирование исходного остатка счета
Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
Теорема
a = b · q + r, где a — делимое, b — делитель, q — неполное частное, r — остаток. 0 ⩽ r < |b|.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Формула деления с остатком
a = b * c + d,
где a — делимое, b — делитель, c — неполное частное, d — остаток.
Эту формулу можно использовать для проверки деления с остатком.
Пример
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:
- 7 * 2 + 1 = 15;
- 2 * 7 + 1 = 15.
Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!
Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.
Самый удобный способ деления — это столбик.
Попрактикуемся в решении.
Пример
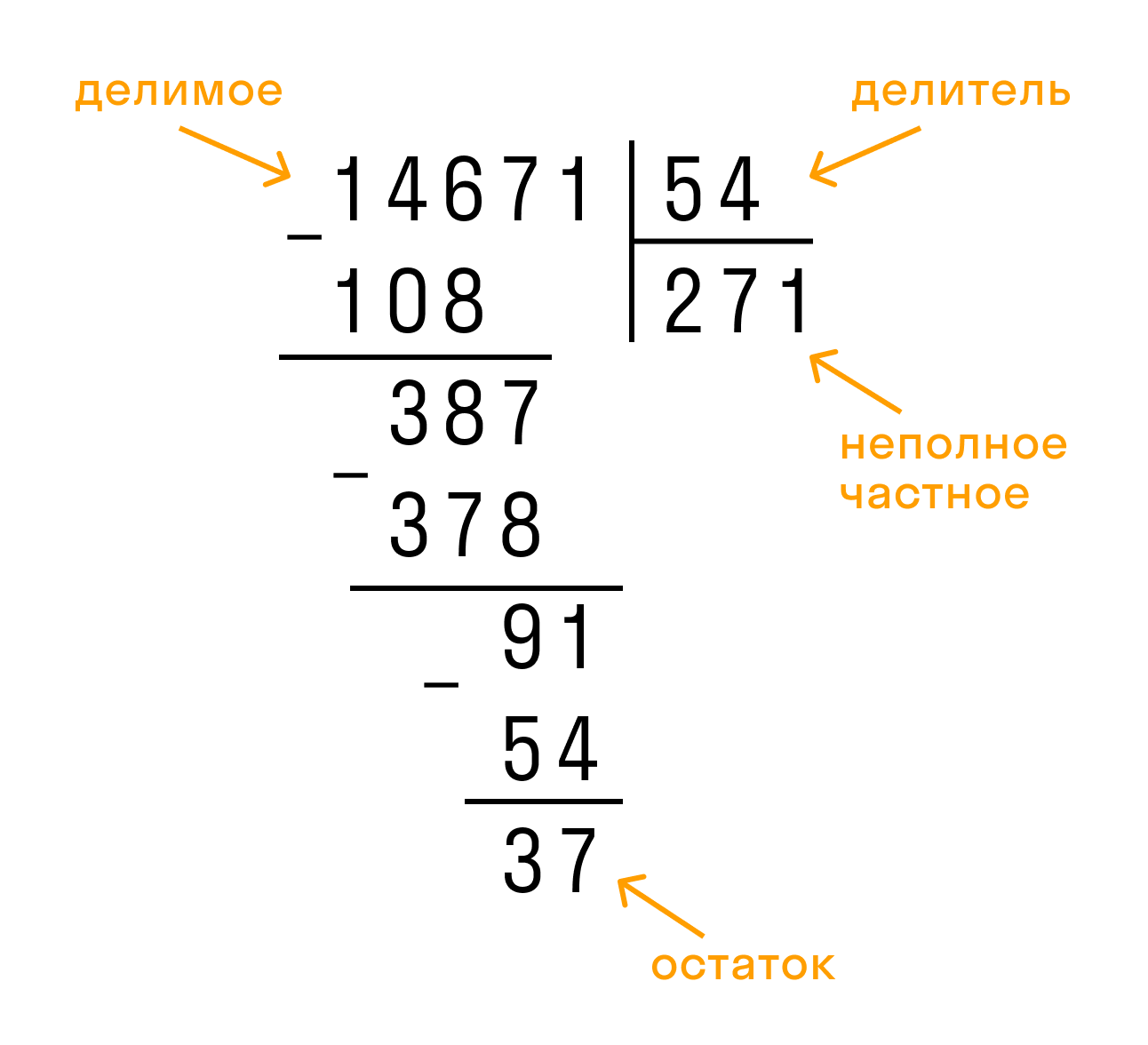
Разделить 14671 на 54.
Как решаем:
Выполним деление столбиком:
Неполное частное равно 271, остаток — 37.
Ответ: 14671 : 54 = 271(остаток 37).
Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
Алгоритм деления положительного числа на целое отрицательное (с остатком):
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя
- получить неполное частное и остаток;
- записать число противоположное полученному.
Пример
Разделить 17 на −5 с остатком.
Как решаем:
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Проверка : a = b * q + r, 17 = −5 * (−3) + 2.
Ответ: 17 : (− 5) = −3 (остаток 2).
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Деление с остатком целого отрицательного числа на целое положительное
Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:
Чтобы получить неполное частное q при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток r будет вычисляться по формуле:
r = a − b * q
Из правила делаем вывод, что при делении получается целое неотрицательное число.
Для точности решения применим алгоритм деления а на b с остатком:
- найти модули делимого и делителя;
- разделить по модулю;
- записать противоположное данному число и вычесть 1;
- использовать формулу для остатка r = a − b * q.
Рассмотрим пример, где можно применить алгоритм.
Пример
Найти неполное частное и остаток от деления −17 на 5.
Как решаем:
Разделим заданные числа по модулю.
Получаем, что при делении частное равно 3, а остаток 2.
Так как получили 3, противоположное ему −3.
Необходимо отнять единицу: −3 − 1 = −4.
Чтобы вычислить остаток, необходимо a = −17, b = 5, q = −4, тогда:
r = a − b * q = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.
Значит, неполным частным от деления является число −4 с остатком 3.
Проверка: a = b * q + r, −17 = 5 * (−4) + 3.
Ответ: (−17) : 5 = −4 (остаток 3).
Деление с остатком целых отрицательных чисел
Сформулируем правило деления с остатком целых отрицательных чисел:
Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:
r = a − b * q
Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.
Алгоритм деления с остатком целых отрицательных чисел:
- найти модули делимого и делителя;
- разделить модуль делимого на модуль делителя;
- получить неполное частное и остаток;
- прибавить 1 к неполному частному;
- вычислить остаток, исходя из формулы r = a − b * q.
Пример
Найти неполное частное и остаток при делении −17 на −5.
Как решаем:
Применим алгоритм для деления с остатком.
Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.
Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.
Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим r = a − b * q = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.
Получилось, что остаток равен 3, а неполное частное равно 4.
Проверка: a = b * q + r, −17 = −5 * 4 + 3.
Ответ: (−17) : (−5) = 4 (остаток 3).
Деление с остатком с помощью числового луча
Деление с остатком можно выполнить и на числовом луче.
Пример 1
Рассмотрим выражение: 10 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.
Решение: 10 : 3 = 3 (остаток 1).
Пример 2
Рассмотрим выражение: 11 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.
Решение: 11 : 3 = 3 (остаток 2).
Метод анализа остатков
В основе метода анализа остатков, который используется при решении ряда задач с целочисленными неизвестными, лежит формула деления с остатком. Суть метода состоит в рассмотрении случаев различных остатков от деления на заданное число, что позволяет в конечном итоге решить поставленную задачу.
В первых трёх примерах, приведённых ниже, в явном виде ищутся остатки от деления одних целых чисел на другие.
Пример №19.
Найти частное и остаток от деления числа (— 23) на 7.
Решение:
Согласно формуле деления с остатком, получаем:
— 23 = — 4 • 7 + 5 , т.е. частное равно — 4, а остаток равен 5.
Пример №20.
Найти сумму остатков, получающихся при делении числа 7263544587435873 на 2, 4, 5, 9, 10, 25.
Решение:
Используя признаки делимости нацело на числа 2,4,5,9,10 и 25, находим остатки:
- остаток от деления на 2 равен 1;
- остаток от деления на 4 равен 1;
- остаток от деления на 5 равен 3;
- остаток от деления на 9 равен 0;
- остаток от деления на 10 равен 3;
- остаток от деления на 25 равен 23.
Суммируя остатки 1 + 1+3+0+3+23, получаем в ответе 31.
Пример №21.
Пусть остаток от деления натурального числа m на 7 равен 3. Найти остаток от деления на 7 числа
Решение:
Из условия следует, что число m имеет вид: 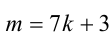
Таким образом, остаток от деления числа 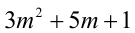
Пример №22.
Доказать, что при любых целых X число 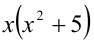
Решение:
Разобьём множество всех целых X на 6 групп в зависимости от остатка при делении на 6, т.е. рассмотрим 6 случаев:
1) Пусть 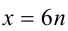
2) Пусть 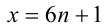
3) Пусть 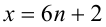
4) Пусть 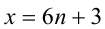
5) Пусть 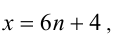
6) Пусть 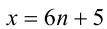
Таким образом, мы рассмотрели все целые числа X и доказали, что всегда (в каждом из шести случаев) выражение 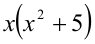
Замечание. Эту задачу можно было решить иначе. Преобразуем данное в условии задачи выражение:
Каждое из двух слагаемых делится нацело на 6 (первое как произведение трёх последовательных целых чисел), поэтому их сумма кратна 6.
Пример №23.
Учительница принесла в класс счётные палочки. Дети раскладывали их в пакетики. Когда разложили по 2 палочки в каждый пакетик, то осталась 1 лишняя палочка. Затем разложили по 13 штук в пакетик, и тогда осталось 7 лишних палочек. Когда же палочки разложили по 9 штук в пакетик, то лишних не осталось. Сколько, самое меньшее, было счётных палочек?
Решение:
Пусть всего было n счётных палочек. Тогда условия задачи приводят к системе
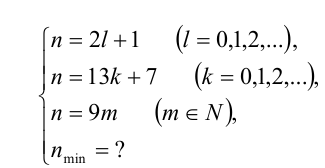
Таким образом, требуется найти наименьшее натуральное нечётное число п , делящееся на 9 и дающее при делении на 13 остаток 7. Заметим, что в силу нечётности 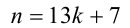
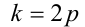
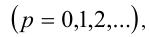
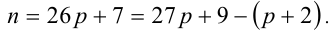
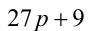
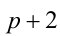
Ответ: самое меньшее — 189 счётных палочек.
Пример №24.
После деления некоторого двузначного числа на сумму его цифр получается 7 и в остатке 6. После деления этого же двузначного числа на произведение его цифр в частном получается 3 и в остатке 11. Найти это двузначное число.
Решение:
Обозначим 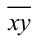
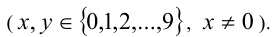
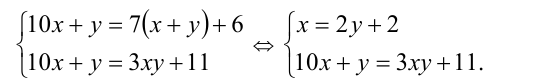
Решая систему методом подстановки, находим единственное решение, удовлетворяющее всем условиям задачи: x= 8, y = 3 . Ответ: 83.
Пример №25.
Целые числа m, n,k не делятся нацело на 3. Доказать, что число 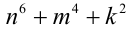
Доказательство. Если 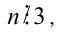
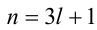
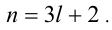
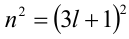
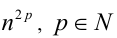
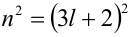
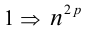
Пример №26.
Доказать, что если 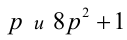
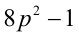
Доказательство. Если 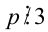
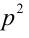
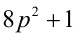
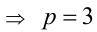
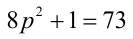
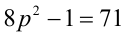
Пример №27.
Решить уравнение в целых числах
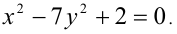
Решение:
Перепишем уравнение в виде: 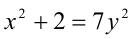
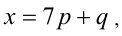
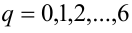
1) Если
2) если
3) если
4) если
5) если
6) если
7) если
Итак, правая часть уравнения делится на 7 нацело (т.е. с остатком 0), а левая часть при этом — с остатками 2, 3, 4, 6. Однако равные числа при делении на одно и то же целое число 7 должны давать одинаковые остатки. Полученное противоречие говорит о том, что данное уравнение не имеет решений в целых числах.
Пример №28.
Найти все пары целых чисел (x;y), удовлетворяющие уравнению
и доказать, что для каждой такой пары сумма 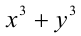
Решение:
Заметим, что левая часть уравнения кратна 3, следовательно, и правая часть должна делиться на 3 нацело. Разобьём множество всех целых y на три группы в зависимости от остатка при делении на 3:
1) Если 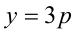
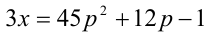
2) Если 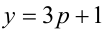
3) Наконец, если 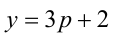
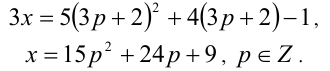
Следовательно, общий вид решений: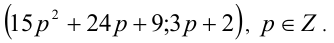
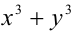
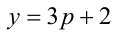
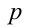
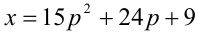
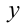
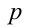


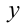
Ответ:
Пример №29.
Решить в целых числах уравнение
Решение:
Так как произвольное целое число 
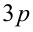
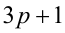
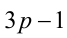
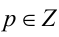
то любое число в кубе или делится нацело на 9, или даёт при делении на 9 в остатке 1 или 8. Аналогично, так как 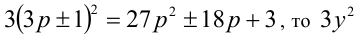
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Предмет математика
Эти страницы возможно вам будут полезны:


















mod(105))
mod(m_1),%20&%20x=(c_2)mod(m_2),....,x=(c_k)mod(m_k))
mod(m_1)\\m_1m_3...m_kx_2=(1)mod(m_2)\\.........\\m_1m_2...m_{k-1}x_k=(1)mod(m_k))
mod%20(m_1m_2...m_k))
mod(3),%20&%20x=(3)mod(5),x=(2)mod(7))
mod(3)=1\\%20&%20(21x_2)mod(5)=1\\(15x_3)mod(7)=1)
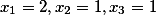
mod(3*5*7)=(233)mod(105))
mod(105)=(233-105-105)mod(105)=23mod(105))