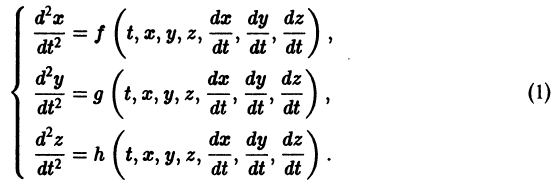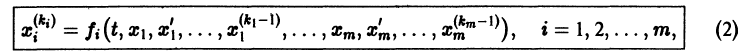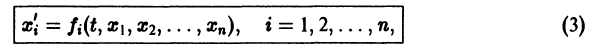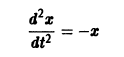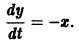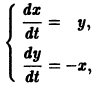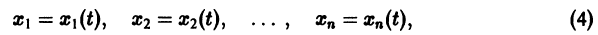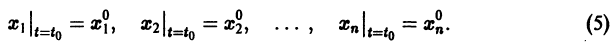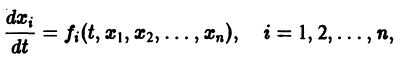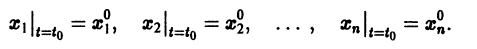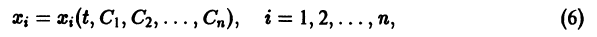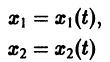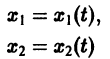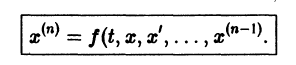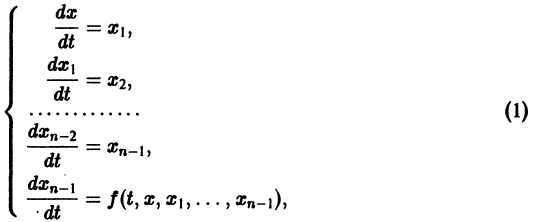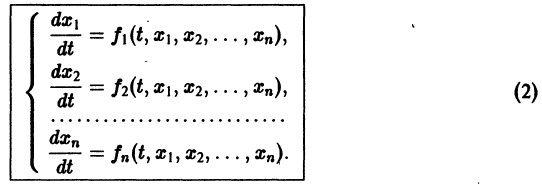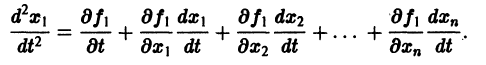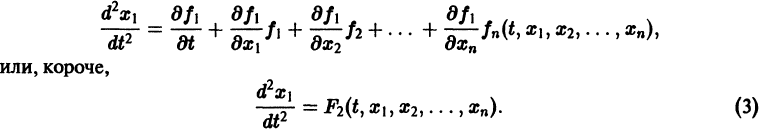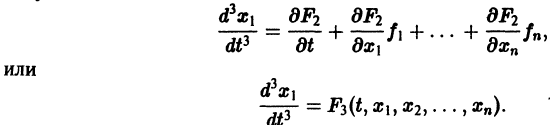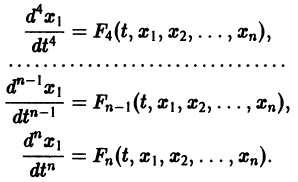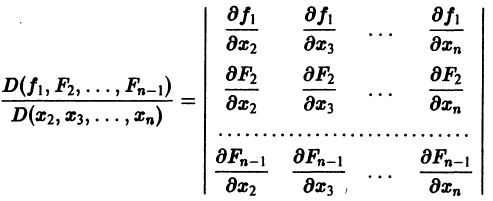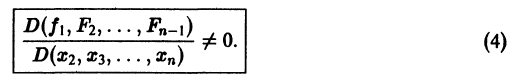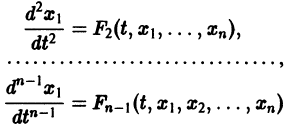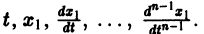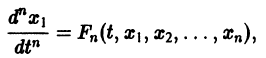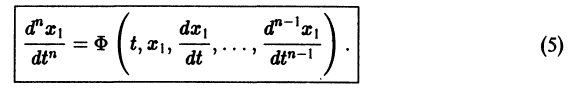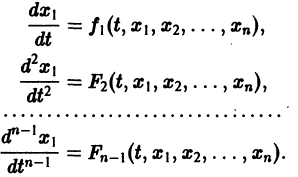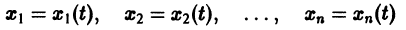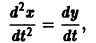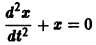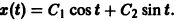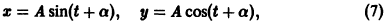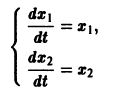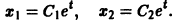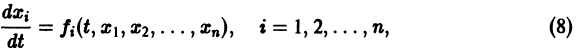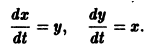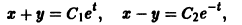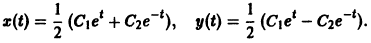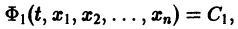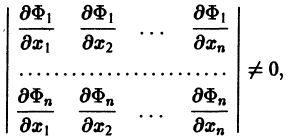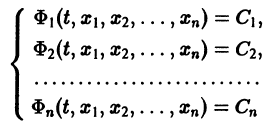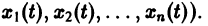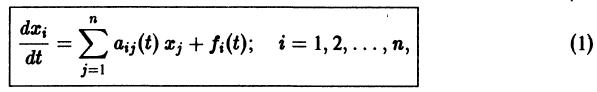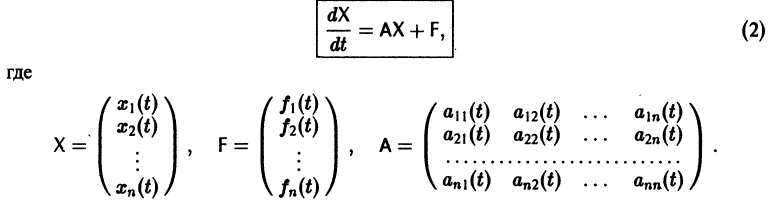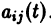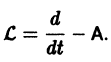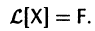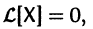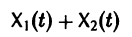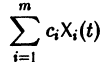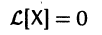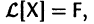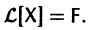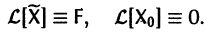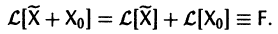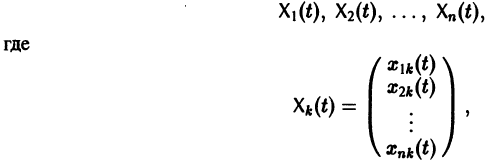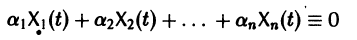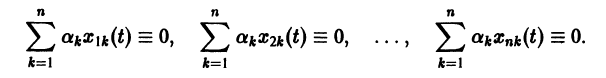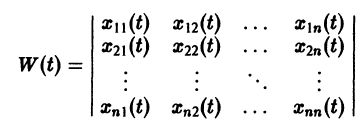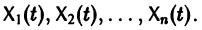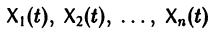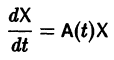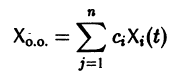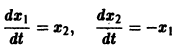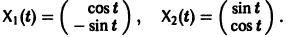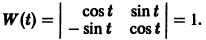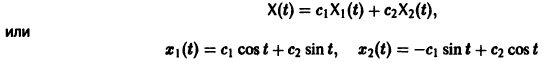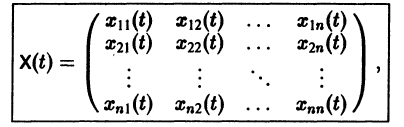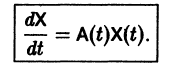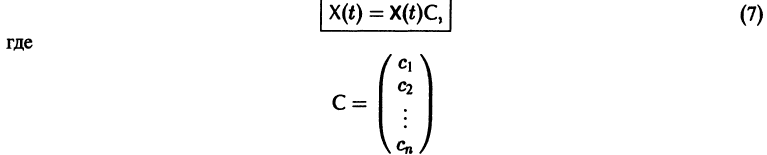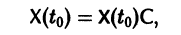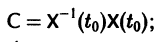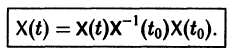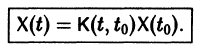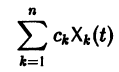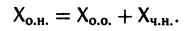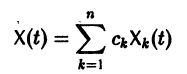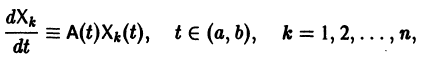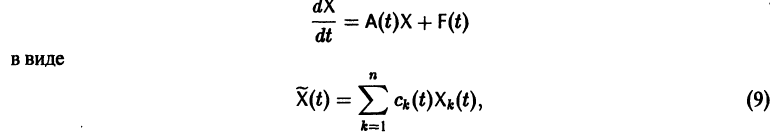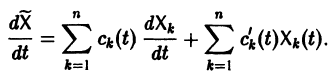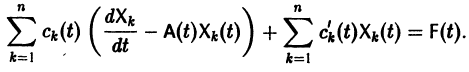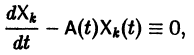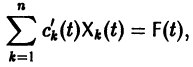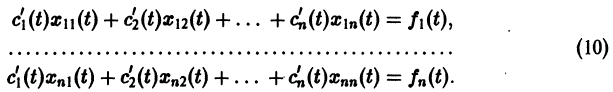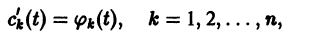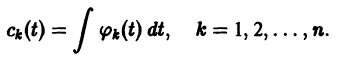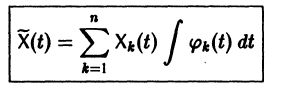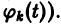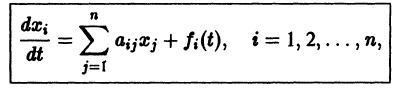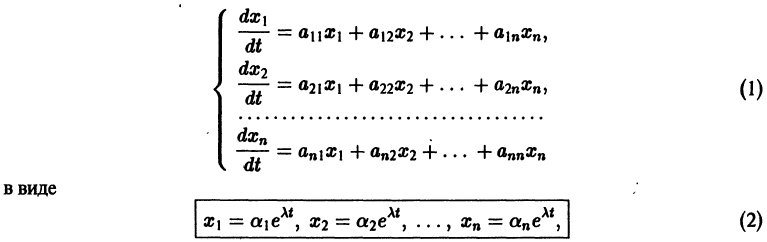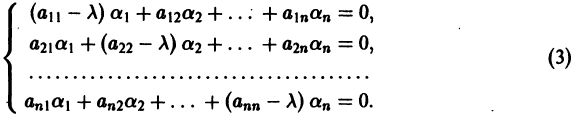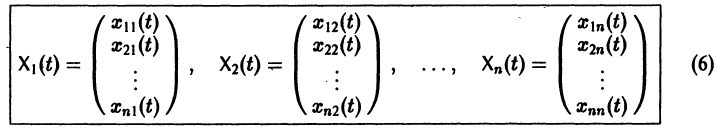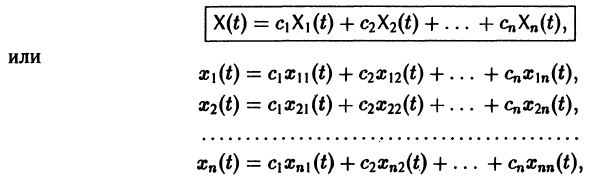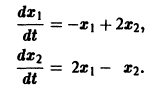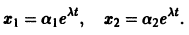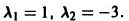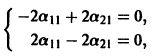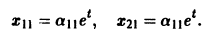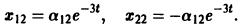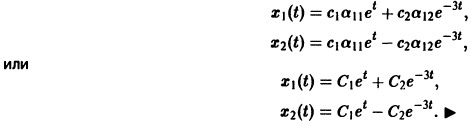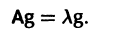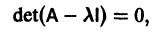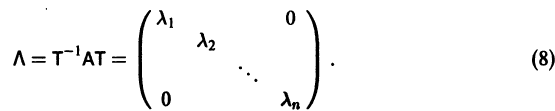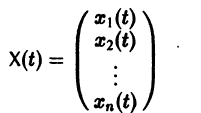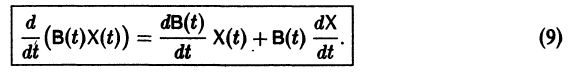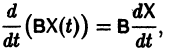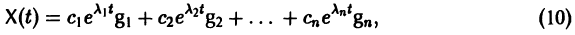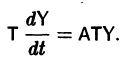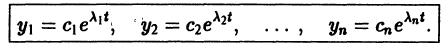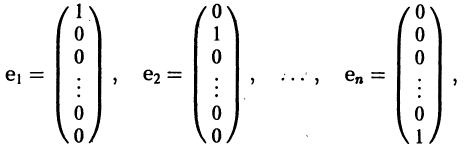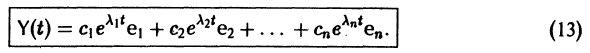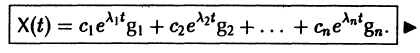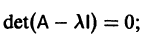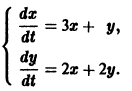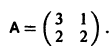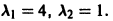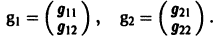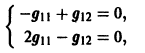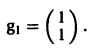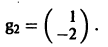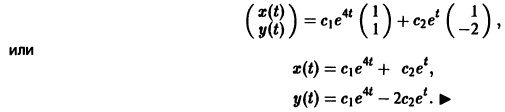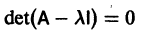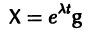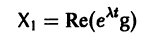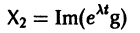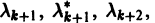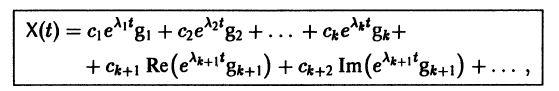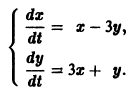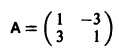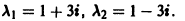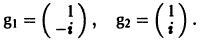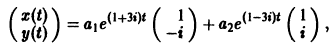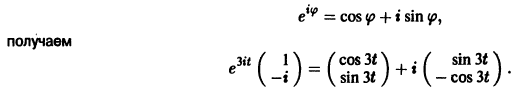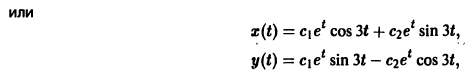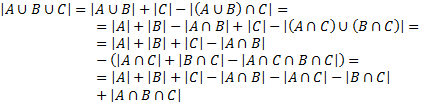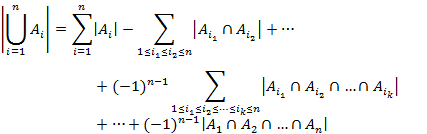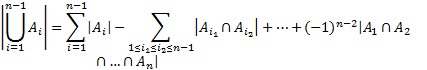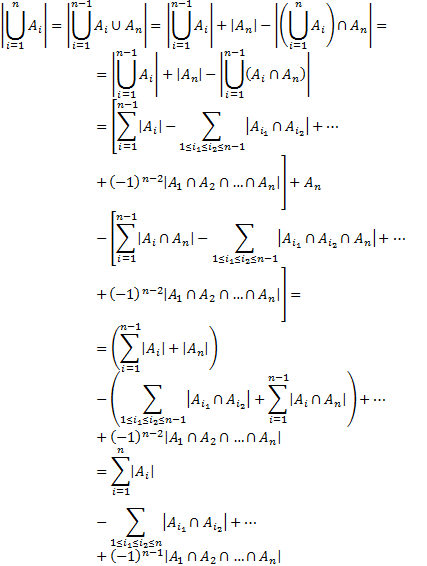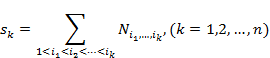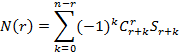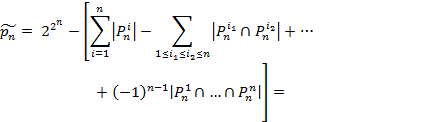Как найти исключенные функции

Метод исключения — сведение системы ДУ к одному уравнению

Частным случаем канонической системы дифференциальных уравнений является одно уравнение n-го порядка, разрешенное относительно старшей производной.

Введением новых функций

это уравнение заменяется нормальной системой уравнений

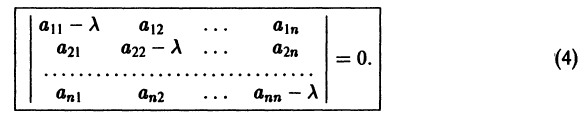
Можно утверждать и обратное, что, вообще говоря, нормальная система уравнений первого порядка

эквивалентна одному уравнению порядка . На этом основан один из методов интегрирования систем дифференциальных уравнений — метод исключения .

Проиллюстрируем этот метод на примере системы двух уравнений:

Здесь — постоянные коэффициенты, а и — заданные функции; и — искомые функции. Из первого уравнения системы (1) находим

Подставляя во второе уравнение системы вместо у правую часть (2), а вместо производную от правой части (2), получаем уравнение второго порядка относительно

где — постоянные. Отсюда находим . Подставив найденное выражение для и в (2), найдем .

Пример 1. Проинтегрировать систему уравнений

Решение. Из первого уравнения системы (3) находим , тогда

Подставляя (4) во второе уравнение системы (3), получаем линейное дифференциальное уравнение с постоянными коэффициентами второго порядка

Общее решение уравнения (5)

Находя производную по от (6), получаем

Общее решение системы (3):

Пример 2. Решить задачу Коши для системы

Решение. Из второго уравнения системы (7) находим

Подставляя (9) и (10) в первое уравнение системы (7), получаем уравнение , общее решение которого

Подставляя (11) в (9), найдем . Общее решение системы (7)

При начальных условиях (8) из (12) получим систему уравнений для определения

решая которую, найдем . Подставляя эти значения и в (12), получаем решение поставленной задачи Коши:

Пример 3. Решить систему уравнений

Решение. Из первого уравнения системы находим

Подставляя эти выражения для и во второе уравнение, получаем

Считая , из последнего уравнения имеем и после интегрирования получим . Теперь легко находим

Общее решение данной системы

Замечание. Не всякая система дифференциальных уравнений может быть сведена к одному уравнению более высокого порядка. Например,

не сводится к одному уравнению второго порядка. Ее общее решение .

Системы дифференциальных уравнений с примерами решения и образцами выполнения

Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.

Решение систем дифференциальных уравнений

К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции 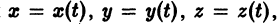выражающие зависимость координат движущейся точки от времени. Система, которая при этом получается, в общем случае имеет вид

Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.

Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями 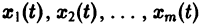аргумента t, назовем канонической систему вида

разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,

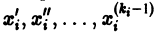
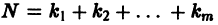
Если в (2) принять за новые вспомогательные функции, то общую каноническую систему (2) можно заменить эквивалентной ей нормальной системой, состоящей из уравнений. Поэтому достаточно рассматривать лишь нормальные системы.

Например, одно уравнение

является мастным случаем канонической системы. Положив 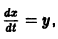в силу исходного уравнения будем иметь

В результате получаем нормальную систему уравнений

эквивалентную исходному уравнению.

Определение:

Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций

дифференцируемых на интервале а

Теорема:

Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений

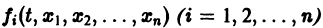
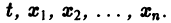
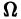
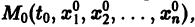
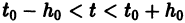
и пусть функции определены в некоторой (n + 1) — мерной области D изменения переменных Если существует окрестность точки в которой функции fi непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным то найдется интервал изменения t, на котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям

Определение:

Система n функций

зависящих от t и n произвольных постоянных 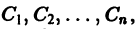называется общим решением нормальной системы (3) в некоторой области существования и единственности решения задачи Коши, если

1) при любых допустимых значениях 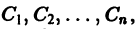система функций (6) обращает уравнения (3) в тождества,

2) в области функции (6) решают любую задачу Коши.

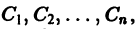
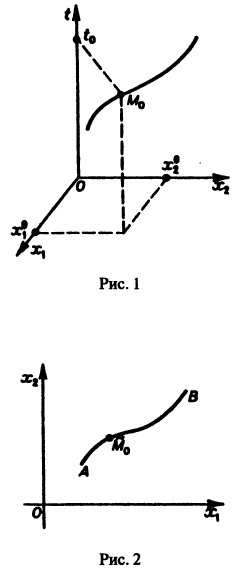
Решения, получающиеся из общего при конкретных значениях постоянных называются частными решениями.

Обратимся для наглядности к нормальной системе двух уравнений,

Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат 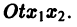Решение

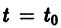
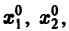
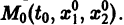
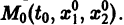
системы (7), принимающее при значения определяет в пространстве некоторую линию, проходящую через точку Эта линия называется интегральной кривой нормальной системы (7). Задача Коши для системы (7) получает следующую геометрическую формулировку: в пространстве переменных t, x1, х2 найти интегральную кривую, проходящую через данную точку (рис. 1). Теорема 1 устанавливает существование и единственность такой кривой.

Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение

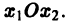
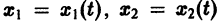
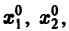
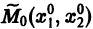
системы — как параметрические уравнения кривой на плоскости Эту плоскость переменных х1х2 называют фазовой плоскостью. В фазовой плоскости решение системы (7), принимающее при t = to начальные значения изображается кривой АВ, проходящей через точку (рис. 2). Эту кривую называют траекторией системы (фазовой траекторией). Траектория системы (7) есть проекция интегральной кривой на фазовую плоскость. По интегральной кривой фазовая траектория определяется однозначно, но не наоборот.

Методы интегрирования систем дифференциальных уравнений

Метод исключения

Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной

Введя новые функции 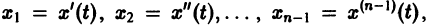заменим это уравнение следующей нормальной системой n уравнений:

т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)

Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.

Делается это так. Пусть имеем нормальную систему

Продифференцируем первое из уравнений (2) по t. Имеем

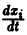
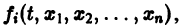
Заменяя в правой части производные их выражениями получим

Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим

Продолжая этот процесс, найдем

Предположим, что определитель

(якобиан системы функций отличен от нуля при рассматриваемых значениях

Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений

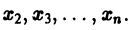
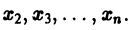
будет разрешима относительно неизвестных При этом выразятся через

Внося найденные выражения в уравнение

получим одно уравнение n-го порядка

Из самого способа его построения следует, что если 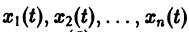есть решения системы (2), то функция х1(t) будет решением уравнения (5).

Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим 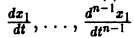и подставим найденные значения как известные функции

от t в систему уравнений

По предположению эту систему можно разрешить относительно 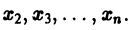т. е найти как функции от t.

Можно показать, что так построенная система функций

составляет решение системы дифференциальных уравнений (2). Пример:

Требуется проинтегрировать систему

Дифференцируя первое уравнение системы, имеем

откуда, используя второе уравнение, получаем

— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид

В силу первого уравнения системы находим функцию

Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.

Функции x(t), y(t) можно представить в виде

откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом 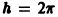и с общей осью х = у = 0, которая также является интегральной кривой (рис. 3).

Исключая в формулах (7) параметр t, получаем уравнение

так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.

При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.

Замечание:

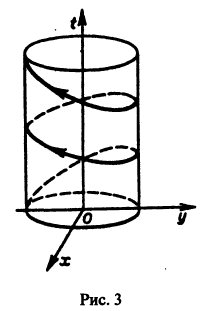
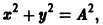
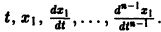
Может оказаться, что функции нельзя выразить через Тогда уравнения n-го порядка, эквивалентного исходной системе, мы не получим. Вот простой пример. Систему уравнений

нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает

Метод интегрируемых комбинаций

Интегрирование нормальных систем дифференциальных уравнений

иногда осуществляется методом интегрируемых комбинаций.

Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.

Пример:

Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:

Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:

Мы нашли два конечных уравнения

из которых легко определяется общее решение системы:

Одна интегрируемая комбинация дает возможность получить одно уравнение

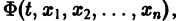
связывающее независимую переменную t и неизвестные функции Такое конечное уравнение называется первым интегралом системы (8). Иначе: первым интегралом системы дифференциальных уравнений (8) называется дифференцируемая функция не равная тождественно постоянной, но сохраняющая постоянное значение на любой интегральной кривой этой системы.

Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций отличен от нуля:

то задача интефирования системы (8) решена (так как из системы

определяются все неизвестные функции

Системы линейных дифференциальных уравнений

Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид

или, в матричной форме,

Теорема:

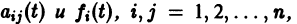
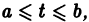
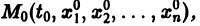
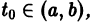
Если все функции непрерывны на отрезке то в достаточно малой окрестности каждой точки где выполнены условия теоремы существования и единственности решения задачи Коши, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (1).

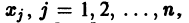
Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, и их частные производные по ограничены, так как эти производные равны непрерывным на отрезке [а,b] коэффициентам

Введем линейный оператор

Тогда система (2) запишется в виде

Если матрица F — нулевая, т. е. 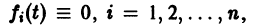на интервале (а,b), то система (2) называется линейной однородной и имеет вид

Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.

Теорема:

Если X(t) является решением линейной однородной системы

то cX(t), где с — произвольная постоянная, является решением той же системы.

Теорема:

двух решений 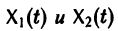однородной линейной системы уравнений является решением той же системы.

Следствие:

с произвольными постоянными коэффициентами сi решений 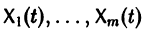линейной однородной системы дифференциальных уравнений

является решением той же системы.

Теорема:

Если 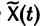есть решение линейной неоднородной системы

a Xo(t) — решение соответствующей однородной системы

будет решением неоднородной системы

Действительно, по условию,

Пользуясь свойством аддитивности оператора 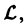получаем

Это означает, что сумма 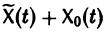есть решение неоднородной системы уравнений

Определение:

называются линейно зависимыми на интервале a

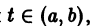
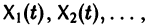
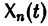
при причем по крайней мере одно из чисел аi, не равно нулю. Если тождество (5) справедливо только при то векторы называются линейно независимыми на (а, b).

Заметим, что одно векторное тождество (5) эквивалентно n тождествам:

называется определителем Вронского системы векторов

Определение:

Пусть имеем линейную однородную систему

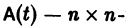
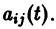
где матрица с элементами Система n решений

линейной однородной системы (6), линейно независимых на интервале а

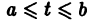
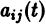
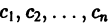
с непрерывными на отрезке коэффициентами является линейная комбинация п линейно независимых на интервале а

() — произвольные постоянные числа).

Пример:

имеет, как нетрудно проверить, решения

Эти решения линейно независимы, так как определитель Вронского отличен от нуля:

Общее решение системы имеет вид

(с1, с2 — произвольные постоянные).

Фундаментальная матрица

Квадратная матрица

столбцами которой являются линейно независимые решения 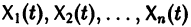системы (6), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению

Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде

— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем

Матрица 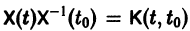называется матрицей Коши. С ее помощью решение системы (6) можно представить так:

Теорема:

О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области 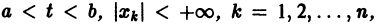линейной неоднородной системы дифференциальных уравнений

с непрерывными на отрезке 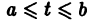коэффициентами aij(t) и правыми частями fi(t) равно сумме общего решения

соответствующей однородной системы и какого-нибудь частного решения 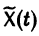неоднородной системы (2):

Метод вариации постоянных

Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).

есть общее решение однородной системы (6), тогда

причем решения Xk(t) линейно независимы.

Будем искать частное решение неоднородной системы

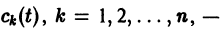
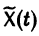
где неизвестные функции от t. Дифференцируя по t, имеем

Подставляя 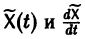в (2), получаем

то для определения 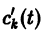получаем систему

или, в развернутом виде,

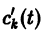
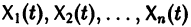
Система (10) есть линейная алгебраическая система относительно определителем которой является определитель Вронского W(t) фундаментальной системы решений . Этот определитель отличен от нуля всюду на интервале a

где 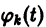— известные непрерывные функции. Интегрируя последние соотношения, находим

Подставляя эти значения 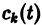в (9), находим частное решение системы (2)

(здесь под символом 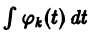понимается одна из первообразных для функции

Системы линейных дифференциальных уравнений с постоянными коэффициентами

Рассмотрим линейную систему дифференциальных уравнений

в которой все коэффициенты 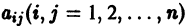— постоянные. Чаще всего такая система интегрируется сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.

Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.

Метод Эйлера

Будем искать решение системы

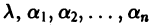
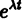
где — постоянные. Подставляя Xk в форме (2) в систему (1), сокращая на и перенося все члены в одну часть равенства, получаем систему

Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными 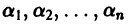имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:

Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно степени n. Из этого уравнения определяются те значения , при которых система (3) имеет нетривиальные решения . Если все корни характеристического уравнения (4) различны, то, подставляя их по очереди в систему (3), находим соответствующие им нетривиальные решения этой системы n, следовательно, находим п решений исходной системы дифференциальных уравнений (1) в виде

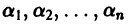
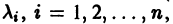
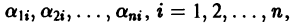
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)

образуют, как можно проверить, фундаментальную систему решений этой системы.

Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид

где произвольные постоянные.

Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.

Пример:

Ищем решение в виде

имеет корни

Система (3) для определения a1, а2 выглядит так:

Подставляя в (*) 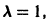получаем

откуда а21 = а11. Следовательно,

Полагая в 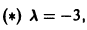находим a22 = — a12, поэтому

Общее решение данной системы:

Матричный метод

Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде

матрица с постоянными действительными элементами

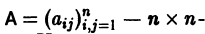
Напомним некоторые понятия из линейной алгебры. Вектор 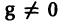называется собственным вектором матрицы А, если

Число называется собственным значением матрицы А, отвечающим собственному вектору g, и является корнем характеристического уравнения

где I — единичная матрица.

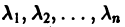
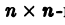
Будем предполагать, что все собственные значения матрицы А различны. В этом случае собственные векторы g1, g2, …gn линейно независимы и существует матрица Т, приводящая матрицу А к диагональному виду, т. е. такая, что

Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.

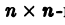
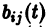
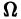
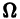
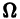
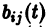
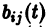
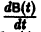
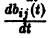
Введем еще следующие понятия. Пусть В(t) — матрица, элементы которой суть функции аргумента t, определенные на множестве . Матрица В(t) называется непрерывной на , если непрерывны на все ее элементы . Матрица В(t) называется дифференцируемой на , если дифференцируемы на все элементы этой матрицы. При этом производной матрицы называется матрица, элементами которой являются производные у соответствующих элементов матрицы В(t).

Пусть B(t) — n х n-матрица,

— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы

В частности, если В — постоянная матрица, то

так как 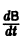есть нуль-матрица.

Теорема:

Если собственные значения 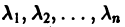матрицы А различны, то общее решение системы (7) имеет вид

где g1, g2,…, gn — собственные векторы-столбцы матрицы А, произвольные постоянные числа.

Введем новый неизвестный вектор-столбец Y(t) по формуле

где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему

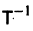
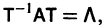
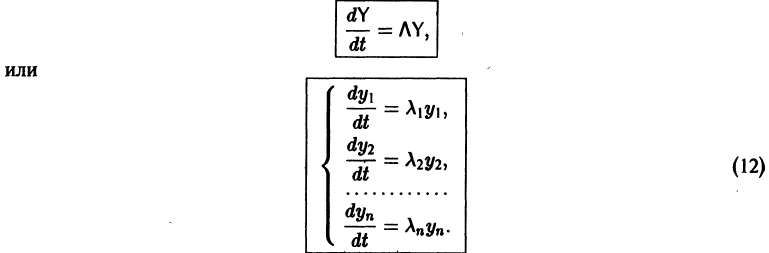
Умножая обе части последнего соотношения слева на и учитывая, что придем к системе

Мы получили систему из n независимых уравнений, которая без труда интегрируется:

Здесь 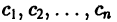— произвольные постоянные числа.

Вводя единичные n-мерные векторы-столбцы

решение Y(t) можно представить в виде

В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы 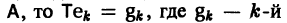собственный вектор матрицы А. Поэтому, подставляя (13) в (11), получим формулу (10):

Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:

1) находим собственные значения 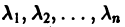матрицы как корни алгебраического уравнения

2) находим все собственные векторы g1, g2,…, gn;

3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).

Пример:

Матрица А системы имеет вид

1) Составляем характеристическое уравнение

Корни характеристического уравнения

2) Находим собственные векторы

Для = 4 получаем систему

откуда g11 = g12, так что

Аналогично для = 1 находим

3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений

Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 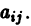системы (7) действительные, то характеристическое уравнение

будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем оно будет иметь и корень *, комплексно сопряженный с . Нетрудно показать, что если g — собственный вектор, отвечающий собственному значению , то * — тоже собственное значение, которому отвечает собственный вектор g*, комплексно сопряженный с g.

При комплексном решение

системы (7) также будет комплексным. Действительная часть

этого решения являются решениями системы (7). Собственному значению * будет отвечать пара действительных решений X1 и -Х2, т. е. та же пара, что и для собственного значения . Таким образом, паре , * комплексно сопряженных собственных значений отвечает пара действительных решений системы (7) дифференциальных уравнений.

Пусть — действительные собственные значения, — комплексные собственные значения. Тогда всякое действительное решение системы (7) имеет вид

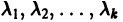
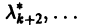
где сi — произвольные постоянные.

Пример:

1) Характеристическое уравнение системы

Его корни

2) Собственные векторы матриц

3) Решение системы

где а1, а2 — произвольные комплексные постоянные.

Найдем действительные решения системы. Пользуясь формулой Эйлера

Следовательно, всякое действительное решение системы имеет

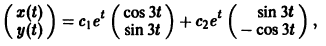
где с1, с2 — произвольные действительные числа.

Понятие о системах дифференциальных уравнений

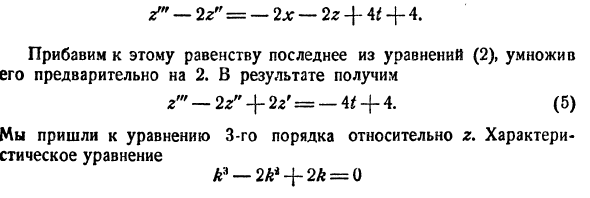
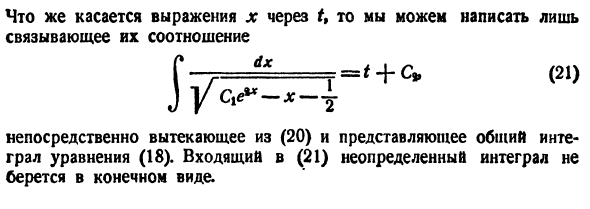
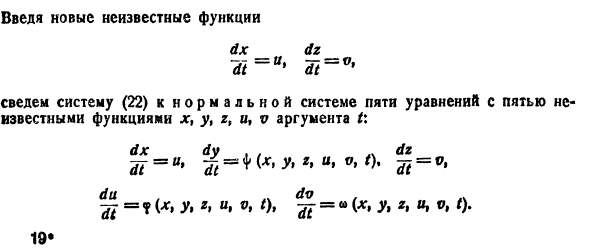
Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Системы дифференциальных уравнений

Этот раздел мы решили посвятить решению систем дифференциальных уравнений простейшего вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2 , в которых a 1 , b 1 , c 1 , a 2 , b 2 , c 2 — некоторые действительные числа. Наиболее эффективным для решения таких систем уравнений является метод интегрирования. Также рассмотрим решение примера по теме.

Решением системы дифференциальных уравнений будет являться пара функций x ( t ) и y ( t ) , которая способна обратить в тождество оба уравнения системы.

Рассмотрим метод интегрирования системы ДУ d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2 . Выразим х из 2 -го уравнения системы для того, чтобы исключить неизвестную функцию x ( t ) из 1 -го уравнения:

d y d t = a 2 x + b 2 y + c 2 ⇒ x = 1 a 2 d y d t — b 2 y — c 2

Выполним дифференцирование 2 -го уравнения по t и разрешим его уравнение относительно d x d t :

d 2 y d t 2 = a 2 d x d t + b 2 d y d t ⇒ d x d t = 1 a 2 d 2 y d t 2 — b 2 d y d t

Теперь подставим результат предыдущих вычислений в 1 -е уравнение системы:

d x d t = a 1 x + b 1 y + c 1 ⇒ 1 a 2 d 2 y d t 2 — b 2 d y d t = a 1 a 2 d y d t — b 2 y — c 2 + b 1 y + c 1 ⇔ d 2 y d t 2 — ( a 1 + b 2 ) · d y d t + ( a 1 · b 2 — a 2 · b 1 ) · y = a 2 · c 1 — a 1 · c 2

Так мы исключили неизвестную функцию x ( t ) и получили линейное неоднородное ДУ 2 -го порядка с постоянными коэффициентами. Найдем решение этого уравнения y ( t ) и подставим его во 2 -е уравнение системы. Найдем x ( t ) . Будем считать, что на этом решение системы уравнений будет закончено.

Найдите решение системы дифференциальных уравнений d x d t = x — 1 d y d t = x + 2 y — 3

Начнем с первого уравнения системы. Разрешим его относительно x :

x = d y d t — 2 y + 3

Теперь выполним дифференцирование 2 -го уравнения системы, после чего разрешим его относительно d x d t : d 2 y d t 2 = d x d t + 2 d y d t ⇒ d x d t = d 2 y d t 2 — 2 d y d t

Полученный в ходе вычислений результат мы можем подставить в 1 -е уравнение системы ДУ:

d x d t = x — 1 d 2 y d t 2 — 2 d y d t = d y d t — 2 y + 3 — 1 d 2 y d t 2 — 3 d y d t + 2 y = 2

В результате преобразований мы получили линейное неоднородное дифференциальное уравнение 2 -го порядка с постоянными коэффициентами d 2 y d t 2 — 3 d y d t + 2 y = 2 . Если мы найдем его общее решение, то получим функцию y ( t ) .

Общее решение соответствующего ЛОДУ y 0 мы можем найти путем вычислений корней характеристического уравнения k 2 — 3 k + 2 = 0 :

D = 3 2 — 4 · 2 = 1 k 1 = 3 — 1 2 = 1 k 2 = 3 + 1 2 = 2

Корни, которые мы получили, являются действительными и различными. В связи с этим общее решение ЛОДУ будет иметь вид y 0 = C 1 · e t + C 2 · e 2 t .

Теперь найдем частное решение линейного неоднородного ДУ y

d 2 y d t 2 — 3 d y d t + 2 y = 2

Правая часть записи уравнения представляет собой многочлен нулевой степени. Это значит, что частное решение будем искать в виде y

= A , где А – это неопределенный коэффициент.

Определить неопределенный коэффициент мы можем из равенства d 2 y

= 2 :
d 2 ( A ) d t 2 — 3 d ( A ) d t + 2 A = 2 ⇒ 2 A = 2 ⇒ A = 1

Таким образом, y

= 1 и y ( t ) = y 0 + y

= C 1 · e t + C 2 · e 2 t + 1 . Одну неизвестную функцию мы нашли.

Теперь подставим найденную функцию во 2 -е уравнение системы ДУ и разрешим новое уравнение относительно x ( t ) :
d ( C 1 · e t + C 2 · e 2 t + 1 ) d t = x + 2 · ( C 1 · e t + C 2 · e 2 t + 1 ) — 3 C 1 · e t + 2 C 2 · e 2 t = x + 2 C 1 · e t + 2 C 2 · e 2 t — 1 x = — C 1 · e t + 1

Так мы вычислили вторую неизвестную функцию x ( t ) = — C 1 · e t + 1 .

Ответ: x ( t ) = — C 1 · e t + 1 y ( t ) = C 1 · e t + C 2 · e 2 t + 1

источники:

http://lfirmal.com/ponyatie-o-sistemah-differencialnyh-uravnenij/

http://zaochnik.com/spravochnik/matematika/differentsialnye-uravnenija/sistemy-differentsialnyh-uravnenij/

Источник

Добавлено 13 сентября 2021 в 02:49

В C++ все функции классифицируются как не выбрасывающие исключения (не генерируют исключения) или потенциально выбрасывающие исключения (могут генерировать исключения).

Рассмотрим следующее объявление функции:

int doSomething(); // может ли эта функция выбросить исключение или нет?

Глядя на типовое объявление функции, невозможно определить, может ли функция выбросить исключение или нет. Хотя комментарии могут помочь определить, генерирует ли функция исключения или нет (и если да, то какие исключения), документация может устареть, а компилятор не использует комментарии.

Спецификации исключений – это языковой механизм, который изначально был разработан как часть спецификации функций для документирования того, какие исключения может вызывать функция. Хотя большая часть спецификаций исключений теперь устарела или удалена, в качестве замены была добавлена другая полезная спецификация исключений, которую мы и рассмотрим в этом уроке.

Спецификатор noexcept

Спецификатор noexcept определяет функцию как не вызывающую исключения и используется в объявлении функции справа от списка параметров:

void doSomething() noexcept; // эта функция не выбрасывает исключения

Обратите внимание, что noexcept на самом деле не мешает функции генерировать исключения или вызывать другие функции, которые потенциально могут генерировать исключения. Скорее, когда генерируется исключение, если оно выходит из функции noexcept, будет вызываться std::terminate. И обратите внимание, что если std::terminate вызывается из функции noexcept, раскручивание стека может произойти, а может и не произойти (в зависимости от реализации и оптимизации), что означает, что перед завершением программы ваши объекты могут быть, а могут и не быть разрушены корректным образом.

Как и функции, отличающиеся только своими возвращаемыми значениями, функции, отличающиеся только спецификацией исключения, так же не могут быть перегружены.

Спецификатор noexcept с логическим параметром

У спецификатора noexcept есть необязательный логический параметр. noexcept(true) эквивалентно noexcept, что означает, что функция не выбрасывает исключения. noexcept(false) означает, что функция потенциально может выбрасывать исключения. Эти параметры обычно используются только в шаблонах функций, где на основе некоторого параметризованного значения шаблонная функция может быть динамически создана как не генерирующая или как потенциально генерирующая исключения.

Какие функции не выбрасывают исключения, а какие потенциально выбрасывают исключения

Функции, которые по умолчанию не выбрасывают исключения:

  • конструкторы по умолчанию;
  • конструкторы копирования;
  • конструкторы перемещения;
  • деструкторы;
  • операторы присваивания копированием;
  • операторы присваивания перемещением.

Однако если какая-либо из перечисленных функций вызывает (явно или неявно) другую функцию, которая потенциально выбрасывает исключения, то указанная функция также будет рассматриваться как потенциально выбрасывающая исключения. Например, если в классе есть член данных с конструктором, потенциально выбрасывающим исключения, то конструкторы данного класса также будут рассматриваться как потенциально выбрасывающие исключения. В качестве другого примера, если оператор присваивания копированием вызывает оператор присваивания, потенциально выбрасывающий исключения, то этот оператор присваивания копированием также будет считаться бросать потенциально выбрасывающим исключения.

Лучшая практика

Если вы хотите, чтобы какие-либо из перечисленных выше функций были не выбрасывающими исключения, явно пометьте их как noexcept (даже если они заданы таким образом по умолчанию), чтобы они случайно не стали потенциально выбрасывающими исключения.

По умолчанию потенциально выбрасывающими исключения могут быть:

  • обычные функции;
  • пользовательские конструкторы;
  • некоторые операторы, например, new.

Оператор noexcept

Оператор noexcept может использоваться внутри функций. Он принимает выражение в качестве аргумента и возвращает true или false, если компилятор считает, что аргумент вызовет исключение или нет. Оператор noexcept проверяется статически во время компиляции и на самом деле не вычисляет входное выражение.

void foo() {throw -1;}
void boo() {};
void goo() noexcept {};
struct S{};

// true; int'ы не выбрасывают исключения
constexpr bool b1{ noexcept(5 + 3) }; 

// false; foo() выбрасывает исключение
constexpr bool b2{ noexcept(foo()) }; 

// false; boo() неявно объявлена noexcept(false)
constexpr bool b3{ noexcept(boo()) }; 

// true; goo() явно объявлена noexcept(true)
constexpr bool b4{ noexcept(goo()) }; 

// true; конструктор по умолчанию struct - по умолчанию noexcept
constexpr bool b5{ noexcept(S{}) };

Оператор noexcept может использоваться для условного выполнения кода в зависимости от того, является ли его аргумент потенциально выбрасывающим исключения или нет. Это необходимо для выполнения определенных гарантий безопасности исключений, о которых мы поговорим в следующем разделе.

Гарантии безопасности исключений

Гарантия безопасности исключений – это договоренность о том, как функции или классы будут вести себя в случае возникновения исключения. Существует четыре уровня безопасности исключений:

  • Нет гарантии – нет никаких гарантий относительно того, что произойдет, если будет выброшено исключение (например, объект класса может остаться в непригодном для использования состоянии).
  • Базовая гарантия – при возникновении исключения утечка памяти не происходит, и объект по-прежнему можно использовать, но программа может быть оставлена в измененном состоянии.
  • Строгая гарантия – если возникнет исключение, утечка памяти не произойдет и состояние программы не изменится. Это означает, что функция должна либо полностью завершиться успешно, либо не иметь побочных эффектов в случае сбоя. Это может быть просто, если сбой произошел до того, как что-либо было изменено; но также это может быть достигнуто путем отката любых изменений, чтобы программа вернулась в состояние до сбоя.
  • Гарантия отсутствия выбросов исключений / сбоев – функция всегда завершается успешно (без сбоя) или со сбоем, но без выброса исключения.

Давайте рассмотрим гарантию без выбросов исключений / без сбоев более подробно:

Гарантия отсутствия выбросов исключений: если функция дает сбой, она не вызывает исключения. Вместо этого она вернет код ошибки или проигнорирует проблему. Гарантии отсутствия выбросов исключений требуются во время раскручивания стека, когда исключение уже обрабатывается; например, все деструкторы должны иметь гарантию отсутствия выбросов исключений (как и любые функции, вызываемые этими деструкторами). Примеры кода, который должен быть не выбрасывающим исключения:

  • деструкторы и функции освобождения/очистки памяти;
  • функции, которые должны вызываться функциями более высокого уровня, не выбрасывающими исключения.

Гарантия отсутствия сбоев: функция всегда будет успешной в том, что она пытается сделать (и, таким образом, никогда не будет необходимости генерировать исключение, поэтому отсутствие сбоев – это немного более строгая форма отсутствия выбросов исключений). Примеры кода, который должен быть без сбоев:

  • конструкторы перемещения и присваивание перемещением (семантика перемещения, описана в главе M);
  • функции обмена (swap-функции);
  • функции очистки/стирания/сброса контейнеров;
  • операции с std::unique_ptr (также рассматриваются в главе M);
  • функции, которые должны вызываться функциями более высокого уровня, не дающими сбоев.

Когда использовать noexcept

Тот факт, что ваш код не генерирует явно никаких исключений, не означает, что вы должны начать использовать noexcept везде, где только можно. По умолчанию большинство функций потенциально выбрасывают исключения, поэтому, если ваша функция вызывает другие функции, есть большая вероятность, что она вызовет функцию, которая потенциально выбрасывает исключения, и, следовательно, так же станет потенциально выбрасывающей исключения.

Политика стандартной библиотеки заключается в использовании noexcept только для функций, которые не должны выбрасывать исключения или давать сбой. Функции, которые потенциально могут генерировать исключения, но на самом деле не генерируют исключения (из-за реализации), обычно не помечаются как noexcept.

Лучшая практика

Используйте спецификатор noexcept в случаях, когда хотите показать гарантию отсутствия сбоев и выбросов исключений.

Лучшая практика

Если вы не уверены, должна ли функция иметь гарантию отсутствия сбоев / выбросов исключений, не помечайте ее как noexcept. Отмена решения об использовании noexcept нарушает обязательства интерфейса перед пользователем в отношении поведения функции. Повышение гарантий путем добавления noexcept позже считается безопасным.

Почему полезно помечать функции как не выбрасывающие исключения

Есть несколько веских причин отмечать функции как не выбрасывающие исключения:

  • Функции, не выбрасывающие исключения, можно безопасно вызывать из функций, которые не безопасны для исключений, например, деструкторов.
  • Функции с noexcept могут позволить компилятору выполнить некоторые оптимизации, которые в противном случае были бы недоступны. Поскольку функция noexcept не может генерировать исключение, компилятору не нужно беспокоиться о сохранении стека выполнения в нераскручиваемом состоянии, что может позволить ему создавать более быстрый код.
  • Также есть несколько случаев, когда знание функции noexcept позволяют нам создавать более эффективные реализации в нашем собственном коде: контейнеры стандартной библиотеки (например, std::vector) не выбрасывают исключения и будут использовать оператор noexcept, чтобы определить, использовать ли в некоторых местах семантику перемещения (быстрее) или семантику копирования (медленнее) (семантику перемещения мы рассмотрим в главе M).

Динамические спецификации исключений

Дополнительные материалы

До C++11 и до C++17 вместо noexcept использовались динамические спецификации исключений. Синтаксис динамических спецификаций исключений использует ключевое слово throw для перечисления типов исключений, которые функция может прямо или косвенно генерировать:

// не генерирует исключения
int doSomething() throw();

// может выбрасывать исключения либо std::out_of_range, либо указатель на int
int doSomething() throw(std::out_of_range, int*); 

// может выбросить что угодно
int doSomething() throw(...);

Из-за таких факторов, как неполные реализации компиляторов, некоторая несовместимость с шаблонами функций, распространенное недопонимание того, как они работают, и тот факт, что стандартная библиотека в основном их не использовала, динамические спецификации исключений были объявлены устаревшими в C++11 и удалены из языка в C++17 и C++20. Для получения более подробной информации смотрите этот документ.

Теги

C++ / CppException / ИсключениеLearnCppnoexceptГарантии безопасности исключенийДля начинающихОбработка ошибокОбучениеПрограммирование

Источник
  1. 1. Инварианты
  2. 2. Виды исключений
  3. 3. std::logic_error
  4. 4. std::invalid_argument
  5. 5. std::domain_error
  6. 6. std::length_error
  7. 7. std::out_of_range
  8. 8. std::future_error
  9. 9. std::runtime_error
  10. 10. std::range_error
  11. 11. std::overflow_error
  12. 12. std::underflow_error
  13. 13. std::system_error
  14. 14. std::ios_base::failure
  15. 15. std::bad_typeid
  16. 16. std::bad_cast
  17. 17. std::bad_weak_ptr
  18. 18. std::bad_function_call
  19. 19. std::bad_alloc
  20. 20. std::bad_array_new_length
  21. 21. std::bad_exception

Что такое исключение? Это ситуация, которая не предусмотрена стандартным поведением программы. Например, попытка доступа к элементу в классе Vector (который мы разбирали в статье про

классы

), который не существует. То есть происходит выход за пределы вектора. В данном случае можно воспользоваться исключениями, чтобы прервать выполнение программы. Это необходимо потому, что

  • Как правило в таких случаях, автор класса

    Vector

    не знает, как пользователь захочет использовать его класс, а также не знает в какой программе этот класс будет использоваться.
  • Пользователь класса

    Vector

    не может всегда контролировать правильность работы этого класса, поэтому ему нужно сообщить о том, что что-то пошло не так.

Для разрешения таких ситуация в C++ можно использовать технику исключений.

Рассмотрим, как написать вызов исключения в случае попытки доступа к элементу по индексу, который не существует в классе Vector. 

double& Vector::operator[](int i)
{
    if (i<0 || size()<=i) throw out_of_range{"Vector::operator[]"};
    return elem[i];
}




  Здесь применяется исключение

  

   out_of_range.

  

  Данное исключение определено в заголовочном файле

  

    .

   



  Оператор

  

   throw

  

  передаёт контроль обработчику для исключений типа

  

   out_of_range

  

  в некоторой функции, которая прямо или косвенно вызывает

  

   Vector::operator

   

  . Для того, чтобы обработать исключения необходимо воспользоваться блоком операторов

  

   try catch.

  


void f(Vector& v)
{
    // ...
    try { // блок обработки функции с исключением
        v[v.size()] = 7; // попытка доступа к элементу за пределами вектора
    }
    catch (out_of_range) { // ловим ошибку out_of_range 
        // ... обработки ошибки out_of_range ...
    }
    // ...
}




  Инварианты

 



  Также блоки

  

   try catch

  

  позволяют производить обработку нескольких различных исключений, что вносит инвариантность в работу механизма исключений C++.
 



  Например, класс вектор при создании может получить неправильный размер вектора или не найти свободную память для элементов, которые он будет содержать.
 


Vector::Vector(int s)
{
    if (s < 0) throw length_error{};
    elem = new double[s];
    sz = s;
}




  Данный конструктор может выбросить исключение в двух случаях:
 


    

  • 
   Если в качестве аргумента
    
   
    
    size
    
   
    
   будет передано отрицательное значение
  
    • 

  • 
   Если оператор
    
   
    
    new
    
   
    
   не сможет выделить память
  
    • 





   length_error

  

  — это стандартный оператор исключений, поскольку библиотека std часто использует данные исключения при своей работе.
 



  Обработка исключений будет выглядеть следующим образом:
 


void test()
{
    try {
        Vector v(−27);
    }
    catch (std::length_error) {
        // обработка отрицательного размера вектора
    }
    catch (std::bad_alloc) {
        // обработка ошибки выделения памяти
    }
}




  Также можно выделить свои собственные исключения.
 



  Виды исключений

 



  Все исключения стандартной библиотеки наследуются от

  

   std::exception.

  



  На данный момент существуют следующие виды исключений:
 


    

  • 
   logic_error
  
    • 

  • 
   invalid_argument
  
    • 

  • 
   domain_error
  
    • 

  • 
   length_error
  
    • 

  • 
   out_of_range
  
    • 

  • 
   future_error (C++11)
  
    • 

  • 
   runtime_error
  
    • 

  • 
   range_error
  
    • 

  • 
   overflow_error
  
    • 

  • 
   underflow_error
  
    • 

  • 
   system_error (C++11)
  
    • 

  • 
   ios_base::failure (начиная с C++11)
  
    • 

  • 
   bad_typeid
  
    • 

  • 
   bad_cast
  
    • 

  • 
   bad_weak_ptr (C++11)
  
    • 

  • 
   bad_function_call (C++11)
  
    • 

  • 
   bad_alloc
  
    • 

  • 
   bad_array_new_length (C++11)
  
    • 

  • 
   bad_exception
  
    • 

  • 
   ios_base::failure (до C++11)
  
    • 




  std::logic_error

 



  Исключение определено в заголовочном файле
  



  Определяет тип объекта, который будет брошен как исключение. Он сообщает об ошибках, которые являются следствием неправильной логики в рамках программы, такие как нарушение логической предпосылки или класс инвариантов, которые возможно предотвратить.
 



  Этот класс используется как основа для ошибок, которые могут быть определены только во время выполнения программы.
 



  std::invalid_argument

 



  Исключение определено в заголовочном файле
  



  Наследован от std::logic_error. Определяет исключение, которое должно быть брошено в случае неправильного аргумента.
 



  Например, на MSDN приведён пример, когда в объект класса bitset из стандартной библиотеки
 


// invalid_arg.cpp  
// compile with: /EHsc /GR  
#include <bitset>  
#include <iostream>  

using namespace std;  

int main( )  
{  
   try   
   {  
      bitset< 32 > bitset( string( "11001010101100001b100101010110000") );  
   }  
   catch ( exception &e )   
   {  
      cerr << "Caught " << e.what( ) << endl;  
      cerr << "Type " << typeid( e ).name( ) << endl;  
   };  
}  
* Output:   
Caught invalid bitset<N> char  
Type class std::invalid_argument  
* 




  В данном примере передаётся неправильная строка, внутри которой имеется символ ‘b’, который будет ошибочным.
 



  std::domain_error

 



  Исключение определено в заголовочном файле
  



  Наследован от std::logic_error. Определяет исключение, которое должно быть брошено в случае если математическая функция не определена для того аргумента, который ей передаётся, например:
 


std::sqrt(-1)




  std::length_error

 



  Исключение определено в заголовочном файле
  



  Наследован от std::logic_error. Определяет исключение, которое должно быть броше в том случае, когда осуществляется попытка реализации превышения допустим пределов для объекта. Как это было показано для размера вектора в начале статьи.
 



  std::out_of_range

 



  Исключение определено в заголовочном файле
  



  Наследован от std::logic_error. Определяет исключение, которое должно быть брошено в том случае, когда происходит выход за пределы допустимого диапазона значений объекта. Как это было показано для диапазона значений ветора в начале статьи.
 



  std::future_error

 



  Исключение определено в заголовочном файле
  



  Наследован от std::logic_error. Данное исключение может быть выброшено в том случае, если не удалось выполнить функцию, которая работает в асинхронном режиме и зависит от библиотеки потоков. Это исключение несет код ошибки совместимый с

  

   std::error_code

  

  .
 



  std::runtime_error

 



  Исключение определено в заголовочном файле
  



  Является базовым исключением для исключений, которые не могут быть легко предсказаны и должны быть брошены во время выполнения программы.
 



  std::range_error

 



  Исключение определено в заголовочном файле
  



  Исключение используется при ошибках при вычислении значений с плавающей запятой, когда компьютер не может обработать значение, поскольку оно является либо слишком большим, либо слишком маленьким. Если значение является значение интегрального типа, то должны использоваться исключения

  

   underflow_error

  

  или

  

   overflow_error

  

  .
 



  std::overflow_error

 



  Исключение определено в заголовочном файле
  



  Исключение используется при ошибках при вычислении значений с плавающей запятой интегрального типа, когда число имеет слишком большое положительное значение, положительную бесконечность, при которой происходит потеря точности, т.е. результат настолько большой, что не может быть представлен числом в формате IEEE754.
 



  std::underflow_error

 



  Исключение определено в заголовочном файле
  



  Исключение используется при ошибках при вычислении значений с плавающей запятой интегрального типа, при которой происходит потеря точности, т.е. результат настолько мал, что не может быть представлен числом в формате IEEE754.
 



  std::system_error

 



  Исключение определено в заголовочном файле
  




   std::system_error

  

  — это тип исключения, которое вызывается различными функциями стандартной библиотеки (как правило, функции, которые взаимодействуют с операционной системой, например, конструктор

  

   std::thread

  

  ), при этом исключение имеет соответствующий

  

   std::error_code

  

  .
 



  std::ios_base::failure

 



  Исключение определено в заголовочном файле
  



  Отвечает за исключения, которые выбрасываются при ошибках функций ввода вывода.
 



  std::bad_typeid

 



  Исключение определено в заголовочном файле
  



  Исключение этого типа возникает, когда оператор

  

   typeid

  

  применяется к нулевому указателю полиморфного типа.
 


#include <iostream>
#include <typeinfo>

struct S { // Тип должен быть полиморфным
    virtual void f();
}; 

int main()
{
    S* p = nullptr;
    try {
        std::cout << typeid(*p).name() << 'n';
    } catch(const std::bad_typeid& e) {
        std::cout << e.what() << 'n';
    }
}




  std::bad_cast

 



  Исключение определено в заголовочном файле
  



  Данное исключение возникает в том случае, когда производится попытка каста объекта в тот тип объекта, который не входит с ним отношения наследования.
 


#include <iostream>
#include <typeinfo>

struct Foo { virtual ~Foo() {} };
struct Bar { virtual ~Bar() {} };

int main()
{
    Bar b;
    try {
        Foo& f = dynamic_cast<Foo&>(b);
    } catch(const std::bad_cast& e)
    {
        std::cout << e.what() << 'n';
    }
}




  std::bad_weak_ptr

 



  Исключение определено в заголовочном файле
  




   std::bad_weak_ptr

  

  – тип объекта, генерируемый в качестве исключения конструкторами

  

   std::shared_ptr

  

  , которые принимают

  

   std::weak_ptr

  

  в качестве аргумента, когда

  

   std::weak_ptr

  

  ссылается на уже удаленный объект.
 


#include <memory>
#include <iostream>
int main()
{
    std::shared_ptr<int> p1(new int(42));
    std::weak_ptr<int> wp(p1);
    p1.reset();
    try {
        std::shared_ptr<int> p2(wp);
    } catch(const std::bad_weak_ptr& e) {
        std::cout << e.what() << 'n';
    }
}




  std::bad_function_call

 



  Исключение определено в заголовочном файле
  



  Данное исключение генерируется в том случае, если был вызван метод

  

   std::function::operator()

  

  объекта

  

   std::function

  

  , который не получил объекта функции, то есть ему был передан в качестве инициализатора nullptr, например, а объект функции так и не был передан.
 


#include <iostream>
#include <functional>

int main()
{
    std::function<int()> f = nullptr;
    try {
        f();
    } catch(const std::bad_function_call& e) {
        std::cout << e.what() << 'n';
    }
}




  std::bad_alloc

 



  Исключение определено в заголовочном файле
  



  Вызывается в том случае, когда не удаётся выделить память.
 



  std::bad_array_new_length

 



  Исключение определено в заголовочном файле
  



  Исключение вызывается в следующих случаях:
 


    

  1. 
   Массив имеет отрицательный размер
  
    2. 

  2. 
   Общий размер нового массива превысил максимальное значение, определяемое реализацией
  
    3. 

  3. 
   Количество элементов инициализации превышает предлагаемое количество инициализирующих элементов
  
    4. 



#include <iostream>
#include <new>
#include <climits>

int main()
{
    int negative = -1;
    int small = 1;
    int large = INT_MAX;
    try {
        new int[negative];           // negative size
        new int[small]{1,2,3};       // too many initializers
        new int[large][1000000];     // too large
    } catch(const std::bad_array_new_length &e) {
        std::cout << e.what() << 'n';
    }
}




  std::bad_exception

 



  Исключение определено в заголовочном файле
  




   std::bad_exception

  

  — это тип исключения в C++, которое выполняется в следующих ситуациях:
 


    

  1. 
   Если нарушается динамическая спецификация исключений
  
    2. 

  2. 
   Если
    
   
    
    std::exception_ptr
    
   
    
   хранит копию пойманного исключения, и если конструктор копирования объекта исключения поймал current_exception, тогда генерируется исключение захваченных исключений.
  
    3. 



#include <iostream>
#include <exception>
#include <stdexcept>

void my_unexp() { throw; }

void test() throw(std::bad_exception)
{
    throw std::runtime_error("test");
}

int main()
{
    std::set_unexpected(my_unexp);
    try {
         test();
    } catch(const std::bad_exception& e)
    {
        std::cerr << "Caught " << e.what() << 'n';
    }
}
Источник

    1. Формула включений и исключений

1.3.1. Объединение комбинаторных конфигураций

Комбинаторные
числа не всегда определяются непосредственно
по известным комбинаторным конфигурациям.
Часто используются различные способы
сведения одних комбинаторных комбинаций
к другим. Простейший из этих способов
– метод включений и исключений. В этом
методе комбинаторная комбинация
представляет собой объединение других
комбинаторных конфигураций, число
которых легко вычислить непосредственно.
Таким образом, возникает задача вычисления
числа комбинаторных конфигураций в
объединении. В простейшем случае
справедлива формула.

Доказательство.
Используем круги Эйлера.

Group 3

Можно
выделить три непересекающихся между
собой области, тогда

Указанные
в этих объединениях множества не
пересекаются, поэтому можно воспользоваться
правилом суммы для определения их
мощности, т.е.

Подставим
из первых двух равенств в 3е, получим

В
более сложном случае имеет место
равенство

Доказательство.

Пример.
Сколько существует натуральных чисел,
меньших 1000, которые не делятся ни на 3,
ни на 5, ни на 7?

Всего
натуральных чисел меньших тысячи 999.Из
них

  1. делятся
    на 3


  2. делятся на 5


  3. делятся на 7


  4. делятся на 3 и 5

  5. 7
    делятся на 3 и 7


  6. делятся на 5 и 7


  7. делятся на 3, на 5 и на 7

В
результате имеем

1.3.2. Принцип включения и исключения

Формула,
известная как принцип включения и
исключения позволяет вычислить мощность
объединения множеств, если известны их
мощности и мощности их пересечений. А
именно, справедлива теорема.

Доказательство.
Проводится методом математической
индукции. При
в силу установленного ранее равенства,
имеем:

т.е.
теорема справедлива.

Предположим,
что формула верна при ,
т.е.

Тогда при nимеем

Т.е.
теорема доказана

Рассмотрим
следующую ситуацию. Множество A
имеет N
элементов с n
одноместными отношениями .
Каждый из N
элементов может обладать или не обладать
любым из этих свойств.


— число элементов, обладающих k
свойствами
и может быть некоторыми другими.

N(0)
– число элементов, не обладающих ни
одним из этих свойств. Это число
определяется формулой включений и
исключений.

Обобщая
эту формулу, получаем выражение,
позволяющее вычислить число элементов,
обладающих R
свойствами.

Пример.
Сколько положительных чисел от 20 до
1000 делятся ровно на одно из чисел 7,11,13.

На
7 делятся 142 числа, из них на 11 делятся
12 чисел, на 13 – 10 чисел.

На
11 делятся 90 числа, из них на 7 делятся 12
чисел, на 13 – 6 чисел.

На
13 делятся 76 числа, из них на 7 делятся 10
чисел, на 12 – 6 чисел.

120
+ 72 + 60 – 4 = 248.

1.3.3. Число булевых функций, существенно зависящих от всех своих переменных

Рассмотрим
применение принципа включения и
исключения на следующем примере. Пусть

число всех булевых функций n
переменных, т.е.

Обозначим

число булевых функций существенно
зависящих от всех n
переменных;
множество булевых функций, у которых
переменная
фиктивная.

Тогда:

Заметим,
что
и

Следовательно

1.3.4. Решето Эратосфена

Одной
из самых больших загадок математики
является расположение простых чисел в
ряду всех натуральных чисел. Иногда два
простых числа идут через одно, (например,
17 и 19, 29 и 31), а иногда подряд идет миллион
составных чисел. Сейчас ученые знают
уже довольно много о том, сколько простых
чисел содержится среди N
первых натуральных
чисел. В этих подсчетах весьма полезным
оказался метод, восходящий еще к
древнегреческому ученому Эратосфену.
Он жил в третьем веке до новой эры в
Александрии.

Эратосфен
занимался самыми различными вопросами
— ему принадлежат интересные исследования
в области математики, астрономии и
других наук. Впрочем, такая разносторонность
привела его к некоторой поверхностности.
Современники несколько иронически
называли Эратосфена «во всем второй»:
второй математик после Евклида, второй
астроном после Гиппарха и т.д.

В
математике Эратосфена интересовал как
раз вопрос о том, как найти все простые
числа среди натуральных чисел от 1 до
N.
Эратосфен считал 1 простым числом. Сейчас
математики считают 1 числом особого
вида, которое не относится ни к простым,
ни к составным числам. Эратосфен придумал
для подсчёта простых чисел следующий
способ. Сначала вычеркивают все числа,
делящиеся на 2 (исключая само число 2).
Потом берут первое из оставшихся чисел
(а именно 3). Ясно, что это число — простое.
Вычеркивают все идущие после него числа,
делящиеся на 3. Первым оставшимся числом
будет 5. Вычеркивают все идущие после
него числа, делящиеся на 5, и т.д. Числа,
которые уцелеют после всех вычеркиваний,
и являются простыми. Так как во времена
Эратосфена писали на восковых табличках
и не вычеркивали, а «выкалывали»
цифры, то табличка после описанного
процесса напоминала решето. Поэтому
метод Эратосфена для нахождения простых
чисел получил название «решето
Эратосфена».

Подсчитаем,
сколько останется чисел в первой сотне,
если мы вычеркнем по методу Эратосфена
числа, делящиеся на 2, 3 и 5. Иными словами,
поставим такой вопрос: сколько чисел в
первой сотне не делится ни на одно из
чисел 2, 3, 5? Эта задача решается по формуле
включения и исключения.

Обозначим
через α1
свойство числа
делиться на 2, через α2
— свойство делимости на 3 и через α3
— свойство делимости на 5. Тогда α1α2
означает, что число делится на 6, α1α3
означает, что оно делится на 10, и α2α3
— оно делится на
15. Наконец, α1α2α3
означает, что число
делится на 30. Надо найти, сколько чисел
от 1 до 100 не делится ни на 2, ни на 3, ни на
5, то есть не обладает ни одним из свойств
α1,
α2,
α3.
По формуле имеем

N(α’1α’2α’3)
= 100 — N(α1)
— N(α2)
— N(α3)
+ N(α1α2)
+ N(α1α3)
+ N(α2α3)
— N(α1α2α3)

Но
чтобы найти, сколько чисел от 1 до N
делится на n,
надо разделить N
на n
и взять целую часть
получившегося частного. Поэтому

N(α1)
= 50, N(α2)
= 33, N(α3)
= 20, N(α1α2)
= 16, N(α1α3)
= 10, N(α2α3)
= 3,

а
значит N(α1α2α3)
= 32.

Таким образом, 32
числа от 1 до 100 не делятся ни на 2, ни на
3, ни на 5. Эти числа и уцелеют после первых
трех шагов процесса Эратосфена. Кроме
них останутся сами числа 2, 3 и 5. Всего
останется 35 чисел.

А из первой тысячи
после первых трех шагов процесса
Эратосфена останется 335 чисел. Это
следует из того, что в этом случае

N(α1)
= 500, N(α2)
= 333, N(α3)
= 200, N(α1α2)
= 166, N(α1α3)
= 100, N(α2α3)
= 66,

а
значит N(α1α2α3)
= 33.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Я обошел метод класса, используя CDetours через инъекцию dll (да я изучаю реверс-инжиниринг) void MyClass::SetData( D3DXVECTOR3& data )и в реальном приложении все работает нормально, функция отключена, и я вижу сообщения отладки (вывод на консоль).

Теперь настоящая проблема в том, что я пытаюсь сделать эту функцию вызовом, если бы она была глобальной функцией, я бы сделал:

typedef void (*SetDataFunc)(D3DXVECTOR3&); //for global functions __cdecl is ok
SetDataFunc SetDataRev = (SetDataFunc)0x00428FD0; //just an example address

then call it:

D3DXVECTOR3 data(0,0,0);
SetDataRev(data);

и все снова будет работать нормально, моя проблема в том, что даже зная адрес MyClass::SetData и используя метод выше, чтобы вызвать его (это действительно называется), но MyClass созданный объект останется прежним, потому что сам вызов не имеет смысла, так как вы не вызываете его из объекта.

Например

MyClass myobj;
myobj.SetData( data ); //ok any members that 'SetData' changes will be changed.

SetDataRevForClass( data ); //not ok, nothing on 'myobj' changed

Как я могу вызвать метод класса «из» myobj на моей длл?

0

Решение

Это зависит от соглашения о вызовах. Вам нужно проверить, как именно функции-члены представлены в вашей перехваченной DLL. На стороне c ++ вышеприведенное объявление и присваивание неверны, тип функции-члена: void (MyClass :: *) (D3DXVECTOR3&). Как это будет переведено, зависит от соглашения о вызовах, но в любом случае указатель на объект MyClass должен быть передан во время вызова.

1

Другие решения

Других решений пока нет …

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти местонахождение телефона по gps
  • Как найти чему равен элемент матрицы
  • Vga graphics card is not guaranteed to operate normally как исправить
  • Синий оттенок на экране ноутбука как исправить
  • Ссд определяется как флешка как исправить