Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Генеральная дисперсия
Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 1
Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Определение 2
Генеральная дисперсия — среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:
С этим понятием также связано понятие генерального среднего квадратического отклонения.
Определение 3
Генеральное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
[{sigma }_г=sqrt{D_г}]
Выборочная дисперсия
Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:
Определение 4
Выборочная совокупность — часть отобранных объектов из генеральной совокупности.
Определение 5
Выборочная дисперсия — среднее арифметическое значений вариант выборочной совокупности.
«Дисперсия: генеральная, выборочная, исправленная» 👇
Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:
Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:
С этим понятием также связано понятие выборочного среднего квадратического отклонения.
Определение 6
Выборочное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:
[{sigma }_в=sqrt{D_в}]
Исправленная дисперсия
Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $frac{n}{n-1}$, то есть
С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:
!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$
Пример задачи на нахождение дисперсии и среднего квадратического отклонения
Пример 1
Выборочная совокупность задана следующей таблицей распределения:
Рисунок 1.
Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.
Решение:
Для решения этой задачи для начала сделаем расчетную таблицу:
Рисунок 2.
Величина $overline{x_в}$ (среднее выборочное) в таблице находится по формуле:
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]
То есть
[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]
Найдем выборочную дисперсию по формуле:
[D_в=frac{sumlimits^k_{i=1}{{{(x}_i-overline{x_в})}^2n_i}}{n}=frac{523,75}{20}=26,1875]
Выборочное среднее квадратическое отклонение:
[{sigma }_в=sqrt{D_в}approx 5,12]
Исправленная дисперсия:
[{S^2=frac{n}{n-1}D}_в=frac{20}{19}cdot 26,1875approx 27,57]
Исправленное среднее квадратическое отклонение:
[S=sqrt{S^2}approx 5,25]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
ЛЕКЦИЯ 13
ТЕМА: СТАТИСТИЧЕСКИЕ
ОЦЕНКИ ПАРАМЕТРОВ ВЫБОРКИ
1.
Точечные оценки параметров распределения.
1.1.
Генеральная средняя.
1.2.
Выборочная средняя.
1.3.
Генеральная дисперсия.
1.4.
Выборочная дисперсия.
1.5.
Исправленная дисперсия.
2.
Интервальные оценки параметров
распределения.
2.1.
Интервальные оценки параметров
нормального распределения.
2.1.1.
Доверительный интервал для оценки
математического ожидания при известном s.
2.1.2.
Доверительный
интервал для оценки математического
ожидания при неизвестном s.
2.1.3.
Доверительный интервал для оценки
дисперсии и среднего квадратического
отклонения.
2.2.
Интервальная оценка вероятности
биноминального распределения по
относительной частоте.
1.
Точечные
оценки параметров распределения.
Пусть
требуется изучить количественный признак
генеральной совокупности. Допустим, что из
теоретических соображений удалось
установить, какое именно распределение
имеет признак. Возникает задача оценки
параметров, которыми определяется это
распределение.
Обычно
в распоряжении исследователя имеются лишь
данные выборки, полученные в результате n
наблюдений (здесь и далее наблюдения
предполагаются независимыми). Через эти
данные и выражают оцениваемый параметр.
Рассматривая значения количественного
признака как независимые случайные
величины, можно сказать, что найти
статистическую оценку неизвестного
параметра теоретического распределения —
это значит найти функцию от наблюдаемых
случайных величин, которая и дает
приближенное значение оцениваемого
параметра.
Итак, статистической
оценкой неизвестного параметра
теоретического распределения называют
функцию от наблюдаемых случайных величин.
Для
того чтобы статистические оценки давали «хорошие»
приближения оцениваемых параметров, они
должны удовлетворять определенным
требованиям: оценка должна быть несмещенной,
эффективной и состоятельной.
Поясним
каждое из понятий.
Несмещенной
называют статистическую оценку Q*, математическое ожидание которой
равно оцениваемому параметру Q при любом объеме выборки, т. е.
M(Q*)
= Q.
Смещенной
называют оценку, математическое ожидание
которой не равно оцениваемому параметру.
Эффективной
называют статистическую оценку, которая (при
заданном объеме выборки п) имеет наименьшую
возможную дисперсию.
При
рассмотрении выборок большого объема (n велико!) к статистическим
оценкам предъявляется требование
состоятельности.
Состоятельной
называют статистическую оценку, которая
при
п®¥
стремится по вероятности
к оцениваемому параметру. Например, если
дисперсия несмещенной оценки при п®¥
стремится
к нулю, то такая оценка оказывается и
состоятельной.
Рассмотрим
точечные оценки параметров
распределения, т.е.
оценки, которые
определяются одним числом Q* =f( x1, x2,…,xn), где x1, x2,…,xn— выборка.
1.1.Генеральная средняя.
Пусть
изучается генеральная совокупность
относительно количественного признака Х.
Генеральной
средней называют среднее арифметическое
значений признака генеральной
совокупности.
Если все
значения признака различны, то
Если значения признака имеют частоты N1, N2, …, Nk, где N1 +N2+…+Nk= N, то
1.2.Выборочная средняя.
Пусть для
изучения генеральной совокупности
относительно количественного признака Х
извлечена выборка объема n.
Выборочной
средней называют среднее арифметическое
значение признака выборочной совокупности.
Если
все значения признака выборки различны, то
если
же все значения имеют частоты n1, n2,…,nk, то
Выборочная
средняя является несмещенной и
состоятельной оценкой
генеральной средней.
Замечание:
Если выборка представлена интервальным
вариационным рядом, то за xi
принимают середины частичных интервалов.
1.3.
Генеральная дисперсия.
Для
того чтобы охарактеризовать рассеяние
значений количественного признака Х генеральной совокупности вокруг
своего среднего значения, вводят сводную
характеристику — генеральную дисперсию.
Генеральной
дисперсией
Dг
называют
среднее арифметическое квадратов
отклонений значений признака генеральной
совокупности от их среднего значения
.
Если
все значения признака генеральной
совокупности объема N
различны, то
Если
же значения признака имеют соответственно
частоты N1, N2, …, Nk, где N1 +N2+…+Nk= N, то
Кроме
дисперсии для характеристики рассеяния значений
признака генеральной совокупности вокруг
своего среднего значения пользуются
сводной характеристикой— средним
квадратическим отклонением.
Генеральным
средним квадратическим отклонением
(стандартом) называют квадратный корень из
генеральной дисперсии:
1.4.Выборочная
дисперсия.
Для
того, чтобы наблюдать рассеяние
количественного признака значений выборки
вокруг своего среднего значения , вводят
сводную характеристику- выборочную
дисперсию.
Выборочной дисперсией
называют
среднее арифметическое квадратов
отклонения наблюдаемых значений признака
от их среднего значения
.
Если все
значения признака выборки различны, то
если же все значения имеют
частоты n1, n2,…,nk, то
Для
характеристики рассеивания значений
признака выборки вокруг своего среднего
значения пользуются сводной
характеристикой — средним квадратическим
отклонением.
Выборочным средним
квадратическим отклоненим называют
квадратный корень из выборочной дисперсии:
Вычисление
дисперсии- выборочной или генеральной,
можно упростить, используя формулу:
Замечание:
если выборка представлена интервальным
вариационным рядом, то за xi
принимают середины частичных интервалов.
1.5.Исправленная
дисперсия.
Выборочная
дисперсия является смещенной оценкой
генеральной дисперсии, т.е. математическое
ожидание выборочной дисперсии не равно
оцениваемой генеральной дисперсии, а равно
Для
исправления выборочной дисперсии
достаточно умножить ее на дробь
получим
исправленную
дисперсию S2. Исправленная дисперсия
является несмещенной оценкой.
В
качестве оценки генеральной дисперсии
принимают исправленную дисперсию.
Для
оценки среднего квадратического
генеральной совокупности используют исправленное среднее
квадратическое отклонение
Замечание:
формулы для вычисления выборочной
дисперсии и исправленной дисперсии
отличаются только знаменателями. При
достаточно больших n
выборочная и исправленная дисперсии мало
отличаются, поэтому на практике
исправленной дисперсией пользуются, если n<30.
Вычислим выборочные характеристики по
выборкам, рассмотренным в
лекции 12 пункт 3.1.(дискретный вариационный
ряд и пункт 3.2.(интервальный вариационный
ряд).
Пример
1. Для
дискретного вариационного ряда:
Среднее
выборочное
Выборочная
дисперсия
Выборочное
среднее квадратическое отклонение
Исправленная
дисперсия
Пример2.
Для интервального вариационного ряда:
За хi примем середины частичных
интервалов:
Для
вычисления выборочной дисперсии
воспользуемся формулой
Выборочное
среднее квадратическое отклонение :
2.
Интервальные
оценки параметров распределения.
Интервальной
называют оценку, которая определяется
двумя числами—концами интервала.
Интервальные оценки позволяют установить
точность и надежность оценок .
Пусть найденная по данным
выборки статистическая характеристика Q* служит оценкой
неизвестного параметра Q. Будем считать Q
постоянным числом (Q может быть и случайной
величиной). Ясно, что Q* тем точнее
определяет параметр Q, чем меньше
абсолютная величина разности |Q—
Q*|. Другими словами, если d>0
и |Q- Q*| <d , то чем
меньше
d
, тем оценка точнее.
Таким
образом, положительное число d характеризует
точность оценки.
Однако статистические
методы не позволяют категорически
утверждать, что оценка Q*
удовлетворяет неравенству |Q- Q*| <d;
можно лишь говорить о
вероятности g,
с которой это неравенство
осуществляется.
Надежностью
(доверительной вероятностью)
оценки
называют вероятность g , с
которой осуществляется неравенство |Q—Q*
| <d .
Обычно
надежность оценки задается наперед, причем
в качестве g берут
число, близкое к единице. Наиболее часто
задают надежность,
равную 0,95; 0,99 и 0,999.
Пусть
вероятность того, что, |Q- Q*| <d равна g:
P(|Q-
Q*| <d)= g.
Заменив
неравенство равносильным ему двойным
неравенством получим:
Р [Q* —d< Q < Q* +d] = g
Это соотношение следует понимать
так: вероятность того, что интервал Q* — d<
Q
< Q* +d заключает
в себе (покрывает) неизвестный параметр Q,
равна g.
Интервал (Q* — d
Q* +d) называется
доверительным интервалом , который
покрывает неизвестный параметр с
надежностью g.
2.1.Интервальные
оценки параметров нормального
распределения.
2.1.1.
Доверительный интервал для оценки
математического ожидания при известном
s.
Пусть количественный признак
генеральной совокупности распределен
нормально. Известно среднее квадратическое
отклонение этого
распределения —s. Требуется
оценить математическое ожидание а
по выборочной средней. Найдем
доверительный интервал, покрывающий а
с надежностью g.
Выборочную среднюю будем
рассматривать как случайную величину ( она
изменяется от выборки к
выборке), выборочные значения признака- как
одинаково распределенные независимые СВ с
математическим ожиданием каждой а
и средним квадратическим отклонением s. Примем
без доказательства, что если величина Х
распределена нормально, то и выборочная
средняя тоже распределена нормально с
параметрами
.
Потребуем,
чтобы выполнялось равенство
Заменив
Х и s, получим
получим
Задача
решена. Число t
находят по таблице функции Лапласа Ф(х).
Пример1.
СВХ распределена нормально и s
=3. Найти доверительный
интервал для оценки математического
ожидания по выборочным средним, если n
= 36 и задана надежность g
=0,95.
Из
соотношения 2Ф(t)= 0,95 ,
откуда Ф(t) = 0,475 по таблице найдем t
: t
=1,96. Точность оценки
Доверительный
интервал
.
Пример2.
Найти минимальный объем выборки, который
обеспечивает заданную точность d =0,3 и
надежность g = 0,975, если
СВХ распределена нормально и s =1,2.
Из равенства
выразим
n:
,
подставим
значения и получим минимльный объем
выборки n ~
81.
2.1.2.
Доверительный интервал для оценки
математического ожидания при неизвестном
s.
Т.к.
мы не знакомы с законами распределения СВ,
которые используются при выводе
формулы, то примем ее без доказательства.
В
качестве неизвестного параметра
s
используют
исправленную дисперсию s2
. Заменяя s на
s, t на величину tg.
Значение
этой величины зависит от надежности
g и объема
выборки n и определяется
по » Таблице значений tg.«
Итак :
и
доверительный интервал имеет вид
Пример1.
Найти доверительный интервал для оценки
математического ожидания с надежностью 0,95,
если объем выборки n =16, среднее выборочное и
исправленная дисперсия соответственно
равны 20,2 и 0,8.
По
таблице приложения найдем tg
по заданной
надежности g =0,95 и n=
16: tg
=2,13. Подставим
в формулу s =0,8 и
tg
=2,13
, вычислим границы доверительного интевала:
,
откуда
получим доверительный интервал (19,774; 20,626)
Смысл
полученного результата: если взять 100
различных выборок, то в 95 из них
математическое ожидание будет находится в
пределах данного интервала, а в 5 из них- нет.
Пример2.
Измеряют диаметры 25 корпусов
электродвигателей. Получены выборочные
характеристики
Необходимо
найти вероятность
(надежность) того, что
—
является доверительным интервалом оценки
математического ожидания при нормальном
распределении.
Из
условия задачи найдем точность d,
составив и решив систему:
Откуда d =10.
Из
равенства
выразим
,
откуда
tg =3,125.
По таблице для найденного
tg и
n=
25 находим g
=0,99.
2.1.3.
Доверительный интервал для оценки
дисперсии и среднего квадратического
отклонения.
Требуется
оценить неизвестную генеральную дисперсию
и генеральное среднее квадратическое
отклонение по исправленной дисперсии, т.е.
найти доверительные интервалы, покрывающие
параметры D и s с заданной надежностью
g.
Потребуем
выполнения соотношения
.
Раскроем
модуль и получим двойное неравенство:
.
Преобразуем:
.
Обозначим
d/s
= q (величина
q
находится по «Таблице значений q»и зависит
от надежности и объема выборки),
тогда доверительный
интервал для оценки генерального среднего
квадратического отклонения имеет вид:
.
Замечание
: Так как s >0, то
если q
>1 , левая граница интервала равна 0:
0<
s
< s ( 1 + q ).
Пример1.
По выборке объема n
= 25 найдено «исправленное» среднее
квадратическое отклонение s
=
0,8. Найти
доверительный интервал, покрывающий генеральное
среднее квадратическое отклонение с
надежностью 0,95.
По
таблице приложения по данным : g
= 0,95; n =25 ,
находим q = 0,32.
Искомый
доверительный интервал 0,8(1- 0,32)< s
< 0,8(1+ 0,32) или
0,544<s
<0,056.
Пример2.
По выборке объема n = 10
найдено s = 0,16. Найти доверительный
интервал, покрывающий генеральное среднее
квадратическое отклонение с надежностью
0,999.
q( n=10, g
=0,999) =
1,8>0.
Искомый
доверительный интервал
0< s <0,16(1+1,8) или 0<
s <0,448.
Так
как дисперсия есть квадрат среднего
квадратического отклонения, то
доверительный интервал, покрывающий
генеральную дисперсию с заданной
надежностью g, имеет вид:
2.2.
Интервальная оценка
вероятности биноминального распределения
по относительной частоте.
Найдем
доверительный интервал для оценки
вероятности по относительной частоте,
используя формулу:
Если
n
достаточно велико и р не очень близка к нулю
и единице, то можно считать, что
относительная частота распределена
приближенно по нормальному закону, причем
М(W)= р.
Заменив Х на относительную частоту ,
математическое ожидание — на вероятность,
получим равенство:
Приступим к
построению доверительного интервала (р1,
р2), который с надежностью g
покрывает
оцениваемый параметр р
Потребуем, чтобы с надежностью g
выполнялось соотношение указанное выше
равенство:
Заменив
,
получим:
Таким образом,
с надежностью g выполняется
неравенство (чтобы получить рабочую
формулу, случайную величину W
заменим неслучайной наблюдаемой
относительной частотой w
и подставим 1- р
вместо q):
Учитывая,
что вероятность р
неизвестна, решим это неравенство
относительно р.
Допустим, что w > р. Тогда
Обе
части неравенства положительны; возведя
их в квадрат, получим равносильное
квадратное неравенство относительно р:
Дискриминант
трехчлена положительный, поэтому корни
действительные и различные:
меньший
корень
больший
корень:
Замечание1:
При больших значениях n
, пренебрегая слагаемыми
,и
учитывая
получим
приближенные формулы для границ
доверительного интервала :
Пример1.
Производят независимые испытания с
одинаковой и неизвестной вероятностью
появления события А в каждом испытании.
Найти доверительный интервал для оценки
вероятности с надежностью 0,95, если в 80
испытаниях событие А появилось 16 раз.
По
условию n =80, m=16,
g =0,95. Относительная
частота
.
Из
соотношения Ф(t)=0,95/2
= 0,475 по таблице находим t = 1,96. Т.к. n<100,
то используем точные формулы, получим :
р1= 0,128, р2= 0,299.
Замечание 2: Если n
мало, то используем для определения концов
доверительного интервала вероятности
события при биноминальном распределении
«Таблицу доверительных границ р1 и р2«. Значения р1 и р2
находят в зависимости от n
и m.
Пример.
В пяти независимых испытаниях событие А
произошло 3 раза. Найти с надежностью 0,95
интервальную оценку для вероятности
события А в единичном испытании.
По
условию задачи n=5, m=3.
Имеет место схема повторных испытаний.
Используя таблицу, находим доверительный
интервал : 0,147<p<0,947.
Контрольные
вопросы
1.
Определение статистической оценки
неизвестного параметра.
2.
Какая оценка называется точечной?
3.
Каким требованиям должны удовлетворять
статистические оценки?
4.
Сформулировать определения
генеральной средней и генеральной
дисперсии.
5.
Записать выражения для вычисления
выборочной средней, выборочной дисперсии и
исправленной дисперсии. Какая из этих
оценок не является несмещенной?
6.
Методики вычисления границ
доверительного интервала
для оценки математического ожидания
нормально распределенной СВ при известном
и неизвестном
s.
7.
Методика вычисления границ
доверительного интервала для оценки
среднего квадратического отклонения
нормально распределенной СВ.
8.
Доверительный интервал вероятности
биноминального распределения по
относительной частоте при больших n , при n<100.
3.Объясните тот факт, что интенсивность перехода может быть величиной как неотрицательной, так и отрицательной. На каких местах в матрице интенсивностей стоят отрицательные элементы, и почему?
4.Как по интенсивности перехода приближённо рассчитать вероятность перехода из
состояния i в состояние j за малое время ∆t ? Рассмотрите раздельно случаи i ≠ j и i = j .
5.Охарактеризуйте систему уравнений Колмогорова для марковского процесса с непрерывным временем и запишите её в матричном виде..
6.Как выглядит условие стационарности марковского процесса с непрерывным временем в матричном виде?
СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ КОЛИЧЕСТВЕННОГО ПРИЗНАКА.
ТОЧЕЧНОЕ И ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ ГЕНЕРАЛЬНЫХ ХАРАКТЕРИСТИК ПО ВЫБОРОЧНЫМ ДАННЫМ
Гистограмма частот. Свойства точечных оценок. Построение доверительного интервала
для оценки математического ожидания случайной величины
Время на выполнение и защиту – 2 часа
Цель работы:
1)изучение метода группировки статистических данных в интервальный ряд для построения гистограмм;
2)анализ свойств точечных статистических оценок;
3)изучение метода доверительных интервалов;
4)изучение ряда функций Excel и Mathcad.
Начальные понятия статистического метода
Целью статистических исследований являются научные и практические выводы об изучаемых явлениях и процессах. Однако статистический метод исследований не занимается глубоким индивидуальным изучением объектов. Его сутью является систематизация, обработка, анализ и использование так называемых статистических данных. Последние представляют собой информацию о том, сколько объектов изучаемой совокупности обладают определёнными (качественными или количественными) признаками. Сами объекты при этом «обезличиваются».
Изучение совокупности однородных объектов относительно некоторого качественного или количественного признака начинается со сбора статистических данных. В зависимости от степени охвата объектов обследование совокупности (наблюдение) может быть сплошным или выборочным. При сплошном наблюдении производится регистрация значения признака для каждого объекта генеральной (т. е. полной) совокупности. При выборочном обследовании из ге-
91
неральной совокупности выделяется выборочная совокупность (выборка). Объ-
ёмом выборки называется число её объектов.
Выборочный метод применяется тогда, когда проведение сплошного обследования нецелесообразно (в том числе, и по причинам экономического характера) или вообще невозможно.
Свойство выборки представлять характеристики генеральной совокупности называется репрезентативностью (по-русски – представительностью). Для того чтобы выборка была репрезентативной, желательно обеспечить случайность отбора объектов. Это означает, что включение каждого объекта генеральной совокупности в выборку должно быть равновероятным.
Другим требованием является достаточно большой объём выборки – на-
столько большой, чтобы обеспечить нужную точность. Например, с целью прогнозирования результатов предстоящих выборов опрашивается примерно 2000 человек, живущих в разных городах и населённых пунктах. При таком объёме выборки статистическая погрешность составляет 2 процентных пункта. Оценивание статистической погрешности может быть выполнено методом доверительных интервалов, изучаемым в данной работе.
Статистическое распределение количественного признака. Гистограмма
Наблюдаемые значения количественного признака (синоним понятия «случайная величина») X , которые в дальнейшем обозначаются символом xi ,
называются вариантами. Последовательность вариантов, записанная в возрастающем порядке, называется вариационным рядом.
Число появлений ni варианта xi в выборке называется выборочной час-
тотой этого варианта; ∑ni = n , где n − объём выборки.
i
Статистическим распределением выборки называется перечень вариантов и их частот (или относительных частот wi = ni / n , где ∑wi =1).
i
Как известно из теории вероятностей, случайные величины (количественные признаки) могут относиться к дискретному или непрерывному типу. Если признак дискретный, то в качестве графика распределения строится полигон частот или полигон относительных частот – ломаная линия, соединяющая точки ( xi , ni ) или ( xi , wi ) .
При большом числе вариантов или непрерывном характере признака вместо отдельных значений используются интервалы, для каждого из которых определяется частота попадания значений признака.
Графическим изображением статистического распределения в случае интервального ряда является гистограмма частот – ступенчатая фигура, каждый прямоугольник которой имеет в качестве основания частичный интервал, а в качестве высоты – соответствующую плотность частоты ni / h , где h – длина
92
интервала. Площадь отдельных столбиков численно равна соответствующим частотам, а площадь всей гистограммы равна объёму совокупности n .
Иногда строится гистограмма относительных частот. В этом случае по оси ординат откладываются значения wi / h. Площадь такой гистограммы
будет равна единице (аналогия: условие нормировки вероятности непрерывной случайной величины).
|
Пример 19. Для определения средней дальности грузоперевозок прове- |
|||||||||||||||
|
Табл. 7.1. Исходные данные |
дено наблюдение за 20 грузами. В табл. |
||||||||||||||
|
7.1 приведена масса каждого груза (в |
|||||||||||||||
|
к примеру 19 |
|||||||||||||||
|
тоннах) и дальность перевозки (в км). |
|||||||||||||||
|
Масса |
Дальность |
||||||||||||||
|
25 |
792 |
Требуется обработать и проанализиро- |
|||||||||||||
|
36 |
432 |
вать данные наблюдений (конкретные |
|||||||||||||
|
32 |
235 |
пункты исследования будут |
уточнены |
||||||||||||
|
27 |
1030 |
ниже). На первом этапе отобразить ста- |
|||||||||||||
|
44 |
1425 |
||||||||||||||
|
тистическое |
распределение грузов по |
||||||||||||||
|
21 |
727 |
||||||||||||||
|
дальности с помощь таблицы и графика. |
|||||||||||||||
|
38 |
159 |
||||||||||||||
|
22 |
980 |
Сгруппируем грузы по дальности |
|||||||||||||
|
12 |
407 |
(без учёта масс перевезённых грузов), |
|||||||||||||
|
23 |
225 |
введя |
интервалы |
0-200, |
200-400, 400- |
||||||||||
|
45 |
527 |
600, 600-800, 800-1000, 1000-1200, 1200- |
|||||||||||||
|
48 |
1299 |
||||||||||||||
|
1400, 1400-1600 км. |
|||||||||||||||
|
57 |
290 |
||||||||||||||
|
Составим статистический ряд рас- |
|||||||||||||||
|
10 |
64 |
||||||||||||||
|
13 |
1216 |
пределения непрерывного количествен- |
|||||||||||||
|
15 |
895 |
ного признака в виде табл. 7.2, опреде- |
|||||||||||||
|
43 |
774 |
лив частоту попадания в каждый интер- |
|||||||||||||
|
23 |
545 |
вал. |
|||||||||||||
|
30 |
755 |
||||||||||||||
|
40 |
958 |
||||||||||||||
|
Табл. 7.2. Статистический ряд распределения |
|||||||||||||||
|
непрерывного количественного признака (пример 19) |
|||||||||||||||
|
Интервал, i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|||||||
|
Начало интервала, |
|||||||||||||||
|
xi−1 |
0 |
200 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
|||||||
|
2 |
|||||||||||||||
|
Конец интервала, |
|||||||||||||||
|
xi+1 |
200 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
|||||||
|
2 |
|||||||||||||||
|
Середина интервала, |
|||||||||||||||
|
xi |
100 |
300 |
500 |
700 |
900 |
1100 |
1300 |
1500 |
|||||||
|
Частота, ni |
2 |
3 |
4 |
4 |
3 |
1 |
2 |
1 |
|||||||
|
Для построения гистограммы частот необходимо для каждого интервала |
|||||||||||||||
|
рассчитать значение величины ni |
/ h ( h = 200– длина интервала). Результат изо- |
||||||||||||||
|
бражён на рис. 7.1. |
93

|
частоты |
0,025 |
||||
|
0,02 |
|||||
|
0,015 |
|||||
|
плотность |
|||||
|
0,01 |
|||||
|
0,005 |
|||||
|
0 |
|||||
|
100 |
300 |
500 |
700 |
900 1100 1300 1500 |
|
|
дальность перевозок, км |
Рис. 7.1. Гистограмма, построенная поданным примера 19
Выборочная средняя
Если данные не сгруппированы и частоты вариантов не определены, то выборочная средняя определяется по формуле
|
1 |
n |
||||
|
x = |
∑xi . |
(7.1) |
|||
|
n i=1 |
|||||
|
В том случае, когда определены частоты ni |
всех значений количественно- |
го признака, они выступают в качестве весов:
|
1 |
k |
||||
|
= |
∑ni xi , |
(7.2) |
|||
|
x |
|||||
|
n i=1 |
где k – число различных вариантов в выборке.
Пример 19 (продолжение). Средняя выборочная дальность перевозок может быть вычислена разными способами. Сначала не будем учитывать массы грузов. Выборочная средняя, рассчитанная по несгруппированным данным
(табл. 7.1) по формуле (7.1), равна x = 686.75. Расчёт по сгруппированным данным (табл. 7.2) с использованием в формуле (7.2) в качестве вариантов xi
|
середин интервалов даёт значение |
x |
= 690. |
||||||
|
Если же учёт масс грузов (mi ) |
необходим, то для определения средней |
|||||||
|
дальности перевозок следует применить формулу |
||||||||
|
n |
||||||||
|
∑xi mi |
||||||||
|
= |
i=1 |
, |
(7.3) |
|||||
|
x |
||||||||
|
n |
||||||||
|
∑mi |
i=1
94

где массы являются аналогом частот (сравните с (7.2)). Числитель (7.3) представляет собой грузооборот (тонно-километры), знаменатель – объём перевозок
|
n |
n |
||
|
(тонны). В нашем случае ∑xi mi = 425567 , |
∑mi = 604 , x = 704.58. |
||
|
i=1 |
i=1 |
Понятие оценки. Несмещённость и состоятельность оценок
Как уже говорилось в описании работы 3, выборочная средняя – среднее значение случайной величины, вычисленное по всем наблюдавшимся значениям – служит статистической оценкой математического ожидания. Уточним это понятие. Определённая числовая характеристика, полученная по выборочным данным, называется статистикой или оценкой. Если оценка даётся одним числом, то она называется точечной.
Математическое ожидание случайной величины X можно записать как
M (X ) = 1 ∑k Ni xi , N i=1
где Ni – генеральные частоты, а N = ∑Ni – объём генеральной совокупности.
Выражение, стоящее в правой части равенства, есть не что иное, как генеральная средняя, т. е. средняя, определённая по всей генеральной совокупности. Таким образом, математическое ожидание признака равно генеральной средней этого признака (неслучайная величина, константа). Напротив, выборочная средняя есть случайная величина
X= 1 ∑n X i ,
n i=1
где каждое слагаемое X i (значение количественного признака в i-м наблюдении) имеет то же распределение, что и X. Можно показать, что
M (X ) = M (X ) ,
т.е. математическое ожидание выборочной средней равно генеральной средней. Практический смысл этого положения: мы имеем возможность оценивать генеральную среднюю по выборке значений признака, причём эта оценка не содержит так называемой систематической ошибки. Иначе говоря, отклонение выборочной средней от генеральной средней есть случайная величина с нулевым математическим ожиданием. (Необходимо подчеркнуть, что всё сказанное относится только к такой выборочной средней, которая рассчитывается по ре-
презентативной выборке).
Величина Θ* называется несмещённой оценкой величины Θ, если M (Θ* ) = Θ (математическое ожидание оценки равно оцениваемой величине). Напротив, если M (Θ* ) ≠ Θ, то Θ* называется смещённой оценкой величины Θ.
95

Таким образом, выборочная средняя – несмещённая оценка генеральной средней.
Согласно теореме Бернулли (см. описание работы 1), выборочные относительные частоты отдельных значений признака ( wi = ni / n ) сходятся по веро-
ятности к генеральным относительным частотам при n →∞:
|
ni |
→ P(X = x |
) = |
Ni |
, n → ∞. |
|
n |
p |
i |
N |
|
Значит, и выборочная средняя с ростом объёма выборки сходится по вероятности к генеральной средней:
X →M (X ), n → ∞.
p
Оценка, сходящаяся по вероятности к истинному значению оцениваемой величины при n →∞, называется состоятельной:
Θ* →Θ, n →∞.
p
Итак, выборочная средняя является состоятельной оценкой генеральной средней.
Характеристики вариации количественного признака: дисперсия и среднеквадратическое отклонение
Пусть известно статистическое распределение некоторого количествен-
ного признака. Выборочной дисперсией D и выборочным среднеквадратиче-
ским отклонением σ количественного признака X называются величины, определяемые формулами:
|
k |
k |
||||
|
∑(xi − x)2 ni |
∑xi2ni |
2 |
= x2 − x2 ; |
||
|
D = i=1 |
= i=1 |
n |
− x |
||
|
n |
(7.4) |
||||
|
σ |
= |
D. |
|||
Здесь, как и прежде, k − это либо число различных вариантов в выборке, либо число интервалов (для интервального ряда). Если данные вообще не сгруппированы, то все ni ≡1, а суммирование проводится от 1 до n.
Об этих величинах уже шла речь в работе 3 (см. формулу (3.7)).
Можно показать, что выборочная дисперсия является смещённой (в сред-
|
нем заниженной) оценкой генеральной дисперсии D(X ): |
|||
|
M (D) = |
n −1 |
D(X ) . |
(7.5) |
|
n |
96

Исправленной выборочной дисперсией называется величина
|
s 2 = |
n |
D , |
(7.6) |
||
|
n −1 |
|||||
|
являющаяся несмещённой оценкой генеральной дисперсии. Величина s = |
s 2 |
называется исправленным среднеквадратическим отклонением.
Считается, что при достаточно больших n (больше чем 30) отношение выборочного и исправленного среднеквадратических отклонений близко к 1, и различием между ними пренебрегают.
Пример 19 (продолжение). Если рассчитать выборочную дисперсию (7.4) по несгруппированным данным (приняв все ni ≡1) без учёта масс грузов, то
получим следующее значение: D =148775. (Без использования компьютера этот расчёт окажется весьма трудоёмким!) Исправленная дисперсия
s 2 = 1920 D =156606 , исправленное среднеквадратическое отклонение s = 395.7 .
Понятие интервальной оценки.
Точность и надёжность оценки, доверительный интервал
Если точечная оценка – это оценка одним числом, то интервальная оцен-
ка указывает два числа – начало и конец интервала, который (с определённой вероятностью) заключает в себе оцениваемую величину.
Пусть Θ* – найденная по выборке точечная оценка неизвестного параметра Θ, с вероятностью γ удовлетворяющая условию Θ − Θ* < δ , то есть
P(Θ − Θ* <δ )=γ .
Тогда:
−полуширина δ симметричного относительно Θ* интервала называется
точностью оценки;
−вероятность γ называется доверительной вероятностью или надёж-
ностью оценки;
− интервал (Θ* −δ, Θ* +δ) , который заключает в себе (покрывает) неизвестный параметр Θ с вероятностью γ , называют доверительным интервалом.
Интервальная оценка генеральной средней (математического ожидания) нормального распределения при известном генеральном среднеквадратическом отклонении
Пусть количественный признак X распределён в генеральной совокупности нормально с известным генеральным среднеквадратическим отклонением σ . По выборке объёма n определена выборочная средняя x . Тогда доверительный интервал для оценки генеральной средней a с надёжностью γ имеет вид
97

|
x − tσ |
< a < x + tσ |
, |
(7.7) |
|
n |
n |
где t определяется выбранной надёжностью оценки. Таким образом, центр доверительного интервала находится в точке x , а полуширина доверительного
интервала составляет δ = tσn .
Величина t определяется равенством γ 
пласа (4.14), таблица значений которой помещена в приложении 2. В частности, для задаваемых обычно значений надёжности имеем:
|
γ |
0.95 |
0.99 |
0.999 |
|
t |
1.96 |
2.57 |
3.3 |
При заданной надёжности с увеличением объёма выборки уменьшается величина δ , т.е. улучшается точность интервальной оценки. При постоянном объёме выборки с ростом требуемой надёжности растёт коэффициент t и, следовательно, ухудшается точность интервальной оценки. Невозможно одновременно повышать надёжность и улучшать точность интервальной оценки, если не увеличивать объём выборки.
Пример 19 (продолжение). В данном случае генеральное среднеквадратическое отклонение σ нам неизвестно. Построение доверительного интервала для оценки генеральной средней при неизвестном σ описано в следующем пункте. Однако для выборок достаточного объёма ( n > 30) обычно принимают неизвестное σ равным выборочному среднеквадратическому отклонению или, что почти то же самое, исправленному среднеквадратическому отклонению s . В нашем случае, правда, n = 20 , но мы используем допущение σ = s в качестве грубого приближения.
Зададим надежность γ = 0,99 и по приложению 2 найдём t = 2,57 . Если теперь грубо принять σ = s , то получим полуширину доверительного интервала δ = 227,9 . Воспользовавшись средним значением x , найденным для несгруппированных данных без учёта масс грузов, получим доверительный интервал для средней дальности перевозок
686,8 −227,9 < a < 686,8 +227,9 458,9 < a <914,7 .
Интервальная оценка генеральной средней нормального распределения при неизвестном генеральном среднеквадратическом отклонении (малая выборка)
В этом случае строим доверительный интервал в виде
|
x − t(γ, n)s |
< a < x + t(γ, n)s |
, |
(7.8) |
|
n |
n |
98
где s – исправленное среднеквадратическое отклонение. Величину t(γ, n) называют коэффициентом Стьюдента. Таблица значений t(γ, n) помещена в приложении 3.
Коэффициент Стьюдента t(γ,n) отличается от величины t , определённой из уравнения γ 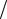
Пример 19 (окончание). Использованное в предыдущем пункте приближение (σ = s ) годится только для больших выборок ( n > 30). В нашем случае
правильнее считать генеральное среднеквадратическое отклонение неизвестным и строить доверительный интервал с помощью коэффициента Стьюдента. Для надёжности γ = 0,99 , согласно приложению 3, t(0,99; 20) = 2,86. Тогда
δ = 253,1. Доверительный интервал для средней дальности перевозок
686,8 −253,1< a <686,8 +253,1 433,7 < a <939,9
оказался шире, чем в предыдущем пункте, т.к. значение генерального среднеквадратического отклонения оценивалось по выборке объёма 20, а не полагалось известным.
Задание для лабораторной работы
Задание 7.1. Воспроизвести на компьютере все этапы анализа примера 19, а именно:
7.1.1.Найти минимальное и максимальное значения дальности в выборке. Построить гистограмму частот для дальности перевозок (без учёта масс перевезённых грузов), введя интервалы 0–200, 200–400, 400–600, 600– 800, 800–1000, 1000– 1200, 1200–1400, 1400–1600.
7.1.2.Найти точечную оценку средней дальности перевозок: а) с учётом масс грузов (по несгруппированным данным);
б) без учёта масс грузов (по несгруппированным и сгруппированным данным).
7.1.3.Найти точечную несмещённую оценку дисперсии дальности перевозок в генеральной совокупности и исправленное отклонение без учёта масс грузов (по несгруппированным данным).
7.1.4.Считая генеральное среднеквадратическое отклонение известным (приняв его равным исправленному среднеквадратическому отклонению), а распределение – нормальным, построить доверительный интервал для средней дальности перевозок с надёжностью 0,99.
7.1.5.Считая генеральное среднеквадратическое отклонение неизвестным, построить доверительный интервал для средней дальности перевозок с надёжностью 0,99.
99
Инструкция по выполнению задания в Excel
Введём в ячейку A1 заголовок: Статистическое изучение дальности гру-
зоперевозок. Запишем в ячейку A3 заголовок Масса, а в ячейки А4:А23 – массы грузов. Поместим в ячейке B3 заголовок Дальн., а в ячейках В4:В23 – значения дальности каждой перевозки. В ячейке A24 введём Надёжн., а в ячейке B24 – заданное значение надёжности интервальной оценки (0,99).
7.1.1. Найдём минимальное и максимальное значения дальности в выборке. Конечно, когда данных немного, это можно сделать и «вручную». Однако, как правило, статистические ряды довольно велики, и имеет смысл воспользоваться функциями рабочего листа. Введём в ячейку D4 текст Минимальная дальность, а в ячейку D5 – Максимальная дальность. Активизируем ячейку H4
и помещаем в неё функцию МИН (Статистические). В качестве аргумента введём диапазон B4:B23. Результатом в ячейке H4 будет число 64.
Теперь поместите в ячейку H5 максимальное значение из того же списка. Единственное отличие в ваших действиях будет заключаться в том, что вместо функции МИН вы должны использовать функцию МАКС. Результатом будет число 1425.
Приступим к нахождению частотного распределения дальности перевозок. Введём в ячейках D7, E7 и F7 тексты Нач., Сер., Кон. соответственно, что будет обозначать начала, середины и концы интервалов. Теперь, согласно условию, в диапазоне D8:D15 должны быть введены числа 0, 200, 400, …, 1400, в
диапазоне E8:E15 – числа 100, 300, 500, …, 1500, в диапазоне F8:F15 – числа 200, 400, 600, …, 1600.
Следующий столбец таблицы будет заполнен эмпирическими частотами, для нахождения которых мы воспользуемся одной из функций рабочего листа.
В ячейке G7 введём текст Частота. Выделим ячейки G8:G15. Щёлкнем на кнопке Вставка функций. В открывшемся диалоговом окне выберем: Статистические, ЧАСТОТА. Мы выбрали функцию, которая, «возвращает распределение частот в виде вертикального массива». Эта функция, в отличие от МИН и МАКС, обязательно должна иметь два аргумента: массив данных и двоичный массив. В первое окно ввода вводим все наблюдавшиеся значения дальности (диапазон B4:B23). Во второе окно ввода – ячейки F8:F15, в которых находятся концы интервалов. В правой части окна появился результат: {2,3,4,4,3,1,2,1,0}. Это и есть искомые частоты. Для того чтобы поместить их в таблицу, щёлкнем на кнопке ОК. В ячейке G8 появилось значение 2, но остальные ячейки столбца остались незаполненными. Дело в том, что результатом обращения к функции ЧАСТОТА является не просто одно число, как это было с функциями МИН или МАКС, а массив (С функциями массива МОБР и МУМНОЖ мы уже встречались в работе 5). Это требует от нас следующих дополнительных действий. Нажмём клавишу [F2], переходя в режим Правка. Теперь нажмём на комбинацию клавиш [CTRL]+[SHIFT] и, не отпуская, на клавишу [ENTER]. Все ячейки G8:G15 должны заполниться числами.
100
Приступим к построению гистограммы частот. тервале необходимо определить плотность частоты ni
Для этого в каждом ин- / h , где h – длина интер-
вала (200). В ячейке H7 введём текст Плотн. Помещаем в ячейку H8 формулу для вычисления плотности частоты внутри 1-го интервала = G8/200. Ячейки H9:H15 заполним с помощью автозаполнения.
В EXCEL существует широкий круг средств графического представления числовых данных. В частности, гистограмма является типом диаграммы, часто используемым в статистике. Выделим в рабочем листе диапазон ячеек, данные из которого должны быть представлены в гистограмме. Удалим название Сер. из ячейки E7 (чтобы программа воспринимала этот столбец как ряд значений аргумента, а не функции). Выделим несмежные диапазоны ячеек: E7:E15 и H7:H15. Для этого придётся после выделения первого диапазона нажать и удерживать кнопку CTRL.
Активизируем кнопку Мастер диаграмм на панели инструментов. На экране появится первое диалоговое окно Мастера диаграмм, в котором можно выбрать тип диаграммы. Мы выберем Гистограмму (обычную) и нажмём кнопку Далее.
Для обработки гистограммы с помощью специальных средств следует активизировать её с помощью двойного щелчка мышью. Форматирование диаграммы может включать в себя вставку или изменение легенды, задание цвета и узора, помещение текста на осях, форматирование осей и т. п. Допустим, что нас не устраивают какие-то элементы графика, например зазор между отдельными столбиками гистограммы. Установив курсор на любом из столбиков, с помощью щелчка правой кнопкой можно открыть контекстное меню и выбрать в нём Формат данных. В диалоговом окне активизируем кнопку Параметры, установим ширину зазора, равную нулю, и щёлкнем на кнопке ОК. Желаемое изменение в график внесено.
Соответствующая гистограмма уже приведена нами на рис. 7.1.
7.1.2.Перейдём к статистическим оценкам. Средняя дальность перевозок
сучётом масс грузов представляет собой частное от деления грузооборота на объём перевозок (7.3). Введем в ячейке D17 текст Грузооборот, а в ячейке H17
–функцию СУММПРОИЗВ (она находится в списке Математические). В качестве аргументов этой функции зададим два массива: масс грузов и дальностей. Результат: 425567 (тонно-километров). В ячейке D18 введем текст Объём перевозок, а в ячейке H18 – функцию СУММ (она находится в том же списке). Результат: 604 (тонны). В ячейке D19 введем текст Ср. дальность (с учётом масс), а в ячейке H19 – формулу, определяющую эту величину (с адресами числителя и знаменателя). Результат: 704.58 (км).
В ячейке D20 введем текст Ср. дальность (без учёта масс), а в ячейке H20 – функцию СРЗНАЧ (она находится в списке Статистические). Её аргументом будет массив дальностей. Результат: 686.75. Более грубый вариант оценки основан на интервальном ряде. В ячейке D21 введем текст Ср. дальность (по сгрупп. данным), а в ячейке H20 – уже знакомую нам функцию СУММПРОИЗВ. В данном случае её аргументами будут следующие два масси-
101
ва: середины интервалов и частόты. Теперь скорректируем формулу в ячейке D21, добавив деление на объём выборки (на 20). Результат: 690 (км).
7.1.3.В ячейке D22 введем текст Исправленная дисперсия, а в ячейке H22
–функцию ДИСП с массивом дальностей в качестве аргумента. Результат: 156606 (км2). Исправленное среднекв. откл. (этот текст введём в ячейке D23) вычисляется как квадратный корень из исправленной дисперсии, но в EXCEL для этой цели существует специальная функция СТАНДОТКЛОН (введите её в ячейке H23). Результат: 395.73 (км). Заметьте, что в работе 3 для вычисления выборочного среднеквадратического отклонения мы использовали другую функцию (СТАНДОТКЛОНП).
7.1.4.Построение интервальной оценки генеральной средней (математического ожидания) можно выполнить с помощью функции ДОВЕРИТ, которая даёт значение полуширины доверительного интервала по считающемуся известным генеральному среднеквадратическому отклонению. Функция
ДОВЕРИТ имеет 3 аргумента: уровень значимости «альфа» (α =1−γ , где γ –
заданное значение надёжности), «стандартное отклонение» (исправленное среднеквадратическое отклонение) и «размер» (объём выборки). В нашем случае α = 0,01, объём выборки составляет 20. Введите текст Полуширина доверит. интерв. в ячейке D24 и функцию =ДОВЕРИТ(1-B24;H23;20) в ячейке H24. Результат: 227.93 (км).
В ячейках D25 и D26 введите текст Нижн. граница доверит. интерв. и
Верхн. граница доверит. интерв. соответственно. Для определения этих границ в ячейке H25 должна быть введена формула =H20-H24, а в ячейке H26 формула =H20+H24. Отметим, что эти формулы можно задать и с помощью функций. Например, мы могли бы использовать для нижней границы доверительного интервала формулу =СРЗНАЧ(…) — ДОВЕРИТ(…), где в скобках должны присутствовать аргументы функций.
7.1.5. Другой вариант построения доверительного интервала для генеральной средней применяется, когда генеральное среднеквадратическое отклонение неизвестно. В этом случае необходимо воспользоваться таблицей коэффициентов Стьюдента (приложение 3), или воспользоваться функцией СТЬЮДРАСПОБР, задавая в качестве «вероятности» величину α =1−γ , в ка-
честве «степеней свободы» – объём выборки, уменьшенный на единицу. Введите значение коэффициента в рабочий лист и завершите выполнение задания самостоятельно. (Для вычисления квадратного корня из объёма выборки воспользуйтесь функцией КОРЕНЬ из списка Математические.)
102
|
A |
B |
C |
D |
E |
F |
G |
H |
|
|
1 |
Статистическое изучение дальности грузоперевозок |
|||||||
|
2 |
||||||||
|
3 |
Масса |
Дальн. |
||||||
|
4 |
25 |
792 |
Минимальная дальность |
64 |
||||
|
5 |
36 |
432 |
Максимальная дальность |
1425 |
||||
|
6 |
32 |
235 |
||||||
|
7 |
27 |
1030 |
Нач. |
Кон. |
Частоты |
Плотн. |
||
|
8 |
44 |
1425 |
0 |
100 |
200 |
2 |
0.01 |
|
|
9 |
21 |
727 |
200 |
300 |
400 |
3 |
0.015 |
|
|
10 |
38 |
159 |
400 |
500 |
600 |
4 |
0.02 |
|
|
11 |
22 |
980 |
600 |
700 |
800 |
4 |
0.02 |
|
|
12 |
12 |
407 |
800 |
900 |
1000 |
3 |
0.015 |
|
|
13 |
23 |
225 |
1000 |
1100 |
1200 |
1 |
0.005 |
|
|
14 |
45 |
527 |
1200 |
1300 |
1400 |
2 |
0.01 |
|
|
15 |
48 |
1299 |
1400 |
1500 |
1600 |
1 |
0.005 |
|
|
16 |
57 |
290 |
||||||
|
17 |
10 |
64 |
Грузооборот |
425567 |
||||
|
18 |
13 |
1216 |
Объём перевозок |
604 |
||||
|
19 |
15 |
895 |
Ср.дальность (с учётом масс |
) |
704.58 |
|||
|
20 |
43 |
774 |
Ср.дальность (без учёта масс) |
686.75 |
||||
|
21 |
23 |
545 |
Ср.дальность по сгрупп. данным |
690 |
||||
|
22 |
30 |
755 |
Исправленная дисперсия |
156606 |
||||
|
23 |
40 |
958 |
Исправленное среднекв. откл. |
395.734 |
||||
|
24 |
Надёжн. |
0.99 |
Полуширина доверит. интерв. (1) |
227,93 |
||||
|
25 |
Нижн. граница доверит. интерв. (1) |
458.82 |
||||||
|
26 |
Верхн. граница доверит. интерв. (1) |
914.68 |
||||||
|
27 |
Коэффициент Стьюдента |
2.86 |
||||||
|
28 |
Полуширина доверит. интерв |
. (2) |
253.078 |
|||||
|
29 |
Нижн. граница доверит. интерв. (2) |
433.672 |
||||||
|
30 |
Верхн. граница доверит. интерв. (2) |
939.828 |
Инструкция по выполнению задания в Mathcad
Присвоим переменной ORIGIN значение, равное 1.
Введём следующие обозначения для вводимых исходных данных и вычисляемых величин:
M – вектор масс грузов;
L – вектор значений дальности каждой перевозки;
γ – заданное значение надёжности интервальной оценки (0,99); Мin – минимальное значение дальности в выборке;
Мax – максимальное значение дальности в выборке; b – вектор, обозначающий границы интервалов;
n – вектор, элементами которого являются частоты, с которыми значения данных попадают в заданные интервалы;
den – вектор плотности частоты;
103
Lam – средняя дальность перевозок с учётом масс грузов; La – средняя дальность перевозок без учёта масс грузов;
Введем исходные данные массы грузов и дальности каждой перевозки, присвоив переменным М и L значения элементов матриц размером 20×1. Переменной nad присвоим значение 0.99 (используя точку, а не запятую).
7.1.1. Найдём минимальное и максимальное значения дальности в выборке. Конечно, когда данных немного, это можно сделать и «вручную». Однако, как правило, статистические ряды довольно велики, и имеет смысл восполь-
зоваться функциями Mathcad max(A, B, C, …) и min(A, B, C, …) категории
Vector and Matrix (Векторы и матрицы), которые возвращают наибольшее и наименьшее из значений A, B, C, … соответственно. В нашем случае в качестве аргументов нужно задать L, а остальные пустые местозаполнители удалить. В результате получим: Min = 64, Max =1425.
Приступим к нахождению частотного распределения дальности перевозок. Введём векторы med, размером 8×1, b – размером 9×1. Согласно условию, в вектор med (середины интервалов) должны быть введены числа 100, 300, 500, …, 1500, в вектор b (границы интервалов) – числа 0, 200, 400, 600, …, 1600.
Для нахождения эмпирических частот используем функцию hist (intvls, data) категории Statistics (Статистика). Эта функция возвращает вектор, элементами которого являются частоты, с которыми значения вектора data попадают в интервалы, заданные параметром intvls. Параметр intvls может быть либо числом интервалов одинаковой длины, либо вектором границ интервалов (см. выше). Обратившись к функции hist (b, L), получим вектор частот n = (2, 3, 4, 4, 3, 1, 2, 1)
Приступим к построению гистограммы частот. Для этого в каждом интервале необходимо определить плотность частоты ni / h , где h – длина интер-
вала (200). Используем для этого вектор den. С помощью дискретных переменных присвоим каждому элементу вектора den соответствующее значение вектора n, деленное на 200.
|
i :=1. .8 |
den |
:= |
ni |
|
i |
200 |
||
Для того чтобы создать график в виде гистограммы нужно сначала по-
строить двумерный график. Для этого щелкните по кнопке 
Затем войдите в диалоговое окно Formatting Currently Selected Graph
(Форматирование) выбранного графика (например, двойным щелчком мыши) и перейдите на вкладку Traces (Графики).
104

|
Установите |
для серии |
данных |
|||||||||||||||||||||||||
|
гистограммы в поле Туре (Тип) эле- |
|||||||||||||||||||||||||||
|
0.02 |
мент списка solidbar (гистограмма) и |
||||||||||||||||||||||||||
|
частоты |
нажмите кнопку ОК. Затем перейдите |
||||||||||||||||||||||||||
|
на вкладку «Подписи» и введите со- |
|||||||||||||||||||||||||||
|
Плотность |
den |
ответствующие подписи |
по |
осям. |
|||||||||||||||||||||||
|
0.01 |
Полученная |
гистограмма |
подобна |
||||||||||||||||||||||||
|
приведенной на рис. 7.2. |
|||||||||||||||||||||||||||
|
7.1.2. Перейдём к статистиче- |
|||||||||||||||||||||||||||
|
0 |
ским оценкам. Средняя дальность пе- |
||||||||||||||||||||||||||
|
ревозок с учётом масс грузов пред- |
|||||||||||||||||||||||||||
|
0 |
500 1000 1500 |
||||||||||||||||||||||||||
|
med |
ставляет собой частное от деления |
||||||||||||||||||||||||||
|
Дальность перевозок, км |
грузооборота |
на |
объём |
перевозок |
|||||||||||||||||||||||
|
Рис. 7.2. Гистограмма частот |
(7.3). Числитель этой формулы мож- |
||||||||||||||||||||||||||
|
но вычислить как скалярное произве- |
|||||||||||||||||||||||||||
дение векторов М и L, знаменатель – как сумму элементов вектора М. Для ввода этой формулы после ввода имени переменной Lam и знака присваивания нажмите клавишу « / » (деление), появится шаблон дроби. В числителе щелкните
по кнопке 
(сумма компонент вектора) и в появившемся шаблоне вставьте имя вектора М . Результат: 704.581(км).
Определим среднюю дальность перевозок без учёта масс. Для этого используем функцию mean(A, B, C, …) категории Statistics (Статистика). Присвоив переменной La значение mean(L), получим результат: 686.75.
Более грубый вариант оценки основан на интервальном ряде. Определим среднюю дальность перевозок по сгруппированным данным с помощью формулы (7.2), используя в качестве вариантов количественного признака середины интервалов. Действуем подобно тому, как выше рассчитывали среднюю дальность с учётом масс грузов, только теперь в числителе дроби будет находиться скалярное произведение векторов med и n, а в знаменателе будет стоять объём выборки (20). Результат: 690 (км).
7.1.3.Найдем исправленную дисперсию, присвоив переменной S2 значе-
ние функции Var(A, B, C, …) категории Statistics (Статистика) с массивом дальностей в качестве аргумента. Результат: 156606 (км2). Исправленное среднеквадратическое отклонение s можно вычислить как квадратный корень из исправленной дисперсии, или с помощью встроенной функции Stdev(A, B, C, …) категории Statistics (Статистика) с тем же массивом дальностей в качестве аргумента. Результат в обоих случаях получим 395.73 (км).
7.1.4.Построение интервальной оценки генеральной средней (математического ожидания) можно выполнить с помощью формулы (7.7)
105
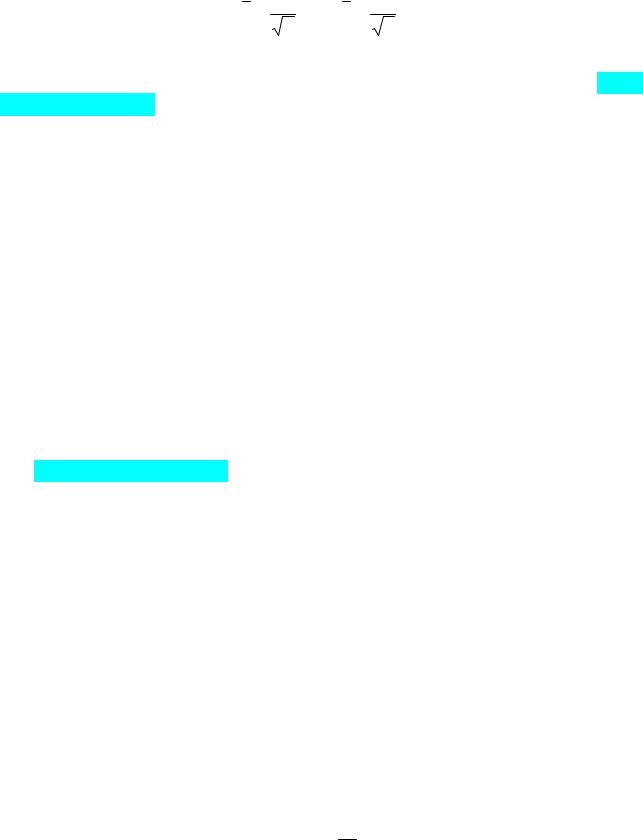
x − tσn < a < x + tσn ,
считая генеральное среднеквадратическое отклонение известным. Величину t можно вычислить с помощью функции qnorm(p, mu, sigma) категории Probability Distribution (Распределение вероятностей), считая случайную величину нормированной (со средним mu =0 и среднеквадратическим отклонением sigma
=1). При этом р нужно взять равным p =1 − α2 . В нашем случае α = 0,01, значит
p = 0,995. Получим коэффициент t=2,576. Нижнюю и верхнюю границы доверительного интервала найдите самостоятельно, используя формулу (7.7). Для
вычисления квадратного корня из объёма выборки воспользуйтесь кнопкой 
686.75 −227.93 < a < 686.75 + 227.93 458.82 < a < 914.68.
7.1.5. Другой вариант построения доверительного интервала для генеральной средней применяется, когда генеральное среднеквадратическое отклонение неизвестно. В этом случае необходимо воспользоваться таблицей коэффициентов Стьюдента (приложение 3), или воспользоваться функцией qt(p, d) категории Probability Distribution (Распределение вероятностей), которая возвращает обратное кумулятивное распределение Стьюдента со степенями свободы d. При этом р задается так же как в предыдущем случае, в качестве «степеней свободы» возьмем объём выборки, уменьшенный на единицу. Получим коэффициент ts=2,861. Завершите выполнение задания самостоятельно, используя формулу (7.8). Для вычисления квадратного корня из объёма выборки воспользуйтесь
кнопкой 
Дополнительное задание
Задание 7.2. Проведите следующий опыт. Генерируйте выборку объёма n =5 случайных чисел, равномерно распределённых в интервале ( 0, 1).
Вычислите выборочную дисперсию D и исправленную дисперсию s2 непосредственно по формулам (7.4) и (7.6) или с помощью предназначенных для этого функций и сравните эти оценки с генеральной дисперсией равномерного распределения, которая в данном случае равна
D(x) =121 .
106
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В данной статье я расскажу о том, как найти среднеквадратическое отклонение. Этот материал крайне важен для полноценного понимания математики, поэтому репетитор по математике должен посвятить его изучению отдельный урок или даже несколько. В этой статье вы найдёте ссылку на подробный и понятный видеоурок, в котором рассказано о том, что такое среднеквадратическое отклонение и как его найти.
Среднеквадратическое отклонение дает возможность оценить разброс значений, полученных в результате измерения какого-то параметра. Обозначается символом (греческая буква «сигма»).
Формула для расчета довольно проста. Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии. Так что теперь вы должны спросить: “А что же такое дисперсия?”
Что такое дисперсия
Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.
Чтобы найти дисперсию последовательно проведите следующие вычисления:
- Определите среднее (простое среднее арифметическое ряда значений).
- Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
- Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).
Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.
| Порода собаки | Рост в миллиметрах |
| Ротвейлер | 600 |
| Бульдог | 470 |
| Такса | 170 |
| Пудель | 430 |
| Мопс | 300 |
Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.
Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:
Среднее мм.
Итак, среднее (среднеарифметическое) составляет 394 мм.
Теперь нужно определить отклонение роста каждой из собак от среднего:
Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:
Дисперсия мм2.
Таким образом, дисперсия составляет 21704 мм2.
Как найти среднеквадратическое отклонение
Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:
мм (округлено до ближайшего целого значения в мм).
Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).
Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.
То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.
Что такое стандартное отклонение
Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.
Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.
Если есть значений, то:
Все остальные расчеты производятся аналогично, в том числе и определение среднего.
Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:
Дисперсия выборки = мм2.
При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).
Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.
Примечание. Почему именно квадраты разностей?
Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:
.
Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?
.
На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:
.
Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.
А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).
Для первого примера получится:
.
Для второго примера получится:
.
Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.
Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.
И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.
О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич
Cumulative probability of a normal distribution with expected value 0 and standard deviation 1
In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values.[1] A low standard deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range.
Standard deviation may be abbreviated SD, and is most commonly represented in mathematical texts and equations by the lower case Greek letter σ (sigma), for the population standard deviation, or the Latin letter s, for the sample standard deviation.
The standard deviation of a random variable, sample, statistical population, data set, or probability distribution is the square root of its variance. It is algebraically simpler, though in practice less robust, than the average absolute deviation.[2][3] A useful property of the standard deviation is that, unlike the variance, it is expressed in the same unit as the data.
The standard deviation of a population or sample and the standard error of a statistic (e.g., of the sample mean) are quite different, but related. The sample mean’s standard error is the standard deviation of the set of means that would be found by drawing an infinite number of repeated samples from the population and computing a mean for each sample. The mean’s standard error turns out to equal the population standard deviation divided by the square root of the sample size, and is estimated by using the sample standard deviation divided by the square root of the sample size. For example, a poll’s standard error (what is reported as the margin of error of the poll), is the expected standard deviation of the estimated mean if the same poll were to be conducted multiple times. Thus, the standard error estimates the standard deviation of an estimate, which itself measures how much the estimate depends on the particular sample that was taken from the population.
In science, it is common to report both the standard deviation of the data (as a summary statistic) and the standard error of the estimate (as a measure of potential error in the findings). By convention, only effects more than two standard errors away from a null expectation are considered «statistically significant», a safeguard against spurious conclusion that is really due to random sampling error.
When only a sample of data from a population is available, the term standard deviation of the sample or sample standard deviation can refer to either the above-mentioned quantity as applied to those data, or to a modified quantity that is an unbiased estimate of the population standard deviation (the standard deviation of the entire population).
Basic examples[edit]
Population standard deviation of grades of eight students[edit]
Suppose that the entire population of interest is eight students in a particular class. For a finite set of numbers, the population standard deviation is found by taking the square root of the average of the squared deviations of the values subtracted from their average value. The marks of a class of eight students (that is, a statistical population) are the following eight values:
These eight data points have the mean (average) of 5:
First, calculate the deviations of each data point from the mean, and square the result of each:
The variance is the mean of these values:
and the population standard deviation is equal to the square root of the variance:
This formula is valid only if the eight values with which we began form the complete population. If the values instead were a random sample drawn from some large parent population (for example, they were 8 students randomly and independently chosen from a class of 2 million), then one divides by 7 (which is n − 1) instead of 8 (which is n) in the denominator of the last formula, and the result is 

Standard deviation of average height for adult men[edit]
If the population of interest is approximately normally distributed, the standard deviation provides information on the proportion of observations above or below certain values. For example, the average height for adult men in the United States is about 70 inches, with a standard deviation of around 3 inches. This means that most men (about 68%, assuming a normal distribution) have a height within 3 inches of the mean (67–73 inches) – one standard deviation – and almost all men (about 95%) have a height within 6 inches of the mean (64–76 inches) – two standard deviations. If the standard deviation were zero, then all men would be exactly 70 inches tall. If the standard deviation were 20 inches, then men would have much more variable heights, with a typical range of about 50–90 inches. Three standard deviations account for 99.73% of the sample population being studied, assuming the distribution is normal or bell-shaped (see the 68–95–99.7 rule, or the empirical rule, for more information).
Definition of population values[edit]
Let μ be the expected value (the average) of random variable X with density f(x):
The standard deviation σ of X is defined as
which can be shown to equal
Using words, the standard deviation is the square root of the variance of X.
The standard deviation of a probability distribution is the same as that of a random variable having that distribution.
Not all random variables have a standard deviation. If the distribution has fat tails going out to infinity, the standard deviation might not exist, because the integral might not converge. The normal distribution has tails going out to infinity, but its mean and standard deviation do exist, because the tails diminish quickly enough. The Pareto distribution with parameter ![{displaystyle alpha in (1,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/782b1d598278b0238ee817c658744e8a7ed3a06e)
Discrete random variable[edit]
In the case where X takes random values from a finite data set x1, x2, …, xN, with each value having the same probability, the standard deviation is
or, by using summation notation,
If, instead of having equal probabilities, the values have different probabilities, let x1 have probability p1, x2 have probability p2, …, xN have probability pN. In this case, the standard deviation will be
Continuous random variable[edit]
The standard deviation of a continuous real-valued random variable X with probability density function p(x) is
and where the integrals are definite integrals taken for x ranging over the set of possible values of the random variable X.
In the case of a parametric family of distributions, the standard deviation can be expressed in terms of the parameters. For example, in the case of the log-normal distribution with parameters μ and σ2, the standard deviation is
Estimation[edit]
One can find the standard deviation of an entire population in cases (such as standardized testing) where every member of a population is sampled. In cases where that cannot be done, the standard deviation σ is estimated by examining a random sample taken from the population and computing a statistic of the sample, which is used as an estimate of the population standard deviation. Such a statistic is called an estimator, and the estimator (or the value of the estimator, namely the estimate) is called a sample standard deviation, and is denoted by s (possibly with modifiers).
Unlike in the case of estimating the population mean, for which the sample mean is a simple estimator with many desirable properties (unbiased, efficient, maximum likelihood), there is no single estimator for the standard deviation with all these properties, and unbiased estimation of standard deviation is a very technically involved problem. Most often, the standard deviation is estimated using the corrected sample standard deviation (using N − 1), defined below, and this is often referred to as the «sample standard deviation», without qualifiers. However, other estimators are better in other respects: the uncorrected estimator (using N) yields lower mean squared error, while using N − 1.5 (for the normal distribution) almost completely eliminates bias.
Uncorrected sample standard deviation[edit]
The formula for the population standard deviation (of a finite population) can be applied to the sample, using the size of the sample as the size of the population (though the actual population size from which the sample is drawn may be much larger). This estimator, denoted by sN, is known as the uncorrected sample standard deviation, or sometimes the standard deviation of the sample (considered as the entire population), and is defined as follows:[6]
where 

This is a consistent estimator (it converges in probability to the population value as the number of samples goes to infinity), and is the maximum-likelihood estimate when the population is normally distributed.[7] However, this is a biased estimator, as the estimates are generally too low. The bias decreases as sample size grows, dropping off as 1/N, and thus is most significant for small or moderate sample sizes; for 
Corrected sample standard deviation[edit]
If the biased sample variance (the second central moment of the sample, which is a downward-biased estimate of the population variance) is used to compute an estimate of the population’s standard deviation, the result is
Here taking the square root introduces further downward bias, by Jensen’s inequality, due to the square root’s being a concave function. The bias in the variance is easily corrected, but the bias from the square root is more difficult to correct, and depends on the distribution in question.
An unbiased estimator for the variance is given by applying Bessel’s correction, using N − 1 instead of N to yield the unbiased sample variance, denoted s2:
This estimator is unbiased if the variance exists and the sample values are drawn independently with replacement. N − 1 corresponds to the number of degrees of freedom in the vector of deviations from the mean, 
Taking square roots reintroduces bias (because the square root is a nonlinear function which does not commute with the expectation, i.e. often ![{textstyle E[{sqrt {X}}]neq {sqrt {E[X]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3dbf273b716d2bdaac95f31a6890ded4645d8709)
As explained above, while s2 is an unbiased estimator for the population variance, s is still a biased estimator for the population standard deviation, though markedly less biased than the uncorrected sample standard deviation. This estimator is commonly used and generally known simply as the «sample standard deviation». The bias may still be large for small samples (N less than 10). As sample size increases, the amount of bias decreases. We obtain more information and the difference between 

Unbiased sample standard deviation[edit]
For unbiased estimation of standard deviation, there is no formula that works across all distributions, unlike for mean and variance. Instead, s is used as a basis, and is scaled by a correction factor to produce an unbiased estimate. For the normal distribution, an unbiased estimator is given by s/c4, where the correction factor (which depends on N) is given in terms of the Gamma function, and equals:
This arises because the sampling distribution of the sample standard deviation follows a (scaled) chi distribution, and the correction factor is the mean of the chi distribution.
An approximation can be given by replacing N − 1 with N − 1.5, yielding:
The error in this approximation decays quadratically (as 1/N2), and it is suited for all but the smallest samples or highest precision: for N = 3 the bias is equal to 1.3%, and for N = 9 the bias is already less than 0.1%.
A more accurate approximation is to replace N − 1.5 above with N − 1.5 + 1/8(N − 1).[8]
For other distributions, the correct formula depends on the distribution, but a rule of thumb is to use the further refinement of the approximation:
where γ2 denotes the population excess kurtosis. The excess kurtosis may be either known beforehand for certain distributions, or estimated from the data.[9]
Confidence interval of a sampled standard deviation[edit]
The standard deviation we obtain by sampling a distribution is itself not absolutely accurate, both for mathematical reasons (explained here by the confidence interval) and for practical reasons of measurement (measurement error). The mathematical effect can be described by the confidence interval or CI.
To show how a larger sample will make the confidence interval narrower, consider the following examples:
A small population of N = 2 has only one degree of freedom for estimating the standard deviation. The result is that a 95% CI of the SD runs from 0.45 × SD to 31.9 × SD; the factors here are as follows:
where 
With k = 1, q0.025 = 0.000982 and q0.975 = 5.024. The reciprocals of the square roots of these two numbers give us the factors 0.45 and 31.9 given above.
A larger population of N = 10 has 9 degrees of freedom for estimating the standard deviation. The same computations as above give us in this case a 95% CI running from 0.69 × SD to 1.83 × SD. So even with a sample population of 10, the actual SD can still be almost a factor 2 higher than the sampled SD. For a sample population N = 100, this is down to 0.88 × SD to 1.16 × SD. To be more certain that the sampled SD is close to the actual SD we need to sample a large number of points.
These same formulae can be used to obtain confidence intervals on the variance of residuals from a least squares fit under standard normal theory, where k is now the number of degrees of freedom for error.
Bounds on standard deviation[edit]
For a set of N > 4 data spanning a range of values R, an upper bound on the standard deviation s is given by s = 0.6R.[10]
An estimate of the standard deviation for N > 100 data taken to be approximately normal follows from the heuristic that 95% of the area under the normal curve lies roughly two standard deviations to either side of the mean, so that, with 95% probability the total range of values R represents four standard deviations so that s ≈ R/4. This so-called range rule is useful in sample size estimation, as the range of possible values is easier to estimate than the standard deviation. Other divisors K(N) of the range such that s ≈ R/K(N) are available for other values of N and for non-normal distributions.[11]
Identities and mathematical properties[edit]
The standard deviation is invariant under changes in location, and scales directly with the scale of the random variable. Thus, for a constant c and random variables X and Y:
The standard deviation of the sum of two random variables can be related to their individual standard deviations and the covariance between them:
where 

The calculation of the sum of squared deviations can be related to moments calculated directly from the data. In the following formula, the letter E is interpreted to mean expected value, i.e., mean.
The sample standard deviation can be computed as:
For a finite population with equal probabilities at all points, we have
which means that the standard deviation is equal to the square root of the difference between the average of the squares of the values and the square of the average value.
See computational formula for the variance for proof, and for an analogous result for the sample standard deviation.
Interpretation and application[edit]
Example of samples from two populations with the same mean but different standard deviations. Red population has mean 100 and SD 10; blue population has mean 100 and SD 50.
A large standard deviation indicates that the data points can spread far from the mean and a small standard deviation indicates that they are clustered closely around the mean.
For example, each of the three populations {0, 0, 14, 14}, {0, 6, 8, 14} and {6, 6, 8, 8} has a mean of 7. Their standard deviations are 7, 5, and 1, respectively. The third population has a much smaller standard deviation than the other two because its values are all close to 7. These standard deviations have the same units as the data points themselves. If, for instance, the data set {0, 6, 8, 14} represents the ages of a population of four siblings in years, the standard deviation is 5 years. As another example, the population {1000, 1006, 1008, 1014} may represent the distances traveled by four athletes, measured in meters. It has a mean of 1007 meters, and a standard deviation of 5 meters.
Standard deviation may serve as a measure of uncertainty. In physical science, for example, the reported standard deviation of a group of repeated measurements gives the precision of those measurements. When deciding whether measurements agree with a theoretical prediction, the standard deviation of those measurements is of crucial importance: if the mean of the measurements is too far away from the prediction (with the distance measured in standard deviations), then the theory being tested probably needs to be revised. This makes sense since they fall outside the range of values that could reasonably be expected to occur, if the prediction were correct and the standard deviation appropriately quantified. See prediction interval.
While the standard deviation does measure how far typical values tend to be from the mean, other measures are available. An example is the mean absolute deviation, which might be considered a more direct measure of average distance, compared to the root mean square distance inherent in the standard deviation.
Application examples[edit]
The practical value of understanding the standard deviation of a set of values is in appreciating how much variation there is from the average (mean).
Experiment, industrial and hypothesis testing[edit]
Standard deviation is often used to compare real-world data against a model to test the model.
For example, in industrial applications the weight of products coming off a production line may need to comply with a legally required value. By weighing some fraction of the products an average weight can be found, which will always be slightly different from the long-term average. By using standard deviations, a minimum and maximum value can be calculated that the averaged weight will be within some very high percentage of the time (99.9% or more). If it falls outside the range then the production process may need to be corrected. Statistical tests such as these are particularly important when the testing is relatively expensive. For example, if the product needs to be opened and drained and weighed, or if the product was otherwise used up by the test.
In experimental science, a theoretical model of reality is used. Particle physics conventionally uses a standard of «5 sigma» for the declaration of a discovery. A five-sigma level translates to one chance in 3.5 million that a random fluctuation would yield the result. This level of certainty was required in order to assert that a particle consistent with the Higgs boson had been discovered in two independent experiments at CERN,[12] also leading to the declaration of the first observation of gravitational waves.[13]
Weather[edit]
As a simple example, consider the average daily maximum temperatures for two cities, one inland and one on the coast. It is helpful to understand that the range of daily maximum temperatures for cities near the coast is smaller than for cities inland. Thus, while these two cities may each have the same average maximum temperature, the standard deviation of the daily maximum temperature for the coastal city will be less than that of the inland city as, on any particular day, the actual maximum temperature is more likely to be farther from the average maximum temperature for the inland city than for the coastal one.
Finance[edit]
In finance, standard deviation is often used as a measure of the risk associated with price-fluctuations of a given asset (stocks, bonds, property, etc.), or the risk of a portfolio of assets[14] (actively managed mutual funds, index mutual funds, or ETFs). Risk is an important factor in determining how to efficiently manage a portfolio of investments because it determines the variation in returns on the asset and/or portfolio and gives investors a mathematical basis for investment decisions (known as mean-variance optimization). The fundamental concept of risk is that as it increases, the expected return on an investment should increase as well, an increase known as the risk premium. In other words, investors should expect a higher return on an investment when that investment carries a higher level of risk or uncertainty. When evaluating investments, investors should estimate both the expected return and the uncertainty of future returns. Standard deviation provides a quantified estimate of the uncertainty of future returns.
For example, assume an investor had to choose between two stocks. Stock A over the past 20 years had an average return of 10 percent, with a standard deviation of 20 percentage points (pp) and Stock B, over the same period, had average returns of 12 percent but a higher standard deviation of 30 pp. On the basis of risk and return, an investor may decide that Stock A is the safer choice, because Stock B’s additional two percentage points of return is not worth the additional 10 pp standard deviation (greater risk or uncertainty of the expected return). Stock B is likely to fall short of the initial investment (but also to exceed the initial investment) more often than Stock A under the same circumstances, and is estimated to return only two percent more on average. In this example, Stock A is expected to earn about 10 percent, plus or minus 20 pp (a range of 30 percent to −10 percent), about two-thirds of the future year returns. When considering more extreme possible returns or outcomes in future, an investor should expect results of as much as 10 percent plus or minus 60 pp, or a range from 70 percent to −50 percent, which includes outcomes for three standard deviations from the average return (about 99.7 percent of probable returns).
Calculating the average (or arithmetic mean) of the return of a security over a given period will generate the expected return of the asset. For each period, subtracting the expected return from the actual return results in the difference from the mean. Squaring the difference in each period and taking the average gives the overall variance of the return of the asset. The larger the variance, the greater risk the security carries. Finding the square root of this variance will give the standard deviation of the investment tool in question.
Population standard deviation is used to set the width of Bollinger Bands, a technical analysis tool. For example, the upper Bollinger Band is given as 
Financial time series are known to be non-stationary series, whereas the statistical calculations above, such as standard deviation, apply only to stationary series. To apply the above statistical tools to non-stationary series, the series first must be transformed to a stationary series, enabling use of statistical tools that now have a valid basis from which to work.
Geometric interpretation[edit]
To gain some geometric insights and clarification, we will start with a population of three values, x1, x2, x3. This defines a point P = (x1, x2, x3) in R3. Consider the line L = {(r, r, r) : r ∈ R}. This is the «main diagonal» going through the origin. If our three given values were all equal, then the standard deviation would be zero and P would lie on L. So it is not unreasonable to assume that the standard deviation is related to the distance of P to L. That is indeed the case. To move orthogonally from L to the point P, one begins at the point:
whose coordinates are the mean of the values we started out with.
|
Derivation of |
|---|
|
The line L is to be orthogonal to the vector from M to P. Therefore: |
A little algebra shows that the distance between P and M (which is the same as the orthogonal distance between P and the line L) 
Chebyshev’s inequality[edit]
An observation is rarely more than a few standard deviations away from the mean. Chebyshev’s inequality ensures that, for all distributions for which the standard deviation is defined, the amount of data within a number of standard deviations of the mean is at least as much as given in the following table.
| Distance from mean | Minimum population |
|---|---|
 |
50% |
 |
75% |
 |
89% |
 |
94% |
 |
96% |
 |
97% |
 |
 [15] [15]
|
 |

|
Rules for normally distributed data[edit]
Dark blue is one standard deviation on either side of the mean. For the normal distribution, this accounts for 68.27 percent of the set; while two standard deviations from the mean (medium and dark blue) account for 95.45 percent; three standard deviations (light, medium, and dark blue) account for 99.73 percent; and four standard deviations account for 99.994 percent. The two points of the curve that are one standard deviation from the mean are also the inflection points.
The central limit theorem states that the distribution of an average of many independent, identically distributed random variables tends toward the famous bell-shaped normal distribution with a probability density function of
where μ is the expected value of the random variables, σ equals their distribution’s standard deviation divided by n1⁄2, and n is the number of random variables. The standard deviation therefore is simply a scaling variable that adjusts how broad the curve will be, though it also appears in the normalizing constant.
If a data distribution is approximately normal, then the proportion of data values within z standard deviations of the mean is defined by:
where 
If a data distribution is approximately normal then about 68 percent of the data values are within one standard deviation of the mean (mathematically, μ ± σ, where μ is the arithmetic mean), about 95 percent are within two standard deviations (μ ± 2σ), and about 99.7 percent lie within three standard deviations (μ ± 3σ). This is known as the 68–95–99.7 rule, or the empirical rule.
For various values of z, the percentage of values expected to lie in and outside the symmetric interval, CI = (−zσ, zσ), are as follows:
| Confidence interval |
Proportion within | Proportion without | |
|---|---|---|---|
| Percentage | Percentage | Fraction | |
| 0.318639σ | 25% | 75% | 3 / 4 |
| 0.674490σ | 50% | 50% | 1 / 2 |
| 0.977925σ | 66.6667% | 33.3333% | 1 / 3 |
| 0.994458σ | 68% | 32% | 1 / 3.125 |
| 1σ | 68.2689492% | 31.7310508% | 1 / 3.1514872 |
| 1.281552σ | 80% | 20% | 1 / 5 |
| 1.644854σ | 90% | 10% | 1 / 10 |
| 1.959964σ | 95% | 5% | 1 / 20 |
| 2σ | 95.4499736% | 4.5500264% | 1 / 21.977895 |
| 2.575829σ | 99% | 1% | 1 / 100 |
| 3σ | 99.7300204% | 0.2699796% | 1 / 370.398 |
| 3.290527σ | 99.9% | 0.1% | 1 / 1000 |
| 3.890592σ | 99.99% | 0.01% | 1 / 10000 |
| 4σ | 99.993666% | 0.006334% | 1 / 15787 |
| 4.417173σ | 99.999% | 0.001% | 1 / 100000 |
| 4.5σ | 99.9993204653751% | 0.0006795346249% | 1 / 147159.5358 6.8 / 1000000 |
| 4.891638σ | 99.9999% | 0.0001% | 1 / 1000000 |
| 5σ | 99.9999426697% | 0.0000573303% | 1 / 1744278 |
| 5.326724σ | 99.99999% | 0.00001% | 1 / 10000000 |
| 5.730729σ | 99.999999% | 0.000001% | 1 / 100000000 |
| 6σ | 99.9999998027% | 0.0000001973% | 1 / 506797346 |
| 6.109410σ | 99.9999999% | 0.0000001% | 1 / 1000000000 |
| 6.466951σ | 99.99999999% | 0.00000001% | 1 / 10000000000 |
| 6.806502σ | 99.999999999% | 0.000000001% | 1 / 100000000000 |
| 7σ | 99.9999999997440% | 0.000000000256% | 1 / 390682215445 |
Relationship between standard deviation and mean[edit]
The mean and the standard deviation of a set of data are descriptive statistics usually reported together. In a certain sense, the standard deviation is a «natural» measure of statistical dispersion if the center of the data is measured about the mean. This is because the standard deviation from the mean is smaller than from any other point. The precise statement is the following: suppose x1, …, xn are real numbers and define the function:
Using calculus or by completing the square, it is possible to show that σ(r) has a unique minimum at the mean:
Variability can also be measured by the coefficient of variation, which is the ratio of the standard deviation to the mean. It is a dimensionless number.
Standard deviation of the mean[edit]
Often, we want some information about the precision of the mean we obtained. We can obtain this by determining the standard deviation of the sampled mean. Assuming statistical independence of the values in the sample, the standard deviation of the mean is related to the standard deviation of the distribution by:
where N is the number of observations in the sample used to estimate the mean. This can easily be proven with (see basic properties of the variance):
(Statistical independence is assumed.)
hence
Resulting in:
In order to estimate the standard deviation of the mean σmean it is necessary to know the standard deviation of the entire population σ beforehand. However, in most applications this parameter is unknown. For example, if a series of 10 measurements of a previously unknown quantity is performed in a laboratory, it is possible to calculate the resulting sample mean and sample standard deviation, but it is impossible to calculate the standard deviation of the mean. However, one can estimate the standard deviation of the entire population from the sample, and thus obtain an estimate for the standard error of the mean.
Rapid calculation methods[edit]
The following two formulas can represent a running (repeatedly updated) standard deviation. A set of two power sums s1 and s2 are computed over a set of N values of x, denoted as x1, …, xN:
Given the results of these running summations, the values N, s1, s2 can be used at any time to compute the current value of the running standard deviation:
Where N, as mentioned above, is the size of the set of values (or can also be regarded as s0).
Similarly for sample standard deviation,
In a computer implementation, as the two sj sums become large, we need to consider round-off error, arithmetic overflow, and arithmetic underflow. The method below calculates the running sums method with reduced rounding errors.[17] This is a «one pass» algorithm for calculating variance of n samples without the need to store prior data during the calculation. Applying this method to a time series will result in successive values of standard deviation corresponding to n data points as n grows larger with each new sample, rather than a constant-width sliding window calculation.
For k = 1, …, n:
where A is the mean value.
Note: Q1 = 0 since k − 1 = 0 or x1 = A1.
Sample variance:
Population variance:
Weighted calculation[edit]
When the values xi are weighted with unequal weights wi, the power sums s0, s1, s2 are each computed as:
And the standard deviation equations remain unchanged. s0 is now the sum of the weights and not the number of samples N.
The incremental method with reduced rounding errors can also be applied, with some additional complexity.
A running sum of weights must be computed for each k from 1 to n:
and places where 1/σ is used above must be replaced by wi/Wn:
In the final division,
and
or
where n is the total number of elements, and n′ is the number of elements with non-zero weights.
The above formulas become equal to the simpler formulas given above if weights are taken as equal to one.
History[edit]
The term standard deviation was first used in writing by Karl Pearson in 1894, following his use of it in lectures.[18][19] This was as a replacement for earlier alternative names for the same idea: for example, Gauss used mean error.[20]
Standard deviation index[edit]
The standard deviation index (SDI) is used in external quality assessments, particularly for medical laboratories. It is calculated as:[21]
Higher dimensions[edit]
The standard deviation ellipse (green) of a two-dimensional normal distribution
In two dimensions, the standard deviation can be illustrated with the standard deviation ellipse (see Multivariate normal distribution § Geometric interpretation).
See also[edit]
- 68–95–99.7 rule
- Accuracy and precision
- Algorithms for calculating variance
- Chebyshev’s inequality An inequality on location and scale parameters
- Coefficient of variation
- Cumulant
- Deviation (statistics)
- Distance correlation Distance standard deviation
- Error bar
- Geometric standard deviation
- Mahalanobis distance generalizing number of standard deviations to the mean
- Mean absolute error
- Pooled variance
- Propagation of uncertainty
- Percentile
- Raw data
- Reduced chi-squared statistic
- Robust standard deviation
- Root mean square
- Sample size
- Samuelson’s inequality
- Six Sigma
- Standard error
- Standard score
- Yamartino method for calculating standard deviation of wind direction
References[edit]
- ^ Bland, J.M.; Altman, D.G. (1996). «Statistics notes: measurement error». BMJ. 312 (7047): 1654. doi:10.1136/bmj.312.7047.1654. PMC 2351401. PMID 8664723.
- ^ Gauss, Carl Friedrich (1816). «Bestimmung der Genauigkeit der Beobachtungen». Zeitschrift für Astronomie und Verwandte Wissenschaften. 1: 187–197.
- ^ Walker, Helen (1931). Studies in the History of the Statistical Method. Baltimore, MD: Williams & Wilkins Co. pp. 24–25.
- ^ Weisstein, Eric W. «Bessel’s Correction». MathWorld.
- ^ «Standard Deviation Formulas». www.mathsisfun.com. Retrieved 21 August 2020.
- ^ Weisstein, Eric W. «Standard Deviation». mathworld.wolfram.com. Retrieved 21 August 2020.
- ^ «Consistent estimator». www.statlect.com. Retrieved 10 October 2022.
- ^ Gurland, John; Tripathi, Ram C. (1971), «A Simple Approximation for Unbiased Estimation of the Standard Deviation», The American Statistician, 25 (4): 30–32, doi:10.2307/2682923, JSTOR 2682923
- ^ «Standard Deviation Calculator». PureCalculators. 11 July 2021. Retrieved 14 September 2021.
- ^ Shiffler, Ronald E.; Harsha, Phillip D. (1980). «Upper and Lower Bounds for the Sample Standard Deviation». Teaching Statistics. 2 (3): 84–86. doi:10.1111/j.1467-9639.1980.tb00398.x.
- ^ Browne, Richard H. (2001). «Using the Sample Range as a Basis for Calculating Sample Size in Power Calculations». The American Statistician. 55 (4): 293–298. doi:10.1198/000313001753272420. JSTOR 2685690. S2CID 122328846.
- ^ «CERN experiments observe particle consistent with long-sought Higgs boson | CERN press office». Press.web.cern.ch. 4 July 2012. Archived from the original on 25 March 2016. Retrieved 30 May 2015.
- ^ LIGO Scientific Collaboration, Virgo Collaboration (2016), «Observation of Gravitational Waves from a Binary Black Hole Merger», Physical Review Letters, 116 (6): 061102, arXiv:1602.03837, Bibcode:2016PhRvL.116f1102A, doi:10.1103/PhysRevLett.116.061102, PMID 26918975, S2CID 124959784
- ^ «What is Standard Deviation». Pristine. Retrieved 29 October 2011.
- ^ Ghahramani, Saeed (2000). Fundamentals of Probability (2nd ed.). New Jersey: Prentice Hall. p. 438. ISBN 9780130113290.
- ^ Eric W. Weisstein. «Distribution Function». MathWorld. Wolfram. Retrieved 30 September 2014.
- ^ Welford, B. P. (August 1962). «Note on a Method for Calculating Corrected Sums of Squares and Products». Technometrics. 4 (3): 419–420. CiteSeerX 10.1.1.302.7503. doi:10.1080/00401706.1962.10490022.
- ^ Dodge, Yadolah (2003). The Oxford Dictionary of Statistical Terms. Oxford University Press. ISBN 978-0-19-920613-1.
- ^ Pearson, Karl (1894). «On the dissection of asymmetrical frequency curves». Philosophical Transactions of the Royal Society A. 185: 71–110. Bibcode:1894RSPTA.185…71P. doi:10.1098/rsta.1894.0003.
- ^ Miller, Jeff. «Earliest Known Uses of Some of the Words of Mathematics».
- ^ Harr, Robert R. (2012). Medical laboratory science review. Philadelphia: F. A. Davis Co. p. 236. ISBN 978-0-8036-3796-2. OCLC 818846942.
External links[edit]
- «Quadratic deviation», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- «Standard Deviation Calculator»



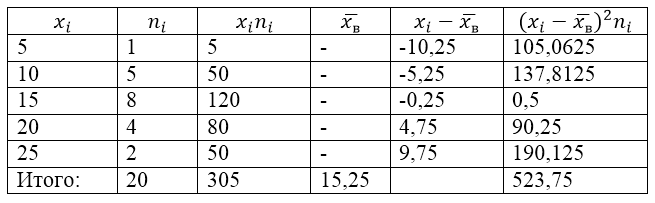










![Rendered by QuickLaTeX.com [ begin{array}{l} 1: 600-394 = 206 \ 2: 470-394 = 76 \ 3: 170-394 = -224\ 4: 430-394 = 36\ 5: 300-394 = -94 end{array} ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-3916a3ccd97d909589dfe1dabb970af0_l3.png)







![{displaystyle mu equiv operatorname {E} [X]=int _{-infty }^{+infty }xf(x),mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb2a61843da0d05619c0dd691dbf3fe315b395ad)
![{displaystyle sigma equiv {sqrt {operatorname {E} left[(X-mu )^{2}right]}}={sqrt {int _{-infty }^{+infty }(x-mu )^{2}f(x),mathrm {d} x}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3a1cfef8ad100fbcae387d9581763f0b389bbc3)
![{textstyle {sqrt {operatorname {E} left[X^{2}right]-(operatorname {E} [X])^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2dd8d466c3ecb05713377fefcb7e7f787b29ce7)
![{displaystyle sigma ={sqrt {{frac {1}{N}}left[(x_{1}-mu )^{2}+(x_{2}-mu )^{2}+cdots +(x_{N}-mu )^{2}right]}},{text{ where }}mu ={frac {1}{N}}(x_{1}+cdots +x_{N}),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/827beb1be760eed3cb07b20d29f01d326f728071)















![{displaystyle sigma (X)={sqrt {operatorname {E} left[(X-operatorname {E} [X])^{2}right]}}={sqrt {operatorname {E} left[X^{2}right]-(operatorname {E} [X])^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3ab12089bd2027790ef060ff7cc2ec05ae2021f)
![{displaystyle s(X)={sqrt {frac {N}{N-1}}}{sqrt {operatorname {E} left[(X-operatorname {E} [X])^{2}right]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/702e9da21c721697e6e81932bf8b7443028f7d6d)







cdot (x_{1}-ell ,x_{2}-ell ,x_{3}-ell )&=0\[4pt]r(x_{1}-ell +x_{2}-ell +x_{3}-ell )&=0\[4pt]rleft(sum _{i}x_{i}-3ell right)&=0\[4pt]sum _{i}x_{i}-3ell &=0\[4pt]{frac {1}{3}}sum _{i}x_{i}&=ell \[4pt]{bar {x}}&=ell end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51526a39caa45834866ae2dc4bb3ed262ba7fbe0)


![{displaystyle {text{Proportion}}leq x={frac {1}{2}}left[1+operatorname {erf} left({frac {x-mu }{sigma {sqrt {2}}}}right)right]={frac {1}{2}}left[1+operatorname {erf} left({frac {z}{sqrt {2}}}right)right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19a6aad42f0352f855f10ad517460517ae848e4f)























