Как найти истинное ускорение

Скорость и ускорение



Скорость точки

В предыдущей статье движение тела или точки определено, как изменение положения в пространстве с течением времени. Для того чтобы более полно охарактеризовать качественные и количественные стороны движения введены понятия скорости и ускорения.

Скорость – это кинематическая мера движения точки, характеризующая быстроту изменения ее положения в пространстве.
Скорость является векторной величиной, т. е. она характеризуется не только модулем (скалярной составляющей), но и направлением в пространстве.

Как известно из физики, при равномерном движении скорость может быть определена длиной пути, пройденного за единицу времени: v = s/t = const (предполагается, что начало отсчета пути и времени совпадают).
При прямолинейном движении скорость постоянна и по модулю, и по направлению, а ее вектор совпадает с траекторией.

Единица скорости в системе СИ определяется соотношением длина/время, т. е. м/с.

Очевидно, что при криволинейном движении скорость точки будет меняться по направлению.
Для того, чтобы установить направление вектора скорости в каждый момент времени при криволинейном движении, разобьем траекторию на бесконечно малые участки пути, которые можно считать (вследствие их малости) прямолинейными. Тогда на каждом участке условная скорость v_п такого прямолинейного движения будет направлена по хорде, а хорда, в свою очередь, при бесконечном уменьшении длины дуги (Δs стремится к нулю), будет совпадать с касательной к этой дуге.
Из этого следует, что при криволинейном движении вектор скорости в каждый момент времени совпадает с касательной к траектории (рис. 1а). Прямолинейное движение можно представить, как частный случай криволинейного движения по дуге, радиус которой стремится к бесконечности (траектория совпадает с касательной).

При неравномерном движении точки модуль ее скорости с течением времени меняется.
Представим себе точку, движение которой задано естественным способом уравнением s = f(t).

Если за небольшой промежуток времени Δt точка прошла путь Δs, то ее средняя скорость равна:

vср = Δs/Δt.

Средняя скорость не дает представления об истинной скорости в каждый данный момент времени (истинную скорость иначе называют мгновенной). Очевидно, что чем меньше промежуток времени, за который определяется средняя скорость, тем ближе ее значение будет к мгновенной скорости.

Истинная (мгновенная) скорость есть предел, к которому стремится средняя скорость при Δt, стремящемся к нулю:

v = lim v_ср при t→0 или v = lim (Δs/Δt) = ds/dt.

Таким образом, числовое значение истинной скорости равно v = ds/dt.
Истинная (мгновенная) скорость при любом движении точки равна первой производной координаты (т. е. расстояния от начала отсчета перемещения) по времени.

При Δt стремящемся к нулю, Δs тоже стремится к нулю, и, как мы уже выяснили, вектор скорости будет направлен по касательной (т. е. совпадает с вектором истинной скорости v). Из этого следует, что предел вектора условной скорости v_п, равный пределу отношения вектора перемещения точки к бесконечно малому промежутку времени, равен вектору истинной скорости точки.

***

Ускорение точки в прямолинейном движении

В общем случае движение точки с изменяющейся во времени скоростью называют ускоренным, при этом считая ускорение, вызывающее уменьшение скорости, отрицательным. Иногда движение, в котором скорость с течением времени уменьшается, называют замедленным.

Ускорение есть кинематическая мера изменения скорости точки во времени. Другими словами — ускорение — это скорость изменения скорости.
Как и скорость, ускорение является величиной векторной, т. е. характеризуется не только модулем, но и направлением в пространстве.

При прямолинейном движении вектор скорости всегда совпадает с траекторией и поэтому вектор изменения скорости тоже совпадает с траекторией.

Из курса физики известно, что ускорение представляет собой изменение скорости в единицу времени. Если за небольшой промежуток времени Δt скорость точки изменилась на Δv, то среднее ускорение за данный промежуток времени составило: а_ср = Δv/Δt.

Среднее ускорение не дает представление об истинной величине изменения скорости в каждый момент времени. При этом очевидно, что чем меньше рассматриваемый промежуток времени, во время которого произошло изменение скорости, тем ближе значение ускорения будет к истинному (мгновенному).
Отсюда определение: истинное (мгновенное) ускорение есть предел, к которому стремится среднее ускорение при Δt, стремящемся к нулю:

а = lim а_ср при t→0     или     lim Δv/Δt = dv/dt.

Учитывая, что v = ds/dt, получим: а = dv/dt = d²s/dt².

Истинное ускорение в прямолинейном движении равно первой производной скорости или второй производной координаты (расстояния от начала отсчета перемещения) по времени.

Единица ускорения — метр, деленный на секунду в квадрате (м/с²).

***

Ускорение точки в криволинейном движении

При движении точки по криволинейной траектории скорость меняет свое направление, т. е вектор скорости является переменной величиной.

Представим себе точку М, которая за время Δt, двигаясь по криволинейной траектории, переместилась в положение М₁ (рис. 1).

Вектор приращения (изменения) скорости обозначим Δv, тогда: Δv = v₁ – v.

Для нахождения вектора Δv перенесем вектор v₁ в точку М и построим треугольник скоростей. Определим вектор среднего ускорения:

а_ср = Δv/Δt.

Вектор а_ср параллелен вектору Δv, так как от деления векторной величины на скалярную направление вектора не меняется.
Вектор истинного ускорения есть предел, к которому стремится отношение вектора приращения скорости к соответствующему промежутку времени, когда последний стремится к нулю:

а = lim Δv/Δt при t→0.

Такой предел называют векторной производной.
Таким образом, истинное ускорение точки в криволинейном движении равно векторной производной скорости по времени.

Из рисунка 1 видно, что вектор ускорения в криволинейном движении всегда направлен в сторону вогнутости траектории.

Так как векторную производную непосредственно вычислять мы не умеем, то ускорение в криволинейном движении будем определять косвенными методами. Так, например, если движение точки задано естественным способом, то применяется теорема о проекции ускорения на касательную и нормаль. Чтобы понять суть этой теоремы, следует рассмотреть понятие кривизны кривых линий.

***



Понятие о кривизне кривых линий

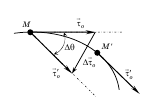
Рассмотрим криволинейную траекторию точки М (рис. 2а).
Угол Δφ между касательными к кривой в двух соседних точках называется углом смежности.

Кривизной кривой в данной точке называется предел отношения угла смежности Δφ к соответствующей длине Δs дуги, когда последняя стремится к нулю.
Обозначим кривизну буквой k, тогда:

k = lim Δφ/Δs   при   Δs → 0.

Рассмотрим окружность радиуса R (см. рисунок 2б).
Так как Δs = RΔφ, то:

k = lim Δφ/Δs = lim Δφ/RΔs = 1/R (при Δs → 0).

Следовательно, кривизна окружности во всех точках одинакова и равна k = 1/R.

Для каждой точки данной кривой можно подобрать такую окружность, кривизна которой равна кривизне кривой в данной точке. Радиус ρ такой окружности называется радиусом кривизны кривой в данной точке, а центр этой окружности – центром кривизны.

Итак, кривизна кривой в данной точке есть величина, обратная радиусу кривизны в данной точке:

k= 1/ρ.

Очевидно, что кривизна прямой линии будет равна нулю, а поскольку радиус кривизны такой линии равен бесконечности.

***

Теорема о проекции ускорения на касательную и нормаль

Проекция ускорения на касательную к траектории называется касательным (тангенциальным) ускорением, а проекция ускорения на нормаль к этой касательной – нормальным ускорением.

Теорема: нормальное ускорение равно квадрату скорости, деленному на радиус кривизны траектории в данной точке; касательное ускорение – первой производной от скорости по времени.

Доказательство этой теоремы основывается на геометрических построениях с учетом приведенных ранее зависимостей перемещения, скорости и ускорения от времени. В данной статье доказательство теоремы не приводится; при необходимости, его можно рассмотреть в других источниках информации.

Итак, на основании теоремы об ускорениях, можно записать:

ап = v²/ρ;     a_τ = dv/dt.

Анализируя формулы касательного и нормального ускорения можно сделать вывод, что касательное ускорение характеризует изменение скорости только по модулю, а нормальное – только по направлению.

Зная величину нормального и касательного ускорения, можно вычислить полное ускорение точки, применив теорему Пифагора:

а = √(а_τ² + а_п²).

Направление ускорения: cos (a_τ,a) = а_τ/а.

Часто касательное и нормальное ускорения рассматривают не как проекции, а как составляющие полного ускорения, т. е. как векторные величины.

Вектор нормального ускорения всегда направлен к центру кривизны, поэтому нормальное ускорение иногда называют центростремительным.

***

Виды движения точки в зависимости от ускорения

Анализируя формулы касательного и нормального ускорений, можно выделить следующие виды движения точки:

а_п = v²/ρ ≠ 0;    a_τ = dv/dt ≠ 0,   — неравномерное криволинейное (рис. 3а);

а_п = v²/ρ ≠ 0;    a_τ = dv/dt = 0,   — равномерное криволинейное (рис. 3б);

а_п = v²/ρ = 0;    a_τ = dv/dt ≠ 0,   — неравномерное прямолинейное (рис. 3в);

a_τ = dv/dt = const ≠ 0;    а_п = v²/ρ ≠ 0,   — равнопеременное криволинейное (рис. 3г);

a_τ = dv/dt = const ≠ 0,    а_п = v²/ρ = 0,   — равнопеременное прямолинейное (рис. 3д);

а_п = v²/ρ = 0;    a_τ = dv/dt = 0,   — равномерное прямолинейное (движение без ускорения) (рис. 3е).

***

Теоремы о проекциях скорости и ускорения на координатную ось

Если движение точки задано координатным способом, то путь (перемещение), скорость и ускорение за промежуток времени Δt можно найти, используя проекции этих величин на координатную ось. Очевидно, что приращение любой из координат при Δt стремящемся к нулю тоже стремится к нулю, и предел такого приращения может быть определен из дифференциальных отношений, устанавливаемых теоремами о проекциях скорости и ускорения:

Теорема: проекция скорости на координатную ось равна первой производной от соответствующей координаты по времени:

v_пx = dx/Δt       v_пy = dy/Δt       v_пz = dz/Δt.

Теорема: проекция ускорения на координатную ось равна второй производной от соответствующей координаты по времени:

a_x = d²x/Δt²       a_y = d²y/Δt²       a_z = d²z/Δt².

Зная проекции скорости или ускорения на координатные оси, можно определить модуль и направление вектора любой из этих величин, используя теорему Пифагора и тригонометрические соотношения.

***

Простейшие движения твердого тела



Среднее и истинное ускорения точки  [c.104]

В пределе при At- 0 получаем истинное ускорение точки, т. е. ускорение точки в момент t или в положении М  [c.105]

Чтобы определить истинное ускорение точки, находим производную от скорости по времени  [c.84]

Такой предел называют векторной производной. Таким образом, истинное ускорение точки в криволинейном движении равно векторной производной скорости по времени.  [c.85]

Определив предел при М О, получим истинное ускорение точки  [c.138]

Среднее ускорение точки за какой-либо промежуток времени зависит от этого промежутка. Если, выбрав ка-кой-либо промежуток времени Д , мы будем затем его уменьшать, то среднее ускорение точки a — Av]At будет изменяться как по модулю, так и по направлению. Однако по мере приближения At к нулю вектор среднего ускорения точки стремится к некоторому определенному пределу. Этот предел называется истинным ускорением точки в данный момент времени или, чаще, просто ускорением точки.  [c.178]

Переходя к пределу при —> О и обозначая проекцию истинного ускорения точки яа ось х через а, получим  [c.187]

Переходя к пределу при А/ —> О, получим истинное ускорение точки как векторную производную от скорости  [c.133]

После того как силовой расчет всех структурных групп проделан, подвижное звено / первичного механизма (рис. 5.4,6) получает статическую определимость. При этом необходимо совершенно четко отметить, что если подвижное звено совершает вращательное движение, то вовсе не обязательно принимать его равномерным. Более того, если искусственно задавать вращение без углового ускорения, то решение уравнения моментов, составленного для по,движного звена первичного механизма, во многих случаях может оказаться далеким от истинного даже при вращении с весьма малым коэффициентом неравномерности, а в иных случаях и попросту абсурдным.  [c.184]

Таким образом, wqm и Wqm не следует смешивать с истинными касательным н нормальным ускорениями точки w- и w .  [c.257]

Этот способ определения положения мгновенного центра ускорений не требует определения угла а путем вычислений. Если положение мгновенного центра ускорений по этому способу определяется графически, то ускорения точек должны быть отложены в масштабе по их истинным направлениям.  [c.261]

Истинное ускорение тела относительно инерциальной системы отсчета (ускорение свободного падения) имеет величину g и направление — Хв, т. е. оно направлено противоположно начальному положению оси Хв вращающейся системы отсчета, неподвижной относительно Земли. Сила тяжести, действующая на тело, не имеет составляющей в направлении уи. Поэтому если взять проекции обеих частей уравнения (72) на направление у в, то получится следующее соотношение  [c.107]

Пример 9.4. Точка движется прямолинейно по закону 4 = Г + 2/ (з — в метрах, / — в секундах). Найти ее среднее ускорение в промежутке между моментами =5 с, Г2 = 7 с, а также ее истинное ускорение в момент /3 = 6 с.  [c.84]

Годографы дают наглядное представление об изменении величин и направлений скоростей и ускорений точки за полный цикл движения механизма (см. годограф скорости точки К на рис. 2.4, в). Векторы абсолютных скоростей или ускорений точки, соответствующие ряду последовательных положений механизма, откладывают в их истинных направлениях от одного полюса, а затем концы векторов соединяют плавной кривой и получают годограф скорости или ускорения точки.  [c.35]

Таким образом, в общем случае истинное движение любого механизма можно представить состоящим из перманентного и начального. Поэтому при кинематическом исследовании механизма достаточна вначале рассмотреть его перманентное движение, а затем начальное, в котором скорости всех его звеньев равны нулю. Следовательно, для изучения начального движения механизма следует построить только план ускорений в этом движении, который будет подобен построенному плану скоростей в перманентном движении. Затем к отрезкам, изображающим векторы ускорений точек механизма в перманентном движении, геометрически прибавляют отрезки, представляющие собой в масштабе векторы ускорений соответствующих точек в начальном движении.  [c.380]

Если в формулу (7-7) ввести коэффициент перегрузки п, т. е. отношение истинного ускорения системы к ускорению, создаваемому силой тяжести на поверхности Земли,то  [c.201]

Максимальное значение в получается, когда i = 45°, и равно приблизительно 6, Если бы значение g истинного ускорения было одинаково на всей земной поверхности, то формула (8) дала бы изменение кажущегося ускорения с широтою. В действительности ускорение g» само является переменною величиною, так  [c.94]

Поэтому, если па графике касательных ускорений в каком-нибудь месте имеется ордината Wt = 35 мм, то соответствующее ей истинное ускорение будет  [c.242]

Аналогично, найдя значение ej по выбранному 5=0, со гласно уравнению (67) определим истинное значение углового ускорения Ё5 при б1 = 0, а также угловые ускорения других звеньев и ускорения точек.  [c.56]

Зная угловое ускорение звена 5, а следовательно, и полное ускорение точки F, можно построить истинный план ускорений.  [c.57]

Угловым ускорением (или также истинным угловым ускорением) точки в момент t называется  [c.383]

Это ложное ускорение Wp будет истинным. По известным векторам истинных ускорений Wp точки /з и ведущей точки А и векторным соотнощениям  [c.456]

Для построения плана ускорений задаемся ускорением точки О, предположив, что оно нормальное, соответствующее истинной ско-  [c.382]

Перейдем от составляющих среднего ускорения к составляющим истинного ускорения, которые обозначим а (касательная составляющая) и а (нормальная составляющая). Так как истинное ускорение представляет собой предел среднего ускорения при At— 0, то и величины его составляющих определятся как пределы соответствующих величин составляющих среднего ускорения.  [c.147]

Таким образом, если известны траектория точки и уравнение движения s = f t), то формулы (112), (113) и (114) позволяют определить величину и направление истинного ускорения, т. е. решить ту задачу, ответ на которую нельзя было получить непосредственно из 50.  [c.149]

При исследовании движения точек механизма, имеющих криволинейные траектории, целесообразно векторы абсолютных скоростей и ускорений точек, соответствующие ряду последовательных положений механизма, откладывать в их истинных направлениях от общих полюсов, а затем концы этих векторов соединять плав-  [c.56]

Принцип Гаусса не связан с вычислением интегралов по времени—это принцип дифференциальный. Истинное движение системы и ее движение по окольному пути сравниваются со свободным движением в каждый момент времени, причем координаты точек и их скорости во всех сравниваемых движениях считаются совпадающими. Ускорения точек будут различными—в свободном движении отсутствуют реакции связей.  [c.264]

Таким образом, 3 и Одд/ не следует смешивать с истинными касательны и нормальным ускорениями точки От и 5 .  [c.202]

На рис. 279, г показаны в масштабе [Ад сплошными линиями отрезки (ис), (т Ь), (тсе) и (u g) ускорений точек С, В, Е к в пер-манентном движении. К ним прибавлены отрезки (сс ), (ЬЬ% (ее ) и (eje , показанные пунктиром, представляющие собою в масштабе ускорения а , а , а и Истинные ускорения точек С, В, Е vi Е с учетом неравномерности вращения ведущего звена равны (рис. 279, г)  [c.185]

Математически Г. п. выражается равенством 6Z=0, в к-ром варьируются только ускорения точек системы при этом предполагается, что силы от ускорения не зависят. Тогда из (1) можно получить др. выражение Г. п. истинное движение механич. системы от.тича-ется от всех др. кинематически возможных движешгй, начинающихся из той же конфигурации и с теми же нач. скоростями, тем, что только для истинного движения в каждый данный момент времени справедливо равенство  [c.418]

---

Скорость
точкиРассмотрим
некоторые основные определения, важные
для последующего изложения. Если
точка за равные промежутки времени
проходит равные отрезки пути, то ее
движение называется равномерным.Скорость
равномерного движения v измеряется
отношением пути s, пройденного точкой
за некоторый промежуток времени, к
величине этого промежутка времени v
= s/t.
Скорость измеряется в единицах длины,
деленных на единицу времени: м/с, см/с,
км/ч и т. д.; 1 км/ч = 0,278 м/с, 1 м/с = = 3,6
км/ч.Если
точка за равные промежутки времени
проходит неравные пути, то ее движение
называется неравномерным.Скорость
неравномерного движения есть величина
переменная и является функцией времени
v
= f (t). Рассмотрим
точку М, которая перемещается по заданной
траектории по некоторому закону s
= f (t) (рис.а).

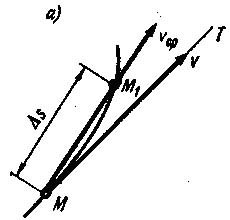
За
промежуток времени t точка М переместится
в положение М1 по
дуге ММ1.
Если промежуток времени t мал, то дугу
можно заменить ее хордой и найти в
первом приближении среднюю скорость
движения точки

 

Средняя
скорость направлена по хорде от точки М к
точке M1.
Истинную скорость найдем путем перехода
к пределу при t—»О

При t—»О направление
хорды в пределе совпадает с направлением
касательной к траектории в точке М,
т. е. значение скорости точки определяется
как производная пути по времени, а
направление ее совпадает с касательной
к траектории в данной точке.

Если
известны проекции скорости на оси
координат, можно определить ее значение
и направление (рис.б):

Ускорение
точкиПри
движении по криволинейной траектории
скорость точки может изменяться и по
направлению, и по величине. Изменение
скорости в единицу времени определяется
ускорением.

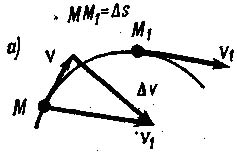
Пусть
точка М (рис.а)
движется по какой-то криволинейной
траектории и за время t переходит
из положения М в
положение M1.
Расстояние, пройденное точкой,
представляет собой дугу ММ1;
ее длину обозначим s.
В положении М точка
имела скорость v, в положении M1 —
скорость v1.
Геометрическую разность скоростей
найдем, построив из точки М вектор v1.

Скорость
точки при перемещении ее из положения М в
положение M1 изменилась
и по величине, и по направлению. Среднее
значение ускорения, характеризующего
отмеченное изменение скорости можно
найти, разделив вектор приращения
скорости v на соответствующее время
движения:

Переходя
к пределу при t—»О получим
истинное ускорение точки как векторную
производную от скорости:

 Найденное
ускорение характеризует изменение
численного значения скорости и ее
направления. Для удобства ускорение
раскладывают на взаимно перпендикулярные
составляющие по касательной и нормали
к траектории движения (рис.б)

Касательная
составляющая 
совпадает
по направлению со скоростью или
противоположна ей. Она характеризует
изменение модуля скорости и соответственно
определяется как производная от функции
скорости:

Нормальная
составляющая 
перпендикулярна
к направлению скорости точки. Она
определяет изменение направления
вектора скорости. Численное значение
нормального ускорения определяется
по формуле:

где r —
радиус кривизны траектории в
рассматриваемой точке.

С

оставляющие 
и 
взаимно
перпендикулярны, и поэтому значение
полного ускоренияопределяется по
формуле:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Скорость изменения скорости

Ускорение
В вакууме (нет сопротивление воздуха ), объекты притягиваются по скорости набора Земли с постоянной скоростью.
Общие символы	a
Единицы СИ	м / с, м · с, мс
Размер	LT

В механике, ускорение— это скорость изменения скорости объекта во времени. Ускорения — это векторные величины (в том смысле, что они имеют величину и направление ). Ориентация ускорения объекта задается ориентацией netсилы, действующей на этот объект. Величина ускорения объекта, описываемая вторым законом Ньютона, является совокупным эффектом двух причин:

• чистый баланс всех внешних сил, действующих на этот объект — величина прямо пропорциональна этой результирующей результирующей силе;
• масса этого объекта, в зависимости от материалов, из которых он сделан — величина обратно пропорциональна к массе объекта.

Единица СИ для ускорения составляет метр в секунду в квадрате (м⋅с, мс 2 { displaystyle { tfrac { OperatorName {m}} { operatorname {s} ^ {2}}}}).

Например, когда транспортное средство стартует с места (нулевая скорость в инерциальной системе отсчета ) и движется по прямой с возрастающей скоростью, оно ускоряется по направлению движения. Если автомобиль поворачивает, происходит ускорение в новом направлении и изменяется вектор движения. Ускорение транспортного средства в текущем направлении движения называется линейным (или тангенциальным во время круговых движений ) ускорением, реакцией, которую пассажиры на борту воспринимают как силу, толкающую их. обратно на свои места. При изменении направления действующее ускорение называется радиальным (или ортогональным во время круговых движений) ускорением, реакцией на которую пассажиры воспринимают как центробежную силу. Если скорость транспортного средства уменьшается, это ускорение в противоположном направлении и математически отрицательное, иногда называемое замедлением, и пассажиры испытывают реакцию на замедление как инерциальную силой толкает их вперед. Такие отрицательные ускорения часто достигаются за счет сжигания ретракет в космических аппаратах. И ускорение, и замедление рассматриваются как изменения скорости. Каждое из этих ускорений (тангенциальное, радиальное, замедление) ощущается пассажирами до тех пор, пока их относительная (дифференциальная) скорость не будет нейтрализована в ссылке для транспортного средства.

Содержание

• 1 Определение и свойства
  • 1.1 Среднее ускорение
  • 1.2 Мгновенное ускорение
  • 1.3 Единицы
  • 1.4 Другие формы
• 2 Тангенциальное и центростремительное ускорение
• 3 Особые случаи
  • 3.1 Равномерное ускорение
  • 3.2 Круговое движение
• 4 Отношение к теории относительности
  • 4.1 Специальная теория относительности
  • 4.2 Общая теория относительности
• 5 Преобразования
• 6 См. Также
• 7 Ссылки
• 8 Внешние ссылки

Определение и свойства

Кинематические величины классической частицы: масса m, положение r, скорость v, ускорение a.

Среднее ускорение

Ускорение — это скорость изменения скорости. В любой точке траектории величина ускорения определяется скоростью изменения скорости как по величине, так и по направлению в этой точке. Истинное ускорение в момент времени t находится в пределе как интервал времени Δt → 0 из Δ v/ Δt

Среднее ускорение объекта за период времени — это его изменение в скорости (Δ v) { displaystyle ( Delta mathbf {v})}, деленное на длительность периода ( Δ t) { displaystyle ( Delta t)}. Математически

a ¯ = Δ v Δ t. { displaystyle { bar { mathbf {a}}} = { frac { Delta mathbf {v}} { Delta t}}.}

Мгновенное ускорение

снизу вверх:

• функция ускорения a (t);
• интеграл ускорения — это функция скорости v (t);
• , а интеграл скорости — функция расстояния s (t).

Между тем, мгновенное ускорение является пределом среднего ускорения за бесконечно малый интервал времени. В терминах исчисления мгновенное ускорение — это производная вектора скорости по времени:

a = lim Δ t → 0 Δ v Δ t = dvdt { displaystyle mathbf {a} = lim _ {{ Delta t} to 0} { frac { Delta mathbf {v}} { Delta t}} = { frac {d mathbf {v}} {dt}}}

Поскольку ускорение определяется как производная от скорости vпо времени t, а скорость определяется как производная от положения, x, с относительно времени ускорение можно представить как вторую производную от xпо t:

a = dvdt = d 2 xdt 2 { displaystyle mathbf {a } = { frac {d mathbf {v}} {dt}} = { frac {d ^ {2} mathbf {x}} {dt ^ {2}}}}

(Здесь и в других местах если движение происходит по прямой, векторные величины могут быть заменены в уравнениях на скаляры.)

На фундаментальную По теореме исчисления можно видеть, что интеграл функции ускорения a (t) равен ve функция локализации v (t); то есть площадь под кривой графика зависимости ускорения от времени (a от t) соответствует скорости.

v = ∫ adt { displaystyle mathbf {v} = int mathbf {a} dt}

Аналогично, интеграл функции j (t) jerk, производной функции ускорения, можно использовать для определения ускорения в определенное время:

a = ∫ jdt { displaystyle mathbf {a} = int mathbf {j} dt}

Units

Ускорение имеет измерения скорости (L / T), разделенные на время, то есть L T. Единица ускорения SI — это метр в секунду в квадрате (мс); или «метр в секунду в секунду», поскольку скорость в метрах в секунду изменяется на величину ускорения каждую секунду.

Другие формы

Объект, движущийся по кругу, например спутник, вращающийся вокруг Земли, ускоряется из-за изменения направления движения, хотя его скорость может быть постоянной. В этом случае говорят, что он испытывает центростремительное (направленное к центру) ускорение.

Правильное ускорение, ускорение тела относительно состояния свободного падения, измеряется прибором, называемым акселерометром.

В классической механике, для тела с с постоянной массой, (векторное) ускорение центра масс тела пропорционально вектору чистой силы (то есть сумме всех сил), действующей на него (второй закон Ньютона ):

F = ma → a = F m { displaystyle mathbf {F} = m mathbf {a} quad to quad mathbf {a} = { frac { mathbf {F}} {m} }}

где F— чистая сила, действующая на тело, m — масса тела, а a— центр массовое ускорение. По мере приближения скорости к скорости света, релятивистские эффекты становятся все более значительными.

Тангенциальное и центростремительное ускорение

Колебательный маятник с отмеченными скоростью и ускорением. Он испытывает как тангенциальное, так и центростремительное ускорение. Компоненты ускорения для криволинейного движения. Тангенциальная составляющая atвозникает из-за изменения скорости перемещения и указывает вдоль кривой в направлении вектора скорости (или в противоположном направлении). Нормальная составляющая (также называемая центростремительной составляющей для кругового движения) acвозникает из-за изменения направления вектора скорости и перпендикулярна траектории, указывая к центру кривизны траектории.

Скорость движения частицу, движущуюся по изогнутой траектории, как функцию времени можно записать как:

v (t) = v (t) v (t) v (t) = v (t) ut (t ), { displaystyle mathbf {v} (t) = v (t) { frac { mathbf {v} (t)} {v (t)}} = v (t) mathbf {u} _ { mathrm {t}} (t),}

, где v (t) равно скорости движения по пути, а

ut = v (t) v (t), { displaystyle mathbf { u} _ { mathrm {t}} = { frac { mathbf {v} (t)} {v (t)}} ,}

a касательный единичный вектор к пути, указывающему в направлении движения в выбранный момент времени. Принимая во внимание как изменяющуюся скорость v (t), так и изменяющееся направление ut, ускорение частицы, движущейся по изогнутой траектории, может быть записано с использованием цепного правила дифференцирования для произведения двух функции времени как:

a = dvdt = dvdtut + v (t) dutdt = dvdtut + v 2 run, { displaystyle { begin {alignat} {3} mathbf {a} & = { frac { mathrm {d} mathbf {v}} { mathrm {d} t}} \ & = { frac { mathrm {d} v} { mathrm {d} t}} mathbf {u} _ { mathrm {t}} + v (t) { frac {d mathbf {u} _ { mathrm {t}}} {dt}} \ & = { frac { mathrm {d} v} { mathrm {d} t}} mathbf {u} _ { mathrm {t}} + { frac {v ^ {2}} {r}} mathbf {u} _ { mathrm {n}} , \ end {alignat}}}

где un- единичный (внутренний) вектор нормали к траектории частицы (также называемой главной нормалью), и r— его мгновенный радиус кривизны, основанный на соприкасающейся окружности в момент времени t. Эти компоненты называются тангенциальным ускорением и нормальным или радиальным ускорением (или центростремительным ускорением при круговом движении, см. Также круговое движение и центростремительная сила ).

Геометрический анализ трехмерных пространственных кривых, который объясняет касательную, (главную) нормальную и бинормальную, описывается формулами Френе – Серре.

Особые случаи

Равномерное ускорение

Вычисление разницы скоростей для равномерного ускорения

Равномерное или постоянное ускорение — это тип движения, при котором скорость объекта изменяется на равную величину в каждый равный период времени.

Часто цитируемый пример равномерного ускорения — это объект в свободном падении в однородном гравитационном поле. Ускорение падающего тела при отсутствии сопротивлений движению зависит только от силы тяжести напряженности g (также называемой ускорением свободного падения). Согласно Второму закону Ньютона сила F g { displaystyle mathbf {F_ {g}}}, действующая на тело, определяется следующим образом:

F g = mg { displaystyle mathbf {F_ {g}} = m mathbf {g}}

Из-за простых аналитических свойств случая постоянного ускорения существуют простые формулы, связывающие смещение, начальная и зависящая от времени скорости и ускорение до истекшего времени :

s (t) = s 0 + v 0 t + 1 2 при 2 = s 0 + v 0 + v (t) 2 t { displaystyle mathbf {s} (t) = mathbf {s} _ {0} + mathbf {v} _ {0} t + { tfrac {1} {2} } mathbf {a} t ^ {2} = mathbf {s} _ {0} + { frac { mathbf {v} _ {0} + mathbf {v} (t)} {2}} т }

v (t) = v 0 + в { displaystyle mathbf {v} (t) = mathbf {v} _ {0} + mathbf {a} t}

v 2 (t) знак равно v 0 2 + 2 a ⋅ [s (t) — s 0] { displaystyle {v ^ {2}} (t) = {v_ {0}} ^ {2} +2 mathbf {a cdot} [ mathbf {s} (t) — mathbf {s} _ {0}]}

где

В частности, движение можно разделить на две ортогональные части, одну с постоянной скоростью, а другую в соответствии с приведенными выше уравнениями. Как показал Галилей, конечным результатом является параболическое движение, которое описывает, например, g., траектория снаряда в вакууме у поверхности Земли.

Круговое движение

Вектор положения r, всегда направлен радиально от начала координат. Вектор скорости v, всегда касательный к траектории движения. Вектор ускорения a, не параллельный радиальному движению, но смещенный на угловое и кориолисово ускорение, не касательный к траектории, но смещение на центростремительное и радиальное ускорения. Кинематические векторы в плоскости полярные координаты. Обратите внимание, что установка не ограничена 2-м пространством, но может представлять плоскость соприкасающейся плоскости в точке произвольной кривой в любом более высоком измерении.

При равномерном круговом движении это движется с постоянной скоростью по круговой траектории, частица испытывает ускорение в результате изменения направления вектора скорости, а его величина остается постоянной. Производная положения точки на кривой по времени, то есть ее скорость, оказывается всегда точно касательной к кривой, соответственно ортогональной радиусу в этой точке. Поскольку при равномерном движении скорость в тангенциальном направлении не меняется, ускорение должно быть в радиальном направлении, указывая на центр окружности. Это ускорение постоянно меняет направление скорости на касательную в соседней точке, тем самым поворачивая вектор скорости по окружности.

• Для заданной скорости v { displaystyle v}величина этого геометрически обусловленного ускорения (центростремительного ускорения) обратно пропорциональна радиусу r { displaystyle r}круга и увеличивается как квадрат этой скорости:

ac = v 2 r. { displaystyle a_ {c} = { frac {v ^ {2}} {r}} ;.}

• Обратите внимание, что для данной угловой скорости ω { displaystyle omega}центростремительное ускорение прямо пропорционально радиусу r { displaystyle r}. Это связано с зависимостью скорости v { displaystyle v}от радиуса r { displaystyle r}.

v = ω r. { displaystyle v = omega r.}

Выражение вектора центростремительного ускорения в полярных компонентах, где r { displaystyle mathbf {r}}— вектор из центра круга частице с величиной, равной этому расстоянию, и учитывая ориентацию ускорения к центру, получаем

ac = — v 2 | г | ⋅ r | г |. { displaystyle mathbf {a_ {c}} = — { frac {v ^ {2}} {| mathbf {r} |}} cdot { frac { mathbf {r}} {| mathbf { r} |}} ;.}

Как обычно при вращении, скорость v { displaystyle v}частицы может быть выражена как угловая скорость относительно точки на расстоянии r { displaystyle r}как

ω = vr. { displaystyle omega = { frac {v} {r}}.}

Таким образом, a c = — ω 2 r. { displaystyle mathbf {a_ {c}} = — omega ^ {2} mathbf {r} ;.}

Это ускорение и масса частицы определяют необходимую центростремительную силу, направленный к центру круга, поскольку результирующая сила, действующая на эту частицу, удерживает ее в этом равномерном круговом движении. Так называемая «центробежная сила », которая, кажется, действует на тело наружу, является так называемой псевдосилой, испытываемой в системе отсчета тело в круговом движении из-за импульса тела, касательного вектора к окружности движения.

При неравномерном круговом движении, т. Е. Скорость по криволинейной траектории меняется, ускорение имеет ненулевую составляющую, касательную к кривой, и не ограничивается главной нормалью, который направлен к центру соприкасающегося круга, который определяет радиус r { displaystyle r}для центростремительного ускорения. Тангенциальная составляющая задается угловым ускорением α { displaystyle alpha}, то есть скоростью изменения α = ω ˙ { displaystyle alpha = { dot { omega}}}угловой скорости ω { displaystyle omega}, умноженной на радиус r { displaystyle r}. То есть

a t = r α. { displaystyle a_ {t} = r alpha.}

Знак тангенциальной составляющей ускорения определяется знаком углового ускорения (α { displaystyle alpha }), и касательная, конечно, всегда направлена ​​под прямым углом к ​​радиус-вектору.

Отношение к теории относительности

Специальная теория относительности

Специальная теория относительности описывает поведение объектов, движущихся относительно других объектов со скоростями, приближающимися к скорости света в вакууме. Ньютоновская механика точно раскрывается как приближение к реальности, действительное с большой точностью на более низких скоростях. Поскольку соответствующие скорости увеличиваются в сторону скорости света, ускорение больше не подчиняется классическим уравнениям.

По мере приближения скорости к скорости света ускорение, создаваемое данной силой, уменьшается, становясь бесконечно малым по мере приближения к скорости света; объект с массой может достичь этой скорости асимптотически, но никогда не достичь ее.

Общая теория относительности

Если состояние движения объекта не известно, невозможно определить, является ли наблюдаемая сила результатом силы тяжести или ускорения — силы тяжести и инерционное ускорение имеет идентичный эффект. Альберт Эйнштейн назвал это принципом эквивалентности и сказал, что только наблюдатели, которые вообще не чувствуют никакой силы, включая силу гравитации, могут сделать вывод о том, что они не ускоряются.

Преобразования

Преобразования между общепринятыми единицами ускорения

Базовое значение	(Гал или см / с)	(фут / с )	(м / с )	(Стандартная сила тяжести, г 0)
1 галлон, или см / с	1	0,0328084	0,01	0,00101972
1 фут / с	30,4800	1	0,304800	0,0310810
1 м / с	100	3,28084	1	0,101972
1 г 0	980,665	32,1740	9.80665	1

См. Также

Ссылки

Внешние ссылки

Викискладе есть материалы, связанные с Ускорение .

• Калькулятор ускорения Простой преобразователь единиц ускорения
• Калькулятор ускорения Калькулятор преобразования ускорения преобразует единицы измерения в квадратный метр в секунду, квадрат в километр в секунду, квадрат миллиметра в секунду и т.д. с метрическим преобразованием.