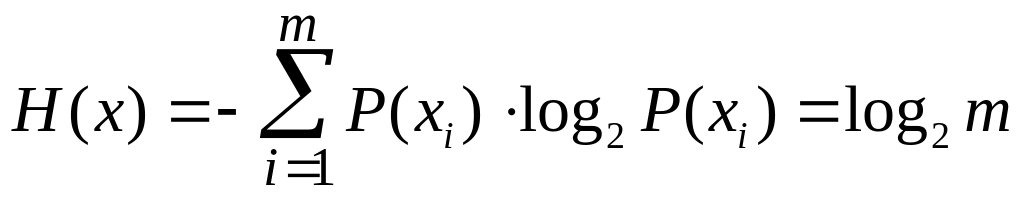Понятие
избыточности означает, что фактическая
энтропия кода или сообщения (Н) меньше,
чем максимально возможная энтропия
(Hmax), т. е. число
символов в сообщении или элементов в
символе кода больше, чем это требовалось
бы при полном их использовании.
Понятие
избыточности легко пояснить следующим
примером.
Выделение
полезного сигнала на уровне помех —
одна из основных проблем передачи
информации. Одним из путей повышения
надёжности передачи сообщений может
быть передача дополнительных символов,
т.е. повышение избыточности сообщений.
Действительно,
по теореме Котельникова (§ 1.7), непрерывное
сообщение (сигнал) можно передать
последовательностью мгновенных отсчетов
его значений с промежутками между ними
:
где
fmax
– верхняя граничная частота в спектре
сигнала.
При
наличии помех промежутки между отсчетами
(Δtn)
необходимо уменьшать, т.е.
В
этом случае мы увеличиваем число отсчетов
и, следовательно, увеличиваем избыточность
сообщения и тем самым повышаем его
помехозащищенность.
Пусть
сообщение из n символов
содержит количество информации I.
Если сообщение обладает избыточностью,
то его (при отсутствии шума) можно
передать меньшим числом символов n0
(n0 < n).
При этом, количества информации (I1
и I1max),
приходящиеся на один символ сообщения,
будут связаны соотношением:
I1
= I/n < I1max
= I/n0
и,
следовательно,
n
∙ I1
= n0
∙
I1max.
За
меру избыточности принимается величина
R:
(2.3)
Таким
образом, избыточность — это свойство,
характеризующее возможность представления
тех же сообщений в более экономной
форме.
При
кодировании избыточных сообщений
возникает определенная исходная
избыточность кодов. Наличие исходной
избыточности уменьшает пропускную
способность каналов и увеличивает
формат сообщений. Вместе с тем в процессе
передачи информации избыточность
сообщений и кодов является средством,
полезным для борьбы с внешними возмущающими
воздействиями и помехами.
По
наличию избыточности коды также делятся
на избыточные и неизбыточные. Для
неизбыточных кодов характерно то, что
они позволяют просто определить различные
символы сообщения. Переход от неизбыточного
кода к избыточному осуществляется путем
добавления позиций в кодовых символах,
которые можно получить либо путем
различных логических операций, выполняемых
над основными информационными позициями,
либо путем использования алгоритмов,
связывающих неизбыточный и избыточный
коды. Например, если есть символы
сообщения А1; А2; А3;
А4, то их можно закодировать в
двоичном неизбыточном коде:
А1
= 00; А2 = 01; А3 = 10; А4
= 11.
Для
получения избыточного кода можно ввести
еще одну позицию, значение которой будет
определяться как сумма значений
предшествующих символов по модулю два:
А1
= 000; А2 = 011; А3 = 101; А4 =
110.
Особенностью
такого кода является то, что он позволяет
обнаружить любую единичную ошибку
(ошибку в одной из позиций кода),
выявившуюся в процессе передачи кода.
-
Эффективное
кодирование. Алгоритм Шеннона-Фено.
Эффективное
кодирование равновероятных символов
сообщений.
Эффективное
кодирование используется в каналах без
шума, т.е. в таких каналах, где помехи
отсутствуют, либо ими можно пренебречь.
Основной задачей кодирования в таком
канале является обеспечение максимальной
скорости передачи информации, близкой
к пропускной способности канала передачи
(§3.4).
В
случае, если все символы алфавита
кодируемого сообщения независимы и их
появление равновероятно, построение
оптимального эффективного кода не
представляет трудностей. Действительно,
пусть Н(х) — энтропия исходного сообщения.
Будем считать, что символы сообщения
(хi) равновероятны
и объем алфавита исходного источника
сообщений равен m.
Следовательно, вероятность появления
любого i-го символа данного
сообщения (P(хi))
будет одинакова, т.е.
,
i=1,.., m
,
а
энтропия сообщения равна (Н(х)):
,
Если
для кодирования используется числовой
код по основанию k (объем
алфавита элементов кодовых символов
равен k), то энтропия
элементов кодовых символов (Н1),
при условии, что элементы символов кода
появляются равновероятно и взаимнонезависимо,
определится из соотношения:
H1
= log2 k
.
Тогда
длина эффективного равномерного кода,
т.е. число элементов в кодовом символе
(lэфф.), может быть
найдена из соотношения:
,
(2.4)
где
m
= k
n.
Эффективное
кодирование неравновероятных символов
сообщений
В
случае, если символы кодируемого
сообщения неравновероятны, в общем виде
правило получения оптимального
эффективного кода неизвестно. Однако
из общих соображений можно представить
принципы его построения.
Очевидно,
что эффективное кодирование будет
оптимальным, если неравномерное
распределение вероятностей появления
символов алфавита источника сообщений
с помощью определенным образом выбранного
кода переводят в равновероятное
распределение вероятностей появления
независимых элементов кодовых символов.
В этом случае среднее количество
информации, приходящееся на один
элемент символа кода, будет максимальным.
Для определения вида кода, удовлетворяющего
этому требованию, можно рассмотреть
«функцию стоимости» (цены передачи
символов сообщения) в виде:
,
(2.5)
где
P(xi) — вероятность
появления i-го символа
алфавита исходного кодируемого сообщения;
m
— объем алфавита;
Wi
— стоимость передачи i-го
символа алфавита, которая пропорциональна
длине кодового слова.
Эффективный
код должен минимизировать функцию Q.
Если передача
всех элементов символов кода имеет
одинаковую стоимость, то стоимость
кодового символа будет пропорциональна
длине соответствующего кодового символа.
Следовательно, в общем случае (при
неравновероятных символах исходного
сообщения) код должен быть неравномерным,
поэтому построение эффективного
кода должно основываться на следующих
принципах:
Длина
кодового символа (ni)
должна быть обратно пропорциональна
вероятности появления соответствующего
символа исходного кодируемого сообщения
(xi);
Начало
более длинного кодового символа не
должно совпадать с началом более
короткого (для возможности разделения
кодовых символов без применения
разделительных знаков);
В
длинной последовательности элементы
символов кода должны быть независимы
и равновероятны.
Теоретическое
обоснование возможности эффективного
кодирования передаваемых по каналу
сообщений обеспечивает теорема,
доказанная К. Шенноном и которая носит
название первая теорема Шеннона или
основная теорема Шеннона о кодировании
для каналов без помех. Эта теорема
гласит, что если источник сообщений
имеет энтропию Н [бит/символ], а канал
обладает пропускной способностью С
[бит/сек] (пропускная способность
характеризует максимально возможное
значение скорости передачи информации),
то всегда можно найти способ кодирования,
который обеспечит передачу символов
сообщения по каналу со средней скоростью
[символ/сек],
где
ε — сколь угодно малая величина.
Обратное
утверждение говорит, что передача
символов сообщения по каналу со средней
скоростью Vср. > Н
невозможна и, следовательно,
[символ/сек].
Эта
теорема часто приводится в иной
формулировке: сообщения источника
сообщений с энтропией Н всегда можно
закодировать последовательностями
элементов кодовых символов с объемом
алфавита k так, что среднее
число элементов символов кода на один
символ кодируемого сообщения (l ср.
) будет сколь
угодно близко к величине H
/ log2 k,
но не менее ее.
Не
вдаваясь в доказательство этой теоремы,
отметим, что эта теорема показывает
возможность наилучшего эффективного
кодирования, при котором обеспечивается
равновероятное и независимое поступление
элементов символов кода, а следовательно,
и максимальное количество переносимой
каждым из них
информации, равное log2
k (бит/элемент) . К
сожалению, теорема не указывает
конкретного способа эффективного
кодирования, она лишь говорит о том, что
при выборе каждого элемента кодового
символа необходимо чтобы он нес
максимальное количество информации,
а, следовательно, все элементы символов
кода должны появляться с равными
вероятностями и взаимнонезависимо.
Исходя
из изложенных принципов, разработаны
ряд алгоритмов эффективного кодирования
как для взаимнонезависимых символов
сообщения, так и для
взаимнозависимых.
Суть их состоит в том, что они сокращают
среднюю длину кодовых символов
путем присвоения кодовых символов
минимальной длины символам исходного
сообщения, которые встречаются наиболее
часто.
Алгоритм
Шеннона-Фено. Суть этого алгоритма,
при использовании двоичного кода (объем
алфавита элементов символов кода равен
2), заключается в следующем.
Все
символы алфавита источника сообщений
ранжируют, т. е. располагают в порядке
убывания вероятностей их появления.
Затем символы алфавита делятся на две
группы приблизительно равной суммарной
вероятности их появления. Все символы
первой группы получают «0» в качестве
первого элемента кодового символа, а
все символы второй группы — «1». Далее
группы делятся на подгруппы, по тому же
правилу примерно равных суммарных
вероятностей, и в каждой подгруппе
присваивается вторая позиция кодовых
символов. Процесс повторяется до
закодирования всех символов алфавита
кодируемого источника сообщений. В
кодовый символ, соответствующий последней
группе, добавляется в качестве последнего
элемента «0» для того, чтобы начальный
элемент символов кода не совпадал с
конечным, что позволяет исключить
разделительные элементы между символами
кода.
Таблица
2.2 иллюстрирует процесс построения кода
Шеннона–Фено на примере источника
сообщений, алфавит которого состоит из
восьми символов.
Таблица
2.2
|
Номер |
Символы |
Вероятности |
Номера |
Кодовые |
|
символа. |
алфавита. |
(Рi). |
Разбиений. |
Символы. |
|
1 |
m1 |
1/2 |
I II III IV V VI VII |
0 |
|
2 |
m2 |
1/4 |
10 |
|
|
3 |
m3 |
1/8 |
110 |
|
|
4 |
m4 |
1/16 |
1110 |
|
|
5 |
m5 |
1/32 |
11110 |
|
|
6 |
m6 |
1/64 |
111110 |
|
|
7 |
m7 |
1/128 |
1111110 |
|
|
8 |
m8 |
1/256 |
11111110 |
На
рис. 2.1 представлен граф кодирования
(кодовое дерево), который показывает,
как «расщепляется» ранжированная
последовательность символов кодируемого
источника сообщений на группы и отдельные
символы и какие кодовые символы
присваиваются группам и отдельным
символам алфавита источника сообщений
на каждом шаге разбиения.
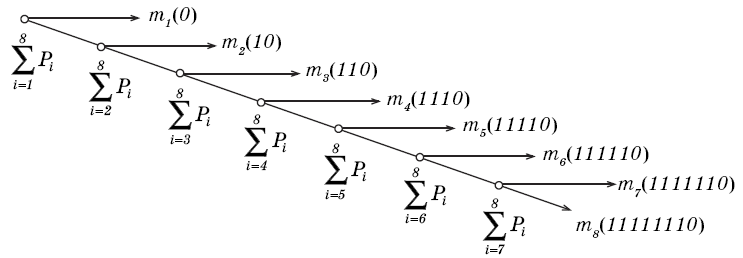
Рис
2.1. Граф кодирования по алгоритму
Шеннона–Фено.
Алгоритм
Шеннона–Фено применим и при иных
числовых основаниях кода (k
> 2). В этом случае алгоритм получения
кода аналогичен рассмотренному примеру,
только алфавит кодируемого источника
сообщений разбивается на k
групп и подгрупп примерно одинаковой
суммарной вероятности.
Представляет
интерес сравнение эффективного
кодирования равномерным кодом и
неравномерным кодом по алгоритму
Шеннона–Фено.
В
качестве примера рассмотрим предложенный
выше (Табл. 2.2) источник сообщений с
объемом алфавита равным 8 и соответствующими
вероятностями появления отдельных
символов (Pi).
Для кодирования используем двоичный
код ( k = 2).
Энтропия
рассмотренного источника сообщений
(Hи) определяется
по формуле Шеннона:
(бит/символ).
Максимально
же возможное значение энтропии источника
сообщений (Hu.max),
при условии равновероятного и взаимно
независимого появления символов,
находится по формуле Хартли:
.
Следовательно,
избыточность рассматриваемого источника
сообщений (Rи) может
быть найдена из соотношения:
Используя
формулу для эффективного равномерного
кода (2.4) при k = 2, получим
значность равномерного двоичного кода
(пр):
и
избыточность равномерного кода (Rрк):
Энтропия
элементов символов равномерного кода
,
т.е. количество информации, приходящееся
на один элемент символа кода, будет
равна:
(бит
/ элемент символа кода). (2.6)
При
использовании эффективного кодирования
по алгоритму Шеннона-Фено соответствующие
информационные параметры кода будут
следующие.
Средняя
длина неравномерного кода (пН)
определяется выражением:
,
(2.7)
где
пi — значность i —
го кодового символа, соответствующего
символу алфавита mi.
Избыточность
неравномерного кода (RНК)
определим из соотношения:
Энтропия
элементов символов эффективного
неравномерного кода
может
быть легко найдена:
(бит/элемент
символа кода). (2.8)
Из
сравнения выражений (2.6) и (2.8) видно, что,
при использовании эффективного
кодирования по алгоритму Шеннона-Фено,
энтропия элементов символов такого
неравномерного кода на 50% выше чем
энтропия элементов символов в случае
использования равномерного кода. Если
предположить, что скорость передачи по
каналу элементов символов кода (W)
одинакова для равномерного и неравномерного
кода, то скорость передачи информации
(V), определяемая выражением
,
где
Н — энтропия элементов символа кода,
также
будет на 50% выше при использовании
эффективного кодирования по алгоритму
Шеннона–Фено по сравнению с равномерным
кодированием.
Алгоритм
Шеннона–Фено часто применяют и для
блочного кодирования. При этом также
существенно повышается эффективность
кодирования. Для иллюстрации такого
кодирования рассмотрим процедуру
эффективного кодирования двоичным
числовым кодом сообщений, генерируемых
источником сообщений с объемом алфавита
равным 2 (m = 2), т.е. с алфавитом, состоящим
только из двух символов m1
и m2 с вероятностями
появления P(m1)
= 0,9 и P(m2)
= 0,1 и, следовательно, с энтропией Н =
0,47.
При
посимвольном кодировании по алгоритму
Шеннона–Фено эффект отсутствует, так
как на каждый символ сообщения будет
приходится один символ кода, состоящий
из одного элемента.
Произведем
теперь кодирование по алгоритму
Шеннона–Фено блоков, состоящих из
комбинаций двух символов источника
сообщений, считая символы
взаимнонезависимыми. Результат приведен
в таблице 2.3.
Таблица
2.3.
|
Блоки |
Вероятности |
Номера |
Кодовые |
|
m1m1 m1m2 m2m1 m2m2 |
0,81 0,09 0,09 0,01 |
I II III |
1 01 001 0001 |
Среднее
число элементов символов кода на один
символ исходного сообщения, вычисленное
по формуле (2.7), равно 0,645, что значительно
ниже, чем при посимвольном кодировании.
Кодирование
блоков, соответствующих комбинациям
из трех символов источника сообщений,
дает еще больший эффект. Результат
приведен в таблице 2.4.
Таблица
2.4.
|
Блоки. |
Вероятности. |
Номера |
Kодовые |
|
m1 |
0,729 |
I |
1 |
|
m2 |
0,081 |
III |
011 |
|
m1 |
0,081 |
II |
010 |
|
m1 |
0,081 |
IV |
001 |
|
m2 |
0,009 |
VI |
00011 |
|
m2 |
0,009 |
V |
00010 |
|
m1 |
0,009 |
VII |
00001 |
|
m2 |
0,001 |
00000 |
В
этом случае среднее число элементов
символов кода на один символ исходного
источника сообщений равно 0,53.
Теоретический
минимум Н = 0,47 может быть достигнут при
кодировании блоков неограниченной
длины.
Алгоритм
Шеннона-Фено не всегда приводит к
однозначному построению кода, так как
при разбиении на подгруппы можно сделать
большей по суммарной вероятности как
верхнюю, так и нижнюю подгруппу. Этого
недостатка лишен алгоритм Хаффмена,
который гарантирует однозначное
построение эффективного кода.
-
Помехоустойчивость.
Корректирующее кодирование.
2.9.
Теоретические основы помехоустойчивого
кодирования
Теоретические
основы помехозащищенного кодирования
сообщений базируются на основной теореме
Шеннона о кодировании для канала с
помехами. Эта теорема гласит:
При
любой производительности источника
сообщений, меньшей чем пропускная,
способность канала, существует такой
способ кодирования, который позволяет
обеспечить передачу всей информации,
создаваемой источником сообщений, со
сколь угодно малой вероятностью ошибки.
Не
существует способа кодирования,
позволяющего вести передачу информации
со сколь угодно малой вероятностью
ошибки, если производительность источника
сообщений больше пропускной способности
канала.
Анализируя
теорему, важно отметить, что она
устанавливает теоретический предел
процесса передачи информации, создаваемой
источником сообщений, со сколь угодно
малой вероятностью ошибки и показывает,
что помехи в канале не накладывают
ограничений на точность и достоверность
передачи сообщений, а ограничения
накладываются лишь на скорость передачи,
при которой может быть достигнута сколь
угодно высокая достоверность передачи.
Теорема,
к сожалению, не указывает конкретных
путей построения кодов, обеспечивающих
надежность передачи, однако она
доказывает, что такие пути существуют.
Для
определения конкретных направлений,
обеспечивающих повышение надёжности
и достоверности передачи сообщений,
обратимся к общей информационной модели
системы передачи сообщений, представленной
на рис. 2.4.

Рис.
2.4. Общая информационная модель системы
передачи сообщений.
Пусть
–
исходное сообщение, генерируемое
источником сообщения, датчик сообщения
преобразует его в сигнал,
затем этот сигнал проходит по каналу и
поступает на приёмник, в котором
преобразовывается в сообщение
:
.
Таким
образом, процесс передачи сообщений
описывается в следующем образом
(Рис.2.5.):
на
передающем конце канала пространство
сообщений
преобразуется
в пространство сигналов
;
на
приёмном конце канала из пространства
сигналов
восстанавливается пространство сообщений
.

Рис.
2.5. Иллюстрация процесса передачи
сообщений по каналу.
При
отсутствии помех выполняется однозначное
соответствие между исходным символом
сообщения (ui)
и принятым символом (vi).
Действительно,
-
,
При
наличии помех сигнал X
при прохождении через канал будет
искажаться и, в общем случае,
,
что приводит к искажению исходного
сообщения и вызывает трудности в
разделении и опознании исходных символов
сообщений. Для безошибочного приёма
необходимо идентифицировать принятое
сообщение v, то есть
определить, какому исходному сообщению
оно соответствует.
Выполнить
эту идентификацию можно следующим
образом. Если собственные шумы в приёмнике
отсутствуют, то можно однозначно
определить принятый сигнал x, соответствующий
полученному сообщению v:
и
определить положение сигнала x в
пространстве сигналов X
(Рис. 2.6.).
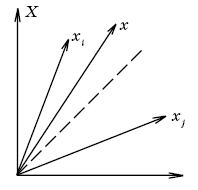
Рис.
2.6. Положение сигнала x в пространстве
сигналов X.
Вектору
x можно присвоить значение ближайшего
к нему известного вектора из пространства
сигналов X , то есть
,
если
для
любого
.
Приемник,
работающий по выше рассмотренному
принципу идентификации, называют
идеальным приемником.
Ошибка
приема идеального приемника (прием
сообщения
вместо переданного
)
происходит лишь тогда, когда сигнал x
под действием помех переходит границу
раздела областей этих сообщений, то
есть тогда, когда
Вероятность
появления такой ошибки может служить
мерой помехоустойчивости или надежности
системы связи (П):
-
(2.9.)
где
–
вероятность появления ошибки на выходе
приемника.
Очевидно,
что с увеличением расстояния между
векторами xi
и xj
помехоустойчивость повышается.
Если
величина помехи ξ определяется как ξ =
xi
— x, то для безошибочного
приема сообщения x
необходимо выполнение условия:
или
-
,
где
И
тогда условие безошибочного приема
запишется в виде:
.
В
случае, если помеха (ξ) имеет плотность
распределения вероятностей f(ξ),
то вероятность появления ошибки
можно определить из выражения:
В
общем случае пространство сообщений U
имеет размерность n
(например, каждый символ этого сообщения
состоит из n элементов).
Тогда условие безошибочного приема
получим из следующих соображений.
Так
как
-
,
то
,
а
-
,
где
– k-я координата пространства
X.
Следовательно,
-
.
Если
и
– независимы, то минимальное расстояние
между сигналами
должно удовлетворять условию:
|
|
где
;
– расстояние
между двумя ближайшими сообщениями.
Корректирующее
кодирование применяют в тех случаях,
когда возможности других более простых
способов повышения помехозащищенности
(таких как многократное повторение или
фильтрация) исчерпаны. Это обусловлено
усложнением систем передачи информации
при введении кодирующих устройств.
Как
следует из выше приведённых выводов
теории помехоустойчивости, основной
практический принцип построения
корректирующих (помехозащищенных) кодов
основывается на допущении, что принятый
кодовый символ после воздействия на
него помехи всегда остается в некоторой
близости от кодового символа, однозначно
соответствующего передаваемому символу
исходного сообщения. Это позволяет в
дальнейшем отождествить принятый символ
с ближайшим к нему символом кодового
алфавита путём нахождения минимального
расстояния из всех расстояний между
принятым символом и всеми символами
кодового алфавита.
Создание
специальных помехоустойчивых цифровых
кодов, позволяющих не только обнаружить,
но и при определенных условиях исправить
возникающие ошибки, основано на увеличении
минимального расстояния между символами
кодового алфавита (dmin)
путём. увеличения избыточности кодов.
Это
достигается введением при кодировании
дополнительных (избыточных) элементов
символов кода, которые удовлетворяют
некоторым дополнительным условиям и
проверка которых дает возможность
обнаружить и исправить ошибки.
Принципы
практического построения корректирующих
кодов удобно продемонстрировать на
примере блочных систематических кодов
(в частности алгебраических кодов), как
наиболее наглядных и широко применяемых.
Для
алгебраических (n, k)
корректирующих кодов избыточность кода
(Rn,
Rk)
определяется выражениями:
,
;
,
,
(2.9)
где
n — число элементов в
кодовом символе;
k
— число информационных элементов в
кодовом символе (или минимально возможное
число элементов в кодовом символе.
Величина
Rk, с
областью изменения от 0 до ∞ предпочтительнее,
так как лучше отвечает смыслу понятия
избыточности.
Коды,
обеспечивающие заданную помехоустойчивость
при минимально возможной избыточности,
называют оптимальными.
Очевидно,
что при оптимальном кодировании, когда
лишние элементы в кодах отсутствуют,
т.е. когда n = k,
избыточность равна 0.
Для
оценки кодов с точки зрения возможности
обнаружения и исправления ошибок
используют понятие кодового расстояния
(число кодовых переходов для двоичных
кодов) dij.
Кодовым
расстоянием (dij)
между кодовыми символами ki
и kj
называют суммарный результат сложения
по модулю mk
одноименных разрядов кодовых символов
ki и
kj:
,
где
;
kik
и kjk
— k разряд кодовых символов
ki и
kj;
— символ
сложения по модулю mk;
mk
— основание кода (основание системы
счисления цифрового кода).
Например,
если даны символы двоичного числового
кода ki
= 10111 и kj
= 01010, то кодовое расстояние между этими
символами равно 4 (dij=
4).
Кодовое
расстояние может быть посчитано и для
числовых кодов с иными основаниями,
отличными от 2.
Кодовое
расстояние иногда называют расстоянием
Хемминга.
2.10.
Некоторые методы построения блочных
корректирующих кодов
1.
Коды, построенные на основе увеличения
кодового расстояния
Идея
обнаружения и исправления ошибок в
таких кодах заключается в следующем.
Для передачи символов сообщения
используют не все N возможных комбинаций
элементов символов кода длиной n, а
только часть из них N0,
которые называются разрешенными
символами кода. Оставшиеся ΔN
комбинаций (ΔN = N – N0)
называют запрещенными. Ошибка
обнаруживается тогда, когда приемник
получает запрещенную комбинацию
элементов символов кода. Всякий код, у
которого ΔN > 0, способен
обнаруживать ошибки в ΔN
случаях из N. Доля обнаруживаемых ошибок
(s) определяется выражением:
.
По
формуле (2.9) легко определить избыточность
такого корректирующего кода (Rk
):
,
где
H(N0
)—энтропия кода с объемом алфавита N0
;
H(N)—энтропия
кода с объемом алфавита N;
n—
число элементов в кодовом символе;
mk—
основание кода.
Исправление
ошибок в корректирующих кодах заключается
в том, что, обнаружив ошибку, определяют
кодовое состояние от полученной
запрещенной комбинации ki
до всех разрешенных символов кода kj
(j=1, 2, …, N0)
и в качестве переданного символа кода
считается тот из разрешенных символов
кода, до которого расстояние минимально.
Таким образом, исправление ошибок
корректирующими кодами производится
с помощью трех последовательных операций:
—
определения кодового расстояния между
принятой кодовой комбинацией и
разрешенными кодовыми символами;
—
отыскания минимального кодового
расстояния;
—
присвоение принятой кодовой комбинации
значения ближайшего к ней (по кодовому
расстоянию) разрешенного кодового
символа.
Например,
в трехзначном равномерном двоичном
коде число возможных кодовых комбинаций
8:
000,
001, 010, 011, 100, 101, 010, 111,
кодовое
расстояние между которыми (dij)
равно 1. Ошибка в любом одном элементе
символа кода превращает передаваемый
разрешенный кодовый символ в другой,
но так же разрешенный.
Если
увеличить кодовое расстояние (dij=2),
т.е. сделать разрешенными кодовые символы
отличающимися в двух элементах (001, 111,
010, 100), то помехозащищенность кода
увеличивается. Действительно, если в
процессе передачи возникает ошибка
только в одном элементе любого разрешенного
символа, то эта комбинация превращается
в запрещенную, что свидетельствует о
появлении одиночной ошибки в символе
кода, хотя и неизвестно какой именно.
Такой код не позволяет выяснить какой
конкретно из передаваемых элементов
искажен, а значит и не позволяет исправить
ошибку.
Если
еще больше увеличить кодовое расстояние
(dij=3), т. е. сделать
разрешенными кодовые символы отличными
друг от друга в трех элементах (например,
111, 000), то помехозащищенность кода еще
более возрастает.
Действительно,
если в процессе передачи произойдет
ошибка в одном или двух элементах любого
из двух разрешенных символов кода, то
возникнет запрещенная комбинация
элементов. Таким образом, применение
этого кода дает возможность обнаружить
две или, если произойдет только одна
ошибка, что более вероятно, то можно
восстановить переданный символ кода.
Из
приведенного примера видно, что для
обнаружения единичной ошибки в символе
кода требуется один избыточный элемент
в символах кода, чтобы обеспечить
минимальное кодовое расстояние
(расстояние между разрешенными символами
(dij))
равное 2, а для исправления в символах
кода одной ошибки необходимо увеличить
минимальное кодовое расстояние между
символами кода (dij)
до 3, т. е. ввести в символы кода два
избыточных элемента. В общем случае для
избыточных кодов справедливо соотношение:
dij
= 1 + p + q ,
где
p ≥ q ;
p—
количество обнаруживаемых ошибок в
символах;
q—
количество исправляемых ошибок в
символах кода.
Свойства
корректирующих кодов по обнаружению и
исправлению ошибок, в зависимости от
величины минимального кодового расстояния
между разрешенными символами, приведены
в таблице 2.7.
Таблица
2.7
|
Характеристика |
Свойства |
||
|
d |
p |
q |
|
|
1 |
0 |
0 |
Отличает |
|
2 |
1 |
0 |
Обнаруживает |
|
3 |
1 |
1 |
Обнаруживает |
|
2 |
0 |
Обнаруживает |
|
|
4 |
2 |
1 |
Обнаруживает |
|
3 |
0 |
Обнаруживает |
|
|
5 |
2 |
2 |
Обнаруживает |
|
3 |
1 |
Обнаруживает |
|
|
4 |
0 |
Обнаруживает |
|
|
и |
2.
Коды, построенные на основе проверки
на четность.
Этот
метод построения помехозащищенных
кодов заключается в том, что в каждый
кодовый символ двоичного кода добавляется
для проверки один избыточный элемент
(0 или 1) так, чтобы общее количество
единиц в каждом символе кода было четным.
Построение такого кода на примере
двухэлементного двоичного кода
представлено в Таблице 2.8.
Таблица
2.8.
|
Неизбьггочные |
Kонтрольный |
Полные обнаруживающие единочную |
|
00 |
0 |
000 |
|
01 |
1 |
011 |
|
10 |
1 |
101 |
|
11 |
0 |
110 |
При
получении символов, таким образом
построенных избыточных кодов, перед их
раскодированием производится проверка
их на четность. При одиночной ошибке
количество единичных элементов в кодовом
символе станет нечетным, что дает
возможность обнаружить ошибку и
осуществить повторную передачу.
Близким
к рассмотренному способу построения
корректирующих кодов является способ
добавления контрольных избыточных
элементов, на основе суммирования по
основанию «2» элементов символов
двоичного кода и на основе простейших
логических операций над элементами
символов кода.
3.
На основе защиты сдвоенными элементами.
В
этом коде количество элементов в символах
двоичного кода удваивается, причем к
каждому элементу «0» приписывается «1»,
а к каждому элементу «1» приписывается
элемент «0». Например, исходный кодовый
символ 11010 по этому методу кодируется
следующим образом:

Рис.
2.7. Метод построения корректирующего
кода на основе защиты сдвоенными
элементами.
Полученный
корректирующий код позволяет обнаружить
одиночную ошибку в каждом разряде путем
сложения по модулю 2 каждой пары элементов
символа корректирующего кода. Если
вследствие единичного сбоя в какой-либо
паре сумма будет равна 0, то это является
сигналом ошибки в данном разряде.
-
Модуляция.
Аналого-цифровое преобразование
(только для ГИС).
Как
отмечалось в предыдущем параграфе, для
передачи сообщений формируются сигналы,
как правило, имеющие два вида параметров:
информационные и селекции.
Параметры
селекции позволяют выделить полезный
сигнал из совокупности сигналов и помех
и обеспечивают эффективную передачу
информацию по каналам связи. Информационные
параметры содержат необходимые сведения
о передаваемом сообщении, то есть именно
в изменении этих параметров и содержится
передаваемое сообщение.
Процесс,
при котором информационные параметры,
предназначенного для передачи сигнала
(сообщения) управляются в соответствии
с законом изменения сформированного и
непосредственно передаваемого по каналу
связи сигнала, будем называть модуляцией.
Сформулированный таким образом
передаваемый сигнал будем называть
модулированным. При этом сигнал,
соответствующий закону изменения
информационного параметра будем называть
модулирующим, сигнал, полученный в
результате преобразования – модулированным,
а сигнал-переносчик – модулируемым.
Модуляцией
называют преобразование одного сигнала,
называемого сигналом-переносчиком
(носителем), в другой сигнал путём
управления информационным параметром
сигнала-переносчика в соответствии с
законом изменения передаваемого
сообщения. Сигнал-переносчик – это
материальная основа, представляющая
собой некий процесс или объект, который
становится носителем информации в
процессе модуляции.
Если
обозначить сигнал-переносчик через
,
передаваемое сообщение через
,
то при модуляции выполняется преобразование
двух сигналов
и
в один модулированный сигнал
,
то есть
.
(1.2)
Для
выделения переданного сообщения
из
необходимо произвести демодуляцию –
преобразование, описываемое оператором
демодуляции D, то есть
.
(1.3)
В
качестве сигнала-переносчика
используются различные виды сигналов.
Если
в качестве сигнала-переносчика выступает
непрерывный сигнал, то говорят о
непрерывных видах модуляции.
В
случае использования в качестве
сигнала-переносчика периодической
последовательности импульсов, говорят
об импульсных видах модуляции.
Модуляции,
при которых информационный параметр
принимает конечное число различных
значений, называют дискретными.
Если
значения сигнала, полученные при
дискретной модуляции, кодируют и передают
в виде цифр, то говорят о цифровой
модуляции, которая используется при
цифровой обработке сигналов.
Классификация
различных видов модуляции обычно
выполняют исходя из:
вида
сигнала-переносчика;
информационного
параметра сигнала;
вида
передаваемого сигнала или сообщения.
Таблица
1.1. иллюстрирует принятую ГОСТом
классификацию различных видов модуляции,
исходя из вида сигнала-переносчика
и вид модулируемого сигнала
.
В
таблице приняты следующие обозначения
для видов модулирующих сигналов
:
A
– детерминированные непрерывные
сигналы;
B
– детерминированные дискретные
последовательности;
C
– случайные стационарные неперывные
сигналы;
D
– случайные стационарные последовательности;
E
– случайные нестационарные непрерывные
сигналы;
F
– случайные нестационарные
последовательности;
G
– дискретные случайные стационарные
последовательности;
H
– дискретные случайные нестационарные
последовательности.
Аналогичные
виды сигналов-переносчиков обозначены
соответсвенно цифрами 1-8.
Таблица
1.1.
|
Виды |
Виды |
|||||||
|
A |
B |
C |
D |
E |
F |
G |
H |
|
|
1 |
A1 |
B1 |
C1 |
D1 |
E1 |
F1 |
G1 |
H1 |
|
2 |
A2 |
B2 |
C2 |
D2 |
E2 |
F2 |
G2 |
H2 |
|
3 |
A3 |
B3 |
C3 |
D3 |
E3 |
F3 |
G3 |
H3 |
|
|
: |
: |
: |
: |
: |
: |
: |
: |
|
8 |
A8 |
B8 |
C8 |
D8 |
E8 |
F8 |
G8 |
H8 |
Выбор
используемого вида модуляции в основном
определяется:
видом
модулирующего сигнала или сообщения;
свойством
канала;
потенциальной
помехустойчивостью;
сложностью
технической реализации;
Как
было показано в §1, для передачи информации
могут использоваться только случайные
сигналы и последовательности, так как
детерминированный сигнал, значения
которого известны, в любой момент
времени, не несет никакой информации.
Поэтому для передачи сообщений не могут
использоваться модулирующие сигналы
А и В.
-
Дискретизация
по уровню и квантование по времени
(только для ГИС).
Дискретизация
по уровню (квантование по уровню)
Сущность
дискретизации (квантовании) по уровню,
как нелинейного преобразования,
заключается в том, что все отсчеты
непрерывного сигнала
,
попадающие в интервал дискретизации
,
представляются одним значением
,
которое называется квантованным. Таким
образом, происходит преобразование
непрерывного сигнала в дискретный.
Процесс дискретизации по уровню
определен, если задана характеристика
дискретизации или квантования (рис.1.3),
которая связывает интервалы дискретизации
и квантованные значения, то есть каждому
интервалу дискретизации ставится в
соответствие квантованное значение
.
Часто интервалы квантования выбирают
одинаковыми и тогда говорят, что
квантование происходит с постоянным
шагом.
Характерной
особенностью операции квантования по
уровню является то, что квантованный
сигнал отличается от оригинала даже
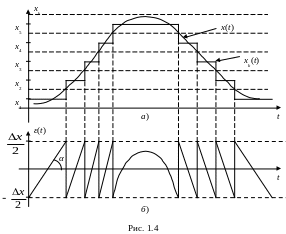
при полном отсутствии шумов. Действительно,
если на вход устройства квантования
подается сигнал
,
а на выходе получаем квантованный сигнал
,
то они будут отличаться друг от друга
на величину
(рис.1.4а).
.
Величину
называют шумом квантования, так как
искажения, вызываемые квантованием по
уровню равносильны искажениям, вызванные
источником шума, то есть искажения
рассматриваются как шум, вводимый в
систему при квантовании. Частота этого
шума зависит от частоты квантуемого
сигнала и превышает его.
Максимальная
амплитуда шума равна шагу квантования,
и поэтому для уменьшения шума необходимо
уменьшать шаг квантования.
Для
определения среднеквадратического
значения ошибки квантования по уровню
предположим, что непрерывный сигнал
имеет равномерную плотность распределения,
интервалы дискретизации
одинаковы по величине и в качестве
квантованных значений
выбираются середины соответствующих
интервалов дискретизации. В этом случае,
при достаточно большом числе интервалов
дискретизации, ошибка квантования
может быть приближенно представлена в
виде графика, состоящего из отрезков
прямых линий с различными наклонами
(рис.1.4б). Эти отрезки ограничены снизу
и сверху половиной шага квантования,
исключения составляют шаги, в которых
сигнал либо минимален, либо максимален.
Если
шаги квантования малы, то среднеквадратическая
ошибка приближенно определяется
среднеквадратическим значением типичного
линейного отрезка.
Для
интервалов времени, заключенных между
и
,
то есть
,
(1.12)
можно
записать уравнение, определяющее
типичный линейный отрезок ошибки
,
(1.13)
где
— наклон отрезка;
t
— время отсчитывается от точки пересечения
отрезком оси t.
Тогда
среднеквадратическая ошибка квантования
может быть определена следующим
выражением:
.
(1.14)
Таким
образом, процесс квантования по уровню
вносит в сигнал шум квантования, причем
среднеквадратическая ошибка квантования
по уровню
зависит от шага квантования и определяется
равенством:
.
(1.15)
Следует
отметить, что полученное выражение
справедливо только в случае выполнения
ограничений, указанных выше и которые
описывают наиболее типичные условия
при выполнении операции дискретизации
по уровню.
В
случае если плотность распределения
сигнала
не постоянна или интервалы дискретизации
(
)
имеют различную величину или квантованное
значение
не равно середине интервала дискретизации
,
выражение для определения среднеквадратической
ошибки может иметь иной вид.
Следует
также отметить, что, как известно из
теории информации, среднее количество
информации (I), содержащееся
в сообщении x, которую
можно выделить из смеси полезного
сигнала и шума определяется выражением:
,
(1.16)
где
– энтропия принятого сообщения;
– энтропия
шума.
Таким
образом, квантование по уровню снижает
среднее количество информации,
содержащееся в сообщении.
Любое сообщение, может быть представлено в различной форме, то есть закодировано различными способами. Разные способы кодирования неравноценны по занимаемому ими количеству информации.
Оптимальным кодом будет тот, при использовании которого среднее значение энтропии, приходящееся на один символ, равно энтропии источника информации.
В большинстве случаев используемые системы кодирования обладают избыточностью, то есть требуют для записи большее количество информации, чем оно содержится в кодируемом сообщении.
Избыточность определяется формулой
[E = 1 — frac{H}{Q}]
где (H) — энтропия сообщения, (Q)- среднее количество информации, приходящееся на один символ кодированного сообщения.
Чем выше избыточность кода, тем больше вероятность безошибочной передачи информации, но тем больший объём требуется для её хранения и большая пропускная способность канала передачи. Естественные человеческие языки характеризуются очень высокой степенью избыточности, также велика избыточность генома высших организмов, хранящегося в молекулах ДНК.
Величина (H /Q) называется экономичностью кода.
Для оптимального кода (H /Q=1) а избыточность отсутствует, то есть (E = 0).
Процесс уменьшения избыточности кодирования называется сжатием информации и применяется для понижения объёма памяти, требуемой для хранения информации. Для сжатия информации, хранящейся в памяти, используются– архиваторы и упаковщики.
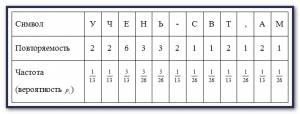
Пример: определить энтропию информации, содержащейся в сообщении «ученье − свет, а не ученье – тьма» и избыточность кода. Каждый символ в сообщении кодируется 1 байтом (8 бит).
Решение: Подсчитаем количество символов в сообщении, для простоты игнорируя пробелы: N=26. Найдём частоту повторения каждого символа (вероятность в сообщении), составив следующую таблицу, приведенную на скрине слева.
Удельная энтропия (энтропия одного символа в сообщении) в битах на символ, равна
[tilde H = 5 cdot frac{1}{{13}}{log _2}13 + frac{3}{{13}}{log _2}frac{{13}}{3} + 2 cdot frac{3}{{26}}{log _2}frac{{26}}{3} + 4 cdot frac{1}{{26}}{log _2}26 approx ]
[ approx frac{5}{{13}} cdot 3.7004 + frac{3}{{13}} cdot 2.1155 + frac{6}{{26}} cdot 3.1155 + frac{4}{{26}} cdot 4.7004 approx 3.3535]
Полная энтропия сообщения (H = 3.3535 cdot 26 = 87.19) бит.
Количество бит, необходимое для кодирования каждого символа одним байтом, составляет (Q = 208;) бит.
Избыточность кода (E=1-87.19/208=0.58=58%).
Похожие публикации: информатика
Избыточное кодирование (англ. redundant encoding) — вид кодирования, использующий избыточное количество информации с целью последующего контроля целостности данных при записи/воспроизведении информации или при её передаче по линиям связи.
| Определение: |
| Код определяет ошибок, если при передаче кодового слова, в котором ошибок, алгоритм декодирования скажет, что есть ошибка. |
| Определение: |
| Код исправляет ошибок, если при передаче кодового слова, в котором ошибок, алгоритм декодирования сможет восстановить исходное слово. |
Код, определяющий одну ошибку
Увеличив объем кода на бит, можно получить возможность определять при передаче наличие одной ошибки. Для этого к коду нужно добавить бит : , такой, чтобы сумма всех единиц была четной. В случае, если контрольная сумма окажется нечетной, следует отправить запрос на повторную посылку элемента, в котором была обнаружена ошибка. Такое кодирование применяется только если вероятность ошибки крайне мала, например, в оперативной памяти компьютера.
Кодирование Хэмминга
Кодирование Хэмминга предусматривает как возможность обнаружения ошибки, так и возможность её исправления.
Рассмотрим простой пример — закодируем четыре бита: . Полученный код будет иметь длину бит и выглядеть следующим образом:
Рассмотрим табличную визуализацию кода:
Как видно из таблицы, даже если один из битов передался с ошибкой, содержащие его -суммы не сойдутся. Итого, зная строку и столбец в проиллюстрированной таблице можно точно исправить ошибочный бит. Если один из битов передался с ошибкой, то не сойдется только одна сумма и очевидно, что можно легко определить, какой бит неверный
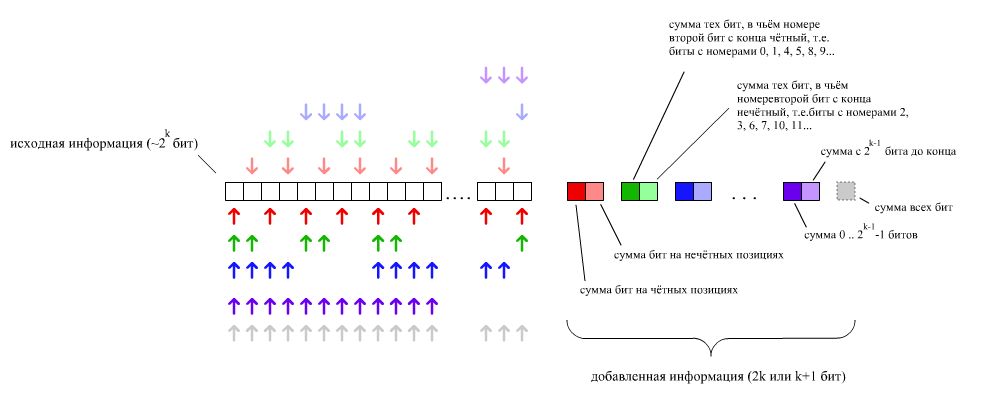
По аналогичному принципу можно закодировать любое число бит. Пусть мы имеем исходную строку длиной в бит. Для получения её кода добавим к ней пар бит по следующему принципу:
- Первая пара: сумма четных бит и сумма нечетных бит
- Вторая пара: сумма тех бит, в чьем номере второй бит с конца ноль и сумма тех бит, в чьем номере второй бит с конца единица
…
- -тая пара: сумма тех бит, в чьем номере -тый бит с конца ноль и сумма тех бит, в чьем номере -тый бит с конца единица
Соответствие добавленной информации исходным битам. Первый вариант кодирования соответствует использованию битов, раскрашенных в тёмные и светлые цвета, оптимизация — в тёмные цвета и серый
Легко понять, что если в одном бите из строки допущена ошибка, то с помощью дописанных пар бит можно точно определить, какой именно бит ошибочный. Это объясняется тем, что каждая пара определяет один бит номера ошибочного бита в строке. Всего пар , следовательно мы имеем бит номера ошибочного бита, что вполне достаточно: общее число бит строки не превосходит .
Теперь заметим, что в случае наличия ошибки в исходной строке, ровно один бит в каждой паре будет равен единице. Тогда можно оставить только один бит из пары. Однако этого будет недостаточно, поскольку если только один добавленный бит не соответствует строке, то нельзя понять, ошибка в нём или в строке. На этот случай можно добавить ещё один контрольный бит — всех битов строки.
Итого, увеличивая код длиной на , можно обнаружить и исправить одну ошибку.
См. также
- Обнаружение и исправление ошибок кодирования
Источники информации
- Wikipedia — Hamming code