Как найти излучательную способность

From Wikipedia, the free encyclopedia

The emissivity of the surface of a material is its effectiveness in emitting energy as thermal radiation. Thermal radiation is electromagnetic radiation that most commonly includes both visible radiation (light) and infrared radiation, which is not visible to human eyes. A portion of the thermal radiation from very hot objects (see photograph) is easily visible to the eye.

The emissivity of a surface depends on its chemical composition and geometrical structure. Quantitatively, it is the ratio of the thermal radiation from a surface to the radiation from an ideal black surface at the same temperature as given by the Stefan–Boltzmann law. The ratio varies from 0 to 1. The surface of a perfect black body (with an emissivity of 1) emits thermal radiation at the rate of approximately 448 watts per square metre at room temperature (25 °C, 298.15 K). All real objects have emissivities less than 1.0, and emit radiation at correspondingly lower rates.^[1]

Emissivities are important in several contexts:

Insulated windows: Warm surfaces are usually cooled directly by air, but they also cool themselves by emitting thermal radiation. This second cooling mechanism is important for simple glass windows, which have emissivities close to the maximum possible value of 1.0. «Low-E windows» with transparent low-emissivity coatings emit less thermal radiation than ordinary windows.^[2] In winter, these coatings can halve the rate at which a window loses heat compared to an uncoated glass window.^[3]

Solar water heating system based on evacuated glass tube collectors. Sunlight is absorbed inside each tube by a selective surface. The surface absorbs sunlight nearly completely, but has a low thermal emissivity so that it loses very little heat. Ordinary black surfaces also absorb sunlight efficiently, but they emit thermal radiation copiously.

Solar heat collectors: Similarly, solar heat collectors lose heat by emitting thermal radiation. Advanced solar collectors incorporate selective surfaces that have very low emissivities. These collectors waste very little of the solar energy through emission of thermal radiation.^[4]
Thermal shielding: For the protection of structures from high surface temperatures, such as reusable spacecraft or hypersonic aircraft, high-emissivity coatings (HECs), with emissivity values near 0.9, are applied on the surface of insulating ceramics.^[5] This facilitates radiative cooling and protection of the underlying structure and is an alternative to ablative coatings, used in single-use reentry capsules.
Passive daytime radiative cooling: Daytime passive radiative coolers use the extremely cold temperature of outer space (~2.7 K) to emit heat and lower ambient temperatures while requiring zero energy input.^[6] These surfaces minimize the absorption of solar radiation to lessen heat gain in order to maximize the emission of LWIR thermal radiation.^[7] It has been proposed as a solution to global warming.^[8]
Planetary temperatures: The planets are solar thermal collectors on a large scale. The temperature of a planet’s surface is determined by the balance between the heat absorbed by the planet from sunlight, heat emitted from its core, and thermal radiation emitted back into space. Emissivity of a planet is determined by the nature of its surface and atmosphere.^[9]
Temperature measurements: Pyrometers and infrared cameras are instruments used to measure the temperature of an object by using its thermal radiation; no actual contact with the object is needed. The calibration of these instruments involves the emissivity of the surface that’s being measured.^[10]

Mathematical definitions[edit]

Hemispherical emissivity[edit]

Hemispherical emissivity of a surface, denoted ε, is defined as^[11]

$varepsilon ={frac {M_{{mathrm {e}}}}{M_{{mathrm {e}}}^{circ }}},$

where

M_e is the radiant exitance of that surface;
M_e° is the radiant exitance of a black body at the same temperature as that surface.

Spectral hemispherical emissivity[edit]

Spectral hemispherical emissivity in frequency and spectral hemispherical emissivity in wavelength of a surface, denoted ε_ν and ε_λ, respectively, are defined as^[11]

${displaystyle {begin{aligned}varepsilon _{nu }&={frac {M_{mathrm {e} ,nu }}{M_{mathrm {e} ,nu }^{circ }}},\varepsilon _{lambda }&={frac {M_{mathrm {e} ,lambda }}{M_{mathrm {e} ,lambda }^{circ }}},end{aligned}}}$

where

M_e,ν is the spectral radiant exitance in frequency of that surface;
M_e,ν° is the spectral radiant exitance in frequency of a black body at the same temperature as that surface;
M_e,λ is the spectral radiant exitance in wavelength of that surface;
M_e,λ° is the spectral radiant exitance in wavelength of a black body at the same temperature as that surface.

Directional emissivity[edit]

Directional emissivity of a surface, denoted ε_Ω, is defined as^[11]

$varepsilon _{Omega }={frac {L_{{{mathrm {e}},Omega }}}{L_{{{mathrm {e}},Omega }}^{circ }}},$

where

L_e,Ω is the radiance of that surface;
L_e,Ω° is the radiance of a black body at the same temperature as that surface.

Spectral directional emissivity[edit]

Spectral directional emissivity in frequency and spectral directional emissivity in wavelength of a surface, denoted ε_ν,Ω and ε_λ,Ω, respectively, are defined as^[11]

${displaystyle {begin{aligned}varepsilon _{nu ,Omega }&={frac {L_{mathrm {e} ,Omega ,nu }}{L_{mathrm {e} ,Omega ,nu }^{circ }}},\varepsilon _{lambda ,Omega }&={frac {L_{mathrm {e} ,Omega ,lambda }}{L_{mathrm {e} ,Omega ,lambda }^{circ }}},end{aligned}}}$

where

L_e,Ω,ν is the spectral radiance in frequency of that surface;
L_e,Ω,ν° is the spectral radiance in frequency of a black body at the same temperature as that surface;
L_e,Ω,λ is the spectral radiance in wavelength of that surface;
L_e,Ω,λ° is the spectral radiance in wavelength of a black body at the same temperature as that surface.

Hemispherical emissivity can also be expressed as a weighted average of the directional spectral emissivities as described in textbooks on «radiative heat transfer».^[10]

Emissivities of common surfaces[edit]

Emissivities ε can be measured using simple devices such as Leslie’s cube in conjunction with a thermal radiation detector such as a thermopile or a bolometer. The apparatus compares the thermal radiation from a surface to be tested with the thermal radiation from a nearly ideal, black sample. The detectors are essentially black absorbers with very sensitive thermometers that record the detector’s temperature rise when exposed to thermal radiation. For measuring room temperature emissivities, the detectors must absorb thermal radiation completely at infrared wavelengths near 10×10⁻⁶ metre.^[12] Visible light has a wavelength range of about 0.4–0.7×10⁻⁶ metre from violet to deep red.

Emissivity measurements for many surfaces are compiled in many handbooks and texts. Some of these are listed in the following table.^[13]^[14]

Photographs of an aluminium Leslie’s cube. The color photographs are taken using an infrared camera; the black and white photographs underneath are taken with an ordinary camera. All faces of the cube are at the same temperature of about 55 °C (131 °F). The face of the cube that has been painted (black or white paint has negligible impact) has a large emissivity, which is indicated by the reddish color in the infrared photograph. The polished face of the cube has a low emissivity indicated by the blue color, and the reflected image of the warm hand is clear.

Material	Emissivity
Aluminium foil	0.03
Aluminium, anodized	0.9^[15]
Aluminium, smooth, polished	0.04
Aluminium, rough, oxidized	0.2
Asphalt	0.88
Brick	0.90
Concrete, rough	0.91
Copper, polished	0.04
Copper, oxidized	0.87
Glass, smooth uncoated	0.95
Ice	0.97-0.99
Iron, polished	0.06
Limestone	0.92
Marble, polished	0.89–0.92
Nitrogen or Oxygen gas layer, pure	~0^[16]
Paint, including white	0.9
Paper, roofing or white	0.88–0.86
Plaster, rough	0.89
Silver, polished	0.02
Silver, oxidized	0.04
Skin, human	0.97–0.999
Snow	0.8–0.9
Polytetrafluoroethylene (Teflon)	0.85
Transition metal disilicides (e.g. MoSi₂ or WSi₂)	0.86–0.93^[5]
Vegetation	0.92-0.96
Water, pure	0.96

Notes:

These emissivities are the total hemispherical emissivities from the surfaces.
The values of the emissivities apply to materials that are optically thick. This means that the absorptivity at the wavelengths typical of thermal radiation doesn’t depend on the thickness of the material. Very thin materials emit less thermal radiation than thicker materials.
Most emissitivies in the chart above were recorded at room temperature (300 K).

[edit]

Absorptivity[edit]

There is a fundamental relationship (Gustav Kirchhoff’s 1859 law of thermal radiation) that equates the emissivity of a surface with its absorption of incident radiation (the «absorptivity» of a surface). Kirchhoff’s law is rigorously applicable with regard to the spectral directional definitions of emissivity and absorptivity. The relationship explains why emissivities cannot exceed 1, since the largest absorptivity—corresponding to complete absorption of all incident light by a truly black object—is also 1.^[10] Mirror-like, metallic surfaces that reflect light will thus have low emissivities, since the reflected light isn’t absorbed. A polished silver surface has an emissivity of about 0.02 near room temperature. Black soot absorbs thermal radiation very well; it has an emissivity as large as 0.97, and hence soot is a fair approximation to an ideal black body.^[17]^[18]

With the exception of bare, polished metals, the appearance of a surface to the eye is not a good guide to emissivities near room temperature. For example, white paint absorbs very little visible light. However, at an infrared wavelength of 10×10⁻⁶ metre, paint absorbs light very well, and has a high emissivity. Similarly, pure water absorbs very little visible light, but water is nonetheless a strong infrared absorber and has a correspondingly high emissivity.

Emittance[edit]

Emittance (or emissive power) is the total amount of thermal energy emitted per unit area per unit time for all possible wavelengths. Emissivity of a body at a given temperature is the ratio of the total emissive power of a body to the total emissive power of a perfectly black body at that temperature. Following Planck’s law, the total energy radiated increases with temperature while the peak of the emission spectrum shifts to shorter wavelengths. The energy emitted at shorter wavelengths increases more rapidly with temperature. For example, an ideal blackbody in thermal equilibrium at 1,273 K, will emit 97% of its energy at wavelengths below 14 μm.^[5]

The term emissivity is generally used to describe a simple, homogeneous surface such as silver. Similar terms, emittance and thermal emittance, are used to describe thermal radiation measurements on complex surfaces such as insulation products.^[19]^[20]^[21]

Measurement of Emittance[edit]

Emittance of a surface can be measured directly or indirectly from the emitted energy from that surface. In the direct radiometric method, the emitted energy from the sample is measured directly using a spectroscope such as Fourier transform infrared spectroscopy (FTIR).^[22] In the indirect calorimetric method, the emitted energy from the sample is measured indirectly using a calorimeter. In addition to these two commonly applied methods, inexpensive emission measurement technique based on the principle of two-color pyrometry.^[23]

Emissivities of planet Earth[edit]

A typical spectrum of Earth’s total outgoing (upwelling) thermal radiation flux under clear-sky conditions, as simulated with MODTRAN. Planck curves are also shown for a range of Earth temperatures.

The emissivity of a planet or other astronomical body is determined by the composition and structure of its outer skin. In this context, the «skin» of a planet generally includes both its semi-transparent atmosphere and its non-gaseous surface. The resulting radiative emissions to space typically function as the primary cooling mechanism for these otherwise isolated bodies. The balance between all other incoming plus internal sources of energy versus the outgoing flow regulates planetary temperatures.^[24]

For Earth, equilibrium skin temperatures range near the freezing point of water (260K±50K). The most energetic emissions are thus within a band spanning about 4-50 μm as governed by Planck’s law.^[25] Emissivities for the atmosphere and surface components are often quantified separately, and validated against satellite- and terrestrial-based observations as well as laboratory measurements. These emissivities serve as input parameters within some meteorlogic and climatologic models.

Earth’s surface emissivities (ε_s) have been inferred with satellite-based instruments by directly observing surface thermal emissions at nadir through a less obstructed atmospheric window spanning 8-13 μm.^[26] Values range about ε_s=0.65-0.99, with lowest values typically limited to the most barren desert areas. Emissivities of most surface regions are above 0.9 due to the dominant influence of water; including oceans, land vegetation, and snow/ice. Globally averaged estimates for the hemispheric emissivity of Earth’s surface are in the vicinity of ε_s=0.95.^[27]

A typical spectrum of infrared radiation transmittance through Earth’s atmosphere. A ‘window’ can be seen between 8 and 14 μm that enables direct transmission of the most intense thermal emissions from Earth’s surface. The remaining portion of the upwelling energy, as well as downwelling radiation back to the surface, undergoes absorption and emission by the various atmospheric components as indicated.

Water also dominates the planet’s atmospheric emissivity and absorptivity in the form of water vapor. Clouds, carbon dioxide, and other components make substantial additional contributions, especially where there are gaps in the water vapor absorption spectrum.^[28] Nitrogen (N
₂) and oxygen (O
₂) — the primary atmospheric components — interact less significantly with thermal radiation in the infrared band.^[29] Direct measurement of Earths atmospheric emissivities (ε_a) are more challenging than for land surfaces due in part to the atmosphere’s multi-layered and more dynamic structure.

Upper and lower limits have been measured and calculated for ε_a in accordance with extreme yet realistic local conditions. At the upper limit, dense low cloud structures (consisting of liquid/ice aerosols and saturated water vapor) close the infrared transmission windows, yielding near to black body conditions with ε_a≈1.^[30] At a lower limit, clear sky (cloud-free) conditions promote the largest opening of transmission windows. The more uniform concentration of long-lived trace greenhouse gases in combination with water vapor pressures of 0.25-20 mbar then yield minimum values in the range of ε_a=0.55-0.8 (with ε=0.35-0.75 for a simulated water-vapor-only atmosphere).^[31] Carbon dioxide (CO
₂) and other greenhouse gases contribute about ε=0.2 to ε_a when atmospheric humidity is low.^[32]

Researchers have also evaluated the contribution of differing cloud types to atmospheric absorptivity and emissivity.^[33]^[34]^[35] These days, the detailed processes and complex properties of radiation transport through the atmosphere are evaluated with radiation transport codes and databases such as MODTRAN/HITRAN. «Effective» atmospheric emissivites for downwelling and upwelling thermal radiation are thereby simulated, and compared to similar results obtained from ground and satellite observations.^[31] An effective global value of ε_a≈0.78 has been estimated from application of an idealized energy-balance model to the planet.^[36]

History[edit]

The concepts of emissivity and absorptivity, as properties of matter and radiation, appeared in the late-eighteenth thru mid-nineteenth century writings of Pierre Prévost, John Leslie, Balfour Stewart and others.^[37]^[38]^[39] In 1860, Gustav Kirchhoff published a mathematical description of their relationship under conditions of thermal equilibrium (i.e. Kirchoff’s law of thermal radiation).^[40] By 1884 the emissive power of a perfect blackbody was inferred by Josef Stefan using John Tyndall’s experimental measurements, and derived by Ludwig Boltzmann from fundamental statistical principles.^[41] Emissivity, defined as a further proportionality factor to the Stefan-Boltzmann law, was thus implied and utilized in subsequent evaluations of the radiative behavior of grey bodies. For example, Svante Arrhenius applied the recent theoretical developments to his 1896 investigation of Earth’s surface temperatures as calculated from the planet’s radiative equilibrium with all of space.^[42] By 1900 Max Planck empirically derived a generalized law of blackbody radiation, thus clarifying the emissivity and absorptivity concepts at individual wavelengths.^[43]

Other radiometric coefficients[edit]

Radiometry coefficients

Quantity	SI units	Notes
Name	Sym.
Hemispherical emissivity	ε	—	Radiant exitance of a surface, divided by that of a black body at the same temperature as that surface.
Spectral hemispherical emissivity	ε_ν ε_λ	—	Spectral exitance of a surface, divided by that of a black body at the same temperature as that surface.
Directional emissivity	ε_Ω	—	Radiance emitted by a surface, divided by that emitted by a black body at the same temperature as that surface.
Spectral directional emissivity	ε_Ω,ν ε_Ω,λ	—	Spectral radiance emitted by a surface, divided by that of a black body at the same temperature as that surface.
Hemispherical absorptance	A	—	Radiant flux absorbed by a surface, divided by that received by that surface. This should not be confused with «absorbance».
Spectral hemispherical absorptance	A_ν A_λ	—	Spectral flux absorbed by a surface, divided by that received by that surface. This should not be confused with «spectral absorbance».
Directional absorptance	A_Ω	—	Radiance absorbed by a surface, divided by the radiance incident onto that surface. This should not be confused with «absorbance».
Spectral directional absorptance	A_Ω,ν A_Ω,λ	—	Spectral radiance absorbed by a surface, divided by the spectral radiance incident onto that surface. This should not be confused with «spectral absorbance».
Hemispherical reflectance	R	—	Radiant flux reflected by a surface, divided by that received by that surface.
Spectral hemispherical reflectance	R_ν R_λ	—	Spectral flux reflected by a surface, divided by that received by that surface.
Directional reflectance	R_Ω	—	Radiance reflected by a surface, divided by that received by that surface.
Spectral directional reflectance	R_Ω,ν R_Ω,λ	—	Spectral radiance reflected by a surface, divided by that received by that surface.
Hemispherical transmittance	T	—	Radiant flux transmitted by a surface, divided by that received by that surface.
Spectral hemispherical transmittance	T_ν T_λ	—	Spectral flux transmitted by a surface, divided by that received by that surface.
Directional transmittance	T_Ω	—	Radiance transmitted by a surface, divided by that received by that surface.
Spectral directional transmittance	T_Ω,ν T_Ω,λ	—	Spectral radiance transmitted by a surface, divided by that received by that surface.
Hemispherical attenuation coefficient	μ	m⁻¹	Radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume.
Spectral hemispherical attenuation coefficient	μ_ν μ_λ	m⁻¹	Spectral radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume.
Directional attenuation coefficient	μ_Ω	m⁻¹	Radiance absorbed and scattered by a volume per unit length, divided by that received by that volume.
Spectral directional attenuation coefficient	μ_Ω,ν μ_Ω,λ	m⁻¹	Spectral radiance absorbed and scattered by a volume per unit length, divided by that received by that volume.

References[edit]

^ The Stefan–Boltzmann law is that the rate of emission of thermal radiation is σT⁴, where σ = 5.67×10⁻⁸ W/m²·K⁴, and the temperature T is in kelvins. See Trefil, James S. (2003). The Nature of Science: An A-Z Guide to the Laws and Principles Governing Our Universe. Houghton Mifflin Harcourt. p. 377. ISBN 9780618319381.
^ «The Low-E Window R&D Success Story» (PDF). Windows and Building Envelope Research and Development: Roadmap for Emerging Technologies. U.S. Department of Energy. February 2014. p. 5.
^ Fricke, Jochen; Borst, Walter L. (2013). Essentials of Energy Technology. Wiley-VCH. p. 37. ISBN 978-3527334162.
^ Fricke, Jochen; Borst, Walter L. (2013). «9. Solar Space and Hot Water Heating». Essentials of Energy Technology. Wiley-VCH. p. 249. ISBN 978-3527334162.
^ ^a ^b ^c Shao, Gaofeng; et al. (2019). «Improved oxidation resistance of high emissivity coatings on fibrous ceramic for reusable space systems». Corrosion Science. 146: 233–246. arXiv:1902.03943. doi:10.1016/j.corsci.2018.11.006. S2CID 118927116.
^ Aili, Ablimit; Yin, Xiaobo; Yang, Ronggui (October 2021). «Global Radiative Sky Cooling Potential Adjusted for Population Density and Cooling Demand». Atmosphere. 12 (11): 1379. doi:10.3390/atmos12111379.
^ Aili, Ablimit; Yin, Xiaobo; Yang, Ronggui (October 2021). «Global Radiative Sky Cooling Potential Adjusted for Population Density and Cooling Demand». Atmosphere. 12 (11): 1379. doi:10.3390/atmos12111379.
^ Chen, Meijie; Pang, Dan; Chen, Xingyu; Yan, Hongjie; Yang, Yuan (2022). «Passive daytime radiative cooling: Fundamentals, material designs, and applications». EcoMat. 4. doi:10.1002/eom2.12153. S2CID 240331557 – via Wiley. Passive daytime radiative cooling (PDRC) dissipates terrestrial heat to the extremely cold outer space without using any energy input or producing pollution. It has the potential to simultaneously alleviate the two major problems of energy crisis and global warming.
^ «Climate Sensitivity». American Chemical Society. Retrieved 2014-07-21.
^ ^a ^b ^c Siegel, Robert (2001). Thermal Radiation Heat Transfer, Fourth Edition. CRC Press. p. 41. ISBN 9781560328391.
^ ^a ^b ^c ^d «Thermal insulation — Heat transfer by radiation — Physical quantities and definitions». ISO 9288:2022. ISO catalogue. 1989. Retrieved 2015-03-15.
^ For a truly black object, the spectrum of its thermal radiation peaks at the wavelength given by Wien’s Law: λ_max = b/T, where the temperature T is in kelvins and the constant b ≈ 2.90×10⁻³ metre-kelvins. Room temperature is about 293 kelvins. Sunlight itself is thermal radiation originating from the hot surface of the sun. The sun’s surface temperature of about 5800 kelvins corresponds well to the peak wavelength of sunlight, which is at the green wavelength of about 0.5×10⁻⁶ metres. See Saha, Kshudiram (2008). The Earth’s Atmosphere: Its Physics and Dynamics. Springer Science & Business Media. p. 84. ISBN 9783540784272.
^ Brewster, M. Quinn (1992). Thermal Radiative Transfer and Properties. John Wiley & Sons. p. 56. ISBN 9780471539827.
^ 2009 ASHRAE Handbook: Fundamentals — IP Edition. Atlanta: American Society of Heating, Refrigerating and Air-Conditioning Engineers. 2009. ISBN 978-1-933742-56-4. «IP» refers to inch and pound units; a version of the handbook with metric units is also available. Emissivity is a simple number, and doesn’t depend on the system of units.
^ The visible color of an anodized aluminum surface does not strongly affect its emissivity. See «Emissivity of Materials». Electro Optical Industries, Inc. Archived from the original on 2012-09-19.
^ Trogler, William C. (1995). «The Environmental Chemistry of Trace Atmospheric Gases». Journal of Chemical Education. 72 (11): 973. Bibcode:1995JChEd..72..973T. doi:10.1021/ed072p973.
^ «Table of Total Emissivity» (PDF). Archived from the original (PDF) on 2009-07-11. Table of emissivities provided by a company; no source for these data is provided.
^ «Influencing factors». evitherm Society — Virtual Institute for Thermal Metrology. Archived from the original on 2014-01-12. Retrieved 2014-07-19.
^ «ASTM C835 — 06(2013)e1: Standard Test Method for Total Hemispherical Emittance of Surfaces up to 1400°C». ASTM International. Retrieved 2014-08-09.
^ Kruger, Abe; Seville, Carl (2012). Green Building: Principles and Practices in Residential Construction. Cengage Learning. p. 198. ISBN 9781111135959.
^ Saad, Abdullah A.; Martinez, Carlos; Trice, Rodney W. (2023-02-13). «Radiation heat transfer during hypersonic flight: A review of emissivity measurement and enhancement approaches of ultra‐high temperature ceramics». International Journal of Ceramic Engineering & Science. doi:10.1002/ces2.10171. ISSN 2578-3270.
^ Saad, Abdullah A.; Martinez, Carlos; Trice, Rodney W. (2023-02-13). «Radiation heat transfer during hypersonic flight: A review of emissivity measurement and enhancement approaches of ultra‐high temperature ceramics». International Journal of Ceramic Engineering & Science. doi:10.1002/ces2.10171. ISSN 2578-3270.
^ Saad, Abdullah A.; Martinez, Carlos; Trice, Rodney W. (2023-02-13). «Radiation heat transfer during hypersonic flight: A review of emissivity measurement and enhancement approaches of ultra‐high temperature ceramics». International Journal of Ceramic Engineering & Science. doi:10.1002/ces2.10171. ISSN 2578-3270.
^ «Climate and Earth’s Energy Budget». NASA Earth Observatory. 14 January 2009. Retrieved 10 October 2022.
^ Petty, Grant W. (2006). A first course in atmospheric radiation (2 ed.). Madison, Wisc.: Sundog Publ. p. 68. ISBN 978-0972903318.
^ «ASTER global emissivity database: 100 times more detailed than its predecessor». NASA Earth Observatory. Retrieved 10 October 2022.
^ «Joint Emissivity Database Initiative». NASA Jet Propulsion Laboratory. Retrieved 10 October 2022.
^ «Remote Sensing: Absorption Bands and Atmospheric Windows». NASA Earth Observatory. 17 September 1999. Retrieved 28 October 2022.
^ Höpfner, M.; Milz, M.; Buehler, S.; Orphall, J.; Stiller, G. (24 May 2012). «The natural greenhouse effect of atmospheric oxygen (O₂) and nitrogen (N₂)». Geophysical Research Letters. 39 (L10706). Bibcode:2012GeoRL..3910706H. doi:10.1029/2012GL051409. ISSN 1944-8007. S2CID 128823108.
^ Liu, Lei; Zhang, Ting; Wu, Yi; Niu, Zhencong; Wang, Qi (2018). «Cloud Effective Emissivity Retrievals Using Combined Ground-Based Infrared Cloud Measuring Instrument and Ceilometer Observations». Remote Sensing. 10 (2033): 2033. Bibcode:2018RemS…10.2033L. doi:10.3390/rs10122033.
^ ^a ^b Mendoza, Victor M..; Vallanueva, Elba E.; Garduno, Rene; Sanchez-Meneses, Oscar (31 January 2017). «Atmospheric emissivity with clear sky computed by E-Trans/HITRAN». Atmospheric Environment. 155: 174–188. Bibcode:2017AtmEn.155..174M. doi:10.1016/j.atmosenv.2017.01.048. ISSN 1352-2310.
^ Staley, D.O.; Jurica, G.M. (1 March 1972). «Effective atmospheric emissivity under clear skies». Applied Meteorology and Climatology. 11 (2): 349–356. Bibcode:1972JApMe..11..349S. doi:10.1175/1520-0450(1972)011<0349:EAEUCS>2.0.CO;2.
^ Graham, Steve (1 March 1999). «Clouds and Radiation». NASA Earth Observatory. Retrieved 28 October 2022.
^ Cox, Stephen K. (1 February 1976). «Observations of cloud infrared effective emissivity». Atmospheric Sciences. 33 (2): 287–289. Bibcode:1976JAtS…33..287C. doi:10.1175/1520-0469(1976)033<0287:OOCIEE>2.0.CO;2.
^ Chylek, Petr; Ramaswamy, V. (1 January 1982). «Simple approximation of infrared emissivity of water clouds». Atmospheric Sciences. 39 (1): 171–177. Bibcode:1982JAtS…39..171C. doi:10.1175/1520-0469(1982)039<0171:SAFIEO>2.0.CO;2.
^ «ACS Climate Science Toolkit — Atmospheric Warming — A Single-Layer Atmosphere Model». American Chemical Society. Retrieved 1 December 2022.
^ Prévost, Pierre (April 1791). «Mémoire sur l’équilibre du feu». Observations Sur la Physique (in French). XXXVIII (1): 314–323.
^ Leslie, John (1804). An Experimental Inquiry into the Nature and Propagation of Heat. Edinburgh: J. Mawman.
^ Stewart, Balfour (1866). An Elementary Treatise on Heat. Oxford, Clarendon Press.
^ Kirchhoff, Gustav (1860). «Ueber das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme and Licht». Annalen der Physik und Chemie. 109 (2): 275–301. Bibcode:1860AnP…185..275K. doi:10.1002/andp.18601850205.
^ Boltzmann, Ludwig (1884). «Ableitung des Stefan’schen Gesetzes, betreffend die Abhängigkeit der Wärmestrahlung von der Temperatur aus der electromagnetischen Lichttheorie» [Derivation of Stefan’s law, concerning the dependency of heat radiation on temperature, from the electromagnetic theory of light]. Annalen der Physik und Chemie (in German). 258 (6): 291–294. Bibcode:1884AnP…258..291B. doi:10.1002/andp.18842580616.
^ Svante Arrhenius (1896). «On the influence of carbonic acid in the air upon the temperature of the ground». Philosophical Magazine and Journal of Science. 41 (251): 237–276. doi:10.1080/14786449608620846.
^ Planck, Max (1901). «Über das Gesetz der Energieverteilung im Normalspektrum». Annalen der Physik. 4 (3): 553–563. Bibcode:1901AnP…309..553P. doi:10.1002/andp.19013090310.

Вопрос 3. Абсолютно черное тело. Серое тело. Закон Кирхгофа.

Опыт
показывает, что любое реальное тело
поглощает излучение различных частот
по разному в зависимости от его
температуры. Поэтому спектральная
поглощательная способность тела
является функцией частотыν
и вид ее
изменяется при изменении температуры
тела T.

По
своему определению поглощательная
способность тела не может быть больше
единицы. При этом тело, у которого
поглощательная способность меньше
единицы и одинакова по всему диапазону
частот, называют серым
телом.

Особое
место в теории теплового излучения
занимает абсолютно
черное тело (АЧТ).
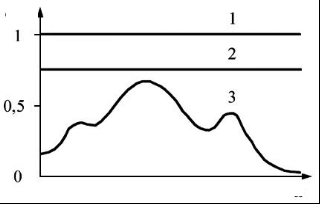
Так Г. Кирхгоф назвал тело, у которого
на всех частотах и при любых температурах
поглощательная способность равна
единице (рис. 16.2,1) . Линия 2 (рис. 16.2,2)
соответствует серому телу, которое
часть энергии отражает. Реальное же
тело всегда отражает часть энергии
падающего на него излучения (рис. 16.2,3),
при этом

Рис.
16.2. Рис. 16.3

поглощательная
способность может изменяться в широких
пределах. Даже сажа приближается по
свойствам к абсолютно черному телу лишь
в оптическом диапазоне.

Абсолютно
черное тело является эталонным телом
в теории теплового излучения. И, хотя в
природе нет абсолютно черного тела,
достаточно просто реализовать его
модель, для которой поглощательная
способность на всех частотах будет
пренебрежимо мало отличаться от единицы.
Такую модель абсолютно черного тела
можно изготовить в виде замкнутой
полости (рис. 16.3), снабженной малым
отверстием, диаметр которого значительно
меньше поперечных размеров полости.
Опыт показывает, что размер отверстия
должен быть меньше 0,1 диаметра полости.
При этом полость может иметь практически
любую форму и быть изготовленной из
любого материала. Если температуру
стенок поддерживать неизменной, то из
отверстия будет выходить излучение,
близкое по своему спектральному составу
к равновесному излучению АЧТ.

В
рассмотренной модели можно считать,
что излучение, падающее на отверстие,
не отражается, а полностью поглощается
внутри полости. Поэтому именно малому
отверстию и приписывается свойство
абсолютно черного тела.

Отметим,
что если стенки полости поддерживать
при некоторой температуре T,
то отверстие будет излучать, и это
излучение с большой степенью точности
можно считать излучением абсолютно
черного тела, имеющего температуру T
независимо от материала стенок.

Между
излучательными и поглощательными
свойствами любого тела должна существовать
связь. Ведь в опыте с равновесным тепловым
излучением (рис. 16.1) равновесие в системе
может установиться только в том случае,
если каждое тело будет излучать в единицу
времени столько же энергии, сколько оно
поглощает. При этом все тела будут
иметь температуру
,
равную температуре оболочки. Это
означает, что тела, интенсивнее поглощающие
излучение какой-либо частоты, будут это
излучение излучать более интенсивно.
Поэтому, в соответствии с таким
принципом детального равновесия,
отношение излучательной и поглощательной
способностей одинаково для всех тел в
природе, включая абсолютно черное тело,
и при данной температуре является одной
и той же универсальной функцией частоты
(длины волны).

Этот
закон теплового излучения, установленный
в 1859 г. Г. Кирхгофом при рассмотрении
термодинамических закономерностей
равновесных систем с излучением, можно
записать в виде соотношений:

, (16.8)

или

…,

где
индексы 1,2,3 и т.д. соответствуют различным
реальным телам.

Сам
закон формулируется следующим образом:

Отношение
излучательной способности любого тела
к его поглощательной способности не
зависит от природы тела и поэтому
является универсальной функцией частоты
и температуры,
т.е.

. (16.9)

Поскольку
поглощательная способность АЧТ
,
то из уравнения (16.9) следует, что
универсальная функция Кирхгофаявляется
спектральной
плотностью энергетической светимости
абсолютно черного тела.
Так как функция
не зависит от природы тел, установление
явного вида этой функции представляло
важную проблему для физиков.

Излучение
абсолютно черного тела имеет универсальный
характер в теории теплового излучения.
Реальное тело излучает при любой
температуре всегда меньше энергии, чем
абсолютно черное тело. Зная излучательную
способность абсолютно черного тела
(универсальную функцию Кирхгофа) и
поглощательную способность реального
тела, из закона Кирхгофа можно определить
энергию, излучаемую этим телом в любом
диапазоне частот или длин волн.

Закон
Кирхгофа описывает только тепловое
излучение тел, а излучение, которое не
подчиняется этому закону, не является
тепловым. Например, при фото — или
хемилюминесценции интенсивность
свечения в ряде спектральных областей
значительно больше, чем у теплового
излучения черного тела, находящегося
при той же температуре.

Соседние файлы в папке физика

Источник

Библиографическое описание:

Тураева, У. Ф. Определение излучательной способности стационарным методом / У. Ф. Тураева, Ш. Ф. Тураев, С. С. Ибрагимов. — Текст : непосредственный // Молодой ученый. — 2013. — № 7 (54). — С. 83-86. — URL: https://moluch.ru/archive/54/6786/ (дата обращения: 29.05.2023).

Обзор методов измерения интегральных радиационных характеристик материалов, проведенный в статьях показывает, что имеются следующие задачи для создания упрощенных методов измерения [1–2].

Так в широко используемом «радиационном методе» необходимо измерение трех параметров — температуры и плотности потока излучения, а также конвективных теплопотерь (при исключении конвективных теплопотерь, как видно необходимо измерение двух величин). Для исключения конвективных теплопотерь и необходимости измерения потока излучения в работах [3–4] была предложена упрощенная нестационарная методика определения интегральной излучательной способности (e_T). Где предлагалось исключение конвективных теплопотерь за счет проведения эксперимента одновременного с двумя образцами — один с известной e_T, второй рабочий. Обе методики были основаны на том, что при одинаковых температурах и для одинаковых перепадов температур оба образца имеют одинаковые конвективные теплопотери. Однако, как известно для нестационарных методов необходимы образцы с одинаковыми размерами и с известными теплофизическими характеристиками (теплоемкость, масса), при этом также необходимо измерять время. Оба эти методы были предложены, но не были реализованы, не была проведена и оценка погрешности этих методов.

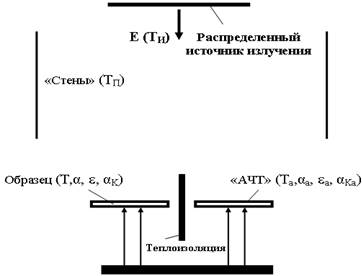
Анализ показал, что возможно развитие предложенных выше методов и разработка на этой основе стационарного метода — измерение излучательной способности по равновесным температурам. Схема нашего стационарного метода приведена на рис.1. Его особенность заключается в следующем. Берутся две тонкие плоские пластины, из одного рабочего материала толщиной порядка 1–5мм и одна из них покрывается сажей. Эти образцы, рабочий и «черный» нагреваются с помощью источника излучения. Измеряются равновесные температуры образцов. Далее, учитывая, что перепады температур в образцах малы, меньше 0.1градуса, а также пренебрегая теплопотерями через боковые стороны пластин и теплопотери через опорные ножки можем записать следующие уравнения баланса.

2_*e_1*s_*Т⁴ +2_* α_К1*(Т-Т₀) = α_1*Е_С + 2_*e_1*s_*Т_П⁴ (1)

2_*e_2*s_*Т_а⁴ +2_*α_К2*(Т_а-Т₀) = α_2*Е_С + 2_*e_1*s_*Т_П⁴ (2)

Рис. 1. Схема определения e_T по равновесным температурам.

При температурах источника близких к температурам нагрева можно также считать, что

α₁ = e₁ и α₂ = e₂ (3)

В этих уравнениях известны температуры образца и «АЧТ», температуры стен (измеряются), температура окружающего воздуха, измеряется и плотность падающего излучения E, а неизвестными являются коэффициенты конвективной теплоотдачи α_К1, α_К2.

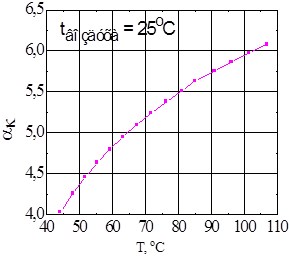
Т. е. из уравнения (2) мы определяем коэффициент конвективной теплоотдачи α_К2. Найдем связь между α_К2 и α_К1. В общем, характер конвективной теплоотдачи на обоих образцах одинаков (одинаковые условия), поэтому различия между ними обусловлены различием в температурах рабочего образца и «АЧТ». Зависимость коэффициента конвективной теплоотдачи от температуры для плоских пластин, охлаждаемых сверху, приведена на рис.2.

Рис. 2. Зависимость коэффициента естественной конвективной теплоотдачи от температуры плоской пластины охлаждаемой сверху.

Как показали предварительные эксперименты различие между температурами рабочего образца и «АЧТ» находится на уровне 10–15⁰, при этом как следует из рис.2. различие между α_К2 и α_К1 не превышает 5 %. Т. е. можно принять, что α_К1 = α_К2. Тогда определяя α_К2 из (2) и подставляя вместо α_К1 из (1) определяем излучательную способность образца. Отметим, что в случае вынужденной конвекции коэффициент теплоотдачи не зависит от температуры образцов, а зависит только от температуры окружающего воздуха.

Оценим основные составляющие относительной погрешности метода d. Они складываются из следующих случайных погрешностей:

Погрешность допущения о малости теплопотерь с боковой поверхности — d_S = 100 % _*(S_Б/(2_*S) = 100 %, которая при r_S = 30мм и h = 2мм равна d_S = 100 % (h /r_S) = 100_*0.033 = 3.3 %;

Погрешность определение температур образца и «АЧТ» термопарами — d_TO = 100 % _*(0.5/90) = 0.6 %;

Погрешность определения плотности падающего потока –d_ПАД 5 % (по паспорту);

Погрешность определение температура окружающего воздуха — d_В = 100 % *(0.2/25) = 0.8 %;

Погрешность допущения, что α_К1 = α_К2 составляет в случае естественной конвекции –d_αК = 5 %, в случае вынужденной конвекции d_αК = 0 %;

Погрешность определения температуры «стен» — d_CТ = 100 %_*(0.5/30) — 1.7 %;

Суммарную относительную погрешность d будем определять по формуле [5].

d = (d_S² + d_TO² +d_TАЧТ² +d_ПАД² +d_В²+d_αК² +d_CТ²)^0.5 = 8 % (4)

Следовательно, практически для всех тел можно определить интегральную излучательную способность и параметр селективности к солнечному излучению по её равновесной температуре, причем, так как равновесные температуры серого и черного тела одинаковы, то в качестве серого тела можно использовать зачерненный рабочий образец.

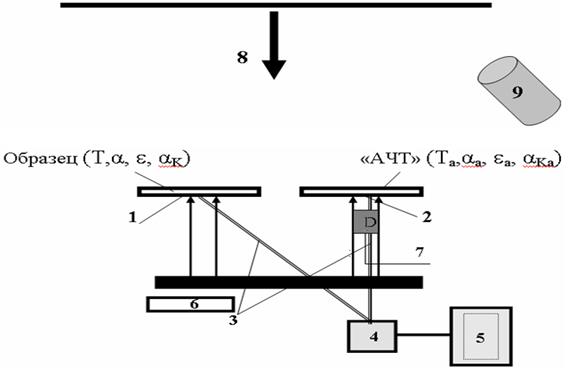
На рис.3 приведена схема установки для измерения излучательной способности, где: 1 — образец e_T, которого необходимо определить; 2 — «черный» образец с известной e_T; 3 — термопары типа ХА; 4 — переключатель; 5 — вольтметр; 6 — термометр; 7 — датчик для измерения потока излучения типа ФОА 022, 8 — распределенный источник излучения, 9 — стандартный актинометр для измерения прямой солнечной радиации с системой автоматического слежения за Солнцем.

Рис. 3. Схема установки для определения излучательной способности.

При разработке экспериментальной установки учитывались требования разработанной методики (см. [1]) — обеспечение равномерного потока на образцах, возможность исключения влияния на образцы остаточного излучения от источника после его выключения (при достижении образцами равновесной температуры), этим и было обусловлено использование кварцевых галогенных ламп, максимально возможное исключение утечек тепла через держатели образцов (игольчатые опоры для образцов), а также обеспечения возможности выполнения при измерениях условия равенства излучательной и поглощательной способности материала (за счет изменения температуры источника излучения). Общий вид экспериментальной установки для измерения излучательной способности e_T различных непрозрачных материалов приведен на рис.4.

Рис. 4. Экспериментальная установка для определения излуательной способности.

Порядок экспериментального определения e_T по разработанной выше методике заключался в следующем. На опорные ножки установки ставятся две пластины (рабочий и «черный») с предварительно закрепленными на их нижней стороны термопарами. Далее включается источник и по достижении образцами равновесных температур источник выключается. На основе полученных данных определяются

коэффициент конвективного теплообмена для черного образца

α_К = [e_Т.АЧТ*(Е_С -2_*s_*(Т_АЧТ⁴ — Т_B⁴)] / [2_*(Т_АЧТ — Т_B)] (5)

излучательная способность рабочего материала

e_Т.ОБР = [2_*α_К*(Т_ОБР-Т₀)] / (Е_С -2_*s_*(Т_ОБР⁴ — Т_B⁴) (6)

Для проверки экспериментальной установки и отработки методики вначале были проведены измерения e_T различных материалов с известными e_T медная и алюминиевая пластины. Было получено для медной пластины e_T = 0.44, а для алюминиевой e_T = 0.32. Эти данные с погрешностью от 8 % до 15 % согласуются с приведенными в литературе [2–4]. Большие отклонения значений e_T были обусловлены с тем, что в эксперименте использовались реальные пластины, и которые специально не обрабатывались. Далее, после отработки метода были исследованы излучательные способности некоторых широко применяемых материалов — краски (белая, красная, зеленая, синяя, черная и серая эмали) и строительные материалы (гипс, шамот, известняк). Цель этих исследований заключалась в определении в последующем их поглощательной способности к солнечному излучению.

Литература:

1. Абдурахманов А., Тураева У. Ф., Клычев Ш. И. Методика определения интегральной излучательной способности приемников солнечного излучения. // Гелиотехника, 2009. — № 4. — С. 62–64.

2. Михеев М. А., Михеева И. М. Основы теплопередачи. — М.: Энергия, 1977. — 344с.

3. Спэрроу Э. М., Сесс Р. Д., Теплообмен излучением. — М.: Энергия, 1977. — 294с.

4. Теплоэнергетика и теплотехника, Общие вопросы, книга 1, Справочник под ред. Григорьева В. А., Зорина В. М., — М.: Энергоиздат, 1987. — 455с.

Основные термины (генерируются автоматически): излучательная способность, конвективная теплоотдача, температура, экспериментальная установка, достижение образцами, зависимость коэффициента, рабочий материал, рабочий образец, стационарный метод, схема установки.

Источник

Задача 202

Условие: Определить излучательную способность поверхности Солнца, если известно, что ее температура равна t=5700ºС и условия излучения близки к излучению абсолютно черного тела. Вычислить также длину волны, при которой будет наблюдаться максимум спектральной интенсивности излучения и общее количество лучистой энергии, испускаемой Солнцем в единицу времени. Диаметр Солнца можно принять равным d=1,391•109 м.

Не подходит эта задача? Посмотрите другие:

Задача 241 Условие задачи : Обмуровка топочной камеры парового котла выполнена из шамотного […]
Задача 200 Условие: Определить, какую долю излучения, падающего от абсолютно черного источника, […]
Задача 240 Условие задачи : Трубопровод диаметром d=120мм проложен в канале размером АхВ=400х400 […]
Задача 196 Условие: В опытной установке для определения степени черноты тел для поддержания […]
Задача 197 Условие: Температуры двух пластин, помещенных в вакуум, равны 127 ºС и 327 ºС. […]
Задача 105 Условие: Определить плотность лучистого теплового потока между двумя, параллельно […]

Источник

Оксид железа
Железо
Грубое железо
Литое железо 0,7-0,9
0,35
0,35
0,7-0,9
0,1-0,3
0,6-0,9
0,4-0,6 0,6-0,9
0,05-0,25
0,5-0,8
— 0,5-0,9
0,05-0,2
0,5-0,7
—

Сталь хол. проката
Листов.сталь
Отполиров. Сталь
Литая сталь
Окислен. Сталь
Нержав. сталь 0,8-0,9
0,35
0,35
0,8-0,9
0,35
0,8-0,90,6-0,7
0,2
0,25-0,4
0,8-0,9
0,2-0,9 0,7-0,9
0,5-0,7
0,1
0,1-0,2
0,7-0,9
0,15-0,8 0,4-0,6
0,1
—
0,7-0,9
0,1-0,8

Источник

Mathematical definitions[edit]

Hemispherical emissivity[edit]

Spectral hemispherical emissivity[edit]

Directional emissivity[edit]

Spectral directional emissivity[edit]

Emissivities of common surfaces[edit]

[edit]

Absorptivity[edit]

Emittance[edit]

Measurement of Emittance[edit]

Emissivities of planet Earth[edit]

History[edit]

Other radiometric coefficients[edit]

See also[edit]

References[edit]

Further reading[edit]

Вопрос 3. Абсолютно черное тело. Серое тело. Закон Кирхгофа.

Библиографическое описание:

Задача 202

Не подходит эта задача? Посмотрите другие: