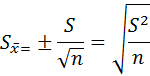Изучаемым
объектам в опыте характерно свойство
изменчивости (варьирования).
Изменчивость эта
обуславливается внешними факторами
(условиями), а также наследственными
особенностями изучаемых объектов
(генетическими).
В математической
статистике 2 вида изменчивости
а)
количественная изменчивость признаков
б)
качественная изменчивость признаков
Количественная
изменчивость
– это изменчивость признаков, которую
можно измерить, взвесить, посчитать.
Количественная изменчивость разделяется
на 2 вида:
-
прерывистая
(дискретная) изменчивость -
непрерывная
изменчивость
Дискретная
изменчивость
— это изменчивость признаков, различия
между значениями которых, обычно выражают
целыми числами (число растений, зёрен
в колосе, количество колосков в колосе
и т.д.)
Непрерывная
изменчивость
— это значение признака, выражающееся
мерами длины, массы, объёма и численные
значения их определяются с «десятыми»
долями. Эти значения находятся в каком-то
интервале.
Качественная
изменчивость
– характеризует изменчивость качественных
признаков (окраска, вкус, консистенция,
форма объекта и др.) Одним из видов
качественной изменчивости является
альтернативная
или двоякая изменчивость.
При этой изменчивости объекты различаются
по какому-то одному признаку. Он может
принимать два взаимоисключающих значения
( всхожесть семян, больные и здоровые
клубни картофеля).
4. Вариационный ряд чисел и его основные статистические характеристики
В
результате выборки мы получим ряд
значений варьирующего признака. Этот
ряд называется
вариационным рядом чисел.
Каждое в отдельности наблюдение является
представителем или элементом вариационного
ряда.
Чтобы выявить
определённую закономерность при анализе
вариационного ряда чисел часто подходят
двумя путями:
-
Можно
группировать эти данные (не сводить их
в таблицу, не разбивать их на группы),
но это неудобно! -
Данные группируют.
Разбивают на классы или группы.
Последовательность
группировки этих данных заключается:
а)
устанавливают количество групп или
классов. Оно зависит от объёма выборки
(n)
n
k
20
— 30
5 — 6
30
– 60 6 –
7
60
– 100 7 –
8
>
100 8 — 15
__
б) К =
2 Количество классов берётся от 5 до
20
в) Устанавливают
интервал или классовый промежуток
, где
– размах варьирования (),
разница между наибольшим ()
и наименьшим (
значениями признака.
г) Затем
данные разносят по классам и рассчитывают
характеристики
вариационного ряда.
1.
Средняя арифметическая выборки
2.
Дисперсия (средний квадрат отклонений)
S2
3.
Стандартное отклонение или среднее
квадратическое S
4.
Коэффициент вариации
V
5.
Ошибка средней арифметической (в
абсолютных единицах)
6.
Относительная ошибка средней арифметической
7.
Доверительный интервал
t
Составляется
вспомогательная таблица, в которой
вычисляются средняя арифметическая
(),
отклонения от средней (),
квадраты отклоненийи суммы квадратов
отклонений
.
1.
Хпрост.
и
Хвзвеш
– это обобщенная характеристика
вариационного ряда (изменчивость)
—
средняя
арифметическая
—
средняя арифметическая
простая,
применяется при n
– не более 10. взвешенная, применяется
при n
Правильность
вычисления
проверяется по равенству 0
в несгруппированном ряду и
0 в сгруппированном (если
найдена без остатка).
Средняя
арифметическая – обобщённая характеристика
всей совокупности в целом, но она не
показывает степень изменчивости
признака. Часто у двух вариационных
рядов
бывает одинакова, а отклонения
индивидуальных значений признака
отразличны,
поэтому для характеристики степени
изменчивости вариационного ряда находят
показатели вариации (изменчивости) –
дисперсию, стандартное отклонение и
коэффициент вариации.
2.
Затем рассчитывается дисперсия
( S2
),
показатель, характеризующий среднюю
меру изменчивости.
где n
–1 – число
степеней свободы (мю)
где f
– частота
класса
3.
Стандартное отклонение (.
Размерность дисперсии и средней
арифметической не совпадает: единица
измерения первой – в квадрате, а второй
– без квадрата. Поэтому, извлекая
квадратный корень из ,
находят показатель варьирования –
среднее квадратическое, или стандартное
отклонение
– это средняя ошибка отдельного
наблюдения, взятого из данной совокупности.
Измеряется она в тех же единицах, что и
изучаемый признак, и вычисляется по
формулам
в
несгруппированном вариационном ряду
в
сгруппированном вариационном ряду
4.
Коэффициент вариации
()
— стандартное отклонение, выраженное в
процентах к средней арифметической.
(%)/
Коэффициент
вариации является показателем однородности
или выравненности объектов по изучаемому
признаку. Изменчивость вариационного
ряда считается:
незначительной
– при
до 10%;
средней
– при
значительной
– при
больше 20%.
В
селекции и семеноводстве используют
коэффициент выравненности (величина
дополняющая коэффициент вариации до
100 %).
В
+ V
= 100 % В = 100 –
V
5.
Ошибка
средней арифметической
().
Средняя арифметическая выборочной
совокупности ()
отличается от средней арифметической
всей генеральной совокупности на
величину ошибки ,
с которой определена средняя выборочной
совокупности ().
прямо пропорциональна стандартному
отклонению (S) и обратно пропорциональна
корню квадратному из числа наблюдений
(n):
Если
вместо S подставить его значение (для
несгруппированного вариационного
ряда), то формула примет вид:
Абсолютная
ошибка ()
позволяет:
а)
установить величину случайной ошибки
в опыте;
б) оценить
существенность различий между средними
урожаями по вариантам;
в) рассчитать
доверительный интервал
6.
Относительная ошибка средней арифметической
().
Сопоставляя среднюю арифметическую
с её ошибкой ,
можно получить представление о точности
определения :
Чем
меньше числовое значение ,
тем точнее проведено наблюдение, т.е. с
меньшей ошибкой определена .
Таким образом, по значению относительной
ошибки можно оценить точность определения
средней арифметической.
При
значении показателя
1-2% — точность определения выборочной
средней отличная, 2-3% — хорошая, 3-5% —
вполне удовлетворительная, 5-7% —
удовлетворительная, больше 7% —
неудовлетворительная
Раньше
— использовали для оценки качества
выполнения полевого опыта и считали,
что если
,
больше 7-8 % то опыт нужно браковать. Но
это не объективно т.к. относительная
ошибка зависит от
и чем больше
,
тем меньше
при
одном и том же числе наблюдений.
7.
Доверительный интервал ().
Величина
даёт возможность вычислить пределы, в
которых находится средняя генеральной
совокупности, — доверительный интервал
для средней. Границы доверительного
интервала равны .
Значение
дано в приложении 2 для принятого уровня
значимости (05 или 01) и числа степеней
свободы n
– 1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое изменчивость выборки? Определение и пример
17 авг. 2022 г.
читать 2 мин
Часто в статистике нас интересуют ответы на такие вопросы, как:
- Каков средний доход домохозяйства в определенном штате?
- Каков средний вес определенного вида черепах?
- Какова средняя посещаемость футбольных матчей колледжа?
В каждом сценарии нас интересует ответ на некоторый вопрос осовокупности , которая представляет все возможные отдельные элементы, которые мы хотим измерить.
Однако вместо сбора данных о каждом человеке в популяции мы собираем данные по выборке популяции, которая представляет собой часть общей популяции.
Например, мы можем захотеть узнать средний вес определенного вида черепах, общая популяция которых составляет 800 особей.
Поскольку поиск и взвешивание каждой черепахи в популяции заняло бы слишком много времени, вместо этого мы собираем простую случайную выборку из 30 черепах и взвешиваем их:
Затем мы могли бы использовать средний вес этой выборки черепах для оценки среднего веса всех черепах в популяции.
Изменчивость выборки относится к тому факту, что среднее значение будет варьироваться от одной выборки к другой.
Например, в одной случайной выборке из 30 черепах среднее значение выборки может оказаться равным 350 фунтам. В другой случайной выборке среднее значение выборки может составлять 345 фунтов. В еще одном образце среднее значение может составлять 355 фунтов.
Существует изменчивость среди выборочных средних.
Как измерить изменчивость выборки
На практике мы собираем только одну выборку для оценки параметра совокупности. Например, мы соберем только одну выборку из 30 морских черепах, чтобы оценить средний вес всей популяции черепах.
Это означает, что мы будем вычислять только одно выборочное среднее ( x ) и использовать его для оценки среднего значения совокупности (μ).
Выборочное среднее = х
Но мы знаем, что среднее значение выборки будет варьироваться от одной выборки к другой. Итак, чтобы учесть эту изменчивость, мы можем использовать следующую формулу для оценки стандартного отклонения выборочного среднего:
Стандартное отклонение выборочного среднего = s / √ n
куда:
- s: Стандартное отклонение выборки
- n: размер выборки
Например, предположим, что мы собрали выборку из 30 морских черепах и обнаружили, что средний вес выборки составляет 350 фунтов, а стандартное отклонение выборки — 12 фунтов. Исходя из этих цифр, мы рассчитываем:
Среднее значение выборки = 350 фунтов
Стандартное отклонение выборочного среднего = 12 / √ 30 = 2,19 фунта.
Это означает, что наша наилучшая оценка среднего веса всех черепах в истинной популяции составляет 350 фунтов, но мы должны ожидать, что среднее значение от одной выборки к другой будет варьироваться со стандартным отклонением около 2,19 фунта.
Одно интересное свойство стандартного отклонения среднего значения выборки заключается в том, что оно естественным образом становится меньше по мере того, как мы используем все большие и большие размеры выборки.
Например, предположим, что мы собираем выборку из 100 морских черепах и обнаруживаем, что средний вес выборки составляет 350 фунтов, а стандартное отклонение выборки составляет 12 фунтов. Затем стандартное отклонение выборочного среднего будет рассчитываться как:
Стандартное отклонение выборочного среднего = 12 / √ 100 = 1,2 фунта.
Наша наилучшая оценка среднего значения выборки по-прежнему будет составлять 350 фунтов, но мы можем ожидать, что среднее значение от одной выборки из 100 морских черепах до следующей выборки из 100 морских черепах будет варьироваться со стандартным отклонением всего в 1,2 фунта.
Другими словами, чем больше размер выборки, тем меньше вариабельность средних значений выборки.
Дополнительные ресурсы
Что такое выборочное распределение?
Введение в центральную предельную теорему
Калькулятор центральной предельной теоремы
Меры разброса (изменчивости) применяются в психологии для численного выражения величины межиндивидуальной вариации признака и показывают, насколько хорошо данные значения представляют данную совокупность.
Минимальное и максимальное
Минимальное (Xmin) — это наименьшее значение измерения (переменной) в выборке.
Максимальное (Xmax) — это самое большое значение измерения (переменной) в выборке.
Сами по себе эти меры не очень информативны. Особенно если величина распределяется по нормальному закону. Но если мы измеряем какое-то конкретное свойство на примере узкой выборки (например, агрессивность людей, страдающих каким-то заболеванием), то минимальное и максимальное значения могут дать возможность качественно описать эту выборку и лучше понимать особенности ее представителей.
Размах
Размах — разность между наибольшим и наименьшим значениями результатов наблюдений, является одной из самых простых мер изменчивости набора числовых значений. Дает информацию о ширине интервала, в котором сосредоточен весь набор числовых данных, геометрически — ширина отрезка, в котором располагаются все значения.
( R = X_{max} — X_{min} )
Простота расчета, наглядность и интуитивная понятность этой характеристики рассеяния значений является очевидным преимуществом перед такими мерами рассеяния как дисперсия и среднее квадратическое отклонение (стандартное отклонение). Существенным недостатком размаха является то, что он не содержит информацию о характере распределения результатов в интервале рассеяния и не устойчив к выбросам, в определенной степени ограничивает его использование.
Пример: допустим у нас есть выборка значений {3,4,5,6,7} где максимальное значение 7, а минимальное 3, получим:
( R = 7 — 3 = 4 )
Минимальное, максимальное и размах измерений свойства у представителей двух независимых выборок (например, мужчин и женщин), представленные в виде графика, позволяют визуально определить наличие различий в проявлении изучаемого свойства. А значит предположить влияние признака (в нашем примере –это пол испытуемых) на выраженность свойства.
Межквартильный размах
В статистике для анализа выборки часто прибегают к более стабильному к выбросам показателю вариации – межквартильному размаху (IQR). Квартиль (Q) – это то значение, которое делит отсортированные (ранжированные) данные на части, кратные одной четверти, или 25%, что равносильно 25-му процентлю или квантилю 0.25. Так, 1-й квартиль (Q1) – это значение, ниже которого находится 25% выборки. 2-й квартиль (Q2) делит выборку данных пополам и равен медиане, ну и 3-й квартиль (Q3) это значение выше которого находится 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями.
( IQR = Q3 -Q1 )
У данного показателя есть одно неоспоримое преимущество: он является робастным.
Пример: допустим у нас есть выборка отсортированных значений {0,1,3,4,5,6,7,100}. Первым делом определяем медиану по которую выборку разделим на две равные части. Медиана у нас 4.5, получаем две выборки {0,1,3,4} и {5,6,7,100}. Теперь для полученых выборок определим медиану. Для первой это будет 2 и это значение будет соответствовать первому квартилю (Q1). Для второй выборки это будет 6.5 и соответствовать третьему квартилю (Q3). Тогда:
( IQR = 6.5 — 2 = 4.5 )
Дисперсия
Один из способов измерения рассеяния данных заключается в том, чтобы определить степень отклонения каждого наблюдения от выборочного среднего. Очевидно, что чем больше отклонение, тем больше изменчивость, вариабельность наблюдений.
Однако мы не можем использовать среднее этих отклонений как меру рассеяния, потому что положительные отклонения компенсируют отрицательные отклонения, их сумма равна нулю. Чтобы решить эту проблему, мы возводим в квадрат каждое отклонение и находим среднее возведенных в квадрат отклонений.
( D = sigma^{2}=frac{sum_{i=1}^n(X_{i}- bar{X})^{2}}{n-1} )
Дисперсия является одним из параметров нормального закона распределения. Чем больше дисперсия, тем более пологими являются «склоны» распределения и длиннее его «хвосты».
Чем выше дисперсия показателей измеряемого свойства (коэффициентов регрессии, значений переменных и т.д.), тем менее устойчивой она будет. Высокая дисперсия исходных данных позволяет предположить высокую значимость в них случайной компоненты, возможном наличии шума, выбросов и аномальных значений.
Пример: допустим у нас есть выборка значений {3,4,5,6,7} первым делом расчитываем выборочное среднее:
( bar{X}=frac{3+4+5+6+7}{5}=frac{25}{5}=5 )
Теперь приступим к расчету дисперсии
( D=frac{(3-5)^{2}+(4-5)^{2}+(5-5)^{2}+(6-5)^{2}+(7-5)^{2}}{5-1} = frac{4+1+0+1+4}{4} = 2.5 )
К сожалению, не существует никаких ориентиров, чтобы интерпретировать величину дисперсии. Тем более, что на ее величину будет влиять размер шкалы измерения. Однако, расчет дисперсии нам необходим для определения следующих статистик.
Стандартное отклонение
Это наиболее распространенный показатель в статистике и теории вероятности, оценивающий среднеквадратичное отклонение случайной величины относительно ее математического ожидания на основе несмещенной оценки ее дисперсии. Измеряется в единицах измерения самой случайной величины.
( sigma=sqrt{D}=sqrt{frac{sum_{i=1}^n(X_{i}- bar{X})^{2}}{n-1}} )
Если перейти на «человеческий» язык, то стандартное отклонение — это показатель того, насколько резво какой-либо показатель меняется со временем или у разных людей. Т.е. чем больше этот показатель, тем сильнее изменчивость ряда значений.
Стандартное отклонение используют для анализа наборов значений. Иногда два набора с одинаковым средним значением могут оказаться совершенно разными по разбросу величин.
Пример: расчитывать стандартное отклонение достаточное легко после того как расчитали дисперсию. Допустим у нас есть все та же выборка {3,4,5,6,7}, для нее мы уже расчитали дисперсию и она равна 2.5, тогда
( sigma=sqrt{2.5} = 1.58113883 )
Синонимы:
- среднее квадратическое отклонение
- среднеквадратичное отклонение
- среднеквадратическое отклонение
- квадратичное отклонение
- стандартный разброс
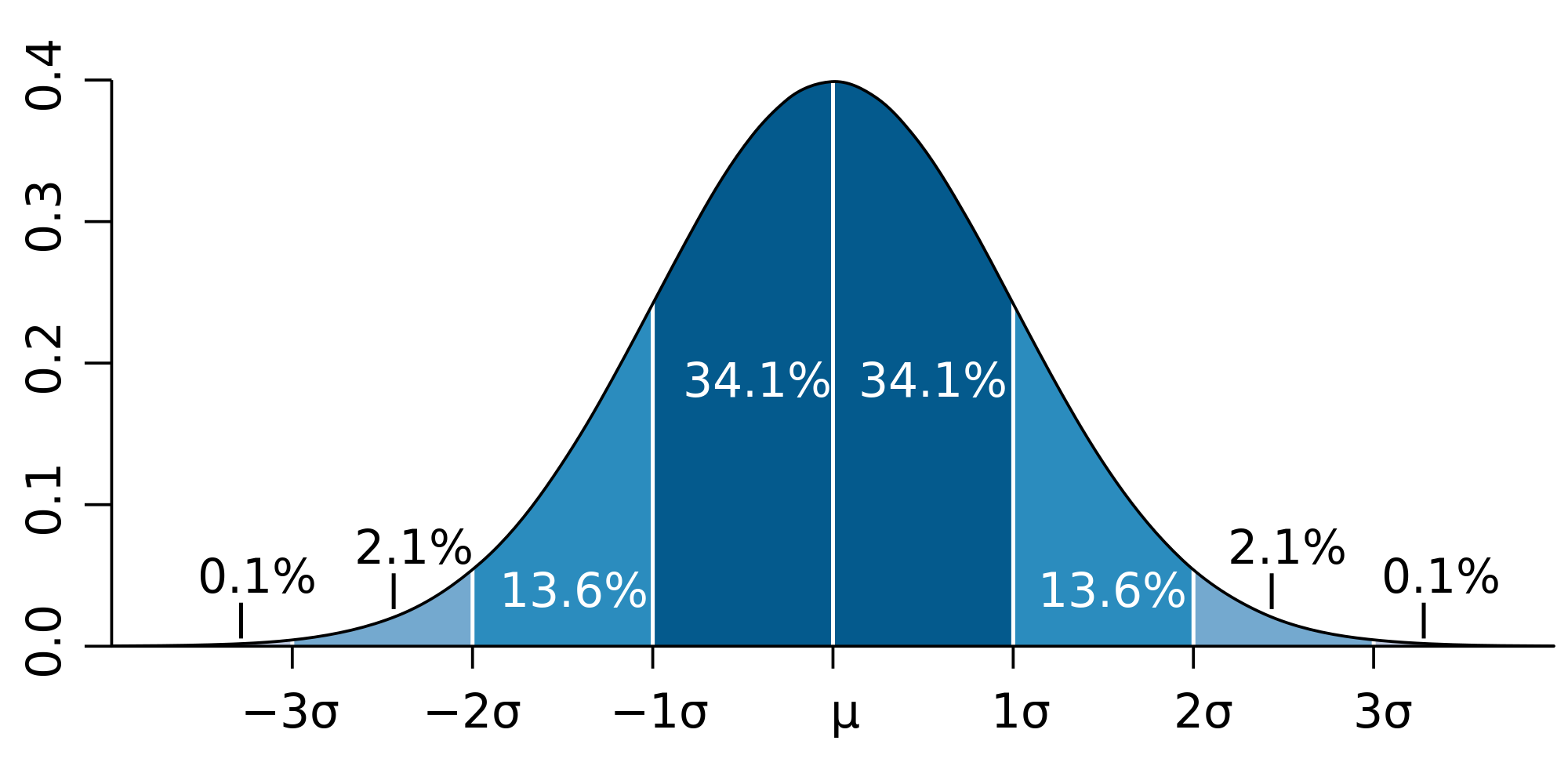
Для психологии расчет стандартного отклонения необходим для определения нормативных интервалов выраженности свойства. Для этого используется «правило трех сигм».
Это правило утверждает, что вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три среднеквадратических отклонения, практически равна нулю. Правило справедливо только для случайных величин, распределенных по нормальному закону, поэтому часто используется в современной психометрике.
Как показано на рисунке интервал [-3σ;-1σ] – это значения, соответствующие низкому уровню выраженности свойства, интервал[-1σ;1σ] – среднему уровню, а интервал [1σ;3σ] – высокому.
Пример:
Мы измеряем беглость мышления по шкале от 0 до 12. Для применения правила нам нужно высчитать среднее выборочное и стандартное отклонение.
Допустим, мы определили, что среднее М = 7, а стандартное отклонение σ = 1,5.
Далее, как показано на рисунке, нам нужно трижды отнять стандартное отклонение от среднего (получим: -1σ = 5,5; -2σ = 4, -3σ = 2,5), и трижды прибавить (1σ = 8,5; 2σ = 10, 3σ = 11,5).
Таким образом получим интервал низких значений [2,5; 5,5]; интервал средних значений [5,5; 8,5]; интервал высоких значений [8,5; 11,5].
Коэффициент вариации
Коэффициент вариации — это величина, используемая в статистике, равная отношению стандартного отклонения случайной величины к ее математическому ожиданию (среднему выборочному). Он применяется для сравнения вариативности одного и того же признака в нескольких совокупностях с различным средним арифметическим. Т.к. коэффициент вариации величина относительная, то обычно она выржаеться в процентах.
( CV = frac{sigma}{bar{X}}cdot100 )
В статистике принято, что:
- если коэффициент вариации меньше 10%, то степень рассеивания данных считается незначительной;
- если от 10% до 20% — средней;
- больше 20% и меньше или равно 33% — значительной.
Если значение коэффициента вариации не превышает 33%, то совокупность считается однородной, а если больше 33%, то — неоднородной.
Пример: берем ранее используемый ряд данных {3,4,5,6,7}, для него у нас посчитано уже и стандартное отклонение и выборочное среднее, получим:
( CV = frac{1.58113883}{5}cdot100 = 31.6227766 )
Исходя из получившегося результата можем утверждать, что степень рассеивания данных значительная, а сама выборка однородная. Если бы мы изучали какое-то свойство, это бы означало, что оно стабильно закрепилось у представителей выборки на уровне, соответствующем среднему выборочному. А значит мы можем смело утверждать, что изучаемое свойство характерно для представителей нашей выборки.