Как найти изменение энергии атома водорода

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

и энергии
нулевых колебаний осциллятора

Некоторые задачи
квантовой механики могут быть решены
или поняты на качественном уровне, если
использовать различные комбинации
законов классической физики и соотношения
неопределенностей Гейзенберга.

Пример 1. Оценим
энергию основного состояния атома
водорода.

Основным
состоянием атома водорода является
состояние с наименьшей энергией (1 –
энергетический уровень).

Полная механическая
энергия атома водорода равна сумме
кинетической энергии вращающегося
электрона вокруг ядра и потенциальной
энергии взаимодействия электрона с
ядром, т. е.

W
= W_к
+ W_р,

где
W_к
=
p²/(2m)
– кинетическая энергия вращающегося
электрона вокруг ядра;

W_р
=
–q_e²/(4₀r)
– потенциальная энергия взаимодействия
электрона с ядром.

При
допущении неопределенности положения
электрона в пределах радиуса его орбиты,
т. е. r

r
и неопределенность импульса в пределах
самого импульса, т. е. р

р.

Тогда на
основании соотношений неопределенностей
Гейзенберга имеем

r

р

h
/(4)

или
по порядку величины р 
h
/2
r.

Если
возьмем равенство

р
= h
/(2r)

и
подставим в формулу кинетической
энергии, то полная энергия атома водорода

W
= h²/(4²m
r²)
– q_e²/(4₀r).

Теперь
перейдем к условию минимума, т. к. нас
интересует состояние с наименьшей
энергией:

dW/dr
= – h²/(4²m
r³)
+ q_e²/(4₀r²)
= 0.

Корень
этого уравнения, соответствующий
минимуму полной энергии W,
равен

r₁
= ₀h²
/ (m
q_e²).

В
квантовой механике, полученное значение
r₁
называют
радиусом первой боровской орбиты.

После вычисления получим r1  510 11 м. Для энергии основного состояния атома водорода получим

W₁
= –
m
q_e⁴
/ (8²₀²h²).

W₁
= –
13,6 эВ

или

W₁
= –
2,176 10
^18Дж.

Пример 2. Энергия
нулевых колебаний одномерного

гармонического
осциллятора.

В
качестве одномерного гармонического
осциллятора рассмотрим колебания груза
на пружине (пружинный маятник), который
характеризуется потенциальной энергией

W_р
=
k
x²
/
2,

представляющий
собой, параболическую потенциальную
яму.

Для
оценки минимально возможной полной
энергии осциллятора применим соотношения
неопределенностей Гейзенберга.

Полная
механическая энергия данного осциллятора

W
= W_к
+ W_р,

где
W_к
=
p_х²
/
(2m)
– кинетическая энергия осциллятора;
W_р
=
k
x²
/
2.

Следовательно,

W
= p_х²
/
(2m)
+ k
x²
/
2.

Согласно
классической механике минимум полной
энергии W
= 0 соответствует х
= 0 и р_х
=
0, т. е. пружинный маятник неподвижен.

При
рассмотрении квантового случая должны
учесть, что одновременно точные значения
координаты (х)
и проекции импульса на ось х (р_х)
указать
невозможно.

Согласно, принципа
неопределенностей Гейзенберга, имеем

х

р_х

h
/(4).

Если
положим, что х

х ; р_х

р_х
или
по порядку величины х 
р_х

h
/ (2),
т. е. р_х

h
/(2x).

При
переходе к равенству р_х
= h
/(2x)
для полной энергии осциллятора будем
иметь

W
= h²
/(8²mx²)
+ k
x²
/
2.

Перейдем
к условию минимума энергии:

dW
/dx
= – h²
/(4²mx³)
+ k
x
= 0.

Корень
этого уравнения запишем в виде

.

Тогда
минимальное значение полной энергии
рассматриваемого квантового осциллятора

W₀
= h
/(2).

или

W₀
= h,

где

– собственная
круговая частота осциллятора; 
= 2.

Данная
оценка отличается от точного значения
только численным множителем 1/2.

Полная
энергия квантового осциллятора
называется энергией нулевых колебаний
гармонического осциллятора.

Перейти к содержимому

Долгое время атом считался мельчайшей неделимой частицей вещества, являющейся носителем его физических свойств. Однако открытие радиоактивности и первой элементарный частицы (электрона) поставило под сомнение факт его неделимости. Почему атом устойчив? Какие физические процессы происходят в атомах? Как атом излучает свет?

Для преодоления противоречий, возникающих при описании строения атома на основе законов классической механики и электродинамики с экспериментальными данными, датский физик Нильс Бор в 1913 г. в работе «О строении атомов и молекул» предложил квантовую модель атома, основанную на двух постулатах.

В современном виде они формулируются следующим образом:

I постулат Бора (постулат стационарных состояний): атом может находиться в особых стационарных (квантовых) состояниях, каждому из которых соответствует определенная энергия. В стационарном состоянии атом не излучает.

Стационарные состояния можно пронумеровать, присвоив им порядковые номера n = 1,2,3,… , причем каждому состоянию соответствует определенное дискретное значение энергии E_n.
Согласно модели Бора стационарным состояниям атома соответствуют определенные (разрешенные) орбиты, по которым электроны движутся вокруг ядра. Бор для простоты полагал, что эти орбиты представляют собой окружности, хотя в общем случае орбиты могут иметь форму эллипса, причем ядро располагается в одном из его фокусов (рис. 194)

Первый постулат противоречит как законам классической механики (энергия движущихся электронов может быть любой), так и законам классической электродинамики (ускоренно движущиеся электроны всегда излучают электромагнитные волны).

II постулат Бора (правило частот): атом может переходить из одного стационарного состояния в другое. При этом переходе может испускаться или поглощаться квант электромагнитной энергии, частота которого определяется разностью энергий атома в данных состояниях:

где  — частота поглощенного или испущенного кванта излучения, E_k, E_n — энергия атома в k-ом и n-ом стационарном состоянии, h — постоянная Планка.
Если  то при переходе происходит излучение энергии, если  то — ее поглощение.

Состояние атома, которому соответствует наименьшая энергия, называется основным, а состояния, которым соответствуют большие значения энергии, — возбужденными. В основном энергетическом состоянии атом может находиться неограниченно долго, а в остальных стационарных состояниях . Это так называемое время жизни атома в возбужденном состоянии.

Как следует из II постулата Бора, частота излучения атома не связана с частотой вращения электрона по орбите, она определяется разностью значений энергии атома E_k и E_n в начальном и конечном состояниях. Переход атома из одного стационарного состояния в другое сопровождается электромагнитным излучением с длиной волны:

(2)

Таким образом, первый постулат Бора позволил объяснить дискретность значений энергии атома, а первый и второй постулаты — линейчатую структуру атомных спектров.
Бор предложил также количественное условие квантования для нахождения радиусов стационарных (разрешенных) круговых орбит электронов:

где n = 1,2,3,…, — номер орбиты, m_e — масса электрона, v_n — модуль скорости электрона на n-й орбите, r — радиус n-й орбиты, h — постоянная Планка.

Таким образом, постулаты Бора основывались на трех экспериментальных предпосылках — результатах исследования атомных спектров, квантовой теории излучения, развитой Планком и Эйнштейном, и ядерной (планетарной) модели атома Резерфорда.
Исходя из постулатов Бора и условия квантования орбит, можно объяснить структуру энергетических уровней простейшего атома — атома водорода, состоящего из ядра (протона) и одного электрона, вращающегося вокруг него.

На основании второго закона Ньютона и закона Кулона, а также условия квантования орбит (3) Бор смог определить радиусы орбит электронов, а также энергии стационарных состояний. Радиус первой (ближайшей к атомному ядру) орбиты электрона (n = 1) определяет размер атома водорода в основном состоянии. Он равен

Из второго закона Ньютона следует, что при движении электрона по круговой орбите радиусом r вокруг ядра с линейной скоростью , сила Кулона   сообщает электрону центростремительное ускорение:

,

(3-1)

где e —  модуль заряда электрона.

Откуда:

(3-2)

Из условия квантования орбит (3) находим модуль скорости на орбите с номером n:

(3-3)

Подставляем выражение (3-3) в соотношение (3-2) и находим радиус стационарной орбиты электрона с номером n:

.

(3-4)

Как видно из формулы (3-4), радиус орбиты возрастает пропорционально .

Модуль скорости электрона на орбите находим, подставляя выражение (3-4) в формулу (3-3):

.

(3-5)

Так как радиус r орбиты может принимать только дискретные (квантованные) значения  (3-3), то и энергия атома в различных стационарных состояниях может также принимать только дискретные значения E_п. Энергия атома водорода определяется только номером орбиты .

Энергия электрона в атоме водорода равна сумме его кинетической энергии E_к при движении по круговой орбите и потенциальной энергии E_п в электростатическом поле ядра. Поскольку взаимодействуют частицы, имеющие заряды противоположных знаков (заряд ядра  , заряд электрона ), то между ними действует сила кулоновского притяжения, и потенциальная энергия их взаимодействия отрицательна:

.

(3-6)

Энергия электрона в атоме совпадает с полной энергией атома — системы, состоящей из атомного ядра и электрона:

.

(3-7)

Подставив в формулу (3-7) выражение для модуля скорости (3-5) и радиуса  n-й орбиты (3-4) для значений энергетических уровней атома  , получаем:

Бор получил выражение для энергии атома водорода:

Поэтому энергия атома водорода (4) фактически определяется только номером орбиты n электрона, так как величина  является постоянной, вследствие того что выражается через фундаментальные постоянные (заряд электрона e, массу электрона , постоянную Планка h, электрическая постоянная ).

Согласно формуле (4) энергия атома водорода в основном состоянии (n = 1) получается равной  = −13,6 эВ, а его энергия в ионизированном состоянии, когда электрон бесконечно далек от ядра () равной . Во втором состоянии (n = 2) энергия  в третьем (n = 3) — и т. д. Энергию атома водорода в любом состоянии можно рассчитать по формуле:

Так как энергия атома водорода может принимать только дискретный набор значений, то говорят, что она квантована.
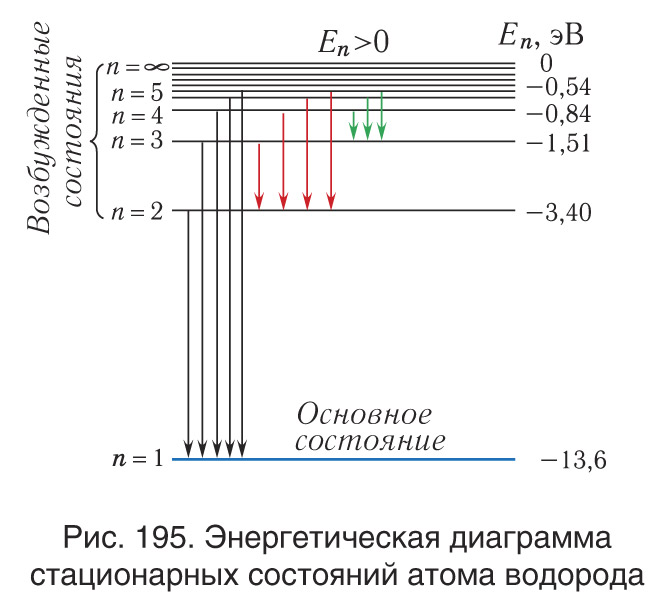
Для наглядного представления стационарных энергетических состояний атома используется энергетическая диаграмма (рис. 195). Графически возможные значения энергии атома изображают в виде схемы уровней энергии (энергетических уровней) — горизонтальных прямых, проведенных на расстояниях в определенном масштабе, соответствующем разностям раз­решенных значений энергии. Переходы атома из одного состояния в другое изображаются на диаграмме вертикальными линиями между соответствующими уровнями. Направление перехода обозначается стрелками.

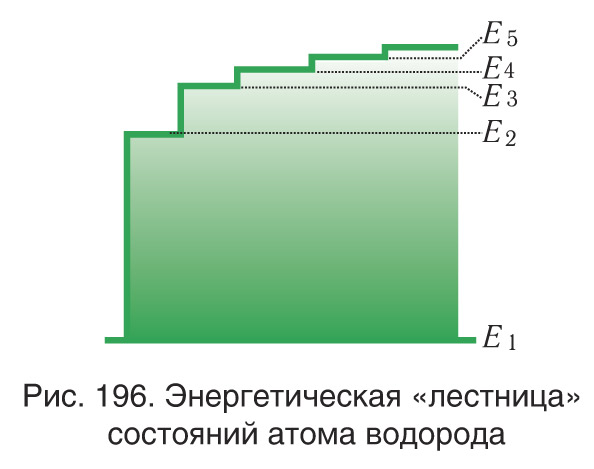
Энергетическую диаграмму можно считать своеобразной «лестницей» с «нижней площадкой» (основным состоянием) и поднимающимися вверх «ступенями» (возбужденными состояниями). Формула для энергетических уровней энергии  атома показывает важную закономерность: чем выше поднимается над основным (первым) уровнем энергетическая «лестница», тем менее «крутыми» становятся ее ступени (на рисунке 196 это хорошо видно при ).

Следовательно, чем дальше электрон от ядра (), тем на меньшую величину отличаются соседние уровни энергии, т.е. густота энергетических уровней растет. Квантовые скачки при этом уменьшаются, вследствие чего переходы между стационарными состояниями атома все больше и больше становятся «похожими» на непрерывное изменение энергии. Энергетическая «лестница» постепенно превращается в пологий «плавный подъем» (см. рис. 196), т.е. энергия становится почти непрерывно меняющейся величиной, как это и было в классической теории.

Процесс удаления электрона из атома называется ионизацией. Для удаления электрона из атома водорода, находящегося в основном состоянии, атому необходимо сообщить энергию  E_и = E_∞ — E₁ = 13,6 эВ
Поэтому эту энергию E_и называют энергией ионизации атома водорода. Следовательно, энергия ионизации равна работе, которую необходимо совершить внешним силам для удаления электрона на «бесконечное» расстояние из атома, находящегося в основном состоянии. Здесь под «бесконечностью» понимается такое расстояние, при котором взаимодей­ствием электрона и ядра можно пренебречь.
Отметим, что выше уровня  (при ) электрон является свободным и может иметь любую энергию.
Энергия

называется энергией связи электрона в атоме водорода.
Энергия связи определяется электромагнитным взаимодействием частиц и является отрицательной величиной, вследствие того, что при образовании атома энергия выделяется. Абсолютное значение энергии связи характеризует прочность связи и устойчивость атома.
Энергия связи по абсолютной величине равна энергии ионизации электрона в атоме:

.

В соответствии с представлениями квантовой механики свободное движение электрона, оторванного от атома, подобно распространению бегущей волны в неограниченном пространстве. Для нее возможны любые значения длин волн. Следовательно, энергия свободного электрона не квантуется, и частота излучения меняется плавно (спектр излучения непрерывный). Вследствие этого линия, обозначенная на энергетической диаграмме n = ∞ , соответствует коротковолновой границе линейчатой структуры излучения (поглощения) атома. К ней примыкает непрерывный спектр излучения электрона

Ионизация сложных атомов может быть однократной (атом теряет один электрон), двукратной (два электрона) и т. д.

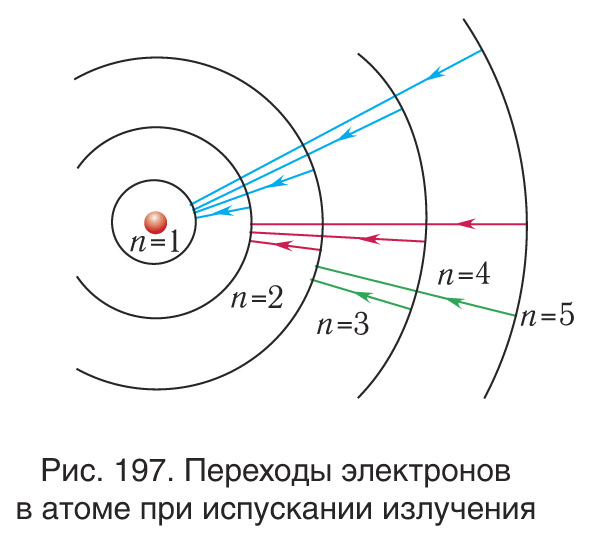
Поскольку при возбуждении атома радиус орбиты электрона возрастает, то испускание излучения атомом происходит при переходах электронов в атоме с внешних орбит на внутренние (рис. 197)

Модель атома Бора позволяет описать не только атом водорода, но и ионизированные атомы (ионы) других элементов, вокруг ядер которых, как и в атоме водорода, движется только один электрон. Такие ионы называются водородоподобными. Примерами таких ионов являются однократно ионизированный атом гелия (), двукратно ионизированный атом лития () и т. д.

Необходимо отметить, что энергия атома может изменяться не только при испускании или поглощении энергии, но и при столкновении атомов. При неупругом столкновении изменяется внутренняя энергия сталкивающихся атомов, и электроны в них переходят на другие уровни энергии.

Таким образом, с помощью модели атома Бора удалось:

Во-первых, вычислить энергию ионизации атома водорода, хорошо согласующуюся с экспериментом. Как теория, так и эксперимент дали значение 
Во-вторых, значительно продвинуться в объяснении закономерностей периодической системы химических элементов Менделеева. Согласно модели атома Бора электроны движутся по определенным орбитам, образующим различные группы — электронные оболочки. Структура электронных оболочек определяет химические свойства элементов, которые периодически повторяются по мере заполнения оболочек электронами. Это позволило «предсказывать» свойства неизвестных элементов; так, например, был открыт элемент с порядковым номером Z = 72 — гафний, по своим свойствам аналогичный цирконию (Z = 40).
Модель атома Бора объяснила основные закономерности спектра атома водорода, хотя частично сохранила классический характер, поскольку в ней предполагалось, что электроны движутся по орбитам вокруг ядра. Однако на основе данной модели не удалось построить теорию более сложных атомов, например объяснить спектр излучения следующего за водородом атома гелия, который содержит всего два электрона. Соответственно, не могло быть и речи об объяснении на основании данной модели строения молекул, так как в них картина движения и взаимодействия электронов и атомных ядер намного сложнее, чем в атомах.
Теория атома Бора явилась важнейшим этапом на пути создания последовательной теории микроскопических явлений — квантовой
механики.

В 1922 г. Нильсу Бору была присуждена Нобелевская премия по физике «за заслуги в исследовании строения атомов и испускаемого ими излучения».

Упражнение 20

1. Сколько различных квантов света N может испустить возбужденный атом водорода, если он находится на четвертом энергетическом уровне?
2. Атом водорода перешел с четвертого энергетического уровня   на второй  . Как при этом изменилась энергия атома?
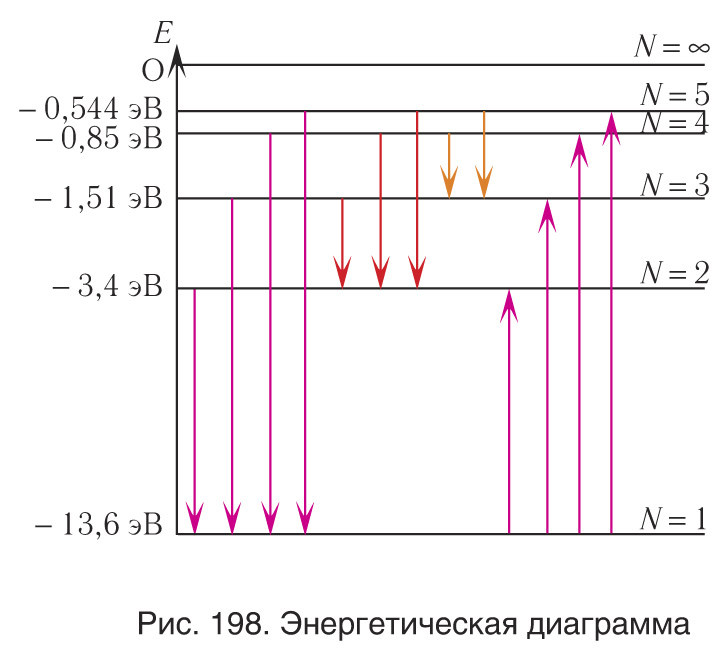
3. Определите, исходя из представленной энергетической диаграммы (рис. 198), какой из переходов соответствует: а) излучению фотона максимальной энергии; б) поглощению фотона максимальной энергии.

4. Определите изменение энергии электрона в атоме водорода, если атом излучает фотон, длина волны которого λ = 486нм.
5. Определите минимальную энергию, которую необходимо сообщить электрону, находящемуся в основном состоянии в атоме водорода, чтобы спектр атома содержал только три спектральные линии.
6. Определите длину волны излучения, которое может вызвать ионизацию атома: а) лития (); б) серебра (); в) калия ().
7. Определите частоту ν поглощенного кванта света, необходимую для того, чтобы атом водорода, с электроном, находящийся на четвертой орбите, мог ионизироваться.
8. Электрон в невозбужденном атоме водорода получил энергию . Определите: а) частоту  поглощенного кванта; б) энергетический уровень, на который он перешел; в) радиус r новой орбиты; г) количество N линий, которое  можно будет увидеть в спектре излучения при переходе на более низкие энергетические уровни. Принять энергию основного состояния атома водорода , радиус первой орбиты  
9. Электрон в модели атома водорода по Бору движется по круговой орбите радиусом . Какую энергию Е должен поглотить атом, чтобы радиус орбиты электрона увеличился в  раза?
10. Рассчитайте радиус третьей и трехсотой орбит электрона в атоме водорода в рамках модели Бора.
11. Определите квантовое число n и энергию E атома водорода, если бы он в возбужденном состоянии имел радиус .
12. Определите отношение модулей электрической и гравитационной сил, действующих на электрон в атоме водорода.
13. Определите радиус первой боровской орбиты электрона в атоме водорода, если бы электрон в атоме был связан с протоном не электрической, а гравитационной силой.
14. Найдите относительное уменьшение массы  атома водорода при переходе электрона с энергетического уровня  в основное состояние на энергетический уровень ?
15. Протон, летевший со скоростью, модуль которой , сталкивается с покоящимся невозбужденным атомом водорода. После столкновения протон летит со скоростью, модуль которой , в том же направлении, а атом переходит в возбужденное состояние. Определите длину волны  излучения, которое может испустить атом, переходя в основное состояние. (Различием масс протона и атома водорода пренебречь.)