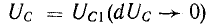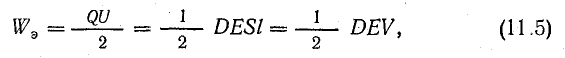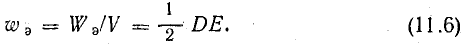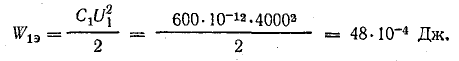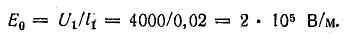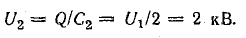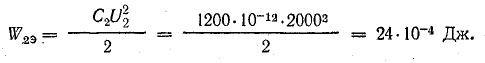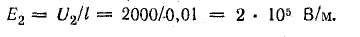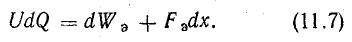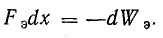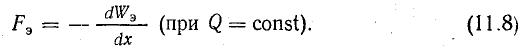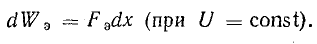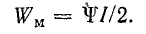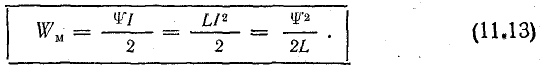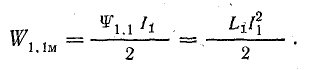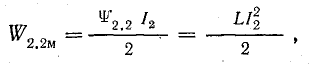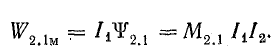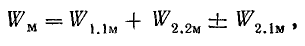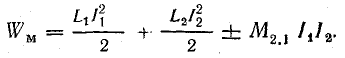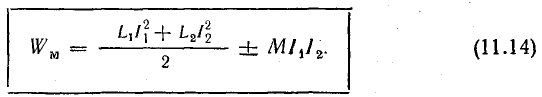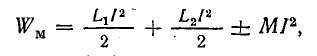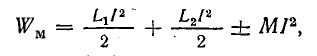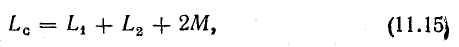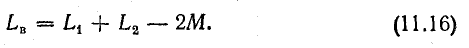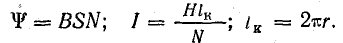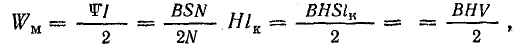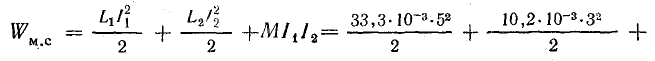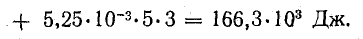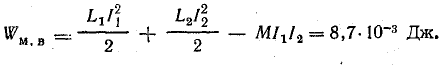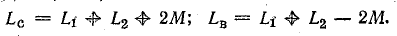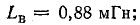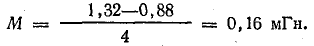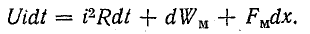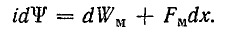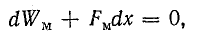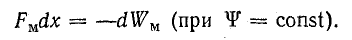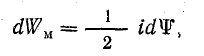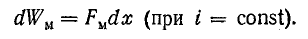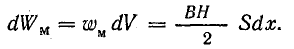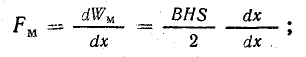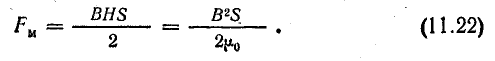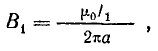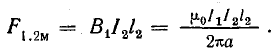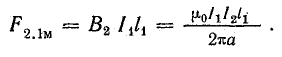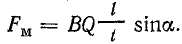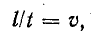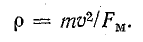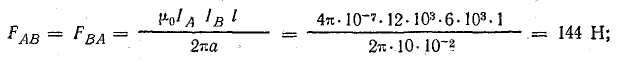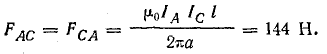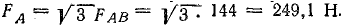Как найти изменение энергии магнитного поля

«Искусство
экспериментатора состоит в том,

чтобы
уметь задавать природе

вопросы
и понимать её ответы».

Майкл
Фарадей

Задача
1.
Какой должна быть сила тока в катушке с индуктивностью 20 мГн, чтобы энергия
магнитного поля составляла 5 Дж?

ДАНО:	СИ	РЕШЕНИЕ Энергия магнитного поля определяется по формуле Из данной формулы выразим искомую силу тока

Ответ:
22,4 А.

Задача
2.
На катушке с индуктивностью 80 мГн поддерживается постоянное напряжение 12 В.
Известно, что сопротивление катушки равно 3 Ом. Найдите энергию, которая
выделится при размыкании цепи. Также найдите ЭДС самоиндукции в катушке,
предполагая, что размыкание произошло за 10 мс.

ДАНО:	СИ	РЕШЕНИЕ Энергия магнитного поля определяется по выражению Запишем закон Ома для участка цепи Тогда с учётом закона Ома энергия магнитного поля равна Запишем закон самоиндукции При размыкании цепи изменение силы тока будет равно току, протекавшему в цепи. Знак минус означает, что сила тока уменьшилась

Ответ:
Энергия магнитного поля – 0,64 Дж; ЭДС самоиндукции – 32 В.

Задача
3.
Соленоид длиной 40 см содержит 5 витков на каждый сантиметр. Найдите энергию
магнитного поля при силе тока в 5 А, если при этом магнитный поток через
поперечное сечение соленоида равен 10 мВб.

ДАНО:	СИ	РЕШЕНИЕ Энергия магнитного поля определяется по формуле Индуктивность соленоида равна отношению магнитного потока к силе тока. В данном случае, это соотношение умножается на число витков, поскольку такой индуктивностью обладает каждый виток соленоида Тогда с учётом последней формулы получаем Количество витков можно определить по формуле

Ответ:
5 Дж.

Задача
4.
При увеличении силы тока в катушке от 3 А до 8 А, энергия магнитного поля
возросла на 20 Дж. Найдите индуктивность этой катушки.

ДАНО:	РЕШЕНИЕ Энергия магнитного поля определяется по формуле Применим эту формулу для начальной и конечной силы тока Изменение энергии магнитного поля можно рассчитать по формуле Тогда

Ответ:
0,73 Гн.

Задача
5.
Катушка с индуктивностью 0,5 Гн включена в цепь. В цепи произошёл скачок
напряжения, изображённый на графике. Известно, что при этом скачке в катушке
возникла ЭДС самоиндукции 10 В. Как изменилась энергия магнитного поля?

ДАНО:

РЕШЕНИЕ Запишем закон самоиндукции Энергия магнитного поля рассчитывается по формуле Из графика видно, что за время 1 с напряжение изменилось от 50 В до 30 В Запишем закон Ома для участка цепи Применим закон Ома для силы тока до и после скачка напряжения Из закона самоиндукции получаем Тогда силы тока до и после скачка напряжения Изменение энергии магнитного поля определяется по выражению Преобразуем эту формулу с учётом выражений для определения силы тока Проверим размерности

Ответ:
энергия уменьшилась на 400 Дж.

Энергия магнитного поля изолированного контура с током.

Для того чтобы в неподвижном контуре создать электрический ток, необходимо включить в цепь источник сторонних э. д.с. Если в цепи течет постоянный ток, то энергия, поступающая в цепь из источника сторонних э. д.с., расходуется на выделение джоулевой теплоты и на совершение работы в потребителе энергии. Индукция магнитного поля, как и его энергия, при этом неизменна. Индукция изменяется с изменением силы тока. Следовательно, источник сторонних э. д.с. передает в цепь энергию на создание магнитного поля в процессе увеличения силы тока. Вычислив работу, совершаемую источником сторонних э. д.с. для увеличения силы тока от нуля до конечного значения, получим энергию магнитного поля, которое связано с этим током.

При изменении потока магнитной индукции, охватываемого контуром, в контуре возникает э. д.с. индукции в соответствии с законом (23.1). У изолированного контура поток электромагнитной индукции Ф возникает за счет магнитного поля, создаваемого током в контуре. При увеличении силы тока возрастает поток Ф, охватываемый током, и в контуре по закону Фарадея возникает э. д.с. индукции, которая в данном случае называется э. д.с. самоиндукции. По правилу Ленца, она направлена так, что препятствует увеличению силы тока. Для увеличения силы тока необходимо, чтобы сторонняя э. д.с. источника была направлена противоположно э. д.с. самоиндукции и равна ей. Таким образом, в процессе роста силы тока источник сторонних э. д.с. совершает работу против э. д.с. самоиндукции. За промежуток времени dt по контуру проходит количество электричества и, следовательно, против э. д.с. самоиндукции источник сторонних сил в течение совершает работу

, (24.1)

Где для использована формула (23.1) . При совершении этой работы происходит превращение энергии источника сторонних э. д.с. в энергию магнитного поля тока в контуре. Поэтому изменение энергии магнитного поля связано с изменением потока соотношением

(24.2)

Индукция магнитного поля тока в соответствии с законом Био-Савара линейно зависит от силы тока. Поэтому при переменной силе тока, протекающего по жесткому неподвижному контуру, картина силовых линий остается прежней, а индукция в каждой точке растет пропорционально силе тока. А это означает, что поток магнитной индукции Ф сквозь фиксированную неподвижную площадь также пропорционален силе тока, и поэтому

(24.3)

Где L – постоянный коэффициент пропорциональности, не зависящий от силы тока и индукции магнитного поля. Этот коэффициент называется индуктивностью контура.

Подставляя обе части (24.3) в (24.2), находим

(24.4)

Интегрируя обе части (24.4) от до некоторого значения I , получаем формулу

, (24.5)

Которая определяет энергию магнитного поля, создаваемого током силы I, текущим по контуру с индуктивностью L.

Это и есть формула, определяющая энергию магнитного поля, созданного током , текущим по контуру с индуктивностью .

Если есть несколько контуров с током, то происходит взаимовлияние контуров друг на друга с помощью так называемых коэффициентов взаимной индукции , . величины определяет индуктивность каждого поля. При наличии нескольких контуров

. (24.6)

Явление самоиндукции.

Рассмотрим явление возникновения в замкнутом контуре при изменении силы тока в этом контуре.

При замыкании ключа в первом случае (а) лампочка мгновенно достигает максимальной яркости и далее горит с постоянным накалом. При размыкании ключа лампочка мгновенно гаснет. Во втором случае (б), где вместо сопротивления включена катушка индуктивности, при замыкании ключа лампочка медленно набирает яркость, а при размыкании гаснет постепенно. Это связано с явлением электромагнитной индукции. Действительно, при замыкании ключа ток нарастает, значит , следовательно , , т. е. в цепи имеется две э. д.с.: , т. е. препятствует нарастанию тока. При размыкании ключа ток в контуре начинает уменьшаться , а значит , , , т. е. поддерживает уменьшающийся ток. С учетом (24.3)

(24.7)

Включение и выключение постоянной э. д.с. в цепи с сопротивлением и индуктивностью.

Если в момент в цепь (рис. б) включается источник сторонней э. д.с. постоянной величины, например, батарея, то сила тока I в цепи начинает расти. Однако за счет роста индукции поля в контуре возникает э. д.с. самоиндукции, действующая противоположно сторонней э. д.с. В результате рост силы тока в цепи замедляется. Для каждого момента времени соблюдается закон Ома, который с учетом (24.7) записывается в виде уравнения

, (24.8)

Где — полное сопротивление в цепи (включая внутреннее сопротивление источника). Это уравнение необходимо решить при начальном условии . Говоря о том, что в каждый момент соблюдается закон Ома, мы предполагаем, что сила тока во всех участках цепи одна и та же, т. е. ток квазистационарен. Решение уравнения (24.8) элементарно

(24.9)

Ток нарастает и установившееся значение силы тока , соответствующее закону Ома для постоянного тока, достигается лишь в смысле предела при бесконечном времени. Учитывая экспоненциальную зависимость силы тока от времени, можно как обычно за время нарастания силы тока в цепи принять такое значение , при котором показатель экспоненты обращается в минус единицу, т. е.

(24.10)

При большой индуктивности в цепи нарастание силы тока происходит медленно. Например, если в цепь включить большую катушку индуктивности и лампу накаливания, то после замыкания цепи проходит значительный промежуток времени, в течение которого лампа разгорается до своего полного постоянного накала.

При выключении постоянного источника сторонних э. д.с. например, закоротив его, можно наблюдать, что сила тока не падает мгновенно до нуля, а уменьшается постепенно. Уравнение для силы тока в этом случае, очевидно, имеет вид

(24.11)

и решается при начальном условии

(24.12)

Время убывания силы тока дается той же формулой (24.10). При достаточно больших индуктивностях после выключения сторонней э. д.с. лампа накаливания в цепи гаснет лишь постепенно в течение заметного промежутка времени. Электродвижущей силой, которая обеспечивает существование тока в цепи в течение этого промежутка времени, является электродвижущая сила самоиндукции, а источником энергии – энергия магнитного поля катушки индуктивности.

Плотность энергии магнитного поля.

Формула (24.5) определяет энергию магнитного поля через ток. Найдем другую формулу, описывающую энергию магнитного поля через его характеристики, т. е. через индукцию и напряженность.

, но , т. е. . Если перейти в этой формуле от линейных токов к объемным токам, то . Преобразуем подынтегральное выражение. Для этого рассмотрим выражение . Тогда мы найдем . После подстановки этого выражения найдем, что

. (24.13)

Но . Оценим второе слагаемое в (24.13). Пусть токи находятся в одной области пространства, а энергию рассматриваем в удаленных областях пространства. Чтобы оценить интеграл при больших значениях r, учтем, что, векторный потенциал пропорционален , т. е. . Напряженность магнитного поля, а. Тогда весь интеграл имеет порядок , а значит при переходе в (24.13.) к интегрированию по всему пространству второй интеграл будет равен нулю и тогда энергия магнитного поля будет определяться формулой:

(24.14)

Формула (24.14) предполагает, что магнитное поле «размазано» по пространству. Плотность энергии магнитного поля:

W (24.15)

В заключение отметим, что формула (24.5) предполагает, что энергия магнитного поля “локализована” в токе, а формула (24.15) – что эта энергия заполняет все пространство.

Содержание:

Энергия электрического и магнитного полей:

Электрическое и магнитное поля обладают энергией, которая накапливается при образовании заряда в электрической системе или образовании тока в электромагнитной системе. В данной главе получены количественные выражения энергии электрического и магнитного полей, а также электрических и электромагнитных сил.

Энергия электрического поля

При зарядке конденсатора энергия запасается в виде энергии электрического поля и может быть возвращена источнику при преобразовании в другой вид энергии.

Выражение энергии через характеристики конденсатора

Заряд конденсатора образуется переносом заряженных частиц с одной обкладки на другую под действием внешнего источника энергии. Работа, совершенная при переносе единицы заряда, численно равна напряжению между обкладками.
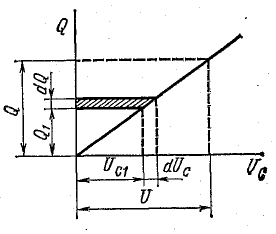
Если бы напряжение в процессе зарядки не изменялось, то энергию можно было бы определить произведением напряжения и заряда [см. формулу (1.5)]. Однако в процессе накопления заряда растет и напряжение, поэтому при определении энергии, затраченной на образование заряда, нужно учесть зависимость между напряжением и зарядом (7.28). Если емкость конденсатора — величина постоянная, зависимость между напряжением и зарядом графически выражается прямой линией (рис. 11.1).

Рис. 11.1. К определению энергии электрического поля

Предположим, что заряд Q₁ увеличился на dQ — величину столь малую, что в пределах изменения заряда напряжение можно считать неизменным:

Выражение энергии через характеристики электрического поля

Выражение (11.2) получено на основе закона сохранения энергии; однако из него непосредственно не следует, что энергия W_э является энергией электрического поля. Можно показать, что эта энергия распределена в электрическом поле.
Для примера рассмотрим равномерное электрическое поле плоского конденсатора (см. рис. 1.6, а).

Поток вектора электрического смещения через любую поверхность, проведенную в диэлектрике параллельно пластинам, равен заряду Q конденсатора, что следует из формулы (7.33): DS = Q.
Напряженность равномерного электрического поля Е = U/l.
Следовательно,

где V — объем диэлектрика, в котором распределено поле, связанное с заряженными пластинами конденсатора.
Отношение энергии к объему диэлектрика дает объемную плотность энергии электрического поля:

Энергия, определенная формулой (11.2) через характеристики проводников, выражена также формулой (11.5) через характеристики электрического поля. Эквивалентность этих формул свидетельствует о том, что энергия системы заряженных тел является энергией электрического поля.

Задача 11.1.

Плоский воздушный конденсатор емкостью 600 пФ при расстоянии между электродами 2 см заряжен до напряжения U = 4 кВ и отключен от источника напряжения. Определить изменение энергии и напряженности электрического поля конденсатора при уменьшении расстояния между электродами вдвое.
Решение. До изменения расстояния между обкладками энергия электрического поля, по формуле (11.3),

Напряженность электрического поля [см. (1.5)]

При уменьшении расстояния между обкладками вдвое емкость конденсатора согласно формуле (7.29) увеличивается вдвое. При этом заряд конденсатора не изменяется (предполагается, что утечки заряда нет).
Вследствие увеличения емкости конденсатора напряжение между обкладками уменьшится во столько же раз [см. формулу (7.28)]:

Энергия электрического поля

Напряженность электрического поля

Механические силы в электрическом поле

Вопрос о механических силах в электрическом поле рассмотрим на примере плоского конденсатора, заряженного от внешнего источника энергии, имеющего напряжение U. Электрическое поле конденсатора будем полагать равномерным.

Энергетический баланс в электростатической системе

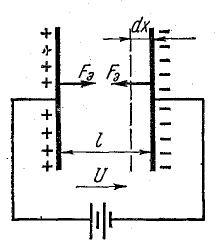
Силы F_э, возникающие вследствие взаимодействия пластин с электрическим полем, приложены к пластинам и направлены так, что они притягиваются. Предположим, что одна из пластин конденсатора свободна, и возможное малое перемещение ее под действием силы F_э обозначим через dх (рис. 11.2).

Рис. 11.2. Механические силы в электрическом поле

В дальнейших рассуждениях будем исходить из того, что при изменении заряда конденсатора не возникает потерь энергии в проводниках в связи с перемещением заряженных частиц и в диэлектрике вследствие изменения напряженности поля.

При таких условиях в соответствии с законом сохранения энергии при изменении заряда конденсатора на dQ за счет энергии внешнего источника изменяется энергия электрического поля на dW_э и совершается механическая работа F_эdx:

Обобщенное выражение электрической силы (первый случай)

Заряд конденсатора остается неизменным (Q = const), т. е. заряженный конденсатор отключен от внешнего источника энергии.
При dQ = 0 работа внешнего источника UdQ = 0. Поэтому
или
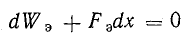
Последнее равенство показывает, что механическая работа, связанная с перемещением пластины, совершается за счет энергии электрического поля.
Действительно, механическая работа, совершаемая электрической силой, положительна (F_эdх > 0), следовательно, изменение энергии электрического поля отрицательно (dW_э < 0). Это значит, что энергия электрического поля в данном случае уменьшается.

Механическую силу, стремящуюся изменить положение пластины конденсатора, можно выразить отношением

Рассуждая аналогично, можно получить зависимость между механическим моментом и углом поворота α, если механическое движение осуществляется в виде вращения одной пластины по отношению к другой:

Изменение расстояния l между пластинами на dх изменит емкость конденсатора. При уменьшении расстояния емкость увеличивается, а напряжение между пластинами уменьшается, что непосредственно следует из формулы (7.28).

Предположим, что расстояние между пластинами увеличивается благодаря действию на пластины внешних механических сил. Энергия в системе возрастает на величину работы, совершенной внешним источником механической энергии. При этом емкость конденсатора уменьшится, а напряжение между пластинами увеличится.

Обобщенное выражение электрической силы (второй случай)

Напряжение между пластинами остается постоянным (U = const), т. е. во время движения пластины конденсатор не отключается от внешнего источника энергии.

При уменьшении расстояния между пластинами увеличивается емкость конденсатора, что при неизменном напряжении влечет за собой увеличение заряда.

Внешний источник энергии должен затратить энергию на увеличение заряда конденсатора в количестве UdQ.

Изменение энергии электрического поля dW_э при изменении заряда, согласно формуле (11.2), 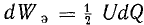, т. е. составляет половину энергии внешнего источника, израсходованной при увеличении заряда конденсатора. Вторая половина энергии расходуется на покрытие механической работы F_эdх, следовательно,

Отсюда

Аналогично, при вращательном движении

Увеличение расстояния между пластинами в результате действия внешних механических сил приведет к уменьшению емкости. Но при постоянном напряжении за уменьшением емкости последуют уменьшение заряда конденсатора и уменьшение энергии электрического поля. В этом случае механическая работа, связанная с перемещением пластины, совершается внешними механическими силами. Величина этой работы численно равна уменьшению энергии электрического поля. Таким образом, источнику электрической энергии возвращается энергия, численно равная удвоенному значению механической работы.

Энергия магнитного поля

При возникновении электрического тока в проводящем контуре одна часть энергии источника питания расходуется на преодоление электрического сопротивления контура и превращается в тепло, а другая запасается в виде энергии магнитного поля.

Энергия магнитного поля уединенного контура или катушки с током

Определим вначале энергию магнитного поля уединенного контура с током I, пользуясь формулой (8.21), согласно которой изменение энергии в магнитной системе связано с изменением потокосцепления.

При этом нужно принять во внимание, что в процессе возникновения тока в контуре его величина не остается постоянной, а увеличивается от 0 до I. Вместе с изменением тока изменяется и потокосцепление [см. формулу (8.23)].
При таких условиях оба множителя в формуле (8.21) являются переменными, поэтому при помощи этой формулы можно определить лишь приращение энергии dW_м за некоторый весьма малый промежуток времени, в течение которого ток в контуре можно считать неизменным:

где i — некоторое промежуточное значение тока между 0 и I, принятое неизменным в течение бесконечно малого промежутка времени; dψ  —приращение потокосцепления за тот же промежуток времени.

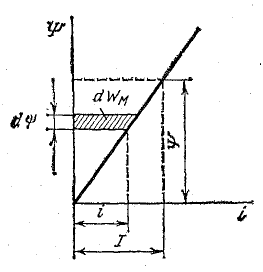
Рис. 11.3. К определению энергии магнитного поля

Если индуктивность контура постоянна, то зависимость между потокосцеплением и током графически изображается прямой линией (рис. 11.3). Изменение энергии при токе i выразится заштрихованным элементом площади [см. формулу (11.12)]. Энергию при потокосцеплении ψ и токе I можно определить суммой таких элементов, т. е. площадью прямоугольного треугольника с катетами ψ и I:

Учитывая формулу (8.23), запишем и другие выражения для определения энергии магнитного поля:

Энергия магнитного поля в системе магнитно-связанных контуров (катушек)

Определим энергию магнитного поля в системе двух магнитно-связанных контуров (катушек) с токами.

Энергия магнитного поля этой системы накапливается в процессе установления токов в обоих контурах, причем в процессе накопления определенное влияние оказывает взаимное потокосцепление.

По закону сохранения энергии, общий запас энергии в магнитном поле не зависит от последовательности установления тока в контурах.
Учитывая это, зададим определенную последовательность установления токов в контурах: сначала ток увеличивается от 0 до I₁ в первом контуре, а после этого — от 0 до I₂ во втором контуре.

При изменении тока в первом контуре изменяется собственное потокосцепление первого контура от 0 до ψ_1.1 и взаимное потокосцепление второго контура от 0 до ψ_1.2.

Энергия в системе определяется только изменением собственного потокосцепления и при установившемся токе I₁ выражается формулой (11.13):

Энергия, определяемая изменением взаимного потокосцепления, равна нулю, так как во втором контуре ток равен нулю.
При изменении тока во втором контуре изменяются собственное потокосцепление второго контура от 0 до ψ_2.2 и взаимное потокосцепление первого контура от 0 до ψ_2.1.
Взаимное потокосцепление второго контура при этом не изменяется, так как ток в первом контуре уже установился.
К запасу энергии W_1.1м добавляются энергия, определяемая изменением собственного потокосцепления второго контура:

н энергия, определяемая изменением взаимного потокосцепления первого контура:

Последняя часть энергии выражена по формуле (8.21), так как магнитное поле второго контура взаимодействует с постоянным током первого контура.
Энергия магнитного поля системы двух контуров с токами

или

Учитывая независимость энергии магнитного поля от последовательности установления токов в контурах или принимая во внимание, что М_2.1 = М_1.2 = М, получим окончательно

Знак перед выражением МI₁I₂ в уравнении (11.14) зависит от способа включения контуров (катушек).

При согласном включении взаимное потокосцепление совпадает по направлению с собственным, поэтому энергия взаимосвязи входит в уравнение со знаком плюс. При встречном включении взаимное потокосцепление направлено против собственного, поэтому энергию взаимосвязи в той же формуле нужно взять со знаком минус.

Индуктивность в системе магнитно-связанных катушек

Рассмотрим частный случай, когда две магнитно-связанные катушки электрически соединены между собой последовательно, в результате чего в обеих катушках ток I один и тот же (см. рис. 8.22).
Энергия магнитного поля такой системы

или

где 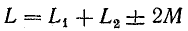— индуктивность системы магнитно-связанных катушек.
При согласном включении

при встречном включении

Выражение энергии через характеристики магнитного поля

Формулами (11.13) и (11.14) энергия выражена через характеристики контуров с токами.

Можно показать, что в данном случае энергия распределена в магнитном поле, окружающем проводники с токами.

Для примера возьмем поле катушки с кольцевым сердечником. Если диаметр сечения сердечника много меньше диаметра самого сердечника, поле можно считать равномерным:

Тогда

где 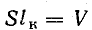— объем сердечника.
Энергия магнитного поля в единице объема

Здесь энергия выражена через характеристики магнитного поля, что свидетельствует о ее принадлежности магнитному полю.

Задача 11.8.

Определить энергию магнитного поля в системе двух обмоток (задача 8.21) при согласном и встречном их включении, если ток в первой обмотке I₁ = 5 А, а во второй I₂ = З А.
Решение. Для определения энергии в магнитно-связанной системе двух обмоток воспользуемся формулой (11.14).
Величины индуктивностей катушек и взаимной индуктивности при неферромагнитном сердечнике не зависят от тока в них, поэтому возьмем их по результатам решения задачи 8.21:
   
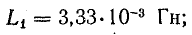
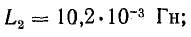
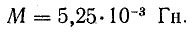
При согласном включении обмоток


При встречном включении

 

Задача 11.9.

Общая индуктивность двух последовательно соединенных катушек (см. рис. 8.22) при согласном включении равна 1,52 мГн, при встречном — 0,88 мГн. Определить взаимную индуктивность катушек.
Решение. Найдем взаимоиндуктивность катушек, решив совместно уравнения (11.15) и (11.16):

Вычтем второе уравнение из первого:

.
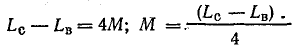
В данном случае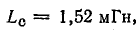  

Механические силы в магнитном поле

В технике широко применяются устройства, в основе работы которых лежит силовое действие магнитного поля (электродвигатели, реле, тяговые и подъемные электромагниты, электроизмерительные приборы и др.).
Электромагнитные силы приходится учитывать при расчете электрических аппаратов, проектировании распределительных устройств электростанций и в других случаях.

Энергетический баланс в электромагнитной системе

Определение электромагнитной силы F_м рассмотрим на примере взаимодействия полюсов электромагнита (рис. 11.4), полагая магнитное поле в воздушном зазоре между полюсами равномерным.

Обозначим ток в обмотке электромагнита через i, сопротивление обмотки — R, возможное малое перемещение одного из полюсов (якоря электромагнита) — dх.
Работа внешнего источника энергии, к зажимам которого подключена обмотка электромагнита, в общем случае расходуется на выделение тепла в обмотке (i²Rdt), на изменение энергии в магнитном поле (dW_м) и механическую работу (F_мdх).

Рис. 11.4. Взаимодействие полюсов электромагнита

Согласно закону сохранения энергии, за малый отрезок времени энергетический баланс в системе выражается уравнением

Два последних слагаемых в правой части уравнения выражают изменение энергии в магнитной системе. Рассмотрим их более подробно. При этом учтем выводы о том, что изменение энергии магнитного поля и работа электромагнитных сил определяются изменением потокосцепления:

Обобщенное выражение электромагнитной силы (первый случай)

Потокосцепление в магнитной системе не изменяется (ψ = const, dψ = 0); это условие обычно соблюдается в электромагнитах переменного тока. Тогда

а

Последнее равенство показывает, что механическая работа, связанная с перемещением якоря электромагнита, совершается за счет энергии магнитного поля. Внешний источник расходует энергию только на выделение тепла.
Механическая работа электромагнитной силы положительна (F_мdx > 0); следовательно, изменение энергии магнитного поля отрицательно (dW_м < 0), т. е. она убывает.

Механическая сила, стремящаяся изменить положение якоря, может быть выражена отношением

Аналогично можно получить зависимость между механическим моментом и углом поворота якоря:

Обобщенное выражение электромагнитной силы (второй случай)

Ток в обмотке электромагнита поддерживается постоянный (i = const). При уменьшении расстояния между полюсами увеличивается индуктивность, что при неизменном токе повлечет за собой увеличение потокосцепления. Внешний источник должен затратить энергию на увеличение потокосцепления в количестве idψ.
Согласно формуле (11.13), энергия магнитного поля изменяется на величину

что составляет половину энергии внешнего источника, а другая расходуется на покрытие механической работы F_мdx.
Следовательно,

Отсюда

Аналогично, для вращательного движения

Таким образом, механическая сила (или момент), стремящаяся изменить положение якоря электромагнита, равна увеличению энергии магнитного поля в расчете на единицу изменения пути (или угла), если ток в обмотке не изменяется.

Увеличение воздушного зазора в результате действия внешней механической силы приведет к уменьшению индуктивности. Но при неизменном токе за этим последует уменьшение потокосцепления и энергии магнитного поля.
Механическая работа, связанная с перемещением якоря, совершается внешними механическими силами. Величина этой работы численно равна уменьшению энергии магнитного поля. Таким образом, источнику электрической энергии возвращается энергия, численно равная удвоенной величине механической работы.

Используя общие выводы и формулы, полученные ранее, найдем выражения для определения электромагнитных сил в конкретных случаях, встречающихся на практике.

Тяговое усилие электромагнита

Отрывная сила (груза, пружины и т. д.) стремится увеличить воздушный зазор между полюсами электромагнита. Предположим, что этот зазор увеличится на dx. При этом объем, в котором распределено магнитное поле, увеличится на (dV = Sdx, где S — площадь полюса.
Изменение энергии магнитного поля составит

Согласно формуле (11.20),

Силы взаимодействия двух параллельных проводов с токами

На практике часто встречается параллельное расположение проводов с токами. Таким образом, например, монтируются шины распределительных устройств электрических станций и подстанций. Для того чтобы правильно выбрать шины и изоляторы, на которых они закреплены, необходимо определить электромагнитные силы взаимодействия между шинами.

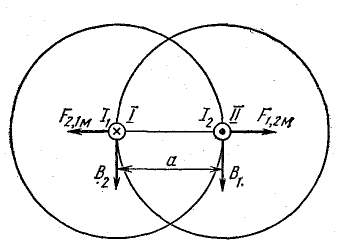
В данном случае силу взаимодействия можно рассматривать как действие магнитного поля тока первого провода I на ток второго II, или наоборот (рис. 11.5).

Рис. 11.5. К определению сил взаимодействия двух параллельных проводов

Согласно формуле (8.10), магнитное поле тока первого провода в месте расположения второго провода характеризуется индукцией

где а — расстояние между осями проводов.
Между направлениями В₁ и I₂ угол α = 90°.
По формуле (8.4), сила, действующая на ток второго провода в поле первого провода,

Аналогичное выражение получается для силы, действующей на ток первого провода в магнитном поле тока второго провода:

Рассматривая взаимодействие равных участков l двух проводов, получим общую формулу

Действие магнитного поля на свободно заряженную частицу

Действие магнитного поля на заряженные частицы, движущиеся вне проводника, например в вакууме, широко используется в технике.
Примерами такого использования могут служить: фокусировка или смещение электронного пучка (луча) в электроннолучевых трубках телевизора и осциллографов или электронных микроскопах, ускорение заряженных частиц для исследования ядерных процессов и т. д.

Для определения силы, которая действует на частицу с зарядом Q, движущуюся в равномерном магнитном поле, можно использовать формулу (8.5), подставив в нее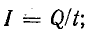  
Рассматривая длину проводника l как путь, пройденный заряженной частицей за время t, отношение l/t можно считать скоростью движения частицы

тогда

где α — угол между направлениями линий магнитной индукции и направлением движения заряженной частицы. При а α= 90^º

Сила F_м, согласно правилу левой руки, направлена перпендикулярно направлению линий магнитной индукции и направлению скорости.
Из механики известно, что при действии на тело постоянной по величине силы перпендикулярно направлению скорости тело движется по окружности радиуса

Подставляя в последнее выражение силу из формулы (11.25), получим

где m — масса заряженной частицы.
Если все величины правой части уравнения (11.26) постоянны, то заряженная частица движется по окружности радиуса ρ в плоскости, перпендикулярной направлению линий магнитной индукции. Угловая скорость движения

Задача 11.11.

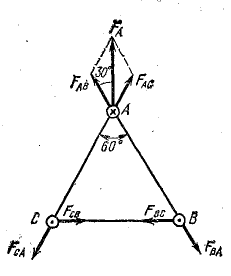
В вершинах А, В, С равностороннего треугольника со стороной а = 10 см расположены три параллельных прямых провода (рис. 11.6). Токи в проводах В и С равны по величине: I_B = I_C = 6000 А и направлены в одну сторону, а ток в третьем проводе I_A = 12 000 А направлен в противоположную сторону. Определить силу, действующую на 1 м длины каждого провода.

Рис. 11.6. К задаче 11.11

Решение. Рассматривая отдельно каждую пару проводов, определим направление сил взаимодействия между ними. При этом будем иметь в виду, что при одинаковом направлении токов провода притягиваются друг к другу, а при разном — отталкиваются. Направления сил показаны на рис. 11.6. Величину их определим по формуле (11.23):


Величину и направление силы F_A, действующей на провод А, определяют векторным сложением составляющих: 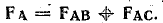 В данном случае складываются две равные силы с углом 60° между их направлениями.
Результирующая сила направлена посредине между составляющими и имеет величину

Содержание книги

Предыдующая страница

§16. Превращение энергии в электрических и магнитных явлениях

16.9 Превращения энергии при изменении индуктивности цепи.

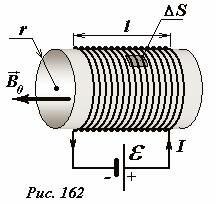
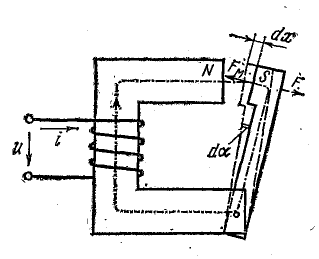
Энергия магнитного поля соленоида зависит от индуктивности последнего. Поэтому при изменении размеров соленоида или изменении материала сердечника в цепи происходят процессы, приводящие к изменению энергии магнитного поля. Для поддержания постоянного электрического тока в цепи, содержащей соленоид, присутствие источника ЭДС обязательно (Рис. 162). Следовательно, нам необходимо принимать во внимание не только изменения магнитного поля соленоида, но и процессы, протекающие на других участках цепи, в том числе и источнике.

Рассмотрим подробно превращения энергии при изменении радиуса соленоида. Для наглядности можно считать, что обмотка соленоида изготовлена из упругой проволоки, способной растягиваться. Прежде всего, обратим внимание, что на обмотку соленоида действуют силы со стороны магнитного поля, создаваемого электрическим током в самой обмотке.

Найдем силы, действующие на обмотку длинного соленоида с плотной намоткой, для которого можно пренебречь краевыми эффектами. Магнитное поле внутри такого соленоида является однородным, вектор индукции направлен вдоль оси соленоида, а его модуль равен

(~B_0 = mu_0 nI) , (1)

где (~n = frac{N}{l}) — плотность намотки, равная числу витков на единицу длины соленоида, I — сила тока в обмотке. Вне соленоида магнитное поле отсутствует.

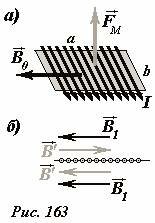
Выделим на поверхности соленоида малую площадку площадью (Delta S = ab) (Рис. 163а). Сила Ампера, действующие на участки витков обмотки, находящиеся на выделенной площадке, направлена перпендикулярно направлению тока и вектору индукции поля. Модуль этой силы рассчитывается по формуле

(~F = I N_1 B_1 b) , (2)

где (N_1 = na) — число витков, лежащих на площадке, B₁ — индукция магнитного поля, создаваемого всеми элементами соленоида, кроме лежащих на площадке.

Вспомните расчет силы, действующей на заряженную пластину конденсатора со стороны электрического поля. При выводе формулы для этой силы мы также учитывали напряженность поля, создаваемого всеми зарядами, кроме находящихся на площадке. Мы показали, что напряженность этого поля в два раза меньше напряженности суммарного поля.

Чтобы определить требуемую индукцию поля, представим суммарное поле в виде суммы полей[~vec B’] — создаваемого током площадки и (~vec B_1) — создаваемого всеми остальными участками обмотки (Рис. 163б). Внутри соленоида эти векторы направлены одинаково и их сумма равна индукции суммарного поля (B’ + B_1 = B_0). Вне соленоида эти векторы направлены противоположно и их сумма равна нулю (B’ — B_1 = 0). Из этих соотношений следует, что индукция поля, действующего на выделенную площадку, в два раза меньше индукции суммарного поля внутри соленоида (~B_1 = frac{B_0}{2}). Таким образом, на выделенную площадку действует сила, которая рассчитывается по формулам

(~F = I N_1 B_1 b = I n frac{B_0}{2} ab = frac{mu_0 n^2 I^2}{2} ab = frac{(mu_0 n I)^2}{2 mu_0} ab = frac{B^2_0}{2 mu_0} ab) . (3)

Найденная сила пропорциональна площади выделенной площадки и направлена перпендикулярно ей, поэтому можно говорить о давлении магнитного поля на поверхность соленоида. Существенно, что величина этого давления равна плотности энергии магнитного поля вблизи площадки

(~p = frac{F}{Delta S} = frac{B^2_0}{2 mu_0} = w_M) . (4)

аналогично тому, что давление электрического поля на поверхность проводника со стороны электрического поля равно плотности энергии этого поля.

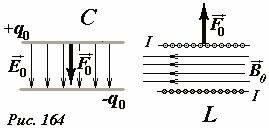
Продолжим сравнение действия электрического поля в конденсаторе и магнитного поля в соленоиде. Самое существенное отличие заключается в направлении действия силы (Рис. 164). На обкладки конденсатора действует сила, направленная внутрь, в сторону части пространства, занятого полем. Если предоставить пластинам возможность двигаться, то сила их взаимодействия приведет к уменьшению расстояния между пластинами, уменьшению объема, занятого полем, уменьшению суммарной энергии поля (при неизменном заряде на пластКурсивное начертаниеинах). При этом энергия электрического поля переходит в кинетическую энергию движущихся пластин.

На обмотку соленоида со стороны магнитного поля действует сила, направленная наружу, в сторону противоположную части пространства, занятого полем. Если обмотка соленоида способна расширятся, то силы взаимодействия приведут к увеличению радиуса обмотки, увеличению объема, занятого полем, увеличению его суммарной энергии (при неизменной силе тока в обмотке). Таким образом, мы приходим к парадоксальному выводу: магнитное поле совершает работу и при этом его энергия увеличивается – отсюда уже недалеко до «вечного двигателя»! Не стоит обольщаться этим «гениальным изобретением», достаточно вспомнить, что для поддержания тока в цепи, в ней должен быть источник, обладающий энергией и отдающий ее в цепь. Кроме того, при движении зараженной пластины в электрическом поле распределение зарядов и их величина могут оставаться неизменными. При движении проводника в магнитном поле распределение электрических токов и их величина изменяются вследствие явления электромагнитной индукции.

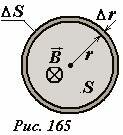
Рассмотрим, какие изменения произойдут в рассматриваемой системе, показанной на рис. 162, при увеличении радиуса обмотки на малую величину Δr (то есть при увеличении площади сечения на величину ΔS — Рис. 165). Изменение силы тока в цепи описывается уравнением закона Ома для полной цепи

(~varepsilon + varepsilon_{ind} = IR) , (5)

где R — полное сопротивление цепи, ε_ind — ЭДС индукции, возникающей в соленоиде, которая определяется законом Фарадея

(~varepsilon_{ind} = -frac{Delta Phi}{Delta t}) , (6)

где (~Phi = NSB = nlS (mu_0 n I) = mu_0 n^2 lSI) — магнитный поток через все N витков катушки (l — длина обмотки). На основании этих законов запишем уравнение

(~varepsilon = IR + frac{Delta Phi}{Delta t}) ,

которое, как обычно, умножим на малую величину заряда Δq, протекающего по цепи за малый промежуток времени Δt, в результате получим соотношение

(~varepsilon Delta q = IR Delta q + frac{Delta Phi}{Delta t} Delta q = IR Delta q + I Delta Phi) . (7)

В данном случае поток через соленоид может изменяться по двум причинам – изменения силы тока и изменения площади поперечного сечения соленоида. Пусть в некоторый момент времени сила тока в обмотке равнялась I, а площадь сечения S, затем за малый промежуток времени Δt сила тока изменилась на ΔI, а площадь — на ΔS. Тогда изменения магнитного потока можно представить в виде

(~Delta Phi = mu_0 n^2 l Delta(IS) = mu_0 n^2 l ((I + Delta I)(S + Delta S) — IS) = mu_0 n^2 l (S Delta I + IDelta S)) ,

на последнем шаге преобразований мы пренебрегли произведением малых величин ΔIΔS. Подставим полученное выражение в уравнение (7)

(~varepsilon Delta q = IR Delta q + I Delta Phi = IR Delta q + I mu_0 n^2 l (S Delta I + IDelta S) = IR Delta q + mu_0 n^2 l S I Delta I + mu_0 n^2 I^2 l Delta S) . (8)

Выясним теперь смысл каждого члена этого уравнения, тем более, что некоторые из них уже встречались нам ранее: [varepsilon Delta q] — работа источника ЭДС по перемещению заряда Δq; [~IR Delta q = I^2 R Delta t] — количество теплоты, выделившееся в цепи при прохождении заряда Δq; [~mu_0 n^2 l S I Delta I = mu_0 n^2 Delta left( frac{I^2}{2}right) Sl = Delta left( frac{mu_0 n^2 I^2}{2}right) Sl = Delta left( frac{B^2}{2mu_0}right) Sl] — (здесь (B = mu_0 n I) — индукция магнитного поля внутри соленоида) изменение энергии магнитного поля вследствие изменения силы тока в соленоиде (изменение энергии поля в первоначальном объеме соленоида);

наконец, последнее слагаемое преобразуется к виду (~mu_0 n^2 I^2 l Delta S = 2 left( frac{B^2}{2mu_0}right) Delta V) и равно удвоенной (!?) энергии магнитного поля в части приращенного объема соленоида ΔV. Смысл половины этого слагаемого, то есть (~left( frac{B^2}{2mu_0}right) Delta V) , понятен – это увеличение энергии поля вследствие увеличения его объема, осталось найти смысл оставшейся величины (~left( frac{B^2}{2mu_0}right) Delta V) . Мы не случайно начали рассуждения данного раздела рассмотрения сил, действующих на обмотку – эти силы увеличивают размер соленоида, следовательно, совершают работу. В результате совершения этой работы увеличивается механическая энергия обмотки – если она упругая и деформируемая, то увеличивается энергия ее упругой деформации, возможно, что часть этой энергии идет на увеличение кинетической энергии расширяющихся витков. Выяснение этих деталей требует более конкретного описания механических свойств обмотки. Не будем их конкретизировать, покажем, что оставшееся слагаемое действительно равно работе сил поля над расширяющейся обмоткой. Еще раз взглянем на выделенную на боковой поверхности соленоида площадку (Рис. 162, 163) со сторонами a и b, на нее действует сила pab (p — давление поля). При смещении этой площадки на расстояние Δr в направлении действия силы, магнитное поле совершает работу (~delta A = F Delta r = pab Delta r = p Delta V_{ab}) , где (Delta V_{ab}) — изменение объема соленоида при смещении рассматриваемой площадки. Так как давление на все точки поверхности соленоида одинаково, то суммарная работа поля по смещению всех участков его поверхности будет равна (A = p Delta V) , где ΔV — полное изменение объема соленоида. Используя формулу (4) для давления магнитного поля, получим, что работа по расширению соленоида равна

(~A = left( frac{B^2}{2mu_0}right) Delta V) .

Таким образом, энергетический баланс и в этом случае сходится: работа, совершенная источником ЭДС по перемещению заряда (varepsilon Delta q), расходуется на:

— преодоление сил сопротивления (в результате чего выделяется теплота (delta Q = IR Delta q));

— увеличение энергии поля, как вследствие изменения его индукции (и плотности энергии) (~Delta W_B = Delta left( frac{B^2}{2mu_0}right) V) , так и вследствие изменения объема, занятого полем (~Delta W_V = left( frac{B^2}{2mu_0}right) Delta V);

— увеличение механической энергии обмотки, которая возрастает благодаря работе поля (~Delta W_{obm} = A = left( frac{B^2}{2mu_0}right) Delta V).

Следующая страница

Если
в контуре с индуктивностью L
течёт ток I,
то в момент размыкания цепи возникает
индукционный ток и им совершается
работа. Эта работа совершается за счёт
энергии исчезнувшего при размыкании
цепи магнитного поля. На основании
закона сохранения и превращения энергию
магнитного поля превращается главным
образом в энергию электрического поля,
за счёт которой происходит нагревание
проводников. Работа может быть определена
из соотношения

dA=ε_смIdt

Так
как
,
то

dA=-LIdI

Уменьшение
энергии магнитного поля равно работе
тока, поэтому

(16.18)

Формула
справедлива для любого контура и
показывает, что энергия магнитного поля
зависит от индуктивности контура и силы
тока, протекающего по нему.

Рассчитаем
энергию однородного магнитного поля
длинного соленоида, индуктивность
которого определяется по формуле L
= μμ₀n²V.
B
этом случае формула энергии примет вид

Учитывая,
что напряжённость поля внутри бесконечно
длинного соленоида Н=In,
получаем

(16.19)

Выразим
энергию через индукцию магнитного поля
B=
μμ₀H:

(16.20)

Или

(16.21)

Вследствие
того, что магнитное поле соленоида
однородно и локализовано внутри
соленоида, энергия распределена по
объёму соленоида с постоянной плотностью

(16.22)

Учитывая
последние три формулы, получаем

Учитывая
правило Ленца, можно заметить, что
явление самоиндукции аналогично
проявлению инертности тел в механике.
Так, вследствие инертности тело не
мгновенно приобретает определённую
скорость, а постепенно. Так же постепенно
происходит и его торможение. То же самое,
как мы видели, происходит и с силой тока
при самоиндукции. Эту аналогию можно
провести и дальше.

и

эти
уравнения эквивалентны.

т.е.
m
~L
, υ~I

Эквивалентны
и формулы

Примеры решения задач

Пример.
В магнитном поле, изменяющемся по закону
B=B₀cosωt
(B₀=5мТл,

ω=5с^-1),
помещён круговой проволочный виток
радиусом r=30см,
причём нормаль к витку образует с
направлением поля угол α=30º. Определите
ЭДС индукции, возникающую в витке в
момент времени t=10с.

Дано:
B=B₀cosωt;
B₀=5мТл=5∙10^-3
Тл;
ω=5с^-1;
r=30см=0,3
м;
α=30º; t=10 с.

Найти:
ε_i.

Решение:
Согласно
закону Фарадея,

,
(1)

Где
магнитный поток, сцепленный с витком
при произвольном его расположении
относительно магнитного поля.

Ф=BScosα.

По
условию задачи B=B₀cosωt,
а площадь кольца S=πr²,
поэтому

Ф=πr²
B₀cosωt∙cosα.
(2)

Подставив
выражение (2) в формулу (1) и продифференцировав,
получаем искомую ЭДС индукции в заданный
момент времени:

Ответ:
ε_i=4,69
мВ.

Пример
В
соленоиде длиной ℓ=50см и диаметром
d=6см
сила тока равномерно увеличивается на
0,3А за одну секунду. Определите число
витков соленоида, если сила индукционного
тока в кольце радиусом 3,1 см из медной
проволоки (ρ=17нОм∙м), надетом на катушку,
I_к=0,3
А.

Дано:
ℓ=50см=0,5
м; d=6см=0,06м;
;r_к=3,1см=3.1∙10^-2м;
ρ=17нОм∙м=17∙10^-9
Ом∙м; I_к=0,3
А.

Найти:
N.

Решение.
При изменении силы тока в соленоиде
возникает ЭДС самоиндукции

(1)

где
—
индуктивность соленоида. Подставив это
выражение в (1)

с
учётом

.

ЭДС
индукции, возникающая в одном кольце,
в N
раз меньше, чем найденное значение ЭДС
самоиндукции в соленоиде, состоящем из
N
витков, т.е.

.
(2)

Согласно
закону Ома, сила индукционного тока в
кольце

,
(3)

где
—
сопротивление кольца. Поскольку ℓ_к=πd,
а S_к=πr_к²,
выражение (3) примет вид

Подставив
в эту формулу выражение (2), найдём искомое
число витков соленоид

.

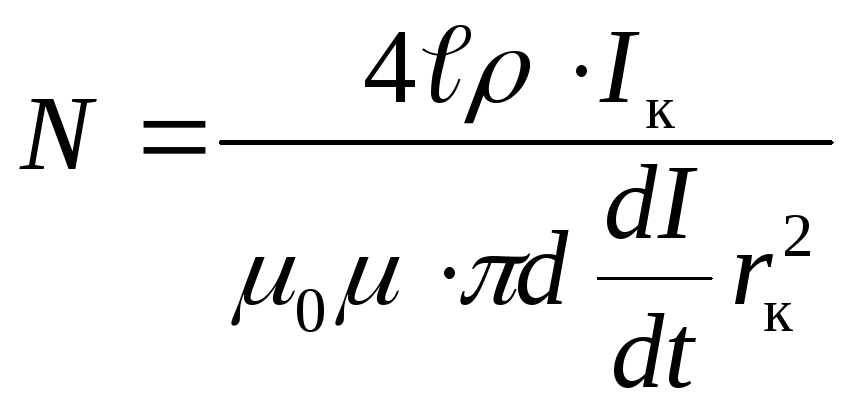
Ответ:
N=150

Пример
В
однородном магнитном поле подвижная
сторона (её длина ℓ=20см) прямоугольной
рамки (см. рисунок) перемещается
перпендикулярно линиям магнитной
индукции со скоростью υ=5 м/с. Определите
индукцию В магнитного поля, если
возникающая в рамке ЭДС индукции ε_i=0,2
В.

Дано:
ℓ=20см=0,2
м; υ=5 м/с; ε_i=0,2
В.

Найти:
B.

Р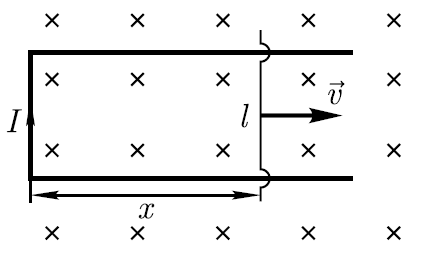ешение.
При движении в магнитном поле подвижной
стороны рамки поток Ф вектора магнитной
индукции сквозь рамку возрастает, что,
согласно закону Фарадея,

,
(1)

приводит
к возникновению ЭДС индукции.

Поток
вектора магнитной индукции, сцепленный
с рамкой,

Ф=Bℓx.
(2)

Подставив
выражение (2) в формулу (1) и учитывая, что
B
и ℓ — величины постоянные, получаем

откуда
искомая индукция магнитного поля

Ответ:
В=0,2 Тл.

Пример
В
однородном магнитном поле с индукцией
В=0,2 Тл равномерно вращается катушка,
содержащая N=600
витков, с частотой n=6
с^-1.
Площадь
S
поперечного сечения катушка 100см².
Ось вращения перпендикулярна оси катушки
и направлению магнитного поля. Определите
максимальную ЭДС индукции вращающейся
катушки.

Дано:
В=0,2
Тл; N=600;
n=6
с^-1;
S=100см²=10^-2
м².

Найти:
(ε_i)_max.

Решение.
Согласно закону Фарадея,

где
Ф – полный магнитный поток, сцеплённый
со всеми витками катушки. При произвольном
расположении катушки относительно
магнитного поля

Ф=NBScosωt,
(1)

где
круговая частота ω=2πn.
Подставив ω в (1), получим

Ф=NBScos2πnt.

Тогда

ε_i=-NBS2πn(-sin2πnt)=2πnNBSsin2πnt,

ε_i=(
ε_i)_max
при
sin2πnt=1, поэтому

(ε_i)_max=2πnNBS

Ответ:
(ε_i)_max=45,2
В.

Пример
Однослойная
длинная катушка содержит N=300
витков, плотно прилегающих друг к другу.
Определите индуктивность катушки, если
диаметр проволоки d=0,7
мм (изоляция ничтожной толщины) и она
намотана на картонный цилиндр радиусом
r=1
см. .

Дано:
N=300;
d=0,7
мм=7∙10^-4
м; r=1
см=10^-2
м.

Найти:
L.

Решение.
Индуктивность катушки

(1)

где
Ф – полный магнитный поток, сцепленный
со всеми витками катушки; I
— сила тока в катушке.

Учитывая,
что полный магнитный поток

Ф=NBS

(N-число
витков катушки; В – магнитная индукция;
S
– площадь поперечного сечения катушки);
магнитная индукция в катушке без
сердечника

(μ₀
– магнитная постоянная; ℓ- длина
катушки), длина катушки

ℓ=Nd

(d-диаметр
проволоки; витки вплотную прилегают
друг к другу), площадь поперечного
сечения катушки

S=πr²,

Получим
осле подстановки записанных выражений
в формулу (1) искомую индуктивность
катушки:

Ответ:
L=1,69
мГн.

Пример
Первичная
обмотка понижающего трансформатора с
коэффициентом трансформации k=0,1
включена в сеть с источником переменного
напряжения с ЭДС ε₁=220
В. Пренебрегая потерями энергии в
первичной обмотке, определите напряжение
U₂
на зажимах вторичной обмотки, если её
сопротивление R₂=5
Ом и сила тока в ней I₂=2А.

Дано:
k=0,1;
ε₁=220
В; R₂=5
Ом; I₂=2А.

Найти:
U₂.

Решение.
В первичной обмотке под действием
переменной ЭДС ε₁
возникает переменный ток I₁,
создающий в сердечнике трансформатора
переменногый магнитный поток Ф, который
пронизывает вторичную обмотку. Согласно
закону Ома, для первичной обмотки

где
R₁
– сопротивление первичной обмотки.
Падение напряжения I₁R₁
при быстропеременных полях мало по
сравнению с ε₁
и ε₂.
Тогда можем записать:

(1)

ЭДС
взаимной индукции, возникающая во
вторичной обмотке,

(2)

Из
выражений (1) и (2) получаем

,

где
—
коэффициент трансформации, а знак «-»
показывает, что ЭДС в первичной и
вторичной обмотках противоположны по
фазе. Следовательно, ЭДС во вторичной
обмотке

ε₂=k
ε₂.

Напряжение
на зажимах вторичной обмотки

U₂=
ε₂-I₂R₂=
kε₁-I₂R₂.

Ответ:
U₂=12
В.

Пример
Соленоид
без сердечника с однослойной обмоткой
из проволоки диаметром d=0,4
мм имеет длину ℓ=0.5 м и поперечное сечение
S=60см².
За какое время при напряжении U=10
В и силе тока I=1,5
А в обмотке выделится количество теплоты,
равное энергии поля внутри соленоида?
Поле считать однородным.

Дано:
d=0,4
мм=0,4∙10^-4
м; ℓ=0,5 м; S=60см²=6∙10^-3
м²;
I=1,5А;
U=10В;
Q=W.

Найти:
t.

Решение.
При прохождении тока I
при напряжении U
в обмотке за время t
выделяется теплота

Q=IUt.
(1)

Энергия
поля внутри соленоида

(2)

где
(N
– общее число витков соленоида). Если
витки вплотную прилегают друг к другу,
то ℓ=Nd,
откуда
.
Подставив выражение для В иN
в
(2), получаем

.
(3)

Согласно
условию задачи, Q=W.
Приравняв выражение (1) и (3),найдём искомое
время:

Ответ:
t
=1,77 мс.

Пример
Катушка
без сердечника длиной ℓ=50 см содержит
N=200
витков. По катушке течёт ток I=1А.
Определите объёмную плотность энергии
магнитного поля внутри катушки..

Дано:
ℓ=50
см=0,5
м;
N=200; I=1 А.

Найти:
ω.

Решение.
Объёмная плотность энергии магнитного
поля (энергия единицы объёма)

,
(1)

где
—
энергия магнитного поля (L
— индуктивность катушки); V=Sℓ-
объём катушки (S
— площадь катушки; ℓ- длина катушки).

Магнитная
индукция поля внутри соленоида с
сердечником с магнитной проницаемостью
μ равна

.

Полный
магнитный поток, сцепленный со всеми
витками соленоида,

.

Учитывая,
что Ф=LI,
получаем формулу для индуктивности
соленоида:

(2)

Подставив
выражение (2) в формулу (1) с учётом того,
что
,
найдём искомую объёмную плотность
энергии магнитного поля внутри катушки:

Ответ:
ω=0,1
Дж/м³.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #