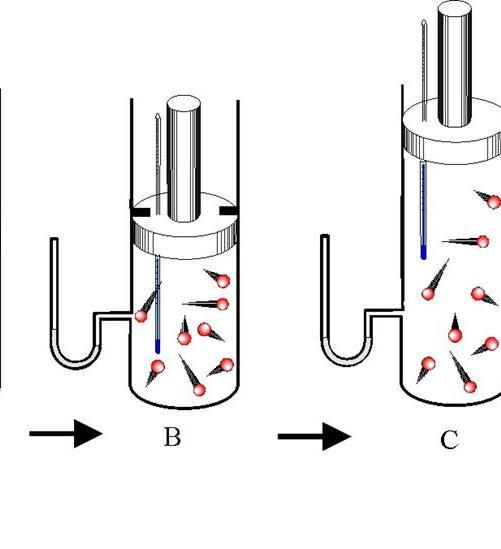
Адиабатный
процесс – это процесс, при котором
рабочее тело не обменивается теплотой
с окружающей средой (dq=0). Для
получения графика процесса вp-vкоординатах выполним некоторые
преобразования.
В
соответствии с первым законом термодинамики
dq=cv·dT+p·dv=c·dT, гдес– теплоёмкость термодинамического
процесса. Тогда можно записать, что
Работа
газа в адиабатном процессе выполняется
за счёт его внутренней энергии. Так как
в адиабатном процессе отсутствует обмен
теплотой с окружающей средой, то в
соответствии с первым законом термодинамики
имеем
l+Δu=0
или
l=-Δu.
Поэтому
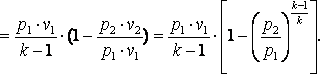
Изменение
энтальпии газа в адиабатном процессе
может быть определено исходя из следующих
соображений:

Энтропия
газа в адиабатном процессе не изменяется,
так как
dq=0.
Поэтому в
T-s
координатах
адиабатный процесс изображается прямой
линией, параллельной оси температур.
6)
При равных условиях энтальпия больше
чем внутренняя энергия, потому что
энтальпия есть теплота при постоянном
давлении, а внутренняя энергия теплота
при постоянном объеме. А из уравнения
Майера известно что Ср
>Сv,
поэтому при равных условиях энтальпия
численно больше внутренней энергии.
1)
Эксергия(эксэргия; отгреч.ek,ех— приставка,
означающая высокую степень, игреч.ergon— работа) — частьэнергии,
равная максимальной полезнойработе,
которую может совершить термодинамическаясистемапри переходе из данного состояния всостояние
равновесиясокружающей
средой. Эксергией иногда
называетсяработоспособностьсистемы. Использование понятия эксергии
даёт возможность количественно определить
влияниенеравновесиятермодинамическихпроцессовнаэффективностьпреобразования энергии, то есть позволяет
вычислять особенностивторого
начала термодинамики: выделить
ту часть энергии, которая не может быть
использована из-за газодинамических
явлений, трения,теплообмена.
Такой подход даёт возможность анализировать
степень термодинамического совершенства
того или другого элемента установки и
не требует предварительной оценки
работоспособности всей установки в
целом.
Эксергия
(от греч. ex —
приставка, обозначающая здесь высокую
степень, и érgon — работа), работоспособность,
термин, применяемый в термодинамике
для обозначения максимальной работы,
которую может совершить система при
переходе из данного состояния в равновесие
с окружающей средой. Работа, совершаемая
системой в каком-либо термодинамическом
процессе, оказывается максимальной
лишь в том случае, если осуществляемый
процесс — равновесный.
ЭКСЕРГИЯ
— термодинамич. ф-ция, определяющая
работоспособностьмассы в поточной системе; макс, кол-во
работы, к-рое может быть получено от
поточной системы в обратимом переходе
её из исходногосостоянияв состояние равновесия с окружающей
средой, имеющей пост, темп-руT0,
энтальпию H0иэнтропию S0(при отсутствии др. источников теплоты,
кроме окружающей среды). Э. является
ф-цией состояния и определяется
приращением энтальпииHи энтропии
S; она равнагдеH-H0и S-S0
соответственно приращение энтальпии
и энтропии.
2)
Часть энергии системы, которая может
быть преобразована в энергию организованных
форм, называется эксергией. Остальная
часть называется анергией. Мерой эксергии
является максимальная полезная работа,
которую можно получить при обратимом
изменении состояния системы от заданного
(при параметрах р,Т) до состояния
равновесия с окружающей средой при
параметрах р0 и Т0. Таким образом, в
отличие от энергии, эксергия является
функцией не только параметров системы,
но и параметров окружающей среды. Поэтому
при расчете эксергии окружающая среда
должна иметь постоянную температуру и
давление.
3)
Параметры окружающей
средыне зависят от параметров
рассматриваемой системы, обычно
предполагаются постоянными и, согласно
указанному определению эксергии, должны
находиться в термодинамич.равновесиис параметрами системы. Однако, строго
говоря, это условие невыполнимо, поскольку
в среде всегда существуют градиенты
т-р, давлений и хим. потенциалов (что в
практич. расчетах можно не учитывать).
Для полной характеристики среды
достаточно знать не более трех параметров
(как правило, т-ру, давление, хим. состав).
До тех пор пока все параметры системы
не сравняются с соответствующими
параметрами среды,равновесиене будет достигнуто и система может
производить определенную работу, т. е.
обладает эксергией. При эксергетическом
анализе работы пром. установок в качестве
окружающей среды принимают
атм.
воздух.
Из самого понятия «эксергия»
следует, что эксергия
окружающей
среды
равна
нулю. Эксергия систем, которые находятся
в равновесии с окружающей средой равны
нулю.
4)
В
соответствии со II
законом термодинамики, для работы
термодинамической системы необходим
не только подвод тепла, но и отвод тепла,
следовательно подведенное тепло

работу.
Т
– рабочая температура рассматриваемой
системы.

температурная функция. В рассматриваемом
примере она оценивает какая часть
подведенной тепловой энергии может
быть превращена в работу.
Покажем,
что эксергетическая температурная
функция

5)
Эксергия
теплового потока — определяется
максимальной работой, которая может
быть получена в обратимой системе
преобразования теплового потока в
работу в интервале между температурой
этого потока и температурой окружающей
среды.
Эксергия
термомеханическая — часть
эксергии потока вещества, определяемая
максимальной работой выравнивания
давления и температуры вещества до
уровня этих параметров в окружающей
среде. Подразделяется на эксергию
термическую, связанную с выравниванием
температур, и эксергию механическую,
связанную с выравниванием давлений.
Эксергия
измеряется в тех же единицах, что и
энергия и работа,- в Дж, эксергия потока
вещества — в Вт, потока теплоты — в Дж/с.
Таким образом, эксергия, характеризуя
качество энергии пром. системы, т. е.
способность быть превращенной в полезную
работу, является универсальной мерой
энергетических ресурсов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Здравствуйте!
У меня возникла такая проблема. Решаю задачу по физической химии ( термодинамике, если быть точнее). По условию при 298 К 0.01 кг кислорода подвергается адиабатическому сжатию с 0.008 до 0.005 кубических метров. Нужно определить конечную температуру, работу сжатия, изменение внутренней энергии и изменение энтальпии. Cv=2,5R.
Как и во всяком задачнике, в конце задачника имеются ответы.
У меня совпали все искомые параметры, кроме изменения энтальпии.
Вопрос: как найти изменение энтальпии при адиабатическом процессе? (ответ: 1335 Дж)
Tконечная=359. 637 К
W=400,352 Дж
deltaU=-400,352 Дж
Я пытался применить формулу deltaH=Cp*(T2-T1), но в ответом не сходится все равно.
Помогите, пожалуйста
Работы, изменения внутренней энерги, энтальпии и энтропи
Изобарный процесс, протекает при постоянном давлении. Уравнение изобарного процесса Р=const.
В соответствии с уравнением политропы Рv n = const политропа превращается в изобару Р=const при показателе политропы n=0.
Теплоемкость изобары cp при n=0 соответствует выражению c=cvк=cp .
Доля теплоты, идущая на увеличение внутренней энергии в изобарном процессе, соответствует величине a=1/к.
Кроме уравнения Р=const, для изобарного процесса можно записать уравнение Tv n-1 = const, которое при n=0 превращается в уравнение T/v=const.
Таким образом, основные величины, характеризующие изобарный процесс, будут представлены выражениями
Р=const, T/v=const, n=0, c=cp, a=1/к.
Теплота изобарного процесса соответствует выражению
а работа изменения объема – выражению
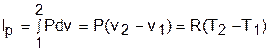
Изменение внутенней энергии, энтальпии и энтропии в изобарном процессе соответствует выражениям
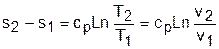
Изохорный процесс, протекает при постоянном объеме.
Уравнение изохорного процесса v=const.
В соответствии с уравнением политропы 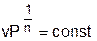
Теплоемкость изохоры при n=±¥ соответствует выражению c=cv. Доля теплоты, идущая на увеличение внутренней энергии в изохорном процессе, соответствует величине a = 1.
Кроме уравнения v=const, для изохорного процесса можно записать уравнение TP (1-n)/n = const, которое при n=±¥ превращается в уравнение T/P=const.
Таким образом, основные величины, характеризующие изохорный процесс, будут представлены выражениями
v = const, T/P = const, n = ±¥, c = cv, a = 1.
Теплота изохорного процесса соответствует выражению
а работа изменения объема равна нулю, т.к. dv=0:
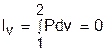
Изменение внутенней энергии, энтальпии и энтропии в изохорном процессе соответствует выражениям
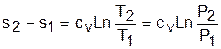
Изотермический процесс, протекает при постоянной температуре. Уравнение изотермического процесса T=const.
В соответствии с уравнением политропы Tv n-1 =const политропа превращается в изотерму Т=const при показателе политропы n=1.
Теплоемкость изотермы при n=1 равна бесконечности: cт=±¥. Доля теплоты, идущая на увеличение внутренней энергии в изотермическом процессе, равна нулю (a = 0).
Кроме уравнения Т=const, для изотемического процесса можно записать уравнение Pv n = const, которое при n=1 превращается в уравнение Pv=const.
Таким образом, основные величины, характеризующие изотермический процесс, будут представлены такими выражениями:
T = const, Pv = const, n = 1, cт = ±¥, a = 0.
Теплота изотермического процесса равна работе, т.к. изменение внутренней энергии идеального газа при Т=const равно нулю:
а работа изменения объема определяется по уравнению
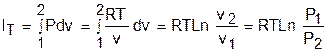
Изменение внутенней энергии и энтальпии в изотермическом процессе для идеального газа равно нулю:
а изменение энтропии определяется выражением
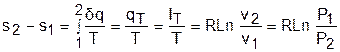
Адиабатный процесс – это процесс без теплообмена с окружающей средой, т.е. для него dq = 0 или q = 0.
Уравнение адиабатного процесса соответствует выражению s=const, т.к. dq=Tds=0 при ds=0. Поэтому адиабатный процесс имеет еще одно название – изоэнтропный процесс.
Теплоемкость адиабаты равна нулю (сs=0), т.к. температура в этом процессе изменяется, а dq=cdT=0.
Показатель политропы при сs=0 будет соответствовать выражению n=cp/cv=к, т.е. показатель политропы в адиабатном процессе равен коэффициенту Пуассона.
Доля теплоты, идущая на увеличение внутренней энергии в адиабатном процессе, равна бесконечности (a=±¥).
Таким образом, основные величины, характеризующие адиабатный процесс, будут представлены выражениями
s = const, Pv к = const, n = к, cs = 0, a = ±¥.
Теплота адиабатного процесса равна нулю, следовательно, для идеального газа в адиабатном процессе работа равна изменению внутренней энергии, взятой с обратным знаком:
Изменение энтальпии в адиабатном процессе ведется традиционно – h2-h1=cp(T2-T1), а изменение энтропии в этом процессе равно нулю – s2-s1=0.
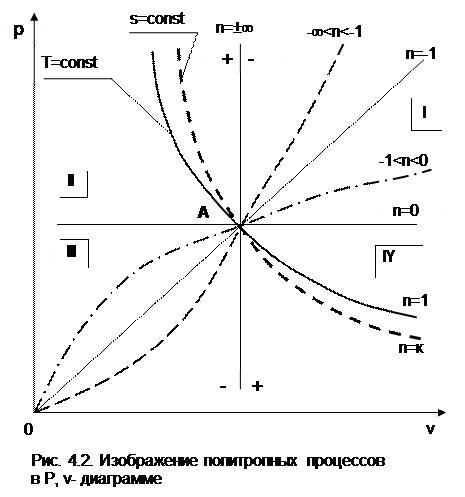
4.3. Изображение политропных процессов
в Р,v и T,s- диаграммах
Политропа в Р,v- диаграмме
На рис.4.2 изображены характерные политропные процессы в Р,v- координатах. Все процессы проведены через общую точку А, что позволяет наглядно сопоставить изображение политроп с различными значениями показателя политропы n.
Показатель политропы определяет характер процесса. В Р,v- координатах политропа описывается уравнением Рv n =const, в соответствии с которым основные процессы будут представлять:
изобара – горизонтальная прямая, n=0, Р=const;
изохора – вертикальная прямая, n=±¥, v=const;
изотерма – равнобокая гипербола с осями асимптот в виде осей координат Р и v, т.к. при n=1 уравнение изотермы p=const/v, причем константа – величина положительная;
адиабата – неравнобокая гипербола, т.к. при n=к>1 уравнение адиабаты Р=const/v к , адиабата круче изотермы.
Политропы при 0 n представляют собой гиперболы, крутизна которых возрастает с увеличением показателя n. Самая крутая из них – изохора (n=¥), а самая пологая – изобара (n=0). Все политропы с положительным показателем n>0 располагаются во II и IV квадрантах относительно точки А.
Политропы с 1 |q|, т.е. в этом случае будет увеличение внутренней энергии (Du=q-l>0) и температуры газа при отводе от него теплоты.
Политропы с отрицательным показателем -¥ -n проходят через начало координат, причем если
n = -1 – это прямая линия,
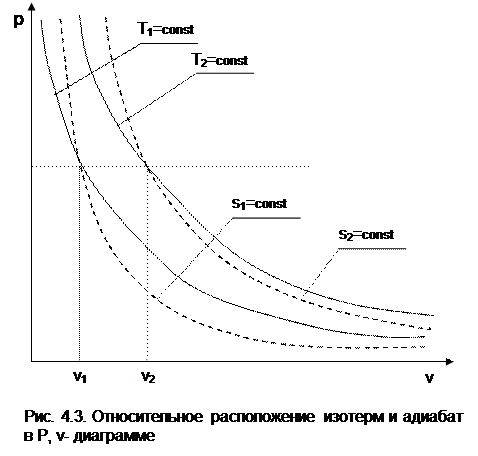
-1 Т1. Кроме этого, исходя из уравнения изобары Т2/Т1=v2/v1, изотермы в P,v- диаграмме находятся одна над другой (или одна правее другой) по
возрастающей, т.к. Т2>T1 только при v2>v1.
Для двух адиабат s1=const и s2=const расстояние между ними по оси v можно оценить по любой изобаре P=const. Исходя из уравнений адиабатного и изобарного процессов,
следует, что точке на данной изобаре с большим объемом будет соответствовать большее значение энтропии, т.е. при v2>v1 будет s2>s1. Следовательно, в Р,v- диаграмме адиабаты (изоэнтропы) чем выше (или правее), тем большее значение энтропии им соответствует.
Для изоэнтропы s2 в уравнении Pv к =const=А2 константа А2 будет больше, чем константа А1 изоэнтропы s1 в уравнении Pv к =const=А1, поскольку при Р=const Pv2 к -Pv1 к =А2-А1>0. Выразив объем из уравнения адиабаты v=const/P 1/к , получим расстояние между двумя адиабатами вдоль оси v в виде выражения
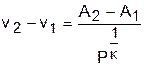
Из этого выражения видно, что с увеличением давления расстояние между адиабатами вдоль оси v в P,v- диаграмме уменьшается, т.е. адиабаты в Р,v- диаграмме не являются эквидистантными кривыми, хотя на всем своем протяжении не пересекаются друг с другом.
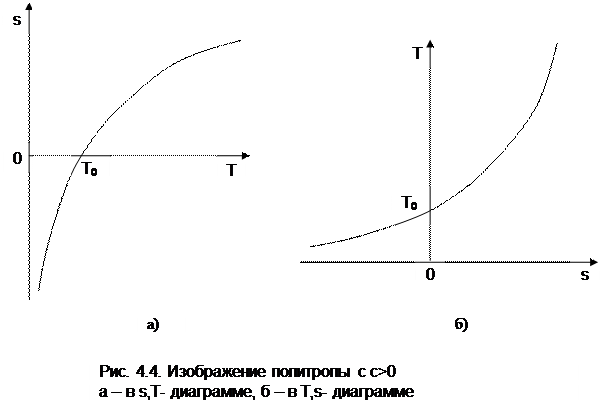
Политропа в T,s- диаграмме
Для политропного процесса идеального газа изменение энтропии определяется уравнением (4.13):
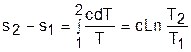
Изображение политропы в Т,s- диаграмме ведется в соответствии с этим уравнением при фиксации начала отсчета энтропии (рис.4.4).
В общем случае начало отсчета энтропии so=0 можно зафиксировать любой парой независимых параметров состояния. Для упрощения анализа политропы зафиксируем so=0 точкой, находящейся на нашей политропе при температуре То. В этом случае второй параметр состояния, определяющий so=0, при расчете абсолютного значения энтропии не потребуется, т.к. он определен своим местонахождением на данной политропе. При необходимости его несложно определить через параметры любой точки на данной политропе, воспользовавшись одним из уравнений политропы, включающим температуру, например
Таким образом, расчетное выражение абсолютного значения энтропии можно представить в виде
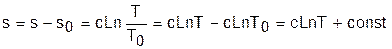
Выражение (4.31) соответствует логарифмической кривой. При положительной теплоемкости c>0 эта кривая в s,T- координатах изображена на рис. 4.4, а. Та же кривая в Т,s- координатах (перевернутых) показана на рис. 4.4, б. Таким образом, в Т,s- координатах политропа представляет логарифмическую кривую.
Политропа с отрицательной теплоемкостью представляет собой логарифмику в виде зеркального отражения политропы с такой же, но положительной теплоемкостью относительно оси Т (рис.4.5).
Причем, если подкасательная любой точки политропы (подкасательная в Т,s- координатах соответствует теплоемкости данной точки процесса) расположена слева от нее, то теплоемкость этой политропы положительная (c>0), если подкасательная расположена справа от точки – теплоемкость политропы отрицательная (с cv. Самая крутая политропа – адиабата, для нее теплоемкость равна нулю. Самая пологая политропа – изотерма, для нее теплоемкость равна бесконечности.
Политропы, проходящие через II и IV квадранты, имеют отрицательную теплоемкость.
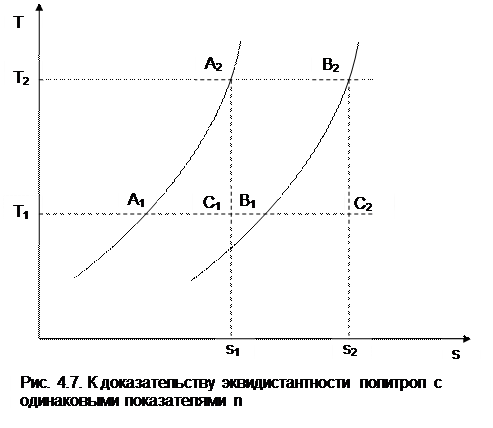
Процессы идеальных газов с одинаковыми показателями политропы в T,s- диаграмме представляют собой эквидистантные по оси s кривые (непересекающиеся, с одинаковым расстоянием друг от друга по оси s). На рис.4.7 изображены в Т,s- диаграмме две политропы идеального газа А1А2 и В1В2 с одинаковым показателем n и соответственно с одинаковыми теплоемкостями. Доказать, что эти политропы эквидистантны несложно. Достаточно рассмотреть расстояние между ними вдоль оси s по двум произвольным изотермам Т1 и Т2. Поскольку теплоемкости этих процессов одинаковые, то изменение энропии на интервале температур Т1-Т2 в этих процессах тоже одинаковое и соответствует отрезкам
А1С1 = В1С2 = 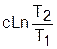
В прямоугольнике С1А2В2С2 противоположные стороны равны (А2В2=С1С2), равны и отрезки А1С1 и В1С2 (А1С1 = В1С2), следовательно, равны и отрезки А1С1 и В1С2 (А1С1 = В1С2). Расстояние между этими политропами по иси s можно рассчитать по формуле оределения изменения энтропии изотермического процесса (4.13) при любой температуре:
s2 — s1
= sB — sA = А1В1 = А2В2 = 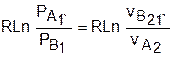
Изобары и изохоры являются частными случаями политроп, следовательно, и они представляют в Т,s- диаграмме эквидистантные по оси s кривые. В Т,s- координатах (рис.4.8) изобары находятся одна над другой по возрастающей, а изохоры одна под другой по возрастающей, т.к. если брать расстояние между ними по изотерме, оно будет равно положительной разности энтропий,
Блог об энергетике
энергетика простыми словами
Основные термодинамические процессы
Основными процессами в термодинамике являются:
- изохорный, протекающий при постоянном объеме;
- изобарный, протекающий при постоянном давлении;
- изотермический, происходящий при постоянной температуре;
- адиабатный, при котором теплообмен с окружающей средой отсутствует;
- политропный, удовлетворяющий уравнению pv n = const.
Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.
При исследовании термодинамических процессов определяют:
- уравнение процесса в p—v иT—s координатах;
- связь между параметрами состояния газа;
- изменение внутренней энергии;
- величину внешней работы;
- количество подведенной теплоты на осуществление процесса или количество отведенной теплоты.
Изохорный процесс

При изохорном процессе выполняется условие v = const.
Из уравнения состояния идеального газа (pv = RT) следует:
т. е. давление газа прямо пропорционально его абсолютной температуре:
Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).
Количество теплоты, подведенной к рабочему телу в процессе 1-2 при cv = const определяется по формуле:
Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:
Изменение энтропии в изохорном процессе определяется по формуле:
Изобарный процесс
Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:
т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.
Работа будет равна:
Количество теплоты при cp = const определяется по формуле:
Изменение энтропии будет равно:
Изотермический процесс
При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:
т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.
Работа процесса будет равна:
Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:
При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.
Изменение энтропии равно:
Адиабатный процесс
Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:
В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.
Обозначим теплоемкость в адиабатном процессе через cад, и условие dq = 0 выразим следующим образом:
Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (cад = 0).
и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:
В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).
kвыхлопных газов ДВС = 1,33
Из предыдущих формул следует:
Техническая работа адиабатного процесса (lтехн) равна разности энтальпий начала и конца процесса (i1 – i2).
Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. В T, s-диаграмме он изображается вертикальной линией.
Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае ds > 0, и процесс называется реальным адиабатным процессом.
Политропный процесс
Политропным называется процесс, который описывается уравнением:
Показатель политропы n может принимать любые значения в пределах от -∞ до +∞, но для данного процесса он является постоянной величиной.
Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p, vи Tв любых двух точках на политропе:
Работа расширения газа в политропном процессе равна:
В случае идеального газа эту формулу можно преобразовать:
Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:
представляет собой теплоемкость идеального газа в политропном процессе.
При cv, k и n = const cn = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.
Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.
Графическое представление политропа в p, v координатах в зависимости от показателя политропа n.
pv 0 = const (n = 0) – изобара;
pv = const (n = 1) – изотерма;
p 0 v = const, p 1/∞ v = const, pv ∞ = const – изохора;
n > 0 – гиперболические кривые,
n По материалам моего конспекта лекций по термодинамике и учебника «Основы энергетики». Автор Г. Ф. Быстрицкий. 2-е изд., испр. и доп. — М. :КНОРУС, 2011. — 352 с.
Адиабатический процесс и уравнения адиабаты для идеального газа. Пример задачи
Адиабатический переход между двумя состояниями в газах не относится к числу изопроцессов, тем не менее, он играет важную роль не только в различных технологических процессах, но и в природе. В данной статье рассмотрим, что представляет собой этот процесс, а также приведем уравнения адиабаты идеального газа.
Кратко об идеальном газе
Идеальным называется такой газ, в котором нет взаимодействий между его частицами, и их размеры равны нулю. В природе, конечно же, не существует идеальных на сто процентов газов, поскольку все они состоят из имеющих размеры молекул и атомов, которые взаимодействуют друг с другом всегда как минимум с помощью ван-дер-ваальсовых сил. Тем не менее, описанная модель часто выполняется с достаточной для решения практических задач точностью для многих реальных газов.

Главным уравнением идеального газа является закон Клапейрона-Менделеева. Он записывается в следующей форме:
Это уравнение устанавливает прямую пропорциональность между произведением давления P на объем V и количества вещества n на абсолютную температуру T. Величина R — газовая константа, которая играет роль коэффициента пропорциональности.
Что это адиабатический процесс?
Адиабатический процесс — это такой переход между состояниями газовой системы, при котором обмена энергией с внешней средой не происходит. При этом изменяются все три термодинамических характеристики системы (P, V, T), а количество вещества n остается постоянным.
Различают адиабатическое расширение и сжатие. Оба процесса происходят только за счет внутренней энергии системы. Так, в результате расширения давление и особенно температура системы сильно падают. Наоборот, адиабатическое сжатие приводит к положительному скачку температуры и давления.
Чтобы не происходил обмен теплом между окружающей средой и системой, последняя должна обладать теплоизолированными стенками. Кроме того, сокращение длительности протекания процесса значительно уменьшает тепловой поток от и к системе.
Уравнения Пуассона для адиабатического процесса
Первый закон термодинамики записывается в таком виде:
Иными словами, сообщенная системе теплота Q идет на выполнение системой работы A и на повышение ее энергии внутренней ΔU. Чтобы написать уравнение адиабаты, следует положить Q=0, что соответствует определению изучаемого процесса. Получаем:
При изохорном процессе в идеальном газе все тепло идет на повышение внутренней энергии. Этот факт позволяет записать равенство:
Где CV — изохорная теплоемкость. Работа A, в свою очередь, вычисляется так:
Где dV — малое изменение объема.
Помимо уравнения Клапейрона-Менделеева, для идеального газа справедливо следующее равенство:
Где CP — изобарная теплоемкость, которая всегда больше изохорной, так как она учитывает потери газа на расширение.
Анализируя записанные выше равенства и проводя интегрирование по температуре и объему, приходим к следующему уравнению адиабаты:
Здесь γ — это показатель адиабаты. Он равен отношению изобарной теплоемкости к изохорной. Это равенство называется уравнением Пуассона для процесса адиабатического. Применяя закон Клапейрона-Менделеева, можно записать еще два аналогичных выражения, только уже через параметры P-T и P-V:
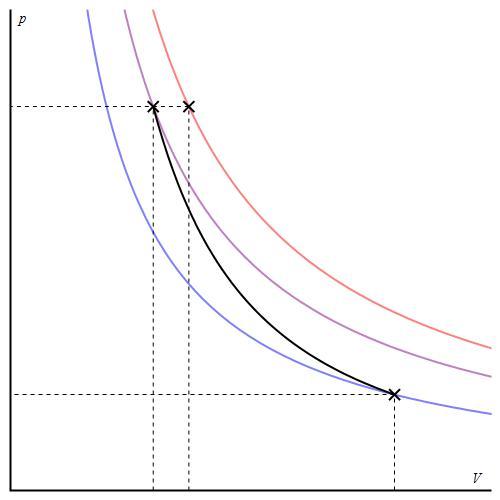
График адиабаты можно привести в различных осях. Ниже он показан в осях P-V.
Цветные линии на графике соответствуют изотермам, черная кривая — это адиабата. Как видно, адиабата ведет себя более резко, чем любая из изотерм. Этот факт просто объяснить: для изотермы давление меняется обратно пропорционально объему, для изобаты же давление изменяется быстрее, поскольку показатель γ>1 для любой газовой системы.
Пример задачи
В природе в горной местности, когда воздушная масса движется вверх по склону, то ее давление падает, она увеличивается в объеме и охлаждается. Этот адиабатический процесс приводит к снижению точки росы и к образованию жидких и твердых осадков.
Предлагается решить следующую задачу: в процессе подъема воздушной массы по склону горы давление упало на 30 % по сравнению с давлением у подножия. Чему стала равна ее температура, если у подножия она составляла 25 oC?
Для решения задачи следует использовать следующее уравнение адиабаты:
Его лучше записать в таком виде:
Если P1 принять за 1 атмосферу, то P2 будет равно 0,7 атмосферы. Для воздуха показатель адиабаты равен 1,4, поскольку его можно считать двухатомным идеальным газом. Значение температуры T1 равно 298,15 К. Подставляя все эти числа в выражение выше, получаем T2 = 269,26 К, что соответствует -3,9 oC.
http://1ku.ru/obrazovanie/58101-adiabaticheskij-process-i-uravnenija-adiabaty-dlja-idealnogo-gaza-primer-zadachi/