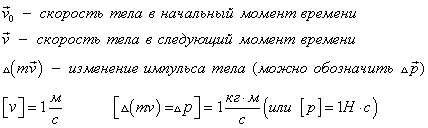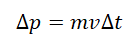Как найти изменение импульса при изменении направления - Исправление недочетов и поиск решений вместе с Examum.ru

Определение

Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:

p = mv

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).

Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.

Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:

10 г = 0,01 кг

Импульс равен:

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

Определение

Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:

p_1отн2 = m₁v_1отн2 = m₁(v₁ – v₂)

p_1отн2 — импульс первого тела относительно второго, m₁ — масса первого тела, v_1отн2 — скорость первого тела относительно второго, v₁ и v₂ — скорости первого и второго тела соответственно в одной и той же системе отсчета.

Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.

Сначала переведем единицы измерения в СИ:

15 т = 15000 кг

p_1отн2 = m₁(v₁ – v₂) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙10³ (кг∙м/с)

Изменение импульса тела

ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:

∆p = p – p₀ = p + (– p₀)

∆p — изменение импульса тела, p — конечный импульс тела, p₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар
	Конечная скорость после удара: v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0.
Абсолютно упругий удар
	Модули конечной и начальной скоростей равны: v = v₀. Модули конечного и начального импульсов равны: p = p₀. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p₀ = 2p.
Пуля пробила стенку
	Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p₀ – p = m(v₀ – v)
Радиус-вектор тела повернул на 180 градусов
	Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p₀ = 2p = 2mv₀
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
	Модули конечной и начальной скоростей равны: v = v₀. Модули конечного и начального импульсов равны: p = p₀. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:

Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.

В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.

Вычисляем:

Второй закон Ньютона в импульсном виде

Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

Или:

F∆t — импульс силы, ∆p — изменение импульса тела

Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Определение

Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.

Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.

Второй закон Ньютона в импульсном виде:

Реактивная сила:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

V = a∆t

Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Определение

Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса

Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.

Закон сохранения импульса в проекции на горизонтальную ось

Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:

положителен, если его направление совпадает с направлением оси ОХ;
отрицателен, если он направлен противоположно направлению оси ОХ.

Важно!

При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m₁v₁ = (m₁ + m₂)v
Неупругое столкновение движущихся тел	± m₁v₁ ± m₂v₂ = ±(m₁ + m₂)v
В начальный момент система тел неподвижна	0 = m₁v’₁ – m₂v’₂
До взаимодействия тела двигались с одинаковой скоростью	(m₁ + m₂)v = ± m₁v’₁ ± m₂v’₂

Сохранение проекции импульса

В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.

Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.

Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:

m₂v₂ = (m₁+ m₂)v

Отсюда скорость равна:

Задание EF17556

Импульс частицы до столкновения равен −p₁, а после столкновения равен −p₂, причём p₁= p, p₂= 2p, −p₁⊥−p₂. Изменение импульса частицы при столкновении Δ−p равняется по модулю:

а) p

б) p√3

в) 3p

г) p√5

Алгоритм решения

1.Записать исходные данные.

2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.

3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.

4.Подставить известные значения и вычислить.

Решение

Запишем исходные данные:

• Модуль импульса частицы до столкновения равен: p₁= p.

• Модуль импульса частицы после столкновения равен: p₂= 2p.

• Угол между вектором начального и вектором конечного импульса: α = 90^о.

Построим чертеж:

Так как угол α = 90^о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:

Δp=√p21+p22

Подставим известные данные:

Δp=√p2+(2p)2=√5p2=p√5

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17695

На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно

б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено

в) в интервалах 0–1 и 1–2 двигалось равномерно

г) в интервалах 0–1 и 1–2 двигалось равноускорено

Алгоритм решения

1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.

2.Сделать вывод о том, как зависит характер движения от импульса.

3.На основании вывода и анализа графика установить характер движения тела на интервалах.

Решение

Импульс тела есть произведение массы тела на его скорость:

p = mv

Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.

На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.

Верный ответ: б.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22730

Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.

Алгоритм решения

1.Записать исходные данные.

2.Записать закон сохранения импульса применительно к задаче.

3.Записать формулу кинетической энергии тела.

4.Выполнить общее решение.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса камня: m₁ = 3 кг.

• Масса тележки с песком: m₂ = 15 кг.

• Кинетическая энергия тележки с камнем: E_k = 2,25 Дж.

Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:

m1v1+m2v2=(m1+m2)v

Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:

m1v1cosα=(m1+m2)v

Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:

Ek=(m1+m2)v22

Отсюда скорость равна:

v=√2Ekm1+m2

Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:

v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2

Подставим известные данные и произведем вычисления:

v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)

Ответ: 6

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22520

Снаряд, имеющий в точке О траектории импульсp₀, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:

а) −−→AB

б) −−→BC

в) −−→CO

г) −−→OD

Алгоритм решения

1.Сформулировать закон сохранения импульса и записать его в векторной форме.

2.Применить закон сохранения импульса к задаче.

3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.

Решение

Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:

−p1+−p2=−p′
1+−p′2

Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:

−p0=−p1+−p2

Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:

−p2=−p0−−p1

Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18122

Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?

Ответ:

а) 27 г

б) 64 г

в) 81 г

г) 100 г

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.

3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.

4.Выполнить решение задачи в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса пластилиновой пули: m = 9 г.

• Скорость пластилиновой пули: v = 20 м/с.

• Максимальный угол отклонения нити: α = 60°.

Переведем единицы измерения величин в СИ:

Сделаем чертеж:

Нулевой уровень — точка А.

После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:

mv=(m+M)V

После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.

Закон сохранения энергии для точки В:

(m+M)V22=(m+M)gh

V22=gh

Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:

V=√2glcosα

Подставим это выражение в закон сохранения импульса для точки А и получим:

Выразим массу груза:

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 20.3k

Источник

I. Механика

Тестирование онлайн

Импульс тела

Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.

Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.

Импульс это векторная величина, которая определяется по формуле

Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости.

Направление вектора импульса всегда совпадает с направлением вектора скорости.

Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.

Импульс силы

Это векторная величина, которая определяется по формуле

Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона

Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.

Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара — 30 м/с. Сила, с которой нога действовала на мяч — 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.

Изменение импульса тела

Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.

1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.

Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.

2) Изменение импульса тела изображено на рисунке

3) Из второго закона Ньютона

Главное запомнить

1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела

Вывод второго закона Ньютона в общем виде

График F(t). Переменная сила

Источник

Предположим, что нам дан график зависимости равнодействующей силы, приложенной к какому-то объекту, от времени.

Допустим, что этот график описывает изменение равнодействующей силы, приводящей в движение маленький кораблик на радиоуправлении массой 2.5 килограмма, который мы запустили плавать в спокойную речку.

В задаче требуется найти скорость тела через 7 секунд после начала движения (в самом начале оно покоилось).

Как же мы будем работать? Во-первых, мы найдем изменение импульса на трех ключевых участках, хорошо видных на рисунке.

Потом через импульс мы узнаем скорость кораблика в интересующий нас момент времени (мы сможем это сделать, так как знаем массу тела и его начальную скорость, которая равна нулю):

varDelta{vec{p}}=vec{p}-vec{p}_0

varDelta{vec{p}}=mvec{v}-mvec{v}_0

varDelta{vec{p}}=mvec{v}

vec{v}=dfrac{varDelta{vec{p}}}{m}

Начнем с того, что найдем изменение импульса в промежутке от 0 до 3 секунд. Для этого нам достаточно найти площадь прямоугольника, находящегося под графиком на этом участке. Почему так? Изменение импульса равно произведению суммы приложенных к телу сил и времени, в течение которого они действовали:

varDelta{vec{p}}=varSigma{vec{F}}varDelta{t}

Если теперь взглянуть на график, можно заметить, что модуль этого произведения совпадает с площадью нашего прямоугольника.

Итак, модуль изменения импульса на первом участке равен:

varDelta{p}=S_Box=ab=4thickspaceН×3thickspaceс=12thickspaceН⋅с

Равнодействующая сила действовала в положительном направлении, поэтому и изменение импульса будет положительно:

varDelta{vec{p}}_1=12thickspaceН⋅с

Используя графический способ нахождения модуля изменения импульса, найдем его и на двух других участках:

varDelta{p}_2=dfrac{1}{2}×4thickspaceН×2thickspaceс=4thickspaceН⋅с

varDelta{p}_3=dfrac{1}{2}×2thickspaceН×1thickspaceс=1thickspaceН⋅с

Добавим направления:

varDelta{vec{p}}_2=4thickspaceН⋅с

varDelta{vec{p}}_3=-,1thickspaceН⋅с

Найдем суммарное изменение импульса:

varDelta{vec{p}}=varDelta{vec{p}}_1+varDelta{vec{p}}_2+varDelta{vec{p}}_3

varDelta{vec{p}}=12thickspaceН⋅с+4thickspaceН⋅с-1thickspaceН⋅с

varDelta{vec{p}}=15thickspaceН⋅с

Осталось узнать скорость кораблика через 7 секунд после начала движения:

vec{v}=dfrac{varDelta{vec{p}}}{m}=dfrac{15thickspaceН⋅с}{2.5thickspaceкг}=6thickspaceм/с

Источник

iSopromat.ru

Пример решения задачи по определению импульса сил, действующих, за определенное время, на материальную точку заданной массы, движущуюся по окружности с постоянной скоростью.

Задача

Материальная точка массой m=10 г движется по окружности с постоянной скоростью 40 см/с.

Найти импульс сил, действующих на точку за время прохождения точкой половины окружности (рисунок 2.3).

Импульс тела, закон сохранения импульса

теория по физике 🧲 законы сохранения

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

p _1отн2— импульс первого тела относительно второго, m₁ — масса первого тела, v _1отн2 — скорость первого тела относительно второго, v ₁и v ₂ — скорости первого и второго тела соответственно в одной и той же системе отсчета.

Сначала переведем единицы измерения в СИ:

Изменение импульса тела

∆ p — изменение импульса тела, p — конечный импульс тела, p ₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар

Конечный импульс тела:

Модуль изменения импульса тела равен модулю его начального импульса:

Абсолютно упругий удар

Модули конечной и начальной скоростей равны:

Модули конечного и начального импульсов равны:

Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:

Пуля пробила стенку

Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:

Радиус-вектор тела повернул на 180 градусов

Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:

Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали

Модули конечной и начальной скоростей равны:

Модули конечного и начального импульсов равны:

Угол падения равен углу отражения:

Модуль изменения импульса в этом случае определяется формулой:

Вычисляем:

Второй закон Ньютона в импульсном виде

Подставим это выражение во второй закон Ньютона и получим:

F ∆t — импульс силы, ∆ p — изменение импульса тела

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Второй закон Ньютона в импульсном виде:

Второй закон Ньютона для ракеты:

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

Выразим ускорение из второго закона Ньютона для ракеты:

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Закон сохранения импульса

Закон сохранения импульса в проекции на горизонтальную ось

положителен, если его направление совпадает с направлением оси ОХ;
отрицателен, если он направлен противоположно направлению оси ОХ.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m₁v₁ = (m₁ + m₂)v
Неупругое столкновение движущихся тел	± m₁v₁ ± m₂v₂ = ±(m₁ + m₂)v
В начальный момент система тел неподвижна	0 = m₁v’₁ – m₂v’₂
До взаимодействия тела двигались с одинаковой скоростью	(m₁ + m₂)v = ± m₁v’₁ ± m₂v’₂

Сохранение проекции импульса

Отсюда скорость равна:

Импульс частицы до столкновения равен − p ₁, а после столкновения равен − p ₂, причём p₁ = p, p₂ = 2p, − p ₁⊥ − p ₂. Изменение импульса частицы при столкновении Δ − p равняется по модулю:

Алгоритм решения

Решение

Запишем исходные данные:

Так как угол α = 90 о , вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:

Δ p = √ p 2 1 + p 2 2

Подставим известные данные:

Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5

pазбирался: Алиса Никитина | обсудить разбор | оценить

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно

б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено

в) в интервалах 0–1 и 1–2 двигалось равномерно

г) в интервалах 0–1 и 1–2 двигалось равноускорено

Материальная точка массой 1 кг равномерно движется по окружности со скоростью 10 м/с. Найти изменение импульса за одну четверть периода; половину периода; период

Ваш ответ

решение вопроса

Основные теоретические сведения

[custom_ads_shortcode1]

Импульс тела

К оглавлению…

Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:

Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с.

Общий импульс системы тел равен векторной сумме импульсов всех тел системы:

Изменение импульса одного тела находится по формуле (обратите внимание, что разность конечного и начального импульсов векторная):

где: pн – импульс тела в начальный момент времени, pк – в конечный. Главное не путать два последних понятия.

Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т.п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения.

Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.

[custom_ads_shortcode2]

Закон сохранения импульса

К оглавлению. . .

При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.

В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса (ЗСИ). Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:

Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:

Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось. Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:

Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.

[custom_ads_shortcode3]

Сохранение проекции импульса

К оглавлению…

Возможны ситуации, когда закон сохранения импульса выполняется только частично, то есть только при проектировании на одну ось. Если на тело действует сила, то его импульс не сохраняется. Но всегда можно выбрать ось так, чтобы проекция силы на эту ось равнялась нулю.

Тогда проекция импульса на эту ось будет сохраняться. Как правило, эта ось выбирается вдоль поверхности по которой движется тело.

[custom_ads_shortcode1]

Многомерный случай ЗСИ. Векторный метод

К оглавлению…

В случаях если тела движутся не вдоль одной прямой, то в общем случае, для того чтобы применить закон сохранения импульса, нужно расписать его по всем координатным осям, участвующим в задаче. Но решение подобной задачи можно сильно упростить, если использовать векторный метод. Он применяется если одно из тел покоится до или после удара. Тогда закон сохранения импульса записывается одним из следующих способов:

Из правил сложения векторов следует, что три вектора в этих формулах должны образовывать треугольник. Для треугольников применяется теорема косинусов.

p = mu

[custom_ads_shortcode2]

Математика

В этом разделе представлены теория и задачи по математике, необходимые для успешной подготовки к ЦТ или ЕГЭ. Список основных тем из школьной математики:

Смотрите также:

m_2

Все учебные материалы
Справочники
Задачники и учебники

[custom_ads_shortcode3]

Физика

В этом разделе представлены теория и задачи по физике, необходимые для успешной подготовки к ЦТ или ЕГЭ. Список основных тем из школьной физики:

Смотрите также:

Все учебные материалы
Справочники
Задачники и учебники

[custom_ads_shortcode1]

Формулы, методы и другая справочная информация

В этом разделе сайта представлены различные списки формул по физике и математике, а также приведена другая необходимая справочная информация. Знание физических и математических формул и методов является одним из ключевых элементов успешной подготовки к ЦТ или ЕГЭ. В этом разделе смотрите:

[custom_ads_shortcode2]

Итоговые тесты по физике и математике

В этом разделе сайта представлены итоговые тесты по физике и математике, которые позволят абитуриентам успешно повторить изученный материал и систематизировать свои знания по физике и математике. Решение этих тестов поможет поступающим успешно сдать ЦТ или ЕГЭ.

Подробнее…

[custom_ads_shortcode3]

Другая полезная информация для абитуриентов

В этом разделе сайта представлены различные советы и рекомендации по подготовке и сдаче ЦТ и ЕГЭ. А также советы о том, как правильно организовать процесс изучения физики и математики дома для абитуриентов. В этом разделе смотрите:

[custom_ads_shortcode1]

Высшая математика

В этом разделе сайта приведена теория, задачи, тесты и формулы по высшей математике. Эта информация поможет поступившим в ВУЗы ученикам разобраться в этом сложном предмете и получить отличные оценки на экзаменах в ВУЗе. Представлена информация в следующих категориях:

Основы высшей математики
Теоретические сведения
Теория вероятностей

[custom_ads_shortcode2]

Материалы для поступающих в Польшу

В этом разделе собраны материалы, которые помогут ученикам подготовится и поступить в польский университет. В основном материалы представляют из себя польские тесты по многим предметам, в том числе по физике и математике, но имеется также и другая полезная информация.

Подробнее…

[custom_ads_shortcode3]

Научно-популярные статьи

В этом разделе собраны различные интересные факты в виде научно-популярных статей, в которых сложные вещи излагаются простым языком без лишних формул. Эти статьи помогут убедиться в особенной занимательности науки, полюбить физику и математику, а также отвлечься и развеяться во время трудоемкой и скучной подготовки к экзаменам.

Подробнее…

Импульс это векторная величина, которая определяется по формуле

Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости. Направление вектора импульса всегда совпадает с направлением вектора скорости.

Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю.

После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.

[custom_ads_shortcode1]

Импульс силы

Это векторная величина, которая определяется по формуле.

Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела. Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара – 30 м/с.

Сила, с которой нога действовала на мяч – 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.

[custom_ads_shortcode2]

Изменение импульса тела

Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание! Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов. Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара. 1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.

Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола. 2) Изменение импульса тела изображено на рисунке

3) Из второго закона Ньютона.

[custom_ads_shortcode3]

Главное запомнить

1) Формулы импульса тела, импульса силы; 2) Направление вектора импульса; 3) Находить изменение импульса тела

[custom_ads_shortcode1]

Вывод второго закона Ньютона в общем виде

[custom_ads_shortcode2]

График F(t). Переменная сила

Импульс силы численно равен площади фигуры под графиком F(t).

Если же сила непостоянная во времени, например линейно увеличивается F=kt, то импульс этой силы равен площади треугольника. Можно заменить эту силу такой постоянной силой, которая изменит импульс тела на ту же величину за тот же промежуток времени

Средняя равнодействующая сила.

Источники:

www.eduspb.com
educon.by
educon.by
fizmat.by

Источник

Импульс. Закон сохранения импульса.
При решении динамических задач необходимо знать какие силы действуют на тело, закон, позволяющий рассчитать конкретную силу. Цель: получить решение задачи механики исходя из начальных условий, не зная конкретного вида взаимодействия.
Законы Ньютона в полученной ранее форме не позволяют решать задачи на движение тела с переменной массой и при скоростях, сравнимых со скоростью света. Цель: получить записи законов Ньютона в форме, справедливой для этих условий.
Импульс силы Векторная физическая величина, являющаяся мерой действия силы за некоторый промежуток времени. – импульс силы за малый промежуток времени t. Вектор импульса силы сонаправлен с вектором силы.	[ I ]= Нс
Импульс тела. (Количество движения) Векторная физическая величина, являющаяся мерой механического движения и равная произведению массы тела на его скорость. Вектор импульса тела сонаправлен с вектором скорости тела.	[ p ]= кг м/с
Основное уравнение динамики.
Из второго закона Ньютона:
Тогда получим: – второй закон Ньютона в импульсной форме
( Dt = t – t₀= t при t = 0).
*Импульс силы равен изменению импульса тела* Вектора импульса силы и изменения импульса тела сонаправлены.
Неупругий удар (шарик “прилипает” к стенке):
Абсолютно упругий удар (шарик отскакивает с прежней по величине скоростью):
Закон сохранения импульса.
До взаимодействия
После взаимодействия

Согласно 3 з-ну Ньютона: , следовательно:
Геометрическая (векторная) сумма импульсов взаимодействующих тел, составляющих замкнутую систему, остается неизменной.
Замкнутой называется система тел, взаимодействующих только друг с другом и не взаимодействующих с другими телами. Можно пользоваться и для незамкнутых систем, если сумма внешних сил, действующих на тела системы, равна нулю, или процесс происходит очень быстро, когда внешними воздействиями можно пренебречь (взрыв, атомные процессы).
В общем виде: т.к. система замкнутая, то , следовательно
Примеры применения закона сохранения импульса: Любые столкновения тел (биллиардных шаров, автомобилей, элементарных частиц и т.д.); Движение воздушного шарика при выходе из него воздуха; Разрывы тел, выстрелы и т.д.

Относительный импульс

Изменение импульса тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар

Абсолютно упругий удар

Пуля пробила стенку

Радиус-вектор тела повернул на 180 градусов

Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали

Второй закон Ньютона в импульсном виде

Реактивное движение

Суммарный импульс системы тел

Закон сохранения импульса

Закон сохранения импульса в проекции на горизонтальную ось

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Сохранение проекции импульса

I. Механика

Тестирование онлайн

Импульс тела

Импульс силы

Изменение импульса тела

Главное запомнить

Вывод второго закона Ньютона в общем виде

График F(t). Переменная сила

iSopromat.ru

Задача

Импульс тела, закон сохранения импульса

теория по физике 🧲 законы сохранения

Относительный импульс

Изменение импульса тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар

Абсолютно упругий удар

Пуля пробила стенку

Радиус-вектор тела повернул на 180 градусов

Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали

Второй закон Ньютона в импульсном виде

Реактивное движение

Суммарный импульс системы тел

Закон сохранения импульса

Закон сохранения импульса в проекции на горизонтальную ось

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Сохранение проекции импульса

Материальная точка массой 1 кг равномерно движется по окружности со скоростью 10 м/с. Найти изменение импульса за одну четверть периода; половину периода; период

Ваш ответ

решение вопроса

Похожие вопросы

Основные теоретические сведения

Импульс тела

Закон сохранения импульса

Сохранение проекции импульса

Многомерный случай ЗСИ. Векторный метод

Математика

Физика

Формулы, методы и другая справочная информация

Итоговые тесты по физике и математике

Другая полезная информация для абитуриентов

Высшая математика

Материалы для поступающих в Польшу

Научно-популярные статьи

Импульс силы

Изменение импульса тела

Главное запомнить

Вывод второго закона Ньютона в общем виде

График F(t). Переменная сила