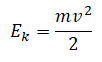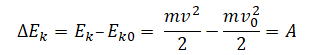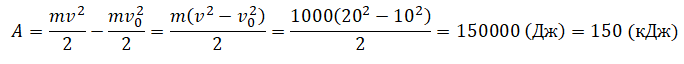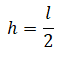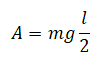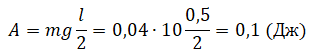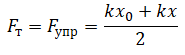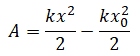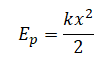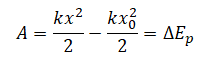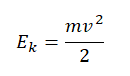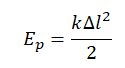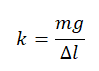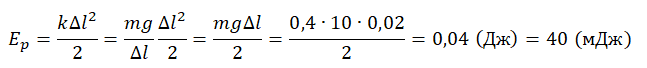Как найти изменение кинетической энергии по графику - Исправление недочетов и поиск решений вместе с Examum.ru

Энергию, которой обладают только движущиеся тела, называют кинетической энергией.

Если тело находится в состоянии покоя, его кинетическая энергия равна нулю.

Кинетическая энергия тела (Eкин) зависит от массы тела (m) и от скорости его движения (v).

Кинетическая энергия прямо пропорциональна массе тела и квадрату его скорости.

Определяют кинетическую энергию по формуле:

Чтобы рассчитать массу или скорость, формулу преобразуют следующим образом:

С увеличением массы тела в линейной зависимости увеличивается также и его кинетическая энергия.

Если масса увеличивается в (2) раза, тогда кинетическая энергия увеличивается также в (2) раза.

Зависимость кинетической энергии от массы можно отобразить на данном графике, если принять скорость тела постоянной и равной (2 м/с).

Рис. (1). График, зависимость кинетической энергии от массы

С увеличением скорости движения тела увеличивается также и его кинетическая энергия в квадратичной зависимости.

Если скорость увеличивается в (2) раза, тогда кинетическая энергия увеличивается в (4) раза.

Зависимость кинетической энергии от скорости движения можно отобразить на данном графике, если принять массу тела постоянной и равной (2 кг).

Рис. (2). График, зависимость кинетической энергии от скорости движения

Пример:

Автомобиль, масса которого (1400 кг), из состояния покоя развивает скорость до значения (5 м/с).

Какова кинетическая энергия автомобиля на конечном этапе движения?

Eкин=m⋅v22=1400⋅522=17500Дж

Источники:

Рис. 1. График, зависимость кинетической энергии от массы. © ЯКласс.
Рис. 2. График, зависимость кинетической энергии от скорости движения. © ЯКласс.

Источник

Энергия.

Работа.
Мощность.
Механическая энергия.
Кинетическая энергия.
Потенциальная энергия тела вблизи поверхности Земли.
Потенциальна яэнергия деформированной пружины.
Закон сохранения механической энергии.
Закон изменения механической энергии.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа силы, мощность, кинетическая энергия, потенциальная энергия, закон сохранения механической энергии.

Мы приступаем к изучению энергии — фундаментального физического понятия. Но предварительно нужно разобраться с другой физической величиной — работой силы.

к оглавлению ▴

Работа.

Пусть на тело действует постоянная сила vec F и тело, двигаясь прямолинейно по горизонтальной поерхности, совершило перемещение vec s . Сила vec F не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате).

Предположим сначала, что векторы силы и перемещения сонаправлены (рис. 1; остальные силы, действующие на тело, не указаны)

Рис. 1.A=Fs

В этом простейшем случае работа определяется как произведение модуля силы на модуль перемещения:

A=Fs . (1)

Единицей измерения работы служит джоуль (Дж): Дж=Н cdot м. Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.

Работа силы, перпендикулярной перемещению, по определению считается равной нулю. Так, в данном случае сила тяжести и сила реакции опоры не совершают работы.

Пусть теперь вектор силы образует с вектором перемещения острый угол alpha (рис. 2).

Разложим силу vec F на две составляющие: $vec F _{parallel }$ (параллельную перемещению) и $vec F _{perp }$ (перпендикулярную перемещению). Работу совершает только $vec F _{parallel }$ . Поэтому для работы силы vec F получаем:

$A=vec F _{parallel }s=Fcosalpha cdot s$ . Итак,

. (2)

Если вектор силы образует с вектором перемещения тупой угол alpha , то работа по-прежнему определяется формулой (2). В этом случае работа оказывается отрицательной.

Например, работа силы трения скольжения, действующей на тело в рассмотренных ситуациях, будет отрицательной, так как сила трения направлена противоположно перемещению. В этом случае имеем:

$alpha=180^{circ}, cos alpha=-1$ , и для работы силы трения получаем:

$A_{TP}=-F_{TP}s=-mu mgs$ ,

где — масса тела, — коэффициент трения между телом и опорой.

Соотношение (2) означает, что работа является скалярным произведением векторов силы и перемещения:

Это позволяет вычислять работу через координаты данных векторов:

$A=F_{displaystyle x}s_{displaystyle x}+F_{displaystyle y}s_{displaystyle y}+F_{displaystyle z}s_{displaystyle z}$ .

Пусть на тело действуют несколько сил $vec F_{1},vec F_{2},..,vec F_{n}$ и vec F — равнодействующая этих сил. Для работы силы vec F имеем:

$A=vec F vec s=(vec F_{1}+vec F_{2}+...+vec F_{n})vec s=vec F_{1}vec s+vec F_{2}vec s+...+vec F_{n}vec s$ ,

или

$A=A_{1}+A_{2}+...+A_{n}$ ,

где $A_{1}, A_{2},...,A_{n}$ — работы сил $F_{1}, F_{2},...,F_{n}$ . Итак, работа равнодействующей приложенных к телу сил равна сумме работ каждой силы в отдельности.

к оглавлению ▴

Мощность.

Часто имеет значение быстрота, с которой совершается работа. Скажем, на практике важно знать, какую работу сможет выполнить данное устройство за фиксированное время.

Мощность — это величина, характеризующая скорость совершения работы. Мощность есть отношение работы ко времени , за которое эта работа совершена:

$N=frac{displaystyle A}{displaystyle t}$ .

Мощность измеряется в ваттах (Вт). 1 Вт = 1 Дж/с, то есть 1 Вт — это такая мощность, при которой работа в 1 Дж совершается за 1 с.

Предположим, что силы, действующие на тело, уравновешены, и тело движется равномерно и прямолинейно со скоростью vec v . В этом случае существует полезная формула для мощности, развиваемой одной из действующих сил vec F .

За время тело совершит перемещение . Работа силы vec F будет равна:

Отсюда получаем мощность:

или

где alpha -угол между векторами силы и скорости.

Наиболее часто эта формула используется в ситуации, когда vec F — сила «тяги» двигателя автомобиля (которая на самом деле есть сила трения ведущих колёс о дорогу). В этом случае , и мы получаем просто:

N=Fv .

к оглавлению ▴

Механическая энергия.

Энергия является мерой движения и взаимодействия любых объектов в природе. Имеются различные формы энергии: механическая, тепловая, электромагнитная, ядерная. . .

Опыт показывает, что энергия не появляется ниоткуда и не исчезает бесследно, она лишь переходит из одной формы в другую. Это самая общая формулировка закона сохранения энергии.

Каждый вид энергии представляет собой некоторое математическое выражение. Закон сохранения энергии означает, что в каждом явлении природы определённая сумма таких выражений остаётся постоянной с течением времени.

Измеряется энергия в джоулях, как и работа.

Механическая энергия является мерой движения и взаимодействия механических объектов (материальных точек, твёрдых тел).

Мерой движения тела является кинетическая энергия. Она зависит от скорости тела. Мерой взаимодействия тел является потенциальная энергия. Она зависит от взаимного расположения тел.

Механическая энергия системы тел равна сумме кинетической энергии тел и потенциальной энергии их взаимодействия друг с другом.

к оглавлению ▴

Кинетическая энергия.

Кинетической энергией тела (принимаемого за материальную точку) называется величина

$K=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ ,

где — масса тела, — его скорость.

Кинетической энергией системы из тел называется сумма кинетических энергий каждого тела:

$K=frac{displaystyle m_{displaystyle 1}v_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}+frac{displaystyle m_{displaystyle 2}v_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}+...+frac{displaystyle m_{displaystyle N}v_{displaystyle N}^{displaystyle 2}}{displaystyle 2}$ .

Если тело движется под действием силы vec F , то кинетическая энергия тела, вообще говоря, меняется со временем. Оказывается, именение кинетической энергии тела за некоторый промежуток времени равно работе силы vec F . Покажем это для случая прямолинейного равноускоренного движения.

Пусть $vec{v_{1}}$ — начальная скорость, $vec{v_{2}}$ — конечная скорость тела. Выберем ось вдоль траектории тела (и, соответственно, вдоль вектора силы vec F ). Для работы силы vec F получаем:

$A=vec{F}vec{s}=F_{x}s_{displaystyle s}=ma_{displaystyle x}s_{displaystyle x}= ma_{displaystyle x}frac{{v_{displaystyle 2x}}^{displaystyle 2}-{v_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2a_{displaystyle x}}=frac{{displaystyle mv_{displaystyle 2x}}^{displaystyle 2}-{displaystyle mv_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2}$ .

(мы воспользовались формулой для $s_{x}$ , выведенной в статье «Равноускоренное движение»). Заметим теперь, что в данном случае проекция скорости отличается от модуля скорости разве что знаком; поэтому ${v_{displaystyle 1x}}^{displaystyle 2}={v_{displaystyle 1}}^{displaystyle 2}$ и ${v_{displaystyle 2x}}^{displaystyle 2}={v_{displaystyle 2}}^{displaystyle 2}$ . В результате имеем:

$A=frac{displaystyle mv_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle mv_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}=K_{displaystyle 2}-K_{displaystyle 1}=Delta K$ ,

что и требовалось.

На самом деле соотношение справедливо и в самом общем случае криволинейного движения под действием переменной силы.

Теорема о кинетической энергии. Изменение кинетической энергии тела равно работе, совершённой приложенными к телу внешними силами за рассматриваемый промежуток времени.

Если работа внешних сил положительна, то кинетическая энергия увеличивается (, тело разгоняется).

Если работа внешних сил отрицательна, то кинетическая энергия уменьшается (, тело замедляет движение). Пример — торможение под действием силы трения, работа которой отрицательна.

Если же работа внешних сил равна нулю, то кинетическая энергия тела за это время не меняется. Нетривиальный пример — равномерное движение по окружности, совершаемое грузом на нити в горизонтальной плоскости. Сила тяжести, сила реакции опоры и сила натяжения нити всегда перпендикулярны скорости, и работа каждой из этих сил равна нулю в течение любого промежутка времени. Соответственно, кинетическая энергия груза (а значит, и его скорость) остаётся постоянной в процессе движения.

Задача. Автомобиль едет по горизонтальной дороге со скоростью и начинает резко тормозить. Найти путь , пройденный автомобилем до полной остановки, если коэффициент трения шин о дорогу равен .

Решение. Начальная кинетическая энергия автомобиля $K_{displaystyle 1}=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ , конечная кинетическая энергия $K_{displaystyle 2}=0$ . Изменение кинетической энергии $Delta K=K_{displaystyle 2}-K_{displaystyle 1}=-frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ .

На автомобиль действуют сила тяжести m vec g , реакция опоры vec N и сила трения vec f . Сила тяжести и реакция опоры, будучи перпендикулярны перемещению автомобиля, работы не совершают. Работа силы трения:

Из теоремы о кинетической энергии теперь получаем:

$Delta K=A Rightarrow - frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}=- mu mgs Rightarrow s=frac{displaystyle v^{displaystyle 2}}{displaystyle 2 mu g}$ .

к оглавлению ▴

Потенциальная энергия тела вблизи поверхности Земли.

Рассмотрим тело массы , находящееся на некоторой высоте над поверхностью Земли. Высоту считаем много меньше земного радиуса. Изменением силы тяжести в процессе перемещения тела пренебрегаем.

Если тело находится на высоте , то потенциальная энергия тела по определению равна:

W=mgh

где — ускорение свободного падения вблизи поверхности Земли.

Высоту не обязательно отсчитывать от поверхности Земли. Как мы увидим ниже (формулы (3), (4)), физическим смыслом обладает не сама по себе потенциальная энергия, но её изменение. А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства.

Найдём работу, совершаемую силой тяжести при перемещении тела. Предположим, что тело перемещается по прямой из точки , находящейся на высоте $h_{1}$ , в точку , находящуюся на высоте $h_{2}$ (рис. 3).

Рис. 3.A=mg(h1-h2)[/math]

Угол между силой тяжести m vec g и перемещением тела vec s обозначим alpha . Для работы силы тяжести получим:

Но, как видно из рис. 3, $s cos alpha=h_{1}-h_{2}$ . Поэтому

$A=mg(h_{1}-h_{2})=mgh_{1}-mgh_{2}$ ,

или

$A=W_{1}-W_{2}$ . (3)

Учитывая, что $W_{1}-W_{2}=-(W_{2}-W_{1})=- Delta W$ , имеем также:

. (4)

Можно доказать, что формулы (3) и (4) справедливы для любой траектории, по которой тело перемещается из точки в точку , а не только для прямолинейного отрезка.

Работа силы тяжести не зависит от формы траектории, по которой перемещается тело, и равна разности значений потенциальной энергии в начальной и конечной точках траектории. Иными словами, работа силы тяжести всегда равна изменению потенциальной энергии с противоположным знаком. В частности, работа силы тяжести по любому замкнутому пути равна нулю.

Сила называется консервативной, если при перемещении тела работа этой силы не зависит от формы траектории, а определяется только начальным и конечным положением тела. Сила тяжести, таким образом, является консервативной. Работа консервативной силы по любому замкнутому пути равна нулю. Только в случае консервативной силы возможно ввести такую величину, как потенциальная энергия.

к оглавлению ▴

Потенциальна яэнергия деформированной пружины.

Рассмотрим пружину жёсткости . Начальная деформация пружины равна $x_{1}$ . Предположим,
что пружина деформируется до некоторой конечной величины деформации $x_{2}$ . Чему равна при этом работа силы упругости пружины?

В данном случае силу на перемещение не умножишь, так как сила упругости меняется в процессе деформации пружины. Для нахождения работы переменной силы требуется интегрирование. Мы не будем приводить здесь вывод, а сразу выпишем конечный результат.

Оказывается, сила упругости пружины также является консервативной. Её работа зависит лишь от величин $x_{1}$ и $x_{2}$ и определяется формулой:

$A=frac{kx_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle kx_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}$ .

Величина

$W=frac{displaystyle kx^{displaystyle 2}}{displaystyle 2}$

называется потенциальной энергией деформированной пружины (x — величина деформации).

Следовательно,

$A=W_{1}-W_{2}=- Delta W$ ,

что полностью аналогично формулам (3) и (4).

к оглавлению ▴

Закон сохранения механической энергии.

Консервативные силы называются так потому, что сохраняют механическую энергию замкнутой системы тел.

Механическая энергия тела равна сумме его кинетической и потенциальной энергий:

E=K+W .

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии их взаимодействия друг с другом.

Предположим, что тело совершает движение под действием силы тяжести и/или силы упругости пружины. Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны $K_{1}$ и $W_{1}$ , в конечном положении — $K_{2}$ и $W_{2}$ . Работу внешних сил при перемещении тела из начального положения в конечное обозначим .

По теореме о кинетической энергии

$K_{2}-K_{1}=A$ .

Но работа консервативных сил равна разности потенциальных энергий:

$A=W_{1}-W_{2}$ .

Отсюда получаем:

$K_{2}-K_{1}=W_{1}-W_{2}$ ,

или

$K_{1}+W_{1}=K_{2}+W_{2}$ .

Левая и правая части данного равенства представляют собой механическую энергию тела в начальном и конечном положении:

$E_{1}=E_{2}$ .

Следовательно, при движении тела в поле силы тяжести и/или на пружине механическая энергия тела остаётся неизменной при отсутствии трения. Справедливо и более общее утверждение.

Закон сохранения механической энергии. Если в замкнутой системе действуют только консервативные силы, то механическая энергия системы сохраняется.

При этих условиях могут происходить лишь превращения энергии: из кинетической в потенциальную и наоборот. Общий запас механической энергии системы остаётся постоянным.

к оглавлению ▴

Закон изменения механической энергии.

Если между телами замкнутой системы имеются силы сопротивления (сухое или вязкое трение), то механическая энергия системы будет уменьшаться. Так, автомобиль останавливается в результате торможения, колебания маятника постепенно затухают и т. д. Силы трения неконсервативны: работа силы трения очевидным образом зависит от пути, по которому перемещается тело между данными точками. В частности, работа силы трения по замкнутому пути не равна нулю.

Снова рассмотрим движение тела в поле силы тяжести и/или на пружине. Вдобавок на тело действует сила трения, которая за рассматриваемый промежуток времени совершает отрицательную работу $A_{TP}$ . Работу консервативных сил (тяжести и упругости) по-прежнему обозначаем .

Изменение кинетической энергии тела равно работе всех внешних сил:

$K_{2}-K_{1}=A+A_{TP}$ .

Но $A=W_{1}-W_{2}$ , следовательно

$K_{2}-K_{1}=W_{1}-W_{2}+A_{TP}$ .

Отсюда

$K_{2}+W_{2}-(K_{1}+W_{1})=A_{TP}$ ,

или

$E_{2}-E_{1}=A_{TP}$ .

В левой части стоит величина $Delta E=E_{2}-E_{1}$ — изменение механической энергии тела:

$Delta E=A_{TP}$ .

Итак,при движении тела в поле силы тяжести и/или на пружине изменение механической энергии тела равно работе силы трения. Так как работа силы трения отрицательна,изменение механической энергии также отрицательно: механическая энергия убывает.
Справедливо и более общее утверждение.

Закон изменения механической энергии. Изменение механической энергии замкнутой системы равно работе сил трения, действующих внутри системы.

Ясно, что закон сохранения механической энергии является частным случаем данного утверждения.

Конечно, убыль механической энергии не противоречит общефизическому закону сохранения энергии. В данном случае механическая энергия превращается в энергию теплового движения частиц вещества и их потенциальную энергию взаимодействия друг с другом, т. е. переходит во внутреннюю энергию тел системы.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Энергия.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Совершение работы телом не проходит бесследно. Рассмотрим, например, часы с пружинным заводом. При заводе часов состояние системы (часового механизма) меняется так, что она приобретает способность совершать работу в течение длительного времени. Пружина поддерживает движение всех колес, стрелок и маятника, испытывающих сопротивление движению, вызванное трением. По мере хода часов способность пружины совершать работу постепенно утрачивается. Состояние пружины меняется.

Если тело или система тел могут совершить работу, говорят, что они обладает механической энергией.

Определение

Механическая энергия — скалярная физическая величина, являющаяся единой мерой всех форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие.

Механическая энергия обозначается буквой E. Единица изменения энергии — Джоуль (Дж).

Виды механической энергии

В механике состояние системы определяется положением тел и их скоростями. Поэтому в ней выделяют два вида энергии: потенциальную и кинетическую.

Определение кинетической энергии

Кинетическая энергия — это энергия, которой обладает движущееся тело. Она обозначается как E_k. Кинетическая энергия тела зависит от его массы и скорости. Численно она равна половине произведения массы тела на квадрат его скорости:

Определение потенциальной энергии

Потенциальная энергия — это энергия взаимодействующих тел. Она обозначается как E_p.

Потенциальная энергия в поле тяготения Земли численно равна произведению массы тела на его высоту (расстояние от поверхности планеты) и на ускорение свободного падения:

Ep=mgh

Потенциальная энергия упруго деформированного тела определяется формулой:

Ep=kx22

k — жесткость пружины, x — ее удлинение.

Пример №1. Мальчик подбросил футбольный мяч массой 0,4 кг на высоту 3 м. Определить его потенциальную и кинетическую энергию в верхней точке.

Потенциальная энергия мяча в поле тяготения Земли равна:

E_p = mgh = 0,4∙10∙3 = 12 (Дж)

В верхней точке полета скорость мяча равна нулю. Следовательно, кинетическая энергия мяча в этой точке тоже будет равна нулю:

E_k = 0 (Дж).

Теорема о кинетической энергии

Изменение кинетической энергии тела равно работе равнодействующей всех сил, действующих на тело:

Эта теорема справедлива независимо от того, какие силы действуют на тело: сила упругости, сила трения или сила тяжести.

Пример №2. Скорость движущегося автомобиля массой 1 т изменилась с 10 м/с до 20 м/с. Чему равна работа равнодействующей силы?

Сначала переведем единицы измерения в СИ: 1 т = 1000 кг. Работа равна изменения кинетической энергии, следовательно:

Работа и потенциальная энергия тела, поднятого над Землей

Величина потенциальной энергии зависит от выбора нулевого уровня энергии. В поле тяготения Земли нулевым уровнем энергии обладает тело, находящееся на поверхности планеты.

Работа силы тяжести

Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:

A = – ∆E_p = –(mgh – mgh₀) = mg(h₀ – h)

Если тело поднимается, сила тяжести совершает отрицательную работу. Если тело падает, сила тяжести совершает положительную работу.

Пример №3. Шарик массой 100 г скатился с горки длиной 2 м, составляющей с горизонталью угол 30^о. Определить работу, совершенную силой тяжести.

Сначала переведем единицы измерения в СИ: 100 г = 0,1 кг. Под действием силы тяжести положение тела относительно Земли изменилось на величину, равную высоте горки. Высоту горки мы можем найти, умножим ее длину на синус угла наклона. Начальная высота равна высоте горки, конечная — нулю. Отсюда:

A = mg(h₀ – h) = 0,1∙10(2∙sin30^o – 0) =2∙0,5 = 1 (Дж)

Потенциальная энергия протяженного тела

Работа силы тяжести

Потенциальная энергия протяженного тела выражается через его центр масс. К примеру, чтобы поднять лом длиной l и массой m, нужно совершить работу равную:

A = mgh

где h — высота центра массы лома над поверхностью Земли. Так как лом однородный по всей длине, его центр масс будет находиться посередине между его концами, или:

Отсюда работа, которую необходимо совершить, чтобы поднять этот лом, будет равна:

Пример №4. Лежавшую на столе линейку длиной 0,5 м ученик поднял за один конец так, что она оказалась в вертикальном положении. Какую минимальную работу совершил ученик, если масса линейки 40 г?

Переведем единицы измерения в СИ: 40 г = 0,04 кг. Минимальная работа, необходимая для поднятия линейки за один конец, равна:

Работа и изменение потенциальной энергии упруго деформированного тела

Вспомним, что работа определяется формулой:

A = Fs cosα

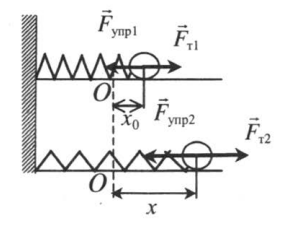
Когда мы сжимаем пружину, шарик перемещается в ту же сторону, в которую направлена сила тяги. Если мы растягиваем ее, шарик перемещается так же в сторону направления силы тяги. Поэтому вектор силы упругости и вектор перемещения сонаправлены, следовательно, угол между ними равен нулю, а его косинус — единице:

Модуль силы тяги равен по модулю силе упругости, поэтому:

Перемещение определяется формулой:

s = x – x₀

Следовательно, работа силы тяги по сжатию или растяжению пружины равна:

Но известно, что потенциальная энергия упруго деформированного тела равна:

Следовательно, работа силы, под действием которой растягивается или сжимается пружина, равна изменению ее потенциальной энергии:

Задание EF18117

На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Какой из представленных вариантов описания движения соответствует данному графику?

Ответ:

а) Тело брошено под углом к горизонту с поверхности Земли и упало в кузов проезжающего мимо грузовика.

б) Тело брошено под углом к горизонту с поверхности Земли и упало на Землю.

в) Тело брошено под углом к горизонту с поверхности Земли и упало на балкон.

г) Тело брошено вертикально вверх с балкона и упало на Землю.

Алгоритм решения

1.Описать изменение кинетической энергии в течение всего времени движения тела.

2.Установить характер движения тела в течение этого времени.

3.Проанализировать все ситуации и выбрать ту, которая не противоречит установленному характеру движения тела.

Решение

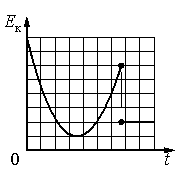
Согласно графику, кинетическая энергия тела сначала уменьшалась, а затем увеличилась. Затем она резко уменьшилась до некоторого значения и осталась постоянной.

Кинетическая энергия тела определяется формулой:

Кинетическая энергия зависит прямо пропорциональной от квадрата скорости. Следовательно, когда уменьшается кинетическая энергия, скорость тоже уменьшается. Когда она возрастает — скорость тоже возрастает. Когда она постоянная — скорость тоже постоянна и не равна нулю.

Если тело брошено под углом к горизонту, скорость сначала будет уменьшаться, так как ускорение свободного падения направлено вниз. Если тело бросить вертикально вверх, скорость тоже сначала будет уменьшаться. Но в этом случае при достижении верхней точки траектории на момент скорость тела будет равна нулю. Следовательно, график зависимости кинетической энергии от времени в этот момент тоже должен быть равен нулю. Но это не так. Поэтому последний вариант ответа не подходит.

Если бы тело упало на неподвижный объект, его скорость относительно Земли стала бы равной нулю. Но так как его кинетическая энергия не равна нулю и является постоянной, тело начало двигаться с постоянной скоростью. Это возможно только в случае, если тело упало на объект, движущийся с постоянной скоростью. Поэтому из всех вариантов ответа подходит только первый, когда тело падает в проезжающий мимо грузовик.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18192

К бруску массой 0,4 кг, лежащему на горизонтальной поверхности стола, прикреплена пружина. Свободный конец пружины тянут медленно в вертикальном направлении (см. рисунок). Определите величину потенциальной энергии, запасённой в пружине к моменту отрыва бруска от поверхности стола, если пружина при этом растягивается на 2 см. Массой пружины пренебречь.

Ответ:

а) 40 мДж

б) 20 мДж

в) 80 мДж

г) 200 мДж

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Сделать чертеж, указать силы, действующие на пружину, выбрать систему отсчета.

3.Записать формулу для вычисления потенциальной энергии в пружине.

4.Выполнить общее решение.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

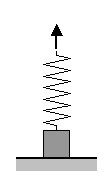
• Масса бруска: m = 4 кг.

• Удлинение пружины: ∆l = 2 см.

Переведем сантиметры в метры:

2 см = 0,02 м

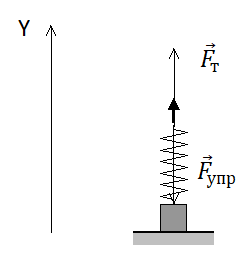
Выполним рисунок. Для описания ситуации нам понадобится только одна ось: Oy.

Потенциальная энергия деформированной пружины определяется формулой:

Так как брусок поднимают за прикрепленную к нему пружину медленно, можно считать, что это движение равномерное (и прямолинейное). Поэтому, согласно второму закону Ньютона:

F_т = F_упр

Чтобы оторвать брусок от поверхности стола, модуль силы тяги должен быть равен модулю силы тяжести. Поэтому:

F_т = F_тяж =F_упр

Или:

mg = k∆l

Теперь можем выразить жесткость пружины:

Подставим жесткость пружины в формулу потенциальной энергии и сделаем вычисления:

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18553

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t– 3t²(все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

1.Записать исходные данные и перевести их единицы измерения величин в СИ.

2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.

3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.

4.Определить перемещение тела и его кинетическую энергию.

5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:

x(t)=x0+v0t+at22

Теперь мы можем выделить кинематические характеристики движения тела:

• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).

Перемещение тела определяется формулой:

s=v0t+at22

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

x(t)=v0t+at22=5t−3t2

Кинетическая энергия тела определяется формулой:

Ek=mv22

Скорость при прямолинейном равноускоренном движении равна:

v=v0+at=5−6t

Поэтому кинетическая энергия тела равна:

Ek=m(5−6t)22=0,22(5−6t)2=0,1(5−6t)2

Следовательно, правильная последовательность цифр в ответе будет: 34.

Ответ: 34

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18678

Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?

Для каждой величины определите соответствующий характер изменения:

1)	увеличилась
2)	уменьшилась
3)	не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Скорость

спутника

Потенциальная энергия спутника

Алгоритм решения

1.Записать закон всемирного тяготения и формулу центростремительного ускорения для движения тела по окружности с постоянной по модулю скоростью.

2.Установить зависимость скорости от высоты спутника над поверхностью Земли.

3.Записать формулу потенциальной энергии и установить, как она зависит от высоты.

Решение

На спутник действует сила притяжения Земли, которая сообщает ему центростремительное ускорение:

F=maц=GmM(R+h)2

Отсюда центростремительное ускорение равно:

aц=GM(R+h)2

Но центростремительное ускорение также равно:

aц=v2(R+h)

Приравняем правые части выражений и получим:

GM(R+h)2=v2(R+h)

v2=MG(R+h)(R+h)2=MG(R+h)

Квадрат скорости спутника обратно пропорционален радиусу вращения. Следовательно, при увеличении высоты увеличивается радиус вращения, а скорость уменьшается.

Потенциальная энергия спутника определяется формулой:

E_p = mgh

Видно, что потенциальная энергия зависит от высоты прямо пропорционально. Следовательно, при увеличении высоты потенциальная энергия спутника тоже увеличивается.

Верная последовательность цифр в ответе: 21.

Ответ: 21

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 11.6k

Источник

График кинетической энергии всех звеньев механизма

Поскольку

ось
абсцисс графика
нужно перенести вниз на величину
ординаты, соответствующей начальной
кинетической энергии.
Однако конкретное значениепока неизвестно; поэтому положение
оси абсцисс показано на рис. 24 условно.

Построение
графика приведенных моментов инерции
и приближенного
графика
.
Для решения уравнения (54) необходимо
иметь график кинетической энергииII
группы звеньев. Определим кинетическую
энергию
через приведенные моменты инерции
этой же группы звеньев. Для этого
построим зависимость.
Построение графикаразберем на примере кривошипно-ползунного
механизма (рис. 22),II
группа звеньев которого включает в себя
звенья 2 и 3.

Для
определения приведенных моментов
инерции звена 2 (шатуна), совершающего
плоское движение, и звена 3 (ползуна),
движущегося поступательно, используем
формулы (34) и (32):

Заменяя
,и переходя к отрезкам с планов возможных
скоростей, получим

Еще
раз обратим внимание на то, что величины
изависят от отношения скоростей точек
механизма, а не от их абсолютного
значения. Отношения скоростей, входящие
в выражения для определенияи,
заменяются для каждого положения
механизма отношением соответствующих
отрезков, взятых с планов возможных
скоростей. Выберем масштаби построим зависимости,ипо углу поворота.
Сложив их, получим график(рис. 25).

Кинетическую
энергию
звеньев 2 и 3 выразим через сумму
приведенных моментов инерцииэтих звеньев:

Кинетическую
энергию
звена 2 представим в виде двух слагаемых:— кинетической энергии звена в
поступательной части движения со
скоростьюи— кинетической энергии во вращательной
части движения вокруг оси, проходящей
через центр массшатуна. В результате получим

Закон
изменения
еще неизвестен. Поэтому для определениявоспользуемся приближенным равенством,
поскольку коэффициент неравномерности— величина малая.

Тогда

(57)

Так
как
,
томожно считать пропорциональной,
а построенную кривуюпринять за приближенную кривую.
Масштаб графика

(58)

При
решении задачи динамики для многоцилиндровых
поршневых машин должен быть построен
график
,

где
n
— число рассматриваемых механизмов,
равное числу цилиндров машины.

Рекомендуется
описанным выше способом получить сначала
график
для механизма, передающего движение от
поршня цилиндра на главный (коленчатый)
вал, а затем в каждом положении
механизма графически или аналитически
просуммироватьn
ординат этой диаграммы, учитывая угол
между осями цилиндров и угол между
кривошипами коленчатого вала.

Так,
например, на рис. 30 показана схема
двухцилиндрового двухтактного двигателя
внутреннего сгорания с рядным
расположением цилиндров. Рабочий
процесс в каждом цилиндре происходит
за один оборот главного вала — начального
вала 1. Угол между кривошипами коленчатого
вала составляет
рад, угол между осями цилиндров равен0.
При таком расположении цилиндров и
таком угле между кривошипами кинематические
процессы механизмов рассматриваемого
двигателя сдвинуты друг относительно
друга на угол
рад. Фазы рабочего процесса в цилиндре
2 сдвинуты по отношению к одноименным
фазам рабочего процесса в цилиндре
1 также на угол,
т.е. на угол поворота главного вала за
время половины цикла.

На
такой же угол сдвинуты изображенные на
рис. 30 графики
идля механизмов цилиндров 1 и 2. После
сложения ординат этих графиков получен
график(рис. 30).

Построение
приближенного графика
.
Согласно уравнению (54) имеем

Следовательно,
для механизма двигателя (см. рис. 22) при
построении кривой
необходимо из ординат кривой(рис. 26) в каждом положении механизма
вычесть отрезки, изображающие величины;
взятые из графика(рис. 25); вычитаемые отрезка должны быть
представлены обязательно втом
же масштабе
,
в каком построена кривая.
Полученная кривая(рис. 26) — приближенная, так как построена
вычитанием из точной кривойприближенных значений.

г) Определение
необходимого момента инерции маховых
масс

Построив
кривую
(рис. 26), найдем на ней точкиF
и N,
соответствующие значениям
и,
и получим согласно уравнению (55)
максимальное изменение кинетической
энергииI
группы звеньев за период цикла

где
— отрезок вмм,
изображавший
в масштабе

Необходимый
момент инерции
подсчитывается по формуле (53)

Допущение,
что
,
при построении графика
,
не вносит заметной ошибки в расчет при
малых значениях.
При значениях,
чтобы избежать завышения маховых масс,
в расчет целесообразно вносить поправку,
пользуясь формулой

(59)

где
и— значения кинетической анергии звеньевII
группы (рис. 25) соответственно в положениях
механизма f
и n,
где кинетическая энергия звеньев I
группы имеет значения
и(рис. 26).

д) Определение
момента инерции дополнительной маховой
массы

По
формуле (53) подсчитывается тот необходимый
момент инерции
,
который обеспечит колебания угловой
скоростив пределах, заданных коэффициентом
неравномерности.
ВI
группу звеньев кроме начального звена
часто входят еще и другие звенья:
роторы различных машин, зубчатые колеса,
подвижные части редукторов и т.д. Все
эти звенья, связанные с начальным
звеном постоянным передаточным
отношением, обладают маховыми массами,
которые влияют на закон движения
начального звена. Если сумма приведенных
моментов инерции этих звеньев оказывается
меньше значения необходимого момента
инерции
,
то в составI
группы звеньев надо вводить дополнительную
маховую массу, момент инерции которой
определяют по формуле

(60)

где
— сумма приведенных моментов инерции
вращающихся деталей, связанных с
начальным звеном постоянным передаточным
отношением.

Напомним,
что если для ротора задан маховой момент
(в технической системе единиц), то его
нужно пересчитать на момент инерции
(см. введение).

Рассмотрим
пример. На рис. 27 показана та часть
механизма машинного агрегата, которая
представляет собой I
группу звеньев. Начальное звено —
коленчатый вал (в)
основного механизма — тихоходный. Поэтому
между ним и электродвигателем поставлена
понижающая передача, состоящая из
редуктора и пары зубчатых колес
и.
Для нашего примера момент инерции
начального звена.

С помощью формулы
(60) определим момент инерции дополнительной
маховой массы, которая размещается на
валу начального звена

Необходимый
момент инерции
получен из динамического расчета.
Приведенные моменты инерции остальных
звеньевI
группы подсчитываются следующим образом:

;

Здесь
и— передаточные функции.

е) Определение
закона движения механизма

Закон движения
начального звена механизма может быть
определен по уравнению (42).

Однако
определив по этому уравнению угловой
скорости затруднено тем, что необходимо
знать начальные условия, которые обычно
для установившегося движения наперед
неизвестны. Поэтому при определении
закона движения воспользуемся тем, что
при малых значениях коэффициента
неравномерности
верхняя часть графика(рис. 26), изображающая изменение
кинетической энергии,
приближенно изображает также изменение
угловой скорости.

В
точках F
и N
кривой
имеет соответственно значенияи.
Масштаб графика угловой скорости
определяется по формуле

(61)

Чтобы
перейти от изменений угловой скорости
к ее полному значению, необходимо
определить положения оси абсцисс графика
.
Для этого через середину отрезка,
изображающего разностьи равного разности ординат точекF
и N
(рис. 26), проводится горизонтальная
штриховая линия, которая является
линией средней угловой скорости
.
Расстояние от линиидо оси абсцисс определяется следующим
образом:

(62)

Получив
положение оси абсцисс графика
,
можно определить,а
по ней и.

Соседние файлы в папке 51A

Источник

На чтение 15 мин Просмотров 2.2к.

Навигация

Кинетическая энергия механической системы
Энергетические характеристики
Теорема об изменении кинетической энергии

Кинетическая энергия механической системы

Кинетической энергиейT материальной точки массы m, движущейся со скоростью V, называют величину

T=mV22 . (47)

Кинетической энергией механической системы называют сумму кинетических энергий включенных в эту систему материальных точек:

T=∑nk=1mV2k2 . (48)

В тех случаях, когда масса системы распределена непрерывно, суммирование в выражении (48) заменяют интегрированием по области распределения.

Найдем связь между значениями кинетической энергии механической системы в двух системах отсчета, одна из которых неподвижна, а другая движется поступательно со скоростью →VA . В этом случае скорость →Vkточки в неподвижной координатной системе и относительная скорость →Vrk связаны соотношением

→Vk=→VA+→Vrk .

Тогда вместо (48) получим

T=MV2A2+M→VA→VrC+Tr . (49)

Здесь →VrC=∑mk→VrkM — относительная скорость центра масс; Tr=∑nk=1mk(Vrk)22 — кинетическая энергия механической системы в подвижной системе координат.

Если за начало координат подвижной системы принимается центр масс механической системы С, то выражение (49) упрощается (теорема Кенига):

T=MV2C2+Tr. (50)

Использование выражений (48) и (50) позволяет сформулировать следующие правила вычисления кинетической энергии твердого тела: при поступательном движении тела массой M со скоростью →V

T=MV22 ; (51)

при вращении с угловой скоростью ω вокруг неподвижной оси z тела с моментом инерции Iz

T=Izω22 ; (52)

при плоскопараллельном движении твердого тела с угловой скоростью ω при значении центрального момента инерции ICz относительно оси, перпендикулярной плоскости движения, и значении IPz момента инерции относительно мгновенной оси вращения

T=MV2C2+ICzω22=IPzω22 ; (53)

при сферическом движении с угловой скоростью вращения ω

и значении момента инерции тела Iξотносительно мгновенной оси вращения ξ

T=Iξω22 ; (54)

в общем случае движения твердого тела

T=MV2C2+ICξω22 . (55)

Здесь момент инерции ICξ вычисляется относительно мгновенной оси Cξтакого сферического движения тела, которое оно совершает в системе осей, перемещающихся поступательно вместе с центром масс С.

В качестве примера вычислим кинетическую энергию механической системы, изображенной на рис.28, как сумму кинетических энергий тел ее формирующих. В этом случае

T=Tпост1+Tврбл+Tпост3+Tвр3=P1˙s212g+I2˙ϕ222+P3˙s232g+I3˙ϕ232 .

С учетом уравнений кинематических связей ˙s1=˙ϕ⋅R и ˙s3=˙ϕ3r3 выражение для кинетической энергии рассматриваемой механической системы с двумя степенями свободы может быть записано через любые две переменные, принятые за независимые. Например, если полагать независимыми s1 и s2, то выражение для кинетической энергии примет вид

T=˙s21(P1R2+I)2gR2+˙s223P34g .

Энергетические характеристики

К энергетическим характеристикам силы относят ее мощность, работу и потенциальную энергию.

Мощностью Nсилы →F, точка приложения которой движется со скоростью →V, называют величину

N=→F⋅→V. (56)

Работа силы d‘Aна элементарном интервале времени dtи соответствующем этому промежутку времени элементарному смещению d→rточки приложения определяется по правилу

d‘A=Ndt=→F⋅→Vdt=→F⋅d→r. (57)

Работой A силы на конечном интервале времени [0;t] и соответствующем изменении радиуса – вектора точки приложения этой силы от →r0 до →r называют величину

A=∫t0Ndt=∫→r→r0→Fd→r . (58)

Работа момента пары сил вычисляется аналогично.

Потенциальная энергия Попределена только в тех случаях, когда выражение (57) представляет собой полный дифференциал П:

d‘A=−dП. (59)

При выполнении условия (59) говорят, что сила потенциальна. Сопоставление формул (57) и (59) позволяет записать соотношения, связывающие проекции силы на оси выбранной координатной системы с функцией П:

Fx=−∂П∂x; Fy=−∂П∂y; Fz=−∂П∂z . (60)

Если точка приложения силы переместилась из положения M1(x1;y1;z1) в положение M2(x2;y2;z2), то путем интегрирования (59) можно получить

A12=−∫M2M1dП=П(x1;y1;z1)−П(x2;y2;z2). (61)

Заметим (см. формулы (57), (60) и (61)), что потенциальная энергия определена с точностью до постоянного слагаемого; отмеченная особенность позволяет полагать потенциальную энергию равной нулю в выбираемой нами точке (например, в начале координат). В последнем случае формула (61) принимает вид

A10=−∫M0M1dП=П(x;y;z). (62)

Иными словами – потенциальная энергия равна работе сил по переводу системы из отклоненного положения в начальное.

В том случае, когда для совокупности сил, действующих на механическую систему, можно записать выражение потенциальной энергии П, механическую систему называют консервативной. Такие механические системы обладают важными особенностями – работа действующих сил не зависит от вида траектории и закона движения по ней; работа при движении по замкнутому контуру равна нулю (см. (61)). Из (60) легко получить условия, при выполнении которых существует функция П:

∂Fx∂y=∂Fy∂x ; ∂Fx∂z=∂Fz∂x ; ∂Fz∂y=∂Fy∂z. (63)

В качестве примера вычислим потенциальную энергию для трех частных, но важных для технических приложений, случаев: действуют сила тяжести, центральная сила и сила упругости пружины.

Для силы тяжести →P=→i0+→j0−→kP выполняются критерии (63); тогда, в соответствии с формулами (58) и (62), имеем

П=A10=∫0z(Fxdx+Fydy+Fzdz)=∫0z(−P)dz=Pz. (64)

Для центральной силы →F=F(r)→rr, модуль которой зависит от расстояния rдо начала координат, так же выполняются критерии (63), поэтому

П=A10=∫r0rF(r)→rrd→r=∫r0rF(r)dr . (65)

Силу упругости пружины можно считать центральной силой, направленной к началу координат; в случае прямой пропорциональности между величиной силы Fx и удлинением x пружины имеем Fx=−cx. В этом случае

П=A10=∫0xFxdx=∫0x(−cx)dx=cx22. (66)

При определении энергетических характеристик системы сил суммируют соответствующие характеристики для всех сил, действующих на механическую систему.

Теорема об изменении кинетической энергии

Умножим уравнения (2.5) скалярно на скорость →Vk и сложим.

∑nk=1mkd→Vkdt→Vk=∑nk=1→Fek→Vk+∑nk=1→Fik→Vk=Ne+Ni ,

где Ne и Ni— мощности внешних и внутренних сил, действующих на механическую систему.

Заметим, что если связи между телами, формирующими систему, допускают деформацию (см. пружину жесткостью c2 в примере 21), то точки приложения равных и противоположно направленных внутренних сил →T2 имеют различные скорости, вследствие чего их суммарная мощность не будет равной нулю.

Изменив порядок суммирования и дифференцирования в левой части равенства, ее можно привести к виду

∑nk=1mkd→Vkdt→Vk=ddt∑nk=1mk→V2k2=ddt∑nk=1mkV2k2=dTdt .

Окончательно имеем запись теоремы об изменении кинетической энергии механической системы в дифференциальной форме:

dTdt=Ne+Ni. (67)

— производная по времени от кинетической энергии механической системы равна мощности всех действующих сил.

В дифференциальной форме, основанной на понятии работы силы за элементарный промежуток времени, получим

dT=(Ne+Ni)dt=d‘Ae+d‘Ai. (68)

Интегрируя (68) на интервале времени [0;t], получим интегральную форму записи теоремы об изменении кинетической энергии

T1−T0=Ae+Ai , (69)

где T1=T(t); T0=T(0); Ae=∫t0Nedt; Ai=∫t0Nidt.

В частном случае, когда для совокупности внешних и внутренних сил системы можно записать выражение потенциальной энергии

d‘Ae+d‘Ai=−dП,

вместо (68) имеем соотношение

d(T+П)=0 . (70)

В такой системе выполняется закон сохранения полной механической энергии

T+П=const ,

а сама система называется консервативной.

Источник