
МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ИНСТИТУТ
(ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
ОСНОВЫ ХИМИЧЕСКОЙ КИНЕТИКИ
Москва 2007
МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Кафедра химии
ОСНОВЫ ХИМИЧЕСКОЙ КИНЕТИКИ
УЧЕБНОЕ ПОСОБИЕ
Утверждено редсоветом МАДИ(ГТУ)
Москва 2007
УДК 544.4 ББК 24.1
Болячевская К. И., Литманович А. А., Остаева Г. Ю., Панасенко А.А., Полякова Е.В.
Основы химической кинетики: Учебное пособие / Под ред. И. М. Паписова. – М.: МАДИ (ГТУ), 2007. – 80 с.
В пособии рассмотрены кинетические закономерности протекания химических реакций. Изложены основные понятия катализа.
Пособие содержит теоретический материал, экспериментальную часть,
примеры решения типовых задач, предлагаемых студентам МАДИ (ГТУ) на контрольных и экзаменационных работах, вопросы для самоконтроля. Приведены варианты домашних заданий по теме «Химическая кинетика» общего курса химии, изучаемого студентами МАДИ (ГТУ).
Пособие предназначено для студентов всех специальностей дневного отделения МАДИ (ГТУ), изучающих тему «Химическая кинетика» в общем курсе химии на кафедре химии МАДИ (ГТУ).
© Московский автомобильно-дорожный институт (государственный технический университет), 2007
Введение
Любая химическая реакция протекает во времени. Некоторые реакции заканчиваются за малые доли секунды, другие осуществляются за минуты, часы, дни; известны реакции, требующие для своего протекания нескольких лет, десятилетий и большего времени. Кроме того, одна и та же реакция может в одних условиях, например при повышенных температурах, протекать быстро, а в других – например, при охлаждении, — медленно.
Интенсивность протекания процесса характеризует скорость химической реакции, которая зависит от многих факторов.
На скорость реакции влияют:
•природа реагирующих веществ;
•реакционная среда;
•концентрации реагентов;
•давление;
•температура;
•присутствие в системе катализаторов;
•размер поверхности раздела (гетерогенные системы);
•внешние воздействия, например, излучения и др.
Весьма важно не только знать, с какой скоростью будет протекать реакция в тех или иных условиях, но и как нужно изменить эти условия для того, чтобы реакция протекала с требуемой скоростью.
Раздел химии, изучающий скорости и механизмы химических реакций, называется химической кинетикой.
1. ОСНОВНЫЕ ПОНЯТИЯ ХИМИЧЕСКОЙ КИНЕТИКИ
Различают гомогенные и гетерогенные химические реакции. Гомогенной называется реакция, протекающая в одной фазе. Гомо-
генная реакция осуществляется во всем объеме системы (в газовой фазе или жидком растворе), например:
H2 (г) + I2 (г) → 2 HI (г)
3
HCl (р-р) + NaOH (р-р) → NaCl (р-р) + H2O (ж).
Гетерогенной называется реакция, протекающая на границе раздела фаз (твердой и жидкой, твердой и газообразной), например:
|
Fe (тв) + 2 HCl (р-р) → Fe Cl2 (р-р) + H2 (г) |
|
|
t,оС |
Fe (тв) + H2O (г). |
|
FeO (тв) + H2 (г) → |
Все реакции подразделяют на простые и сложные.
Простой (элементарной) называется реакция, протекающая в одну стадию (элементарный акт).
Количество частиц (молекул, атомов, ионов), принимающих участие в элементарной реакции, определяет ее молекулярность.
Мономолекулярная реакция — реакция с участием одной частицы. Например, реакция, связанная с распадом молекулы:
H2 → 2H SO2Cl2 → SO2 + Cl2.
Бимолекулярная реакция – реакция, протекающая в результате взаимодействия в элементарном акте двух молекул:
H2 + I 2 → 2HI
2NO → N2O2.
Тримолекулярные реакции – реакции, требующие одновременного столкновения трех частиц:
2NO + H2 → N2O + H2O.
Чаще всего встречаются мономолекулярные и бимолекулярные реакции. Реакции с молекулярностью больше трех неизвестны, что связано с крайне малой вероятностью одновременного столкновения четырех и более частиц.
Большинство химических реакций являются сложными.
Сложные реакции – это многостадийные реакции, протекающие через ряд элементарных (простых) реакций.
К сложным реакциям относятся последовательные, параллель-
ные, цепные, фотохимические и некоторые другие реакции.
4
В последовательных реакциях
A →B →C
продукт, образованный в предыдущей стадии, является одновременно исходным веществом для последующей стадии. Общая скорость процесса определяется скоростью наиболее медленной стадии, которая называется лимитирующей.
В параллельных реакциях исходные вещества претерпевают превращение одновременно в двух или нескольких направлениях по следующей схеме:
В
A
D
Общая скорость процесса определяется скоростью наиболее быстрой стадии.
Совокупность элементарных реакций, из которых складывается сложная химическая реакция, называется механизмом реакции.
2. СКОРОСТЬ ХИМИЧЕСКИХ РЕАКЦИЙ
Существуют различные химические и физические методы определения скорости реакции. За ходом химической реакции можно наблюдать по изменению какого-нибудь свойства вещества: вязкости раствора, его оптической плотности, потенциала электрода, теплопроводности, объема выделяющегося газа и др. Но все способы выражения скорости реакции в конечном итоге сводятся к изменению количества вещества.
Скорость химической реакции равна изменению количества вещества в единицу времени в единице реакционного пространст-
ва. Для гомогенных процессов реакционное пространство представляет собой объем, заполненный реагентами, для гетерогенных процессов — поверхность раздела фаз.
5
2.1.Гомогенные химические реакции
Взамкнутой системе, в которой объем не меняется, отношение количества вещества к объему системы представляет собой молярную концентрацию.
Скорость гомогенной реакции равна изменению концентрации какого-либо из веществ, вступающих в реакцию, или образующихся
врезультате ее, в единицу времени.
Зависимости концентраций исходных веществ или продуктов реакции от времени называются кинетическими кривыми.
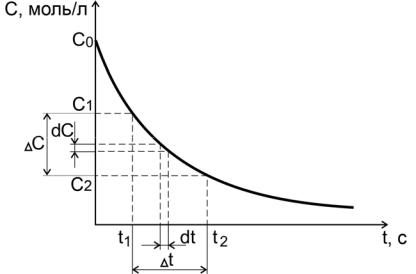
Пусть за промежуток времени от t1 до t2 молярная концентрация некоторого реагирующего исходного вещества уменьшилась от С1 до
С2 (рис. 1).
Рис. 1. Средняя и истинная скорости реакции для исходного вещества
Скорость реакции в данный промежуток времени будет равна
|
υ = − |
С2 − |
С1 |
. |
|
t2 − |
|||
|
t1 |
В ходе реакции количества исходных веществ во времени убывают, количества продуктов реакции увеличиваются. Скорость является положительной величиной, поэтому перед отношением в правой
6
части уравнения ставят знак «минус», если ее определяют по расходу исходного вещества, и знак «плюс», если ее определяют по увеличению концентрации продукта реакции.
В общем случае
|
υ = ± |
С2 −С1 |
= ± |
C . |
||||
|
(2.1) |
|||||||
|
t2 − t1 |
t |
||||||
|
Отношение изменения концентрации одного из реагирующих |
|||||||
|
веществ к промежутку времени |
C2 − C1 |
выражает среднюю ско- |
|||||
|
t2 − t1 |
|||||||
|
рость реакции. |
Входе реакции изменяются концентрации реагирующих веществ
исоответственно скорость реакции. Средняя скорость реакции тем
ближе к истинной скорости, чем меньше промежуток времени t. За бесконечно малый промежуток времени dt концентрация изменится на бесконечно малое значение dC.
Скорость реакции в данный момент времени или, мгновенная (истинная) скорость реакции, представляет собой первую производ-
|
ную концентрации реагирующего вещества по времени |
|
|
υ = ± dC . |
(2.2) |
|
dt |
Производные концентрации по времени, входящие в выражение для мгновенной скорости реакции, находятся как тангенсы углов наклона касательных к кинетическим кривым в точках, соответствующих различным моментам времени от начала химической реакции (рис.2).
Из определения скорости и анализа уравнения (2.1) следует, что скорость реакции имеет единицу измерения [моль·л-1·с-1] (иногда [моль·м-3·с-1], [моль·л-1·ч-1] и т.п.).
7
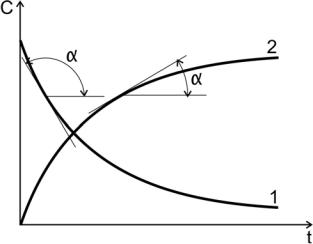
Рис. 2. Кинетические кривые:
1 — для исходного вещества; tgα< 0 ; 2 – для продукта реакции; tgα> 0
При описании кинетического процесса необходимо указывать вещество, по отношению к которому была измерена скорость («скорость по веществу»). Рассмотрим в качестве примера следующую реакцию:
N2 + 3H2 = 2NH3.
Из уравнения реакции видно, что если за какой-то период времени t в реакцию вступит n молей N2, то за это же время прореагирует 3n молей Н2 и образуется 2n молей NH3. Следовательно, скорости реакции по каждому из веществ различны, однако, разделив эти скорости на стехиометрический коэффициент, соответствующий этому ве-
|
ществу в уравнении реакции, |
получим одну и ту же величину — просто |
|||||||
|
«скорость реакции» |
||||||||
|
υ = − |
dCN2 |
= − |
1 |
dCH2 |
= |
1 |
dCNH3 |
. |
|
dt |
3 dt |
2 dt |
8
2.2. Зависимость скорости гомогенной химической реакции от концентрации реагирующих веществ
Чтобы произошло химическое взаимодействие, необходимо столкновение реагирующих частиц. При одной и той же температуре количество столкновений растет с увеличением количества реагирующих частиц в единице объема, т.е. с возрастанием концентрации реагентов. Соответственно, скорость реакции повышается с увеличением концентрации реагирующих веществ.
Выведенное на основе экспериментальных данных уравнение, выражающее зависимость скорости от концентраций реагирующих веществ, показывает, что скорость химической реакции пропорциональна произведению концентраций реагентов в степенях, называемых порядками реакции по реагентам и определяемых опытным путем.
Уравнение, устанавливающее зависимость скорости от концентрации реагирующих веществ, называется дифференциальным кинетическим уравнением реакции.
Например, для реакции аА + bB = cC + dD выражение для скорости реакции будет иметь следующий вид:
где k – коэффициент пропорциональности, называемый константой скорости реакции; [A] и [B] — молярные концентрации реагирующих веществ; n и m — показатели степеней при концентрациях реагентов
(порядки реакции по веществам А и B).
Общим порядком, или просто порядком реакции, называется ве-
личина, равная сумме показателей степеней при концентрациях реагентов в кинетическом уравнении реакции (n+m). Порядок реакции равен сумме порядков по реагирующим веществам.
Константа скорости k – постоянная величина (при T = const) и не зависит от концентрации реагентов. Она определяется природой реагирующих веществ и зависит от температуры.
9
Из уравнения (2.3) следует, что при единичных концентрациях реагирующих веществ (например, [A] = [B] = 1 моль/л) константа скорости реакции численно равна скорости реакции.
Из этого же уравнения видно, что размерность константы скорости реакции зависит от порядка реакции, поскольку размерность скорости реакции для всех гомогенных реакций одинакова. Единицу измерения константы скорости реакции определяют из анализа размерностей.
Порядок реакции зависит от ее сложности.
Для простой (элементарной) реакции стехиометрическое уравнение передает механизм процесса, стехиометрические коэффициенты уравнения реакции совпадают с порядками по реагентам, молекулярность совпадает с общим кинетическим порядком.
Для необратимой элементарной реакции зависимость скорости от концентрации реагентов выражается законом действующих масс.
При постоянной температуре скорость элементарной химической реакции пропорциональна произведению концентраций реагирующих веществ в степенях, равных их стехиометрическим коэффициентам.
Рассмотрим необратимые элементарные реакции разного вида и применим к ним закон действующих масс.
1. Скорость реакции первого порядка А → продукты, характеризуется кинетическим уравнением
υ = k [A].
Константа скорости реакции первого порядка имеет размерность
[с-1].
Например, для термораспада диметилового эфира
CH3OCH3 → CH4 + H2 + CO, υ = k [CH3OCH3]
10
2. Скорость реакции второго порядка в соответствии с законом действующих масс равна:
2А → продукты, υ = k [А]2;
А + В → продукты, υ = k [А] [В]. Размерность константы скорости реакции второго порядка
[л· моль-1·с-1].
Например, для реакции разложения иодида водорода
2 HI → H2 + I2 υ = k [ HI]2.
Или, для реакции этерификации уксусной кислоты этанолом
CH3COOH + C2H5OH → CH3COOC2H5 + H2O,
υ= k [CH3COOH] [C2H5OH].
3.Скорость реакции третьего порядка
|
A + B + C → продукты, |
υ = k [А] [В] [C], |
|
2A + B → продукты, |
υ = k [А]2 [B]; |
|
3A → продукты, |
υ = k [А]3. |
Размерность константы скорости третьего порядка [л²· моль-2·с-1]. Например, реакция взаимодействия оксида азота с хлором
2NO + Cl 2 → 2NOCl, υ = k [NO]2 [Cl 2].
Закон действующих масс справедлив только для элементарных реакций.
В большинстве случаев реакции многостадийны.
Для сложных (многостадийных) реакций порядки реакции по реагентам не совпадают со стехиометрическими коэффициентами, общий порядок реакции не равен сумме стехиометрических коэффициентов.
Порядок сложной реакции может быть целым, дробным числом и даже равным нулю.
Порядок сложной реакции определяют экспериментально.
11
Например, реакция: 2N2O5 = 2N2O4 + O2 является сложной и протекает по стадиям:
|
N2O5 = N2O3 + O2 |
(а) |
|
N2O3 = NO2 + NO |
(б) |
|
NO + N2O5 = 3NO2 |
(в) |
|
2NO2 = N2O4. |
(г) |
|
Наиболее медленно протекает стадия (а), т.е. эта стадия явля- |
|
|
ется лимитирующей. Скорость стадии (а) и соответственно |
всей |
|
сложной реакции будет равна |
|
|
υ ≈ υa = ka [N2O5]. |
Так, приведенная выше сложная реакция имеет первый порядок по оксиду азота (V) и общий первый порядок.
2.3. Графический метод определения констант дифференциального кинетического уравнения
Определим константы дифференциального кинетического уравнения для следующей реакции:
аА + bB → продукты.
Зависимость скорости от концентраций выражается уравнением
(2.3)
υ = k[A]n [B]m .
Прологарифмируем это выражение
lnυ= lnk + nln[A]+ mln[B]. (2.4)
Так как величины k, n и m для рассматриваемой реакции (при T = const) являются постоянными и не зависят от концентрации реагентов, то для их нахождения достаточно определить зависимость скорости реакции от концентрации одного из реагентов при фиксированной концентрации другого реагента.
Пусть в трех опытах концентрация вещества А будет постоянной и равной [A]0, тогда в уравнении (2.4) сумма (lnk + nln[A]0 ) будет тоже
величиной постоянной, обозначим ее
12
|
lnk + nln[A]0 = D . |
|
|
Тогда уравнение (2.4) можно переписать как |
|
|
lnυ= mln[B]+D . |
(2.5) |
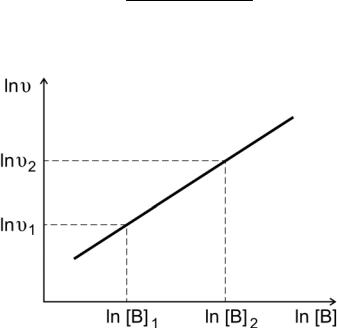
Зависимость (2.5) представляет собой в координатах ln[B] — lnυ уравнение прямой линии, тангенс угла наклона которой к оси абсцисс численно равен порядку реакции по веществу В.
По экспериментальным данным строят график зависимости lnυ от ln[B] (рис. 3) и находят порядок реакции по веществу B
m = lnυ2 − lnυ1 . ln[B]2 − ln[B]1
Рис.3. Определение порядка реакции по веществу В
В последующих опытах определяют скорость реакции при различных исходных концентрациях вещества А и постоянной концентрации [B]0. Находят порядок реакции по веществу А
|
n = |
ln υ2 − |
ln υ1 |
||
|
. |
||||
|
ln[A] |
2 |
− |
ln[A] |
|
|
1 |
Из уравнения (2.3) с учетом найденных порядков реакции по веществам А и В рассчитывают константу скорости
13

ki = [A]i nυ[iB]i m ,
где υi , [A]i, [B]i — экспериментальные данные, относящиеся к одному опыту.
2.4. Зависимость концентрации реагирующих веществ от времени для реакции первого порядка. Интегральное кинетическое уравнение
На практике чаще всего интересует не само значение скорости химической реакции, а то, сколько вещества израсходовано или образовалось к определенному моменту времени после начала реакции.
Рассмотрим эту задачу на примере реакции первого порядка
А → продукты.
Скорость такой реакции выражается следующим уравнением:
|
υ= k[A] . |
(2.6) |
||
|
В дифференциальном виде |
|||
|
− |
d[A] |
= k[A]. |
(2.7) |
|
dt |
|||
Перепишем это уравнение в следующем виде:
−d[[AA]] =kdt ,
ивозьмем определенный интеграл от обеих частей уравнения от исходного состояния ([A]0, t0 = 0) до текущего момента ([A]t, t):
|
− |
[A]t d[A] |
t |
|
|
∫ |
=k ∫dt . |
||
|
[A] |
|||
|
[A]0 |
0 |
Решение этого уравнения приводит к следующей зависимости:
|
[A] |
t |
= [A] |
0 |
• e− kt |
(2.8) |
или
(2.9)
14

ln[A]t = ln[A]0 − kt .
Соотношения (2.8) и (2.9) являются интегральными кинетиче-
скими уравнениями реакции первого порядка.
Зная исходную концентрацию вещества [A]0 и константу скорости реакции k, можно рассчитать концентрацию [A]t через любое время t после начала реакции.
Если же известны исходная концентрация [A]0 и концентрация реагирующего вещества [A]t через какое-то время t после начала ре-
|
акции, то можно рассчитать константу скорости этой реакции |
|||
|
1 |
[A]0 |
||
|
k = t ln |
. |
||
|
[A]t |
(2.10) |
Часто для характеристики скорости реакции пользуются временем полупревращения t1/2 (для реакции первого порядка чаще говорят «период полураспада»). t1/2 — это время, за которое прореагирует по-
ловина исходного вещества [A]t = [A2]0 . Тогда, исходя из уравнения
(2.10), получим следующие зависимости:
|
k = |
1 |
ln |
[A]0 |
= ln2 = |
0,693 ; |
||
|
[A]0 / 2 |
(2.11) |
||||||
|
t1/ 2 |
t1/ 2 |
t1/ 2 |
|||||
|
t |
= 0,693 . |
(2.12) |
|||||
|
1/ 2 |
k |
15
2.5.Скорость гетерогенной химической реакции
Вгетерогенной химической реакции взаимодействие реагентов происходит на поверхности раздела фаз.
Скорость гетерогенной реакции измеряется изменением количества какого-либо из веществ, вступающих в реакцию или образующихся в результате ее, за единицу времени на единице поверхности раздела фаз
|
υ = ± dn |
1 |
, |
(2.13) |
|
|
S |
||||
|
dt |
где n – количество вещества какого-либо компонента реакционной системы, моль; t – время, с; S – площадь поверхности раздела фаз, м2.
Из уравнения (2.13) следует, что скорость гетерогенной химической реакции имеет единицу измерения [моль· м -2 ·с -1]. Гетерогенные химические реакции являются сложными, многостадийными процессами. В ходе гетерогенной реакции можно выделить три характерные стадии.
1.Подвод реагирующих веществ к поверхности раздела фаз.
2.Химическая реакция на поверхности раздела фаз.
3.Отвод продуктов реакции из реакционной зоны.
Скорость суммарного гетерогенного процесса определяется наиболее медленной (лимитирующей) стадией.
Если наиболее медленно протекающими являются первая или третья стадии, связанные с переносом вещества, то скорость такого процесса определяется конвекцией (переносом массы газа или жидкости) или диффузией (самопроизвольным выравниванием концентраций) и практически не зависит от скорости протекания самой химической реакции.
При усилении конвекции скорость возрастает. Так, реакция горения угля протекает тем быстрее, чем интенсивнее подается к углю кислород
C (тв) + O2 (г) = CO2 (г).
16
При отсутствии конвекционного потока процесс может лимитироваться диффузией. Толщина диффузионного слоя уменьшается при перемешивании. Интенсивное перемешивание увеличивает скорость общего процесса. Например, растворение солей в водных растворах кислот
MgCO3 (тв) + 2 HNO3 (ж) = Mg(NO3)2 (р-р) + H2O (ж) + CO2 (г).
Если скорость переноса веществ больше, чем скорость химического превращения, т.е. наиболее медленной стадией является вторая стадия, то скорость протекания всего процесса определяется собственно химической реакцией и можно применить закон действующих масс.
При этом надо иметь в виду, что реакция протекает на поверхно-
сти раздела фаз, поэтому общая скорость химической реакции будет зависеть от концентрации жидкого или газообразного вещества, а также от площади соприкосновения фаз. Концентрация твердого вещества не входит в выражение для скорости реакции.
При измельчении твердого вещества скорость реакции будет возрастать из-за увеличения площади поверхности. Например, скорость реакции
CaCO3 (тв) + 2HCl (р-р) = CaCl2 (р-р) + H2O (ж) + CO2 (г)
зависит от концентрации соляной кислоты и площади поверхности раздела фаз. Скорость реакции порошкообразного карбоната кальция с кислотой выше скорости взаимодействия мраморной крошки с кислотой из-за увеличения площади контакта. Уравнение скорости в общем виде
υ= k [HCl]m ·S,
где m – порядок реакции по кислоте; S – площадь поверхности, м2. Порядок реакции m может совпадать со значением стехиометри-
ческого коэффициента, если лимитирующей стадией процесса является собственно простая химическая реакция.
17
2.6. Зависимость скорости химической реакции от температуры
2.6.1.Уравнение Аррениуса
Вбольшинстве случаев скорость химической реакции увеличивается при повышении температуры.
Зависимость константы скорости реакции от температуры выражается уравнением Аррениуса
|
− |
Ea |
(2.14) |
||
|
RT |
, |
|||
|
k = A e |
||||
|
где k — константа скорости реакции; |
||||
|
A — константа, называемая |
предэкспоненциальным |
|||
|
множителем; |
e — основание натурального логарифма; Еa — энергия активации, Дж/моль;
Т — температура, К;
R — газовая постоянная, 8,31 Дж/моль К.
2.6.2. Энергия активации
Для того чтобы произошла реакция, необходимо преодолеть отталкивание электронных оболочек молекул и разорвать или ослабить связи между атомами. На это надо затратить определенную энергию.
Энергия активации в элементарных реакциях – минимальная энергия реагентов (атомов, молекул и др. частиц), достаточная для того, чтобы они вступили в химическую реакцию, т. е. для пре-
одоления барьера на поверхности потенциальной энергии, отделяющего реагенты от продуктов реакции.
Потенциальный барьер – максимум потенциальной энергии, через который должна пройти система в ходе элементарного акта химического превращения.
18
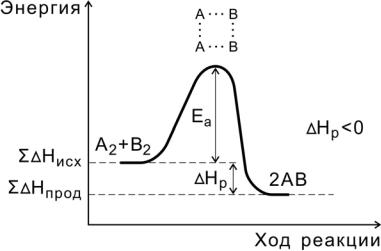
В ходе реакции вещества переходят в неустойчивое промежуточное состояние, характеризующееся большим запасом энергии. Это состояние называется активированным комплексом или переходным состоянием. Именно для его образования необходима энергия активации (рис. 4, 5).
Число частиц, входящих в активированный комплекс, определяет молекулярность данной стадии реакции.
Неустойчивый активированный комплекс существует очень короткое время (10−15 с). Он распадается с образованием исходных веществ или продуктов реакции.
Рис. 4. Энергетическая диаграмма экзотермической реакции
Переходное состояние возникает в ходе как прямой, так и обратной реакций (рис. 6). Разность энергий активации прямой и обратной реакций равна изменению внутренней энергии (тепловому эффекту) реакции
Нр = Еа(пр) — Еа (обр).
В макроскопической химической кинетике энергия активации – параметр Еa, входящий в уравнение Аррениуса (2.14). В общем случае сложных реакций параметр Еa является функцией энергий активации отдельных стадий, и определяемая энергия активации называется эффективной (эмпирической, кажущейся).
19
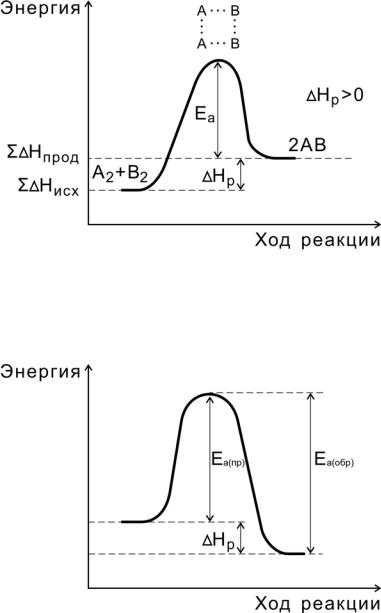
Рис. 5. Энергетическая диаграмма эндотермической реакции
Рис.6. Соотношение между энергиями активации прямой
иобратной реакций и теплового эффекта
2.6.3.Распределение молекул по энергиям
Элементарный акт химической реакции происходит не при любом столкновении молекул, а только при столкновении молекул, которые обладают повышенным запасом кинетической энергии. Молеку-
20
лы, обладающие такой энергией, называются активными молекулами.
Если сталкивающиеся молекулы не обладают такой энергией, то столкновение будет неэффективным – не приведет к образованию новой молекулы. Если же кинетическая энергия сталкивающихся молекул достаточна, то столкновение может привести к перестройке атомов и образованию молекулы нового вещества.
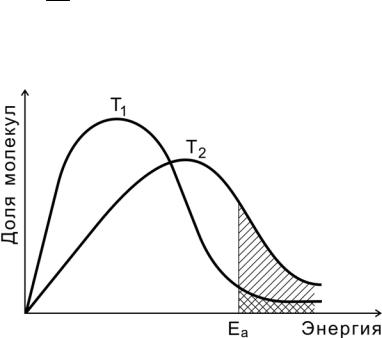
На рис. 7 показано распределение молекул идеального газа по кинетической энергии согласно статистическому закону МаксвеллаБольцмана при двух разных температурах.
Доля молекул с энергией, превышающей энергию активации Еа (доля активных молекул), с повышением температуры резко возрастает (площадь заштрихованной области).
− Ea
Величина e RT в уравнении Аррениуса (2.14) численно равна доле активных молекул.
Рис. 7. Распределение молекул по энергиям при двух разных температурах (Т2 > Т1)
Чем выше температура, тем больше в системе активных молекул, тем выше скорость реакции.
21

2.6.4. Энтропия активации. Стерический фактор
Кроме энергии активации важным условием осуществления химической реакции является ориентация молекул в момент столкновения. Большую роль играют размеры и форма молекул, место расположения реакционно-способных атомов или групп атомов в молекуле.
Вероятность необходимой для взаимодействия ориентации молекул при столкновении
W = nвзаим ,
nобщ
где, nвзаим — число способов ориентации, приводящих к взаимодействию; nобщ — общее число возможных способов ориентации.
Энтропия активации (в расчете на 1 моль) по уравнению Больц-
мана
Sa = R lnW .
Вероятность необходимой ориентации
Sa
W = e R .
Чем больше вероятность необходимой для реакции ориентации, т.е. чем больше значение энтропии активации и чем меньше значение энергии активации, тем выше скорость реакции и, соответственно, константа скорости
|
Sa |
− |
Ea |
(2.15) |
||
|
k = Z • e R |
RT , |
||||
|
• e |
где Z – коэффициент пропорциональности.
Для бимолекулярных реакций Z – это число столкновений частиц в единице объема за единицу времени (1с, 1 см3).
Уравнение (2.15) называют основным уравнением химической кинетики. Энергия активации и энтропия активации являются теми факторами, посредством которых сказывается влияние природы реагирующих веществ на скорость реакции.
22

Sa
Множитель e R называется стерическим фактором (или стерическим множителем, или фактором вероятности).
Sa
Стерический фактор e R ются в уравнении Аррениуса множитель А.
и частота столкновений Z учитыва- (2.14) через предэкспоненциальный
2.6.4. Применение уравнения Аррениуса
Энергию активации можно рассчитать по экспериментальным данным графическим или аналитическим способами, используя уравнение Аррениуса
− Ea
k = A e RT ,
|
представив его в логарифмическом виде |
|||
|
ln k = ln A − |
Еa |
. |
(2.16) |
|
RT |
Графический способ
Рис. 8. Зависимость константы скорости реакции от температуры
23

По экспериментальным значениям константы скорости реакции
1
при различных температурах строят график зависимости lnk = f (T )
(рис. 8).
По тангенсу угла наклона прямой к оси абсцисс вычисляют энергию активации
Ea = −R tgα.
Аналитический способ
Если предположить, что для выбранной реакции величины А и Еа постоянны в небольших пределах температур от Т1 до Т2, то уравнение Аррениуса (2.16) можно применить для двух различных темпе-
|
ратур (Т2> Т1; k (Т2) = k2; k (Т1) = k1) |
||||||||||||||||
|
ln k |
= ln A − |
Еa |
; |
|||||||||||||
|
1 |
RT1 |
|||||||||||||||
|
ln k |
2 |
= ln A − |
Еa |
. |
||||||||||||
|
RT2 |
||||||||||||||||
|
В результате вычитания первого уравнения из второго получим |
||||||||||||||||
|
В результате вычитания первого уравнения из второ- |
(2.17) |
|||||||||||||||
|
го получим |
||||||||||||||||
|
ln |
k2 |
= |
Ea |
T2 −T1 |
, |
|||||||||||
|
k |
T T |
|||||||||||||||
|
R |
||||||||||||||||
|
1 |
1 |
2 |
||||||||||||||
|
следовательно, |
||||||||||||||||
|
Ea = R |
T1T2 |
ln |
k2 |
. |
||||||||||||
|
(2.18) |
||||||||||||||||
|
T2 −T1 |
k1 |
Под символом логарифма находится отношение констант скоростей реакции при двух температурах, поэтому константы можно заменить любыми пропорциональными им величинами при тех же температурах. Например, вместо констант скоростей можно подставить скорости реакции, если исходные концентрации реагирующих веществ при измерении скоростей в обоих опытах были одинаковы и скорость
24
изменилась только под влиянием изменения температуры. Тогда получим следующие выражения:
|
ln |
υ2 |
= |
Ea |
T2 −T1 |
; |
(2.19) |
|||
|
T T |
|||||||||
|
υ |
R |
||||||||
|
1 |
1 |
2 |
|||||||
|
Ea = R |
T1T2 |
ln |
υ2 . |
(2.20) |
|||||
|
T2 −T1 |
υ1 |
3.КАТАЛИТИЧЕСКИЕ РЕАКЦИИ
3.1.Основные понятия
Катализаторы — вещества, изменяющие скорость реакции и остающиеся к концу реакции химически неизменными.
Явление изменения скорости реакции под действием таких веществ называется катализом.
Реакции, протекающие под действием катализаторов, называют-
ся каталитическими реакциями.
Реакции, в которых катализатором является продукт реакции,
называются автокаталитическими.
Важным свойством катализаторов является селективность (избирательность) их действия, проявляющаяся в увеличении скорости только определенной из нескольких возможных реакций.
Вещества, малые примеси которых могут сильно снижать или полностью подавлять активность катализатора, называются катали-
тическими ядами.
Промоторы – вещества, которые увеличивают активность катализаторов, хотя сами таковыми не являются.
По фазовому принципу различают гомогенный и гетерогенный катализ.
25
3.2. Сущность каталитического действия
Катализ обусловлен промежуточным химическим взаимодействием реагирующих веществ с катализатором, в результате которого открывается новый реакционный путь. Ускорение процессов с помощью катализаторов достигается за счет того, что появляются новые механизмы, при которых медленные стадии заменяются более быстрыми.
Реакция превращения веществ А и В в вещество АВ с участием катализатора К осуществляется по следующей схеме:
A + K → AK
АК + В → АВ + К
————————————-
А + В → АВ.
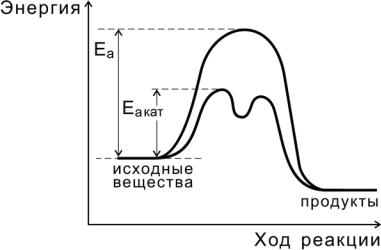
Независимо от механизма действия роль катализатора с точки зрения энергетики реакции сводится, как показано на рис. 9, к снижению энергии активации (Еакат < Еа ), за счет чего увеличивается константа скорости реакции.
Рис.9. Реакция с участием катализатора
26
Катализатор может также способствовать необходимой для взаимодействия молекул ориентации.
Катализатор не влияет на константу химического равновесия и не смещает положение химического равновесия.
Энергия активации прямой и обратной реакций при введении катализатора уменьшается на одинаковую величину.
Катализатор ускоряет прямую и обратную реакции, т.е. сокращает время достижения равновесия при подходе к нему как со стороны исходных веществ, так и со стороны продуктов.
3.3. Гомогенный катализ
Гомогенным называют катализ, при котором катализатор и реагирующие вещества находятся в одной фазе (газовой или жидкой).
Примером гомогенного газофазного каталитического процесса может служить окисление диоксида серы SO2 до триоксида SO3. Без катализатора диоксид серы очень медленно окисляется кислородом. При производстве серной кислоты камерным способом процесс окисления диоксида серы до триоксида катализируется оксидом азота (II), который открывает для реакции новый путь, не включающий медленной стадии взаимодействия диоксида серы с молекулярным кислородом
2 SO2 (г) + О2 (г) NO( Г ) →2 SO3 (г).
Катализатор NO вступает в реакцию с кислородом О2 , образуя промежуточный продукт NO2,
2NO (г) + O2 (г) = 2NO2(г) .
NO2 затем реагирует с SO2 по реакции
2SO2 (г) + 2NO2 (г) = 2SO3 (г) + 2NO (г),
27
в результате которой получается конечный продукт и выделяется катализатор в химически неизменном виде и первоначальном количестве.
К преимуществам гомогенного катализа можно отнести высокую эффективность действия катализаторов, так как реакция идет во всем объеме сосуда. Но практическое выделение продуктов из реакционной смеси может быть затруднено.
3.4. Гетерогенный катализ
Гетерогенным называют катализ, при котором катализатор и реагирующие вещества находятся в разных фазах.
Процесс идет на границе раздела фаз. Обычно катализатор представляет собой твердое вещество, а реагенты находятся в газе или жидкости.
Механизмы действия гетерогенных катализаторов включают в себя следующие основные стадии:
1)движение реагирующих веществ к поверхности катализатора;
2)адсорбцию реагентов поверхностью катализатора;
3)взаимодействие реагентов на поверхности;
4)десорбцию продуктов реакции с освобождением поверхности катализатора;
5)отвод продуктов реакции из реакционной зоны.
Взависимости от условий проведения процесса и его особенностей лимитирующей может оказаться любая из этих стадий.
Адсорбция может способствовать разрыхлению и поляризации определенных химических связей, активировать реагирующие молекулы, обеспечивая на поверхности катализатора их благоприятную взаимную ориентацию в течение времени, необходимого для взаимодействия.
Активность гетерогенного катализатора зависит от величины и свойств его поверхности. Количество активных центров (участков, на которых обеспечиваются оптимальные условия реакции) определяет-
28
ся составом поверхностного слоя, способом приготовления катализатора и обработки его поверхности. Обычно применяют тонко измельченные порошки, пористые структуры с высокоразвитой поверхностью, в том числе пористые носители с нанесенным слоем катализатора.
Во многих случаях гетерогенный катализ протекает с помощью переходных металлов и их соединений (Pt, Pd, Rh, Fe, Ni, CuO, V2O5, NiO, Fe2O3, Cr2O3 и др.).
Примерами гетерогенного катализа являются вышерассмотренная реакция окисления диоксида серы SO2 до триоксида SO3, но уже в присутствии твердого катализатора V2O5 или Pt
|
2SO2(г) + O2(г) |
V O , Pt |
|
|
2 5 → 2SO3(г) |
||
|
или реакция синтеза аммиака |
||
|
N2 (г) + 3H2 (г) |
Fe, V |
2 NH3 (г). |
|
→ |
Гетерогенный катализ удобен тем, что катализатор не смешивается с реагентами, поэтому не возникает проблемы отделения его от продуктов реакции. Но с течением времени активная поверхность твердых катализаторов может измениться.
4.ХИМИЧЕСКОЕ РАВНОВЕСИЕ
4.1.Состояние равновесия
Реакции, протекающие при одних и тех же условиях одновременно в противоположных направлениях, называются обратимыми.
Рассмотрим простую обратимую реакцию, которая протекает в закрытой системе
A + B ↔ C + D.
Скорость прямой реакции описывается уравнением
υпр = kпр [A][B] ,
29
где υпр – скорость прямой реакции; kпр – константа скорости прямой
реакции.
С течением времени концентрации реагентов А и В уменьша-
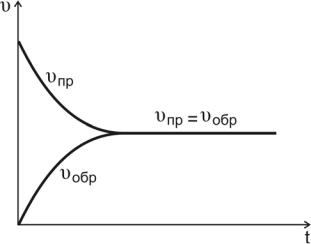
ются, скорость реакции снижается (рис.10, кривая υпр ).
Рис.10. Изменение скоростей прямой и обратной реакций во времени
Реакция между А и В приводит к образованию веществ C и D, молекулы которых при столкновениях могут вновь дать вещества А и В.
Скорость обратной реакции описывается уравнением
υобр = kобр[C][D],
где υобр – скорость обратной реакции; kобр – константа скорости об-
ратной реакции.
По мере того как концентрации веществ C и D возрастают, скорость обратной реакции увеличивается (рис.10, кривая υобр ).
В какой-то момент времени скорости прямой и обратной реакций становятся равными
30

υпр = υобр.
Такое состояние системы называется состоянием равновесия.
В состоянии равновесия концентрации всех его участников перестают меняться во времени. Такие концентрации называются
равновесными.
Химическое равновесие – это динамическое равновесие. Неизменность концентраций веществ, присутствующих в закрытой системе, есть следствие непрерывно идущих химических процессов. Скорости прямой и обратной реакций не равны нулю, а нулю равна наблюдаемая скорость процесса.
Равенство скоростей прямой и обратной реакций – это кинетическое условие химического равновесия.
4.2. Константа равновесия
При равенстве скоростей прямой и обратной реакций
υпр = υобр
справедливо равенство
kпр[A][B] = kобр[C][D],
где [A], [B], [С], [D] – равновесные концентрации веществ.
Поскольку константы скоростей не зависят от концентраций, равенство можно записать иначе:
kпр = [C][D] . kобр [A][B]
Отношение констант скоростей прямой и обратной реакций (kпр/kобр ) называют константой химического равновесия:
|
kпр |
[C][D] |
(4.1) |
||||
|
Kc |
= |
= |
[A][B] |
. |
||
|
kобр |
||||||
|
31 |
[CO]
Рассмотрим сложную реакцию
aA + bB ↔ cC + dD
Любую сложную химическую реакцию можно представить в виде ряда простых реакций. Для каждой из простых реакций можно записать кинетическое уравнение прямой и обратной реакций и соответствующие им выражения для констант равновесия. Константа равновесия сложной реакции равна произведению констант равновесия простых реакций, описывающих ее механизм
Kc = K1 K2 K3 KKi .
Поэтому в суммарное выражение для константы равновесия равновесные концентрации войдут в степенях их стехиометрических коэффициентов
|
с |
d |
(4.2) |
||
|
Kc |
= |
[C]a |
[D]b . |
|
|
[A] |
[B] |
В выражение константы равновесия гетерогенной реакции входят только концентрации веществ, находящихся в жидкой или газообразной фазе.
Концентрации твердых веществ не входят в выражение константы равновесия гетерогенной реакции.
Например, выражение для константы равновесия следующей реакции
СО2 (г) + С(тв) ↔ 2СО(г)
записывается так:
2
Kc = [CO2 ] .
Уравнение константы равновесия показывает, что в условиях равновесия концентрации всех веществ, участвующих в реакции, связаны между собой. Численное значение константы равновесия определяет, каким должно быть соотношение концентраций всех реагирующих веществ при равновесии.
32
Изменение концентрации любого из этих веществ влечет за собой изменение концентраций всех остальных веществ. В итоге устанавливаются новые равновесные концентрации, но соотношение между ними вновь соответствует константе равновесия.
Величина константы равновесия зависит от природы реагирующих веществ и температуры.
Константа равновесия, выраженная через молярные концентрации реагирующих веществ Kc и константа равновесия, выраженная
через равновесные парциальные давления Kp (см. «Основы химиче-
ской термодинамики»), связаны между собой соотношениями
K p = Kc (RT ) ν ;
|
Kc = |
K p |
, |
||
|
(RT ) |
ν |
|||
где Δν — изменение числа газообразных молей в реакции. Стандартное изменение энергии Гиббса равно
GTo = −RT lnKp ,
а также
GTo = Ho −T So.
После приравнивания правых частей уравнений
− RT lnKp = Ho −T So
или
|
Ho |
So |
(4.3) |
|||||
|
lnK |
p |
= − |
+ |
. |
|||
|
RT |
R |
||||||
Уравнение (4.3) не только устанавливает вид зависимости константы от температуры, но и показывает, что константа определяется природой реагирующих веществ.
Константа равновесия не зависит от концентраций реагентов (как и константа скорости реакции), механизма реакции, энергии акти-
вации, от присутствия катализаторов. Смена механизма, например,
33
при введении катализатора не влияет на численное значение константы равновесия, но может изменить скорость достижения равновесного состояния.
4.3. Расчет равновесного состава продуктов химической реакции
Зная величины констант равновесия при данных условиях и используя стехиометрические соотношения реакции (закон сохранения массы), рассчитывают равновесный состав продуктов по следующей схеме.
1.Пишут уравнение реакции.
2.Пишут под формулами уравнения начальные концентрации исходных веществ (в моль/л). Если начальные концентрации продуктов реакции не оговариваются в условии задачи, они обычно принимаются равными нулю.
А + b В ↔ c С + D
|
Начальное |
[А]0 |
[В]0 |
[С]0 |
0 |
|
состояние |
||||
|
Число молей |
1 |
b |
c |
1 |
|
по уравнению |
||||
|
Изменение |
x |
b x |
c x |
x |
|
концентраций |
||||
|
Равновесное |
[А]0 — x |
[В]0 – bx |
[С]0 + c x |
x |
|
состояние |
3. Принимают, что в ходе реакции до состояния равновесия прореагировало x моль/л какого-либо вещества. Обычно за x принимают изменение концентрации того реагента, стехиометрический коэффициент при котором в уравнении реакции наименьший, чтобы из-
34

бежать дробных коэффициентов при неизвестном x. Например, прореагировало x моль/л вещества А.
4.По уравнению реакции определяют изменение концентраций других веществ.
5.Определяют равновесные концентрации веществ. При протекании реакции в прямом направлении до состояния равновесия происходит уменьшение концентраций исходных веществ и увеличение концентраций продуктов реакции.
6.Пишут выражение закона действующих масс. Подставляют в него найденные значения равновесных концентраций.
[C]с[D] Kc = [A][B]b ,
Kc = ([C]0 + cx)c • (x) b . ([A]0 — x) • ([B]0 — bx)
7. Решают уравнение с одним неизвестным. При этом учитывают, что отрицательный корень не имеет физического смысла, и убыль концентрации исходного вещества не может быть больше величины самой концентрации (начальная концентрация исходного вещества не может быть меньше его остаточной равновесной концентрации).
8. Находят равновесные концентрации.
[А] = [А]0— x; [B] = [B]0 — b x; [C] = [С]0 + cx; [D] = x.
Приведенная схема расчета может быть применена также для определения исходных (начальных) молярных концентраций, если известны равновесные концентрации реагентов.
35

4.4. Смещение химического равновесия. Принцип Ле Шателье
Истинное химическое равновесие является динамическим и подвижным: изменение внешних условий (температуры, давления, концентраций реагирующих веществ) ведет к смещению равновесия в сторону прямой или обратной реакции. Характер влияния внешних факторов на равновесные системы выражает принцип Ле Шателье.
Если на систему, находящуюся в состоянии равновесия, оказать внешнее воздействие, то смещение равновесия происходит в сторону той реакции (прямой или обратной), которая ослабляет эффект внешнего воздействия.
Равновесное состояние в системе
H2 (г) + I2 (г) → 2 HI (г)
характеризуется (для одной и той же температуры) константой равновесия
Kc = [H[H]I][2 ] .
2 I2
Если, например, в систему добавить водород, т.е. увеличить его концентрацию, то скорость прямой реакции увеличится (в соответствии с законом действующих масс)
υпр = kпр [H2] [I 2], υпр > υобр ,
равновесие сместится вправо. Концентрация йодоводорода будет увеличиваться, а концентрация водорода и йода будет уменьшаться. Процесс будет протекать до тех пор, пока не установится новое равновесие. Новые равновесные концентрации всех компонентов будут другими, но соотношение между ними, определяемое константой равновесия, останется постоянным.
36
Если в систему ввести дополнительное количество йодоводорода, то скорость обратной реакции увеличится
υобр = kобр [HI] 2 , υобр > υпр ,
равновесие сместится влево.
Удаление из системы продуктов (или продукта) реакции ведет к смещению равновесия в сторону прямой реакции, а уменьшение концентрации исходных (или исходного) веществ приводит к сдвигу равновесия в направлении обратной реакции.
4.4.2. Изменение давления
Повышение давления (уменьшение общего объема) вызывает смещение равновесия в направлении уменьшения общего количества молей газообразных веществ, т.е. в направлении, приводящем к понижению давления.
При уменьшении давления (увеличении общего объема) равновесие смещается в сторону увеличения количества молей газообразных веществ, т.е. в направлении, приводящем к возрастанию давления.
Рассмотрим, в каком направлении сместится равновесие в сис-
теме
CO (г) + Cl2 (г) ↔ COCl2 (г),
если при неизменной температуре увеличить давление путем уменьшения объема газовой смеси?
В реакцию вступают 2 моля, а образуется 1 моль газообразных веществ. Прямая реакция при постоянном объеме сопровождается уменьшением давления. Если увеличить общее давление в системе, то согласно принципу Ле Шателье равновесие сместится в сторону прямой реакции.
Это можно доказать расчетами. Скорость прямой реакции рав-
на
37
υпр = kпр [СО][Сl2],
скорость обратной реакции равна
υобр = kобр [COCl2].
При повышении давления объем системы уменьшился, например, в 3 раза. Тогда концентрации всех реагентов увеличатся в 3 раза. При этом скорость прямой реакции увеличивается в 9 раз:
|
υ |
= k |
пр |
(3 [CO]) (3 [Cl2]) = k |
пр |
32 [CO][Cl2] = 9 υ . |
|
пр |
пр |
Скорость обратной реакции увеличивается только в 3 раза:
υобр = kобр (3[СОCl2]) = 3 kобр [СОCl2] = 3 υобр .
Таким образом, равновесие этой реакции будет смещаться в сторону накопления СОCl2 в системе до тех пор, пока не установится вновь состояние химического равновесия.
Для реакций, протекающих без изменения числа молей газообразных веществ, изменение давления (или общего объема) не влияет на химическое равновесие и равновесный состав продуктов.
Для реакции
H2 (г) + I2 (г) ↔ 2 HI (г)
количество молей газообразных веществ слева и справа от знака равновесия равно. При изменении давления скорости прямой и обратной реакций изменяются одинаково, а их отношение будет оставаться неизменным. В этом случае изменение давления не влияет на положение равновесия.
Рассмотрим влияние разбавления реагирующей смеси инерт-
ным газом на химическое равновесие.
1. Если разбавление ведется при постоянных давлении и температуре (изобарно-изотермический процесс), объем системы при накачивании инертного газа увеличивается (он пропорционален количест-
38

nRT
ву вещества n газов, V = p . Следовательно, молярные концентра-
ции Ci = nVi и парциальные давления pi = nni p исходных веществ и
продуктов реакции уменьшаются (ni ,ni‘ = const ;ni – число молей i — го исходного вещества, ni‘ – число молей i — го продукта реакции). Создается эффект уменьшения общего давления, ведущий к смещению равновесия в соответствующем направлении.
2. Если разбавление осуществляется при постоянных объеме и температуре (изохорно-изотермический процесс), то при накачивании инертного газа, например, в автоклав, общее давление возрастает пропорционально увеличению количества вещества газов в системе
|
p = nRT |
. При |
n |
,n‘ = const |
молярные концентрации |
C |
i |
= |
ni |
и парци- |
|
|
V |
||||||||||
|
V |
i |
i |
||||||||
|
альные давления pi = Ci RT |
исходных веществ и продуктов сохраня- |
ются постоянными. В этом случае разбавление инертным газом не влияет на химическое равновесие.
4.4.3. Влияние температуры
|
Зависимость константы равновесия от температуры |
Kp = f (T ) |
|||||||||||||||||
|
выражается уравнением |
||||||||||||||||||
|
lnK |
p |
= |
− |
Ho 1 |
+ |
So |
, или |
lnK |
p |
= |
A |
+ B , |
(4.4) |
|||||
|
T |
||||||||||||||||||
|
R Т |
R |
|||||||||||||||||
|
где A = − |
Ho |
; B = |
So |
. |
||||||||||||||
|
R |
||||||||||||||||||
|
R |
Выражение (4.4) представляет собой уравнение прямой в коорди-
натах T1 —ln Kp , тангенс угла наклона которой к оси абсцисс
39
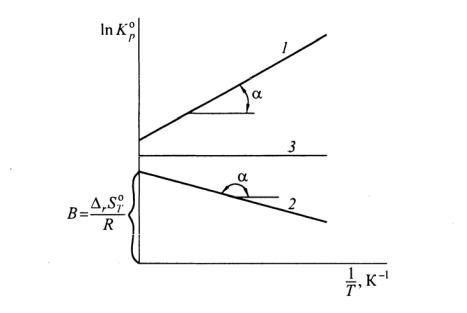
|
tgα = A = − |
Ho |
, а отрезок, отсекаемый на оси ординат, |
B = |
So |
|
|
R |
|||||
|
R |
|||||
|
(рис. 11). |
|||||
Рис. 11. Зависимость логарифма константы равновесия от обратной абсолютной температуры для разных типов реакции:
1 – экзотермическая ( H o< 0); 2 – эндотермическая ( Ho> 0); 3 – реакция с нулевым тепловым эффектом ( Ho= 0)
Для экзотермической реакции ( Ho< 0, tgα> 0) угол наклона прямой к оси абсцисс положителен, для эндотермических процессов
|
( Ho> 0, |
tgα < 0) отрицателен, для реакций с нулевым тепловым эф- |
|
фектом ( |
Ho= 0, tgα= 0) равен 0 (рис. 11, прямые 1, 2, 3 соответст- |
|
венно). |
1. Для экзотермических процессов Ho< 0 при увеличении тем-
пературы значения Kp уменьшаются, что соответствует смещению
равновесия в сторону обратной (эндотермической) реакции. Например, для реакции синтеза аммиака из азота и водорода,
N2(г) + 3H2 (г) ↔ 2NH3(г),
40
которая является экзотермической ( Ho< 0), первое слагаемое в уравнении (4.4) будет положительным. С повышением температуры его абсолютная величина будет уменьшаться. Это приведет к умень-
|
шению K |
p |
независимо от знака So . |
Уменьшение Kp означает, что в выражении константы равнове-
сия числитель (концентрации продуктов реакции) уменьшается, а знаменатель (концентрации исходных веществ) увеличивается.
Равновесие смещается в сторону обратного эндотермического процесса разложения аммиака.
2. Для эндотермических процессов Ho> 0 при увеличении тем-
пературы значения Kp увеличиваются, что соответствует смещению равновесия в сторону прямой (экзотермической) реакции.
|
Например, в реакции |
|
|
N2O4 (г) ↔ 2 NO2 (г), |
H o = 57,4 кДж. |
Ho> 0, т.е. прямая реакция — эндотермическая. Следовательно, первое слагаемое в уравнении (4.4) отрицательно. При увеличении температуры его абсолютная величина уменьшается и независимо от знака So константа увеличивается.
Увеличение Kp означает, что в выражении константы равнове-
сия числитель (концентрации продуктов реакции) увеличивается, а знаменатель (концентрации исходных веществ) уменьшается. Равновесие смещается в сторону прямой реакции.
Зная знак Ho, можно сказать, в каком направлении будет изменяться константа равновесия при изменении температуры.
Повышение температуры приводит к смещению равновесия в направлении реакции, сопровождающейся поглощением теплоты и охлаждением системы, т.е. в сторону эндотермической реакции.
При понижении температуры равновесие смещается в сторону экзотермической реакции.
41
Смесь, состоящая из частиц растворителя, растворяемого вещества и продуктов их взаимодействия, называется раствором. Это гомогенные структуры однородной консистенции, состоящие из двух либо нескольких компонентов. Решение задач на растворы – определение их концентрации, степени растворимости веществ, условий протекания растворообразующих процессов.
Задачи на растворы по химии
Чистое вещество либо смесь нескольких компонентов, попадая в растворитель, могут проявлять свойства:
- хорошей растворимости;
- малой растворимости;
- быть нерастворимыми.
При растворении в воде образуются многочисленные атомно-молекулярные связи. Их количество зависит от коэффициента растворимости – химической величины, которая рассчитывается путем деления массы растворяемого вещества на массу растворителя.
Кроме этого, в задачах могут присутствовать массовая доля вещества, растворенного в соответствующем растворителе.
Как решать задачи с процентными растворами
Растворы с выраженной концентрацией активного (растворенного) вещества носят название процентных. В задачах по химии ставятся цели определить содержание массы растворенного вещества, массы образовавшегося либо первоначального раствора, процентного содержания вещества до или после растворения.
Растворы, о которых идет речь в задачах по химии, обладают общими свойствами:
- они однородны;
- смешивание компонентов происходит за малый отрезок времени, как и изменение их концентрации;
- в результате смешивания двух (или более) растворов с различной концентрацией, происходит не только увеличение общей массы и объема раствора, но и усреднение процентного содержания растворенного вещества.
Поэтому существуют общие принципы их решения. Так, увеличение концентрации происходит в результате упаривания (испарения растворителя), а уменьшение – разбавления. В результате смешения может наблюдаться как увеличение, так и уменьшение, в зависимости от конкретных условий задачи.
В любом случае характеристики начального и конечного продуктов будут различаться, поэтому важно, данные в условии сведения не перепутать. Для этого применяется их нумерация.
Чтобы грамотно составить алгоритм решения, часто бывает полезно использовать уравнение химической реакции относительно активного вещества либо кислоты.
Концентрация растворов и способы ее выражения
На бытовом уровне понятие концентрации раствора выражается в отношении массы растворенного вещества к массе раствора, выраженном в процентах. Однако правомерно более широкое определение, охватывающее различные способы выражения концентрации.
Концентрация раствора – количественный показатель состава активного вещества в растворе, выраженное в определенных единицах и заключенное в единице массы или объема. Выражается в долях, процентах, массовых долях, молярности, мольных долях, титрах. Из них чаще применяются молярность и мольная доля.
1. О массовой доле ((omega)) идет речь в задачах, когда можно составить соотношение масс растворенного компонента и всего раствора. Для ее выражения существует формула:
(omega=M_{в-ва}div M_{р-ра})
Выражается она в процентах либо долевых частях единицы.
2. Молярность (по-другому – молярная концентрация) или (С) показывает сколько молей растворяемого компонента содержится в литре раствора. Ее формула имеет вид:
(С=ndiv V)
где (n) – это растворенное вещество в молях. Исходя из его значения, раствор может быть одномолярным (содержит 1 моль в 1 литре), децимолярным (0,1 моля в 1 л), сантимолярным (0,01 моль) и т.д.
3. Концентрация моляльная (обозначается (С_х)) – моляльность – показатель количества (n) молей растворенного компонента в 1 кг растворителя ((M_{р-ля})).
(C_x=ndiv M_{р-ля})
4. Для определения содержания (в граммах) вещества в 1 л раствора применяется понятие «титр» ((Т)).
(T=M_{в-ва}div V_{р-ра})
5. Под растворимостью ((S)) понимают максимальную массу растворяемого вещества, способного раствориться в 100 г растворителя:
(S=(M_{в-ва}div M_{р-ля})times100 {})
6. Коэффициент растворимости ((K_s)) – показатель, который определяется отношением массы вещества к массе растворителя при условии получения насыщенного раствора при обозначенной температуре:
(K_s=M_{в-ва}div M_{р-ля})
Решение задач на упаривание растворов
Выпаривание раствора происходит в результате испарения воды, что ведет за собой уменьшение общего объема и массы. В то же время масса растворенного вещества остается без изменений. Существуют случаи, когда, кроме растворителя, испаряется растворенное вещество, если оно обладает повышенной летучестью.
Пример. Водный раствор аммиака
Рассмотрим пример решения задачи на упаривание.
Условие: В наличии 800 г раствора с 15%-ной концентрацией определенного вещества. Нужно увеличить его массовую долю на 5%. Сколько г воды должно испариться?
Этапы решения:
- Какова масса вещества в первичном растворе?
(M_в=omega_вtimes M_р=0,15×800=120)г, где (M_в) — масса вещества, (M_р) — масса раствора
Найденное значение останется постоянным, поскольку при выпаривании изменения массы растворенного вещества не происходит. Значит M’=120г
2. (M_р=M_вdivomega_в= 120÷0.2=600)г
3. Теперь можно найти массу испаренной воды:
(M{исп;в}=M_р-M’=800-600=200)г
Решение задач на разбавление растворов
В результате процесса разбавления масса того вещества, которое растворено, не меняется в отличие от массы всего раствора и растворителя.
Задача
Масса имеющегося раствора NaCl 200г, его концентрация – 15%. К раствору добавлено 40г воды. Определить массовую долю NaCl в конце реакции.
Решение
1. Определение массы раствора в конце процесса:
(M’=M_{р-ра}+M_{добH2O}=240)г
2. Определение массы NaCl в начале процесса:
(M_{NaCl}=(omega_{NaCl}times M_р)div100%=15%times200гdiv100%=30 {})г
В конечном растворе (M’_ {NaCl}=M_{NaCl})
3. Определение массовой доли NaCl в конце процесса:
(omega’_{NaCl}=M_{NaCl}div M’_рtimes100%=12,5%)
Решение задач на концентрирование растворов
Повышение концентрации происходит при добавлении вещества в раствор. При этом конечная масса растворенного вещества равна сумме первоначального содержимого и того, который добавлен.
Задача. Имеется 180 г раствора с 8%-ной концентрацией соли (формула NaCl). В этот раствор всыпали еще 20 г поваренной соли. Какая массовая доля NaCl получилась в конце реакции?
Решение
1. Определение окончательной массы раствора:
(M’_р=M_р+M_{доб}=200)г
2. Определение конечной массы NaCl:
M’=M+Mдоб
Следовательно, нужно найти (M) – массу в начале процесса.
(M=(omega_{NaCl}times M_р)÷100%=14,4)г
Тогда (M’=14,4г+20г=34,4)г
3. Определение массовой доли NaCl в конечном продукте:
(omega’=M’_{NaCl}div M’_рtimes100%=17,2%)
Решение задач на смешение растворов
Смешение растворов с различной концентрацией растворенного вещества происходит с соблюдением «конверта Пирсона». Это – диагональная модель, при которой нельзя складывать массовые доли, а можно – лишь массы растворенных компонентов и растворов.
Задача
Дано два раствора с массами (M) и (M_1). Массовые доли растворенного вещества обозначим соответственно (ω) и (ω_1). В конечном продукте аналогичная величина – (ω_3). Необходимо приготовить третий раствор с отличной от имеющихся концентраций.
Решение
1. Определение общей массы растворенного вещества:
(M_1omega_1+M_2omega_2=omega_3(M_1+M_2))
2. Математические действия:
(M_1(omega_1-omega_3)=M_2=(omega_3-omega_2))
(M_1div M_2=(omega_3-omega_2)div(omega_1-omega_3))
Следовательно, согласно этому математическому выражению, и нужно взять соотношение растворов.
Задачи на определение процентной концентрации раствора
Задача 1
Какая процентная концентрация раствора (KNO_3), если нормальная равна (0,2) моль/л. Плотность равна (1) г/мл.
Решение:
1. Определение массы раствора объемом (1000) мл:
(M=rhotimes V=1times1000=1000)г
2. Составление и решение следующей пропорции:
(20,0)г (KNO_3) — (1000) г раствора
(Х_г) — (100) г раствора
(Х=2,02) г или (ω=2,02%)
Задача 2
Нужно приготовить (300) г 25%-ного раствора соли, имея 60%-ный и 10%-ный. Сколько нужно взять таких компонентов (m1 и m2)?
Для решения применим правило Креста:
1. Определение веса одной из 50-ти частей образуемого раствора:
(300div5=6)
2. Определение массы каждой части (m_1) и (m_2):
(m_1=6times15=90)
(m_2=6times35=210)
Задача 3
Используя 250г 45%-ного раствора соли, нужно понизить его концентрацию до 10%. Сколько воды необходимо использовать?
Концентрация соли в воде, используемой в качестве добавки, равна 0.
По методу креста образуется 45 частей раствора:
Решение
1. Масса одной части первичного раствора равна: (250div10=25)г
2. Определение массы воды, что необходима: (25times35=875)г
С целью проверки можно выполнить следующие действия:
1. Определение массы конечного продукта-раствора:
(875+25=1125г)
2. Для исходного раствора действует пропорция:
В 250г 40%-ного р-ра содержится Хг соли
в 100 г – 45г
Отсюда Х=112,5 г соли
3. Определение конечной концентрации раствора:
1125 г раствора – 112,5 соли
100г – Х
Х=10г или 10%
Следовательно, нужно взять 875 г воды.
Решать задачи на растворы – интересное занятие! Знание основных закономерностей будет полезно с теоретической и практической точек зрения. Однако бывают случаи, когда нужно быстро сдать контрольную либо перепроверить собственные решения. Тогда можно обратиться на сайт ФениксХелп.
Как решать задачи на концентрацию
Концентрация – это относительное содержание некоего компонента в более сложном составе. Как правило, концентрация того или иного вещества определяется в растворах или смесях различных веществ. В молекулярно-кинетической теории под концентрацией понимают количество молекул газа в единице объема.

Вам понадобится
- — растворы разных концентраций;
- — вода;
- — калькулятор.
Инструкция
Чтобы найти концентрацию вещества растворенного в воде, используйте понятие массовых долей этих веществ. Для этого сложите массу воды и вещества, которое в ней растворяется. После этого поделите массу растворяемого вещества на массу раствора, а результат умножьте на 100%. Получившееся число и будет концентрацией вещества в растворе. Например, если в 200 г воды, добавить 50 г поваренной соли, то поручим 240 г раствора. Поделите массу соли на массу раствора и умножьте на 100% (50∙100/240=20). Концентрация поваренной соли в растворе составляет 20%.
Чтобы решить задачу на изменение концентрации, начала найдите массу раствора, который должен быть при изменении концентрации при данной массе растворяемого вещества, которую найдите, используя данные о массе раствора. После этого вычислите, сколько растворителя в него нужно добавить. Например, концентрация сахара в 160 г раствора равна 20 %. Сколько нужно долить воды, чтобы концентрация раствора стала 10%? Определите массу сахара в растворе для этого массу раствора умножьте на концентрацию вещества и поделите на 100%, получите 160∙20/100=32 г. Для того, чтобы получить раствор концентрацией 10%, его общая масса должна быть 32∙100/10=320 г. Для получения 10% раствора долейте еще 320-160=160 г воды.
Поскольку концентрация молекул газа равна их количеству в единице объема, чтобы ее найти, поделите количество молекул газа N, на объем V, который они занимают n=N/V. Если такой возможности нет, то для определения концентрации воспользуйтесь одним из следствий из основного уравнения молекулярно-кинетической теории. Чтобы найти концентрацию молекул газа, поделите его давление на постоянную Больцмана k=1,38∙10^(-32) и температуру газа, измеренную в Кельвинах n=p/(k∙T).
Источники:
- как работать над концентрацией
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Концентрации исходных веществ
Равновесие гомогенной системы СО + Cl2 = COCl2 установилось при следующих концентрациях: [Cl2] = 0,4 моль/л; [CO]=0,1 моль/л; [COCl2] = 4 моль/л. Вычислите концентрации исходных веществ в начальный момент.
Решение задачи
Рассмотрим обратимую химическую реакцию:
Для нахождения концентрации исходных веществ учтем, что, если известно изменение концентрации одного из веществ, то по уравнению реакции можно найти изменения концентраций всех других веществ, составляющих реакционную систему.
Для нахождения концентрации исходных веществ CO и Cl2 учтем, что, согласно уравнению реакции, из 1 моль CO и 1 моль Cl2 образуется 1 моль COCl2. Поскольку по условию задачи в каждом литре системы образовалось 4 моль вещества COCl2, то при этом было израсходовано 4 моль CO и 4 моль Cl2. Таким образом, искомые концентрации исходных веществ равны:
C(CO) = 0,1 + 4 = 4,1 (моль/л);
C(Cl2) = 0,4 + 4 = 4,4 (моль/л).
Ответ:
концентрация исходного вещества CO 4,1 моль/л;
концентрация исходного вещества Cl2 4,4 моль/л.
