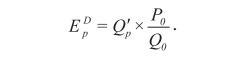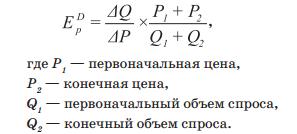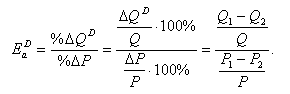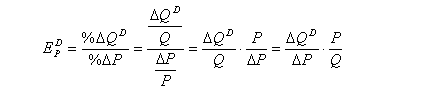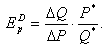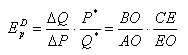Важную роль в
изучении возможных реакций со стороны
экономических агентов на изменения
цены играет понятие эластичности.
Эластичность
показывает степень реакции одной
величины на изменения другой, например,
изменение объема спроса в связи с
изменением цены. Такая реакция может
быть слабой или сильной, и, естественно,
будут менять свою форму кривые спроса
и предложения. Знакомство с аппаратом
эластичности начнем с эластичности
спроса.
Эластичность –
безразмерная величина, значение которой
не зависит от того, в каких единицах мы
измеряем цены, объем или другие величины.
|
Эластичность |
Различают
эластичность спроса по цене, эластичность
спроса по доходу и перекрестную
эластичность.
Эластичность
спроса по цене.
|
Эластичность |
На рис. 5.20 представлены
две кривые спроса, в первом случае
изменения цены с 7 до 4 руб. не привело к
резкому увеличению спроса (εd
= 0,3), во
втором случае спрос резко возрос (εd
= 1,22).
Спрос называется
неэластичным,
если при изменении цены объем спроса
изменяется незначительно. Спрос на
товар называют эластичным,
если при изменении цены объем спроса
существенно изменяется.
Итак, эластичность
спроса по цене (εрd)
показывает степень воздействия изменения
цены на изменение количества продукции,
на которую предъявлен спрос.
Эластичность
определяется как отношение процентного
изменения объема спроса к процентному
изменению цены.
.
Коэффициент
эластичности спроса по цене, как правило,
является отрицательной величиной, так
как с ростом цены объем спроса падает,
но в экономической теории принято
пользоваться абсолютным значением
этого показателя, поэтому знак «минус»
порой не ставят, но при расчетах принимают
во внимание.
|
Коэффициент |
Например,
εРd
=-2.
Это означает, что снижение цены (рост)
на 1% приводит к росту (снижению) объема
спроса на 2%.
Эластичности
взаимно обратных функций являются
взаимо-обратными величинами:
εРd
=1/
εdР
,
где εРd
—
коэффициент
эластичности спроса по цене,
εdР
—
коэффициент эластичности цены по спросу.
Поясним
вышеизложенное на примере. Пусть
эластичность спроса по цене равна -0,6
(снижение цены на 1% приведет к росту
объема спроса на 0,6%). Определим коэффициент
эластичности цены по спросу:
εdР=1/
εРd=
1/-0,6=
—1,66.
εdР
=
-1,66
– это означает, что рост объема спроса
на 1% приведет к сокращению цены на 1,66%
Эластичность
линейной функции спроса изменяется от
0 до -∞. Различают пять типов эластичности:
|
1) |
Р Р2 Р1 Q1 |
|
2) |
Р Р2 Р1 Q1 |
|
3) |
Р Р2 Р1 Q2 |
|
4) QD=a— |
Р Р2 εРd Р1 Q2 |
|
5) |
Р εРd= Р Q1 |
На степень
эластичности спроса влияет целый ряд
факторов:
1) наличие заменителей:
чем больше товаров–субститутов, тем
эластичней спрос на данный товар;
2) удельный вес
товара в бюджете потребителя: чем выше
удельный вес, тем выше ценовая эластичность;
3) размер дохода;
4) вид
товара: является ли товар предметом
роскоши (спрос на такие товары эластичен)
или предметом первой необходимости
(спрос на них неэластичен);
5) размер
запаса: чем больше запас, тем более
эластичен спрос;
6)
рассматриваемый период: в краткосрочном
периоде благо неэластично, в долгосрочном
— эластично. Например, в краткосрочном
периоде потребеление электроэнергии
неэластично, так как мы не можем быстро
отказаться от имеющихся электроприборов,
а в долго-срочном — довольно эластично,
поскольку мы будем заменять электро-емкие
приборы более экономичными.
Различают
точечную
и дуговую эластичность.
При небольших изменениях цены или объема
спроса или в случае вычисления эластичности
в конкретной ситуации (точке) используется
формула точечной эластичности, а при
значительных – дуговой эластичности.
Дуговая эластичность
– это показатель средней реакции объема
спроса на изменение цены товара на
некотором отрезке D1D2
(рис. 5.21). Ее определяют с учетом средней
точки.

Точечная
эластичность
характеризует относительное изменение
одного фактора, например объема спроса,
при бесконечно малом изменении другого,
например цены. Для ее расчета используют
слудеющие формулы:

или, взяв производную
от функции спроса:

где
Q’(P)
– производная функции спроса по цене,
Р1
– цена в конкретной точке, Q1
– объем спроса в конкретной точке.
Точечную эластичность
можно определить и графическим способом,
если провести касательную к кривой
спроса в искомой точке. Наклон кривой
спроса в любой точке определяется
значением тангенса угла касательной с
осью 0Х
(рис. 5.22). Ошибочно считают, что значение
точечной эластичности обратно
пропорционально тангенсу угла наклона
α, в формуле точечной эластичности
только значение (∆Q/∆P)
обратно пропорционально тангенсу угла
наклона α.
∆Q/∆P
= —tg
α,
тогда
tg
α =∆Р/∆Q.
Р
Р1
Наклон кривой
спроса будет постоянным на всем ее
протяжении и идентифицирован в виде
ценового коэффициента
b
(кривая спроса задается линейной функцией
QD
= a
— b∙P),
который является величиной обратной
наклону кривой спроса, т.е.
b
= 1/(∆P∕∆Q)=
∆Q
∕∆Р.
Подставим это
выражение в классическую формулу
точечной эластичности и получим:

Перекрестная
эластичность.
Спрос на товар
зависит также и от цен на другие товары.
|
Эластичность |
Коэффициент
перекрестной эластичности
спроса представляет собой отношение
изменения объема спроса на товар ί
к вызвавшему его изменению цены на товар
ј:
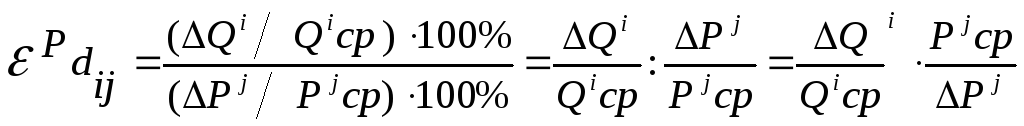
Различают
дуговую и точечную перекрестную
эластичность.
Дуговая
эластичность —
это показатель средней реакции объема
спроса одного товара на изменение цены
на другой товар на некотором отрезке.
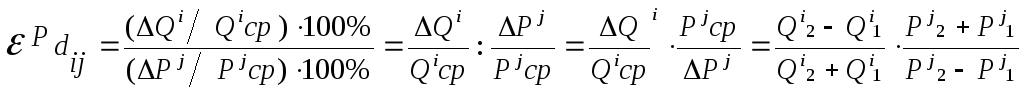
Точечная
эластичность
характеризует линейную зависимость
между ценой одного товара и объемом
спроса на другой. Для ее расчета используют
следующую формулу:
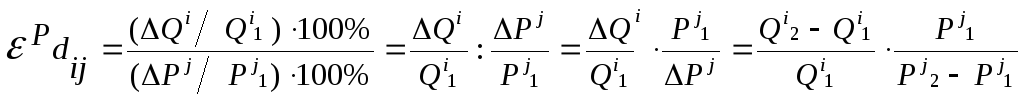
Коэффициент
перекрестной эластичности может быть
как положительной, так и отрицательной
величиной (рис. 5.23), он указывает на тип
взаимосвязи благ, то есть его абсолютное
значение отражает степень этой
взаимосвязи. Чем выше перекрестная
эластич-ность спроса, тем выше степень
заменяемости благ, чем меньше вели-чина
перекрестной эластичности, тем больше
взаимодополняемость благ.
Это важно для
разработки общей и ценовой с тратегии
организаций, поскольку следует принимать
во внимание не только возможность
конкуренции товаров-субститутов
(заменяемых товаров), но и наличие и
ценовые тенденции взаимодополняемых
товаров (например связаны между собой
рынок жилья и рынок строительных
материалов, рынок автомобилей и рынок
автомобильного топлива).
Блага
взаимозаменяющие (рис.
5.23 а): 0 <
εРdij
< ∞.
Коэффициент
перекрестной эластичности будет
положительной величиной и изменяться
в пределах от 0 до ∞. Это означает, что
при изменении цены на благо j
спрос на благо i
изменится в том же направлении. Например,
снижение цены на благо j
вызовет снижение спроса на благо i
и наоборот.
Взаимодополняемые
блага (рис.
5.23 б): εРdi
<
0.
Коэффициент
перекрестной эластичности будет
отрицательной величиной. Это означает,
что при изменении цены на благо j
спрос на благо i
изменяется
в противоположном направлении. Например,
снижение цены на благо j
вызовет
рост спроса на благо i,
и
наоборот.
Блага,
независящие друг от друга в потреблении
(рис. 5.23 в) имеют нулевую перерестную
эластичность, то есть рост цен на один
товар никак не связан ни с потребелнием,
ни с изменением спроса на другой товар.
Практическая
значимость эластичности спроса
состоит в том, что различные случаи
эластичности непосредственно влияют
на получаемую выручку производителем
(TR)
и расходы потребителей.
TR
=
P∙
Q,
где Р—
цена данного товара, Q
– количество купленного товара.
З
начение эластичности будет различным
в разных точках кривой (рис. 5.24).
Эластичность
линейной функции спроса изменяется от
0 (в точке пересечения кривой линейной
спроса и осью абсцисс) до ∞ (в точке
пересечения кривой линейной спроса и
осью ординат).
Если
спрос по цене эластичный
(εРd
>1),
то снижение цены вызовет рост выручки
(поскольку незначительное снижение
цены приведет к большему в процентном
выражении росту объема спроса). Рост
цены вызовет сокращение выручки
(поскольку незначительное повышение
цены приведет к большему в процентном
выражении сокращению объема спроса).
Если
спрос по цене неэластичен (εРd
<1),
то снижение цены приведет к падению
выручки. Рост цен вызовет рост выручки.
В средине
отрезка 0Q
получим единственную точку на линейной
кривой спроса с единичной эластичностью,
в которой выручка максимальна и неизменна
при любом изменении цены. В этом случае
повышение доходности и рентабельности
производства возможно за счет неценовых
факторов.
Соседние файлы в папке Микроэкономика Часть 1
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Татьяна Васильевна Болотова
Эксперт по предмету «Экономика»
Задать вопрос автору статьи
Классификация формул для расчета эластичности
Известно, что такие параметры как цена и объем спроса реагируют на изменения. Эта реакция на изменения отражается в таких законах как закон спроса и закон предложения. По таким законам можно судить об изменениях качественно. Для того чтобы можно было определить такие изменения на количественном уровне, используется индикатор эластичности спроса или рассчитывается эластичность.
Для этого используются формулы, с помощью которых можно получить намного больше информации о поведении потребителей и продавцов на рынке.
Итак, определить, как изменяется спрос от изменений цены можно с помощью следующих видов формул:
- эластичность спроса по цене;
- точечная;
- дуговая.
Первая формула представлена на рисунке ниже. Данная формула используется тогда, когда нужно рассчитать индикатор эластичности (Е) в относительном выражении.
С помощью такой формулы можно измерить следующее: как переменился объем спроса, если цена на какое-либо благо изменилась на 1 %.
Обратите внимание, что на изменение цен влияют следующие факторы:
- уровень необходимости, полезности товара для потребителей;
- доля заменителей на рынке;
- доля расходов на определенное благо в бюджете покупателей;
- фактор времени.
Точная формула расчета
Такая формула применяется в том случае, если изменения в цене незначительны. Тогда индикатор эластичности рассчитывается с помощью производной.
На рисунке ниже представлена формула расчета по точному методу расчета.
«Формулы эластичности спроса» 👇
Приблизительная формула расчета
Однако, если сдвиги в цене становятся значительными, то в таком случае применяется формула, представленная ниже.
Замечание 1
Эта формула применяется потому, что величины, на которую изменяется спрос и величины, на которую изменяется цена, становятся слишком разными. То есть изменения между начальной и, например, конечной ценой очень большие.
Поэтому лучше будет рассчитать дуговой индикатор эластичности. В таком случае эластичность будет определяться не в одной конкретной точке, как в предыдущей формуле, а в средней точке, как в формуле на рисунке выше.
Интерпретация результатов расчета по формулам
Обратите внимание, что в связи с законами спроса, цена и спрос будут иметь разнонаправленное изменение. По этой причине полученное число будет отрицательное. По отрицательному или положительному значению можно найти угол наклона спроса.
Однако, на практике часто применяется оценка с помощью абсолютного значения индикатора эластичности.
Самые распространенные индикаторы и их интерпретация представлены на рисунке ниже.
Для того, чтобы интерпретировать полученный результата значение берется по модулю, то есть без учета математического знака. По модулю отрицательность не учитывается.
Однако, при интерпретации расчетов в формулах существуют и крайние случаи. Рассмотрим их более подробно.
Выделяются следующие крайние случаи:
- эластичность нулевая;
- эластичность бесконечная.
В первом случае предполагается, что кривая спроса на графике будет строго вертикальной. А это значит, что изменения в объемах спроса будут равны 0 при разных ценах. То есть в таком случае спрос будет строго и абсолютно неэластичен. Пример, такой ситуации, это, например, необходимое лекарство, вода для человека в пустыне.
Во втором случае кривая спроса на графике будет в виде горизонтальной прямой. А это значит, что изменения объема спроса будут до бесконечности значимыми даже, если цена практически не будет меняться. То есть индикатор будет абсолютно эластичен.
Пример такой ситуации. Допустим, на рынке совершенной конкуренции фермер будет продавать зерно по определенной цене. При этом на данной территории нет разнообразия рынков сбыта. Тогда даже при незначительном росте цен потребители могут отказаться от покупки и приобретать товар у других продавцов дешевле. Однако, даже при незначительном снижении цен потребители могут значимо увеличить объем покупок.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
5.5. Эластичность спроса по цене: углубление анализа
Анализируя поведение потребителя, мы обосновали закон спроса. Если цена на товар растёт, то, ceteris paribus (при прочих равных условиях), величина спроса на этот товар на рынке уменьшается, и наоборот. Но вот на сколько? Это зависит от чувствительности спроса к изменению цены, то есть от ценовой эластичности спроса. Знание эластичности спроса по цене имеет большое практическое значение. В правильной оценке эластичности спроса заинтересованы и фирмы, и правительство.
Напомним, что для измерения эластичности
используется коэффициент эластичности
спроса (ED), который
в самом общем виде представляет собой отношение процентного изменение величины
спроса к процентному изменению цены:
(1)
Коэффициент эластичности
показывает, на сколько процентов
изменится спрос, если цена изменится на 1 %. Поскольку цена и величина спроса
изменяются (по закону спроса) в противоположном друг другу направлении,
постольку коэффициент эластичности имеет знак «минус» , который, впрочем,
экономисты по молчаливому соглашению часто опускают. К примеру, | Еd | для электроэнергии равняется 0,13 – это значит, что если тариф на электроэнергию
повысится на 1 % , то спрос на неё понизится на 0,13 %. Если тариф повысится на 10 %, то спрос
понизится на 1,3 % и т.д.
Напомним также, что в зависимости от
степени чувствительности спроса к изменению цены можно выделить пять видов
эластичности:
1. Эластичный
спрос. Покупатели чувствительны к изменению цены. Спрос в
процентном отношении изменяется больше, чем цена, то есть для эластичного спроса | Еd
| >
1,0;
2. Неэластичный
спрос. Покупатели нечувствительны к изменению цены. Спрос в
процентном отношении изменяется меньше, чем цена, то есть для эластичного спроса | Еd
| <
1,0;
3. Единичная
эластичность спроса. Спрос в процентном отношении
изменяется так же как цена, то есть для
этого вида спроса | Еd | =
1,0;
4. Совершенно
эластичный спрос. Покупатели гиперчувствительны к
изменению цены. Например, при ничтожно малом повышении цены спрос стремится к
бесконечно малой величине. Для этого вида спроса| Еd | =
∞. На графике кривая спроса представляет собой прямую линию параллельную
абсциссе;
5. Совершенно
неэластичный спрос. Покупатели абсолютно нечувствительны к
изменению цены. При любом процентном изменении цены величина спроса остаётся
неизменной. Для этого вида спроса | Еd
| = 0.
На графике кривая спроса представляет собой прямую линию параллельную
ординате.
Существуют два способа точного
измерения эластичности. Ценовую эластичность спроса можно определить: (1) в
некотором диапазоне изменения цены – на отрезке (дуге) кривой спроса. Этот
способ измерения называется дуговой
эластичностью; (2) для определённого уровня цены, то есть в некоторой точке
кривой спроса. Этот способ называется точечной
эластичностью.
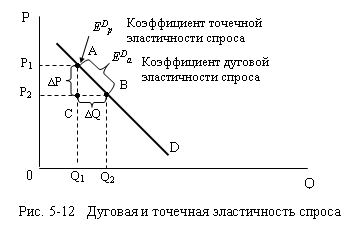
измеряется в ценовом диапазоне Р1
– Р2 на отрезке АВ
кривой спроса, а точечная – для уровня цены Р1 в точке А.
Выведем формулу для дуговой эластичности спроса.
Поскольку в приведенной выше формуле не ясно, какое
значение Q: Q1 или Q2, берётся
за базу, а это может сильно повлиять на результат измерения, экономисты
договорились брать среднее арифметическое значение. То есть, Q = (Q1 + Q2 /2. То же самое делается
по отношению к цене, выступающей в качестве базы: Р = (Р1 + Р2)/2. Тогда формула коэффициента
дуговой эластичности спроса по цене примет окончательный вид:
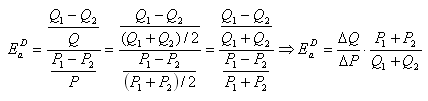
Дуговая эластичность спроса используется в случае
значительного изменения цены. Если же это изменение незначительно, то
целесообразно использовать точечную эластичность спроса. Коэффициент точечной
эластичности спроса легко выводится из формулы (2):
Посмотрим на рис. 5-12 и представим, что ∆P сжимается
так, что точка С приближается
вплотную к точке А. Тогда ∆Q также
сжимается и точка В стремится к точке
А как к своему пределу. Если мы
примем ∆P и, следовательно,
∆Q за
бесконечно малые величины, то получим измерение ценовой эластичности в точке А:
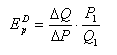
 Математическое приложение 5-2
Математическое приложение 5-2
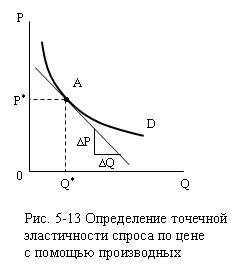
через производные. Предположим, требуется определить ЕDp в точке А кривой спроса на рис. 5-13:
Тогда
при бесконечно малом изменении Р
«скорость» изменения Q
будет dQ/dP и формула примет
вид:
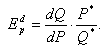
Коэффициент ценовой эластичности спроса
в точке можно определить по уравнению функции
спроса. Линейное уравнение имеет вид: QD = a – bP (например, QD = 10 – 2P). Коэффициент b показывает,
на сколько единиц изменяется величина спроса при изменении цены на 1 рубль (в
нашем примере b = — 2, что
означает, что каждый раз, когда цена изменяется на 1 рубль, величина спроса
изменяется в противоположном направлении на 2 единицы). То есть -b = -∆Q/∆Р = наклону
кривой спроса.
Тогда,
подставив b в уравнение (3) получим:
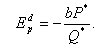
Пример.
Пусть функция спроса описывается
уравнением: QD
= 10 – 2P.
Определить ценовую эластичность спроса при Р* = 4.
Решение:
Подставим в уравнение (5) все данные, получим:
Измерение
точечной эластичности спроса геометрическим способом («правило РАРО»). Есть
простой способ измерения эластичности в любой точке кривой спроса с помощью
линейки. Этот способ известен как «правило РАРО» (PAPO rule).
Правило
РАРО гласит: чтобы
определить точечную эластичность нужно измерить расстояние от точки до
абсциссы, РА (point
– abscissa),
и
расстояние от точки до ординаты, РО (point – ordinate), а
затем отнести первое ко второму, то есть ЕD = РА/РО.
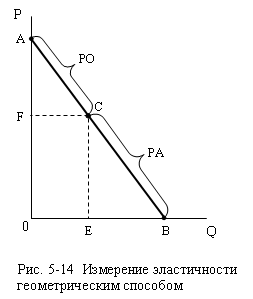
Выведем правило,
используя рис. 5-14. Определим эластичность в точке С.
Так как АОВ и СЕВ – подобные треугольники, то
и
Но (при пересечении сторон угла параллельными прямыми по
сторонам угла отсекаются пропорциональные отрезки).
И,
следовательно
СВ
– это расстояние от точки, в которой измеряется эластичность, до абсциссы (РА),
а СА – это расстояние от той же точки
до ординаты (РО).
На рис. 5-14 РА= 5,5
см., а РО = 4 см. Следовательно, ЕD=
5,5:4 = 1,375.
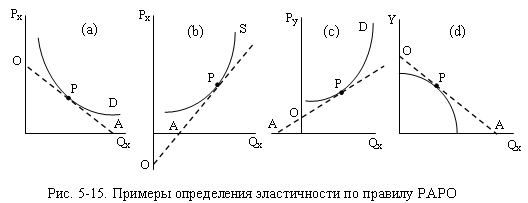
Правило РАРО универсально. Оно позволяет
определить эластичность спроса по цене, доходу, перекрёстную эластичность
спроса, эластичность предложения. Правило применимо и тогда, когда линии спроса
и предложения являются кривыми. В этом случае отрезки РА и РО находятся на
касательной, проведённой через интересующую нас точку на кривой спроса или
предложения (примеры приведены на рис. 5-15).
На рис. 5-15а спрос
в точке Р имеет единичную эластичность по цене (РА=РО). На рис. 5-15b ценовая
эластичность предложения в точке Р меньше единицы (PA<PO), то есть предложение
неэластично. На рис. 5-15с перекрёстная эластичность спроса на товар Х по цене
товара У больше единицы (PA>PO), то есть спрос эластичен. На
рис. 5-15d спрос на низший товар Х эластичен по доходу У (PA>PO).
Эластичность нельзя
отождествлять с наклоном кривой спроса (наклон линии представляет собой
отношение горизонтального изменения к вертикальному, то есть -∆Q/∆Р.
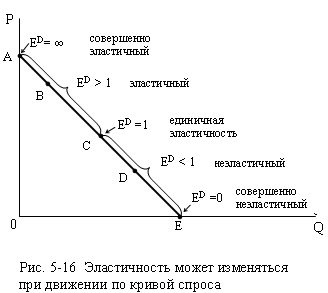
Рассмотрим рис. 5-16. В каждой точке кривой
спроса наклон одинаков. Поэтому в
формуле (5) — b является постоянной величиной. В то же время отношение P/Q при
движении по кривой спроса меняется. Поэтому эластичность в разных точках кривой
спроса будет разной. Применим «правило РАРО» для расчёта коэффициента
эластичности. В точке А эластичность
равна бесконечности (= АЕ/0). В точке В эластичность больше 1 ( = ВЕ/АВ).
В точке С, которая находится в середине кривой спроса эластичность равна единице (так как СЕ = СА, то СЕ/СА = 1). В точке D она меньше
единицы (= DE/DA). И
наконец, в Е эластичность равна 0 (= 0/AE).
1) горизонтальная кривая спроса (эластичность в каждой точке равна бесконечности);
2) вертикальная кривая спроса (в каждой точке эластичность равна нулю);
3) кривая спроса, имеющая форму равносторонней гиперболы;
В последнем случае кривая описывается уравнением обратной пропорциональности:
,
где
с – есть некоторая постоянная величина.
Применительно к функции спроса уравнение
выглядит:
Тогда, учитывая, что с – это коэффициент при цене, который мы раньше обозначали как b, получим:
Следовательно, кривая спроса, имеющая форму
равносторонней гиперболы, имеет единичную эластичность (в любой её точке
эластичность спроса по цене равна –1).
Почему эластичность спроса по цене для
разных товаров различна? Основные факторы, определяющие эластичность:
1. Наличие
доступных товаров-субститутов. Чем больше таких товаров, тем больше эффект
замещения при изменении цены данного товара и тем эластичнее спрос.
2. Доля
расходов на товар в бюджете потребителя. Чем она больше, тем больше эффект
дохода и тем эластичнее спрос. Это зависимость помогает понять, почему при
высоких ценах (в верхней части кривой спроса) спрос эластичен, а при низких
ценах (нижняя часть кривой спроса) неэластичен. Более высокая цена
означает большую долю в расходах
потребителя при фиксированном бюджете.
3. Направление
эффекта дохода. В случае нормальных товаров эффект дохода усиливает эффект замещения
и спрос становится эластичнее. Для низших товаров эффект дохода ослабляет
действие эффекта замещения и спрос поэтому менее эластичен.
4. Время,
прошедшее после изменения цены. Чем продолжительнее этот период, тем больше
возможности у потребителя найти замещающие товары и тем эластичнее спрос.
повышение средней цены на зерно в России в 2003 году с 2,5 тыс. до 4,5 тыс.руб. за тонну улучшило положение сельхозпроизводителей, увеличив их доходы. В то же время повышение платы за проезд в муниципальном транспорте города Томска в 2003 г. с 3,5 до 4,5 рублей привело к тому, что выручка у Трамвайно-троллейбусного управления значительно упала.
Поскольку выручка определяется как произведение цены товара на количество проданного товара (ТR = P·Q), то результат зависит от того будет ли процентное изменение количества
больше или меньше процентного изменения цены, то есть от ценовой эластичности
спроса. Так, если цена повысится на 10 %, а физический объём продаж вследствие
этого сократится на 20 % (эластичность спроса по цене равна 2,0 – спрос эластичен), то выручка уменьшится.
Общее правило таково: при эластичном спросе доходы (расходы)
изменяются в направлении противоположном изменению цены. При неэластичном
спросе доходы (расходы) изменяются в том же направлении, что и цена. В случае единичной эластичности доход не
изменяется.
Все возможные случаи отражены в таблице 5-1.
|
Эластичность |
Цена |
Цена |
|
Эластичный спрос (>1) |
TR падает |
TR растёт |
|
Единичная эластичность (=1) |
TR не меняется |
TR не меняется |
|
Неэластичный спрос (<1) |
TR растёт |
TR падает |
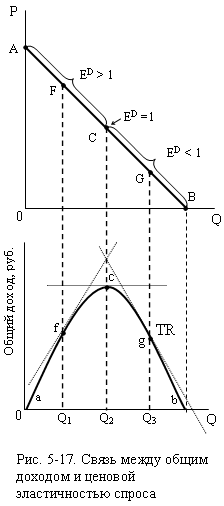
На рис.
5-17 показана связь между общим доходом (расходами) и ценовой эластичностью
спроса. Предположим, что цена товара всё время понижается, и мы движемся по
кривой спроса (на верхнем рисунке) вниз из точки А в точку В. На отрезке АС,
где спрос эластичен, снижение цены будет перекрываться ещё большим ростом (в
процентном отношении) величины спроса. Общий доход, следовательно, будет расти
(участок ас на нижнем рисунке). На
участке СА, где спрос неэластичен дальнейшее снижение цены вызывает уже меньший
рост (в процентном отношении) спроса, и доход падает (участок сb). В точке С, где
эластичный спрос переходит в неэластичный (эластичность равна единице) доход
перестаёт расти, достигая максимума при объёме Q2.
 Математическое приложение 5-3
Математическое приложение 5-3
Связь между ценовой эластичностью спроса и общим доходом можно определить с помощью методов предельного анализа.
Общий доход, TR = P∙Q. Следовательно,
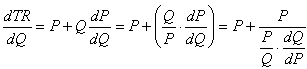
Так как ценовая эластичность спроса равна
(2)
то, подставив (2) в (1), получим:
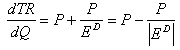
Таким образом, когда спрос эластичен, то есть │ED│ > 1, то
TR изменяется в том же направлении, что и Q, и в направлении противоположном Р (для нормальной, нисходящей кривой спроса).
Когда спрос имеет единичную эластичность, то есть │ED│ = 1, то
TR с изменением Q не меняется.
Когда спрос неэластичен, то есть │ED│ < 1, то
TR изменяется в направлении противоположном Q и в том же направлении что и Р (для нормальной кривой спроса).
Снова обратимся к рис. 5-17. Возьмём на кривой спроса точку F, в которой спрос эластичен. С понижением цены объём спроса будет расти. Изменение общего дохода, обусловленное бесконечно малым увеличением объёма продаж при уровне Q1, то есть dTR/dQ, показывается наклоном касательной к кривой общего дохода в точке f. Этот наклон положителен. Следовательно, общий доход будет увеличиваться.
При единичной эластичности спроса (точка С), наклон касательной к кривой общего дохода в точке с будет равен 0. Следовательно общий доход при объёме продаж Q2, не изменяется ни в сторону увеличения, ни в сторону уменьшения. Он достигает максимума.
Наконец, при неэластичном спросе, к примеру, в точке G, при снижении цены общий доход будет уменьшаться. Об этом говорит отрицательный наклон касательной к кривой общего дохода в точке g.
Основными понятиями экономики являются спрос и предложение, находящиеся в тесной зависимости от рыночных условий. Для понимания реакции потребителей на тот или иной продукт необходимо анализировать показатели эластичности – коэффициенты.
Процентная реакция ценового изменения дохода от реализации товаров на изменение предложения товара на рынке.
Факторы, влияющие на эластичность
- доступность товаров заменителей;
- изменение потребительских доходов;
- временной интервал воздержания от покупки товара.
Коэффициент эластичности предназначен для определения роста или понижения покупательского интереса в результате изменения цен на товары производителей.
K=ΔQ/ΔPK= Delta Q / Delta P,
где ΔQDelta Q – изменение величины реализованных товаров,
ΔPDelta P – изменение цен на реализованные товарные группы.
Значения коэффициента эластичности
- Высокое – незначительные изменения в товарных ценах, которые приводят к повышению предложения на товары или спроса на них (доступные, повседневные продукты в большом количестве на рынке);
- Низкое – резкое повышение цен приводит к необходимости отказа от покупки незначительной доли потребителей товаров (необходимые для ежедневного потребления товары).
Чем выше значение коэффициента эластичности, тем более чувствителен сбыт продукции к ценовым колебаниям.
Виды коэффициента эластичности
- Эластичность по цене необходима для определения зависимости объема продаж и рыночной цены. В результате расчета можно оценить снижение спроса от повышения цены группы товаров на 1%.
- Перекрестная эластичность позволяет оценить взаимное влияние разных товаров друг на друга, т.е. процент повышения цены одного товара в результате снижения спроса на другой. Для независимых товаров (субститутов) коэффициент стремится к 1. Для комплементарных (зависимых) товаров коэффициент меньше 0.
Сферы применения коэффициента эластичности
- анализ политики государства;
- определение дохода предприятий;
- оценка отраслевой стабильности;
- выбор инвестиционных проектов;
- прогнозирование торговли на международных рынках;
- оценки эффективности мероприятий по продвижению товаров.
Примеры решения задач
Пример 1
Найти коэффициент эластичности, если прогнозируется повышение цен на 10%, при понижении спроса на 5%.
Решение
По формуле эластичности
K=ΔQ/ΔP=(−5%)/(10%)=−0,5K= Delta Q / Delta P = (-5%)/(10%)=-0,5
Ответ: Коэффициент эластичности −0,5-0,5, спрос неэластичен по цене.
Пример 2
Определить эластичность спроса по цене, если в текущем месяце цена на товар составила 80 руб., в следующем цена увеличится до 85 руб., в результате чего будет продано не 1500 штук товара, а 1800 штук.
Решение
- Изменение цены (85−80)/80=0,0625=6,25%(85-80)/80 = 0,0625 = 6,25%
- Изменение спроса (1800−1500)/1500=0,2=20%(1800-1500)/1500 = 0,2 =20%
- Коэффициент эластичности
K=ΔQ/ΔP=(20%)/(6,25%)=3,2K= Delta Q / Delta P =(20%)/(6,25%)=3,2
Ответ: Спрос эластичен по цене и равен 3,23,2.
Расчет коэффициента эластичности позволяет оценить собственникам предприятий финансовые результаты в случае повышения или понижения цен, оценить собственные силы и позиции, предвидеть риск банкротства, а также смоделировать поведение инвесторов и поставщиков. Сторонние фирмы и государство могут оценить влияние косвенных мер на рыночные структуры, и целесообразность нововведений.