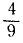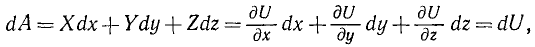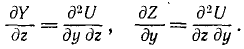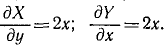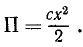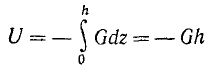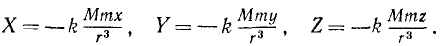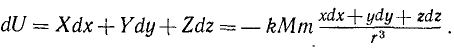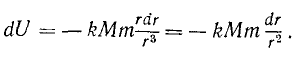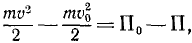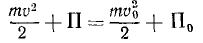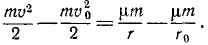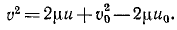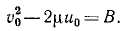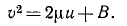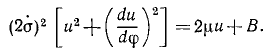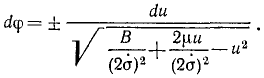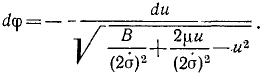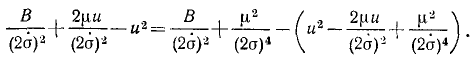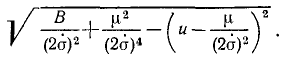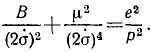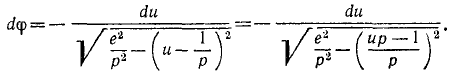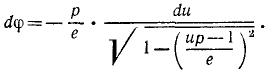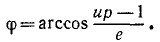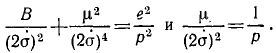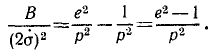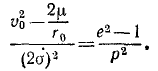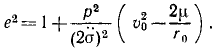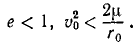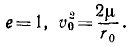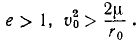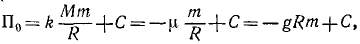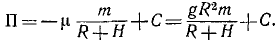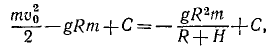Как найти изменение потенциальной энергии системы - Исправление недочетов и поиск решений вместе с Examum.ru

Однородным электрическим полем называют такое электрическое поле, вектор напряжённости которого не зависит от точки пространства ((vec{r(t)} =const)), где (vec{r(t)}) — радиус-вектор исследуемой точки.

Потенциальные и непотенциальные силы в электродинамике

Все силы можно разделить на потенциальные и непотенциальные.

Работа потенциальной силы зависит только от начального и конечного положения тела и от формы траектории не зависит. Сила Кулона является потенциальной.

Потенциальность кулоновских сил позволяет говорить о потенциальной энергии заряда в поле электрических сил. По определению потенциальной энергии полагается, что изменение потенциальной энергии при его переносе из точки (А) в точку (Б) в любом электрическом поле — это работа кулоновских сил при перемещении заряда между этими точками, взятая со знаком минус:
(A=-(E_Б-E_А)). ((1))

Энергия системы заряженных тел

Вокруг заряженного тела появляется электрическое поле, которое оказывает действие на другие заряды. Таким образом, система, состоящая из какого-либо набора заряженных тел, обладает потенциальной энергией, которую обычно называют кулоновской или электрической.

Изменение потенциальной энергии заряда в однородном электрическом поле

Рассмотрим изменение потенциальной энергии положительного заряда (q), если переместить его в однородном электрическом поле из точки (А) в точку (Б) по красной траектории (рис. (1)).

Рис. (1). Перемещение заряда в однородном поле

Она изменяется так же, как если бы заряд перемещался по прямой (чёрной) траектории, поскольку работа потенциальной силы зависит только от начальной и конечной точки траектории.

Сила, действующая на него, постоянна:
(vec{F}=q vec{E}). ((2))
Если ввести радиус-векторы начала и конца этой траектории (vec{r}_А) и (vec{r}_Б) соответственно, то перемещение этого заряда:
(vec{r}=(vec{r}_Б — vec{r}_А)). ((3))
Работу кулоновской силы можно записать как скалярное произведение силы на перемещение:
(A=vec{F}cdot {r}=q vec{E} (vec{r}_Б — vec{r}_А) ). ((4))
Выбрав за ноль потенциальной энергии начальную точку ((vec{r}_А)), перепишем формулу ((1)) в виде:

(A=-E_Б). ((5))

Из формулы ((4)) получим, что потенциальная энергия заряда, который расположен в точке с радиус-вектором (vec{r}_Б=vec{r}) в однородном электрическом поле, равна скалярному произведению радиус-вектора на вектор напряжённости электрического поля:
(E= -A=-q vec{E} cdot vec{r} ), ((6))
что в координатном виде может быть записано как:
(E=-q (E_x x+E_у y+E_z z).) ((7))

Энергия взаимодействия точечных зарядов

Для того чтобы найти энергию взаимодействия точечных зарядов, рассмотрим систему из двух положительных зарядов (q_1) и (q_2). Положим, что заряд (q_1) неподвижен.

Рассмотрим, какую работу совершит электрическое поле, которое создано зарядом (q_1), при перемещении заряда (q_2) из точки (А) в точку (Б) по красной траектории (рис. (2)).

Рис. (2). Перемещение заряда в поле точечного заряда

Как и в случае однородного электрического поля, вместо красной траектории будем рассматривать чёрную траекторию, где из точки (А) в точку (С) заряд перемещается вдоль линии, соединяющей эти два заряда, а из точки (С) в точку (Б) — по дуге окружности, центром которой является первый заряд.

В таком случае работа электрического поля на дуге (СБ) будет нулевой:

(A=vec{F} cdot vec{r}=|F|cdot |r|cos(pi/2)=0,) ((8))

поскольку сила Кулона всегда перпендикулярна перемещению. На участке (АС) сила Кулона сонаправлена с перемещением, а по модулю:
( F(r)=frac{k q_1q_2}{r^2}), ((9))
поэтому работу электрического поля можно рассчитать как:

(A=F(r_A)r+F(r_A+Delta r)Delta r+F(r_A+2Delta r) Delta r+F(r_A+3Delta r) Delta r+ldots +)

(+F(r_C-2Delta r) Delta r+ F(r_C-Delta r) r=sum limits_{r=r_A}^{r_C}F(r)Delta r=sum limits_{r=r_A}^{r_C} frac{k q_1 q_2}{r^2} cdot Delta r.) ((10))
В пределе, когда (Delta r) мало, эта сумма равна:
(A=-frac{k q_1 q_2}{r}). ((11))
Сравнивая формулы ((1)) и ((11)), получаем, что потенциальная энергия взаимодействия точечных зарядов:
(E=frac{k q_1q_2}{r}.) ((12))

Энергия системы (n) точечных зарядов

Если рассматривать систему, состоящую из (n) точечных зарядов, то её потенциальная энергия:
( E=frac{1}{2} sum limits_{i neq j} frac{k q_i q_j}{r_{i,j}}=frac{1}{2} left(frac{k q_1 q_2}{r_{12}}+frac{k q_2 q_1}{r_{21}}+frac{k q_2 q_3}{r_{23}}+frac{k q_3 q_2}{r_{32}}+ldots right),) ((13))
где (r_{i,j}) — это расстояние между (i)-м и (j)-м точечными зарядами, а множитель (frac{1}{2}) появляется из-за того, что в сумме дважды учитывается потенциальная энергия взаимодействия (i)-го и (j)-го точечных зарядов.

Свойство линий напряжённости электрического поля

Поскольку сила Кулона потенциальна, то, если перемещать заряд по любому замкнутому контуру, работа силы Кулона равна нулю.
Отсюда вытекает, что линия напряжённости электростатического поля не замкнута.
Докажем это от противного: предположим, что линия электрического поля замкнута (рис. (3)).

Рис. (3). Замкнутая линия электрического поля

Но тогда при перемещении положительного заряда по замкнутой линии электрического поля работа электрического поля будет равна:
(A=sum vec{F} cdot vec{r}). ((14))
Каждый член этой суммы положителен, поскольку сила всегда сонаправлена с перемещением (рис. (3)).

Мы пришли к противоречию. Следовательно, линии электрического поля не замкнуты.

Источники:

Рис. 1. Перемещение заряда в однородном поле. © ЯКласс.

Рис. 2. Перемещение заряда в поле точечного заряда. © ЯКласс.

Рис. 3. Замкнутая линия электрического поля. © ЯКласс.

Источник

1. Определение потенциальной энергии

В предыдущем параграфе мы говорили о работе, которую может совершить тело за счет уменьшения своей скорости, а теперь нас будет интересовать работа, которую может совершить тело или система тел вследствие изменения положения тел.

Рассмотрим примеры.

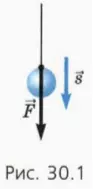
Работа поднятого груза. Когда подвешенный на тросе груз равномерно движется вниз, он действует на трос силой, направленной тоже вниз (рис. 30.1).

Эта сила обусловлена силой тяжести: она совершает работу, действуя на груз, а груз совершает работу, действуя на трос.

Итак, благодаря действию силы тяжести груз может совершить работу при движении вниз.

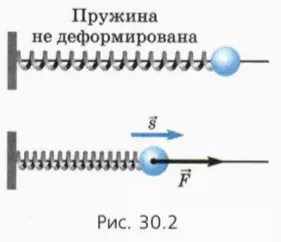
Работа пружины. Когда деформация пружины уменьшается, пружина действует на тело силой упругости, направленной так же, как перемещение тела (рис. 30.2). При этом пружина совершает положительную работу.

Итак, деформированная пружина может совершить работу при возвращении в недеформированное состояние.

В рассмотренных примерах работу совершают силы тяготения и силы упругости. Как мы уже знаем, общая важная особенность этих сил состоит в том, что при движении по замкнутой траектории (когда тело возвращается в начальное положение) работа этих сил равна нулю. (Такие силы называют консервативными. Если между телами замкнутой системы действуют только консервативные силы, то, как мы увидим далее, механическая энергия системы сохраняется («консервируется»).)

Благодаря этому для системы тел, взаимодействующих посредством сил тяготения и упругости, можно определить потенциальную энергию как величину, характеризующую способность системы тел совершать работу и зависящую только от взаимного положения тел.

Потенциальная энергия системы тел характеризует ее способность совершать работу вследствие изменения взаимного положения взаимодействующих тел.

Если система тел совершает положительную работу, потенциальная энергия системы уменьшается. А если система тел совершает отрицательную работу, ее потенциальная энергия увеличивается. При этом

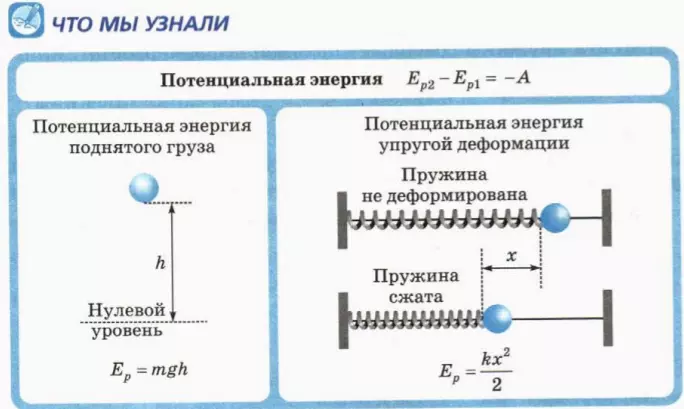
изменение потенциальной энергии системы тел равно работе сил упругости и тяготения, действующих со стороны тел системы, взятой со знаком минус:

E_p2 – E_p1 = –A (1)

Здесь E_p1 и E_p2 обозначают начальную и конечную потенциальную энергию системы тел.

(Мы приводим определение потенциальной энергии, применимое к механическим явлениям. В дальнейшем мы расширим и уточним это определение.)

? 1. Как изменяется потенциальная энергия системы «камень + Земля», когда камень движется вверх? вниз? Объясните свои ответы.

? 2. Как изменяется потенциальная энергия пружины, когда деформация уменьшается? увеличивается? Объясните свои ответы.

Нулевой уровень потенциальной энергии. Из формулы (1) следует, что физический смысл имеет только изменение потенциальной энергии: оно измеряется работой, совершенной телами системы.

Поэтому нулевой уровень потенциальной энергии (состояние системы, которому сопоставляется нулевое значение потенциальной энергии) выбирают так, чтобы упростить расчеты.

2. Потенциальная энергия поднятого груза

Когда груз массой m равномерно перемещается вертикально вниз на расстояние h, он совершает положительную работу mgh, потому что он действует на опору или поднес направленной вниз силой (весом груза), равной силе тяжести.

Следовательно, при уменьшении высоты груза на h потенциальная энергия груза уменьшается на mgh. (Важно понимать, что это потенциальная энергия системы взаимодействующих тел – груза и Земли.) Если сопоставить нулевой уровень потенциальной энергии наинизшему положению груза, то

потенциальная энергия груза массой m, поднятого на высоту h, выражается формулой

E_p = mgh. (2)

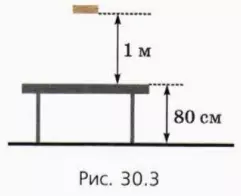
? 3. Брусок массой 200 г поднят на высоту 1 м над поверхностью стола высотой 80 см (рис. 30.3).

а) Чему равна потенциальная энергия бруска, если за нулевой уровень потенциальной энергии бруска принять уровень стола? уровень пола?
б) Чему равно изменение потенциальной энергии бруска при его падении на стол, если за нулевой уровень потенциальной энергии бруска принять уровень стола? уровень пола?

Эти примеры подтверждают, что имеет значение только изменение потенциальной энергии. Оно измеряется работой, совершенной телом или системой тел, и не зависит от выбора нулевого уровня потенциальной энергии.

3. Потенциальная энергия упругой деформации

При возвращении в недеформированное состояние сила упругости пружины совершает положительную работу

A = (kx²)/2.

При этом потенциальная энергия пружины уменьшается на такую же величину. Если нулевому уровню потенциальной энергии сопоставить состояние недеформированной пружины, то

потенциальная энергия деформированной пружины жесткостью k выражается формулой

Ep = (kx²)/2, (3)

где x – деформация пружины.

Потенциальную энергию, выражаемую формулой (3), называют также потенциальной энергией упругой деформации. Она зависит от квадрата деформации. Поэтому потенциальная энергия сжатой пружины равна потенциальной энергии растянутой пружины, если модуль деформации пружины в обоих случаях один и тот же.

? 4. В начальном состоянии пружина жесткостью 200 Н/м сжата на 1 см. Как изменилась потенциальная энергия пружины, если в конечном состоянии:
а) пружина не деформирована?
б) сжата на 2 см?
в) растянута на 1 см?
г) растянута на 2 см?

? 5. Шар массой 200 г подвешен к пружине жесткостью 100 Н/м и находится в равновесии, Шар поднимают так, чтобы пружина стала недеформированной, и отпускают без толчка.
а) На какую высоту подняли шар?
б) Как изменилась потенциальная энергия шара за время, в течение которого он возвращался в положение равновесия?
в) Как изменилась за то же время потенциальная энергия пружины?
г) Как изменилась за то же время потенциальная энергия системы «шар + Земля + пружина»?

Дополнительные вопросы и задания

6. С высоты 20 м над поверхностью земли свободно без начальной скорости падает камень массой 300 г. За нулевой уровень потенциальной энергии камня примите уровень земли.
а) Чему равна потенциальная энергия камня в начальный момент?
б) Чему равна потенциальная энергия камня через 1 с после начала движения?
в) Через какое время после начала движения потенциальная энергия камня уменьшилась в 2 раза по сравнению с ее начальным значением?

7. Шар массой 1 кг брошен с поверхности земли с начальной скоростью 20 м/с под углом 30º к горизонту. Считайте, что сопротивлением воздуха при движении шара можно пренебречь.
а) До какой максимальной высоты поднялся шар?
б) Как изменилась потенциальная энергия шара за время подъема?

8. По реке с постоянной скоростью плывет плот. Как изменяется со временем:
а) кинетическая энергия плота?
б) потенциальная энергия плота?

9. Когда сжатую пружину сжали еще на 2 см, ее потенциальная энергия увеличилась в 9 раз.
а) Во сколько раз модуль конечной деформации пружины больше, чем модуль начальной деформации?
б) Чему равен модуль начальной деформации пружины?

10. Две пружины жесткостью 100 Н/м и 400 Н/м соединены последовательно. Систему соединенных пружин растянули на 5 см.
а) Чему равна деформация более мягкой пружины?
б) Чему равна деформация более жесткой пружины?
в) Потенциальная энергия упругой деформации какой пружины больше, и во сколько раз?

Источник

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические
43,662
гуманитарные
33,654
юридические
17,917
школьный раздел
611,978
разное
16,905

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Источник

Энергия.

Работа.
Мощность.
Механическая энергия.
Кинетическая энергия.
Потенциальная энергия тела вблизи поверхности Земли.
Потенциальна яэнергия деформированной пружины.
Закон сохранения механической энергии.
Закон изменения механической энергии.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа силы, мощность, кинетическая энергия, потенциальная энергия, закон сохранения механической энергии.

Мы приступаем к изучению энергии — фундаментального физического понятия. Но предварительно нужно разобраться с другой физической величиной — работой силы.

к оглавлению ▴

Работа.

Пусть на тело действует постоянная сила vec F и тело, двигаясь прямолинейно по горизонтальной поерхности, совершило перемещение vec s . Сила vec F не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате).

Предположим сначала, что векторы силы и перемещения сонаправлены (рис. 1; остальные силы, действующие на тело, не указаны)

Рис. 1.A=Fs

В этом простейшем случае работа определяется как произведение модуля силы на модуль перемещения:

A=Fs . (1)

Единицей измерения работы служит джоуль (Дж): Дж=Н cdot м. Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.

Работа силы, перпендикулярной перемещению, по определению считается равной нулю. Так, в данном случае сила тяжести и сила реакции опоры не совершают работы.

Пусть теперь вектор силы образует с вектором перемещения острый угол alpha (рис. 2).

Разложим силу vec F на две составляющие: $vec F _{parallel }$ (параллельную перемещению) и $vec F _{perp }$ (перпендикулярную перемещению). Работу совершает только $vec F _{parallel }$ . Поэтому для работы силы vec F получаем:

$A=vec F _{parallel }s=Fcosalpha cdot s$ . Итак,

. (2)

Если вектор силы образует с вектором перемещения тупой угол alpha , то работа по-прежнему определяется формулой (2). В этом случае работа оказывается отрицательной.

Например, работа силы трения скольжения, действующей на тело в рассмотренных ситуациях, будет отрицательной, так как сила трения направлена противоположно перемещению. В этом случае имеем:

$alpha=180^{circ}, cos alpha=-1$ , и для работы силы трения получаем:

$A_{TP}=-F_{TP}s=-mu mgs$ ,

где — масса тела, — коэффициент трения между телом и опорой.

Соотношение (2) означает, что работа является скалярным произведением векторов силы и перемещения:

Это позволяет вычислять работу через координаты данных векторов:

$A=F_{displaystyle x}s_{displaystyle x}+F_{displaystyle y}s_{displaystyle y}+F_{displaystyle z}s_{displaystyle z}$ .

Пусть на тело действуют несколько сил $vec F_{1},vec F_{2},..,vec F_{n}$ и vec F — равнодействующая этих сил. Для работы силы vec F имеем:

$A=vec F vec s=(vec F_{1}+vec F_{2}+...+vec F_{n})vec s=vec F_{1}vec s+vec F_{2}vec s+...+vec F_{n}vec s$ ,

или

$A=A_{1}+A_{2}+...+A_{n}$ ,

где $A_{1}, A_{2},...,A_{n}$ — работы сил $F_{1}, F_{2},...,F_{n}$ . Итак, работа равнодействующей приложенных к телу сил равна сумме работ каждой силы в отдельности.

к оглавлению ▴

Мощность.

Часто имеет значение быстрота, с которой совершается работа. Скажем, на практике важно знать, какую работу сможет выполнить данное устройство за фиксированное время.

Мощность — это величина, характеризующая скорость совершения работы. Мощность есть отношение работы ко времени , за которое эта работа совершена:

$N=frac{displaystyle A}{displaystyle t}$ .

Мощность измеряется в ваттах (Вт). 1 Вт = 1 Дж/с, то есть 1 Вт — это такая мощность, при которой работа в 1 Дж совершается за 1 с.

Предположим, что силы, действующие на тело, уравновешены, и тело движется равномерно и прямолинейно со скоростью vec v . В этом случае существует полезная формула для мощности, развиваемой одной из действующих сил vec F .

За время тело совершит перемещение . Работа силы vec F будет равна:

Отсюда получаем мощность:

или

где alpha -угол между векторами силы и скорости.

Наиболее часто эта формула используется в ситуации, когда vec F — сила «тяги» двигателя автомобиля (которая на самом деле есть сила трения ведущих колёс о дорогу). В этом случае , и мы получаем просто:

N=Fv .

к оглавлению ▴

Механическая энергия.

Энергия является мерой движения и взаимодействия любых объектов в природе. Имеются различные формы энергии: механическая, тепловая, электромагнитная, ядерная. . .

Опыт показывает, что энергия не появляется ниоткуда и не исчезает бесследно, она лишь переходит из одной формы в другую. Это самая общая формулировка закона сохранения энергии.

Каждый вид энергии представляет собой некоторое математическое выражение. Закон сохранения энергии означает, что в каждом явлении природы определённая сумма таких выражений остаётся постоянной с течением времени.

Измеряется энергия в джоулях, как и работа.

Механическая энергия является мерой движения и взаимодействия механических объектов (материальных точек, твёрдых тел).

Мерой движения тела является кинетическая энергия. Она зависит от скорости тела. Мерой взаимодействия тел является потенциальная энергия. Она зависит от взаимного расположения тел.

Механическая энергия системы тел равна сумме кинетической энергии тел и потенциальной энергии их взаимодействия друг с другом.

к оглавлению ▴

Кинетическая энергия.

Кинетической энергией тела (принимаемого за материальную точку) называется величина

$K=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ ,

где — масса тела, — его скорость.

Кинетической энергией системы из тел называется сумма кинетических энергий каждого тела:

$K=frac{displaystyle m_{displaystyle 1}v_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}+frac{displaystyle m_{displaystyle 2}v_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}+...+frac{displaystyle m_{displaystyle N}v_{displaystyle N}^{displaystyle 2}}{displaystyle 2}$ .

Если тело движется под действием силы vec F , то кинетическая энергия тела, вообще говоря, меняется со временем. Оказывается, именение кинетической энергии тела за некоторый промежуток времени равно работе силы vec F . Покажем это для случая прямолинейного равноускоренного движения.

Пусть $vec{v_{1}}$ — начальная скорость, $vec{v_{2}}$ — конечная скорость тела. Выберем ось вдоль траектории тела (и, соответственно, вдоль вектора силы vec F ). Для работы силы vec F получаем:

$A=vec{F}vec{s}=F_{x}s_{displaystyle s}=ma_{displaystyle x}s_{displaystyle x}= ma_{displaystyle x}frac{{v_{displaystyle 2x}}^{displaystyle 2}-{v_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2a_{displaystyle x}}=frac{{displaystyle mv_{displaystyle 2x}}^{displaystyle 2}-{displaystyle mv_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2}$ .

(мы воспользовались формулой для $s_{x}$ , выведенной в статье «Равноускоренное движение»). Заметим теперь, что в данном случае проекция скорости отличается от модуля скорости разве что знаком; поэтому ${v_{displaystyle 1x}}^{displaystyle 2}={v_{displaystyle 1}}^{displaystyle 2}$ и ${v_{displaystyle 2x}}^{displaystyle 2}={v_{displaystyle 2}}^{displaystyle 2}$ . В результате имеем:

$A=frac{displaystyle mv_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle mv_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}=K_{displaystyle 2}-K_{displaystyle 1}=Delta K$ ,

что и требовалось.

На самом деле соотношение справедливо и в самом общем случае криволинейного движения под действием переменной силы.

Теорема о кинетической энергии. Изменение кинетической энергии тела равно работе, совершённой приложенными к телу внешними силами за рассматриваемый промежуток времени.

Если работа внешних сил положительна, то кинетическая энергия увеличивается (, тело разгоняется).

Если работа внешних сил отрицательна, то кинетическая энергия уменьшается (, тело замедляет движение). Пример — торможение под действием силы трения, работа которой отрицательна.

Если же работа внешних сил равна нулю, то кинетическая энергия тела за это время не меняется. Нетривиальный пример — равномерное движение по окружности, совершаемое грузом на нити в горизонтальной плоскости. Сила тяжести, сила реакции опоры и сила натяжения нити всегда перпендикулярны скорости, и работа каждой из этих сил равна нулю в течение любого промежутка времени. Соответственно, кинетическая энергия груза (а значит, и его скорость) остаётся постоянной в процессе движения.

Задача. Автомобиль едет по горизонтальной дороге со скоростью и начинает резко тормозить. Найти путь , пройденный автомобилем до полной остановки, если коэффициент трения шин о дорогу равен .

Решение. Начальная кинетическая энергия автомобиля $K_{displaystyle 1}=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ , конечная кинетическая энергия $K_{displaystyle 2}=0$ . Изменение кинетической энергии $Delta K=K_{displaystyle 2}-K_{displaystyle 1}=-frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}$ .

На автомобиль действуют сила тяжести m vec g , реакция опоры vec N и сила трения vec f . Сила тяжести и реакция опоры, будучи перпендикулярны перемещению автомобиля, работы не совершают. Работа силы трения:

Из теоремы о кинетической энергии теперь получаем:

$Delta K=A Rightarrow - frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}=- mu mgs Rightarrow s=frac{displaystyle v^{displaystyle 2}}{displaystyle 2 mu g}$ .

к оглавлению ▴

Потенциальная энергия тела вблизи поверхности Земли.

Рассмотрим тело массы , находящееся на некоторой высоте над поверхностью Земли. Высоту считаем много меньше земного радиуса. Изменением силы тяжести в процессе перемещения тела пренебрегаем.

Если тело находится на высоте , то потенциальная энергия тела по определению равна:

W=mgh

где — ускорение свободного падения вблизи поверхности Земли.

Высоту не обязательно отсчитывать от поверхности Земли. Как мы увидим ниже (формулы (3), (4)), физическим смыслом обладает не сама по себе потенциальная энергия, но её изменение. А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства.

Найдём работу, совершаемую силой тяжести при перемещении тела. Предположим, что тело перемещается по прямой из точки , находящейся на высоте $h_{1}$ , в точку , находящуюся на высоте $h_{2}$ (рис. 3).

Рис. 3.A=mg(h1-h2)[/math]

Угол между силой тяжести m vec g и перемещением тела vec s обозначим alpha . Для работы силы тяжести получим:

Но, как видно из рис. 3, $s cos alpha=h_{1}-h_{2}$ . Поэтому

$A=mg(h_{1}-h_{2})=mgh_{1}-mgh_{2}$ ,

или

$A=W_{1}-W_{2}$ . (3)

Учитывая, что $W_{1}-W_{2}=-(W_{2}-W_{1})=- Delta W$ , имеем также:

. (4)

Можно доказать, что формулы (3) и (4) справедливы для любой траектории, по которой тело перемещается из точки в точку , а не только для прямолинейного отрезка.

Работа силы тяжести не зависит от формы траектории, по которой перемещается тело, и равна разности значений потенциальной энергии в начальной и конечной точках траектории. Иными словами, работа силы тяжести всегда равна изменению потенциальной энергии с противоположным знаком. В частности, работа силы тяжести по любому замкнутому пути равна нулю.

Сила называется консервативной, если при перемещении тела работа этой силы не зависит от формы траектории, а определяется только начальным и конечным положением тела. Сила тяжести, таким образом, является консервативной. Работа консервативной силы по любому замкнутому пути равна нулю. Только в случае консервативной силы возможно ввести такую величину, как потенциальная энергия.

к оглавлению ▴

Потенциальна яэнергия деформированной пружины.

Рассмотрим пружину жёсткости . Начальная деформация пружины равна $x_{1}$ . Предположим,
что пружина деформируется до некоторой конечной величины деформации $x_{2}$ . Чему равна при этом работа силы упругости пружины?

В данном случае силу на перемещение не умножишь, так как сила упругости меняется в процессе деформации пружины. Для нахождения работы переменной силы требуется интегрирование. Мы не будем приводить здесь вывод, а сразу выпишем конечный результат.

Оказывается, сила упругости пружины также является консервативной. Её работа зависит лишь от величин $x_{1}$ и $x_{2}$ и определяется формулой:

$A=frac{kx_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle kx_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}$ .

Величина

$W=frac{displaystyle kx^{displaystyle 2}}{displaystyle 2}$

называется потенциальной энергией деформированной пружины (x — величина деформации).

Следовательно,

$A=W_{1}-W_{2}=- Delta W$ ,

что полностью аналогично формулам (3) и (4).

к оглавлению ▴

Закон сохранения механической энергии.

Консервативные силы называются так потому, что сохраняют механическую энергию замкнутой системы тел.

Механическая энергия тела равна сумме его кинетической и потенциальной энергий:

E=K+W .

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии их взаимодействия друг с другом.

Предположим, что тело совершает движение под действием силы тяжести и/или силы упругости пружины. Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны $K_{1}$ и $W_{1}$ , в конечном положении — $K_{2}$ и $W_{2}$ . Работу внешних сил при перемещении тела из начального положения в конечное обозначим .

По теореме о кинетической энергии

$K_{2}-K_{1}=A$ .

Но работа консервативных сил равна разности потенциальных энергий:

$A=W_{1}-W_{2}$ .

Отсюда получаем:

$K_{2}-K_{1}=W_{1}-W_{2}$ ,

или

$K_{1}+W_{1}=K_{2}+W_{2}$ .

Левая и правая части данного равенства представляют собой механическую энергию тела в начальном и конечном положении:

$E_{1}=E_{2}$ .

Следовательно, при движении тела в поле силы тяжести и/или на пружине механическая энергия тела остаётся неизменной при отсутствии трения. Справедливо и более общее утверждение.

Закон сохранения механической энергии. Если в замкнутой системе действуют только консервативные силы, то механическая энергия системы сохраняется.

При этих условиях могут происходить лишь превращения энергии: из кинетической в потенциальную и наоборот. Общий запас механической энергии системы остаётся постоянным.

к оглавлению ▴

Закон изменения механической энергии.

Если между телами замкнутой системы имеются силы сопротивления (сухое или вязкое трение), то механическая энергия системы будет уменьшаться. Так, автомобиль останавливается в результате торможения, колебания маятника постепенно затухают и т. д. Силы трения неконсервативны: работа силы трения очевидным образом зависит от пути, по которому перемещается тело между данными точками. В частности, работа силы трения по замкнутому пути не равна нулю.

Снова рассмотрим движение тела в поле силы тяжести и/или на пружине. Вдобавок на тело действует сила трения, которая за рассматриваемый промежуток времени совершает отрицательную работу $A_{TP}$ . Работу консервативных сил (тяжести и упругости) по-прежнему обозначаем .

Изменение кинетической энергии тела равно работе всех внешних сил:

$K_{2}-K_{1}=A+A_{TP}$ .

Но $A=W_{1}-W_{2}$ , следовательно

$K_{2}-K_{1}=W_{1}-W_{2}+A_{TP}$ .

Отсюда

$K_{2}+W_{2}-(K_{1}+W_{1})=A_{TP}$ ,

или

$E_{2}-E_{1}=A_{TP}$ .

В левой части стоит величина $Delta E=E_{2}-E_{1}$ — изменение механической энергии тела:

$Delta E=A_{TP}$ .

Итак,при движении тела в поле силы тяжести и/или на пружине изменение механической энергии тела равно работе силы трения. Так как работа силы трения отрицательна,изменение механической энергии также отрицательно: механическая энергия убывает.
Справедливо и более общее утверждение.

Закон изменения механической энергии. Изменение механической энергии замкнутой системы равно работе сил трения, действующих внутри системы.

Ясно, что закон сохранения механической энергии является частным случаем данного утверждения.

Конечно, убыль механической энергии не противоречит общефизическому закону сохранения энергии. В данном случае механическая энергия превращается в энергию теплового движения частиц вещества и их потенциальную энергию взаимодействия друг с другом, т. е. переходит во внутреннюю энергию тел системы.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Энергия.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Содержание:

Потенциальное силовое поле и силовая функция:

Силовым полем называют часть пространства, приведенную какими-либо телами в такое состояние, при котором в каждой ее точке на данную материальную частицу действует сила, зависящая только от положения частицы и от времени, но не от ее скорости

Силовое поле

Пусть к материальной частице находящейся внутри некоторой области (части пространства), приложена сила, обусловленная наличием каких-либо тел. Если материальная частица передвигается в этой области, то действующая на нее сила может изменяться в зависимости от положения частицы или же оставаться постоянной. Эта сила может изменяться и со временем, но не должна зависеть от скорости частицы. Такую часть пространства называют силовым полем, причем силовое поле называют стационарным, если силы его не зависят от времени, и нестационарным, если силы поля с течением времени меняются.

Так, например, наша планета находится под действием силы притяжения к Солнцу. Эта сила обратно пропорциональна квадрату расстояния Земли от Солнца, т. е. зависит от положения Земли относительно Солнца, но не зависит от времени, и поле тяготения к Солнцу является стационарным силовым полем.

Тяготением Ньютон объяснил (1687 г.) морские приливы и отливы. Его теория, усовершенствованная главным образом Д. Бернулли, рассматривает океан как водяной покров, окружающий твердый земной шар. Капли воды, находящиеся ближе к Луне, притягиваются к ней сильнее, чем более удаленные капли. Вследствие «приливного ускорения» (рис. 221), т. е. геометрической разности ускорений, которые Луна сообщает центру земного шара и каплям водяной оболочки Земли, возникает движение воды такого характера, как будто обращенная к Луне часть океана притягивается ею, а противоположная отталкивается. Поэтому навстречу вращению Земли (т. е. с В на 3) всегда бежит по океану приливная волна (но не течение!). Аналогичное явление получается от притяжения к Солнцу, но расстояние до Солнца так велико по сравнению с размерами Земли, что приливное ускорение от притяжения к Солнцу составляет всего

Силовой функцией называют такую функцию координат точек стационарного поля, полный дифференциал которой равен элементарной работе сил поля

Силовая функция силового поля

Дано какое-либо стационарное поле и пусть существует некоторая функция координат

U = U (х, у, г), (237)

обладающая тем свойством, что ее частные производные по х, у и г являются однозначными функциями координат и равны проекциям X, Y и Z силы поля на соответствующие оси координат, т.е.

(238)

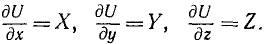
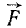
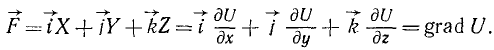
Функцию U называют силовой функцией, а силу поля, проекции которой на оси равны частным производным от силовой функции по этим осям, называют градиентом силовой функции:

(239)

Геометрическое место точек, в которых силовая функция имеет одинаковое значение

U (х, у, z) = const (240)

называют эквипотенциальной поверхностью, или поверхностью уровня. Все силовое поле можно представить заполненным непрерывным множеством бесконечно близких друг другу поверхностей уровня. Для каждого мгновения существуют определенные поверхности уровня и в нестационарных силовых полях

U (х, у, z, t) = const. (240′)

Во всякой точке поля градиент (239) направлен по нормали к поверхности уровня.

Подставив в выражение (221) элементарной работы вместо X, Y и Z эти значения, получим

т. е. элементарная работа силы поля равна полному дифференциалу силовой функции

dA=dU (241)

Для существования силовой функции должны удовлетворяться определенные соотношения между проекциями силы поля. Продифференцируем по z второе из равенств (238), а третье продифференцируем по у, получим

Ha основании свойств частных производных можем написать следующие равенства:

и аналогично (242)

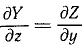
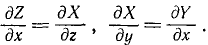
Задача №1

Существует ли силовая функция в стационарном силовом поле, если проекции силы поля на оси координат зависят от координат материальной точки следующим образом X-2xy; Y =x²; Z = 0?

Решение. Для ответа на вопрос воспользуемся равенством (242)

Следовательно, условия (242) выполняются.
Ответ. Да, существует.

Потенциальным полем называют такое стационарное силовое поле, в котором работа силы поля, приложенной к материальной частице, зависит только от начального и конечного положений этой частицы

Потенциальное силовое поле

Стационарное поле, в котором выполняются эти условия, т. е. имеется силовая функция U, называют потенциальным полем. Пусть в потенциальном поле движется материальная частица, перемещающаяся с произвольной скоростью и безразлично по какой траектории из одного положения, которое мы примем за начальное, в какое-либо другое, которое мы назовем конечным. Обозначим через U₀ значение силовой функции в той точке поля, которую мы приняли за начальное положение частицы, а через U — в конечной точке и затем, проинтегрировав левую и правую части равенства (241) в соответствующих пределах от 0 до А и от U₀ до U, получим

A = U- U₀. (243)

Таким образом, независимо от скорости частицы и формы траектории работа силы потенциального поля равна разности значений силовой функции в конечной и в начальной точках траектории. Пусть имеется такое положение точки, для которого значение силовой функции равно нулю. Назовем это положение нулевым и примем его за начальное (U₀ = 0). В таком случае

A = U

Следовательно, силовая функция выражает ту работу, которую производит сила поля при переходе материальной частицы из нулевого положения в данное.

Потенциальная энергия материальной точки равна работе сил потенциального поля при переходе точки из данного положения в нулевое

Потенциальная энергия материальной частицы

Наряду с силовой функцией U нам понадобится величина П, связанная с силовой функцией простой зависимостью

П = — U (244)

и называемая потенциальной энергией.

Равенство (244) вместе с предыдущим равенством позволяют выяснить физическую сущность этого понятия: потенциальная энергия материальной точки, находящейся в каком-либо данном положении, равна работе силы потенциального поля при переходе точки из данного положения в нулевое.
Поясним это следующими примерами.

Потенциальная энергия пружины

Сжатая пружина обладает потенциальной энергией, обусловленной упругими деформациями в материале пружины. Если пружина сжата на величину х, то, как было показано (227), при переходе ее в ненапряженное состояние сила упругости может совершить работу 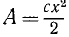. Эта способность сжатой пружины совершить работу является потенциальной энергией пружины:

Так же выразится и потенциальная энергия растянутой пружины.

Потенциальная энергия тела в поле тяжести

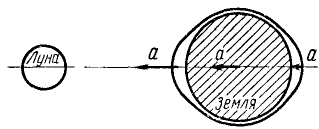
Материальная частица или тяжелое тело, поднятое на некоторую высоту, обладает потенциальной энергией, равной той работе, которую совершит сила тяжести при опускании тела до «нулевого положения». Однако нулевое положение в поле силы тяжести не может быть так естественно определено, как в поле упругой силы. Для пружины и вообще в случаях упругих сил нулевым положением является то, при котором отсутствует деформация. Для тяжелого тела нулевым положением может быть уровень пола, уровень земли и т. д. Уровень, относительно которого отсчитывают потенциальную энергию тела, поднятого на некоторую высоту, может быть выбран совершенно условно. Но эта условность в выборе нулевого положения не сказывается на расчетах, так как в расчеты всегда входит не полная потенциальная энергия, а ее изменение. Нужно лишь отсчитывать потенциальную энергию относительно одного и того же уровня. Поэтому для определения потенциальной энергии тела в поле силы тяжести мы построим систему прямоугольных координатных осей, направив ось Oz вертикально вверх, но не будем пока уточнять положение начала отсчета и определим проекции силы тяжести:

X = O; У = 0; Z = -G.

Условия (242) существования силовой функции удовлетворяются. Определим дифференциал силовой функции:

Xdx + Ydy + Zdz = — Gdz — dU.

Интегрируя, найдем силовую функцию силы тяжести:

U = — Gz+ C.

Постоянная интеграции C зависит от начала отсчета, но изменение U-U₀ силовой функции от начала отсчета не зависит. Интегрирование можно провести и в пределах. Выберем, например, за нулевое положение уровень моря и пусть тело поднято на высоту h, тогда

и

П = + Gh.

Нетрудно видеть, что изменение П—П₀ потенциальной энергии тела при заданном изменении его высоты одинаково, выразим ли мы ее как П=Gh или П = Gz+С, и не зависит от С.

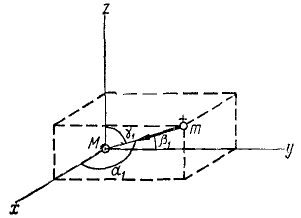
Силовая функция поля всемирного тяготения

По закону всемирного тяготения планеты притягиваются к Солнцу с силой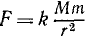 , где M — масса Солнца, m—масса планеты и k— постоянная величина. Построив систему координат с началом в центре Солнца (рис. 222), определим проекции силы на оси, для чего умножим модуль силы на ее направляющие косинусы:

Получим

Рис. 222

Взяв частные производные от этих величин по х, у и г, можно показать, что условия (242) существования силовой функции выполняются, а следовательно, силовая функция существует. Найдем эту функцию:

Числитель дроби в правой части есть rdr, в чем можно убедиться, продифференцировав равенство r² = x² + y² + z^2, поэтому

Интегрируя, находим силовую функцию ньютонианского поля:
(245)

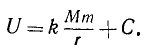
Или, если ввести гауссово число μ-kM, то

(245′)

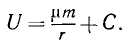
Потенциальная энергия выражается той же величиной, но взятой с обратным знаком.

При движении материальной частицы под действием силы потенциального поля сумма кинетической и потенциальной энергий частицы остается постоянной

Закон сохранения механической энергии

На материальную частицу, находящуюся в потенциальном поле, действует сила этого поля, поэтому при движении частицы ее скорость, а следовательно, и кинетическая энергия ее в общем случае меняются. Выражая в уравнении (232) работу А равенством (243), найдем зависимость изменения кинетической энергии от изменения силовой функции:

(246)

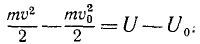
Это равенство называют интегралом кинетической энергии. Оно показывает, что изменение кинетической энергии материальной частицы, движущейся в потенциальном поле, равно изменению силовой функции, не зависит от пути материальной частицы, а зависит лишь от ее начального и конечного положений в потенциальном поле.

Если в равенстве (246) силовую функцию мы выразим посредством (244) через потенциальную энергию, то получим

откуда

и вообще

(247)

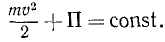
Таким образом, если материальная частица движется в потенциальном поле под действием сил этого поля, то во всякое мгновение при всяком положении частицы сумма ее кинетической и потенциальной энергий есть величина постоянная. Равенство (247) выражает закон сохранения механической энергии и имеет применение в тех случаях, если на частицу не действуют никакие силы, кроме сил потенциального поля. Поэтому потенциальные поля называют также консервативными (от лат. Conservativus—сохраняющий).

Так, например, закон сохранения механической энергии справедлив при движении планет в поле ньютонианского тяготения: чем ближе к Солнцу находится планета на своей эллиптической орбите, тем меньше ее потенциальная энергия и соответственно больше кинетическая (см. § 44 — закон площадей). Скорость периодических комет, движущихся по очень вытянутым эллипсам, в перигелии во много тысяч раз превышает их скорость в афелии, но в любой точке орбиты сумма кинетической и потенциальной энергий кометы есть для этой кометы величина постоянная.

Вывод первого закона Кеплера из закона всемирного тяготения Ньютона

Задача №2

Определить траекторию небесного тела (планеты, кометы, космического корабля), движущегося под действием тяготения к Солнцу, подчиняясь закону всемирного тяготения Ньютона.
Решение. Задача относится к обратным задачам динамики: определить движение по заданной силе. Для решения воспользуемся интегралом кинетической энергии

(246)

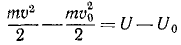
или, применительно к данной задаче и в виду (245′)

Определим из этого равенства υ₂ и заменим радиус-вектор его обратной величиной :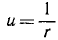

Для упрощения записи введем обозначение

Тогда

Это значение υ₂ внесем в первую формулу Бине (191):

Решим это уравнение относительно dφ:

Если мы отсчитываем φ от какого-либо начального положения, в котором радиус-вектор возрастает, а следовательно, его обратная величина 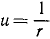убывает, то du имеет отрицательный знак и

Для интегрирования преобразуем выражение, стоящее под знаком корня, прибавив к подкоренному количеству и вычтя из него :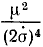

Выражение, взятое в скобки, представляет полный квадрат разности двух количеств, и радикал принимает следующий вид:

Сумма двух первых членов в подкоренном количестве должна быть больше отрицательного третьего члена, потому что в противном случае φ было бы мнимой величиной. Введем обозначение

Положим, кроме того, как это мы уже приняли при решении задачи № 129, что 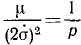и перепишем уравнение в следующем виде:

Разделим числители и знаменатели на :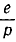

В правой части равенства мы имеем дифференциал арккосинуса от аргумента 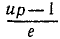. Теперь интегрирование не составляет труда и, учитывая, что постоянная интеграции равна нулю, получаем

Решим это уравнение относительно :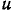

Мы получили уравнение конического сечения в полярных координатах.

Ответ.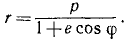. Траектория—коническое сечение.

Задача №3

По данным предыдущей задачи определить условия, при которых траекторией небесного тела является эллипс, парабола или гипербола.

Решение. В обозначениях, принятых в предыдущей задаче, напишем:

Как видно из конечного результата предыдущей задачи, величины р и e имеют следующий геометрический смысл: р является параметром, а е—эксцентриситетом. Вводя в квадрат второе из принятых обозначений и вычитая из первого, найдем:

Подставим вместо В в левую часть равенства его значение, принятое в предыдущей задаче:

Из этого соотношения определим квадрат эксцентриситета:

В аналитической геометрии показано, что у эллипса эксцентриситет меньше единицы, у параболы равен единице и у гиперболы больше единицы. Как видно из написанного равенства, эксцентриситет меньше единицы, равен единице или больше единицы в зависимости от того, является ли выражение, стоящее в скобках, отрицательным, нулем или положительным.
Ответ. Эллипс:

Парабола:

Гипербола:

Задача №4

Тело брошено с поверхности Земли вверх по вертикальной линии с начальной скоростью υ₀. Определить величину H поднятия тела, принимая во внимание, что сила притяжения изменяется обратно пропорционально квадрату расстояния от центра Земли; сопротивлением воздуха пренебрегаем. Радиус Земли R = 6370 км, υ₀=1 км/сек.

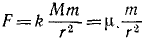
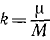
Решение. Рассматриваем движение тела в поле тяготения Земли. На тело действует одна лишь сила , где — коэффициент пропорциональности, M — масса Земли и m— масса тела.

Коэффициент μ=gR² для силы земного притяжения определен в задаче № 155.

Начальная кинетическая энергия тела 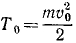, конечная Т=0; начальная потенциальная энергия

конечная

Приравняем сумму энергий в начале движения сумме энергий в конце движения:

откуда находим 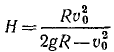и, подставляя числовые значения, получаем ответ.
Ответ. H = 51 км.

При движении тела в поле тяжести вблизи земной поверхности на тело, кроме силы тяжести, действуют различные диссипативные силы, например сила сопротивления воздуха, поэтому закон сохранения механической энергии здесь неприменим: происходит рассеяние механической энергии, переход ее в другие немеханические виды. Вместе с тем и немеханические виды энергии могут переходить в механическую энергию. Переход не только механической, но и всякой другой энергии из данного вида в эквивалентное количество энергии всякого другого вида подчинен всеобщему закону сохранения и превращения энергии, изучаемому в курсах физики. Согласно этому закону во всякой изолированной системе сумма энергий всех видов (кинетической, потенциальной, тепловой, электрической и т. д.) остается постоянной.

Открытие закона сохранения механической энергии (выражаясь точнее, вывод равенства 246) обычно приписывают Гельмгольцу. Но он провел разработку лишь математической стороны вопроса, однако физическая сущность равенств (246) и (247) не могла получить правильного освещения в трудах Гельмгольца, понимавшего движение не как внутренне присущий материи атрибут, а как нечто внешнее по отношению к материи, «существо которой», по выражению Гельмгольца, «в самом себе представляется для нас покоящимся и бездейственным».

Открытие же всеобщего закона сохранения и превращения энергии приписывают обычно Р. Майеру или Джоулю. Но никакое крупнейшее открытие не может принадлежать одному человеку. В частности, открытие этого закона было подготовлено трудами Декарта, Гюйгенса, Лейбница, Ломоносова, Сади Карно и многих других ученых. Постановка этой проблемы и, в частности, изучение перехода тепловой энергии в механическую было вызвано в первой половине XIX в. развитием промышленности и применением паровых машин, практически осуществляющих этот переход.

Потенциальная энергия механической системы зависит только от положения точек системы в потенциальном поле

Потенциальная энергия системы

Чтобы лучше осветить физическую сторону вопроса, мы все формулы и формулировки в этой главе дали для реальной материальной частицы. Они останутся, конечно, без изменения, если материальную частицу мы заменим материальной точкой, являющейся абстрактным образом материального тела. Они применимы и к такой материальной системе, в которой сумма работ всех сил, приложенных к точкам системы, при перемещении системы из одного положения в другое не зависит от траекторий точек. В частности, они применимы к абсолютно твердому телу, так как работа внутренних сил твердого тела равна нулю.

Очевидно, что потенциальная энергия системы, математически выражается функцией координат всех точек системы

П = П (x₁, y_l, z_l, …, x_n, у_n, z_n),

причем полный дифференциал этой функции, взятый с обратным знаком, равен сумме элементарных работ сил потенциального поля, приложенных к точкам системы. Такое поле является консервативным, т. е. при движении системы в таком поле под действием только сил этого поля сумма кинетической и потенциальной энергий системы сохраняет постоянное значение.

Равновесные положения механической системы в потенциальном поле, при которых потенциальная энергия системы достигает минимума, устойчивы

Теорема Лежен Дирихле

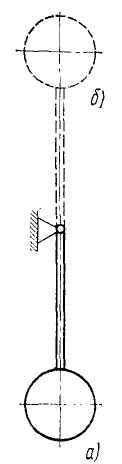
Отметим интересные свойства равновесия механических систем в потенциальном поле:

если система находится в покое в потенциальном поле и занимает положение, при котором потенциальная энергия П минимальна (а следовательно, силовая функция U имеет максимум), то система находится в устойчивом равновесии, т. е., будучи незначительно выведена из этого положении, она стремится вернуться к нему, совершая около него малые колебания;
наоборот, если потенциальная энергия при равновесии системы имеет максимум, то система находится в состоянии неустойчивого равновесия и, будучи выведена из этого состояния, не может остаться близкой к первоначальному положению равновесия.

Так, например, на рис. 223, а и б изображен физический маятник в состоянии равновесия, но в положении, изображенном на рис. 223, а, потенциальная энергия маятника минимальна и равновесие устойчиво, а на рис. 223, б потенциальная энергия максимальна и равновесие неустойчиво. Такой маятник является механической системой с одной степенью свободы. Колебания CiicreM со многими степенями свободы складываются из простых колебаний около положения устойчивого равновесия. Указанный Лагранжем метод изучения колебаний (см. § 52) имеет громадное применение в различных отраслях науки и техники и, в частности, в теории вибрации машин.

Рис. 223

Обобщенные координаты системы
Сложение двух сил
Разложение силы на две составляющие
Определение равнодействующей сходящихся сил
Колебания материальной точки
Количество движения
Момент количества движения
Мощность и работа силы

Источник