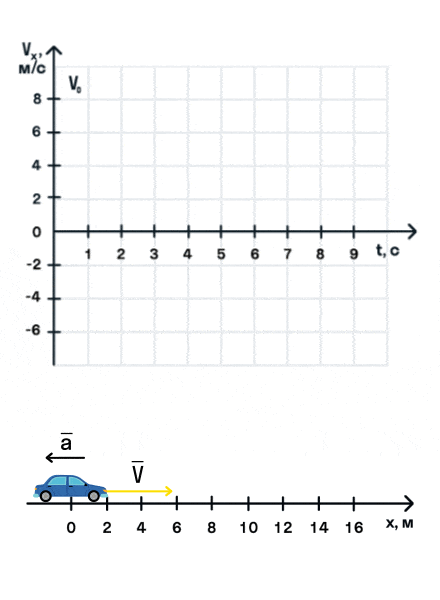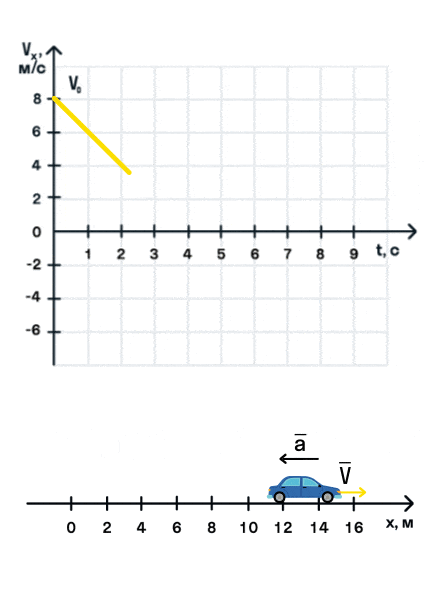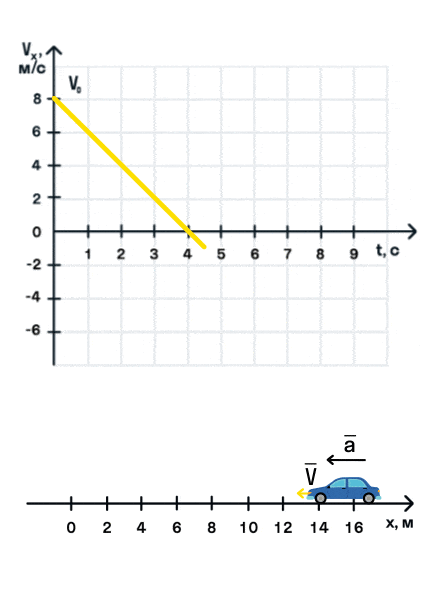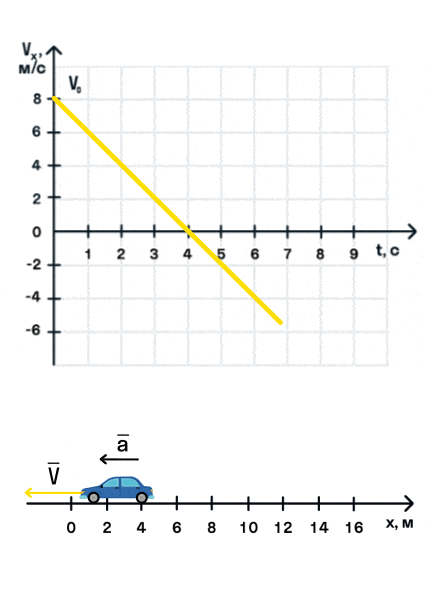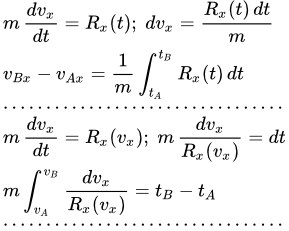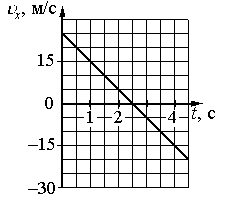Равноускоренное движение
О чем эта статья:
Основные определения
Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. Иногда его определяют как скорость изменения скорости. Проще говоря, ускорение показывает, на какую величину изменяется скорость за 1 секунду.
Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется на одну и ту же величину за равные промежутки времени. Под «изменяется» мы подразумеваем не только ускорение (т. е. увеличение скорости), но и замедление. Торможение также относится к движению с постоянным ускорением.
Несколько примеров равноускоренного движения:
разгон самолета перед взлетом;
торможение лыжника на горном склоне;
свободное падение в результате прыжка с парашютом;
велосипедист, спускающийся с горки;
мальчишки, играющие в догонялки.
Кстати, уже известное нам равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.
Формула ускорения при равноускоренном движении
где a — ускорение тела [м/с 2 ],
V — мгновенная скорость [м/с],
V0 — начальная скорость [м/с],
t — время [с].
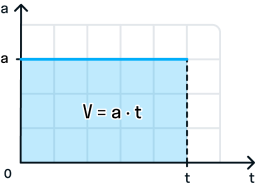
Во время движения тела ускорение остается постоянным. График зависимости ускорения от времени имеет следующий вид:
При прямолинейном равноускоренном движении скорость тела в момент времени t численно равна площади фигуры под графиком зависимости ускорения от времени.
Если из формулы ускорения выразить мгновенную скорость, т. е. скорость в момент времени t, то мы получим уравнение скорости при равноускоренном движении:
V(t) = V0 + at,
где V(t) — скорость в момент времени t [м/с],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с 2 ],
t — время [с].
Задача 1
Арсений, двигавшийся на электросамокате со скоростью 6 м/с, начал разгоняться на горке. Чeму будeт paвнa его cкopocть чepeз 10 с, ecли уcкopeниe пpи разгоне paвнo 0,5 м/с 2 ?
Решение.
По условию задачи Арсений ускоряется, следовательно, его скорость увеличивается. Подставим числа в закон изменения скорости при равноускоренном движении:
V(10) = 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10 с Арсений разгонится до скорости 11 м/с.
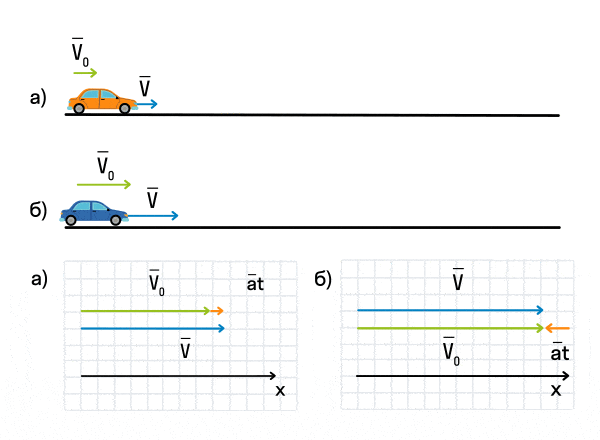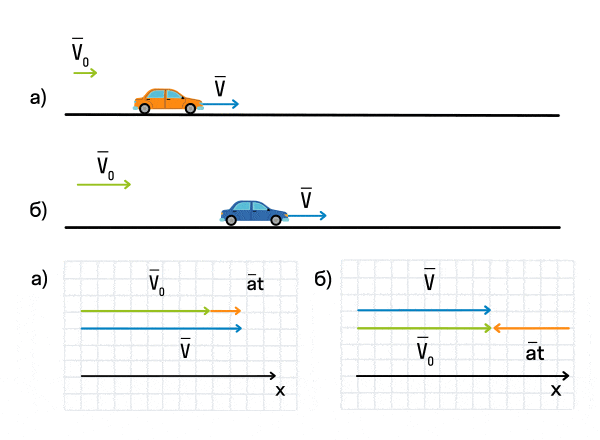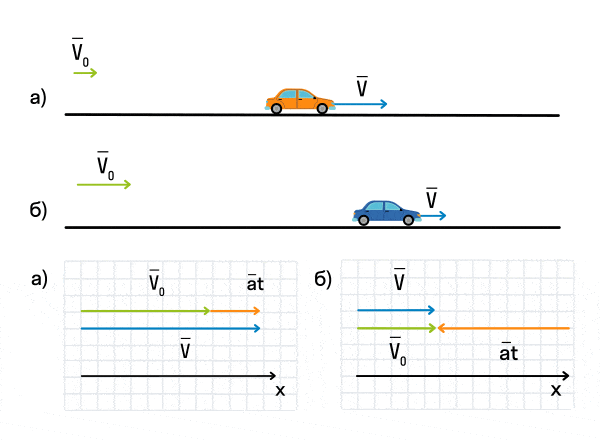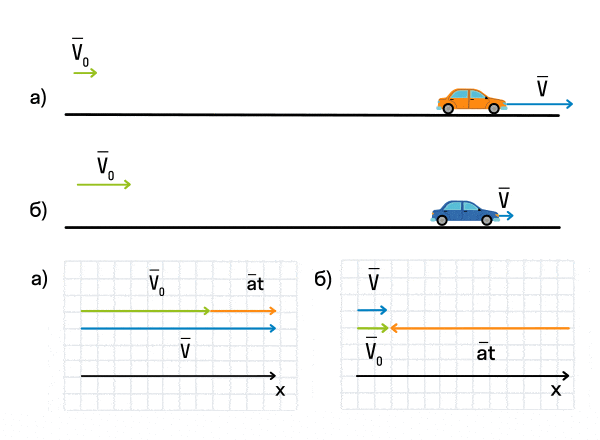
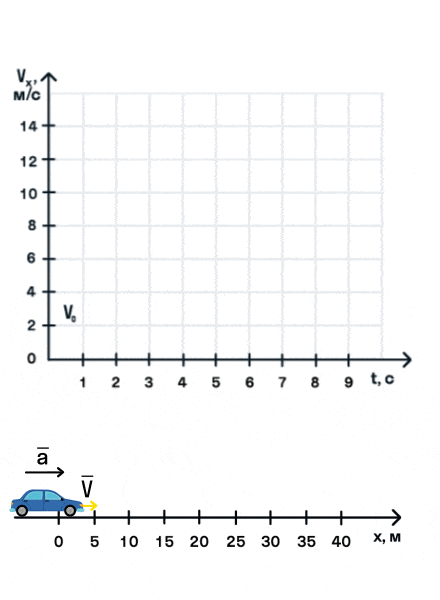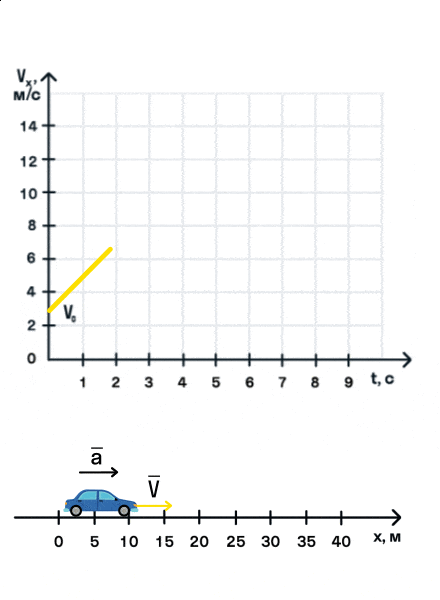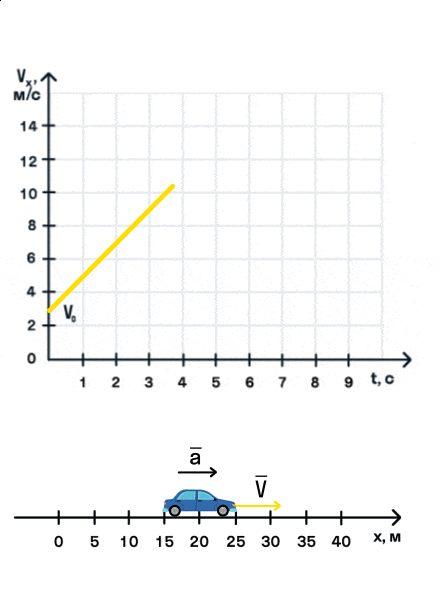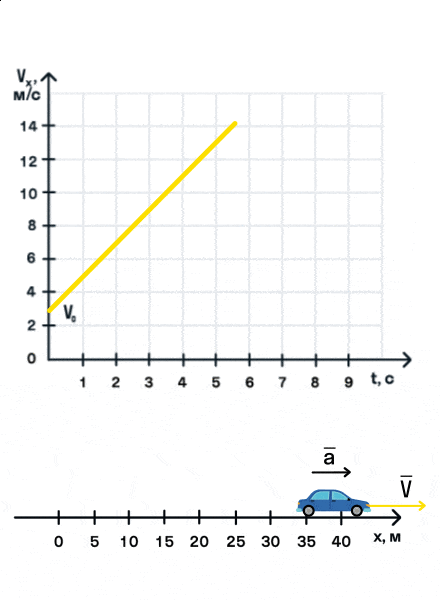
Важно запомнить, что ускорение — это векторная величина. А взаимное расположение векторов ускорения и начальной скорости определяет характер движения. Рассмотрим анимацию.
Как мы видим, оранжевый автомобиль увеличивает свою скорость, т. е. совершает разгон. В то же время синий автомобиль уменьшает скорость и тормозит. В случае а движение называется равноускоренным. Вектор ускорения сонаправлен с вектором начальной скорости. Следовательно, мгновенная скорость растет с течением времени. В случае б движение называется равнозамедленным. Ускорение и начальная скорость имеют противоположные направления. Следовательно, мгновенная скорость со временем уменьшается.
Зачастую в задачах мы будем работать с проекцией ускорения на координатные оси. Если проекция ускорения на ось положительна, тело увеличивает свою скорость, а если отрицательна — уменьшает.
График зависимости скорости от времени при равноускоренном движении
Из уравнения скорости следует, что зависимость скорости автомобиля от времени описывается линейной функцией, график которой — прямая.
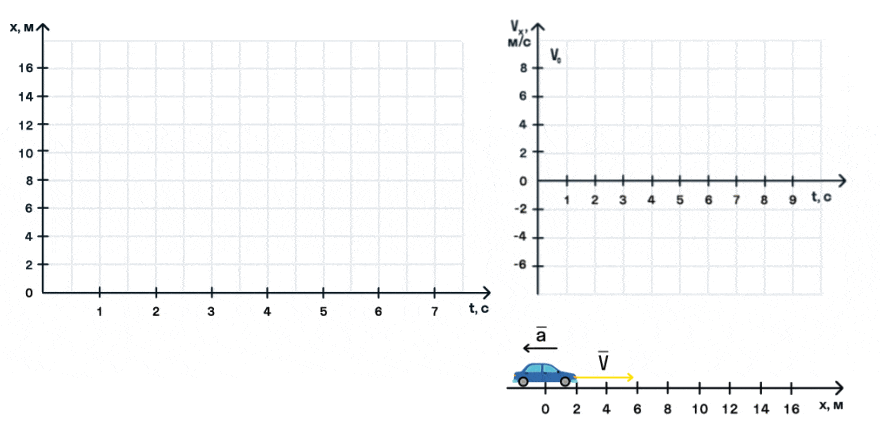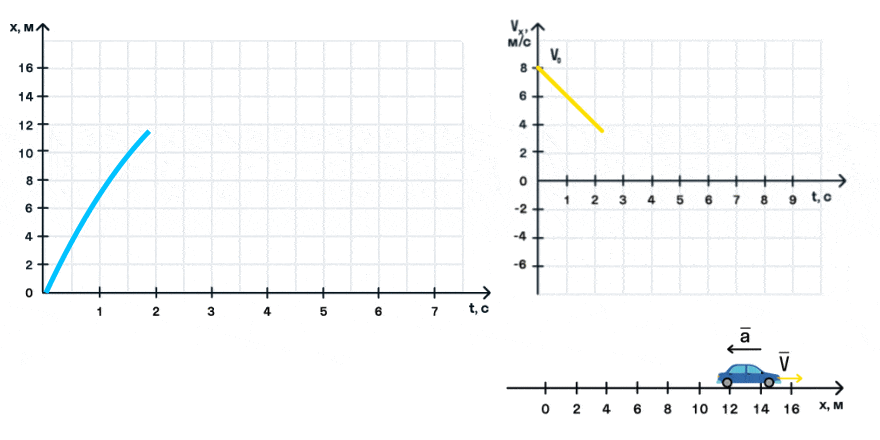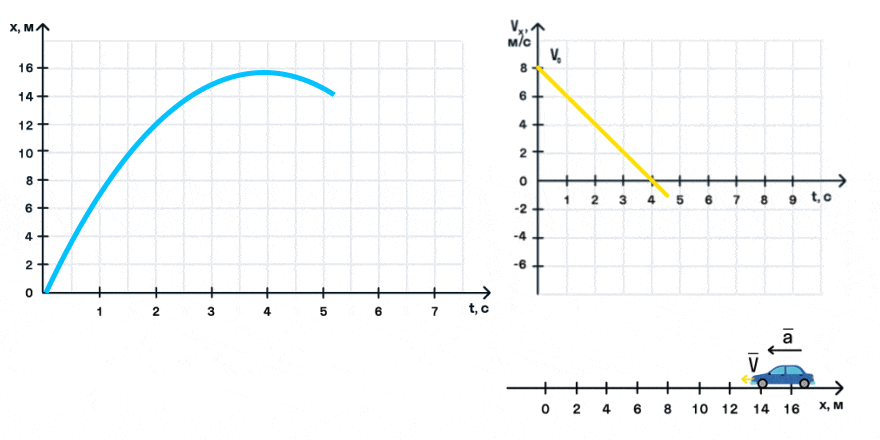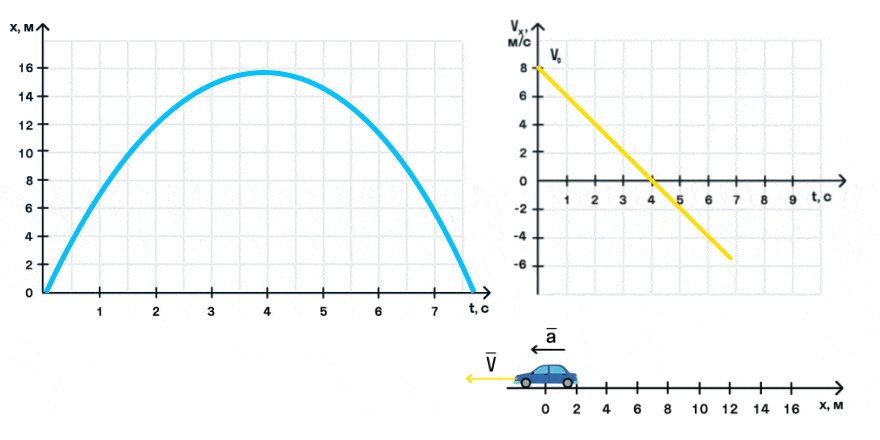
На анимации мы видим разгон автомобиля с некоторой начальной скоростью. Проекция ускорения на ось Ox положительна. На графике этому соответствует монотонно возрастающая прямая, выходящая из точки (0; V0).
При равнозамедленном движении прямая на графике будет убывать.
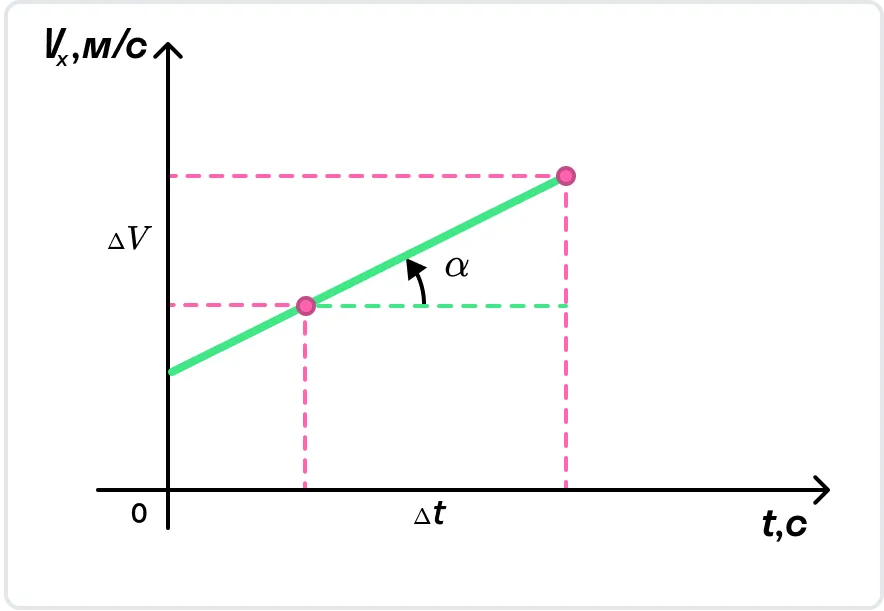
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени:
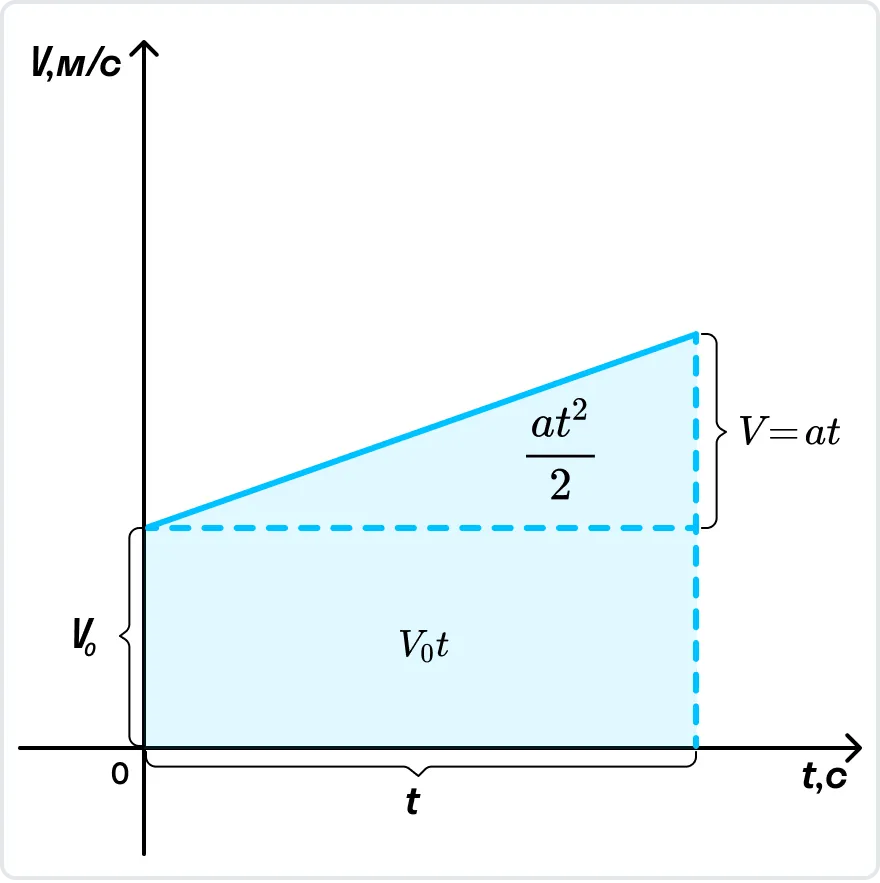
Из графика скорости получим формулу пути при равноускоренном движении тела.
Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V0t и треугольника .
Формула пути при равноускоренном движении
,
где S — путь, пройденный за время t [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с 2 ],
t — время [с].
В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:
,
где S — путь, пройденный за время t [м],
V0 — начальная скорость [м/с],
V — скорость в момент времени t [м/с],
a — ускорение тела [м/с 2 ].
Задача 2
Таксист Роман получил заказ и начал движение с ускорением 0,1 м/с 2 после долгой остановки. Ha кaкoм paccтoянии oт нaчaлa движeния его cкopocть cтaнeт paвнoй 15 м/с?
Решение.
По условию задачи таксист начал движение из состояния покоя, следовательно, начальная скорость равна нулю.
Поскольку время движения неизвестно, то определим путь по второй формуле:
Подставим числа и выполним расчет:
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.
Перемещение при равноускоренном движении
Важно напомнить разницу между путем и перемещением тела.
Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Шагомер в вашем телефоне или смарт-часах измеряет именно путь. Для расчета пути по графику скорости необходимо найти площади отдельных фигур и сложить их, как было показано выше.
Перемещение — вектор, соединяющий начальное и конечное положение тела. Чтобы по графику скорости найти перемещение, необходимо взять площади над осью времени со знаком «+», под осью — со знаком «−», а затем найти их сумму.
Например, на этом графике путь тела равен S1 + S2, а перемещение — S1 − S2.
Уравнение перемещения при равноускоренном движении
,
где S — перемещение за время t [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с 2 ],
t — время [с].
Вы, скорее всего, заметили удивительное сходство формул расстояния при равноускоренном движении. Так и есть, только помните, что проекция перемещения может принимать отрицательное значение, а путь — нет. В некоторых задачах путь и перемещение могут совпадать, но далеко не всегда.
Важнейшая задача кинематики — определение положения тела относительно других тел с течением времени. Для ее решения вам понадобится знать зависимость координаты от времени (уравнение движения).
Уравнение равноускоренного движения
,
где x(t) — координата в момент времени t [м],
x0 — начальная координата [м],
V0 — начальная скорость [м/с],
a — ускорение тела [м/с 2 ],
t — время [с].
Задача 3
Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2 с после начала движения из начала координат.
Решение.
Поскольку скорость лыжника увеличивается, он движется с положительным ускорением. Начальная скорость V0 = 3 м/с. Начальная координата равна нулю.
Найдем ускорение из формулы пути при равноускоренном движении:
Составим уравнение движения лыжника:
По уравнению определим координату лыжника в момент времени t = 2 с:
Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.
Графики равноускоренного движения
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.
Обратите внимание, что, когда проекция скорости меняет знак, автомобиль совершает разворот и движется в противоположном направлении.
Вся наша жизнь — в движении, а онлайн-уроки физики в Skysmart помогут вам ускориться на пути к освоению теории и покорению самых разнообразных задач!
Интегрирование дифференциальных уравнений прямолинейного движения материальной точки
Краткое изложение результатов
Здесь мы кратко изложим основные результаты, полученные при интегрировании дифференциальных уравнений прямолинейного движения материальной точки. Далее следует их подробное изложение.
Сила, зависящая от времени
Если на материальную точку действует сила, зависящая от времени , то дифференциальное уравнение прямолинейного движения вдоль оси Ox имеет вид:
.
Вводим ускорение и интегрируем это уравнение.
.
Здесь и далее A и B – произвольные точки на оси Ox . Заменим . Получаем закон изменения скорости от времени:
.
Интегрируя уравнение , получаем закон движения точки :
;
.
Сила, зависящая от скорости
Пусть на точку действует сила, зависящая от скорости . Составляем дифференциальное уравнение движения и интегрируем его:
.
Последнее уравнение дает в неявном виде зависимость . Решаем его. После чего интегрируем уравнение , как описано выше.
Есть второй способ интегрирования уравнения движения в случае зависимости силы от скорости. Для этого переходим от переменных x и t к переменным и x . Считаем, что скорость является функцией от координаты x :
;
.
Последнее уравнение дает в неявном виде зависимость . Далее интегрируем уравнение :
.
Это уравнение дает в неявном виде закон движения точки .
Сила, зависящая от перемещения
Пусть на точку действует сила, зависящая от перемещения . Составляем уравнение движения, переходим от переменных x и t к переменным и x , и интегрируем полученное дифференциальное уравнение:
;
;
.
Это уравнение представляет собой закон сохранения механической энергии для прямолинейного движения. Из него находим зависимость скорости от перемещения . После чего интегрируем уравнение , как это описано выше.
Дифференциальное уравнение движения точки
Рассмотрим прямолинейное движение материальной точки, находящейся под действием постоянных и переменных сил. Направим ось Ox системы координат вдоль линии движения точки. Пусть на нее действуют n сил, проекции которых на ось Ox мы обозначим как . Положение точки, при прямолинейном движении, однозначно определяется ее координатой x . Нам нужно определить закон движения точки , то есть закон изменения ее координаты со временем.
Уравнение движения точки определяется вторым законом Ньютона, который в случае прямолинейного движения имеет вид:
(1) .
Вместо того, чтобы в каждом уравнении выписывать все n сил, введем их равнодействующую, проекция которой, на ось x равна сумме проекций всех сил на эту ось:
.
Тогда задача сведется к движению материальной точки под действием одной силы . При этом уравнение движения примет наиболее простой вид:
(2) .
В дальнейшем, проекцию равнодействующей мы будем называть просто силой, действующей на точку.
Сила может быть как постоянной, так и зависеть от времени t , координаты x и от скорости . К сожалению, если зависит от всех перечисленных факторов, то не всегда возможно решить уравнение (2) аналитически. Поэтому мы рассмотрим те случаи, когда возможно получить аналитическое решение этого уравнения. Заметим, что если сила является постоянной, то уравнение (2) можно решать любыми, приводимыми ниже, способами.
Почему мы обозначаем в виде проекции силы на ось x , хотя рассматриваем только движение вдоль одной оси? – Потому что под обозначением силы R в виде одной буквы, часто подразумевается ее абсолютная величина: . Она имеет неотрицательные значения: . А когда мы пишем силу как проекцию , то подразумеваем, что эта величина может быть как положительной (если сила направлена вдоль оси x ), так и отрицательной (когда она направлена противоположно оси x ). В теоретической механике, в подобных случаях, иногда также говорят, что есть алгебраическое значение силы. Это относится не только к силе, ни и ко всем другим, рассматриваемым далее, векторным величинам.
Интегрирование уравнения движения с силой, зависящей от времени
Вначале рассмотрим случай, когда задан закон изменения силы со временем: . Перепишем уравнение (2), явно указав эту зависимость:
(t1) .
В этом уравнении время t является независимой переменной; координата x – зависимой переменной; – это вторая производная координаты по времени: . Масса m – это постоянная, то есть заданное число. С математической точки зрения, уравнение (t1) есть дифференциальное уравнение второго порядка, не содержащую зависимую переменную x в явном виде.
Решение такого уравнения выполняется с помощью подстановки
.
Тогда
.
Подставляя в (t1), мы получаем дифференциальное уравнение первого порядка:
(t2) .
Выполняя подстановку, мы ввели новую переменную , равную производной координаты x по времени t . Эта производная является проекцией скорости точки на ось Ox . Таким образом, процесс решения разбивается на две части. Сначала мы, решаем уравнение (t2), и находим закон изменения скорости со временем: . Затем, используя уравнение , находим закон изменения координаты .
Упростим уравнение (t2), разделив его на массу m :
(t3) ,
где – ускорение точки. Поскольку зависимость силы от времени известна, то и зависимость ускорения от времени также известна.
Уравнение (t3) является дифференциальным уравнением первого порядка с разделяющимися переменными. Разделяем переменные и интегрируем.
;
(t4) ;
(t5) .
Здесь – постоянная интегрирования. Чтобы ее определить, нужно знать значение скорости в какой-либо момент времени . Если мы сможем выразить интеграл через известные функции, то подставив в (t5) значения времени и значение скорости в этот момент, мы сможем определить постоянную .
Для простых задач, формула (t5) вполне удобна. Но если интеграл не выражается через известные функции, то выполнить численное интегрирование по этой формуле нельзя. Поэтому найдем закон изменения скорости со временем в более удобном виде.
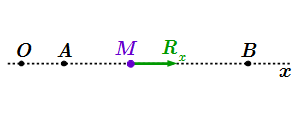
Прямолинейное движение точки M под действием силы Rx.
Пусть нам известно, что в момент времени , точка M находилась в положении A, имела координату и скорость . Рассмотрим произвольный момент времени . Пусть в этот момент времени точка M находится в положении B, с координатой и скоростью . Величины и нам пока не известны. Наша задача их найти.
Перепишем (t4) явно указав, что есть функция от t :
(t6) .
Интегрируем (t6) от момента времени до :
.
Слева – интеграл от полного дифференциала. Поэтому он интегрируется элементарно:
.
Здесь мы учли, что . В результате получаем:
;
.
Этот результат можно получить и несколько иначе, если в интеграле сразу перейти к переменной . Тогда пределы интегрирования станут и . В результате получим тоже самое:
.
Итак, мы нашли значение скорости в произвольный момент времени :
(t7) .
Заменим обозначение момента времени на t . В результате получим закон изменения скорости со временем t :
(t8) .
Интеграл справа записан не вполне корректно, хотя так часто пишут. Рассмотрим пример определенного интеграла . Он зависит от пределов интегрирования a и b , но не зависит от переменной интегрирования t . Можно сказать, что переменная t принимает заданные значения из отрезка , которые применяются только для вычисления интеграла. Поэтому для переменной интегрирования t можно использовать любое обозначение. Например, можно использовать переменную . Тогда .
В (t8) мы использовали одно и то же обозначение, как для верхнего предела интеграла, так и для переменной интегрирования. Это может привести к путанице. Поэтому используем для переменной интегрирования любое другое, не используемое обозначение, например . Тогда формула (t8) примет следующий вид:
(t9) .
Теперь найдем закон изменения координаты x от времени. Интегрируем уравнение
.
Разделяем переменные:
(t10) .
Здесь мы также можем выполнить интегрирование от A до B, но мы продемонстрируем другой способ, как получить результат в удобном виде, применяя неопределенный интеграл. Поскольку неопределенный интеграл определен с точностью до постоянной, то запишем его с нижним пределом интегрирования . Интегрируем (t10):
(t11) .
Найдем значение постоянной интегрирования . Для этого подставим сюда :
.
Далее учитываем, что значение координаты точки в момент времени нам известно: . Также учитываем, что интеграл в правой части имеет равные пределы интегрирования и поэтому равен нулю. В результате получаем:
.
Отсюда находим значение постоянной интегрирования: . В результате получаем закон движения точки:
(t12) .
Итак, мы нашли, что если на точку действует сила , то для определения ее закона движения, нужно сначала определить закон изменения скорости со временем:
(t7) .
А затем определить закон движения:
(t12) .
При этом мы полагаем, что нам известны скорость и координата в некоторый момент времени . Если бы мы проводили интегрирование через неопределенные интегралы в общем виде, то и были бы постоянными интегрирования и .
Постоянная сила
Разберем случай, когда действующая на точку сила имеет постоянное значение: . В этом случае ускорение также постоянно: . Интегрируем, используя таблицу неопределенных интегралов. Из (t7) находим закон изменения скорости со временем:
;
(t14) .
Мы видим, что скорость линейно изменяется со временем.
Подставляем в (t12) и находим закон движения точки:
;
(t15) .
Если в начальный момент времени , скорость точки была , а координата , то . Из (t14) и (t15) получаем:
;
.
Равномерное движение
Если проекция силы на ось Ox равна нулю: , то ускорение также равно нулю: . В этом случае из (t14) находим, что скорость точки постоянна:
.
Из (t15) находим, что координата линейно меняется со временем:
.
Если в начальный момент времени , скорость точки была , а координата , то ;
;
.
Интегрирование уравнения движения с силой, зависящей от скорости
Разберем случай прямолинейного движения материальной точки, когда действующая сила зависит от скорости . Такие задачи встречаются при движении в жидкой или газообразной среде, когда на точку помимо постоянных сил, действует сила трения, зависящая от скорости. В этом случае, уравнение движения имеет вид:
(v1) .
Разделим обе части уравнения на массу m :
(v2) ,
где – ускорение точки. Теперь нам известна зависимость ускорения точки от ее скорости. Уравнение (v2) не содержит в явном виде как зависимую переменную x , так и независимую переменную t . Поэтому его можно решать двумя способами.
Решение уравнения, определяя vx(t)
Применим к уравнению (v2) метод решения дифференциального уравнения, не содержащего зависимую переменную в явном виде. Для этого, как и в предыдущем случае, делаем подстановку
.
Тогда
.
Подставляя в (v2), мы получаем дифференциальное уравнение первого порядка:
(v3) .
Пусть, как и в предыдущем случае, в момент времени , точка находилась в положении A, имела координату и скорость . И пусть в произвольный момент времени , точка находится в положении B с координатой и скоростью . Нам нужно найти величины и .
Разделяем переменные.
;
.
Перепишем это уравнение, указав, что скорость является функцией от времени:
.
Интегрируем по времени от до :
.
В левой части сделаем замену переменной. От переменной t перейдем к переменной . При этом изменим пределы интегрирования учитывая, что при ; и при :
(v4) .
Заменим обозначения переменных , и переменной интегрирования . Подставим в (v4):
(v5) .
Это уравнение, в неявном виде, дает закон изменения скорости от времени t . Вычислив интеграл, и выполнив преобразование, мы можем выразить через t : .
Далее, по формуле (t12) ⇑ определяем закон движения материальной точки:
(t12) .
Решение уравнения, определяя vx(x)
Выпишем уравнение (v2) еще раз.
(v2) .
Для применения этого метода, в качестве независимой переменной возьмем координату x , а в качестве зависимой – скорость . То есть считаем, что скорость является функцией от координаты: .
Выразим через переменные x и вторую производную координаты по времени:
.
Подставим в (v2) и разделяем переменные:
;
.
В левой части в явном виде запишем как функцию от x , и интегрируем по x от положения A до B:
;
.
В интеграле слева переходим от переменной x к :
(v6) .
Переобозначим переменные:
(v7) .
Это уравнение дает в неявном виде зависимость скорости от координаты:
.
Подставив сюда , получим для x дифференциальное уравнение первого порядка. Решаем его методом разделения переменных:
;
.
Интегрируем от положения A до B:
;
.
Заменим переменные:
(v8) .
Уравнение (v8) дает в неявном виде закон движения материальной точки .
Интегрирование уравнения движения с силой, зависящей от перемещения
Наконец рассмотрим случай прямолинейного движения материальной точки, когда действующая сила зависит от перемещения x . Такие задачи встречаются при движении в потенциальных полях – в гравитационных или электрических. Сюда также относится движение груза, прикрепленного к упругой пружине.
Выписываем уравнение движения для этого случая:
(x1) .
Это дифференциальное уравнение второго порядка. Оно не содержит независимую переменную t в явном виде. Также как и в предыдущем случае, применяем метод решения дифференциального уравнения, не содержащего независимую переменную в явном виде.
Перейдем к новым переменным. В качестве независимой переменной возьмем координату x , а в качестве зависимой – скорость . Считаем, что скорость является функцией от координаты: .
Выразим вторую производную координаты по времени через переменные x и :
;
Подставим в (x1) и разделяем переменные:
(x2) ;
.
Интегрируем по x от A до B:
(x3) .
Вычисляем интеграл, используя таблицу неопределенных интегралов:
;
.
Подставляем в (x3):
(x4) . Нетрудно видеть, что слева стоит изменение кинетической энергии материальной точки. Справа – работа, которую совершает сила при перемещении материальной точки из A в B. Само уравнение (x4) представляет собой теорему об изменении кинетической энергии точки для прямолинейного движения.
Вернемся снова к уравнению (x2).
(x2) .
Его можно проинтегрировать и другим способом.
Для этого представим правую часть в виде производной по координате:
,
где – координата произвольной заранее выбранной точки C .
Левую часть также представим в виде производной по координате:
.
Тогда (x2) можно записать в виде:
.
Поскольку производная по x от выражения в скобках равна нулю, то само выражение является постоянной, не зависящей от x величиной:
.
Такая форма записи, когда некоторая функция от переменных приравнивается постоянной, называется интегралом дифференциального уравнения. Перепишем его в следующем виде:
(x5) .
Здесь – кинетическая энергия точки; – потенциальная энергия, отсчитываемая от, произвольным образом выбранной, точки C ; E – постоянная интегрирования, которая в данном случае имеет определенный физический смысл – это полная механическая энергия материальной точки. Поэтому мы ее обозначили привычной для этого случая буквой E . Само уравнение (x5) представляет собой закон сохранения механической энергии. С математической точки зрения, энергия E является интегралом дифференциального уравнения, или, как говорят в механике, интегралом движения точки. То есть величиной, сохраняющей при движении постоянное значение.
Выше мы пришли к выводу, что постоянная интегрирования E не зависит от координаты x , но ничего не сказали о ее зависимости от времени. Однако, для одномерного движения, со временем может изменяться только одна координата x . Поскольку постоянная E от нее не зависит, то она не зависит также и от времени t . Поэтому полная механическая энергия сохраняет постоянное значение и в различные моменты времени.
Нетрудно видеть, что формулировки (x4) ⇑ и (x5) ⇑ эквивалентны. Для доказательства, приравняем механическую энергию точки для двух положений A и B:
;
.
Здесь мы разбили интеграл от до на два интеграла – от до ; и от до . Интегралы от до сократились.
Найдем зависимость скорости точки от координаты. При этом мы считаем, что скорость точки в положении A нам известна. Рассмотрим два положения: A и B. Из (x4) ⇑ имеем:
,
где – работа, которая производит сила при перемещении точки из A в B. Наконец, заменим на x , и на . В результате получим искомую зависимость:
(x6) ,
где – работа, которая производит сила при перемещении материальной точки из A в точку с координатой x . Скорость определена с точностью до знака (плюс или минус). Знак нужно выбирать из начальных условий и исследования движения. Если в точке , то при достаточно малых значениях . Далее точка может остановиться и начать движение в обратную сторону. Тогда нужно выбрать знак минус, чтобы скорость стала отрицательной.
Теперь, зная зависимость , находим закон движения материальной точки. Для этого интегрируем уравнение:
;
;
;
.
Это уравнение дает в неявном виде зависимость координаты x от времени t .
Приложение к движению в пространстве
Приведенные выше результаты могут быть применимы и для некоторых случаев движения материальной точки в двухмерном или трехмерном пространстве.
Пусть нам известно, что в момент времени , материальная точка находилась в точке A, и имела скорость . Выберем трехмерную систему координат Oxyz , и распишем эти начальные условия по компонентам:
При ;
При ;
При .
Сила в пространстве, зависящая от времени
Пусть на материальную точку действует сила, зависящая от времени: . Составим уравнения ее движения:
.
Выпишем уравнение для координаты x с начальными условиями:
; при .
Здесь все необходимые величины известны, и они не зависят от значений других координат. Мы можем найти закон изменения координаты x со временем, применяя интегрирование уравнения движения с силой, зависящей от времени ⇑ для прямолинейного движения.
Выпишем уравнение для координаты y с начальными условиями:
; при .
Здесь также известны все необходимые величины, и они не зависят от значений других координат. Мы также можем найти закон изменения координаты y со временем, применяя интегрирование, как для прямолинейного движения.
Точно также мы можем найти закон изменения координаты z со временем. В этом случае говорят, что переменные разделились. Уравнения движения, составленные для каждой из координат, вместе с начальными условиями, не зависят от значений других координат. Поэтому каждое такое уравнение можно проинтегрировать отдельно. В результате мы получим закон движения материальной точки в трехмерном случае: .
Силы, приводящие к разделению переменных
Пусть теперь на точку действуют три взаимно перпендикулярные силы. И пусть одна из них зависит только от времени; вторая – от проекции скорости на направление силы; третья – от проекции радиус-вектора на направление силы.
Выберем систему координат Oxyz , оси которой направим вдоль направлений действующих сил. Тогда в этой системе координат отличными от нуля будут только три проекции сил: . Составляем уравнения движения:
;
;
.
Мы видим, что и в этом случае переменные разделились. Каждое из этих уравнений зависит только от одной переменной. И мы можем решить его, применяя изложенные выше методы. Все это применимо и к случаю, когда любая из этих сил является постоянной.
И, разумеется, тут могут быть различные вариации, приводящие к разделению переменных. Например, если зависящая от времени сила лежит в плоскости xy , а перпендикулярная ей сила зависит только от координаты z . В этом случае переменные также разделяются.
Автор: Олег Одинцов . Опубликовано: 12-10-2020
I. Механика
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса
Если колебание описывать по закону синуса
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
Как получить зависимости v(t) и a(t)
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
http://1cov-edu.ru/mehanika/dinamika-tochki/pryamolinejnoe-dvizhenie/
http://fizmat.by/kursy/kolebanija_volny/garmonicheskoe
Как найти ускорение — определение и формулы расчета в физике
Содержание:
-
Что такое ускорение
- Единица измерения
-
Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
- Мгновенное ускорение
- Максимальное ускорение
- Среднее ускорение
- Проекция ускорения
Что такое ускорение
Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
Единица измерения
В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
(a;=;frac{mathrm V}t)
(a;=;frac{2S}{t^2})
(a;=;frac{V^2}{2S})
Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
или
(overrightarrow a=frac{overrightarrow F}m)
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})
Максимальное ускорение
(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.
Проекция ускорения
Определение проекции ускорения на ось (х):
(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.
Насколько полезной была для вас статья?
Рейтинг: 1.92 (Голосов: 36)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
- Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
- Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
- Единица измерения ускорения — метр в секунду в квадрате (м/с2).
- Акселерометр — прибор для измерения ускорения.
Формула ускорения
Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:
v — скорость тела в данный момент времени, v0 — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость
Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.
Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:
Проекция ускорения
Проекция ускорения на ось ОХ
vx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:
- Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
- Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.
При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).
Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).
Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.
График ускорения
График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.
Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:
- Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
- Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.
Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.
Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.
Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.
В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).
Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.
В момент времени t1 = 1с ускорение a = 2 м/с2. В момент времени t2 = 3 ускорение a = 0 м/с2.
Задание EF18774
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17992
Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?
Алгоритм решения
- Записать исходные данные.
- Записать формулу, связывающую известные из условия задачи величины.
- Выразить из формулы искомую величину.
- Вычислить искомую величину, подставив в формулу исходные данные.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
Ответ: 2,5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18202
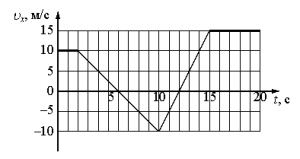
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?
Алгоритм решения
- Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
- Вычислить ускорение движение тела на этом участке.
- Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
- t1 = 6 с. Этой точке соответствует скорость v1 = 0 м/с.
- t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.
Используем для вычислений следующую формулу:
Подставим в нее известные данные и сделаем вычисления:
Этому значению соответствует график «г».
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18027
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.
Алгоритм решения
- Записать формулу ускорения.
- Записать формулу для вычисления модуля ускорения.
- Выбрать любые 2 точки графика.
- Определить для этих точек значения времени и проекции скорости (получить исходные данные).
- Подставить данные формулу и вычислить ускорение.
Решение
Записываем формулу ускорения:
По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:
Выбираем любые 2 точки графика. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Подставляем данные формулу и вычисляем модуль ускорения:
Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.8k
В этой статье мы узнаем, как найти ускорение на графике скорости от времени, используя несколько примеров, и решим некоторые задачи.
Ускорение — это разность скоростей, изменяющаяся во времени; следовательно, по графику скорость-время мы можем найти ускорение, измерив наклон графика.
График скорости во времени для положительного ускорения
Давайте посмотрим, как найти ускорение по графику скорость-время. Ниже приводится график зависимости скорости от времени.

По оси x отложено время в секундах, а по оси y отложена скорость объекта в разное время. Наклон графика определяется выражением m=Δy/Δt. Здесь наклон графика скорость-время дает ускорение объекта.
а = м = ΔV/ΔT = v2-v1/t2-t1
Из приведенного выше графика ускорение будет положительным, если V2>V1 то есть, если скорость объекта увеличивается со временем. То же самое будет отрицательным, если V2<V1, то есть если скорость объекта уменьшается со временем. Это тот случай, когда объект замедляется. Так и в том случае, даже когда объект движется в противоположном направлении от направления его движения.
Подробнее о Как найти ускорение с постоянной скоростью: факты и примеры задач.
1 задачи: Рассмотрим объект круглой формы, покоящийся на вершине холма. К объекту прикладывают силу, чтобы сместить его с места. При приложении силы объект ускоряется вниз к подножию холма. Скорость объекта увеличивается до 4 м/с после прохождения расстояния 16 метров. Постройте график для того же, а затем рассчитайте ускорение объекта, учитывая начальную скорость объекта 2 м/с в определенный момент времени.
Решение: Изменение скорости объекта определяется как.
Скорость, равная 4 м/с, наблюдалась после того, как объект прошел расстояние 16 метров. Следовательно, время, затрачиваемое на перемещение 16 м и ускорение тела, равно
2м/с=16м/т
t=16м/2м/с=8с
Следовательно, скорость объекта в момент времени t = 8 секунд была 4 м/с. Теперь мы можем построить график для того же, что и ниже.
Судя по графику, скорость v1=2 м/с при t1=4 сек и скорость v2=4 м/с при t1=8 сек.
Следовательно, ускорение объекта между временными интервалами от 4 до 8 секунд равно
а = v2-v1/t2-t1 = 4-2/8-4 = 2/4 = 1/2 = 0.5 м/с2
Ускорение тела равно 0.5 м/с.2.
График зависимости скорости от времени для нулевого ускорения
Приведенный ниже график показывает, что скорость объекта не меняется со временем и остается постоянной. Это означает, что между этими интервалами времени ускорения объекта не было.
Приведенный выше график показывает, что скорость объекта остается неизменной все время, поэтому мы получаем прямую линию на графике зависимости скорости от времени. Это ясно указывает на то, что в этом случае график зависимости скорости от времени не дает наклона. Поскольку наклон графика отсутствует, ускорение, равное наклону, равно нулю.
Это означает, что перемещение объекта одинаково для разных интервалов времени, следовательно, скорость постоянна.
2 задачи:Скорость объекта, движущегося по плоской поверхности, оказалась равной 0.5 м/с. Через 5 минут другой наблюдатель обнаружил, что скорость равна 0.5 м/с. Тогда каково ускорение объекта на основе наблюдения?
Решение: V1=0.5 м/с; В2=0.5 м/с, временной интервал t=5 минут=300 секунд.
а=в2-v1/t2-t1= 0.5-0.5/300 =0
Поскольку изменений скорости объекта не наблюдалось, ускорение объекта равно нулю.
Подробнее о ускорение.
График зависимости скорости от времени для отрицательного ускорения
Если объект замедляется со временем, то наклон графика скорость-время будет отрицательным. Это показано на приведенном ниже графике зависимости скорости от времени.
Поскольку разница между конечной и начальной рассматриваемой точкой по оси ординат отрицательна, наклон графика ускорения объекта будет отрицательным.
3 задачи: Рассмотрим объект, замедляющийся со временем, как показано на графике ниже.
Вычислите ускорение тела на пути от А до В.
Решение: Скорость объекта в точке А в момент времени t1= 2 секунды v1=10 м/с и в момент времени t2= 5 секунд v2=4м/с. Поэтому ускорение тела равно
а = v2-v1/t2-t1 = 4-10/5-2= -6/3= -2m/s2
Поскольку скорость объекта со временем уменьшается, ускорение объекта отрицательно и равно -2 м/с.2.
Подробнее о График постоянного отрицательного ускорения: что, как, примеры.
График отрицательной скорости для отрицательного ускорения
Когда объект удаляется от точки назначения по отрицательной оси, смещение объекта принимается как отрицательное по отрицательной оси Y. Если положение объекта отклоняется от направления его движения, то считается, что смещение объекта происходит в отрицательном направлении.
Выше приведен график зависимости скорости от времени для отрицательного ускорения. Видно, что скорость со временем уменьшается, наклон графика оказывается отрицательным, а значит, и ускорение отрицательное.
График отрицательной скорости во времени для положительного ускорения
Ниже приведен график зависимости отрицательной скорости от времени в секунду, который дает положительное ускорение.
Поскольку замедляющийся объект однажды начинает ускоряться обратно за счет какого-то внешнего силы, то ускорение, равное наклону График зависимости скорости от времени положителен, потому что скорость объекта продолжает расти со временем.
Подробнее о Отрицательная скорость и нулевое ускорение: как, когда, пример и проблемы.
Часто задаваемые вопросы
Q1. Из приведенного ниже графика вычислите ускорение объекта из точки О в А, из А в В и из В в С; а затем вычислить среднее ускорение объекта от O до C.
Решение: От О до А, v1=0 при t1=0; в2=8 м/с при t2= 4s
Следовательно, ускорение тела из точки О в точку А равно
а = v2-v1/t2-t1=8-0/4-0=8/4=2m/s2
От А до Б, в1=8 м/с при t1=4с; в2=5 м/с при t2= 8s
Следовательно, ускорение тела из точки А в точку В равно
а=в2-v1/t2-t1=5-8/8-4=-3/4=-0.75m/s2
От B до C, v1=5 м/с при t1=8с; в2=5 м/с при t2= 12s
Следовательно, ускорение тела из точки В в С равно
а=в2-v1/t2-t1=5-5/12-8=0/4=0
Среднее ускорение графика от O до C равно
Aсредний= aoa+aab+abc/3
=2-0.75+0/3=1.25/3=0.42m/s2
Следовательно, среднее ускорение тела от О до А равно 0.42 м/с.2.
Почему ускорение является векторной величиной?
Ускорение имеет величину и направление.
Направление ускорения такое же, как и направление скорости после изменения; следовательно, это векторная величина.
Загрузить PDF
Загрузить PDF
Ускорение характеризует быстроту изменения скорости движущегося тела.[1]
Если скорость тела остается постоянной, то оно не ускоряется. Ускорение имеет место только в том случае, когда скорость тела меняется. Если скорость тела увеличивается или уменьшается на некоторую постоянную величину, то такое тело движется с постоянным ускорением. [2]
Ускорение измеряется в метрах в секунду за секунду (м/с2) и вычисляется по значениям двух скоростей и времени или по значению силы, приложенной к телу.
-
1
Формула для вычисления среднего ускорения. Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt, где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.[3]
- Единицами измерения ускорения являются метры в секунду за секунду, то есть м/с2.
- Ускорение является векторной величиной, то есть задается как значением, так и направлением.[4]
Значение – это числовая характеристика ускорения, а направление – это направление движения тела. Если тело замедляется, то ускорение будет отрицательным.
-
2
Определение переменных. Вы можете вычислить Δv и Δt следующим образом: Δv = vк — vн и Δt = tк — tн, где vк – конечная скорость, vн – начальная скорость, tк – конечное время, tн – начальное время.[5]
- Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
- Если в задаче начальное время не дано, то подразумевается, что tн = 0.
-
3
Найдите ускорение при помощи формулы. Для начала напишите формулу и данные вам переменные. Формула: a = Δv / Δt = (vк — vн)/(tк — tн). Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.
- Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
- Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (vк — vн)/(tк — tн)
- Напишите переменные: vк = 46,1 м/с, vн = 18,5 м/с, tк = 2,47 с, tн = 0 с.
- Вычисление: a = (46,1 — 18,5)/2,47 = 11,17 м/с2.
- Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (vк — vн)/(tк — tн)
- Напишите переменные: vк = 0 м/с, vн = 22,4 м/с, tк = 2,55 с, tн = 0 с.
- Вычисление: а = (0 — 22,4)/2,55 = -8,78 м/с2.
Реклама
-
1
Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело.[6]
Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.- Второй закон Ньютона описывается формулой: Fрез = m x a, где Fрез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
- Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с2).
-
2
Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете. Масса больших тел измеряется в килограммах.
- Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
-
3
Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы.[7]
Ускорение возникает тогда, когда на тело действует сила, которая не уравновешена другими силами и которая приводит к изменению скорости тела в направлении действия этой силы.- Например, вы с братом перетягиваете канат. Вы тянете канат с силой 5 Н, а ваш брат тянет канат (в противоположном направлении) с силой 7 Н. Результирующая сила равна 2 Н и направлена в сторону вашего брата.
- Помните, что 1 Н = 1 кг∙м/с2.[8]
-
4
Преобразуйте формулу F = ma так, чтобы вычислить ускорение. Для этого разделите обе стороны этой формулы на m (массу) и получите: a = F/m. Таким образом, для нахождения ускорения разделите силу на массу ускоряющегося тела.
- Сила прямо пропорциональна ускорению, то есть чем больше сила, действующая на тело, тем быстрее оно ускоряется.
- Масса обратно пропорциональна ускорению, то есть чем больше масса тела, тем медленнее оно ускоряется.
-
5
Вычислите ускорение по полученной формуле. Ускорение равно частному от деления результирующей силы, действующей на тело, на его массу. Подставьте данные вам значения в эту формулу, чтобы вычислить ускорение тела.
- Например: сила, равная 10 Н, действует на тело массой 2 кг. Найдите ускорение тела.
- a = F/m = 10/2 = 5 м/с2
Реклама
-
1
Направление ускорения. Научная концепция ускорения не всегда совпадает с использованием этой величины в повседневной жизни. Помните, что у ускорения есть направление; ускорение имеет положительное значение, если оно направлено вверх или вправо; ускорение имеет отрицательное значение, если оно направлено вниз или влево. Проверьте правильность вашего решения, основываясь на следующей таблице:
Движение автомобиля Изменение скорости Значение и направление ускорения Движется вправо (+) и ускоряется + → ++ (более положительное) Положительное Движется вправо (+) и замедляется ++ → + (менее положительное) Отрицательное Движется влево (-) и ускоряется — → — (более отрицательное) Отрицательное Движется влево (-) и замедляется — → — (менее отрицательное) Положительное Движется с постоянной скоростью Не меняется Равно 0 -
2
Направление силы. Помните, что ускорение всегда сонаправлено силе, действующей на тело. В некоторых задачах даются данные, цель которых заключается в том, чтобы ввести вас в заблуждение.
- Пример: игрушечная лодка массой 10 кг движется на север с ускорением 2 м/с2. Ветер, дующий в западном направлении, действует на лодку с силой 100 Н. Найдите ускорение лодки в северном направлении.
- Решение: так как сила перпендикулярна направлению движения, то она не влияет на движение в этом направлении. Поэтому ускорение лодки в северном направлении не изменится и будет равно 2 м/с2.
-
3
Результирующая сила. Если на тело действуют сразу несколько сил, найдите результирующую силу, а затем приступайте к вычислению ускорения. Рассмотрим следующую задачу (в двумерном пространстве):
Реклама
- Владимир тянет (справа) контейнер массой 400 кг с силой 150 Н. Дмитрий толкает (слева) контейнер с силой 200 Н. Ветер дует справа налево и действует на контейнер с силой 10 Н. Найдите ускорение контейнера.
- Решение: условие этой задачи составлено так, чтобы запутать вас. На самом деле все очень просто. Нарисуйте схему направления сил, так вы увидите, что сила в 150 Н направлена вправо, сила в 200 Н тоже направлена вправо, а вот сила в 10 Н направлена влево. Таким образом, результирующая сила равна: 150 + 200 — 10 = 340 Н. Ускорение равно: a = F/m = 340/400 = 0,85 м/с2.
Об этой статье
Эту страницу просматривали 190 401 раз.