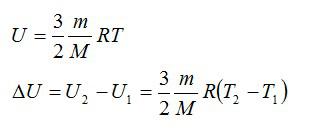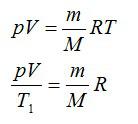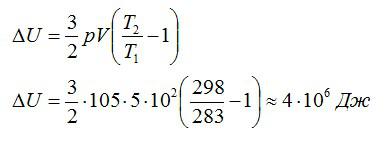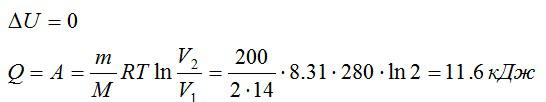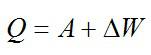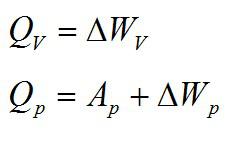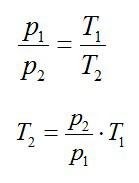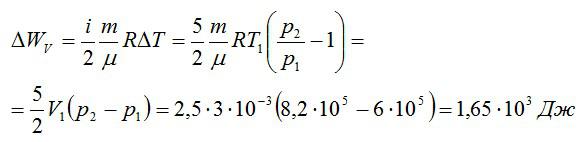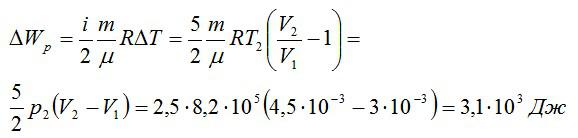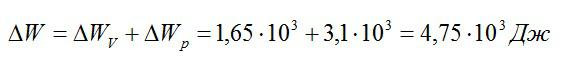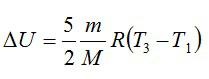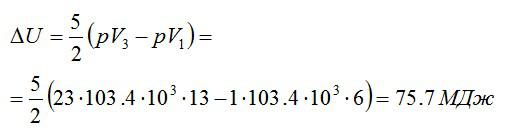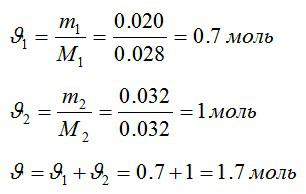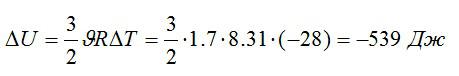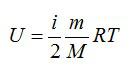Как найти изменение внутренней энергии шаров

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Решение задач – занятие, которое любит далеко не каждый. Здесь мы стараемся сделать так, чтобы оно занимало у вас поменьше времени без ущерба для качества самого решения. Тема этой статьи — задачи на внутреннюю энергию.

Подписывайтесь на наш телеграм и читайте полезные материалы для студентов каждый день!

Решение задач: внутренняя энергия

Прежде чем приступать к задачам на внутреннюю энергию тела, посмотрите общую памятку по решению физических задач. И пусть под рукой на всякий случай всегда будут основные физические формулы.

Задача №1. Изменение внутренней энергии

Условие

Воздушный шар объёмом 500 м3 наполнен гелием под давлением 105 Па. В результате нагрева температура газа в аэростате поднялась от 10 °С до 25 °С. Как увеличилась внутренняя энергия газа?

Решение

Для решения будем использовать формулу внутренней энергии идеального газа:

Массу гелия выразим из уравнения Клапейрона-Менделеева:

Тогда можно записать:

Ответ: 4 МДж.

Задача №2. Внутренняя энергия и работа

Условие

Азот массой 200 г расширяется изотермически при температуре 280 К, причем объём газа увеличивается в 2 раза. Найти:

1. Изменение ∆U внутренней энергии газа.
2. Совершенную при расширении газа работу А.
3. Количество теплоты Q, полученное газом.

Решение

Так как процесс изотермический, то изменение внутренней энергии равно нулю, а работа равна количеству теплоты, полученному газом:

Ответ: 0; 11,6 кДж; 11,6 кДж.

Задача №3. Изменение внутренней энергии при изобарном и изохорном процессе

Условие 

Кислород занимает объём V1= 3 л при давлении p1= 820 кПа. В результате изохорного нагревания и изобарного расширения газ переведён в состояние с объёмом V2= 4,5 л и давлением p2= 600 кПа. Найти количество теплоты, полученное газом; изменение внутренней энергии газа. 

Решение

Теплота, подведенная к газу, идет на совершение работы и изменение внутренней энергии:

В изохорном и изобарном процессе соответственно:

Изохорное нагревание:

Изменение внутренней энергии при изохорном процессе:

Изменение внутренней энергии при изобарном процессе:

Общее изменение внутренней энергии:

Ответ: 4,75 кДж.

Задача №4. Изменение внутренней энергии двухатомного газа

Условие

Кислород массой 2 кг занимает объём 6 м3 и находится под давлением 1 атм. Газ был нагрет сначала при постоянном давлении до объёма 13 м3, а затем при постоянном объёме – до давления 23 атм. Найти изменение внутренней энергии газа.

Решение

Изменение внутренней энергии находим по формуле:

Эту форму можно преобразовать, используя уравнение Клапейрона-Менделеева:

Ответ: 75,7 МДж.

Задача №5. Внутренняя энергия смеси газов

Условие

В закрытом сосуде находится масса m1 = 20 г азота и масса m2 = 32 г кислорода. Определить изменение ΔU внутренней энергии смеси газов при охлаждении ее на ΔТ = 28 К. 

Решение

Знак «минус» означает, что внутренняя энергия уменьшается.

Ответ: -539 Дж.

Вопросы на тему «Внутренняя энергия тела»

Вопрос 1. Что такое внутренняя энергия?

Ответ. Для начала, внутренняя энергия чего? Бутылки с пивом, воздуха в шарике, тазика с водой? Все макроскопические тела обладают энергией, заключенной внутри них: атомы твердого тела колеблются в кристаллической решетке около положений равновесия, молекулы газа находятся в постоянном хаотическом движении и т.д.

По определению:

Внутренняя энергия вещества – это энергия, которая складывается из кинетической энергии всех атомов и молекул, и потенциальной энергии их взаимодействия друг с другом.

Для идеального газа с числом степеней свободы i внутренняя энергия вычисляется по формуле:

Вопрос 2. От чего зависит внутренняя энергия идеального газа?

Ответ. Эта величина не зависит от объёма и определяется только температурой.

Вопрос 3. Как изменяется внутренняя энергия тела?

Ответ. Если тело совершает работу, его внутренняя энергия уменьшается. Например, газ передвигает поршень. Если же работа совершается над телом, то внутренняя энергия увеличивается.

Вопрос 4. Что такое функция состояния?

Ответ. Функция состояния – это один из параметров, которым можно описать термодинамическую систему. Функция состояния не зависит от того, как система пришла в то или иное состояние, а определяется несколькими переменными состояния.
Внутренняя энергия – это функция состояния термодинамической системы. В общем случае она зависит от температуры и объёма. 

Вопрос 5. Можно ли изменить внутреннюю энергию тела, не совершая над ним работы?

Ответ. Да, еще один способ изменения внутренней энергии – теплопередача. В процессе теплопередачи внутренняя энергия тел изменяется.

Нужна помощь в решении задач по любой теме и других студенческих заданий? Профессиональный студенческий сервис поспособствует в выполнении работы вне зависимости от ее сложности.

ЛАБОРАТОРНАЯ
РАБОТА.

«Изучение
законов сохранения энергии и импульса
при ударе».

Цель
работы:

1. изучить
   теорию, абсолютно упругого и неупругого
   ударов;

2. экспериментально
   проверить законы сохранения механической
   энергии и импульса при, абсолютно
   упругом и неупругом ударе двух шаров;

3. определить
   время и среднюю силу взаимодействия
   при упругом ударе.

Приборы
и принадлежности:

Прибор для
исследования столкновений шаров FPM–08,
технические весы, набор шаров, разновесы,
ножницы, липкая лента.

1. Краткая теория.

При соударении
шаров силы взаимодействия резко
изменяются с расстоянием между центрами
масс, и весь процесс взаимодействия
протекает в очень малом пространстве
и за очень короткий промежуток времени.
Такое взаимодействие называют ударом.
Различают два вида ударов. Если шары
являются, телами абсолютно упругими,
то удар называют, абсолютно упругим
(или просто упругим). Если же шары (или
хотя бы один из них) являются телами,
абсолютно неупругими, удар называют,
абсолютно неупругим (или просто
неупругим). Абсолютно упругое и абсолютно
неупругие тела идеализированные модели.
На самом деле всякий удар (шаров) является,
строго говоря, неупругим. Однако, в
одних случаях, с некоторым приближением,
удар можно считать абсолютно упругим
(например, удар двух шаров из стали),
других абсолютно неупругим (шары из
пластилина, свинца).

При абсолютно
неупругом ударе потенциальная энергия
упругой деформации не возникает (шары
деформируются и не восстанавливают
свою первоначальную форму); кинетическая
энергия тел частично или полностью
превращается во внутреннюю энергию;
после удара тела движутся с одинаковой
скоростью (как одно тело), либо покоятся.
При таком ударе выполняется только
закон сохранения импульса. Закон
сохранения механической энергии не
соблюдается механическая энергия
частично или полностью переходит во
внутреннюю.

При абсолютно
упругом ударе полная механическая
энергия тел сохраняется. Сначала
кинетическая энергия частично или
полностью переходит в потенциальную
энергию упругой деформации. Затем, за
счёт сил упругости, тела принимают
первоначальную форму, и потенциальная
энергия упругой деформации переходит
в кинетическую тела отталкивают друг
друга. Скорости тел после удара
определяются из законов сохранения
суммарной энергии и суммарного импульса
тел до и после удара.

Ограничимся
рассмотрением центрального удара двух
однородных шаров. Удар называется
центральным, если происходит вдоль
линии, проходящей через центры шаров.
Из соображений симметрии ясно, что после
удара шары будут двигаться вдоль той
же прямой, что и до удара. Предположим,
что шары движутся только поступательно
(скользят на поверхности, не вращаются)
и образуют замкнутую систему, либо
внешние силы, приложенные к шарам,
уравновешивают друг друга.

а) Абсолютно
неупругий удар.

Обозначим массы
шаров m₁
и m₂ ,
скорости шаров до удара v₁
и v₂,
скорости шаров после удара v΄₁
и v΄₂.
Шары могут двигаться как в одном, так и
в противоположных направлениях (рис.
1).

т₁ т₂

Х

а)

т₁
т₂

Х

б)

Рис. 1.

После
удара шары движутся как одно тело массой
(m₁
+ m₂)
со скоростью
.
В этом случае хотя бы часть кинетической
энергии переходит во внутреннюю энергию
(шары нагреваются).

По закону сохранения
импульса:

 _до
=  _после,

–  _до суммарный
импульс шаров до взаимодействия равен
суммарному импульсу системы после
взаимодействия 
_после

Скорость шаров после
взаимодействия:

. (1)

Так как удар центральный, то
все векторы скоростей лежат на одной
прямой. Принимая эту прямую за ось 
и проецируя векторы скоростей на эту
ось, получим скалярное уравнение, в
котором скорости имеют алгебраический
знак (положительный, если они направлены
в сторону положительных значений X)

. (2)

Из уравнения (2) видно, что если
шары до удара двигались в одну сторону
(рис.1,б), то после удара они будут двигаться
в ту же сторону, так как V₁
>V₂.
Если же до удара шары двигались навстречу
друг другу (рис. 1,а), то после удара они
будут двигаться в ту сторону, куда
двигался шар, имевший больший импульс.
Если один из шаров покоился (например,
второй, V₂
= 0), то скорость шаров после удара:

, (3)

а двигаться они будут в ту же
сторону, куда двигался первый шар до
удара.

Используя закон
сохранения полной энергии

,

можно определить Q
изменение внутренней энергии шаров
(энергию, переходящую в тепловую форму):

Q =
.

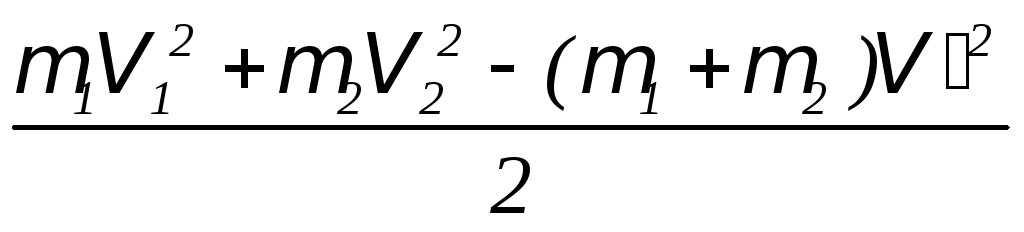
Подставляя вместо V
´ из формулы (2) получим:

².

Таким образом, изменение
внутренней энергии системы двух шаров
пропорционально квадрату относительной
скорости шаров.

Неупругий удар
двух тел используется на практике: а)
для изменения формы тела при ковке,
чеканке и т.д. и б) для забивания гвоздей,
свай и др. В этом случае обычно одно из
соударяющихся тел до удара покоится;
V₂
= 0. Тогда обозначив через W_к1=
– кинетическую энергию первого тела
до взаимодействия получим,

(4)

Число

показывает, какая часть кинетической
энергии первого тела расходуется на
деформацию. Оставшаяся часть

кинетической энергии первого тела
переходит в кинетическую энергию обоих
тел. Эта энергия расходуется затем на
преодоление сил сопротивления среды.
Чем больше
,
тем больше энергия ударяющего тела
расходуется на деформацию и тем меньше
её остаётся в виде кинетической энергии
тел после удара. Отсюда следует, что
если нужно энергию ударяющего тела
использовать для деформации, то масса
покоящегося тела должна быть много
больше массы движущегося тела
.В
этом случае

и работа деформации будет приближаться
по значению W_k1.
Поэтому тело, которое подвергается
деформации, помещают на очень массивную
наковальню.

Если энергию
ударяющего тела необходимо использовать
для перемещения второго тела в среде,
то m₂
должна быть намного меньше массы
ударяющего тела почти вся кинетическая
энергия первого тела будет переходить
в кинетическую энергию обоих тел. По
этой причине масса молотка во много раз
превосходит массу гвоздя.

б) Абсолютно
упругий удар.

При абсолютно
упругом ударе на первом этапе тела
деформируются, часть кинетической
энергии тел переходит в потенциальную
энергию упругой деформации. На втором
этапе за счёт сил упругой деформации
тела приобретают первоначальную форму
– потенциальная энергия упругой
деформации переходит вновь в кинетическую
энергию тел. Таким образом, при абсолютно
упругом ударе внутренняя энергия системы
соударяющихся тел не меняется, тела не
нагреваются.

Рассмотрим
замкнутую систему, состоящую из двух
абсолютно упругих шаров массами m₁
и m₂.
Удар – центральный. Шары перемещаются
без вращения (скользят) со скоростями

и
.
Силами трения пренебрегаем. Выведем
формулу для определения скоростей шаров

после удара.

Запишем законы сохранения
энергии и импульса системы шаров для
двух моментов времени: t₁
– момент времени пред началом соударения;
t₂
момент времени, соответствующий концу
взаимодействия шаров.

(5)

(6)

Преобразуем эти уравнения:

(7)

(8)

При записи уравнения (6)
использовано:

Поделив уравнение (8) на (7)
получим:

, (9)

откуда

(10)

Подставим

в уравнение (6)

Из последнего
уравнения определим скорость первого
шара после удара:

. (11)

Если
из уравнения (9) определить

и подставить

в уравнение (6), то после преобразований
получим выражение для определения
скорости движения второго шара после
удара
:

. (12)

Выражения
для

(11) и

(12) отличаются только перестановкой
индексов 1 и 2. Это естественно, поскольку
шары в процессе соударения совершенно
равноправны и безразлично, какой из них
считать первым, а какой вторым.

Рассмотрим
конкретные случаи. Пусть шары перемещаются
навстречу друг другу вдоль оси Х (рис.
1, а). В этом случае проекция вектора

равна
модулю вектора, взятому со знаком плюс
(V_1x
= V₁),
а проекция вектора
–
модулю вектора, взятому со знаком минус
(V_2x
= –V₂
). С учётом
знаков скорости шаров после удара
определяться по формулам:

, (13)

. (14)

Направление движения и величины скоростей
после взаимодействия зависят от
соотношения масс и скоростей до удара.

Особый
интерес представляет случай, когда
массы шаров одинаковы: m₁
= m₂.
При этом условии из (13) и (14) получается,
что

и
.

Следовательно, шары
равной массы при центральном ударе
обмениваются скоростями. В частности,
если один из шаров до соударения покоился,
то после удара он движется с такой же
скоростью, какую имел первоначально
другой шар, который после удара
остановился. При центральном абсолютно
упругом ударе шар полностью передаёт
свою кинетическую энергию неподвижному
шару той же массы.

Если
масса второго шара много больше массы
первого шара

или

и к тому же, массивный шар покоился (),
то из уравнений (13–14) следует, что:

,

.

Это
очень важный результат. Он показывает,
что если некоторое тело массой m₁
ударяется абсолютно упруго о другое
тело, масса которого m₂
бесконечно велика по отношению к m₁,
то ударившееся тело отскакивает без
изменения модуля скорости и следовательно,
без изменения кинетической энергии.
Пример удар стального шарика о наковальню.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

T₁ = 400 Дж, T₂ = 100 Дж, m₁ = m₂. Обозначу массу одного шарика через m. Необходимо вычислить: ΔТ₁, ΔТ₂, ΔU.

Из формулы кинетической энергии выражаю скорости:

v₁ = √(2T₁/m),

v₂ = √(2T₂/m).

Общую скорость шариков после столкновения обозначу как v’. По закону сохранения импульса:

mv₁ + mv₂ = 2mv’,

v’ = (v₁ + v₂) / 2 = (√T₁ + √T₂) / √(2m).

Кинетические энергии обеих шариков после неупругого столкновения одинаковы, так как одинаковы массы и также скорости. Обозначу кинетическую энергию каждого шарика после столкновения как T’, тогда кинетическая энергия обеих шариков равна 2T’.

T’ = (mv’²) / 2 = (√T₁ + √T₂)² / 4 = 225 Дж.

2T’ = 450 Дж.

Изменение общей кинетической энергии обеих шариков ΔТ = 450 − (400 + 100) = −50 Дж. Изменение внутренней энергии обеих шариков ΔU = −ΔT = 50 Дж.

Изменение кинетической энергии каждого из шариков:

ΔT₁ = 225 − 400 = −175 Дж,

ΔT₂ = 225 − 100 = 125 Дж.

Ответ: ΔT₁ = −175 Дж, ΔT₂ = 125 Дж, ΔU = 50 Дж.

Пластилиновый шар, двигаясь по гладкой горизонтальной плоскости, столкнулся с покоящимся металлическим шаром и прилип к нему. Как в результате изменились следующие физические величины: суммарная кинетическая энергия шаров, внутренняя энергия шаров, величина суммарного импульса шаров? Для каждой величины определите соответствующий характер изменения.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.