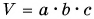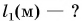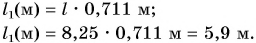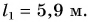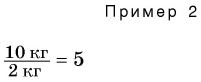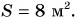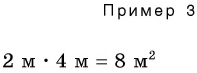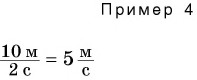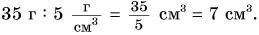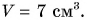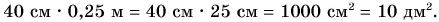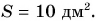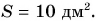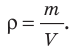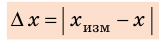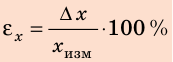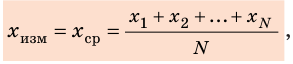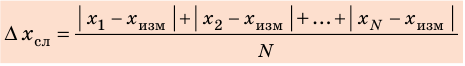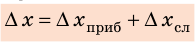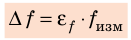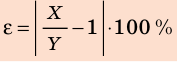План урока:
Измерить – значит сравнить
Числа «карлики» и числа «великаны»
Как измерить длину. Погрешности измерений
Площадь и ее измерение
Измерение объема. Мензурка
Измерить – значит, сравнить
На помощь человеку приходят числа, используя которые можно было сравнить предметы по величине. Так в одном известном мультфильме длину удава измеряли в «попугаях», сравнивая величину удава с длиной попугая.
Из мультфильма «38 попугаев».
Длина удава 38 «попугаев». Понятно, что удав в 38 раз длиннее попугая. Но попугаи бывают разными. Если взять другого попугая, тот же удав будет, например, 45 «попугаев». Что делать?
Нужно найти тело, принимаемое за единицу измерения, с которой сравниваются другие тела.
В практической деятельности человеку приходится часто измерять длину, массу и время. В разных странах вводились разные единицы измерения этих величин. Существовали такие единицы, как «лошадиная сила», локоть, бочка. Но ведь и локоть, и бочка могут быть разными, поэтому о точности выполнения работы говорилось приблизительно.

Сравнивать нужно только однородные физические величины. Длину тела нужно сравнивать с длиной другого тела, а массу тела – только с массой другого тела, принятого за единицу измерения. Так массу удава из мультфильма можно было сравнить с массой обезьянки. Удав имеет массу 195 «обезьянок». Что бы это значило?
Выход был найден, когда ввели систему единиц СИ. Чтобы измерить любую величину, нужно сравнить ее с однородной величиной, принятой за единицу. Как же выбирают эти единицы?
Наиболее распространено измерение длины, размеров пройденного пути, расстояния. Все эти величины измеряются в метрах. Один метр получили следующим образом. Взяли одну сорока миллионную часть меридиана, который проходит через столицу Франции – Париж. Длину этой части и приняли за 1 метр. На стержне, изготовленном из иридия и платины, нанесли два деления, расстояние между которыми равно одному метру. Такой сплав меньше всего подвержен температурному влиянию, которое может изменить длину тела. Это стержень и есть эталон длины, с которым сравнивают единицу длины во многих странах мира. Метровые линейки – это многочисленные копии эталона, которыми как раз и можно пользоваться.
Эталон длины
(Источник)
Первый эталон метра был изготовлен из латуни в 1795 г. С 1960 г. используется изготовленный с помощью электронных технологий эталон из сплава иридия и платины.
Существует и эталон массы, равный одному килограмму. Он также изготовлен из сплава иридия и платины.
(Источник)
Эталоны длины и массы хранятся в г. Севр, вблизи Парижа, где располагается Международная палата мер и весов. В 1960 году метр начали сравнивать с величинами, относящимися к разделу «Световые явления». Подробности о свете изучаются в старших классах.
Со светом связана и единица времени – 1 секунда. А до 1960 года (год введения СИ) за основу подсчета времени брали время оборота Земли вокруг Солнца – 1 год, который по календарю состоит из 12 месяцев. Месяцы делятся на сутки – время полного оборота Земли вокруг своей оси, сутки — 24 часа, в каждом из которых 60 минут. А одна шестидесятая часть минуты и есть одна секунда.
Время «хранят» при помощи очень точных часов – устройств, предназначенных для измерения времени. Действие любых часов основано на повторяющихся процессах – колебаниях. Чем меньше период (время одного полного колебания), тем часы более точные.
При изучении быстро протекающих процессов требуется измерять миллиардные и еще более мелкие доли секунды. Для этого служат атомные часы.

Ученик седьмого класса, конечно же, умеет измерять длину и время, массу продуктов определяют продавцы с помощью весов.
По мере изучения физики будет идти знакомство с различными физическими величинами, способами и приборами их измерения. А сейчас надо знать:
- чтобы измерить физическую величину, ее надо сравнить с однородной величиной, принятой за единицу;
- за основу физических величин берутся эталонные значения, то есть образец сравнения.
- для всех величин существуют свои способы, устройства и единицы измерения.
Числа «карлики» и числа «великаны»
Солнечная система. Лапка мухи под микроскопом.
Чтобы достать до Альфа Центавры, звезды, ближайшей к Солнечной системе, надо со скоростью света (300 000 км/с) лететь четыре года. Расстояния до небесных тел огромны.
К звездам. (Источник)
Если определить расстояние от Земли до Солнца, то оно выразится числом 150 000 000 000 м. А бывают числа с еще большим количеством нулей. Масса Земли в килограммах выражается числом с 24 нулями. Такие числа называют «гигантами». Их записывать и использовать очень неудобно.
Существует способ краткой записи больших чисел в виде степени. Например, 1 000 000 = 106. 10 – основание, а 6 – показатель степени.
Используя этот способ, расстояние от нашей планеты до Солнца запишется так:
150 000 000 000 = 15 ∙ 1010 м – это промежуток называется астрономической единицей (1 а.е.) и служит единицей сравнения в Солнечной системе.
До Альфа-Центавры расстояние в 270 000 а.е., или 4 световых года. Световой год – это тоже астрономическая единица измерения расстояния. Астрономия – наука о космосе и космических телах. (1 св. год = 9,46 ∙ 1015 м = 68 000а.е.).
Фото двойной звезды Альфа созвездия Центавра. (Источник)
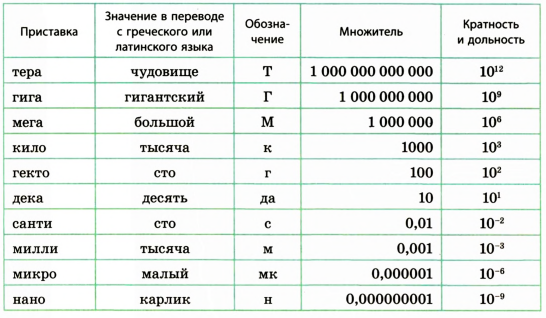
Большие числа записываются при помощи кратных приставок. Например, километр – это тысяча метров, килограмм – тысяча граммов. Приставка «кило» обозначает «тысяча». Есть и другие приставки, которые обозначают умножение величины на число, кратное десяти. Примеры и форма записи даны в таблице кратных приставок.
Используя эти приставки можно записывать очень большие числа.
1 а.е. = 150 000 000 000 м = 150 ∙ 109 м = 150Гм;
1 св. год = 9 460 000 000 000 м = 9,46 ∙ 1012 м = 9,46 Тм;
А теперь о числах – «карликах». Если сделать попытку измерить толщину одного листа книги, то сразу это не получится. Надо действовать по простому плану:
- отобрать в книге некоторое число страниц N (N = 100, например);
- измерить толщину L этих страниц (пусть L = 11 мм);
- найти толщину одной страницы d по формуле d = L/N.
Получится d = 0,11 мм = 0, 00011 м. Это число очень маленькое.
Такой способ измерения малых величин называется методом рядов. Он достаточно прост.
Размеры пшена. Толщина проволоки.
Но существуют и гораздо меньшие величины. Маленькие числа, так называемые «карлики», также записывают при помощи степеней или дольных приставок. (С приставками деци, санти, милли знакомятся еще в начальной школе).
Число меньше единицы, поэтому показатель степени – отрицательное число. Оно показывает количество цифр после запятой. Например, 0, 00011 м = 11 ∙ 10-5 м.
Число 0,00000625 можно записать по-разному, применяя степень:
625 ∙ 10-8, 62,5 ∙ 10-7, 6,25 ∙ 10-6 и т. д.
Очень маленькие числа по-другому можно записывать, используя таблицу дольных приставок.
Например, при изготовлении сверхточных приборов (телескопов, микроскопов и др.), детали ошлифовываются до очень гладкой поверхности. Неровности должны быть меньше 2,5 ∙ 10-6 м или 2,5 мкм.
Большие и маленькие числа помогают человеку в различных отраслях деятельности: в науке, промышленности, медицине и т.д.
Как измерить длину. Погрешности измерений
На практике измерить длину отрезка достаточно просто:
- Приложить линейку к отрезку.
- Совместить ноль с началом отрезка.
- Определить число, соответствующее концу отрезка.
- Записать результат измерения.
В приведенном примере длина отрезка 9,9 см. Как точен этот результат? Он точен до 1 мм, так как на линейке нет меньших делений. Не надо путать значения слов «штрих» и «деление».

Численное значение самого маленького деления шкалы прибора называется ценой деления.
Чтобы определить цену деления прибора (например, линейки), нужно взять любые два рядом стоящие числа и их разность поделить на число делений между ними (т.е. промежутков между штрихами).
Цена деления линейки = (7 см – 6 см)/10 = 0,1 см = 1 мм.
И чтобы начать измерение, прежде всего надо найти цену деления прибора, который используется в данном случае. Любое измерение дает некоторую погрешность, зависящую от качества прибора. Поэтому ее называют погрешностью прибора.
Шкалы различных приборов. (Источник)
Известно, что измерить какую-то величину – это значит сравнить ее с эталоном. На практике пользуются не эталонами, а специальными приборами (линейка, часы и др.), которые являются копиями с эталонов, изготовленными с определенной точностью. Абсолютно точных измерений не бывает. При использовании линейки допускается погрешность отсчета, которая равна половине цены деления прибора (0,5 мм). Сумма погрешностей прибора и отсчета называется абсолютной погрешностью. Она равна цене деления прибора.
Абсолютная погрешность обозначается значком Δ (дельта). Для школьной линейки Δ = 1 мм. Δ показывает, на сколько совершается ошибка при использовании того или иного прибора. Для более точных измерений используется штангенциркуль. В устройстве штангенциркуля заложено две шкалы, неподвижная (Δ = 1 мм) и подвижная (Δ = 0,1 мм).
Штангенциркуль. Микрометр.
А вот при помощи микрометра, где используется не перемещение шкалы, а ее вращение измерить длину можно с точностью до 0,01 мм. Но это еще не предел. В очень точных технологиях определяются размеры с точностью до 10-7м, в научных разработках точность возрастает во много раз. Но для этого нужны сверхточные приборы.
На практике, используя приборы, необходимо учитывать качество измерения. Величина, которая помогает это учесть, называется относительной погрешностью σ (сигма) и выражается в процентах.
σ = Δ / L ( L – измеренная величина)
Пример: Требуется замерить длину L отрезка различными приборами: 1) линейкой, 2) штангенциркулем и 3) микрометром. Длина отрезка получилась 55 мм. Какова относительная погрешность этих трех измерений?
1) Δ1 = 1 мм, L = 55 ± 1 мм, σ1 = 1 мм / 55 мм ≈ 0,018 (1,8%);
2) Δ2 = 0,1 мм, L = 55 ± 0,1 мм, σ2 = 0,1 мм / 55мм ≈ 0,0018 (0,18);
3) Δ3 = 0,01 мм, L = 55 ± 0,01 мм, σ3 = 0,01 мм / 55мм ≈ 0,00018 (0,018%).
Как видно, более точный прибор (микрометр) дает меньший процент ошибки.
Для каждого конкретного измерения в технике, практической деятельности человека и в науке существует своя точность измерения, в соответствии с которой применяются измерительные приборы.
Площадь и ее измерение
С измерением длин очень тесно связано измерение площадей. Из математики известны формулы площадей квадрата и прямоугольника. У квадрата все стороны равны, поэтому достаточно измерить одну сторону, а у прямоугольника противоположные стороны равны, поэтому надо знать длину и ширину. Площадь обозначается буквой S, и формулы для расчета площадей следующие:
Sкв = a2, Sпр = а ∙ в. Единицей измерения площади является квадратный метр (м2).
Для измерения малых площадей применяются см2 и мм2, а большие площади – в км2. В сельском хозяйстве для измерения земельных участков используют внесистемные единицы: гектар (га) – для больших, ар (а) или «сотка» — для небольших (приусадебных или дачных) участков земли. 1га = 10 000 м2, 1 а = 100 м2.
Очень часто на практике имеют дело с различными кругами. Это может быть цирковая арена, крышка стола, разрез ствола дерева. Формула нахождения площади круга: S = πR2. (π (пи) – это бесконечная дробь ≈ 3,14 подробно изучается в курсе алгебры).
Арена цирка. Круглый стол. Спил дерева.
А как определить площадь, ограниченную произвольной кривой линией? Такая площадь может быть у озера, полянки в лесу, листочка с дерева.
Существует правило нахождения площади тел произвольной формы:
- Разбить всю поверхность на равные квадраты с известной площадью.
- Подсчитать количество целых квадратов.
- Подсчитать число нецелых квадратов и поделить это число на два. (Это будет примерное количество целых квадратов).
- Сложить результаты пунктов 2 и 3.
- Умножить площадь одного квадрата на общее число целых квадратов.
Площадь больших территорий изображают в условном масштабе или фотографируют, применяют прием разбиения на квадраты и находят площадь фотографии. Используя масштаб вычисляют реальную площадь поверхности.

Довольно часто площадь приходится находить в географии. Каждое государство, область, город имеют свои площади. В строительстве – любое здание имеет площадь, которую необходимо знать строителям. В сельском хозяйстве ведется постоянный учет площадей для посевных культур.
Измерение объема. Мензурка
При измерении пространства нужно перейти к трем измерениям, так как представление о пространстве дает объем. Известны формулы объемов параллелепипеда, куба, шара, цилиндра.

Объем любого тела измеряется в кубических метрах (есть кратные и дольные единицы). Из математики известны формулы объемов:
Vпар = а ∙ в ∙ с (произведение длины, ширины и высоты),
Vк = а3 (а — ребро куба),
Vцил = π ∙ r2 ∙ h (r — радиус основания, h – высота цилиндра),
Vш = 4/3 π ∙ R3 (R – радиус шара).
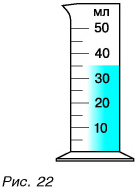
О вычислении объемов более сложной, но правильной, формы рассказывается в старших классах. А как определить объем, например, камня, форма которого может быть самой различной? Для измерения объемов таких тел используется специальный и очень простой прибор, который называется мензурка (или измерительный цилиндр). Это стеклянный сосуд с делениями. При помощи этого цилиндра легко найти объемы сыпучих тел и жидкостей. Для этого достаточно их засыпать вещество или налить в мензурку жидкость и, зная цену деления, определить объем.

На мензурке обычно ставится единица измерения в миллилитрах. Литр – это широко применяемая единица объема, равная одной тысячной кубического метра. 1 мл = 1 см3 = 10-6 м3.
Определить объем камня или любого другого тела неправильной формы с помощью мензурки можно при условии, что тело имеет размеры, позволяющие опустить его в мензурку.

Налить в мензурку воду и зафиксировать ее объем. Прикрепить тело неправильной формы к нити. Осторожно опустить полностью в воду. Уровень воды поднимется ровно на столько, чему равен объем тела.
Пользуясь измерительным цилиндром, нельзя забывать, что это прибор, имеющий шкалу, а значит, результат получится с погрешностью.
Основной единицей длины служит метр (м). Первоначально за образец (эталон) метра было принято расстояние между двумя штрихами на специально изготовленном платино-иридиевом стержне длины 102 см, хранящемся в Международном бюро мер и весов в Париже (рис. 14). Материал и форма сечения стержня н условия его хранения были выбраны так, чтобы наилучшим образом обеспечить неизменность образца. В частности, были приняты меры для поддержания постоянной температуры стержня. Тщательно выполненные вторичные эталоны — копии этого образца — хранятся в институтах мер и весов разных стран.
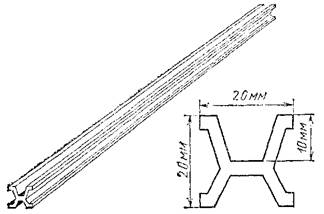 |
| Рис. 14. Первоначальный эталон метра (общий вид и сечение) |
Предполагалось изготовить образец метра равным одной сорокамиллионной части длины земного меридиана. Когда выяснилась недостаточная точность измерений на земной поверхности, то не стали заменять изготовленный образец или вносить поправки на основе более точных измерений, а решили сохранить сам образец в качестве единицы длины. Этот образец примерно на 0,2 мм меньше, чем 1/40 000 000 часть меридиана.
Кроме этой основной единицы, в науке и технике применяют и другие единицы — десятичные кратные и дольные от метра:
- километр (1 км=1000 м);
- сантиметр (1 см=0,01 м);
- миллиметр (1 мм=0,001 м);
- микрометр (1 мкм=0,001 мм=0,000001 м);
- нанометр (1 нм=0,000000001 м).
В Англии, США и некоторых других странах широко распространены так называемые английские меры длины:
- дюйм = 25,4 мм;
- фут = 12 дюймов = 304.8 мм;
- миля сухопутная («статутная») = 1609 м;
- миля морская («адмиралтейская») = 1852 м (длина одной минуты дуги земного меридиана).
Старые русские меры длины составляли:
- вершок = 4,445 см;
- аршин = 28 дюймов = 16 вершков = 0,7112 м;
- сажень = 3 аршина = 2,1336 м;
- верста = 500 сажен = 1,0668 км;
- русская миля = 7 верст = 7,4676 км.
Обилие разных единиц длины (а также и единиц других физических величин) весьма неудобно на практике. Поэтому были разработаны международные стандартные определения единиц всех физических величин. Сборник этих определений называют системой единиц СИ (от слов Systeme Internationale — Международная система). С 1963 г. в СССР и ряде других стран СИ рекомендована для применения во всех областях науки и техники.
Согласно этой системе метр определен как длина, равная 1 650 763,73 длины волны оранжевого света, излучаемого специальной лампой, в которой под действием электрического разряда светится газ криптон-86. Число длин воли выбрано так, чтобы эта единица длины совпадала возможно точнее с парижским метром. Поэтому за единицу и не была выбрана длина, на которой укладывалось бы какое-либо круглое число (например, один миллион) длин волн. Эту новую единицу длины можно воспроизводить (оптическим путем) с большей точностью, чем архивный образец. Очень удобно, что для воспроизведения единицы длины не нужно обращаться к какому-то единственному хранящемуся образцу, а достаточно изготовить специальную криптоновую лампу и наблюдать испускаемый ею свет.
На практике для измерения длины, в том числе и для измерения расстояний между двумя положениями точки на траектории, применяют копии вторичных эталонов: стержни, линейки или ленты с делениями, равными длине эталона, либо его части (сантиметры, миллиметры). При измерении начало измерительной линейки совмещают с одним концом измеряемого отрезка и отмечают то ее деление, против которого окажется второй конец отрезка. Если второй конец не совпадает ни с одним из делений линейки, то «на глаз» оценивают, на какой доле расстояния между делениями он оказался.
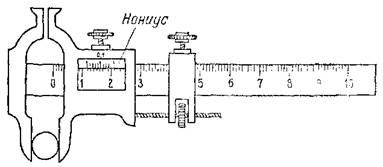 |
| Рис. 15. Штангенциркуль с нониусом |
Для уменьшения неизбежной ошибки отсчета применяют различные вспомогательные приспособления. На рис. 15 изображено одно из них — нониус, установленный на штангенциркуле. Нониус представляет собой добавочную шкалу, передвигаемую вдоль основной шкалы. Деления ноииуса меньше деления основной шкалы на 0,1 их размера; например, если деление основной шкалы равно 1 мм, то деление нониуса равно 0,9 мм. На рисунке видно, что диаметр измеряемого шарика больше 11 мм, но меньше 12 мм. Чтобы найти, сколько десятых долей миллиметра составляет остающаяся дробная часть деления, смотрят, который из штрихов нониуса совпадает с каким-нибудь из штрихов основной шкалы. На нашем рисунке это девятый штрих нониуса. Значит, восьмой, седьмой и т. д. штрихи нониуса окажутся впереди ближайших к ним предыдущих штрихов основной шкалы на 0,1 мм, 0,2 мм и т. д., а начальный штрих нониуса окажется на 0,9 мм впереди ближайшего к нему предыдущего штриха основной шкалы. Отсюда следует, что диаметр шара равен стольким целым миллиметрам, сколько их укладывается от начала основной шкалы до начала шкалы нониуса (11 мм), и стольким десятым долям миллиметра, сколько делений нониуса укладывается от начала шкалы нониуса до совпадающих штрихов (0,9 мм). Итак, измеряемый диаметр шарика равен 11,9 мм.
Таким образом, нониус позволяет измерять расстояния с точностью до 1/10 деления шкалы.
Физика > Длина
Длина в физике – физическая мера. Узнайте, как обозначается длина в физике, формула, как найти длину, какой буквой делают обозначение, единица измерения.
Длина отображает физическое измерение дистанции, которая в системе единиц отображена в метрах.
Задача обучения
- Различать СИ (система единиц) и обычные единицы длины.
Основные пункты
- Единицей СИ выступает метр.
- Один метр – дистанция, которую свет преодолевает в вакууме за 1/299 792 458 секунды.
- Единицы на счетчике разработаны вокруг числа 10.
Термин
Длина – физическая удаленность между объектами.
Давайте разберемся в том, что собою представляет длина в физике. Длина – измерение физической дистанции. Многие характеристики наблюдения строятся на определении длины. От нее зависит дистанция между объектами, степень силы, оказываемая объектом, и скорость перемещения. Чтобы точно описать длину, необходимо полагаться на общепринятую единицу измерения в физике.
Известно, что в различных частях мира используют разные единицы измерения длины (например, в США – дюйм). Обычно, если речь идет о региональном масштабе, то проблем не возникает. Но при сотрудничестве между странами появляются нестыковки. Именно поэтому возникла необходимость в стандартной единице измерения, принятой на международном уровне. Таким образом, выбор пал на метр, потому что он лучше всего сотрудничает со скоростью света.
Один метр вычисляет дистанцию, которую свет преодолевает за 1/299 792 458 секунды. Все показатели основываются на счетчике с кратностью в 10. Например, 1 км = 1000 м.
Измерение длины, площади, объема и времени
- Лабораторная работа №1. Измерение длины ребер, площади поверхности и объема прямоугольного параллелепипеда. Погрешность прямых и косвенных измерений
- Лабораторная работа №2. Измерение времени с помощью секундомера. Погрешность серии прямых измерений
п.1. Лабораторная работа №1. Измерение длины ребер, площади поверхности и объема прямоугольного параллелепипеда. Погрешность прямых и косвенных измерений
Цель работы
Научиться измерять длину с помощью линейки, определять площадь поверхности и объем прямоугольного параллелепипеда, находить абсолютные и относительные погрешности косвенных измерений.
Теоретические сведения
 |
Прямоугольный параллелепипед – это многогранник с шестью гранями, каждая из которых является прямоугольником. Прямоугольный параллелепипед имеет три измерения: длину, ширину и высоту. |
Пусть
длина (AD=BC=A_1 D_1=B_1 C_1=a)
ширина (AB=CD=A_1 B_1=C_1 D_1=b)
высота (AA_1=BB_1=CC_1=DD_1=c)
Площади верхней и нижней грани равны (S_1=ab), площади передней и задней граней равны (S_2=ac), площади левой и правой граней равны (S_3=bc).
Площадь поверхности прямоугольного параллелепипеда равна сумме площадей всех шести граней: $$ S_{пов}=2S_1+2S_2+2S_3=2(ab+ac+bc) $$ Объем прямоугольного параллелепипеда равен произведению всех трех измерений: $$ V=abc $$
Пусть измерения проводятся ученической линейкой с ценой деления (triangle=1 мм).
Тогда инструментальная погрешность измерений равна половине цены деления: $$ d=frac{triangle}{2}=0,5 мм $$ Абсолютная погрешность измерений при работе с линейкой равна инструментальной погрешности, поэтому для всех измерений: (triangle a=triangle b=triangle c=d=0,5 мм)
Относительные погрешности измерений (в долях, без процентов): $$ delta_a=frac{triangle a}{a}=frac da, delta_b=frac{triangle b}{b}=frac db, delta_c=frac{triangle c}{c}=frac dc $$ Выведем необходимые формулы.
Рассмотрим нижнюю грань. Её площадь (S_1=ab) является произведением двух длин.
Значит, относительная погрешность измерения площади равна сумме относительных погрешностей длин: $$ delta_{S1}=delta_a+delta_b $$ Аналогично для остальных граней: $$ delta_{S2}=delta_a+delta_c, delta_{S3}=delta_b+delta_c $$ Абсолютная погрешность измерения площади нижней грани: $$ triangle S_1=S_1cdotdelta_{S1}=abcdot(delta_a+delta_b)=abcdotleft(frac da+frac dbright)=abdcdotleft(frac ab+frac1bright)=abdcdotfrac{b+a}{ab}= d(a+b) $$ Аналогично для остальных граней: $$ triangle S_2=S_2cdotdelta_{S2}=d(a+c), triangle S_3=S_3cdotdelta_{S3}=d(b+c) $$ Абсолютная погрешность суммы измерений равна сумме абсолютных погрешностей. Получаем для площади поверхности: begin{gather*} triangle S_{пов}=2(triangle S_1+triangle S_2+triangle S_3)=2(d(a+b)+d(a+c)+d(b+c))=\ =2d(a+b+a+c+b+c)=4d(a+b+c) end{gather*}
Абсолютная погрешность определения площади поверхности прямоугольного параллелепипеда равна: $$ triangle S_{пов}=4d(a+b+c) $$ где (d) – инструментальная погрешность линейки, (a,b,c) — измеренные значения длины, ширины и высоты.
Найдем погрешность определения объема.
Объем равен произведению трех измерений, значит, относительная погрешность для объема равна сумме относительных погрешностей измерений: $$ delta_v=delta_a+delta_b+delta_c=frac da+frac db+frac dc=dleft(frac 1a+frac 1b+frac 1cright)=dcdotfrac{bc+ac+ab}{abc} $$ Абсолютная погрешность для объема: $$ triangle V=vcdotdelta_v=abccdot dcdotfrac{bc+ac+ab}{abc} = d(bc+ac+ab)=dcdotfrac{S_{пов}}{2} $$
Абсолютная погрешность определения объема прямоугольного параллелепипеда равна: $$ triangle V=dcdotfrac{S_{пов}}{2} $$ где (d) – инструментальная погрешность линейки, (S_{пов}) — площадь поверхности.
Приборы и материалы
Ученическая линейка, книга (или деревянный брусок).
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Измерьте длину, ширину и высоту книги (бруска), (a,b,c).
3. Найдите площадь поверхности (S_{пов}) и объем (V).
4. Найдите абсолютные погрешности (triangle S_{пов}) и (triangle V).
5. Найдите относительные погрешности в процентах: $$ delta_{S_{пов}}=frac{triangle S_{пов}}{S_{пов}}cdot 100text{%}, delta_V=frac{triangle V}{V}cdot 100text{%} $$ 6. Дополнительное задание. Определите толщину одного листа книги, абсолютную и относительную погрешность этой величины.
7. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Инструментальная погрешность линейки (d=frac{1 мм}{2}=0,5 мм)
Результаты измерений:
a=218 мм
b=147 мм
c=32 мм
Площадь поверхности: begin{gather*} S_{пов}=2(ab+ac+bc)=2(218cdot 147+218cdot 32+147cdot 32)=\ =2(32046+6976+4704)=87452 (мм^2) end{gather*} Объем: $$ V=abc=218cdot 147cdot 32=1025472 (мм^2) $$ Абсолютная погрешность определения площади поверхности (округляем до двух значащих цифр с избытком): $$ triangle S_{пов}=4d(a+b+c)=4cdot 0,5cdot (218+147+32)=2cdot 397=794 (мм^2)approx 800 (мм^2) $$ Полученную величину площади поверхности также округляем до сотен. Получаем: $$ S_{пов}=(87500pm 800) (мм^2) $$ Абсолютная погрешность определения объема: $$ triangle V=dcdotfrac{S_{пов}}{2}=0,5cdotfrac{87452}{2}=21863 (мм^3)approx 22000 (мм^3) $$ Полученную величину объема также округляем до тысяч. Получаем: $$ V=(1025000pm 22000) (мм^3) $$
Относительные погрешности (округляем до двух значащих цифр с избытком): begin{gather*} delta_{S_{пов}}=frac{triangle S_{пов}}{S_{пов}}cdot 100text{%}=frac{800}{87500}cdot 100text{%} approx 0,92text{%}\ delta_v=frac{triangle V}{V}cdot 100text{%}=frac{22000}{1025000}cdot 100text{%}approx 2,2text{%} end{gather*} Измеряем толщину книги между обложками: (h=23 мм)
Количество страниц в книге (N=688)
Количество листов в 2 раза меньше. Получаем толщину одного листа: $$ t=frac{h}{N/2}=frac{2h}{N}=frac{2cdot 23}{688}approx 0,0669 (мм)=66,9 (мк) $$ Количество листов – величина точная, без погрешностей.
Абсолютная погрешность для толщины листа зависит только от (triangle h): $$ triangle t=frac 2Ntriangle h=frac 2N d=frac{2}{688}cdot 0,5approx 0,0015 (мм)=1,5 (мк) $$ Толщина листа: $$ t=(66,9pm 1,5) мк $$ Относительная погрешность: $$ delta_t=frac{triangle t}{t}cdot 100text{%}=frac{1,5}{66,9}cdot 100text{%}approx 2,3text{%} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения проводились с помощью линейки с инструментальной погрешностью (d=0,5 мм).
Получена площадь поверхности книги $$ S_{пов}=(87500pm 800) мм^2, delta_{S_{пов}}approx 0,92text{%} $$ Объем книги: $$ V=(1025000pm 22000) мм^3, delta_Vapprox 2,2text{%} $$ Определяя толщину листа, мы использовали способ рядов и увеличили абсолютную точность измерений от 0,5 мм до 1,5 мк. Толщина листа: $$ t=(66,9pm 1,5) мк, delta_tapprox 2,3text{%} $$ С наибольшей точностью определена площадь поверхности, т.к. для нее относительная погрешность меньше всех.
С наименьшей относительной точностью определена толщина листа, зато абсолютная точность для этой величины очень высока – 1,5 микрона.
п.2. Лабораторная работа №2. Измерение времени с помощью секундомера. Погрешность серии прямых измерений
Цель работы
Научиться измерять время с помощью секундомера, определять абсолютную и относительную погрешность величины, полученной в серии прямых измерений.
Теоретические сведения
Математическим маятником называют груз небольших размеров, подвешенный на тонкой невесомой нерастяжимой нити.
Периодом колебаний математического маятника называют время, за которое он возвращается в исходную точку.
При отклонении математического маятника на малые углы (до 20°) период его колебаний (T) остается постоянной величиной. В действительности колебания постепенно затухают, но при достаточно длинной нити и тяжелом грузике, затухания происходят медленно.
Приборы и материалы
Секундомер, штатив, грузик на длинной нитке (не менее 50 см).
Ход работы
1. Закрепите нитку с грузиком в лапке штатива, как показано на рисунке.
2. Определите цену деления секундомера.
3. Отклоните грузик на небольшой угол, отпустите его и с помощью секундомера измерьте время, за которое маятник совершит 10 полных колебаний.
4. Повторите опыт 5 раз.
5. С помощью алгоритма определения истинного значения и абсолютной погрешности в серии измерений (см. §3 данного справочника) найдите точное значение и абсолютную погрешность времени 10 колебаний.
6. Найдите точное значение и абсолютную погрешность периода колебаний (T), рассчитайте относительную погрешность результата измерений.
7. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Определение цены деления секундомера
 |
Два ближайших пронумерованных деления на основной шкале: begin{gather*} a=5 с\ b=10 с end{gather*} Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.
Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
Инструментальная погрешность секундомера равна половине цены деления: (d=frac{triangle}{2}=0,1 c)
Измерения времени 10 колебаний
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t, c) | 15,3 | 14,9 | 15,2 | 15,5 | 15,1 | 76,0 |
| (triangle c) | 0,1 | 0,3 | 0 | 0,3 | 0,1 | 0,8 |
Найдем среднее время для 10 колебаний: begin{gather*} t_0=frac{15,3+14,9+15,2+15,5+15,1}{5}=frac{76,0}{5}=15,2 (c) end{gather*} Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_0): $$ triangle_1=|15,3-15,2|=0,1; triangle_2=|14,9-15,2|=0,3 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0,1+0,3+0+0,3+0,1}{5}=frac{0,8}{5}=0,16 (c) $$ Среднее абсолютное отклонение больше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,16right}=0,16 text{c} $$ Результат измерения времени 10 колебаний: begin{gather*} t=t_0pmtriangle t, t=(15,20pm 0,16) c end{gather*} Период колебаний в 10 раз меньше: $$ T=frac{1}{10}(t_0pmtriangle t), T=(1,520pm 0,016) c $$ Относительная погрешность измерений: $$ delta_T=frac{triangle T}{T_0}cdot 100text{%}=frac{0,016}{1,520}cdot 100text{%}approx 1,1text{%} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения проводились с помощью секундомера, для которого была определена цена деления (triangle=0,2 с) и соответствующая инструментальная погрешность (d=frac{triangle}{2}=0,1 с).
В данном случае абсолютная погрешность может быть заметно больше инструментальной, и поэтому для ее определения потребовалась серия экспериментов.
Полученный в серии из 5 экспериментов результат измерения времени 10 колебаний: $$ t=(15,20pm 0,16) c $$ Искомый период колебаний маятника: $$ T=(1,520pm 0,016) c, delta_T=1,1text{%} $$
Содержание:
Явления природы и свойства тел в физике описывают с помощью терминов, например: движение, траектория, состояние спокойствия. Описывая движение (рис. 4.1), можно указать, куда движется тело (вперед, назад или вверх), большое оно или маленькое; движется по пря-мой или поворачивает (влево или вправо), а может, вообще не движется. Такая характеристика движения является качественной.
Нас интересуют и количественные характеристики: с какой скоростью двигался автомобиль, какое расстояние он проехал. Количественной характеристикой тела или явления является физическая величина. Физическая величина описывает определенное свойство тела или явления. Она характеризуется числовым значением и единицей измерения. Например: автомобиль проехал путь в 30 километров. Сокращенно можно записать S = 30 км.
Каждая физическая величина имеет свое на-звание и символ, которым она обозначается.
Чтобы описать явление падения определенного тела, можно применить такие физические величины, как масса тела, высота, время падения. Физические величины обычно обозначают латинскими или греческими буквами. Массу тела обозначают буквой «m», высоту – буквой «h», время – буквой «t». Например, если тело массой 2 килограмма упало с высоты 5 метров за одну секунду, то пишут: m = 2 кг, h = 5 м, t = 1 с, употребляя общепринятые сокращения: кг – килограмм, м – метр, с – секунда.
Если нас интересует единица измерения физической величины, а не ее числовое значение, то эту величину пишут в квадратных скобках. Например, диаметр трубы составляет d = 3,2 см, а название единицы измерения (размерность): [d] =см.
Почему нужно измерять:
Начертите на листе бумаги горизонтальный отрезок. Потом проведите от середины этого отрезка перпендикулярный к нему отрезок такой же длины «на глаз». Измерьте длину отрезков линейкой, и вы убедитесь, что вертикальный отрезок короче. Вот почему нужно проводить измерения.
Средства измерения
Прямые измерения физических величин осуществляют с помощью приборов. Длину измеряют линейкой, время – с помощью часов, массу – на весах. Для определения размеров очень малых тел или больших расстояний используют более сложные приборы. Измерить физическую величину – значит сравнить ее с определенной мерой, которая является копией общепринятого образца-эталона. Эталонов немного, и хранятся они в специальных метрологических лабораториях.
История:
Для измерения времени использовали вытекание или капанье воды в сосуд с делениями или пересыпание песка – водяные или песочные часы (рис. 4.2). Движение Солнца по небу давало возможность измерять время с помощью солнечных часов (рис. 4.3). Такими часами люди пользовались несколько тысячелетий, однако они имели существенный недостаток – были довольно неточными.
Рис. 4.3. Солнечные часы
В настоящее время появились очень точные кварцевые часы, которые отсчитывают время в на-ручных часах, мобильном телефоне или компьютере. Для потребностей навигации и науки используют атомные часы, которые «ходят» настолько точно, что допускают ошибку в одну секунду за 500 000 лет!
Для измерения длины надо иметь образец, дли-на которого соответствует общепринятым единицам измерения. Сейчас это 1 м. Эталон (образец) метра хранится в метрологических лабораториях, главная из которых находится в г. Севре (Франция). Измерить длину можно еще и в других единицах измерения – канцелярскими скрепками, например, или спичками и сказать: мой рост составляет 80 скрепок или 36 спичечных коробков. Однако у других людей скрепки или спички могут оказаться другого размера, что усложнит обмен информацией. В давние времена так и было: пользовались футами (длина ступни – 30 см), дюймами (длина последней фаланги большого пальца, приблизительно 2,5 см), ярдами, пядями, саженями, локтями.
Инициаторами перехода на метрическую систему единиц были французы. Согласно договоренности, один метр определили как одну сорокамиллионную часть длины меридиана, который проходит через Париж. Для определения длины меридиана достаточно было измерять его часть, которая простирается от юга Испании до севера Норвегии. Начался этот процесс во время Великой французской революции. Днем рождения метрической системы мер считают 10 декабря 1799 г.
На территории нашей страны метрическая система мер была введена специальным декретом 14 сентября в 1918 г. Переход на новые стандарты измерений связан с изменением привычек, необходимостью переиздания справочников, переоборудования метрических лабораторий, с переподготовкой персонала и тому подобным. Все это стоит довольно дорого. США, например, переход на новые стандарты обошелся в 11 млрд. долларов.
Международная система единиц измерения – СИ
В связи с потребностью международного сотрудничества в 1960 году большинство стран мира подписали соглашение о единой Международной системе еди-ниц измерения SI – Systeme International (на русском языке – СИ).
Рис. 4.4. Эталон метра хранится в Международном бюро мер и весов в Париже
Рис. 4.5. Эталон килограмма
В СИ есть 7 основных единицы измерения, которые обеспечены соответствующими эталонами. Остальные единицы измерения могут быть выражены через основные единицы. Для начала нам понадобятся три основные единицы: метр, килограмм и секунда.
Эталон метра изображен на рис. 4.4. Это рельс определенного профиля, длина которого составляет одну сорокамиллионную часть меридиана, проходящего через Париж. Первый эталон метра был изготовлен во Франции в 1795 году.
В 1983 году эталон длины был изменен: теперь метр определен как расстояние, которое проходит свет в вакууме за 1/299 792 458 долю секунды.
Эталон килограмма – цилиндр из платиново-иридиевого сплава, высота которого равна его диаметру и составляет 39 мм (рис. 4.5).
С эталоном секунды вы ознакомитесь в 11 классе.
Таблица 4.1
| Величина | Символ | Размерность | |
| рус. | междунар. | ||
| Длина | l | м | m |
| Масса | m | кг | kg |
| Время | t | с | s |
| Площадь | S, | м2 | m2 |
| Объем | V | м3 | m3 |
| Скорость | v | м/с | m/s |
Площадь в СИ измеряют в м2 (квадратные метры), объем – в м3 (кубические метры).
В таблице 4.1 единицы площади, объема и скорости являются производны-ми единицами, их размерности происходят от основных единиц измерения.
В расчетах используют также кратные и дольные единицы.
Кратные единицы – это единицы, которые больше основных единиц в 10, 100, 1000 и больше раз. Например: 1 дм = 10 см = 101 см, 1 м = 100 см = 102 см, 1 км = 1000 м = 103 м, 1 кг = 1000 г = 103 г.
Дольные единицы – это единицы, которые меньше основных единиц в 10, 100, 1000 и больше раз: 1 см = 0,01 м = 10–2 м, 1 мм = 0,1 см = 10–1 см.
С единицами времени несколько иначе: 1 мин. = 60 с, 1 час = 3600 с. Дольными являются лишь 1 мс (миллисекунда) = 0,001 с = 10–3 с и 1 мкс (микросекунда)= = 0,000001 с = 10–6 с.
Для обозначения кратных и дольных единиц используют приставки (табл. 4.2).
Таблица 4.2 Приставки для обозначения кратных и дольных единиц
| Кратность | Приставка | Обозначение | Пример | ||
| русское | международное | русское | международное | ||
| 102 | гекто | hecto | г | h | 5 гПа (гектопаскаль) = = 500 Па |
| 103 | кило | kilo | к | k | 6 кг (килограмм) = 6000 г |
| 106 | мега | mega | М | M | 2 МДж (мегаджоуль) = = 2 000 000 Дж |
| 109 | гига | giga | Г | G | 1 ГГц (гигагерц) = = 1 000 000 000 Гц |
| Дольность | |||||
| 10–1 | деци | deci | д | d | дм – дециметр |
| 10–2 | санти | centi | с | c | см – сантиметр |
| 10–3 | милли | milli | м | м | мл – миллилитр |
| 10–6 | микро | micro | мк | µ | мкм – микрометр, микрон |
| 10–9 | нано | nano | н | n | нм – нанометр |
Итоги
- Физические величины количественно описывают свойства тел и явлений.
- Физические величины характеризуются названием, символом, числовым значением и единицей измерения.
- В международной системе единиц измерения (СИ) основные механические единицы измерения физических величин – метр, килограмм и секунда.
- Измерить физическую величину – значит сравнить ее с мерой-эталоном.
Физические величины
Физические тела и явления характеризуют физическими величинами. Некоторые из них вам уже знакомы из курса природоведения: это длина, площадь, объем, масса, сила. Рассмотрим их подробнее.
В науке используют единицы физических величин, определенные Международной системой единиц, которую сокращенно называют1 SI — от английских слов System International, что означает «международная система».
Длина, Площадь, Объем
Длиной характеризуют физические тела и, например, путь, пройденный телом за время его движения. За единицу длины в SI принят2 I метр (м).
На линейках и мерных лентах (рулетках) нанесены деления, обозначающие сотые и тысячные доли метра — сантиметры и миллиметры (рис. 3.1).
Единицы площади и объема определяют с помощью единицы длины: единицей площади является I м2 (площадь квадрата со стороной I м), а единицей объема — I м3 (объем куба с ребром I м).
Объем жидкости измеряют с помощью измерительных цилиндров, называемых часто мензурками (рис. 3.2). Длину, площадь и объем задают их числовыми значениями. Физические величины, которые задают только числовыми значениями, называют скалярными.
Время
Всякое физическое явление длится в течение определённого промежутка времени. За единицу времени в S1 принята 1 секунда (с), 60 с составляют 1 минуту (мун), а 60 минут — 1 час (ч).
Время измеряют часами (рис. 3.3). Они представляют собой обычно устройства, в которых повторяется определенный процесс. Например, в маятниковых часах повторяются колебания маятника. Сегодня чаще используют кварцевые часы, в которых колеблются крошечные кристаллы кварца.
Перемещение и скорость
При движении тело изменяет свое положение в пространстве.
Перемещением тела называют направленный отрезок, проведенный из начального положения тела в его конечное положение.
Перемещение задают числовым значением (длиной указанного отрезка) и направлением. Физические величины, которые характеризуют числовым значением и направлением, называют векторными:
Значение векторной величины называют ее модулем.
Векторную величину обозначают буквой со стрелкой, а модуль — той же буквой без стрелки. Так, перемещение обычно обозначают 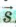

Скоростью тела называют физическую величину, равную отношению перемещения тела к промежутку времени, в течение которого произошло это перемещение.
Скорость, как и перемещение, является векторной величиной, то есть ее характеризуют модулем и направлением. Например, скорости двух встречных автомобилей могут быть равными по модулю, но направлены они противоположно. Скорость обозначают обычно 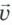
Единицей скорости в SI является 1 метр в секунду (м/с). Тело, которое движется с такой скоростью, за 1 с перемещается на 1 м, — это скорость прогулки. Рекорд скорости в беге — чуть больше 10 м/с.
Скорость современных реактивных самолетов достигает почти километра в секунду (км/с), а космических кораблей — даже больше 10 км/с. Но ни одно тело не может двигаться со скоростью, превышающей скорость света в вакууме, которая равна примерно 300 000 км/с.
Для измерения скорости автомобилей и мотоциклов используют спидометры1 (рис. 3.4-3.6). Они показывают обычно скорость в километрах в час (км/ч). Вы, наверное, замечали, что во время движения автомобиля стрелка спидомстра обычно «покачивается». Дело в том, что скорость автомобиля при движении обычно изменяется.
Масса
Каждое физическое тело имеет определенную массу. Массы двух тел можно сравнить, измерив, как изменяются их скорости при взаимодействии друг с другом: скорость тела большей массы изменяется меньше, чем скорость тела меньшей массы.
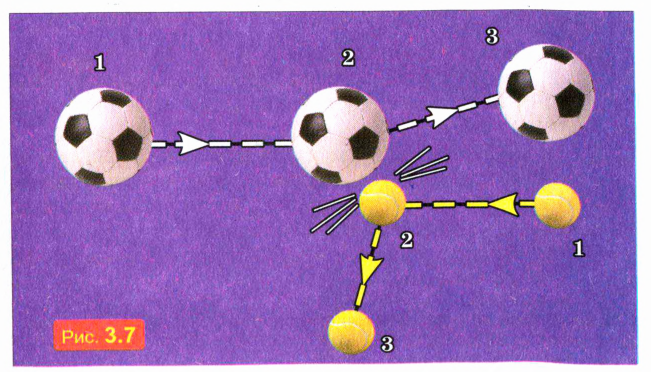
Например, на рис. 3.7 схематически показано столкновение, футбольного и теннисного мячей (цифры обозначают положение мячей в три последовательных момента времени). Мы видим, что при столкновении скорость футбольного мяча изменилась намного меньше, чем скорость теннисного. Значит, масса футбольного мяча намного больше массы теннисного мяча.
Далее мы расскажем о намного более простом способе измерения массы тел, который обычно и используют на практике.
Единицей массы в S1 является 1 килограмм (кг). Это примерно масса одного литра воды. Международный эталон килограмма представляет собой металлический цилиндр из специального сплава.
Сила
Мерой взаимодействия тел является сила: чем больше сила, действующая на тело, тем больше изменяется скорость этого тела за 1 с. Сила является векторной величиной: ее задают числовым значением и направлением. На рисунках силу обозначают стрелкой, начало которой находится в точке приложения силы.
Единицу силы в честь Ньютона назвали ньютоном (Н)1. Сила в 1 Н, приложенная к движущемуся телу массой 1 кг в направлении движения тела, увеличивает его скорость за каждую секунду на 1 м/с,
Чтобы вы представили себе, что такое сила в 1 Н, приведем пример: когда вы держите полное ведро воды, то прикладываете к нему силу, равную примерно 100 Н. При этом приложенная вами сила уравновешивает силу, с которой Земля притягивает то же самое ведро с водой.
Силу, с которой Земля притягивает предметы, называют силой тяжести. В многочисленных опытах было установлено, что сила тяжести, действующая на тело, пропорциональна его массе.
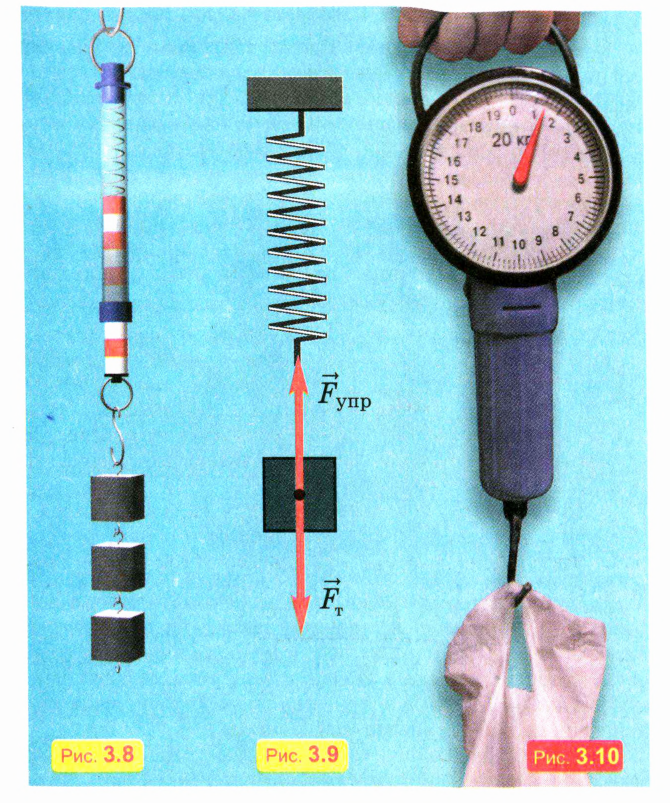
Силу измеряют динамометром2. На рис. 3.8 показан пружинный динамометр, действие которого основано на том, что удлинение пружины пропорционально значению растягивающей ее силы.
На рис. 3.9 схематически изображены силы, действующие на тело, подвешенное к динамометру: это сила тяжести со стороны Земли и сила упругости со стороны пружины. Если тело находится в покое, сила упругости уравновешивает силу тяжести, то есть направлена противоположно ей и равна ей по модулю.
Значит, по удлинению пружины в этом случае можно найти значение силы тяжести. А это, в свою очередь, позволяет рассчитать массу тела, поскольку сила тяжести пропорциональна массе тела.
Таким образом, массу тела можно найти с помощью взвешивания. Пружинные весы (рис. 3.10) — это динамометр, шкала которого размечена (проградуирована) так, что она показывает массу подвешенного груза.
Что называется физической величиной
Издавна люди для более точного описания каких-нибудь событий, явлений, свойств тел и веществ используют их характеристики. Например, сравнивая тела, которые нас окружают, мы говорим, что книга меньше, чем книжный шкаф, а конь больше кошки. Это означает, что объем коня больше объема кошки, а объем книги меньше объема шкафа.
Объем — пример физической величины, которая характеризует общее свойство тел занимать ту или иную часть пространства (рис. 1.15, а). При этом числовое значение объема каждого из тел индивидуально.
Рис. 1.15. Для характеристики свойства тел занимать ту или иную часть пространства мы используем физическую величину объем (а, б), для характеристики движения — скорость (б, в)
Общая характеристика многих материальных объектов или явлений, которая может приобретать индивидуальное значение для каждого из них, называется физической величиной.
Еще одним примером физической величины может служить известное вам понятие «скорость*. Все движущиеся тела изменяют свое положение в пространстве с течением времени, однако быстрота этого изменения для каждого тела различна (рис. 1.15, б, в). Так, самолет за 1 с полета успевает изменить свое положение в пространстве на 250 м, автомобиль — на 25 м, человек — на 1 м, а черепаха — всего на несколько сантиметров. Поэтому физики и говорят, что скорость — это физическая величина, которая характеризует быстроту движения.
Нетрудно догадаться, что объем и скорость,— это далеко не все физические величины, которыми оперирует физика. Масса, плотность, сила, температура, давление, напряжение, освещенность — это лишь малая часть тех физических величин, с которыми вы познакомитесь, изучая физику.
Что означает измерить физическую величину
Для того чтобы количественно описать свойства какого-либо материального объекта или физического явления, необходимо установить значение физической величины, которая характеризует данный объект или явление.
Значение физических величин получают путем измерений (рис. 1.16— 1.19) или вычислений.
Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу.
Приведем пример из художественной литературы: «Пройдя шагов триста по берегу реки, маленький отряд вступил под своды дремучего леса, извилистыми тропами которого им надо было странствовать на протяжении десяти дней*. (Ж. Верн «Пятнадцатилетний капитан*)
Герои романа Ж. Верна измеряли пройденный путь, сравнивая его с шагом, то есть единицей измерения служил шаг. Таких шагов оказалось триста. В результате измерения было получено числовое значение (триста) физической величины (пути) в избранных единицах (шагах).
Рис. 1.20. Если бабушка и внук будут измерять расстояние в шагах. то они всегда будут получать разные результаты
Очевидно, что выбор такой единицы не позволяет сравнивать результаты измерений, полученные разными людьми, поскольку длина шага у всех разная (рис. 1.20). Поэтому ради удобства и точности люди давным-давно начали договариваться о том, чтобы измерять одну и ту же физическую величину одинаковыми единицами. Ныне в большинстве стран мира действует принятая в I960 году Международная система единиц измерения, которая носит название «Система Интернациональная* (СИ) (рис. 1.21).
В этой системе единицей длины является метр (м), времени — секунда (с); объем измеряется в метрах кубических (м3), а скорость — в метрах в секунду (м/с). Об остальных единицах СИ вы узнаете позже.
Кратные и дольные единицы
Из курса математики вы знаете, что для сокращения записи больших и малых значений разных величин пользуются кратными и дольными единицами.
Кратные единицы — это единицы, которые больше основных единиц в 10, 100, 1000 и более раз.
Дольные единицы — это единицы, которые меньше основных в 10, 100, 1000 и более раз.
Для записи кратных и дольных единиц используют приставки. Например, единицы
Рис. 1.21. Основные единицы Международной системы (СИ)
длины, кратные одному метру,— это километр (1000 м), декаметр (10 м). Единицы длины, дольные одному метру,— это дециметр (0,1 м), сантиметр (0,01 м), микрометр (0,000001 м) и так далее.
В таблице приведены наиболее часто употребляемые приставки.
Приставки, служащие для образования кратных и дольных единиц
Измерительные приборы
Измерение физических величин ученые проводят с помощью измерительных приборов. Простейшие из них — линейка, рулетка — служат для измерения расстояния и линейных размеров тела. Вам также хорошо известны такие измерительные приборы, как часы — прибор для измерения времени, транспортир — прибор для измерения углов на плоскости, термометр — прибор для измерения температуры и некоторые другие (рис. 1.22, с. 20). Со многими измерительными приборами вам еще предстоит познакомиться.
Большинство измерительных приборов имеют шкалу, которая обеспечивает возможность измерения. Кроме шкалы, на приборе указывают единицы, в которых выражается измеренная данным прибором величина*.
По шкале можно установить две наиболее важные характеристики прибора: пределы измерения и цену деления.
Пределы измерения — это наибольшее и наименьшее значения физической величины, которые можно измерить данным прибором.

————————————————
Цена деления — это значение наименьшего деления шкалы измерительного прибора.
Например, верхний предел измерений медицинского термометра (рис. 1.23) равен 42 °С, нижний — 34 °С, а цена деления шкалы этого термометра составляет 0,1 °С.
Напоминаем: чтобы определить цену деления шкалы любого прибора, необходимо разность двух любых значений величин, указанных на шкале, разделить на количество делений между ними.
Итоги:
Общая характеристика материальных объектов или явлений, которая может приобретать индивидуальное значение для каждого из них, называется физической величиной.
Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу.
В результате измерений мы получаем значение физических величин.
Говоря о значении физической величины, следует указать ее числовое значение и единицу.
Для измерения физических величин пользуются измерительными приборами.
Для сокращения записи числовых значений больших и малых физических величин используют кратные и дольные единицы. Они образуются с помощью приставок.
Точность измерений
Теперь вы знаете, что означает измерить физическую величину. И в повсе дневной жизни вам уже приходилось выполнять множество простейших измерений. Но насколько точными были ваши измерения? Можно ли получить абсолютно точное значение физической величины?
Попробуем разобраться в этих непростых вопросах.
Оцениваем размеры и проверяем результат:
Начнем с проверки вашего глазомера.
Оцените на глаз длину иглы, изображенной на рис 1.24. А теперь давайте проверим, насколько результат вашей оценки соответствует действительности, то есть измерим длину той же иглы с помощью линейки. Для этого:
- — приложим линейку к игле так, чтобы «ноль» на ее шкале совпал с одним концом иглы (рис. 1.25);
- — определим значение деления шкалы, напротив которого расположен ее другой конец.
Мы видим, что он расположен возле отметки 5 см. Отсюда делаем вывод, что длина иглы около 5 см. Если результат вашей предварительной оценки совпадает с этим значением, то у вас хороший глазомер. Определить на глаз размер более точно нам не удастся.
Результат измерений:
Если нам нужен более точный результат, придется обратить внимание на то, что кончик иглы немного более чем на два миллиметра выступает за отметку 5 см. Итак, более точная длина иглы — 5,2 см, или 52 мм.
Вы можете возразить, что это тоже неточно.
Да, неточно! Именно поэтому принято всегда указывать точность, с которой выполнено измерение.
В первом случае наше измерение выполнено с точностью до 1 см, а во втором — с точностью до 0,1 см.
Чтобы произвести еще более точное измерение, необходимо учесть длину той части иглы, которая выступает за отметку 52 мм, и тогда точность повысится до 0,01 см. Но для этого нам придется использовать измерительный прибор с еще меньшей ценой деления, то есть более точный, но даже тогда мы не можем утверждать, что измерили иглу совершенно точно.
Причин для этого достаточно: это и несовершенство конструкции прибора, и погрешности, которые возникают при проведении опыта (например, начало иглы невозможно абсолютно точно совместить с «нулем» линейки). Таким образом, даже если измерение проводится более тщательно и с помощью более совершенного прибора, точность возрастает, но погрешностей все равно не избежать.
Чтобы уменьшить погрешность, измерение можно выполнить несколько раз, а затем вычислить среднее значение всех полученных результатов (наити их среднее арифметическое).
Точность измерений
Однако не следует думать, что чем точнее измерение, тем лучше: излишняя точность не всегда целесообразна.
Предположим, что вместо длины иглы вам необходимо измерить длину крышки стола. В этом случае нет необходимости учитывать десятые и сотые доли миллиметра, поскольку, измеряя длину стола в разных местах, мы получим величины, отличающиеся на несколько миллиметров. Поэтому долями миллиметра в этом случае можно пренебречь. Также нет смысла измерять длину стены с точностью до одного миллиметра (рис. 1.26).
Из этого можно сделать вывод, что необходимую точность измерения определяет цель эксперимента.
Чаще всего важно не значение погрешности, а то, какую часть от всей измеренной величины составляет возможная погрешность.
Если портной, выкраивая брюки, ошибется на 1 мм, вы этого даже не заметите. А вот если, втягивая нить в ушко иглы, он всякий раз будет ошибаться на 1 мм (рис. 1.27), то едва ли брюки вообще когда-либо будут сшиты.
Роль измерений в физике. Прямые и косвенные измерения
Наука начинается с тех пор, как начинают измерять… Д. И. Менделеев
Вдумайтесь в слова известного ученого. Из них ясна роль измерений в любой науке, особенно в физике. Но, кроме того, измерения важны в практической жизни. Можете ли вы представить свою жизнь без измерений времени, массы, длины, скорости движения, расхода электроэнергии и т. д.?
Как измерить физическую величину? Для этой цели используются измерительные приборы. Некоторые из них вам уже известны. Это разного вида линейки, часы, термометры, весы, транспортиры и др.
Измерительные приборы бывают цифровые и шкальные. В цифровых приборах результат измерений определяется цифрами. Это электронные приборы — часы, термометр, счетчик электроэнергии (рис. 19) и др.
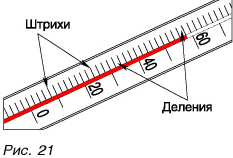
Линейка, стрелочные часы, термометр бытовой, весы, транспортир (рис. 20) — это шкальные приборы. Они имеют шкалу. По ней определяется результат измерений. Вся шкала расчерчена штрихами на деления (рис. 21). Одно деление это не один штрих, как иногда ошибочно считают некоторые учащиеся, а промежуток между двумя ближайшими штрихами. На рисунке 22 на шкале мензурки от значения 10 мл до значения 20 мл два деления, но три штриха. Приборы, которые мы будем использовать в лабораторных работах, в основном шкальные.
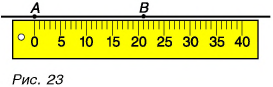
Что значит измерить физическую величину? Измерить физическую величину — значит сравнить ее с однородной величиной, принятой за единицу. Например, чтобы измерить длину отрезка прямой между точками A и В, нужно приложить линейку и по ее шкале (рис. 23) определить, сколько миллиметров укладывается между точками А и В. Однородной величиной, с которой проводилось сравнение длины отрезка АВ, в данном случае была длина, равная 1 мм.
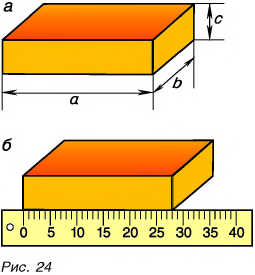
Если физическая величина измеряется непосредственно путем снятия данных со шкалы прибора, то такое измерение называют прямым. Например, приложив линейку к разным ребрам бруска, мы определим его длину а, ширину b и высоту с (рис. 24, а). Значение длины, ширины и высоты мы определили непосредственно, сняв данные со шкалы линейки. Из рисунка 24, б следует: a = 28 мм. Это прямое измерение.
А как определить объем бруска? Надо провести прямые измерения его длины а, ширины b и высоты с, а затем по формуле
вычислить объем бруска.
В этом случае мы говорим, что объем бруска определили по формуле, т. е. косвенно, и измерение объема называется косвенным измерением.
В физике измерения физических величин чаще всего косвенные. В дальнейшем вы убедитесь в этом сами.
Главные выводы:
- Измерительные приборы бывают цифровые и шкальные.
- При прямых измерениях физическая величина определяется непосредственно по шкале прибора.
- При косвенных измерениях физическая величина определяется по формуле.
Для любознательных:
Изучая строение человеческого тела и работу его органов, ученые проводят множество измерений. Оказывается, в человеке массой примерно 70 кг около 6 л крови. Сердце человека в спокойном состоянии сокращается 60—80 раз в минуту. За одно сокращение оно выбрасывает в среднем 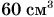
В течение суток кровь человека около 360 раз проходит через почки, очищаясь там от вредных веществ. Общая протяженность почечных кровеносных сосудов составляет приблизительно 18 км. Ведя здоровый образ жизни, мы помогаем нашему организму работать без сбоев!
Единицы измерения физических величин
Чтобы решить, как быстрее доехать до вокзала — на трамвае или на такси, сравнивают скорости движения этих транспортных средств. Скорость — физическая величина. Она количественно описывает физическое явление — движение. Если скорость автомобиля 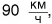
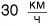
В физике для описания физических явлений и свойств используется множество физических величин: длина, сила, давление и др. Каждая физическая величина имеет символическое обозначение, числовое значение и единицу измерения. Например, длина бруска 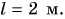
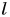
Исторически сложилось так, что у разных народов и государств единицы измерения одних и тех же физических величин различались. Часто это были единицы, соответствующие размерам частей тела человека, массе семени бобов и т. д. Пользоваться такими единицами было неудобно, особенно в торговле между разными государствами.
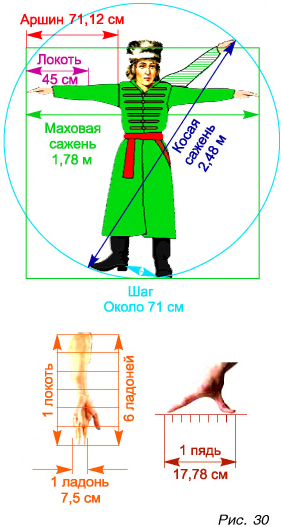
Например, в Англии для измерения длины использовался фут (1 фут = 30,5 см), а на Руси — аршин (1 аршин = 71,1 см) (рис. 30). Нужно было упорядочить систему единиц, сделать ее удобной в использовании всеми странами. В 1960 г. ввели единую Международную систему единиц (сокращенно СИ — Систему Интернациональную). Ею пользуется большинство стран. Основными единицами в СИ являются: метр (м) — для длины, килограмм (кг) — для массы, секунда (с) — для промежутка времени, Кельвин (К) — для температуры.
Но всегда ли удобно измерять время в секундах, а длину — в метрах? Оказывается, нет. Например, время движения поезда из Минска в Москву измеряют в часах (ч), а путь — в километрах (км). Единицы 1 ч и 1 км — это неосновные (кратные) единицы СИ. Между основными и неосновными единицами существует связь. Так, 1 км = 1000 м, 1 ч = 3600 с.
Основные единицы измерения имеют эталоны. Эталоны хранятся в г. Севре (Франция) в Международном бюро мер и весов. На рисунке 31 приведен эталон килограмма — цилиндр из плати но-иридиевого сплава. По эталону делают копии, которыми пользуются разные страны. Позже вы познакомитесь с эталонами других единиц измерения.
Для любознательных
Эталонная база страны обеспечивает единство измерений и является частью национального достояния. В Беларуси, как и в других странах, ведется работа по исследованию и созданию эталонных комплексов. В Белорусском государственном институте метрологии созданы эталоны массы, времени (см. рис.), температуры и др.
Главные выводы
- Каждая физическая величина имеет символическое обозначение, числовое значение и единицу измерения.
- Основными единицами СИ являются: метр, килограмм, секунда, Кельвин и др.
- Основные единицы измерения имеют свои эталоны.
Пример №1
В одной из книг немецкого путешественника XVII в. есть такие строки: «Шелковая материя, привозимая с Востока, называется русскими «китайкой», и каждый кусок содержит ни больше ни меньше как восемь с четвертью аршин». Сколько метров в куске материи?
Дано:
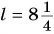
1 аршин = 71,1 см = 0,711 м
Решение
Так как 1 аршин = 71,1 см = 0,711 м, то длина восьми с четвертью аршин в метрах будет равна:
Ответ:
- Заказать решение задач по физике
Действия над физическими величинами
В математике можно складывать, вычитать и сравнивать любые числа. А какие действия можно производить над физическими величинами?
Действия сложения, вычитания и сравнения над физическими величинами можно производить только в том случае, если они однородны, т. е. представляют одну и ту же физическую величину.
Мы можем складывать длину с длиной, вычитать из массы массу, сравнивать промежуток времени с промежутком времени (пример 1). Смешно и нелепо было бы складывать 4 м и 5 кг или вычитать 30 с из 9 кг. А вот умножать и делить можно как однородные, так и разные физические величины.
В примере 2 делятся не только числовые значения (10 : 2 = 5), но и единицы физических величин (кг : кг = 1). Результат показывает, во сколько раз одна физическая величина (масса) больше другой.
В примере 3 умножаются числовые значения 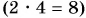
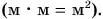
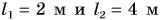
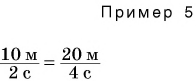
В примере 4 в результате деления двух разных физических величин — длины 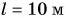
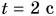
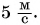
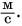
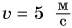
В примере 5 знак равенства относится не только к числовым значениям, но и к единицам. Знак равенства поставить нельзя, если сравнить 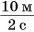
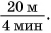
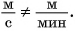
Для любознательных:
Большие единицы времени — год и сутки — дала нам сама природа. Но час, минута и секунда появились благодаря человеку.
Принятое в настоящее время деление суток восходит к глубокой древности. В Вавилоне применялась не десятичная, а шестидесятеричная система счисления. Поскольку 60 делится без остатка на 12, сутки у вавилонян состояли из 12 равных частей. В Древнем Египте было введено деление суток на 24 часа. Позже появились минуты и секунды. То, что в 1 часе 60 минут, а в 1 минуте 60 секунд, — наследие шестидесятеричной системы счисления Вавилона.
Главные выводы:
- Складывать, вычитать и сравнивать можно только однородные физические величины.
- Умножение и деление разнородных величин приводит к появлению новой физической величины.
Пример №2
Выберите значения физических величин, которые можно складывать: 120 г, 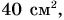
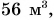
Решение
Однородными физическими величинами в данном случае являются массы тел: 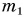
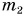
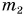
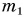
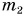
Следовательно, m = 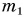
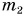
Ответ: результатом сложения является масса m = 168 г.
Пример №3
Определите физические величины, получившиеся в результате
выполнения следующих действий: 1) 35 г : 5 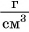
Решение
1) Найдем отношение двух физических величин, разделив их числовые значения и единицы:
Мы получили физическую величину — объем
2) Чтобы умножить две однородные физические величины, необходимо выразить их в одних единицах, например в сантиметрах (см):
Мы получили физическую величину — площадь
Ответ: 1) в результате деления двух физических величин разного рода (массы и плотности) получена третья физическая величина — объем 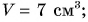
физические величины и их измерение
Чем отличается язык физики (и любой другой точной науки) от обычного? язык физики интернационален: он создавался лучшими умами человечества, его однозначно понимают в любом уголке нашей планеты. язык физики объективен: каждое его понятие однозначно, оно имеет один смысл, который может измениться (чаще всего — расшириться) только благодаря опытам. Как и методы научного познания, язык физики родился из практики.
Что такое физическое исследование и каковы его методы
Вспомним, с чего начинается исследовательская работа ученых. Прежде всего — это наблюдение за определенным явлением (телом или материалом) и размышления над его сущностью.
Наблюдение — это восприятие природы с целью получения первичных данных для последующего анализа. Далеко не всегда наблюдения приводят к правильным выводам. Поэтому, чтобы опровергнуть или подтвердить собственные выводы, ученые проводят физические исследования.
Физическое исследование — это целенаправленное изучение явлений и свойств природы средствами физики.
| Методы физических исследований | |
|---|---|
| экспериментальный | теоретический |
| Эксперимент — исследование физического явления в условиях, находящихся под контролем исследователя. В своей основе физика является экспериментальной наукой: большинство ее законов основаны на фактах, установленных опытным путем. | Анализ данных, полученных в результате экспериментов, формулирование законов природы, объяснение конкретных явлений и свойств на основе этих законов, а главное — предвидение и теоретическое обоснование (с широким использованием математики) еще не известных явлений и свойств. |
Какие наблюдения, теоретические и экспериментальные исследования вы провели бы, чтобы исследовать свечение обычной лампы накаливания?
Теоретические исследования проводят не с конкретным физическим телом, а с его идеализированным аналогом — физической моделью, которая должна учитывать только некоторые основные свойства исследуемого тела. Так, изучая движение автомобиля, мы иногда используем его физическую модель — материальную точку (рис. 2.1, а).
Эту модель используют, если размеры тела не существенны для теоретического описания, то есть в модели «материальная точка» учитывается только масса тела, а его форма и размеры во внимание не принимаются. А вот если нужно выяснить, как на движение автомобиля влияет сопротивление воздуха, целесообразно применить уже другую физическую модель — она должна учитывать и форму, и размеры автомобиля (рис. 2.1, б), но может не учитывать, например, размещение пассажиров в салоне. Чем больше выбрано соответствующих параметров для исследования физической системы «автомобиль», тем точнее можно предвидеть «поведение» этой системы.
Рис. 2.1. Определяя скорость и время движения автомобиля, можно применять физическую модель «материальная точка» (а); выясняя аэродинамические свойства автомобиля, эту физическую модель применять нельзя (б)
Целесообразно ли использовать физическую модель «материальная точка», если инженеры должны рассчитать устойчивость автомобиля?
Как измерить физическую величину
Описывая, например, движение автомобиля, мы используем определенные количественные характеристики: скорость, ускорение, время движения, силу тяги, мощность и т. п.
Из предыдущего курса физики вы знаете, что количественную меру свойства тела, физического процесса или явления называют физической величиной. Значение физической величины устанавливают в ходе измерений, которые, в свою очередь, бывают прямые и косвенные. При прямых измерениях величину сравнивают с ее единицей (метром, секундой, килограммом, ампером и т. п.) с помощью измерительного прибора, проградуированного в соответствующих единицах (рис. 2.2).
Рис. 2.2. Современные приборы для прямого измерения температуры (а); массы (б); скорости движения (в)
Назовите несколько физических величин, значения которых вы находили с помощью прямых измерений. В каких единицах измеряют эти величины? какими приборами? При косвенных измерениях величину вычисляют по результатам прямых измерений других величин, связанных с измеряемой величиной некоторой функциональной зависимостью. Так, чтобы найти среднюю плотность ρ тела, нужно с помощью весов измерить массу m тела, с помощью, например, мензурки измерить его объем V, а затем массу разделить на объем:
Построение системы единиц
В конце XVIII в., после Великой французской революции, перед французскими учеными была поставлена задача создать систему единиц на научной основе. В результате появилась метрическая система единиц. В 1960 г. была создана Международная система единиц CИ, которая со временем стала в мире доминирующей.
Основные единицы СИ
- килограмм (1 кг, 1 kg) единица массы
- метр (1 м, 1 m) единица длины
- секунда (1 с, 1 s) единица времени
- ампер (1 А, 1 А) единица силы тока
- моль (1 моль, 1 mol) единица количества вещества
- кельвин (1 К, 1 K) единица температуры
- кандела (1 кд, 1 kd) единица силы света
Исторически единицы физических величин связывали с определенными телами или природными процессами. Так, 1 метр был связан с размерами планеты Земля, 1 килограмм — с определенным объемом воды, 1 секунда — с суточным вращением Земли. Позже для каждой единицы был создан эталон — средство (или комплекс средств) для воспроизведения и хранения единицы физической величины. Основные эталоны хранились (и хранятся сейчас) в Международном бюро мер и весов (г. Севр, Франция).
Сейчас все большее распространение получают методы построения системы единиц, основанные на особенностях излучения и распространения электромагнитных волн, а также на фундаментальных физических константах. Рассмотрим основные этапы создания системы единиц на примерах метра и килограмма.
Напомним, что для удобства записи больших и малых значений физических величин используют кратные и дольные единицы. Кратные единицы больше основных единиц в 10, 100, 1000 и более раз. Дольные единицы меньше основных единиц в 10, 100, 1000 и более раз.
Названия кратных и дольных единиц включают в себя специальные префиксы. Например, километр (1000 м, или 103 м) — кратная единица длины, миллиметр (0,001 м, или 10–3 м) — дольная единица длины (см. табл. 1).
Таблица 1. Префиксы для образования названий кратных и дольных единиц
| Префикс | Символ | Множитель |
| атто- | а | 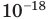 |
| фемто- | ф | 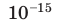 |
| пико- | п | 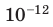 |
| нано- | н | 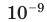 |
| микро- | мк | 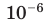 |
| милли- | м | 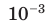 |
| санти- | с | 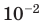 |
| кило- | к | 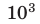 |
| мега- | М | 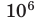 |
| гига- | Г | 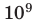 |
| тера- | Т | 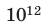 |
| пета | п | 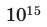 |
| экса | е | 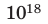 |
Погрешности измерений
При измерении любой физической величины обычно выполняют три последовательные операции: 1) выбор, проверка и установка прибора (приборов); 2) снятие показаний прибора (приборов); 3) вычисление искомой величины по результатам измерений (при косвенных измерениях); 4) оценка погрешности.
Например, нужно измерить на местности расстояние около 5 м. Разумеется, что для этого не следует брать ученическую линейку, — удобнее воспользоваться рулеткой. Все приборы имеют определенную точность. Расстояние в 5 м, как правило, не требуется определять с точностью до миллиметра, поэтому шкала рулетки может и не содержать соответствующих делений.
Рис. 2.3. Штангенциркуль. Точность измерения изображенным прибором — сотые доли миллиметра
А вот если для ремонта лабораторного крана необходимо определить размер шайбы, целесообразно воспользоваться штангенциркулем (см. рис. 2.3). Однако даже с помощью сверхточного прибора нельзя выполнить измерения абсолютно точно. Всегда есть погрешности измерений — отклонение значения измеренной величины от ее истинного значения. Модуль разности между измеренным (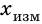
Отношение абсолютной погрешности к измеренному значению измеряемой величины называют относительной погрешностью измерения 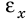
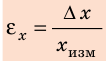
Погрешности при измерениях бывают случайные и систематические.
Случайные погрешности
Случайные погрешности связаны с процессом измерения: измеряя расстояние рулеткой, невозможно проложить ее идеально ровно; отсчитывая секундомером время, прибор невозможно мгновенно включить и выключить и т. д. Чтобы результаты были более точными, измерения проводят несколько раз и определяют среднее значение измеряемой величины:
где 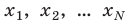
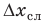
Если измерение проводилось один раз, будем считать, что случайная погрешность равна половине цены деления шкалы прибора.
Систематические погрешности
Систематические погрешности связаны прежде всего с выбором прибора: невозможно найти рулетку с идеально точной шкалой, идеально равноплечие рычаги и т. п. Систематические погрешности определяются классом точности прибора, поэтому их часто называют погрешностями прибора. В процессе эксплуатации точность приборов может снижаться, поэтому их необходимо периодически калибровать при помощи специального оборудования. Абсолютные погрешности некоторых приборов, используемых в школе, приведены в табл. 2. Если используются другие приборы, будем считать, что абсолютная погрешность прибора равна половине цены деления его шкалы.
Абсолютная погрешность прямого измерения (∆x) учитывает как систематическую погрешность, связанную с прибором (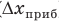
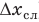
Обратите внимание! Приведенные формулы очень упрощены. Ученые используют более сложные методы расчетов погрешностей.
Таблица 2. Абсолютные погрешности некоторых физических приборов
| Физический прибор | Цена деления шкалы прибора | Абсолютная погрешность прибора |
| Линейка ученическая | 1 мм | ±1 мм |
| Лента измерительная | 0,5 см | ±0,5 см |
| Штангенциркуль | 0,1 мм | ±0,05 мм |
| Цилиндр измерительный | 1 мл | ±1 мл |
| Секундомер | 0,2 с | ±1 с за 30 мин |
| Динамометр учебный | 0,1 Н | ±0,05 Н |
| Термометр лабораторный | 1 °С | ±1 °С |
Как определить погрешности косвенных измерений
Многие физические величины невозможно измерить непосредственно. Их косвенное измерение включает два этапа: 1) методом прямых измерений находят значения определенных величин, например x, y; 2) по соответствующей формуле вычисляют искомую величину f. Как в таком случае определить абсолютную ∆f и относительную 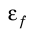
- Относительную погрешность определяют по специальным формулам (см. табл. 3).
- Абсолютную погрешность определяют по относительной погрешности:
- Если эксперимент проводят, чтобы выяснить, выполняется ли некое равенство (например, X Y= ), то относительную погрешность экспериментальной проверки равенства X Y= можно оценить по формуле:
Таблица 3. Некоторые формулы для определения относительной погрешности
| Функциональная зависимость | Относительная погрешность |
|---|---|
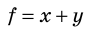 |
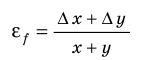 |
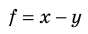 |
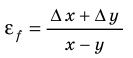 |
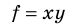 |
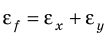 |
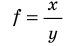 |
|
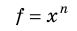 |
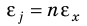 |
Как правильно записать результаты
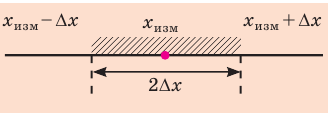
Абсолютная погрешность эксперимента определяет точность, с которой имеет смысл вычислять измеряемую величину. Абсолютную погрешность ∆x обычно округляют до одной значащей цифры с завышением, а результат измерения xизм — до величины разряда, оставшегося после округления в абсолютной погрешности. Окончательный результат х записывают в виде:
Абсолютная погрешность — положительная величина, поэтому 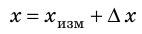
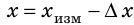
Рис. 2.4. Абсолютная погрешность измерения определяет интервал, в котором находится истинное значение измеряемой величины
Пример. Пусть измеряли ускорение свободного падения (g). После обработки экспериментальных данных получили: 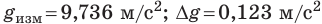
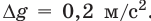
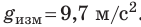
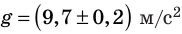
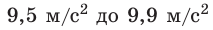
Рис. 2.5. Табличное значение: 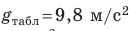
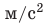
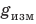
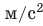
- Точность измерений и погрешности
- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Что изучает физика
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс