Применение размерности для проверки правильности решения физических задач
Разделы: Физика
Цели:
- шире использовать полученные теоретические знания по физике;
- вооружить учащихся большим набором способов решения задач.
1. Понятие размерности
Для начала упорядочим некоторые понятия, с которыми мы имели дело раньше и с теми, которые встретятся нам в будущем. К таким физическим понятиям относятся: наименование, название физической величины, в выбранной системе единиц, размерность, обозначение и определяющее уравнение.
Разберём это на некоторых примерах взятых из раздела «Механика» и знакомых нам. Для краткости сведём всё это в таблицу.
Наименование
S
S = a 3
кв. метр
L 2
V
V = а 3
куб. метр
L 3
V
V = S/t
м/с; м с –1
метр в сек.
L T –1
а
а = 
м/с 2 ; м с –2
метр в секунду
за секунду
L T –2


кг/м 3 ; кг м –3
кг на куб. метр
M L –3
| Название физ. величины | Обозначение | Определяющее уравнение | Размерность |
| Площадь | |||
| Объём | |||
| Скорость | |||
| Ускорение | |||
| Плотность |
Это простые и часто встречающиеся понятия, причём название физической величины вытекает из определяющего её уравнения. Но ряд физических величин имеют «клички». Название величины не следует прямо, как прежде, из определяющего уравнения.
Наименование величины – сила. Название единицы измерения – Ньютон. Вспомним материал 7-го класса. Что такое Ньютон? Это такая сила, которая за 1 секунду изменяет скорость тела массой 1 кг на 1 метр в секунду. Примером одной из сил является вес тела. Мы знаем, что вес тела равен Р = mg, где m – масса тела , а g – ускорение свободного падения.
Из физики 8-го класса мы знаем, что ускорение измеряется в м/с 2 . Значит, если речь идёт о весе тела Р, то он равен произведению массы тела на ускорение. Отсюда можно сделать вывод, что и любая другая сила F равна произведению массы тела на полученное в результате действия силы ускорение, т.е. F = ma.
Обратим внимание на то, что, если масса тела равна 1 кг и полученное ускорение равно 1 м/с 2 , то и сила будет равна единице силы, то есть 1-му Ньютону. Тогда размерность Ньютона будет
[ F ] = кг 
Каждой такой единице присуща ей размерность, которая показывает, из каких основных единиц системы СИ «приготовлена», «сделана» такая единица, в какой степени входят в состав этой величины основные единицы и где они находятся в числителе или в знаменателе.
Что такое определяющее уравнение? Это уравнение, которое следует из определения физической величины.
1. Скорость – это физическая величина равная отношению пути, пройденного телом, ко времени за которое этот путь пройден. Отсюда следует определяющее уравнение V = S/t.
2. Работа – это физическая величина равная произведению силы, приложенной к телу на путь, который прошло тело под действием этой силы. Отсюда следует определяющее уравнение: A = F S.
До введения интернациональной системы единиц (СИ), существовал несколько систем единиц.
Так в одной из них основными единицами были: единица массы – грамм; единица длины – сантиметр; единица времени – секунда. Эта система единиц называлась СГС.
Были и другие системы единиц. Но масса есть масса в любой системе. Будь она в кг, или в г, или в мг. Поэтому, независимо от выбранной системы единиц, принято размерность выражать в символах. Масса – М. Длина – L. Время – Т.
В таблице выше соответствующая колонка называется просто размерность.
Задачи для самостоятельного решения.
1. Определить размерность Джоуля. Определяющее уравнение A = F S
2. Определить размерность Ватта. Определяющее уравнение N = A / t
3. Определить размерность Герца. Определяющее уравнение = 1 / Т
4. Определить размерность Паскаля. Определяющее уравнение р = F/S
5. Определить размерность момента силы. Определяющее уравнение М = F L.
2. Проверка правильности решения задач по размерности
«Видкиль воно взялось и на щоб воно сдалось» Украинская пословица.
Откуда взялась размерность мы рассмотрели. Рассмотрим где, и как она может быть применена и её особенности.
Рассмотрим решение нескольких задач:
1. Определить расстояние между Землёй и Солнцем, если луч света, двигаясь со скоростью 3 х 108 м/с, проходит это расстояние примерно за 8,5 минут?
2. Какое расстояние по прямой может пройти ракета за 1 минуту, двигаясь от места старта с ускорением 20 м/с 2 ?
3. Автомобиль, двигаясь со скоростью 54 км/ч, пошел на обгон и в течение 10 секунд двигался с ускорением 2 м/с 2 . Какой путь прошел автомобиль за это время?
4. Автомобиль, двигаясь со скоростью 54 км/ч, перед поворотом в течение 10 секунд двигался равнозамедленно с ускорением – 2 м/с 2 . Какой путь прошел автомобиль за это время?
Проанализируем решение этих задач.
1. Что общего было в этих задачах? (Определялся путь S)
2. В чём различие в этих задачах? (В каждой задаче описывается различное движение, а значит, применяются различные уравнения для определения пути)
То есть различие в том, что одна и та же величина (путь) определяется через различные величины. В № 1 через V и t. В № 2 через а и t. В № 3 и № 4 через Vо, a, t.
Эти величины имеют различные размерности, а в результате произведенных действий получается во всех случаях одна и та же размерность – метр.
Произведём, не используя модулей этих величин, предлагаемые действия только с размерностями.
1. S = V t = 2. S = . 3.4. S = V0t ± = ± =L±L= L
Отсюда следует закономерность: В правильно составленном уравнении, размерность правой его части равна размерности его левой части.
Эту закономерность можно применить для проверки правильности решения задач.
Допустим, задачу №3 решили с ошибкой (она очень часто встречается), записав
уравнение так S = Vо + at 2 /2 , тогда S = 15 + 2 х 10 2 /2 = 65 (м). Так как правильный ответ неизвестен, то неясно, как проверить правильность решения, и найти причину ошибки.
То ли ошибка в вычислениях, то ли в преобразованиях, то ли в неправильном написании правильно выбранного уравнения?
Проверяя правильность решения по наименованию можно найти причину ошибки.
Как это сделать? Вместо модулей величин подставить размерности величин и сравнить размерности левой и правой части уравнения. (использовать, указанную выше, закономерность )
Отсюда следует, L =/= 1 + Т. Задача решена неверно. Где ошибка? В правой части уравнение представляет двучлен. Одна его часть имеет размерность L, а другая L/T. Как из этого выражения L/T получить L? Нужно умножить его на Т. Тогда получим размерность первого члена L. Первый член и второй член правой части уравнения будут иметь размерность L, то есть L + L = L. Левая и правая части будут иметь одинаковую размерность. Значит, первый член правой части уравнения должен иметь вид не Vо, а Vо t.
Теперь, предположим, решающий допустил другую ошибку. В уравнении S = Vоt +at 2 /2 вместо знака «+» поставил знак «–». Поможет ли здесь метод размерности указать на ошибку? Решение задачи № 4 говорит о том, что задача решена правильно. L = L – L = L, но модуль величины другой.
Отсюда следует второй вывод: метод размерностей может подсказать ошибочность физического направления решения, но не может подсказать ошибочность математического действия.
Решим несколько задач по кинематике и сделаем проверку их правильности решения, применив метод размерности.
Задача № 1.
За время равное 2 с, тело, двигаясь прямолинейно и равноускоренно, прошло путь 20 м. Его скорость при этом увеличилась в 3 раза. Определить ускорение тела.
Сделаем проверку решения методом размерности.
Размерности левой и правой части уравнения совпадают, значит, задача решена правильно.
Задача №2.
Тело, двигаясь от остановки равноускоренно, за первые 5 секунд движения прошло путь 10 м. Какой путь пройдёт это тело за 10 секунд от начала движения?
Задача № 3. Тело, двигаясь равноускоренно, за 5 секунд движения прошло путь 100 м , а за 10 сек. – 300 м. Определить начальную скорость движения тела.
Мы проделали громоздкие преобразования. Не допустили ли мы ошибку? Воспользуемся знанием закономерности размерности и проверим свою работу.
L T–1 = Следовательно, задача решена верно.
Подставим числовое значение входящих величин и получим числовой ответ задачи.
V0 = (м/с)
Задача №4. Во сколько раз скорость пули при вылете её из ствола винтовки больше скорости этой пули при прохождении ею 1/3 ствола?
Практическая работа № 1 Физические величины. Применение теории размерностей
Практическая работа № 1
Физические величины. Применение теории размерностей
Цель работы: научить студентов пользоваться международной системой физических единиц и приобрести практические навыки применения теории размерностей.
Характер выполнения работы: каждый студент выполняет работу индивидуально.
Общепринятые или установленные законодательным путём характеристики (меры) различных свойств, общих в качественном отношении для многих физических объектов (физических систем, их состояний и происходящих в них процессов), но в количественном отношении индивидуальных для каждого из них, называются физическими величинами.
Таким образом, под термином «физическая величина» понимают свойство, общее в качественном отношении многим физическим объектам, но в количественном отношении индивидуальное для каждого из них.
Количественным выражением этого свойства в объекте является размер физической величины, а числовой оценкой её размера – значение физической величины. Физическая величина, которой по определению присвоено числовое значение, равное единице, называют единицей физической величины.
В любой системе единиц существует лишь одна основная единица данной физической величины.
Международная система единиц (СИ) была принята в 1960г. на XI генеральной конференции по мерам и весам. В нашей стране данная система введена в действие с 1 января 1982г., в соответствии с ГОСТ 8.417 – 81 «ГСИ. Единицы физических величин».
В настоящее время она характеризуется как когерентная система единиц, состоящая из семи основных, двух дополнительных и ряда производных единиц, число которых не ограничено.
Основные и дополнительные единицы СИ приведены в табл. 1.
Производные единицы Международной системы единиц образуются из основных и дополнительных единиц СИ на основании законов, устанавливающих связь между физическими величинами, или уравнений по которым определяют физическую величину.
Единицы могут быть дольными и кратными от единиц СИ.
Кратной единицей называют единицу, которая в целое число раз больше системной или внесистемной единицы.
Дольной единицей называют единицу, которая в целое число раз меньше системной или внесистемной единицы.
Единицы физических величин СИ
Основные
Сила электрического тока
радиан
Все приставки пишутся слитно с наименованием основной единицы, к которой они присоединяются (килограмм, миллиметр). Присоединение двух и более приставок не допускается.
Для образования наименьших кратных и дольных единиц физических величин используют приставки изложенные в табл. 2.
Качественной характеристикой измеряемых величин является их размерность. Она отражает её связь с основными величинами и зависит от выбора последних.
Размерность обозначается символом dim, происходящим от слова dimension, которое в зависимости от контекста может переводится как размер, и как размерность.
Размерность основных физических величин обозначается соответствующими заглавными буквами. Для длины, массы, времени, например dim l = L; dim m = M; dim t = T.
Множители и приставки для образования десятичных
кратных и дольных единиц и их наименований
Множитель
от какого слова
из какого языка
шесть раз по 103
пять раз по 103
При определении размерности производных величин руководствуются следующими правилами:
1. Размерность левой и правой части не могут не совпадать так как сравниваться между собой могут только одинаковые свойства, объединяя левые и правые части уравнений, отсюда можно прийти к выводу, что алгебраически суммироваться могут только величины, имеющие одинаковые размерности.
2. Алгебра размерностей мультипликативна, т. е. состоит из одного единственного действия – умножения.
2.1. Размерность произведения нескольких величин равна произведению их размерностей. Так, если зависимость между значениями величин Q, A, B, C имеет вид Q = A B C, то
dim Q = dim A dim B dim C
2.2. Размерность частного при делении одной величины на другую равна отношению их размерностей, Q = A/B, то
dim Q = dim A/dim B
2.3. Размерность любой величины, возведённой в некоторую степень, равна её размерности в той же степени, так, если
dim Q = dim A = dimn A
Например, если скорость определять по формуле V = l/t, то
dim V = dim l/dim t = L/T = LT-1
Если сила по второму закону Ньютона F = m a, где a = V/t – ускорение тела, то
dim F = dim m dim a = ML/T2 = LMT-2
Таким образом, всегда можно выразить размерность производной физической величины за размерность основных физических величин с помощью степенного одночлена dim Q = Lб Mв Tг, где L, M, T, … — размерности соответствующих основных физических величин; б, в, г, … — показатели размерности. Каждый из показателей размерности может быть положительным или отрицательным целым или дробным числом, нулём. Если все показатели размерности равны нулю, то такая величина называется безразмерной. Теория размерностей повсеместно применяется для оперативной проверки правильности сложных формул. Если размерности правой и левой частей уравнений не совпадают, т. е. не выполняется правило 1, то в выводе формулы, следует искать ошибку.
Порядок выполнения работы
В начале занятия студенты должны охарактеризовать общие правила конструирования систем единиц. Далее следует ознакомиться с основными и производными единицами системы СИ, с правилами написания обозначений единиц:
— обозначения единиц ставят после их числовых значений и помещают в строку с ними;
— в обозначениях единиц точку и знак сокращения не ставят;
— в буквенных обозначениях отношений единиц в качестве знака деления должна применяться только одна черта: косая или прямая. При применении косой черты обозначения единиц в числителе и знаменателе помещают в строку, произведение обозначений единиц в знаменателе заключают в скобки, например, Вт/(м2·К). Допускается вместо знака черты применять обозначения единиц в виде произведений единиц, возведённых в степени ; Вт·м-2 ·К-1.
Затем студенты должны ознакомиться с принципом образования наименьших кратных и дольных единиц.
В конце занятия следует выполнить ряд заданий, представленных преподавателем по применению теории размерностей, ответить на вопросы, касающиеся данной темы. Оформить отчёт.
Для проверки качества усвоения материала по теории размерностей рекомендуется выполнить следующие задания.
По определяющим уравнениям выразить размерности физических величин:
ускорение a = V/t;
плотность с = m·V;
По размерности физических величин определить основные формулы и обозначить единицы измерений:
удельный вес L3M-1;
динамическая вязкость L-1MT-1;
поверхностное натяжение MT-2;
магнитная проводимость L2MT-2I-2;
удельное электрическое сопротивление L3MT-2I-2;
1.Каковы правила конструирования систем единиц?
2.Назовите основные и дополнительные единицы системы СИ?
3.Как образуются кратные и дольные единицы Международной системы единиц?
4.Что называют единицей физической величины?
5.Принципы образования производных единиц Международной системы?
6.Что такое физическая величина?
7.Что такое размер физической величины?
8.Какие единицы являются дольными, кратными от единиц СИ?
9.Что такое системные, внесистемные единицы?
10.Какие существуют правила написания обозначения единиц?
ГОСТ 8.417.-81. ГСИ. Единицы физических величин.
2. Коротков , стандартизация и сертификация [Электронный ресурс]: учебное пособие/ , — Электрон. текстовые данные.— Томск: Томский политехнический университет, 2015.— 187 c.
Глава 3. ТЕОРИЯ ВОСПРОИЗВЕДЕНИЯ
И ПЕРЕДАЧИ ИХ РАЗМЕРОВ
3.1. Системы физических величин и их единиц
В науке, технике и повседневной жизни человек имеет дело с разнообразными свойствами окружающих нас физических объектов. Эти свойства отражают процессы взаимодействия объектов между собой. Их описание производится посредством физических величин. Для того чтобы можно было установить для каждого объекта различия в количественном содержании свойства, отображаемого физической величиной, в метрологии введены понятия ее размера и значения.
Размер физической величины — это количественное содержание в данном объекте свойства, соответствующего понятию «физическая величина». Например, каждое тело обладает определенной массой, вследствие чего тела можно различать по их массе, т.е. по размеру интересующей нас ФВ.
Значение физической величины — это оценка ее размера в виде некоторого числа принятых для нее единиц. Его получают в результате ее измерения или вычисления в соответствии с основным уравнением измерения Q = q [ Q ], связывающим между собой значение ФВ Q , числовое значение q и выбранную для измерения единицу [ Q ]. В зависимости от размера единицы будет меняться числовое значение ФВ, тогда как размер ее будет одним и тем же.
Единица физической величины — это ФВ фиксированного размера, которой условно присвоено числовое значение, равное единице, и которая применяется для количественного выражения однородных ФВ. Размер единиц ФВ устанавливается путем их законодательно закрепленного определения метрологическими органами государства.
Важной характеристикой ФВ является ее размерность dim Q — выражение в форме степенного многочлена, отражающее связь данной величины с основными ФВ; коэффициент пропорциональности в нем принят равным единице:
где L , М, Т, I — условные обозначения основных величин данной системы; a , b , g , h — целые или дробные, положительные или отрицательные вещественные числа. Показатель степени, в которую возведена размерность основной величины, называют показателем размерности. Если все показатели размерности равны нулю, то такую величину называют безразмерной.
Размерность ФВ является более общей характеристикой, чем определяющее ее уравнение связи, поскольку одна и та же размерность может быть присуща величинам, имеющим разную качественную природу и различающимся по форме определяющего уравнения. Например, работа силы F на расстоянии L описывается уравнением A 1 = FL . Кинетическая энергия тела массой m , движущегося со скоростью v , равна А2 = mv 2 / 2. Размерности этих качественно различных величин одинаковы.
Над размерностями можно производить действия умножения, деления, возведения в степень и извлечение корня. Понятие размерности широко используется:
• для перевода единиц из одной системы в другую;
• для проверки правильности сложных расчетных формул, полученных в результате теоретического вывода;
• при выяснении зависимости между величинами;
• в теории физического подобия.
Описание свойства, характеризуемого данной ФВ, осуществляется на языке других, ранее определенных величин. Эта возможность обуславливается наличием объективно существующих взаимосвязей между свойствами объектов, которые, будучи переведенными на язык величин, становятся моделями, образующими в своей совокупности систему уравнений, описывающих данный раздел физики. Различают два типа таких уравнений:
1. Уравнения связи между величинами — уравнения, отражающие законы природы, в которых под буквенными символами понимаются ФВ. Они могут быть записаны в виде, не зависящем от выбора единиц измерений входящих в них ФВ:
Коэффициент К не зависит от выбора единиц измерений, он определяет связь между величинами. Например, площадь треугольника S равна половине произведения основания L на высоту h : S = = 0,5 Lh . Коэффициент К = 0,5 появился в связи с выбором не единиц измерений, а формы самих фигур.
2. Уравнения связи между числовыми значениями физических величин — уравнения, в которых под буквенными символами понимают числовые значения величин, соответствующие выбранным единицам. Вид этих уравнений зависит от выбранных единиц измерения. Они могут быть записаны в виде:
где Ке — числовой коэффициент, зависящий от выбранной системы единиц. Например, уравнение связи между числовыми значениями площади треугольника и его геометрическими размерами имеет вид при условии, что площадь измеряется в квадратных метрах, а основание и высота соответственно в метрах и миллиметрах:
C помощью уравнений связи между числовыми значениями ФВ формулируются определения одних величин на языке других и указываются способы их нахождения. Совокупность ФВ, образованная в соответствии с принятыми принципами, когда одни величины принимаются за независимые, а другие являются их функциями, называется системой физических величин.
Обосновано, но в общем произвольным образом выбираются несколько ФВ, называемых основными. Остальные величины, называемые производными, выражаются через основные на основе известных уравнений связи между ними. Примерами производных величин могут служить: плотность вещества, определяемая как масса вещества, заключенного в единице объема; ускорение — изменение скорости за единицу времени и др.
В названии системы ФВ применяют символы величин, принятых за основные. Например, система величин механики, в которой в качестве основных используются длина ( L ), масса (М) и время (Т), называется системой LMT . Действующая в настоящее время международная система СИ должна обозначаться символами LMTIQNJ , соответствующими символам основных величин: длине ( L ), массе (М), времени (Т), силе электрического тока ( I ), температуре ( Q ), количеству вещества ( N ) и силе света ( J ).
Совокупность основных и производных единиц ФВ, образованная в соответствии с принятыми принципами, называется системой единиц физических величин. Единица основной ФВ является основной единицей данной системы. В Российской Федерации используется система единиц СИ, введенная ГОСТ 8.417-81 «ГСИ. Единицы физических величин». В качестве основных единиц приняты метр, килограмм, секунда, ампер, кельвин, моль и канделла (табл. 3.1).
Основные и дополнительные единицы физических величин
http://pandia.ru/text/80/436/3549.php
http://ks-invest.ru/metrology/gl-17.html
Заказать задачи по любым предметам можно здесь от 10 минут
Как решать дифференциальные уравнения
СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ
- Основные понятия и определения
-
- Определения
- Типы уравнений
- Алгоритм решения
- Дифференциальные уравнения первого порядка
-
- ДУ с разделяющимися переменными
- Однородные ДУ
- Линейные неоднородные ДУ
- ДУ Бернулли
- ДУ в полных дифференциалах
- Дифференциальные уравнения второго порядка
-
- ДУ допускающие понижение порядка
- Линейные однородные ДУ с постоянными коэффицентами
- Линейные неоднородные ДУ с постоянными коэффициентами
- Метод Лагранжа
Введите уравнение
Условия к задаче (необязательно)
Пример 1 Пример 2 Правила ввода
Дифференциальные уравнения бывают обыкновенными и в частных производных. В этой статье мы будем говорить об обыкновенных уравнениях и о том, как их решать.
Основные понятия и определения
Определения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие функцию $y(x)$ только от одной неизвестной переменной (например, $x$).
Рассмотрим это на следующих практических примерах. $$ y’ = xy $$ $$ y» = 1 $$
Итак, в первом диффуре присутствует независимая переменная $x$, неизвестная функция $y(x)$ и производная этой функции $y'(x)$. А во втором случае нет $x, y(x),y'(x)$, а есть только вторая производная функции $y»(x)$. Значит, для того, чтобы уравнение называлось дифференциальным необязательно иметь $y(x)$ и $x$, а должно быть производная $y(x)$ любого порядка.
Порядок дифференциального уравнения – это порядок старшей производной неизвестной функции $y(x)$ в уравнении.
В первом случае максимальная производная первого порядка, значит, и само ДУ первого порядка. А во втором случае уравнение имеет вторую производную $y»(x)$, поэтому это ДУ второго порядка.
Общее решение дифференциального уравнения – это семейство функций $y = f(x,C)$, при подстановке которых в заданное исходное уравнение мы получаем равенство левой и правой части. Здесь $C$ произвольная константа. Процесс нахождения таких решений называется интегрированием дифференциального уравнения.
Частное решение дифференциального уравнения – это решение, полученное из общего решения, путем нахождения константы $C$ из дополнительных условий в задаче.
Типы уравнений
- ДУ первого порядка
– с разделяющимися переменными
– однородные
– линейные неоднородные
– уравнение Бернулли - ДУ второго порядка
– уравнения допускающие понижение порядка
– однородные с постоянными коэффициентами
– неоднородные с постоянными коэффициентами
Алгоритм решения
- По старшей производной функции $y(x)$ определить порядок ДУ
- Зная порядок, определить тип уравнения
- Узнав тип, подобрать подходящий метод решения
- Используя метод, найти общее решение
- Получить частное решение из общего путем вычисления неизвестной $C$
В некоторых случаях для решения дифференциальных уравнений удобно переписать производные в таком виде (например, это нужно для ДУ с разделяющимися переменными). $$y’ = frac{dy}{dx}$$
ОБЯЗАТЕЛЬНО! Чтобы успешно решать дифференциальные уравнения необходимо уметь находить интегралы. Поэтому, если вы забыли данную тему, то её нужно вспомнить!
| Пример 1 |
| Дана функция $y = Ce^{frac{x^2}{2}} $. Проверить является ли функция решением дифференциального уравнения $y’ = xy$ |
| Решение |
|
Для того, чтобы проверить является ли функция решением нужно подставить её в исходное ДУ. Найдем производную функции. $$y’ = (Ce^{frac{x^2}{2}})’ = Ce^{frac{x^2}{2}} cdot (frac{x^2}{2})’ = Ce^{frac{x^2}{2}} cdot x = Cxe^{frac{x^2}{2}}$$ Теперь подставим $y’$ и $y$ в исходное уравнение. $$ Cxe^{frac{x^2}{2}} = x Ce^{frac{x^2}{2}} $$ Получили равенство левой и правой части, значит, функция $y = Ce^{frac{x^2}{2}} $ является общим решением ДУ. |
| Ответ |
| $$y = Ce^{frac{x^2}{2}} $$ |
Дифференциальные уравнения первого порядка
ДУ с разделяющимися переменными
Уравнения такого типа имеют следующий вид: $$ f_1(x)g_1(y)dy = f_2(x)g_2(y)dx$$ Общее решение такого ДУ нужно находить путем разделения переменных с иксами и с игреками: $$int frac{g_1(y)}{g_2(y)}dy = int frac{f_2(x)}{f_1(x)}dx$$
СОВЕТ: Если не удается определить тип диффура первого порядка, то рекомендуем мысленно попытаться разделить переменные иксы от игреков. Возможно перед вами хитрое дифференциальное уравнение с разделяющимися переменными.
Алгоритм нахождения общего решения:
- Переписываем производные через $y’ = frac{dy}{dx}$
- Разделяем все $y$ в левую часть уравнения, а все $x$ в правую
- Интегрируем обе части уравнения
| Пример 2 |
| Найти общее решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = xy$ |
| Решение |
|
Видим, что в условии задачи присутствует производная от неизвестной функции $y(x)$ первого порядка. Значит, перед нами диффур 1-го порядка. Забегая вперед скажем, что данный диффур из задачи является дифференциальным уравнением с разделяющимися переменными. Что это означает? Это означает, что можно в уравнении перенести всё что содержит $y$ в левую часть равенства, а то, что содержит $x$ перенести в правую часть. То есть разделить «игрики» от «иксов» по разные стороны. Но прежде, чем это делать стоит переписать производную таким образом: $$y’ = frac{dy}{dx}$$ После замены производной игрека исходное уравнение приобретает такой формат: $$frac{dy}{dx} = xy$$ Теперь, как сказали ранее, начинаем отделять игрики от иксов по разные стороны. Для этого обе части уравнения необходимо умножить на $dx$, а ещё разделить на $y$. $$ frac{dy}{y} = xdx $$ Теперь необходимо проинтегрировать обе части уравнения, чтобы получить функцию $y$. Для этого навешиваем значок интеграла на обе части уравнения. $$ int frac{dy}{y} = int xdx $$ Вспоминаем, что левый интеграл равен натуральному логарифму, а правый интеграл $frac{x^2}{2}$. А так как интеграл неопределенный, то необходимо прибавить константу $C$. $$ ln|y| = frac{x^2}{2} + C $$ Теперь необходимо вытащить $y$ для того, чтобы записать окончательный ответ в виде общего решения. Для этого вспоминаем, что игрик в $ln|y| = x$ равен $y = e^x$. Поэтому продолжая решать наше уравнение получаем. $$ y = e^{frac{x^2}{2} + C} $$ Далее вспоминаем свойство степеней $a^{x+y} = a^x cdot a^y$. Таким образом делаем преобразования нашего уравнения. Так как $e^C$ это константа, то её можно переписать следующим видом $e^C = C$. И после этого получаем окончательный ответ исходного уравнения, называемый общим решением. $$ y = Ce^{frac{x^2}{2}} $$ |
| Ответ |
| $$ y = Ce^{frac{x^2}{2}} $$ |
| Пример 3 |
| Найти частное решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = frac{2x}{1+x^2}$, если $y(0) = 0$. |
| Решение |
|
Начнем решать с того, что представим производную в исходном уравнении в виде $y’ = frac{dy}{dx}$: $$ frac{dy}{dx} = frac{2x}{1+x^2} $$ Теперь разделяем переменные иксы от игреков по разные стороны равенства путем умножения обеих частей уравнения на $dx$: $$ dy = frac{2x}{1+x^2} dx $$ Навешиваем знак интеграла на левую и правую часть, а затем решаем интегралы: $$ int dy = int frac{2x}{1+x^2} dx $$ $$ y = int frac{2x}{1+x^2} dx $$ Замечаем, что $(1+x^2)’ = 2x$. Поэтому $2x$ можно занести под знак дифференциала, чтобы решить интеграл: $$ y = int frac{d(1+x^2)}{1+x^2} = ln (1+x^2) + C $$ Получили общее решение $y = ln (1+x^2) + C$. В условии задачи просят найти частное решение при условии $y(0) = 0$. Это означает, что нужно из последного условия найти константу $C$. Из $y(0) = 0$ видно, что $x = 0$, а $y = 0$. Подставляем их в общее решение дифференциального уравнения и вычисляем $C$: $$ln(1+0^2)+C = 0$$ $$ln 1+C = 0$$ $$0 + C = 0$$ $$C=0$$ Теперь заменив в общем решении $C$ на ноль, получаем частное решение: $$y = ln(1+x^2)$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = ln(1+x^2)$$ |
Однородные ДУ
Чтобы проверить является ли предложенное уравнение однородным нужно заменить $x$ и $y$ на $lambda x$ и $lambda y$. Производную $y’$ заменять не нужно. Если все $lambda$ после элементарных преобразований удастся уничтожить, то перед вами однородное дифференциальное уравнение первого порядка.
Решается по следующему алгоритму:
- Проверить уравнение на однородность с помощью $lambda$
- Привести уравнение к виду $y’ = f(frac{y}{x})$
- Выполнить замену $frac{y}{x} = t$ и $y’ = t’x+t$
- Решить уравнение методом разделяющихся переменных
| Пример 4 |
| Найти общее решение дифференциального уравнения первого порядка $$y’ = frac{y}{x} — 1$$ |
| Решение |
|
Так как разделить переменные не получается, то проверим уравнение на однородность. Для этого вместо $x$ и $y$ выполним подстановку $lambda x$ и $lambda y$: $$y’ = frac{lambda y}{lambda x} — 1$$ Выполняем сокращение $lambda$ в числителе и знаменателе: $$y’ = frac{y}{x} — 1$$ После сокращения все $lambda$ уничтожились, значит перед нами однородное дифференциальное уравнение первого порядка. Решим его с помощью замены $frac{y}{x} = t$ и $y’ = t’x + t$: $$ t’x + t = t — 1$$ Переносим $t$ в одну сторону и тем самым уничтожаем его: $$ t’x = -1 $$ Теперь это ДУ с разделяющимися переменными. Запишем его в привычном для него виде: $$ frac{dt}{dx} x = -1 $$ Разделим переменные домножением на $dx$ и делением на $x$ обеих частей равенства: $$dt = -frac{dx}{x}$$ Интегрируем обе части: $$int dt = — int frac{dx}{x}$$ $$t = -ln|x|+C$$ Выполняем назад замену $t = frac{y}{x}$: $$frac{y}{x} = -ln|x|+C$$ Умножаем обе части на $x$, чтобы получить окончательный ответ общего решения: $$y = -xln|x| +Cx$$ |
| Ответ |
| $$y = -xln|x| +Cx$$ |
| Пример 5 |
| Решить дифференциальное уравнение первого порядка $xy+y^2=(2x^2+xy)y’$ |
| Решение |
|
Сперва проверим уравнение на однородность. Подставляем $lambda$ вместо $x$ и $y$. $$lambda x cdot lambda y + (lambda y)^2 = (2 (lambda x)^2 + lambda xcdot lambda y)y’$$ После вынесения $lambda$ слева и справа за скобки получаем $$ lambda^2(xy+y^2) = lambda^2(2x^2+xy)y’,$$ где все $lambda$ сокращаются. А это подтвержает однородность уравнения. Перед тем, как выполнить замену $t = frac{y}{x}$ нужно привести исходное уравнение к виду $y = f(frac{y}{x})$. Для этого разделим левую и правую часть равенства на $x^2$: $$frac{y}{x}+frac{y^2}{x^2} = (2+frac{y}{x})y’.$$ Теперь производим замену $t = frac{y}{x}$ и $y’ = t’x+t$ в преобразованном уравнении: $$t+t^2=(2+t)(t’x+t).$$ Раскрываем скобки и сокращаем одинаковые слагаемые $$t+t^2 = 2t’x+2t+t’xt+t^2$$ $$2t’x+t’xt=-t.$$ Далее в полученном уравнении разделяем переменные $t$ и $x$ по разные стороны знака равенства. Для этого выносим за скобку $t’x$ $$t’x(2+t)=-t.$$ Делим на $t$ обе части уравнения $$t’xfrac{2+t}{t}=-1.$$ Представляем производную $t’ = frac{dt}{dx}$ и переносим $dx$ и $x$ в правую часть равенства $$frac{2+t}{t}dt = -frac{dx}{x}.$$ Интегрируем обе части уравнения $$int frac{2+t}{t}dt = — int frac{dx}{x}$$ $$int frac{2}{t}dt+int dt = -int frac{dx}{x}$$ $$2ln|t|+t = -ln|x|+C.$$ Выполняем обратную замену $t = frac{y}{x}$: $$2ln|frac{y}{x}|+frac{y}{x}=-ln|x|+C.$$ Упрощаем полученное равенство с помощью элементарных преобразований и свойств натурального логарифма $$2ln|y|-2ln|x|+frac{y}{x} = -ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+ln|C|$$ $$2ln|y|+frac{y}{x}=ln|Cx|$$ $$ln y^2+frac{y}{x}=ln|Cx|$$ $$ln y^2 = ln|Cx|-frac{y}{x}$$ $$y^2 = Cxe^frac{-y}{x}.$$ Привели решение к такому виду через $y^2$. Это называется общим интегралом дифференциального уравнения. Ответ в таком виде остается в таком формате. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y^2 = Cxe^frac{-y}{x}$$ |
Линейные неоднородные ДУ
Линейное неоднородное дифференциальное уравнение 1-го порядка имеет следующий вид $$y’+p(x)y=q(x).$$
Для его решения существует два способа: метод Бернулли и вариация произвольной постоянной. В первом методе нужно сделать замену на произведение двух функций $y = uv$, а во втором способе необходимо найти неизвестную функцию $C(x)$.
Алгоритм метода Бернулли:
- Выполняем замену $y=uv$ и $y’ = u’v+uv’$
- Находим функции $u(x)$ и $v(x)$ с помощью решения системы двух уравнений
- Подставляем найденные $u(x)$ и $v(x)$ в уравнение $y=uv$, чтобы получить ответ
Алгоритм метода вариации произвольной постоянной:
- Решаем исходное уравнение в качестве однородного методом разделяющихся переменных
- В полученном общем решении заменяем константу $C$ на функцию $C(x)$
- Подставляем общее решение и его производную в исходное уравнение, чтобы найти $C(x)$
- Полученное $C(x)$ подставляем в общее решение однородного уравнения и записываем ответ
| Пример 6 |
| Найти частное решение дифференциального уравнения первого порядка методом Бернулли $xy’-2y=2x^4$, если $y(1)=0$. |
| Решение |
|
Приводим уравнение к виду $y’+p(x)y=q(x)$ путем деления на $x$ обеих частей равенства $$y’-2frac{y}{x}=2x^3.$$ Делаем замену в полученном уравнении на $y=uv$ и $y’=u’v+uv’$ $$u’v+uv’-2frac{uv}{x}=2x^3.$$Выносим за скобку $u$, чтобы в дальнейшем составить систему уравнений: $$u’v+u(v’-2frac{v}{x})=2x^3.$$ Теперь приравниваем к нулю выражение в скобках и составляем систему уравнений $$begin{cases} v’ — 2frac{v}{x} = 0 \ u’v = 2x^3 end{cases},$$ в которой начнем сначала решать первое уравнение для нахождения функции $v(x)$. Разделяем в нём переменные $$begin{cases} frac{dv}{dx} = 2frac{v}{x} \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} frac{dv}{v} = 2frac{dx}{x} \ u’v = 2x^3 end{cases}.$$ Интегрируем первое уравнение в системе, чтобы получить функцию $v(x)$ $$begin{cases} ln|v| = 2ln|x| \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} v = x^2 \ u’v = 2x^3 end{cases}.$$ Теперь, зная, чему равно $v$ подставляем его во второе уравнение $$begin{cases} v=x^2 \ u’x^2 = 2x^3 end{cases} Leftrightarrow begin{cases} v=x^2 \ u = x^2+C end{cases}.$$ Записываем общее решение дифференциального уравнения $$y = uv Rightarrow y = x^4+Cx^2.$$ В условии задачи требуется найти частное решение из условия $y(1)=0$. Подставим в найденное общее решение $x=1$ и $y=0$, чтобы вычислить $C$ $$1^4+Ccdot 1^2 = 0 Rightarrow C = -1. $$ С учётом, что $C=-1$ записываем частное решение дифференциального уравнения $$y = x^4 — x^2.$$ |
| Ответ |
| $$y = x^4 — x^2$$ |
| Пример 7 |
| Найти общее решение дифференциального уравнения первого порядка $y’sin x-ycos x = 1$ методом вариации произвольной постоянной $C$. |
| Решение |
|
Перепишем уравнение в виде $$ y’ — y frac{cos x}{sin x} = frac{1}{sin x} .$$ Теперь записываем однородное дифференциальное уравнение $$y’ — y frac{cos x}{sin x} = 0,$$ решим его методом разделяющихся переменных: $$frac{dy}{dx} = y frac{cos x}{sin x}$$ $$int frac{dy}{y} = int frac{cos x}{sin x} dx.$$ Слева получается натуральный логарифм, а справа заносим косинус под знак дифференциала, чтобы получить логарифм синуса: $$ln|y| = ln|sin x| + C$$ $$y = Csin x.$$ Теперь заменяем константу $C$ на функцию $C(x)$ в полученном решении и находим производную $$y = C(x)sin x Rightarrow y’ = C'(x)sin x+ C(x)cos x.$$ Подставляем $y$ и $y’$ в неоднородное уравнение и решаем его относительно $C(x)$: $$C'(x)sin x+ C(x)cos x — C(x)sin x frac{cos x}{sin x} = frac{1}{sin x}$$ $$C'(x)sin x = frac{1}{sin x}$$ $$C'(x) = frac{1}{sin^2 x}.$$ В последнем уравнении можно разделить переменные, что и делаем, а затем интегрируем: $$ d(C(x)) = int frac{dx}{sin^2 x}$$ $$C(x) = -ctg x + C.$$ Берем решение $y = C(x)sin x$ и подставляем в него найденное $C(x) = -ctg x + C$ $$y = (-ctg x + C) sin x = Csin x — cos x.$$ Таким образом получили общее решение дифференциального уравнения $y = Csin x — cos x$. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = Csin x — cos x$$ |
ДУ Бернулли
Дифференциальное уравнение Бернулли имеет следующий вид $$y’ + g(x)y = f(x)y^alpha qquad (alpha neq 0), (alpha neq 1).$$
Алгоритм решения:
- Выполняем подстановку $y = z^frac{1}{1-alpha}$
- После подстановки получаем линейное уравнение $z’+p(x)z=q(x)$
- Решив линейное уравнение делаем обратную замену $z = y^{1-alpha}$
| Пример 8 |
| Найти общее решение дифференциального уравнения первого порядка $y’+y=xy^2$. |
| Решение |
|
Это уравнение Бернулли. Видим, что $alpha = 2$. Значит делаем замену на $y = z^frac{1}{1-alpha} = z^{-1}$. Отсюда $y’ = -frac{1}{z^2} cdot z’$. После подстановки в исходное уравнение имеем $$ -frac{z’}{z^2}+frac{1}{z}=frac{x}{z^2}.$$ Умножаем обе части равенства на $(-z^2)$, чтобы привести уравнение к линейному ДУ $$z’-z=-x, $$ которое можно решить методом Бернулли, либо вариацией произвольной постоянной. Выберем первый способ. Применяем подстановку $y=uv$ и $y’=u’v+uv’$ для последнего уравнения $$u’v+uv’-uv=-x.$$ Выносим за скобку $u$, чтобы затем построить систему уравнений для нахождения функций $u(x)$ и $v(x)$ $$u’v+u(v’-v) = -x.$$ Приравниваем к нулю скобку и получаем систему $$begin{cases} v’-v = 0 \ u’v = -x end{cases}.$$ Начинаем решать её с первого уравнения. Разделяем в нем переменные и затем интегрируем $$begin{cases} int frac{dv}{v} = int dx \ u’v = -x end{cases} Leftrightarrow begin{cases} ln|v| = x \ u’v = -x end{cases} Leftrightarrow begin{cases} v = e^x \ u’v = -x end{cases}. $$ Зная, что $v = e^x$ подставляем его во второе уравнение системы и решаем $$begin{cases} v = e^x \ u’ = -frac{x}{e^x} end{cases} Leftrightarrow begin{cases} v = e^x \ u = int (-x)e^{-x} dx end{cases}.$$ Для взятия интеграла воспользуемся методом интегрирования по частям $$u = int (-x)e^{-x} dx = begin{vmatrix} u = -x & du = -dx \ dv = e^{-x}dx & v = -e^{-x} end{vmatrix} = xe^{-x} — int e^{-x} dx = xe^{-x} +e^{-x} + C$$ Итак, получаем, что $$z = uv Rightarrow z = (xe^{-x} + e^{-x}+C) e^x = Ce^x +x + 1. $$ Вспоминаем, что была ещё одна замена в самом начале решения задачи $y = z^{-1}$, поэтому общее решение выглядит следующим образом $$y = frac{1}{Ce^x + x + 1}.$$ |
| Ответ |
| $$y = frac{1}{Ce^x + x + 1}$$ |
ДУ в полных дифференциалах
Дифференциальные уравнения в полных дифференциалах имеют следующий вид $$P(x,y) dx + Q(x,y) dy = 0, $$ при выполнении условия $frac{partial P}{partial y} = frac{partial Q}{partial x} $.
Алгоритм решения заключается в том, чтобы найти функцию $U(x,y)=C$, полный дифференциал которой, есть исходное ДУ:
- Проверяем условие, подтверждающее, что перед нами ДУ в полных дифференциалах
- Получаем $U(x,y)$ интегрируя функцию $P(x,y)$ по переменной $x$. В результате этого появится неизвестная функция $varphi(y)$
- Дифференцируем $U(x,y)$ по $y$ и приравниваем к $Q(x,y)$, чтобы найти $varphi(y)$
| Пример 9 |
| Найти общий интеграл $U(x,y)=C$ дифференциального уравнения $$(2x+5y)dx+(5x+3y^2)dy=0.$$ |
| Решение |
|
Убедимся, что данное уравнение в полных дифференциалах. Для этого проверим условие $frac{partial P}{partial y} = frac{partial Q}{partial x} $. Находим производные $$ P’_y = (2x+5y)’_y = 5, Q’_x = (5x+3y^2)’_x = 5, $$ и видим, что условие выполняется $P’_y=P’_x=5$. Находим функцию $U(x,y)$ беря интеграл по $x$ от функции $P(x,y)$ $$U(x,y) = int (2x+5y) dx = x^2 + 5yx + varphi(y).$$ Далее необходимо продифференцировать найденную $U(x,y)$ по $y$ $$U’_y = 5x + varphi'(y).$$ Осталось найти неизвестную функцию $varphi(y)$ приравняв $U’_y$ к $Q(x,y)$: $$5x + varphi'(y) = 5x+3y^2$$ $$varphi'(y) = 3y^2$$ $$varphi(y) = int 3y^2 dy = y^3 + C.$$ Теперь зная чему равна $varphi(y)$ подставляем её в $U(x,y)$ $$U(x,y)=x^2+5xy+y^3+C.$$ Записываем ответ в таком виде $$x^2+5xy+y^3 = C.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$x^2+5xy+y^3 = C.$$ |
Дифференциальные уравнения второго порядка
ДУ допускающие понижение порядка
Дифференциальные уравнения, допускающие понижение порядка бывают двух видов:
- Без функции $y$: $F(x,y’,y»)=0$
- Без переменной $x$: $F(y,y’,y»)=0$
Для решения таких диффуров в первом случае делаем замену $y’ = p(x)$, а во втором $y’ = p(y)$.
| Пример 10 |
| Найти частное решение дифференциального уравнения второго порядка $xy»+y’=0$ при условиях $y(1) = 0$ и $y'(1)=1$. |
| Решение |
|
Видим, что данный дифур попадает под первый случай, когда отсутствует в уравнении $y$, а есть только его производные. Значит, делаем замену $y’ = p(x)$ $$xp’+p=0.$$ Данное уравнение имеет разделяющиеся переменные. Начнем с того, что перепишем уравнение через $p’ = frac{dp}{dx}$ $$xfrac{dp}{dx} = -p.$$ Разделяем переменные налево и направо от знака равенства и затем интегрируем: $$ frac{dp}{p} = -frac{dx}{x}$$ $$ int frac{dp}{p} = -int frac{dx}{x}$$ $$ln|p| = -ln|x|+C_1.$$ Теперь избавимся от логарифмов, чтобы получить $p$: $$p = e^{-ln|x| + C_1}$$ $$p = frac{C_1}{x}.$$ Вспоминаем про ранее выполненную замену $$y’ = p(x) = frac{C_1}{x}.$$ Интегрируем для того, чтобы найти $y$ $$y = int frac{C_1}{x} dx = C_1 ln|x| + C_2.$$ Таким образом, общее решение дифференциального уравнения $$y = C_1 ln|x| + C_2.$$ Займемся поиском частного решения. Для этого используем два дополнительных равенства из условия задачи: $$y(1) = 0 Rightarrow C_1 ln|1| + C_2 = 0 Rightarrow C_2 = 0$$ $$y'(1)=1 Rightarrow frac{C_1}{1} = 1 Rightarrow C_1 = 1.$$ Записываем частное решение дифференциального уравнения $$y = ln|x|.$$ |
| Ответ |
| $$y = ln|x|$$ |
| Пример 11 |
| Найти частное решение дифференциального уравнения второго порядка $$yy»+y’^2 = 1, qquad y(0) = 1, y'(0) = 1.$$ |
| Решение |
|
Видим, что в диффуре отсутствует в явном виде переменная $x$, поэтому необходимо сделать замену $y’ = p(y)$ и отсюда $y» = p'(y)cdot y’ = p'(y)p$. Делаем замену и получаем уравнение $$yp'(y)p + p^2 = 1,$$ которое решим методом разделения переменных: $$ypfrac{dp}{dy} = 1-p^2$$ $$frac{p}{1-p^2}dp = frac{1}{y}dy.$$ Далее по плану необходимо проинтегрировать обе части уравнения, чтобы получить $p$ $$int frac{p}{1-p^2}dp = int frac{1}{y}dy.$$ В первом интеграле заносим под знак дифференциала $1-p^2$, чтобы получился натуральный логарифм, а во втором, используя таблицу интегрирования можно сразу записать ответ: $$-frac{1}{2} int frac{d(1-p^2)}{1-p^2} = ln|y| + C $$ $$-frac{1}{2} ln|1-p^2| = ln|y| + C.$$ Необходимо избавиться от логарифмов. Умножим обе части равенства на $(-2)$, а затем занесем эту двойку над икреком: $$ln|1-p^2| = -2ln|y|+C$$ $$ln|1-p^2| = ln frac{1}{y^2} + C.$$ Итак, теперь убирая логарифмы получаем: $$1-p^2 = C frac{1}{y^2}$$ $$p^2 = 1 — Cfrac{1}{y^2}$$ $$(y’)^2 = 1 — Cfrac{1}{y^2}.$$ Теперь найдем значение константы $C$ благодаря дополнительным условиям задачи $y = 1$ и $y’ = 1$. Подставляем их в последнее уравнение $$1^2 = 1 — Cfrac{1}{1^2} Rightarrow C = 0.$$ Зная теперь, что $C=0$ подставляем его в уравнение $(y’)^2 = 1 — Cfrac{1}{y^2}$: $$(y’)^2 = 1$$ $$y’ = pm 1.$$ Из условия помним, что $y’ = 1 > 0$, значит, берем только решение $y’ = 1$ и продолжаем его решать интегрированием $$y = int 1 dx = x + C.$$ Осталось найти снова постоянную $C$ теперь уже из условия $y(0) = 1$ $$y(0) = 0 + C = 1 Rightarrow C = 1.$$ Вот теперь можно записать ответ в виде частного решения, которое требовалось найти по условию данной задачи $$y = x + 1.$$ |
| Ответ |
| $$y = x + 1$$ |
Линейные однородные ДУ с постоянными коэффицентами
Линейность дифференциального уравнения заключается в том, что в уравнение входит неизвестная функция $y(x)$ и её производные только в первой степени, между собой не перемножаясь. Однородность определяется тем, что уравнение не содержит свободного члена. То есть он равен нулю.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами выглядит следующим образом $$y»+py’+qy = 0.$$ Чтобы его решить необходимо составить характиристический многочлен и найти его корни. Для этого нужно заменить $y$ на $lambda$, степень которых будет соответствовать порядку производной $$y» Rightarrow lambda^2, qquad y’ Rightarrow lambda, qquad y Rightarrow 1.$$
В зависимости от получившихся корней имеем общее решение в различных видах:
- Действительные корни $lambda_1 neq lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2e^{lambda_2 x}$
- Действительные корни $lambda_1 = lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2xe^{lambda_1 x}$
- Комплексные корни $lambda_{1,2} = alphapmbeta i$, тогда $y = C_1e^{alpha x}cos beta x + C_2e^{alpha x}sin beta x$.
| Пример 12 |
| Найти общее решение дифференциального уравнения второго порядка $y»+y’-2y = 0$. |
| Решение |
|
Первым делом составляем характеристический многочлен. Заменяем $y$ на $lambda$ со степенями соответствующими порядку производной $y$ $$lambda^2 + lambda -2 = 0.$$ Обратите внимание, что $y$ имеет производную нулевого порядка, поэтому он заменяется на $lambda^0 = 1$. Итак, перед нами квадратное уравнение, начинаем решать: $$lambda_{1,2} = frac{-1pm sqrt{1^2-4cdot 1 cdot (-2)}}{2cdot 1} = frac{-1pm 3}{2}$$ $$lambda_1 = -2, qquad lambda_2 = 1.$$ Так как получили отличающиеся действительные корни, то общее решение записывается следующим образом $$y = C_1 e^{-2x} + C_2 e^{x}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = C_1 e^{-2x} + C_2 e^{x}$$ |
Линейные неоднородные ДУ с постоянными коэффициентами
Линейное неоднородное ДУ с постоянными коэффициентами отличается от предыдущего типа уравнений наличием правой части от знака равенства $$y»+py’+q = f(x).$$
Общее решение такого диффура складывается из двух частей: общего решения однородного уравнения и частного решения неоднородного уравнения $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}.$$
Частное решение неоднородного уравнения $y_text{ч.н.}$ подбирается исходя из вида правой части дифференциального уравнения. Затем в нём неизвестные постоянные находятся методом неопределенных коэффициентов.
| № | Правая часть | Корни характеристического многочлена | Вид частного решения |
| 1 | $$P_n (x)$$ | Число 0 не является корнем характеристического уравнения. | $$tilde{P_n}(x)$$ |
| Число 0 – корень характеристического уравнения кратности $S$. | $$x^s tilde{P_n}(x)$$ | ||
| 2 | $$P_n (x) e^{alpha x}$$ | Число $alpha$ не является корнем характеристического уравнения. | $$tilde{P_n} (x) e^{alpha x}$$ |
| Число $alpha$ является корнем характеристического уравнения кратности $S$. | $$x^s tilde{P_n} (x) e^{alpha x}$$ | ||
| 3 | $$P_n (x) cos beta x + Q_m (x) sin beta x$$ | Число $pm ibeta$ не является корнем характеристического уравнения. | $$tilde {P_n} cos beta x + tilde{Q_m} sin beta x$$ |
| Число $pm ibeta$ является корнем характеристического уравнения кратности $S$. | $$x^s (tilde {P_n} cos beta x + tilde{Q_m} sin beta x)$$ | ||
| 4 | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ | Число $alpha pm ibeta$ не является корнем характеристического уравнения. | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Число $alpha pm ibeta$ является корнем характеристического уравнения. | $$x^s e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Пример 13 |
| Найти общее решение дифференциального уравнения второго порядка $y»+y = 4xcos x$. |
| Решение |
|
Сначала находим общее решение однородного уравнения $$y» + y = 0.$$ Строим характеристический многочлен $$lambda^2 + 1 = 0,$$ и находим его корни $$lambda_{1,2}=pm i.$$ Записываем получившееся общее решение однородного уравнения $$y_text{о.о.} = C_1 cos x + C_2 sin x.$$ Теперь необходимо подобрать частное решение неоднородного уравнения. Для этого смотрим на правую часть исходного уравнения и видим, что здесь многочлен первой степени умножается на косинус. Значит, необходимо выбрать из таблицы 3й случай. Причем корень характеристического уравнения совпадает с аргументом косинуса. Это значит, что требуется домножение на $x$ $$y_text{ч.н.} = x[(Ax+B)cos x + (Cx+D)sin x].$$Упростим последнее равенство и найдем от него вторую производную: $$y_text{ч.н.} = (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x$$ $$y’_text{ч.н.} = (2Ax+B)cos x-(Ax^2+Bx)sin x + (2Cx+D)sin x + (Cx^2 + Dx) cos x.$$ Упростим $y’_text{ч.н}$ для удобства нахождения второй производной $$y’_text{ч.н.} = (2Ax+B+Cx^2+Dx)cos x + (2Cx+D-Ax^2-Bx)sin x.$$ Теперь можно найти вторую производную $$y»_text{ч.н.} = (2A+2Cx+D)cos x-(2Ax+B+Cx^2+Dx)sin x + (2C-2Ax-B)sin x + (2Cx+D-Ax^2-Bx)cos x.$$ Упрощаем последнее выражение $$y»_text{ч.н.} = (2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x.$$ Подставляем найденные $y_text{ч.н.}$ и $y»_text{ч.н.}$ в исходный диффур из «дано» задачи $$(2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x + (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x = 4xcos x.$$ Упрощаем его $$(2A+4Cx+2D)cos x + (2C-4Ax-2B)sin x = 4xcos x.$$ Теперь подгоняем левую часть под правую, так чтобы можно было применить метод неопределенных коэффициентов и найти неизвестные $A,B,C,D$ $$(2A+2D)cos x+4Cxcos x + (2C-2B)sin x+(-4Ax)sin x = 4xcos x.$$ Смотрим на левую и правую часть и составляем систему $$begin{cases} 2A+2D = 0 \ 4C=4 \ 2C-2B=0 \ -4A = 0 end{cases} Leftrightarrow begin{cases} D=0 \ C= 1 \ B=1 \ A = 0end{cases}.$$ Подставляем полученные коэффициенты в частное решение неоднородного уравнения $$y_text{ч.н.} = xcos x + x^2sin x.$$ Теперь вспоминая, что $y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}$ можем записать окончательный ответ $$y_text{о.н.} = C_1 cos x + C_2 sin x + xcos x + x^2sin x.$$ |
| Ответ |
| $$y = C_1 cos x + C_2 sin x + xcos x + x^2sin x$$ |
| Пример 14 |
| Найти общее решение дифференциального уравнения второго порядка $y»+y’=5x+2e^x$. |
| Решение |
|
Сначала найдем общее решение однородного дифференциального уравнения $$y»+y’=5x+2e^x.$$ Составляем характеристический многочлен однородного уравнения и находим его корни: $$lambda^2 + lambda = 0$$ $$lambda(lambda + 1) = 0$$ $$lambda_1 = 0, qquad lambda_2=-1.$$ Теперь можно записать общее решение $$y_text{о.о.} = C_1 + C_2e^{-x}.$$ Далее необходимо по правой части исходного неоднородного уравнения найти его частное решение путем подбора, используя данные таблицы. Первое слагаемое есть многочлен первой степени. И так как один из корней характеристического уравнения является нулем кратности 1, то решение ищем в виде $y = (Ax+B)x$. Второе слагаемое представляет собой произведение многочлена нулевой степени на экспоненту. Так как аргумент экспоненты не совпадает с одним из корней характеристического многочлена, то подбор будем делать в виде $y = Ce^x$. В итоге правую часть будем искать в виде суммы $$y_text{ч.н.} = (Ax+B)x+Ce^x.$$ Находим первую и вторую производную последней функции: $$y’ = 2Ax+B+Ce^x$$ $$y»=2A+Ce^x.$$ Подставляем полученные производные $y’$ и $y»$ в исходное дифференциальное уравнение: $$2A+Ce^x+2Ax+B+Ce^x = 5x+2e^x$$ $$2Ax+B+2A+2Ce^x=5x+2e^x.$$ Далее необходимо, используя метод неопределенных коэффициентов, найти значения $A,B,C$ составив систему уравнений $$begin{cases} 2A=5 \ 2C=2 \ B+2A = 0 end{cases} Leftrightarrow begin{cases} A=frac{5}{2} \ C=1 \ B=-5 end{cases}.$$ Подставляем найденные коэффициенты и получаем частное решение неоднородного уравнения $$y_text{ч.н.} = (frac{5}{2}x-5)x + e^x = frac{5}{2}x^2 — 5x + e^x.$$ Таким образом теперь можно записать общее решение неоднородного диффура $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}=C_1 + C_2e^{-x} + frac{5}{2}x^2 — 5x + e^x.$$ |
| Ответ |
| $$y = C_1 + C_2e^{-x} + frac{5}{2}x^2 — 5x + e^x$$ |
Метод Лагранжа
Данный метод позволяет решать линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами даже в тех, случаях, когда правая часть уравнения не подходит под табличный вид. В этом случае целесообразно применить данный метод решения.
- Находим общее решение однородного уравнения $y = C_1 y_1(x) + C_2 y_2(x)$
- Варьируем постоянные $C_1$ и $C_2$ на функции $C_1(x)$ и $C_2(x)$
- Решаем систему методом Крамера $begin{cases} C_1 ‘(x) y_1 (x) + C_2 ‘(x) y_2 (x) = 0 \ C_1 ‘(x) y_1 ‘(x) + C_2 ‘(x) y_2 ‘(x) = f(x) end{cases} $
- Получаем $C_1(x)$ и $C_2(x).$
| Пример 15 |
| Найти частное решение дифференциального уравнения $$y»-2y’+y=frac{e^x}{x}, text{ при } y(1)=e, y'(1)=3e.$$ |
| Решение |
|
Так как правая часть диффура не подходит под табличный формат, то не получится подбирать частное решение по правой части как делали это в предыдущем примере. Воспользуется методом Лагранжа или как его еще называют вариация произвольной постоянной. Для начала найдем общее решение однородного уравнения $$y»-2y’+y=0.$$ Составляем характеристический многочлен и находим его корни: $$lambda^2-2lambda+1=0$$ $$(lambda-1)^2 = 0 Rightarrow lambda = 1 text{ с кратностью 2}.$$ Так как корень кратный, то общее решение однородного уравнения записывается следующим образом $$y = C_1 e^x + C_2 xe^x.$$ Теперь необходимо варьировать постоянные $C_1$ и $C_2$ на соответствующие функции $C_1 (x)$ и $C_2 (x)$. Теперь получившееся решение следует записать в виде $y = C_1 (x) e^x + C_2 (x) xe^x$. Здесь заметим, что $y_1 = e^x$ и $y_2 = xe^x$. Это нужно для дальнейшего хода решения, а именно построения системы уравнений. Составляем систему уравнений и решаем её методом Крамера $$begin{cases} C_1 ‘(x) e^x+C_2 ‘(x) xe^x = 0 \C_1 ‘(x) e^x + C_2 ‘(x) (e^x+xe^x) = frac{e^x}{x} end{cases}.$$ Находим главный определитель системы $$Delta = begin{vmatrix} e^x & xe^x \ e^x & e^x+xe^x end{vmatrix} = e^x(e^x+xe^x)-xe^{2x} = e^{2x}.$$ Вычисляем дополнительные определители: $$Delta_1 = begin{vmatrix} 0 & xe^x \ frac{e^x}{x} & e^x + xe^x end{vmatrix} = -xe^x frac{e^x}{x} = e^{2x}$$ $$Delta_2 = begin{vmatrix} e^x & 0 \ e^x & frac{e^x}{x} end{vmatrix} = e^x frac{e^x}{x} = frac{e^{2x}}{x}.$$ Итак, получаем решение системы уравнений $$C_1 ‘(x) = frac{Delta_1}{Delta} = frac{e^{2x}}{e^{2x}} = 1, qquad C_2 ‘(x) = frac{Delta_2}{Delta} = frac{e^{2x}}{x} frac{1}{e^{2x}} = frac{1}{x}.$$ Далее интегрируем полученные решения, чтобы избавиться от производной: $$C_1(x) = int 1 dx = x+tilde{C_1}$$ $$C_2(x)=int frac{dx}{x}=ln|x|+tilde{C_2}.$$ Подставляем полученные $C_1(x)$ и $C_2(x)$ в общее решение однородного уравнения и записываем общее решение неоднородного дифференциального уравнения $$y = (x+tilde{C_1}) e^x + (ln|x|+tilde{C_2}) xe^x.$$ По условию нам требуется найти частное решение при условиях $y(1)=e$ и $y'(1)=3e$. Поэтому находим сначала производную $$y’=e^x+(x+tilde{C_1})e^x+e^x+(ln|x|+tilde{C_2})(e^x+xe^x), $$ раскрываем скобки $$y’ = 2e^x+xe^x+tilde{C_1}e^x+e^xln|x|+xe^xln|x|+tilde{C_2}e^x+tilde{C_2}xe^x,$$ а затем составляем систему уравнений $$begin{cases} y'(1)=3e+tilde{C_1}e+2tilde{C_2}e = 3e \ y(1) = e+tilde{C_1}e + tilde{C_2}e = e end{cases} Rightarrow begin{cases} tilde{C_1}+2tilde{C_2}=0 \ tilde{C_1}+tilde{C_2}=0 end{cases} Rightarrow begin{cases} tilde{C_2} = 0 \ tilde{C_1}=0 end{cases}.$$ Теперь можно записать частное решение к задаче $$y = xe^x + xln|x|e^x = xe^x(1+ln|x|).$$ |
| Ответ |
| $$y = xe^x(1+ln|x|)$$ |
Однородные дифференциальные уравнения
и приводящиеся к ним
Однородные уравнения
Функция называется однородной функцией своих аргументов измерения
, если справедливо тождество
.
Например, функция есть однородная функция второго измерения, так как
При имеем функцию нулевого измерения. Например,
есть однородная функция нулевого измерения, так как
Дифференциальное уравнение вида называется однородным относительно
и
, если
есть однородная функция своих аргументов нулевого измерения. Однородное уравнение всегда можно представить в виде
(1)
Вводя новую искомую функцию , уравнение (1) можно привести к уравнению с разделяющими переменными:
Если есть корень уравнения
, то решение однородного уравнения будет
или
(прямая, проходящая через начало координат).
Замечание. При решении однородных уравнений необязательно приводить их к виду (1). Можно сразу делать подстановку .
Пример 1. Решить однородное уравнение .
Решение. Запишем уравнение в виде так что данное уравнение оказывается однородным относительно
и
. Положим
, или
. Тогда
. Подставляя в уравнение выражения для
и
, получаем
. Разделяем переменные:
. Отсюда интегрированием находим
, или
.
Так как , то, обозначая
, получаем
, где
или
. Заменяя
на
, будем иметь общий интеграл
.
Отсюда общее решение: .
При разделении переменных мы делили обе части уравнения на произведение , поэтому могли потерять решение, которые обращают в ноль это произведение.
Положим теперь и
. Но
в силу подстановки
, а из соотношения
получаем, что
, откуда
. Непосредственной проверкой убеждаемся, что функции
и
также являются решениями данного уравнения.
Пример 2. Рассмотреть семейство интегральных кривых однородного уравнения
. Показать, что касательные в соответственных точках к кривым, определяемым этим однородным дифференциальным уравнением, параллельны между собой.
Примечание: Будем называть соответственными те точки на кривых , которые лежат на одном луче, выходящем из начала координат.
Решение. По определению соответственных точек имеем , так что в силу самого уравнения
, где
и
— угловые коэффициенты касательных к интегральным кривым
и
, в точках
и
соответственно (рис. 12).
Уравнения, приводящиеся к однородным
А. Рассмотрим дифференциальное уравнение вида
(3)
где — постоянные, а
— непрерывная функция своего аргумента
.
Если , то уравнение (3) является однородным и оно интегрируется, как указано выше.
Если хотя бы одно из чисел отлично от нуля, то следует различать два случая.
1) Определитель . Вводя новые переменные
и
по формулам
, где
и
— пока неопределенные постоянные, приведем уравнение (3) к виду
Выбирая и
как решение системы линейных уравнений
(4)
получаем однородное уравнение . Найдя его общий интеграл и заменив в нем
на
, a
на
, получаем общий интеграл уравнения (3).
2) Определитель . Система (4) в общем случае не имеет решений и изложенный выше метод неприменим; в этом случае
, и, следовательно, уравнение (3) имеет вид
. Подстановка
приводит его к уравнению с разделяющимися переменными.
Пример 3. Решить уравнение .
Решение. Рассмотрим систему линейных алгебраических уравнений
Определитель этой системы .
Система имеет единственное решение . Делаем замену
. Тогда уравнение (5) примет вид
Это уравнение является однородным уравнением. Полагая , получаем
, откуда
.
Разделяем переменные
Интегрируя, найдем или
.
Возвращаемся к переменным :
или
Пример 4. Решить уравнение .
Решение. Система линейных алгебраических уравнений несовместна. В этом случае метод, примененный в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку
,
. Уравнение примет вид
Разделяя переменные, получаем
отсюда
Возвращаясь к переменным , получаем общий интеграл данного уравнения
Б. Иногда уравнение можно привести к однородному заменой переменного . Это имеет место в том случае, когда в уравнении все члены оказываются одинакового измерения, если переменному
приписать измерение 1, переменному
— измерение
и производной
— измерение
.
Пример 5. Решить уравнение .
Решение. Делаем подстановку , где
пока произвольное число, которое мы выберем позже. Подставляя в уравнение выражения для
и
, получим
или
Заметим, что имеет измерение
имеет измерение
,
имеет измерение
. Полученное уравнение будет однородным, если измерения всех членов одинаковы, т.е. если выполняется условие
, или
.
Положим ; исходное уравнение принимает вид
или
Положим теперь . Тогда это уравнение примет вид
, откуда
.
Разделяем переменные в этом уравнении . Интегрируя, найдем
или
Заменяя через
, получаем общий интеграл данного уравнения
Уравнение имеет еще очевидное решение , которое получается из общего интеграла при
, если интеграл записать в виде
, а затем перейти к пределу при
. Таким образом, функция
является частным решением исходного уравнения.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
For common nomenclature of base quantities used in this article, see physical quantity. For 4-vector modifications used in relativity, see four-vector.
In physics, defining equations are equations that define new quantities in terms of base quantities.[1] This article uses the current SI system of units, not natural or characteristic units.
Description of units and physical quantities[edit]
Physical quantities and units follow the same hierarchy; chosen base quantities have defined base units, from these any other quantities may be derived and have corresponding derived units.
Colour mixing analogy[edit]
Defining quantities is analogous to mixing colours, and could be classified a similar way, although this is not standard. Primary colours are to base quantities; as secondary (or tertiary etc.) colours are to derived quantities. Mixing colours is analogous to combining quantities using mathematical operations. But colours could be for light or paint, and analogously the system of units could be one of many forms: such as SI (now most common), CGS, Gaussian, old imperial units, a specific form of natural units or even arbitrarily defined units characteristic to the physical system in consideration (characteristic units).
The choice of a base system of quantities and units is arbitrary; but once chosen it must be adhered to throughout all analysis which follows for consistency. It makes no sense to mix up different systems of units. Choosing a system of units, one system out of the SI, CGS etc., is like choosing whether use paint or light colours.
In light of this analogy, primary definitions are base quantities with no defining equation, but defined standardized condition, «secondary» definitions are quantities defined purely in terms of base quantities, «tertiary» for quantities in terms of both base and «secondary» quantities, «quaternary» for quantities in terms of base, «secondary», and «tertiary» quantities, and so on.
Motivation[edit]
Much of physics requires definitions to be made for the equations to make sense.
Theoretical implications: Definitions are important since they can lead into new insights of a branch of physics. Two such examples occurred in classical physics. When entropy S was defined – the range of thermodynamics was greatly extended by associating chaos and disorder with a numerical quantity that could relate to energy and temperature, leading to the understanding of the second thermodynamic law and statistical mechanics.[2]
Also the action functional (also written S) (together with generalized coordinates and momenta and the Lagrangian function), initially an alternative formulation of classical mechanics to Newton’s laws, now extends the range of modern physics in general – notably quantum mechanics, particle physics, and general relativity.[3]
Analytical convenience: They allow other equations to be written more compactly and so allow easier mathematical manipulation; by including a parameter in a definition, occurrences of the parameter can be absorbed into the substituted quantity and removed from the equation.[4]
- Example
As an example consider Ampère’s circuital law (with Maxwell’s correction) in integral form for an arbitrary current carrying conductor in a vacuum (so zero magnetization due medium, i.e. M = 0):[5]
using the constitutive definition
and the current density definition
similarly for the displacement current density
leading to the displacement current
we have
which is simpler to write, even if the equation is the same.
Ease of comparison: They allow comparisons of measurements to be made when they might appear ambiguous and unclear otherwise.
- Example
A basic example is mass density. It is not clear how compare how much matter constitutes a variety of substances given only their masses or only their volumes. Given both for each substance, the mass m per unit volume V, or mass density ρ provides a meaningful comparison between the substances, since for each, a fixed amount of volume will correspond to an amount of mass depending on the substance. To illustrate this; if two substances A and B have masses mA and mB respectively, occupying volumes VA and VB respectively, using the definition of mass density gives:
- ρA = mA / VA , ρB = mB / VB
following this can be seen that:
- if mA > mB or mA < mB and VA = VB, then ρA > ρB or ρA < ρB,
- if mA = mB and VA > VB or VA < VB, then ρA < ρB or ρA > ρB,
- if ρA = ρB, then mA / VA = mB / VB so mA / mB = VA / VB, demonstrating that if mA > mB or mA < mB, then VA > VB or VA < VB.
Making such comparisons without using mathematics logically in this way would not be as systematic.
Construction of defining equations[edit]
Scope of definitions[edit]
Defining equations are normally formulated in terms of elementary algebra and calculus, vector algebra and calculus, or for the most general applications tensor algebra and calculus, depending on the level of study and presentation, complexity of topic and scope of applicability. Functions may be incorporated into a definition, in for calculus this is necessary. Quantities may also be complex-valued for theoretical advantage, but for a physical measurement the real part is relevant, the imaginary part can be discarded. For more advanced treatments the equation may have to be written in an equivalent but alternative form using other defining equations for the definition to be useful. Often definitions can start from elementary algebra, then modify to vectors, then in the limiting cases calculus may be used. The various levels of maths used typically follows this pattern.
Typically definitions are explicit, meaning the defining quantity is the subject of the equation, but sometimes the equation is not written explicitly – although the defining quantity can be solved for to make the equation explicit. For vector equations, sometimes the defining quantity is in a cross or dot product and cannot be solved for explicitly as a vector, but the components can.
Angular momentum; scalar and vector components.
- Examples
Electric current density is an example spanning all of these methods, Angular momentum is an example which doesn’t require calculus. See the classical mechanics section below for nomenclature and diagrams to the right.
Elementary algebra
Operations are simply multiplication and division. Equations may be written in a product or quotient form, both of course equivalent.
-
Angular momentum Electric current density Quotient form Product form
Vector algebra
There is no way to divide a vector by a vector, so there are no product or quotient forms.
-
Angular momentum Electric current density Quotient form N/A Product form Starting from since L = 0 when p and r are parallel or antiparallel, and is a maximum when perpendicular, so that the only component of p which contributes to L is the tangential |p| sin θ, the magnitude of angular momentum L should be re-written as
Since r, p and L form a right-hand triad, this leads to the vector form
Elementary calculus
- The arithmetic operations are modified to the limiting cases of differentiation and integration. Equations can be expressed in these equivalent and alternative ways.
-
Current density Differential form Integral form where dA means a differential area element (see also surface integral).
Alternatively for integral form
Vector calculus
-
Current density Differential form Integral form where dA = ndA is the differential vector area.
Tensor analysis
Vectors are rank-1 tensors. The formulae below are no more than the vector equations in the language of tensors.
-
Angular momentum Electric current density Differential form N/A Product/integral form Starting from the components are Li, rj, pi, where i, j, k are each dummy indices each taking values 1, 2, 3, using the identity from tensor analysis
where εijk is the permutation/Levi-Cita tensor, leads to
Using the Einstein summation convention,
Multiple choice definitions[edit]
Sometimes there is still freedom within the chosen units system, to define one or more quantities in more than one way. The situation splits into two cases:[6]
Mutually exclusive definitions: There are a number of possible choices for a quantity to be defined in terms of others, but only one can be used and not the others. Choosing more than one of the exclusive equations for a definition leads to a contradiction – one equation might demand a quantity X to be defined in one way using another quantity Y, while another equation requires the reverse, Y be defined using X, but then another equation might falsify the use of both X and Y, and so on. The mutual disagreement makes it impossible to say which equation defines what quantity.
Equivalent definitions: Defining equations which are equivalent and self-consistent with other equations and laws within the physical theory, simply written in different ways.
There are two possibilities for each case:
One defining equation – one defined quantity: A defining equation is used to define a single quantity in terms of a number of others.
One defining equation – a number of defined quantities: A defining equation is used to define a number of quantities in terms of a number of others. A single defining equation shouldn’t contain one quantity defining all other quantities in the same equation, otherwise contradictions arise again. There is no definition of the defined quantities separately since they are defined by a single quantity in a single equation. Furthermore, the defined quantities may have already been defined before, so if another quantity defines these in the same equation, there is a clash between definitions.
Contradictions can be avoided by defining quantities successively; the order in which quantities are defined must be accounted for. Examples spanning these instances occur in electromagnetism, and are given below.
- Examples
Mutually exclusive definitions:
The magnetic induction field B can be defined in terms of electric charge q or current I, and the Lorentz force (magnetic term) F experienced by the charge carriers due to the field,
where 


or integral form,
However, only one of the above equations can be used to define B for the following reason, given that A, r, v, and F have been defined elsewhere unambiguously (most likely mechanics and Euclidean geometry).
If the force equation defines B, where q or I have been previously defined, then the flux equation defines ΦB, since B has been previously defined unambiguously. If the flux equation defines B, where ΦB, the force equation may be a defining equation for I or q. Notice the contradiction when B both equations define B simultaneously and when B is not a base quantity; the force equation demands that q or I be defined elsewhere while at the same time the flux equation demands that q or I be defined by the force equation, similarly the force equation requires ΦB to be defined by the flux equation, at the same time the flux equation demands that ΦB is defined elsewhere. For both equations to be used as definitions simultaneously, B must be a base quantity so that F and ΦB can be defined to stem from B unambiguously.[6]
Equivalent definitions:
Another example is inductance L which has two equivalent equations to use as a definition.[7][8]
In terms of I and ΦB, the inductance is given by
in terms of I and induced emf V
These two are equivalent by Faraday’s law of induction:
substituting into the first definition for L
and so they are not mutually exclusive.
One defining equation – a number of defined quantities
Notice that L cannot define I and ΦB simultaneously — this makes no sense. I, ΦB and V have most likely all been defined before as (ΦB given above in flux equation);
where W = work done on charge q. Furthermore, there is no definition of either I or ΦB separately – because L is defining them in the same equation.
However, using the Lorentz force for the electromagnetic field:[9][10][11]
as a single defining equation for the electric field E and magnetic field B is allowed, since E and B are not only defined by one variable, but three; force F, velocity v and charge q. This is consistent with isolated definitions of E and B since E is defined using F and q:
and B defined by F, v, and q, as given above.
Limitations of definitions[edit]
Definitions vs. functions: Defining quantities can vary as a function of parameters other than those in the definition. A defining equation only defines how to calculate the defined quantity, it cannot describe how the quantity varies as a function of other parameters since the function would vary from one application to another. How the defined quantity varies as a function of other parameters is described by a constitutive equation or equations, since it varies from one application to another and from one approximation (or simplification) to another.
- Examples
Mass density ρ is defined using mass m and volume V by but can vary as a function of temperature T and pressure p, ρ = ρ(p, T)
The angular frequency ω of wave propagation is defined using the frequency (or equivalently time period T) of the oscillation, as a function of wavenumber k, ω = ω(k). This is the dispersion relation for wave propagation.
The coefficient of restitution for an object colliding is defined using the speeds of separation and approach with respect to the collision point, but depends on the nature of the surfaces in question.
Definitions vs. theorems: There is a very important difference between defining equations and general or derived results, theorems or laws. Defining equations do not find out any information about a physical system, they simply re-state one measurement in terms of others. Results, theorems, and laws, on the other hand do provide meaningful information, if only a little, since they represent a calculation for a quantity given other properties of the system, and describe how the system behaves as variables are changed.
- Examples
An example was given above for Ampere’s law. Another is the conservation of momentum for N1 initial particles having initial momenta pi where i = 1, 2 … N1, and N2 final particles having final momenta pi (some particles may explode or adhere) where j = 1, 2 … N2, the equation of conservation reads:
Using the definition of momentum in terms of velocity:
so that for each particle:
and
the conservation equation can be written as
It is identical to the previous version. No information is lost or gained by changing quantities when definitions are substituted, but the equation itself does give information about the system.
One-off definitions[edit]
Some equations, typically results from a derivation, include useful quantities which serve as a one-off definition within its scope of application.
- Examples
In special relativity, relativistic mass has support and detraction by physicists.[12] It is defined as:
where m0 is the rest mass of the object and γ is the Lorentz factor. This makes some quantities such as momentum p and energy E of a massive object in motion easy to obtain from other equations simply by using relativistic mass:
However, this does not always apply, for instance the kinetic energy T and force F of the same object is not given by:
The Lorentz factor has a deeper significance and origin, and is used in terms of proper time and coordinate time with four-vectors. The correct equations above are consequence of the applying definitions in the correct order.
Magnetic field deflecting a charged particle, pseudo-defining magnetic rigidity for the particle.
In electromagnetism, a charged particle (of mass m and charge q) in a uniform magnetic field B is deflected by the field in a circular helical arc at velocity v and radius of curvature r, where the helical trajectory inclined at an angle θ to B. The magnetic force is the centripetal force, so the force F acting on the particle is;
reducing to scalar form and solving for |B||r|;
serves as the definition for the magnetic rigidity of the particle.[13] Since this depends on the mass and charge of the particle, it is useful for determining the extent a particle deflects in a B field, which occurs experimentally in mass spectrometry and particle detectors.
See also[edit]
- Constitutive equation
- Defining equation (physical chemistry)
- List of electromagnetism equations
- List of equations in classical mechanics
- List of equations in fluid mechanics
- List of equations in gravitation
- List of equations in nuclear and particle physics
- List of equations in quantum mechanics
- List of optics equations
- List of relativistic equations
- Table of thermodynamic equations
Footnotes[edit]
- ^ Warlimont, pp 12–13
- ^ P.W. Atkins (1978). Physical chemistry (2nd ed.). Oxford University Press. pp. 124–131. ISBN 0-19-855148-7.
- ^ E. Abers (2004). Quantum Mechanics (2nd ed.). Addison Wesley. p. 14. ISBN 978-0-13-146100-0.
- ^ P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN 0-7195-3382-1.
- ^ I.S. Grant; W.R. Phillips; Manchester Physics (2008). Electromagnetism (2nd ed.). John Wiley & Sons. pp. 186–188. ISBN 978-0-471-92712-9.
- ^ a b P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (2nd ed.). John Murray. p. 6. ISBN 0-7195-3382-1.
- ^ P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (2nd ed.). John Murray. p. 405. ISBN 0-7195-3382-1.
- ^ I.S. Grant; W.R. Phillips; Manchester Physics (2008). Electromagnetism (2nd ed.). John Wiley & Sons. pp. 231–234. ISBN 978-0-471-92712-9.
- ^ See, for example, Jackson p 777–8.
- ^ J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. pp. 72–73. ISBN 0-7167-0344-0.. These authors use the Lorentz force in tensor form as definer of the electromagnetic tensor F, in turn the fields E and B.
- ^ I.S. Grant; W.R. Phillips; Manchester Physics (2008). Electromagnetism (2nd ed.). John Wiley & Sons. p. 122. ISBN 978-0-471-92712-9.
- ^ H.D. Young; R.A. Freedman (2008). University Physics – With Modern Physics (12th ed.). Addison-Wesley (Pearson International). pp. 1290–1291. ISBN 978-0-321-50130-1.
- ^ I.S. Grant; W.R. Phillips; Manchester Physics (2008). Electromagnetism (2nd ed.). John Wiley & Sons. ISBN 978-0-471-92712-9.
Sources[edit]
- P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN 0-7195-3382-1.
- G. Woan (2010). The Cambridge Handbook of Physics Formulas. Cambridge University Press. ISBN 978-0-521-57507-2.
- A. Halpern (1988). 3000 Solved Problems in Physics, Schaum Series. Mc Graw Hill. ISBN 978-0-07-025734-4.
- R.G. Lerner; G.L. Trigg (2005). Encyclopaedia of Physics (2nd ed.). VHC Publishers, Hans Warlimont, Springer. pp. 12–13. ISBN 978-0-07-025734-4.
- C.B. Parker (1994). McGraw Hill Encyclopaedia of Physics (2nd ed.). McGraw Hill. ISBN 0-07-051400-3.
- P.A. Tipler; G. Mosca (2008). Physics for Scientists and Engineers: With Modern Physics (6th ed.). W.H. Freeman and Co. ISBN 978-1-4292-0265-7.
- L.N. Hand; J.D. Finch (2008). Analytical Mechanics. Cambridge University Press. ISBN 978-0-521-57572-0.
- T.B. Arkill; C.J. Millar (1974). Mechanics, Vibrations and Waves. John Murray. ISBN 0-7195-2882-8.
- H.J. Pain (1983). The Physics of Vibrations and Waves (3rd ed.). John Wiley & Sons. ISBN 0-471-90182-2.
- J.R. Forshaw; A.G. Smith (2009). Dynamics and Relativity. Wiley. ISBN 978-0-470-01460-8.
- G.A.G. Bennet (1974). Electricity and Modern Physics (2nd ed.). Edward Arnold (UK). ISBN 0-7131-2459-8.
- I.S. Grant; W.R. Phillips; Manchester Physics (2008). Electromagnetism (2nd ed.). John Wiley & Sons. ISBN 978-0-471-92712-9.
- D.J. Griffiths (2007). Introduction to Electrodynamics (3rd ed.). Pearson Education, Dorling Kindersley. ISBN 978-81-7758-293-2.
Further reading[edit]
- L.H. Greenberg (1978). Physics with Modern Applications. Holt-Saunders International W.B. Saunders and Co. ISBN 0-7216-4247-0.
- J.B. Marion; W.F. Hornyak (1984). Principles of Physics. Holt-Saunders International Saunders College. ISBN 4-8337-0195-2.
- A. Beiser (1987). Concepts of Modern Physics (4th ed.). McGraw-Hill (International). ISBN 0-07-100144-1.
- H.D. Young; R.A. Freedman (2008). University Physics – With Modern Physics (12th ed.). Addison-Wesley (Pearson International). ISBN 978-0-321-50130-1.








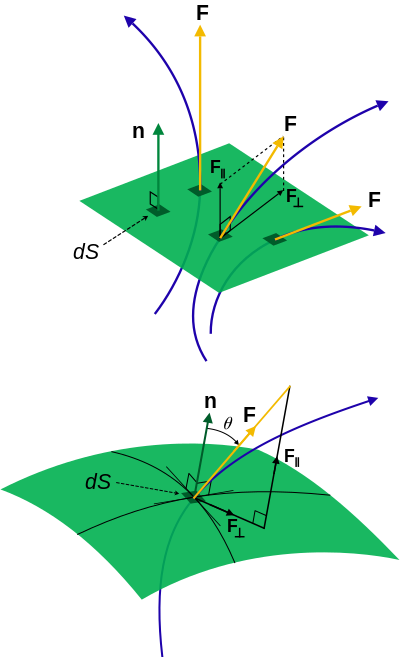



































![mathbf{F} = q left [ mathbf{E} + left ( mathbf{v} times mathbf{B} right )right ] ,,!](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee2c2b4c70c1037f1645968977057dc6d06d7073)















