Между основными оригиналами и изображениями
|
Функция (f(t) |
Изображение |
|
1 |
|
|
|
|
|
cos |
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примеры нахождения изображений сложных функций
1.
.
Так
как
,
то применяя теорему дифференцирования,
найдем
Следовательно,
.
2.
Применять
теорему дифференцирования пять раз,
конечно, неудобно. Представим
в виде
Так
как
,
то по теореме смещения изображения
Теперь
по теореме линейности находим
3.
Представим
в виде
Для функции
изображение известно:
По
теореме дифференцирования изображения
—
.
Следовательно,
4.
Так
как
то
5.
Так
как
то
Учитывая,
что
,
по теоремам подобия и линейности
получим
Замечания.
1.
Грубой ошибкой будет представление
изображения заданных функций в виде
произведения изображений, соответствующих
каждому из сомножителей, так как
умножению оригиналов в пространстве
оригиналов соответствует другая
операция в пространстве изображений
[4,5].
2.
Решение приведенных задач возможно
различными способами. В пособии указан
лишь один из возможных способов решения.
3.2. Обратное преобразование Лапласа
При
практическом применении преобразования
Лапласа всегда приходится решать
обратную задачу — построение оригинала
по его изображению. Общий метод построения
оригинала f(t) по заданному изображению
F(p) базируется на теореме
обращения (
формуле Меллина ):
(3.22)
где
интегрирование проводится по любой
бесконечной прямой 7 0Re p = 7g 0,
лежащей в полуплоскости абсолютной
сходимости интеграла Лапласа [7,8].
Непосредственно формулой (3.22) для
нахождения оригинала по известному
изображению пользуютя редко. При
нахождении оригинала по его изображению
обычно применяют таблицы соответствия
между оригиналами и их изображениями
[5] и свойства преобразования Лапласа.
В
самом распространенном случае, когда
изображение F(p) является дробно —
рациональной функцией вида
,
где
A(p) и B(p) — многочлены, причем степень
многочлена B(p) больше степени многочлена
A(p), оригинал может быть найден разложением
дроби A(p)
/B(p) на простейшие.
Пример.
Дано изображение
Найти
оригинал f(t) = F(p).
Разложим
заданную дробь на простейшие:
Приводя
к общему знаменателю, получим
.
При
p = 0 1 = -8A,
При
p = 2 5 = 16B,
следовательно,
A = -1/8, B = 5/16.
Приравнивая
далее коэффициенты, например, при
и
в левой и правой частях равенства,
получим
Поэтому
Применяя
теорему линейности, окончательно найдем
Пример.
Найти оригинал по его изображению
Разложение
данной дроби на простейшие имеет вид
После
приведения к общему знаменателю получим
При
p
= 0 1 = -3A,
откуда A
= — 1/3;
при
p = 3 1 = 9C, откуда C = 1/9.
Приравнивая
далее коэффициенты при
в правой и левой частях равенства,
получим уравнение 0 = B + C, из которого
следует B = — 1/9.
Итак,
Если
знаменатель рациональной дроби B(p)
имеет простые не-
нулевые
корни
,
то есть если
то
оригинал функции F(p) может быть найден
по формуле
(3.23)
Пример.
Найти оригинал по его изображению
Здесь,
Корни
знаменателя
.
Следовательно,
Поэтому
Если
один из простых корней знаменателя B(p)
равен нулю, то есть B(p) можно представить
в виде
,
где,
то оригинал находится по формуле
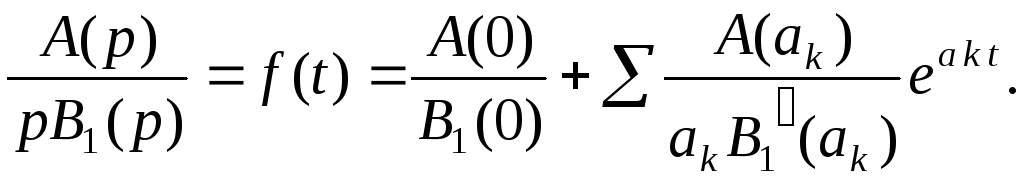
Здесь
суммирование
распространяется
на все ненулевые корни
многочлена
Пример.
Найти оригинал по его изображению
.
Здесь
Корни
знаменателя
.
Поэтому
Применяя
формулу
(3.24), находим
Если
знаменатель рациональной дроби
представляет собой квадратный трехчлен,
корни которого комплексные, удобно
представить его в виде суммы квадратов
слагаемых и применить теорему смещения
изображения.
Пример.
Найти оригинал по его изображению
Соседние файлы в папке Метода по ОДУ теория
- #
27.02.2014452.61 Кб841.DOC
- #
- #
27.02.2014720.9 Кб1542.DOC
- #
27.02.2014497.66 Кб1643.doc
Примеры решений задач по операционному исчислению (преобразованию Лапласа)
Операционное (символическое) исчисление – это один из методов математического анализа, позволяющий в
некоторых случаях свести исследование и решение дифференциальных, псевдодифференциальных, интегральных уравнений, к более простым алгебраическим задачам.
Изучая преобразование Лапласа, мы вводим оригинал функции $f(t)$ и ее изображение $F(p)$, находимое по формуле:
$$F(p) = int_0^infty f(t) e^{-pt}dt$$
Для быстроты и удобства решения задач составлена таблица изображений и оригиналов, которая, наряду с теоремами (линейности, подобия, смещения, запаздывания), свойствами и правилами дифференцирования и интегрирования изображения/оригинала, постоянно используется в решении примеров.
В этом разделе вы найдете готовые задания разного типа: восстановление оригинала или изображения функции, нахождение свертки функций, решение ДУ, систем ДУ или интегральных уравнений с помощью преобразования Лапласа и т.д.
Лучшее спасибо — порекомендовать эту страницу
Как найти изображение функции
Задача 1. Найти изображение данного оригинала, или оригинала, удовлетворяющего данному уравнению
$$f(t)=frac{e^{2t}-e^{-3t}}{t}.$$
Задача 2. Пользуясь определением, найти изображение функции $f(t)=3^t$.
Задача 3. Найти изображение функции: $int_0^t cos tau cdot e^{-3tau}dtau. $
Задача 4. Найти изображение оригинала $f(x)$ двумя способами:
1) Вычислив интеграл $F(p) = int_0^infty f(x) e^{-px}dx$;
2) Воспользовавшись таблице изображений и свойствами преобразования Лапласа.
Оригинал задается формулой (курсочно-линейная функция, см. файл).
Как найти оригинал функции
Задача 5. Найти оригинал изображения $F(p)$, где
$$F(p)=frac{2p-1}{(p^2-4p+13)^2}.$$
Задача 6. Найти оригинал изображения
$$F(p)=frac{15p^2+3p+34}{(p^2+4p+8)(p^2-6p+5)}.$$
Задача 7. Найти оригинал для функции с помощью вычетов
$$F^*(p)=frac{1}{e^{4p}-625}.$$
Как решить ДУ (систему ДУ) операционным методом
Задача 8. Найти частное решение дифференциального уравнения с заданными начальными условиями операторным методом
$$x’+x=4e^t, x(0)=2.$$
Задача 9. Найти решение задачи Коши методами операционного исчисления
$$x»+2x’+2x=te^{-t}, quad x(0)=0, x'(0)=0.$$
Задача 10. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.
$$x’=x-y,\
y’=x+y,\
x(0)=2, y(0)=1.$$
Задача 11. Методом операционного исчисления найти решение задачи Коши для ДУ 3-го порядка
$$x»’+x»-2x’-5x=5e^t, quad x(0)=0, x'(0)=1, x»(0)=2.$$
Задача 12. Решите задачу Коши для системы дифференциальных уравнений с помощью преобразования Лапласа.
$$frac{dx}{dt}=x-2y,\
frac{dy}{dt}=x+3y,\
x(0)=0, y(0)=1. $$
Задача 13. C помощью формулы Дюамеля найти решение уравнения
$$x»’+x’=tg t, quad x(0)=x'(0)=x»(0)=0.$$
Задача 14. Решить систему ДУ с помощью преобразования Лапласа
$$
x’=-y+z,\
y’=z, quad x(0)=1, \
z’=-x+z;\
y(0)=z(0)=1/2.
$$
Как решить интегральное уравнение
Задача 15. Методом операционного исчисления найти решение интегрального уравнения
$$ y(t)=cos t +int_0^t (t-tau)^2 y(tau)d tau. $$
Задача 16. Решить интегральное уравнение
$$ int_0^t ch (tau) x(t-tau)d tau = t. $$
Как найти свертку функций
Задача 17. Найти свертку функций $f(t)=1$ и $phi(t)=sin 5t$.
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей, оформление производится в Word, срок от 1 дня.
Подробнее о решении заданий с преобразованием Лапласа
Дополнительная информация
- Онлайн-помощь по математическому анализу
- Дифференциальные уравнения — задачи с решениями
- Как решать ДУ с помощью операционного исчисления
Преобразование Лапласа и его свойства
Основные определения
1. Оригинал — это комплекснозначная функция действительного аргумента
, которая удовлетворяет следующим условиям:
а) при
;
б) на любом конечном отрезке функция
имеет не более чем конечное число точек разрыва первого рода;
в) имеет ограниченный рост, т.е. возрастает не быстрее показательной функции: существуют такие постоянные
и
, что
при
.
Замечания 5.1
1. Величина называется показателем роста функции
. Для любой ограниченной функции, являющейся оригиналом, можно принять
.
2. Обозначим , если пределы существуют и конечны.
3. Совокупность всех оригиналов называется пространством оригиналов.
4. В точке разрыва первого рода функция имеет конечные односторонние пределы:
.
Пример 5.1
2. Изображение функции — функция
комплексного переменного
, определяемая равенством
(5.1)
Область существования этой функции определяется областью сходимости интеграла Лапласа, стоящего в правой части равенства (5.1). Исследование интeгpaлa позволяет определить эту область и установить свойства функции . Имеет место следующее утверждение.
Утверждение 5.1. Если функция , является оригиналом, то интеграл Лапласа сходится абсолютно в области
(рис. 5.1) , где
— показатель роста оригинала. Внутри этой области, т.е. на любом замкнутом подмножестве
, интеграл сходится равномерно и определяет аналитическую функцию
.
Замечания 5.2
1. Утверждение 5.1 аналогично свойствам степенных рядов, сходящихся в круге и равномерно сходящихся внутри этого круга, где сумма ряда является аналитической функцией.
2. Свойство аналитичности изображения имеет важное значение в теории и практике применения преобразования Лапласа, так как позволяет использовать в пространстве изображений методы теории аналитических функций, в частности разложения функций в ряды и теорию вычетов.
3. Совокупность всех изображений называется пространством изображений.
4. Переход, определяющий изображение по оригиналу
, называется преобразованием Лапласа:
(5.2)
Запись означает, что оригиналу
соответствует изображение
.
5. Оригинал по изображению находится с помощью обратного преобразования Лапласа по формуле обращения
(5.3)
где путь интегрирования — любая прямая , параллельная мнимой оси и лежащая правее прямой
(рис. 5.1).
Непосредственное применение формулы обращения часто затруднительно. Поэтому на практике пользуются методами, изложенными ранее.
Замечания 5.3
1. Для преобразования Лапласа используются различные обозначения, на пример и
, что означает: оригиналу
соответствует изображение
и изображению
соответствует оригинал
. В некоторых учебниках вместо аргумента
применяется
, то есть
и
.
2. Для компактной записи оригиналов используется единичная ступенчатая функция
(5.4)
где — точка приложения (рис. 5.2). Так как во многих практических задачах аргумент
имеет смысл текущего времени, то
также называется моментом приложения единичной ступенчатой функции. В системах автоматического регулирования и управления функция
рассматривается как типовой входной сигнал.
При функция
является функцией Хевисайда:
(5.5)
Тогда, если функция удовлетворяет условиям «б», «в» в определении оригинала (п. 1), но не удовлетворяет условию «а», то функция
будет оригиналом, так как
Далее под заданной с помощью аналитической формулы функцией , там, где это не вызывает недоразумений, будем понимать произведение этой функции на функцию Хевисайда, а множитель
опускать.
3. Функции , являющиеся изображениями, удовлетворяют необходимому условию: если
есть изображение, то
при
. Поэтому функции
не являются изображениями. Однако в практических задачах функции типа
и другие встречаются. Это требует расширения понятий оригинала и изображения.
Класс оригиналов можно расширить, включив в него функции, которые могут быть не ограничены в окрестности некоторых конечных точек, но такие, что интеграл Лапласа от них, тем не менее, сходится абсолютно в некоторой полуплоскости . К числу таких обобщенных оригиналов относятся степенная функция
при
и некоторые другие.
4. Во всякой точке , являющейся точкой разрыва функции
, правая часть формулы (5.3) равна
.
Примеры 5.2-5.3
Пример 5.2. Найти изображение единичной функции Хевисайда .
Решение. Так как функция ограничена, то в качестве показателя роста можно положить
. По формуле (5.2) имеем
так как из равенства следует, что
при
.
Пример 5.3. Найти изображение функции , где
— действительное число.
Решение. Показателем роста можно считать . По формуле (5.2)
так как из равенства следует, что
при
.
Свойства преобразования Лапласа
Будем предполагать, что рассматриваемые далее функции являются оригиналами. Соответствующие им изображения (при
) обозначим
.
1. Линейность. Если — оригиналы, то для любых комплексных чисел
, функция
также является оригиналом и справедливо равенство
(5.6)
Заметим, что для функции существенно, что все слагаемыс являются оригиналами, так как, например, функция
является оригиналом, а слагаемые
и
не являются.
Справедливо и обратное утверждение: если — изображения, то
Здесь также важно, что слагаемые функции являются изображениями, поскольку из того, что
— изображение, не следует, что
— изображения. Например, функция
является изображением, а слагаемые
и
не являются.
Примеры 5.4-5.5
Пример 5.4. Найти изображение функции .
Решение. Из примера 5.2 имеем , а из примера 5.3 при
имеем
. Тогда согласно свойству линейности для оригинала
получаем
.
Пример 5.5. Найти изображение функции .
Решение. Используя формулу Эйлера (2.11), получаем .
Из примера 5.3 при и
следует:
. Тогда по свойству линейности
2. Подобие (теорема подобия). Для любого из
следует
(5.7)
и обратно: .
Пример 5.6
Найти изображение функции .
Решение. Из примера 5.5 следует, что . Тогда по теореме подобия
3. Смещение (теорема смещения). При любом комплексном из
следует
(5.8)
то есть умножению оригинала на соответствует смещение изображения на
.
Пример 5.7
Найти изображение функции .
Решение. Из примера 5.6 следует . Тогда по теореме смещения
.
Запаздывание оригинала
4. Запаздывание (теорема запаздывания). Для любого из
следует
(5.9)
где (рис. 5.3), т.е. запаздыванию оригинала на
соответствует умножение изображения на
.
Примеры 5.8-5.10
Пример 5.8. Найти изображение функции .
Решение. В примере 5.5 получено . По теореме запаздывания при
имеем
.
Пример 5.9. Найти оригиналы по изображениям: a) ; б)
.
а) Из примера 5.7 следует, что при изображению
соответствует оригинал
. Тогда по теореме запаздывания при
имеем
б) По формуле 3 из табл. 5.1 .По теореме запаздывания при
получаем
. Заметим, что для похожего, но отличного от полученного, оригинала
(его можно записать в виде
) изображение имеет вид
.
Пример 5.10. Найти изображение функции , график которой представлен на рис. 5.4.
С учетом (5.4) представим функцию в виде
.
Из примера 5.2 имеем . Применяя свойства линейности и запаздывания, получаем
Заметим, что, находя предел при в последнем выражении, можно получить изображение δ-функции
Замечание 5.4. Дельта-функция часто встречается в инженерных приложениях как идеализация импульса конечной длительности. В теории автоматического регулирования и управления δ-функция вместе с единичной ступенчатой являются типовыми входными воздействиями.
Очевидно, изображение дельта-функции не удовлетворяет необходимому условию (п.2 замечаний 5.3). Этот факт свидетельствует о практическом требовании расширения понятия оригинала. Дельта-функция относится к обобщенным функциям и задается соотношением
(5.10)
Дифференцирование оригинала
5. Если функции являются оригиналами и
, то
(5.11)
где .
Примеры 5.11-5.12
Пример 5.11. Найти изображение , если
.
Решение. Из примера 5.7 следует, что при имеем
.
Найдем . Согласно (5.11)
.
Пример 5.12. Найти изображение выражения с начальными условиями
.
Решение. Пусть , тогда
. В примере 5.2 получено
. Используя свойство линейности, имеем
Интегрирование оригинала
Если функция является оригиналом и
, то
(5.12)
т.е. интегрированию оригинала соответствует деление изображения на .
Пример 5.13
Найти изображение интеграла от функции
.
Решение. Из примера 5.6 следует, что . Тогда
, то есть
.
Дифференцирование изображения
Если функция является оригиналом и
. то
(5.13)
Примеры 5.14-5.15
Интегрирование изображения
Если функция является оригиналом, то из
следует
(5.14)
Пример 5.16
Найти изображение функции .
Решение. Функция является оригиналом, так как
(условие «в») и точка
является точкой разрыва первого рода (условие «б»). Из примера 5.13 следует
.
Отсюда .
Умножение изображений (теорема Бореля)
Из и
следует
(5.15)
т.е. свертке оригиналов соответствует произведение изображений. Функция определяется формулой
(5.16)
и называется сверткой оригиналов и
.
Пример 5.17
Найти оригинал, соответствующий изображению .
Решение. Представим в виде произведения изображений:
.
Из примеров 5.6 и 5.13 следует .
Согласно (5.15),(5.16) получаем искомый оригинал:
Дифференцирование свертки (интеграл Дюамеля)
10. Согласно свойствам 9 и 5 найдем преобразование Лапласа от производной свертки двух функций:
С другой стороны,
или, применяя правило дифференцирования интеграла, зависящего от параметра, имеем
Здесь при дифференцировании интеграла, зависящего от параметра, применялась формула Лейбница, которая для общего случая имеет вид
Объединяя полученные результаты, можно записать:
(5.17)
Формула (5.17) называется интегралом Дюамеля. Интеграл Дюамеля применяется для решения дифференциальных уравнений.
Пример 5.18
Найти оригиналы, соответствующие изображениям: a) ; б)
.
Решение. а) Заметим, что здесь нельзя непосредственно воспользоваться теоре мой Бореля, так как в произведении множитель
не является изображением (не выполняется необходимое условие).
Представим изображение в виде произведения . Из примера 5.3 вытекает
Тогда по формуле (5.17) имеем
Можно решить этот пример с помощью теоремы Бореля, представив изображение в виде
Тогда, используя свойство линейности и теорему Бореля, получаем
б) Представим изображение в виде произведения:
Из примера 5.6 при и
следует
Тогда по формуле (5.17) получаем
Теорема о связи «начальных» и «конечных» значений оригинала и изображения
Начальное значение оригинала находится по формуле
(5.18)
Если существует конечный предел , то
(5.19)
Из соотношений (5.18),(5.19) следует, что для нахождения начальных и конечных значений оригинала не требуется знания оригинала, а достаточно иметь соответствующее изображение. На практике соотношение (5.19) применяется, например, для нахождения установившегося значения выходного сигнала в системах автоматического регулирования.
Пример 5.19
Найти начальное и конечное значения оригинала, которому соответствует изображение .
Решение. Согласно (5.18) и (5.19) имеем
С другой стороны, из примера 5.7 следует, что
поэтому легко убедиться в правильности полученного результата.
Полученные решения примеров 5.2–5.17 позволяют сформировать таблицу преобразования Лапласа. Табл. 5.1 является фрагментом более полных таблиц, используемых далее при решении примеров и задач.
Нахождение изображения по оригиналу
Для нахождения изображения требуется применить свойства преобразования Лапласа Так, чтобы к функции или ее составляющим можно было применить результаты, содержащиеся в табл. 5.1.
Таблица 5.1. Таблица основных преобразований Лапласа
Посмотреть
Пример 5.21
Найти изображения функций:
a) ; б)
;
в) ; г)
;
д) ; е)
;
ж) ; з)
.
Решение
а) Согласно формуле 12 из табл. 5.1 . По свойству дифференцирования изображения (формула (5.13) при
):
или
.
Поэтому .
Можно решать иначе, используя формулу 10 из табл. 5.1 при а = 3 и свойство смещения при
и
.
б) Применим свойства линейности и интегрирования изображения. Так как в силу формул 1 и 9 из табл. 5.1 , то согласно (5.14)
в) По формуле 9 из табл. 5.1 . Функцию fit) можно записать, используя единичную ступенчатую функцию:
. Поэтому для нахождения изображения следует применить теорему запаздывания (5.9) к оригиналу
при
г) Согласно теореме смещения (5.8) и с учетом результата п. «в» имеем
, так как
.
д) По теореме запаздывания (5.9) при и по формуле 7 из табл. 5.1 при
получаем
е) Используя свойства линейности, запаздывания и формулы 6,1,8 из табл. 5.1, получаем
ж) По формуле 19 из табл. 5.1 находим . По свойству интегрирования изображения (формула (5.14)):
По свойству интегрирования оригинала (5.12): .
з) Используем формулу косинуса разности и запишем оригинал в виде суммы:
По свойству линейности получаем:
Заметим, что здесь и результаты пп. «в» и «з» различны так как оригиналами являются разные функции.
Нахождение изображений функций, заданных графиком
При решении прикладных задач оригинал часто задан графиком. Это может быть, например, входной сигнал, действующий на систему автоматической регулирования. В этом случае рекомендуется сначала записать аналитическое выражение оригинала с помощью единичной ступенчатой функции (5.4), привести полученное выражение к виду, удобному для применения табл. 5.1 и свойстве преобразования Лапласа.
Пример 5.22
Найти изображения функций, заданных графиками на рис. 5.5.
Решение.
а) Представим функцию в виде .
По формуле 3 из табл.5.1 и теореме запаздывания (формула (5.9) при )
б) Запишем функцию в виде .
По формулам 1,3 из табл. 5.1 и (5.6), (5.9) имеем .
в) Запишем изображенную функцию в виде .
По формулам 1,3 из табл. 5.1 и (5.6), (5.9) имеем .
г) Представим функцию в виде
По формулам 3 из табл. 5.1 и (5.6), (5.9) имеем .
д) Запишем функцию в форме
По формулам З из табл. 5.1 и (5.6), (5.9) .
е) Представим изображенную функцию в виде
По формулам 1,3 из табл. 5.1 и (5.6), (5.9) .
ж) Запишем функцию в форме .
По формуле 8 из табл. 5.1 и по теореме запаздывания .
з) Представим функцию в виде .
По формуле 6 из табл. 5.1 при и (5.9) при
имеем
и) Представим функцию в виде .
Используя формулы 2 из табл. 5.1 и (5.6), (5.9), получаем .
Нахождение изображений периодических функций
Во многих приложениях используются оригиналы, являющиеся периодическими функциями.
Пусть — оригинал с периодом
(рис. 5.6,в), образованный повторением функции
(рис. 5.6,б):
Для нахождения изображения периодической функции
следует:
1. Найти изображение функции .
2. Найти изображение по формуле
(5.20)
Пример 5.23.
Найти изображения функций, представленных на рис. 5.7.
Решение
а) По графику (рис. 5.7,в) получаем
Поэтому .
Поскольку , по формуле (5.20) находим
б) По графику (рис. 5.7,б) имеем , тогда
. По формуле (5.20) при
имеем
в) Функция, изображенная на рис. 5.7,в , имеет период . Запишем аналитическое выражение для
и соответствующее изображение
По формуле (5.20) получаем .
г) Для функции, изображенной на рис. 5.7,г, изображением для является
(см. пример 5.22 п.»ж»). Тогда по формуле (5.20) при
получаем
.
Нахождение оригинала по изображению
Непосредственное применение формулы обращения (5.3) затруднительно, поэтому для нахождения оригинала применяются теоремы разложения и правила преобразования изображения к виду, представленному в табл. 5.1.
Применение теорем разложения
Теорема 5.1 (первая теорема разложения). Если функция аналитична в некоторой окрестности бесконечно удаленной точки и ее разложение в ряд по степеням
имеет вид
, то функция (5.21) является оригиналом, соответствующим изображению
.
(5.21)
Теорема 5.2 (вторая теорема разложения). Если изображение является однозначной функцией и имеет лишь конечное число особых точек
лежащих в конечной части плоскости, то
(5.22)
Замечания 5.5
1. Формула (5.21) может быть записана в виде . Задача нахождения оригинала при выполнении условий теоремы сводится к нахождению коэффициентов разложения функции в ряд Лорана в окрестности бесконечно удаленной точки.
2. Формула (5.22) принимает наиболее простой вид в случае — рационального изображения, т.е.
, где
— многочлены степеней /пил соответственно, не имеющие общих корней. Если все полюсы
функции
простые, то по формуле (4.24) получаем
, а формула (5.22) принимает вид
(5.23)
3. Если при выполнении условий п.2 коэффициенты многочлена — лействительные числа, то его комплексные корни, как известно, являются по парно сопряженными. Нахождение суммы вычетов в таких точках можно заме нить нахождением действительной части вычета в одной из них. Действительио, вычет в точке
, используя свойства сопряженных чисел, можно записать следующим образом:
Это означает, что вычет в точке есть число, сопряженное вычету в точке
, а сумма таких чисел равна их удвоенной действительной части:
Пример 5.24
Найти оригиналы для функций:
a) ;
б) .
Решение. В случае «а» для решения задачи используем теорему 5.1, а в случае «б» — теорему 5.2.
а) Используем типовые разложения
Для заданных изображений получаем:
Согласно первой теореме разложения
б) Представим в виде
где — простые полюсы функции
. По второй теореме разложения
Тот же результат можно получить, пользуясь пп. 2 и 3 замечаний 5.5:
Функция имеет четыре простых полюса:
.
Так как вычет в простом полюсе находится по формуле , то по второй теореме разложения
Функция имеет два полюса: простой
и полюс второго порядка
.
По второй теореме разложения . Находим вычеты
получаем окончательный ответ .
Применение таблицы и свойств преобразования Лапласа
Приведем ряд известных приемов нахождения оригинала.
1. Если изображение отличается от табличного на постоянный множитель, то его следует умножить и одновременно поделить на этот множитель, а затем воспользоваться свойством линейности.
Пример 5.25
2. Изображение, заданное в виде дроби , разлагается на сумму дробей.
Пример 5.26
Найти оригинал для функций: а) ; б)
; в)
.
Решение. Представим дроби в виде суммы двух слагаемых, а затем воспользуемся свойством линейности и формулами из табл. 5.1:
а) ;
б) .
в) представим в виде
. По формулам 4,6 из табл. 5.1 находим
.
3. Если знаменатель дроби содержит квадратный трехчлен, то в нем выде ляется полный квадрат: . При этом числитель дроби представляется в виде многочлена от
.
Пример 5.27
Найти оригиналы для функций: a) ; б)
.
Решение. а) Выделим полный квадрат в знаменателе дроби и воспользуемся табл. 5.1 (по формуле 12 из табл. 5.1 при ):
б) Используем представление
По формулам 19,20 из табл. 5.1 и по теореме смещения (формула (5.8))
Можно решить эту задачу иначе, используя вторую теорему разложения (см. п. «б» примера 5.24):
4. Если оригинал представляет собой правильную рациональную дробь, то следует разложить ее на простейшие дроби и для каждой из полученных дробей найти оригинал.
Примеры 5.28-5.29
Пример 5.28. Найти оригиналы для функций:
а) ; б)
; в)
; г)
.
Решение. а) Представим в виде
, где
— неопределенные коэффициенты.
Отсюда следует равенство .
Приравнивая коэффициенты при одинаковых степенях , получаем систему уравнений для нахождения неопределенных коэффициентов:
Решая ее, получаем
и
По формулам 1,12,13 из табл. 5.1 .
б) Представим в виде
, где
— неопределенные коэффициенты.
Отсюда .
Подставляя последовательно , получаем
и поэтому
По формулам 6,7 из табл. 5.1 находим .
в) Представим изображение в виде . Отсюда
При получаем
, поэтому
По свойству линейности и по формуле 6 из табл. 5.1 получаем
Можно решить эту задачу иначе, используя вторую теорему разложения (см. п. «б» примера 5.24):
г) Представим в виде
, где
— неопределенные коэффициенты.
Из равенства при
получаем
, поэтому
.
По формуле 6 из табл. 5.1 имеем .
Можно также решить эту задачу иначе, используя вторую теорему разложения (см. п. «б» примера 5.24 и п. «в» данного примера):
Пример 5.29. Найти оригиналы для функций: a) ; б)
.
Решение. а) Решим пример различными способами.
Первый способ. Воспользуемся разложением дроби на элементарные:
По формулам 2,3,6,7 из табл. 5.1 получаем .
Второй способ. Применим вторую теорему разложения, учитывая, что и
— полюсы второго порядка функции
Третий способ. Обозначим . Тогда
. Рассмотрим функцию
. По свойству интегрирования оригинала (формула (5.12)) получаем
Заметим, что . Применяя еще раз свойство интегрирования оригинала, имеем
Четвертый способ. Представим изображение в виде произведения
, где
.
По формулам 3 и 7 из табл. 5.1 . Далее по теореме Бореля (формула (5.15))
б) Решим пример также несколькими способами.
Первый способ. Воспользуемся разложением дроби на элементарные:
По формуле 9 из табл. 5.1 получаем .
Второй способ. Применим вторую теорему разложения с учетом пп. 2,3 замечаний 5.5:
Третий способ. Представим изображение в виде произведения:
Отсюда . По теореме Бореля
Четвертый способ. Используем формулу 37 из табл. 5.1. При получаем
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Преобразованием Лапласа некоторой функции
называется интегральное преобразование вида:
Функция
называется оригиналом, функция
— изображением. Причём
является функцией комлексной переменной, т.е.
.
В качестве примера, найдём изображение
функции оригинала
.
Для этого нам необходимо воспользоваться приведённой выше формулой и
вычислить интеграл:
То, что функция
является изображением функции
записывается как
или
.
Важным свойством
преобразования Лапласа
является то, что если
, то
Указанное свойство активно используется при
решении дифференциальных уравнений
поскольку позволяет сводить последние к алгебраическим.
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha позволяет найти преобразование Лапласа практически любой, даже очень сложной функции.
Интегральное преобразование Лапласа онлайн, калькулятор изображения функций.
Теория функций комплексного переменного.
: x^a
модуль x: abs(x)
: Sqrt[x]
: x^(1/n)
: a^x
: Log[a, x]
: Log[x]
: cos[x] или Cos[x]
 : sin[x] или Sin[x]
: sin[x] или Sin[x] : tan[x] или Tan[x]
: tan[x] или Tan[x] : cot[x] или Cot[x]
: cot[x] или Cot[x] : sec[x] или Sec[x]
: sec[x] или Sec[x] : csc[x] или Csc[x]
: csc[x] или Csc[x] : ArcCos[x]
: ArcCos[x] : ArcSin[x]
: ArcSin[x] : ArcTan[x]
: ArcTan[x] : ArcCot[x]
: ArcCot[x] : ArcSec[x]
: ArcSec[x] : ArcCsc[x]
: ArcCsc[x] : cosh[x] или Cosh[x]
: cosh[x] или Cosh[x] : sinh[x] или Sinh[x]
: sinh[x] или Sinh[x] : tanh[x] или Tanh[x]
: tanh[x] или Tanh[x] : coth[x] или Coth[x]
: coth[x] или Coth[x] : sech[x] или Sech[x]
: sech[x] или Sech[x] : csch[x] или Csch[е]
: csch[x] или Csch[е] : ArcCosh[x]
: ArcCosh[x] : ArcSinh[x]
: ArcSinh[x] : ArcTanh[x]
: ArcTanh[x] : ArcCoth[x]
: ArcCoth[x] : ArcSech[x]
: ArcSech[x] : ArcCsch[x]
: ArcCsch[x]
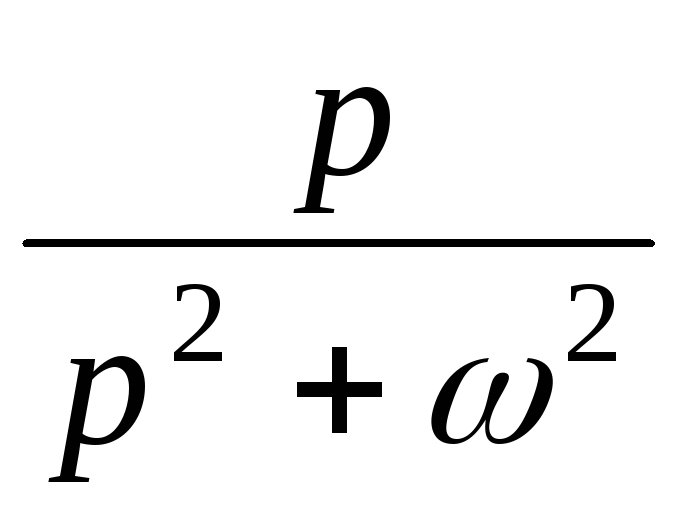


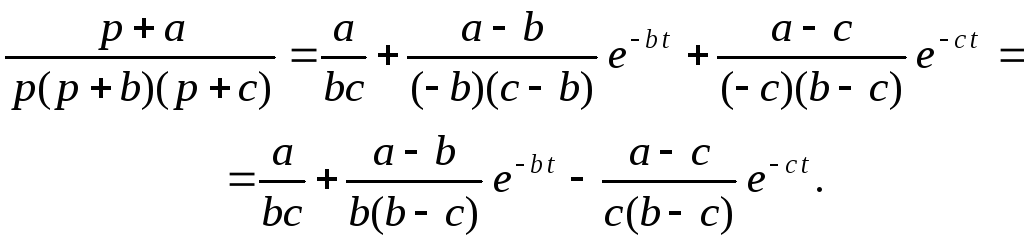
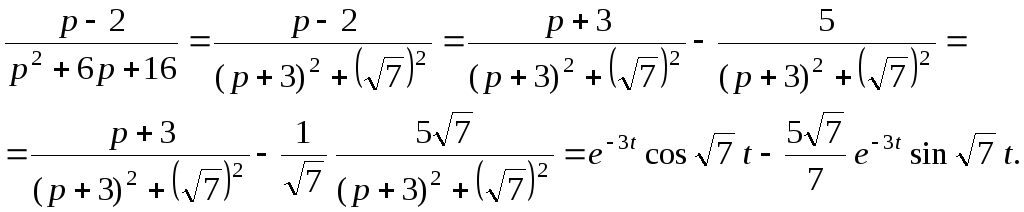
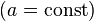
 : x^a
: x^a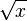 : Sqrt[x]
: Sqrt[x]![sqrt[n]{x}](https://upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) : x^(1/n)
: x^(1/n) : a^x
: a^x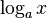 : Log[a, x]
: Log[a, x]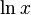 : Log[x]
: Log[x] : cos[x] или Cos[x]
: cos[x] или Cos[x]