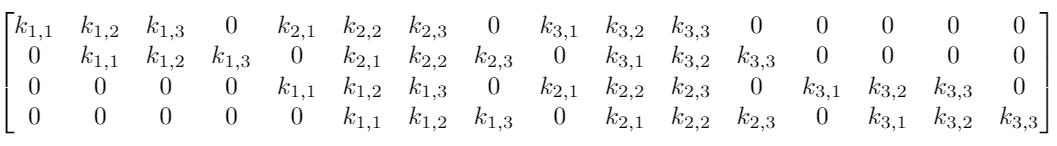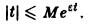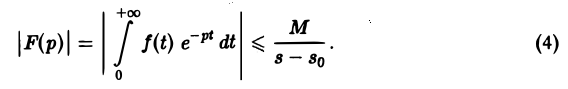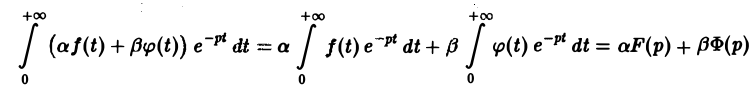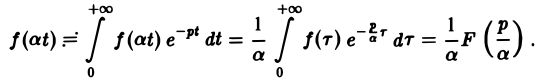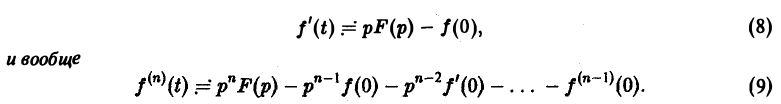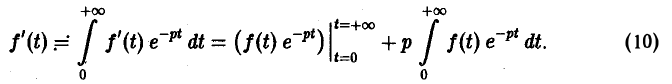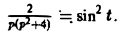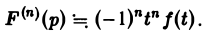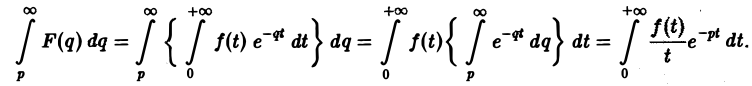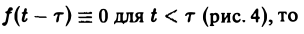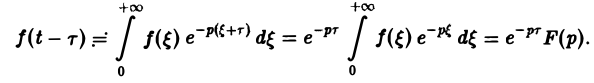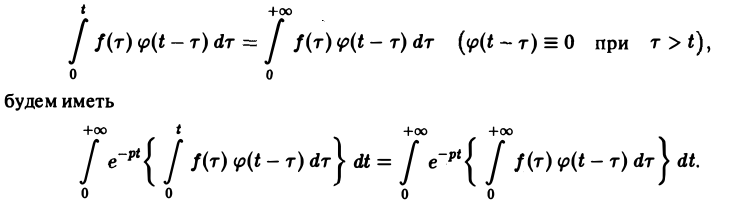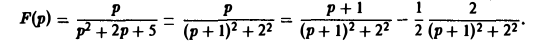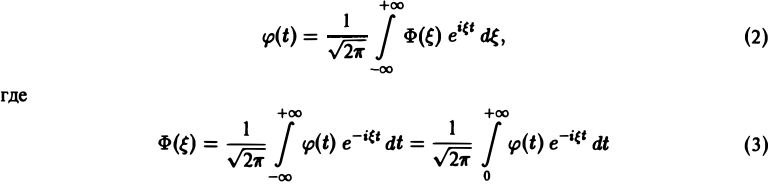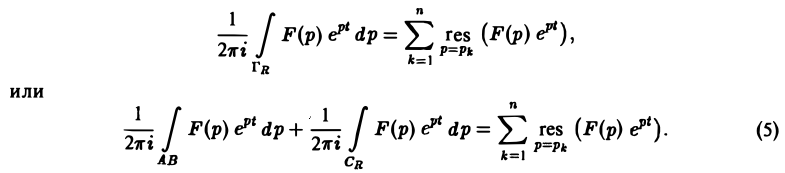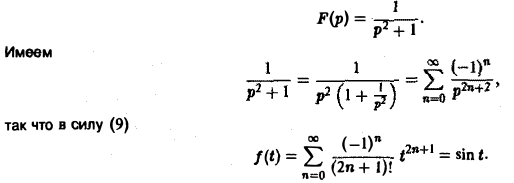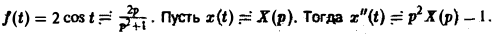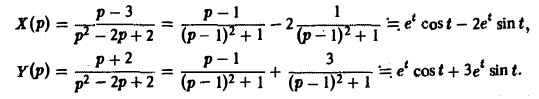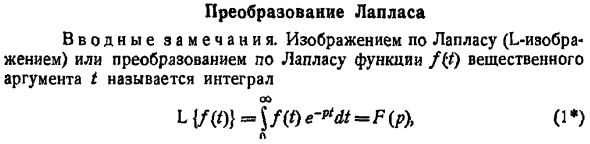При помощи анимированных изображений и визуализаций слоев CNN-сетей раскрываем широко применяемое в моделях глубокого обучения понятие свертки.
В современных фреймворках глубокого обучения сверточные слои в моделях нередко представляются в виде однострочного кода. Само же понятие свертки обычно остается для начинающих аналитиков труднодоступным, как и лежащие в его основе понятия ядра, фильтра, канала и т. д. Тем не менее, свертка представляет собой мощный и расширяемый инструмент, позволяющий разреживать взаимодействия нейронов, находить общие параметры, работая одинаковым образом со входными данными различного размера. Сравним механики операции свертки и полносвязной нейросети.
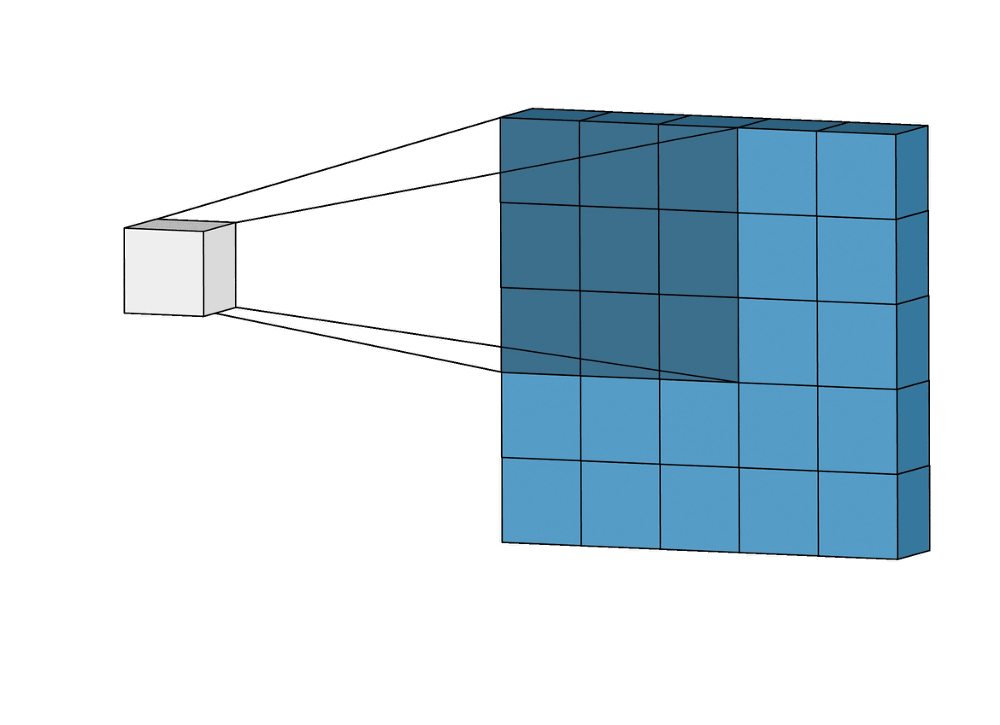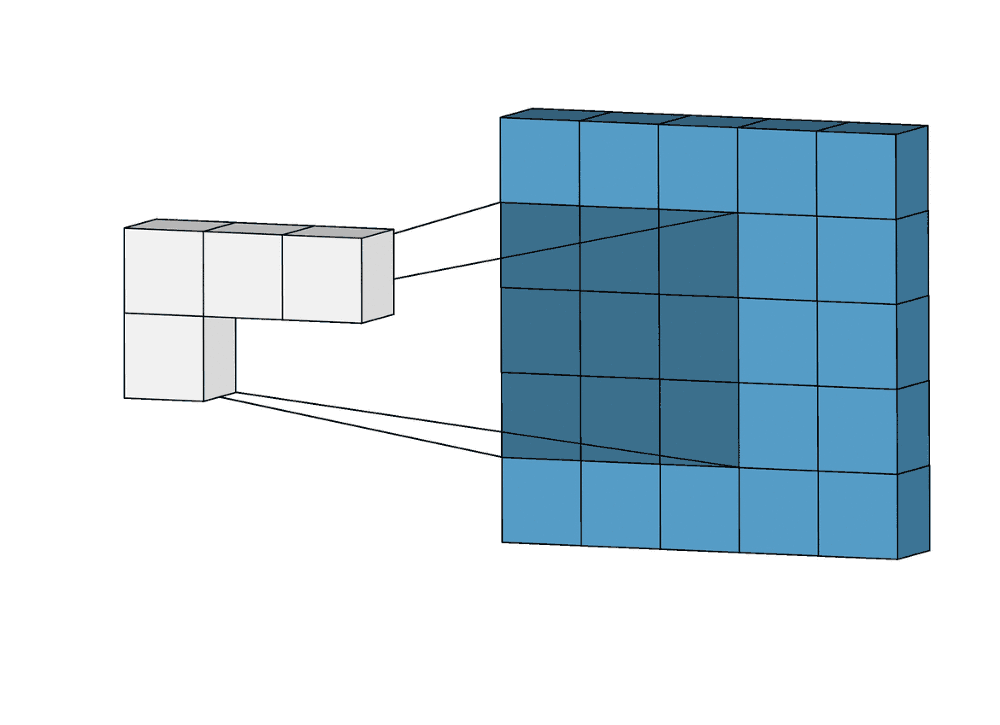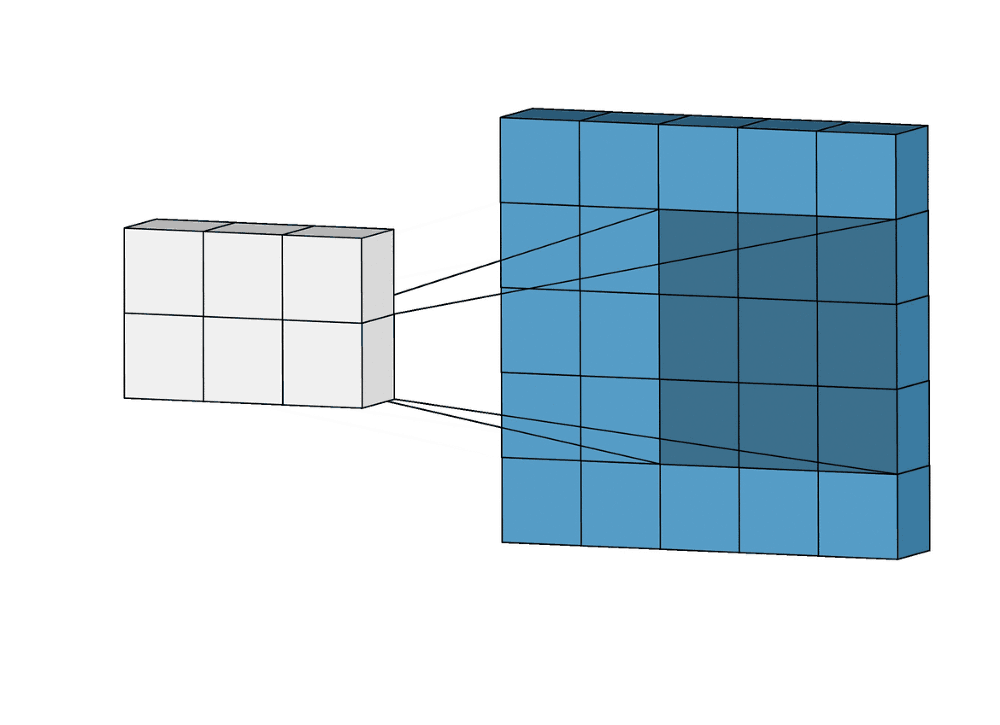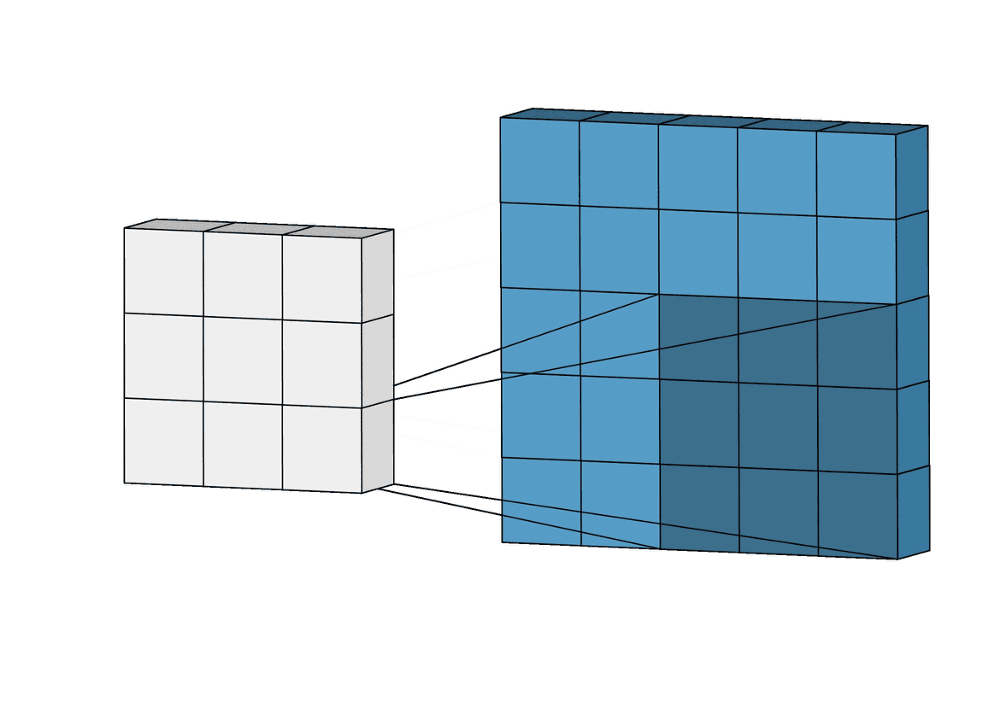
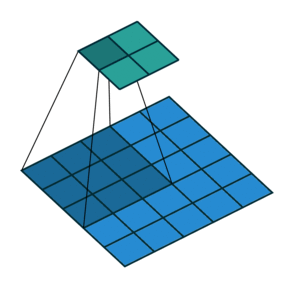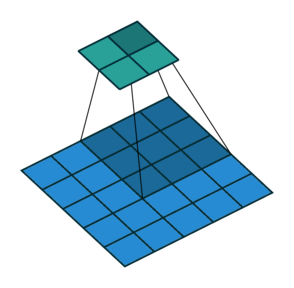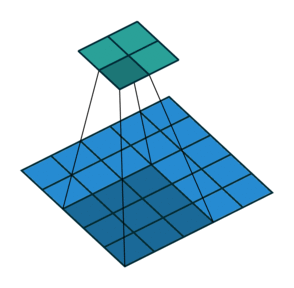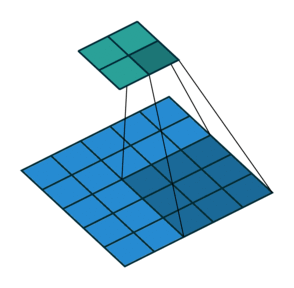
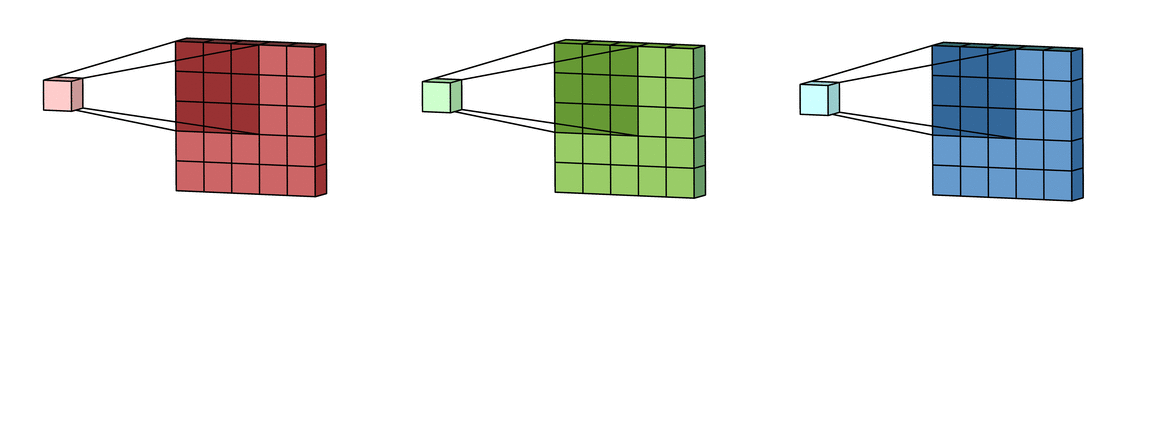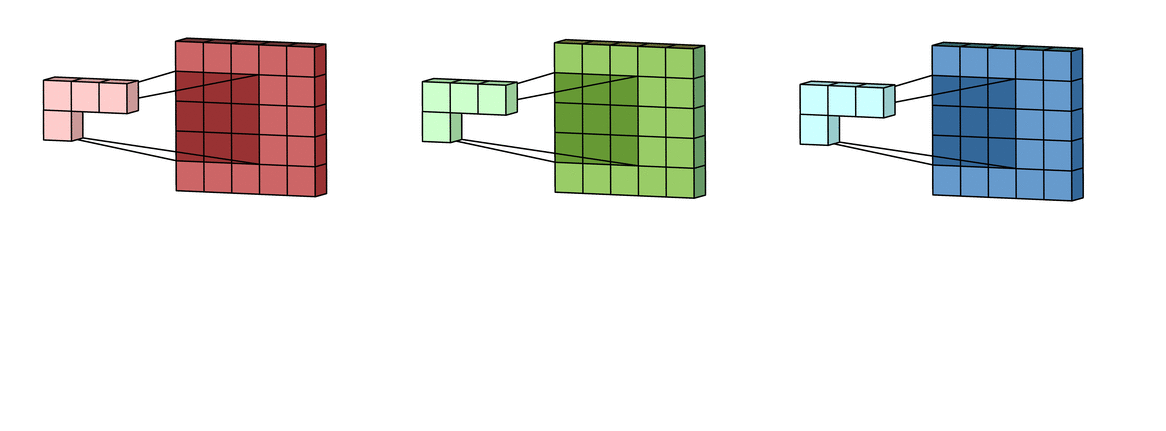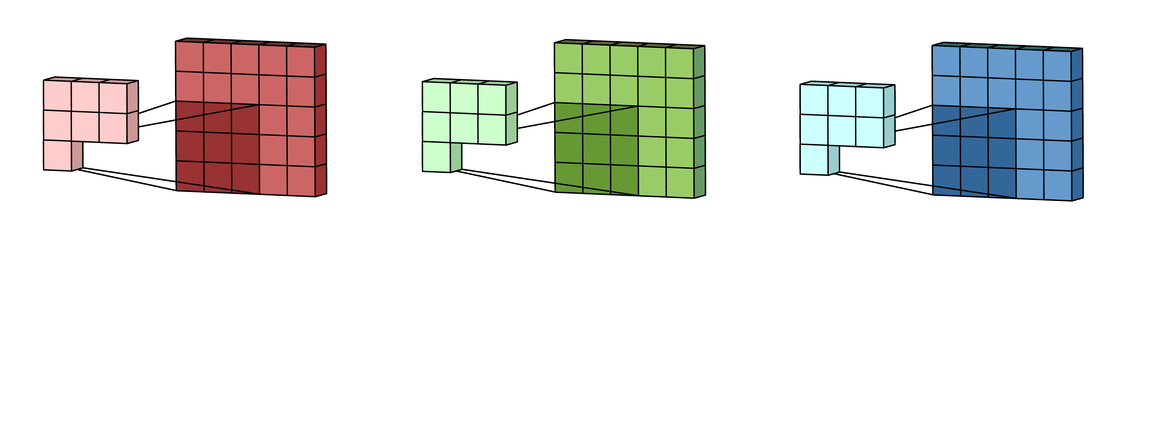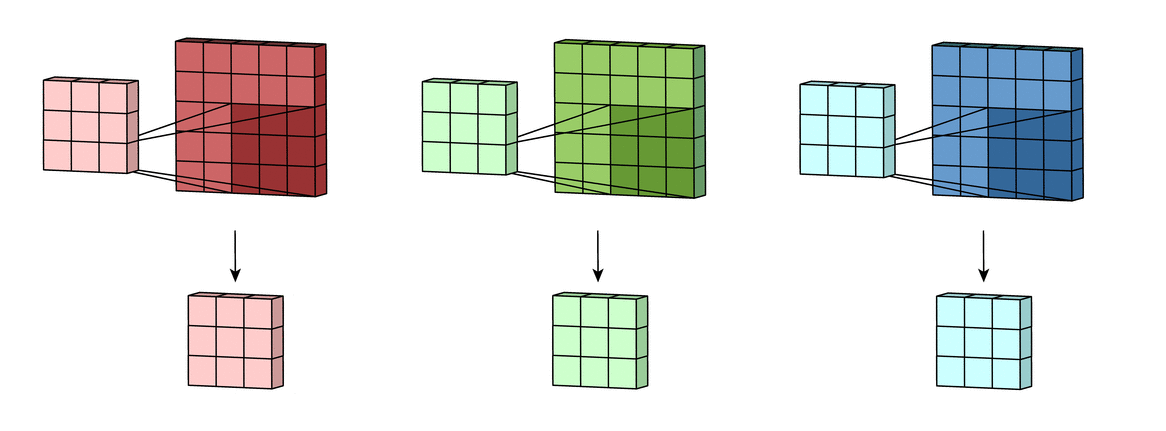
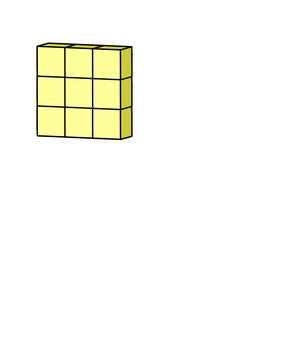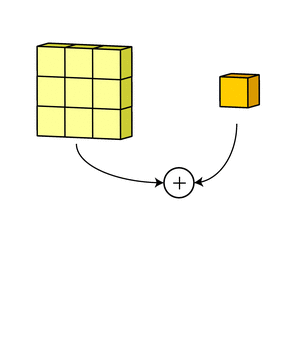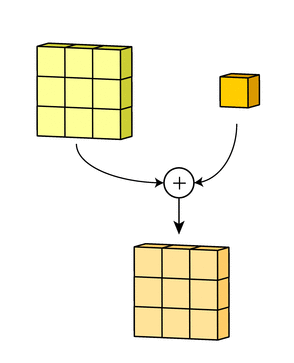
Суть операции свертки на примере черно-белых изображений
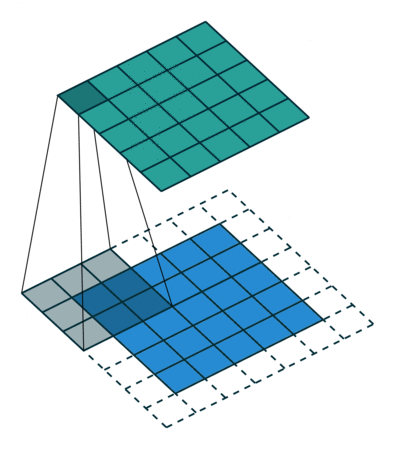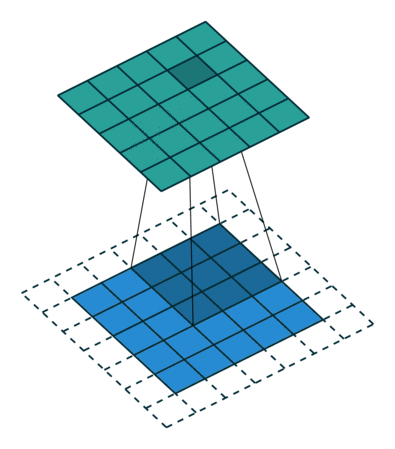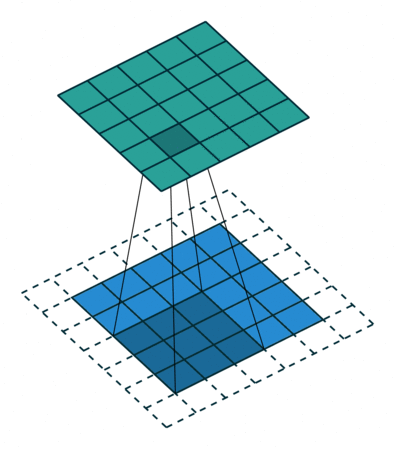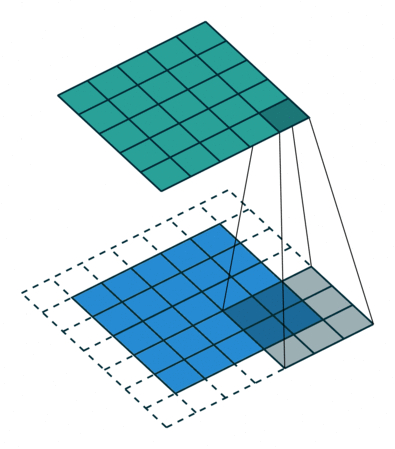
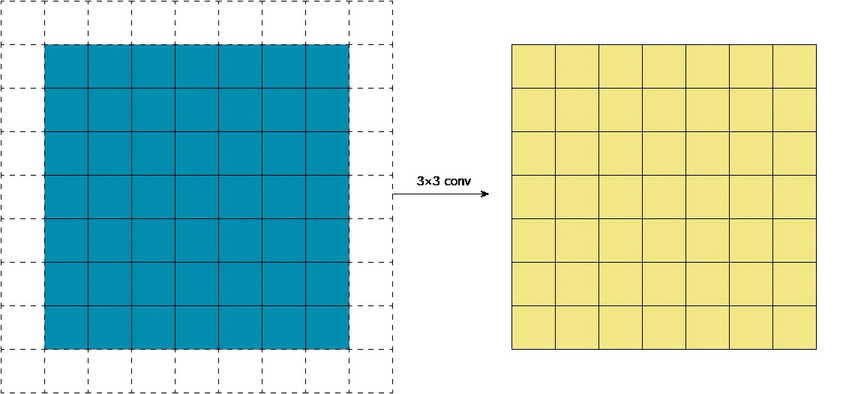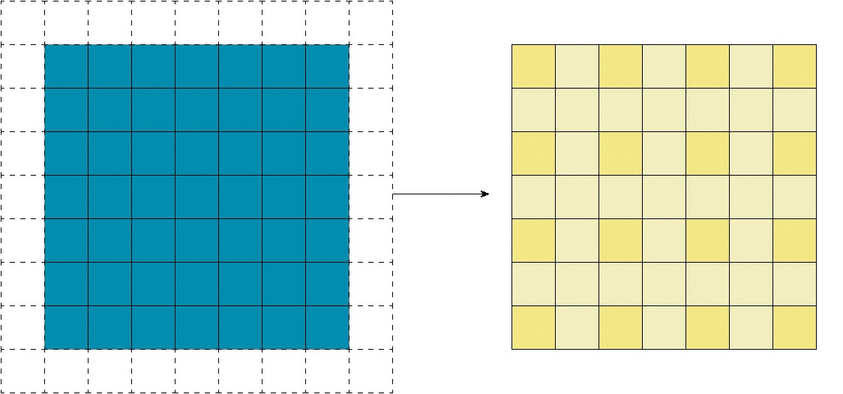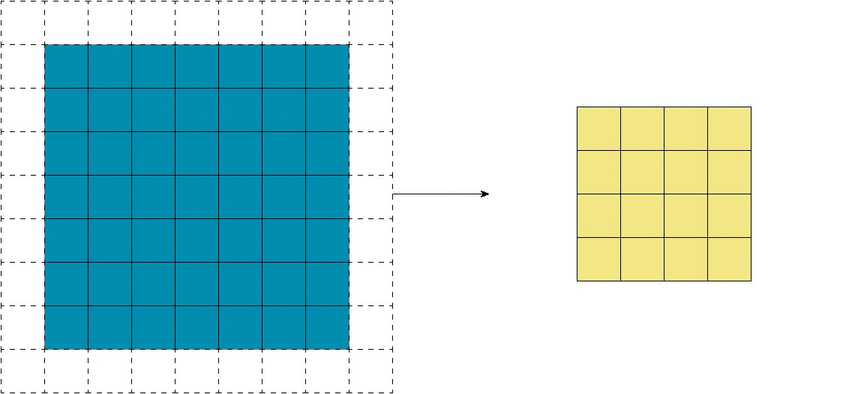
В математическом отношении в двумерной свертке нет ничего сложного. Имеется ядро – небольшая матрица весов. Это ядро «скользит» по двумерным входным данным, выполняя поэлементное умножение для той части данных, которую сейчас покрывает. Результаты перемножений ячеек суммируются в одном выходном пикселе. В случае сверточных нейросетей ядро определяется в ходе обучения сети. Начальные веса, аналогично случаю перцептрона, могут иметь рандомные значения, и корректируются в процессе обучения.
Перемножение и суммирование повторяются для каждой локации, по которой проходит ядро. Двумерная матрица входных признаков преобразуется в двумерную матрицу выходных. Выходные признаки, таким образом, являются взвешенными суммами входных признаков. Число входных признаков в комбинации для одного выходного признака определяет размер ядра.
Такой подход контрастирует с полносвязными сетями. Так, в приведенном выше примере имеется 5×5=25 входных признаков и 3×3=9 выходных. Если бы это были два полносвязных слоя, весовая матрица состояла бы из 25×9=225 весовых параметров. При этом каждая функция вывода была бы взвешенной суммой всех входов. В случае свертки, взвешенная сумма берется только по числу весов ядра. И в рассмотрении одновременно участвуют только близлежащие элементы.
Свертка соответствует модели иерархий абстрактных представлений: совокупность пикселей обобщается до ребер, те – до паттернов, и, наконец, до самого объекта. Малозначимые детали отфильтровываются в процессе перехода к более абстрактным образам.
Некоторые распространенные методы
Обратим внимание на два характерных метода, связанных с операцией свертки: дополнение отступа (padding) и выбор шага (strides).
Нулевой отступ
В вышеприведенном примере скольжение ядра «обрезает» исходный двумерный массив по краю, преобразуя матрицу 5×5 в 3×3. Краевые пиксели теряются из-за того, что ядро не может распространяться за пределы края. Однако иногда необходимо, чтобы размер выходного массива был тем же, что и у входных данных.
Чтобы решить эту задачу, исходный массив можно дополнить «поддельными» пикселями. Например, в виде краевого поля, окружающего массив. Если в качестве значений берутся нули, говорят о «нулевом отступе» (zero padding).
Шаги
Еще чаще стоит задача субдискретизации – уменьшения размерности выходного сигнала в сравнении с исходным. Это обычное явление в сверточных нейросетях, где размер пространственных измерений уменьшается при увеличении количества каналов. Одним из способов является применение объединяющего (pooling) слоя. За счет отбора средних/максимальных значений из каждых соседствующих счетверенных ячеек 2×2 можно уменьшить размерность исходной сетки вдвое. Другой подход – использовать шаг свертки.
Идея шага состоит в том, чтобы при скольжении ядра пропускать часть позиций массива. Значения шага 1 означает выбор каждого пикселя сетки. Шаг 2 означает отбор пикселей на расстоянии в два пикселя с пропуском одного промежуточного, и так далее.
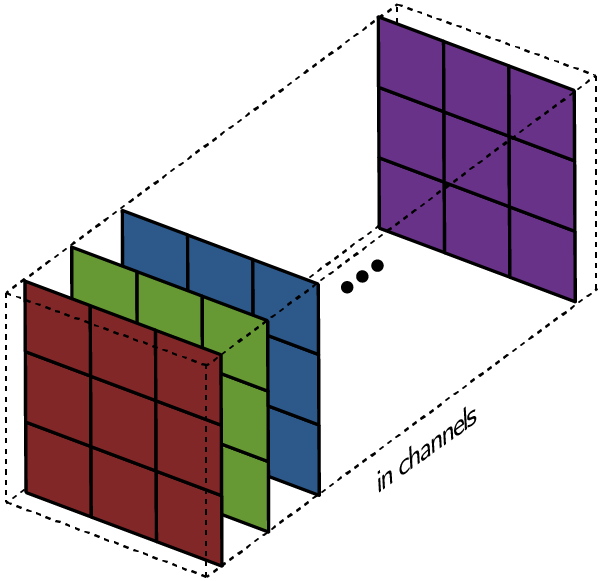
Многоканальная версия – цветные изображения
Вышеприведенные диаграммы соответствуют лишь изображениям с одним входным каналом. На практике большинство изображений имеют три канала: красный, зеленый и синий.
В случае с одним каналом термины фильтр и ядро взаимозаменяемы. Для цветного изображения они различны. Фильтр – это коллекция ядер, каждое из которых соответствует одному каналу. Ядро фильтра скользит по данным канала, создавая их обработанную версию. Значимость ядер определяется взаимным отношением их весов. Например, ядро для красного канала может быть более значимым в модели, чем другие ядра фильтра, тогда будут больше и соответствующие веса.
Каждая из обработанных в своих каналах версий суммируется для формирования общего канала.
В выходном терминале может присутствовать линейное смещение, независимое от функций каждого из ядер и свойственное лишь выходному каналу.
Математическая подоплека свертки – особенности линейного преобразования
Предположим, что у нас есть вход 4×4. Мы хотим преобразовать его в сетку 2×2. Если мы используем сеть прямого распространения, потребуется входной вектор из 16 нейронов, полностью связанных с 4 выходными нейронами. Такую ситуацию можно визуализировать весовой матрицей w.
Хотя операция ядерной свертки может показаться вначале немного странной, она является линейным преобразованием. Если бы мы использовали ядро K размера 3 для тех же размеров входа и выхода, эквивалентная матрица линейного преобразования выглядела бы следующим образом:
Для матрицы с 16×4=64 элементами имеется всего 9 нетривиальных параметров, подлежащих оптимизации вместо 64 весовых параметров для полносвязной двухслойной нейронной сети. Обнуление значительной части параметров обусловлено локальностью применяемой операции. Помимо ускорения расчетов, свертка приводит и к лучшей инвариантности относительно размеров входных данных.
Впрочем это не объясняет, почему такой подход может быть не менее эффективным, чем полносвязная сеть. Ядро, формирующее выходной сигнал, представляет взвешенную комбинацию небольшой области близкорасположенных пикселей. Но в то же время операция взаимодействия с ядром применяется одинаково ко всему изображению.
Локальность свертки
Если бы это был какой-то другой тип данных, а не изображения (например, набор категориальных данных), обобщение, осуществляемое сверткой, могло бы привести к катастрофе. В выходных признаках появлялась бы отсутствовавшая исходно корреляция.
В то же время любое изображение с точки зрения математики представляет собой совокупность правил взаимного расположения элементов. Использование фильтров для поиска элементов изображений – это одна из старых идей компьютерного зрения. Например, для обнаружения контуров можно использовать фильтр Собеля. В отличие от обучаемых ядер сверточных нейронных сетей, ядро этого фильтра имеет фиксированные веса:
Для фонового неба, не содержащего краевых элементов большинство пикселей на изображении имеют одинаковые значения. Суммарные значения выхода ядра в этих местах равны нулю. Для части изображения с вертикальными границами в местах границ существует разница между пикселями слева и справа от края. Ядро, вычисляя эту ненулевую разницу, определяет положение контуров. Повторимся, ядро работает каждый раз только с локальными областями 3×3, обнаруживая аномалии в локальном масштабе.
Применяя один и тот же подход ко всему изображению, можно получить результат для всего массива. Аналогично свертка с транспонированным ядром позволяет выделить горизонтальные края.
Визуализация признаков при помощи оптимизации
Целая отрасль исследований в сфере глубокого обучения посвящена тому, чтобы сделать модели нейронных сетей интерпретируемыми. Одним из мощных инструментов для подобного рода задач является предложенная в работе 2017 года визуализация признаков при помощи оптимизации. Идея в корне простая: оптимизировать изображение, инициализированное шумом, так, чтобы активировать фильтр как можно сильнее.
На трех изображениях ниже представлены визуализации трех различных каналов для первого сверточного слоя GoogleNet. Хотя слои детектируют различные типы контуров, все они являются низкоуровневыми детекторами.
На двух следующих изображениях представлены примеры визуализации фильтров сверточных слоев второго и третьего уровней.
Одна из важных вещей: изображения после операции свертки – это все еще изображения. Операция действует эквивариантно: если изменяется вход, то выход изменяется так же.
Элементы, находившиеся в левом верхнем углу, после свертки имеют соответствующие отображения также в левом верхнем углу. Как бы глубоко ни заходили детекторы признаков, они все равно будут работать на очень маленьких ядерных участках. Неважно, насколько глубоко происходит свертка, но вы не можете обнаружить лица из сеток размером 3х3. Здесь возникает идея локальной зоны восприимчивости (receptive field).
Зона восприимчивости свертки
Существенной составляющей архитектуры сверточной нейронной сети является уменьшение объема данных от входа к выходу модели с одновременным увеличением глубины канала. Как упоминалось ранее, обычно это делается при помощи выбора шага свертки или pooling-слоев. Зона восприимчивости определяет, какая площадь оригинальных входных данных из исходной сетки обрабатывается на выходе. На изображениях ниже представлен пример шагающей свертки с выкидыванием промежуточных пикселей.
Ниже представлены примеры визуализации признаков набора блоков свертки, показывающие постепенное увеличение сложности. Расширение поля восприимчивости позволяет сверточным слоям комбинировать низкоуровневые признаки (линии, края) в более высокоуровневые (кривые, текстуры).
Сеть развивается от небольшого количества низкоуровневых фильтров на начальных этапах (64 в случае GoogleNet) до очень большого количества фильтров (1024 в финальной свертке), каждый из которых находит специфичный высокоуровневый признак. Переход от уровня к уровню обеспечивает иерархию распознавания образов.
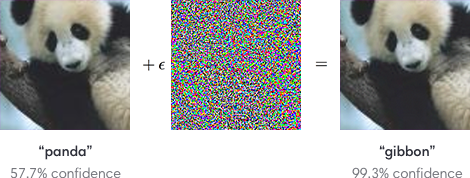
Обобщающие процессы свертки имеет свою оборотную сторону – возможность подделки изображений под удовлетворение особенностей распознающих фильтров. На изображениях ниже человек в обоих случаях узнает фотографии панды. А сверточные нейросети можно запутать, добавив шум, подстроенный под фильтры распознавания других образов.
Однако именно сверточные нейронные сети позволили компьютерному зрению пройти путь от простых приложений до сложных продуктов и услуг, таких как распознавание лиц и улучшение качества медицинских диагнозов.
Источник
Другие материалы по теме
- Учебный план освоения глубокого обучения и нейросетей за 6 недель
- Нейронные сети: наиболее полные и понятные видеолекции
- Мнения топовых людей из индустрии Data Science о развитии отрасли
20.2.9.1. Свёртка функций и её свойства.
Определение.
Сверткой
функций f1(t)
и f2(t)
называется функция 
.
Свёртка обозначается
символом 
:
.
Если f1(t)
и f2(t)
— функции-оригиналы, то их свёртка — тоже
функция-оригинал, показатель роста
которой превышает наибольший из
показателей роста функций f1(t)
и f2(t)
не больше, чем на 1. Действительно, пусть
,
,
,
тогда 
,
так как t
< e
t.
Свёртка функций
коммутативна: 
,
в этом легко убедиться, заменив в
интеграле 
переменную 
на 
.
Можно показать,
что свёртка обладает свойством
ассоциативности, т.е. что 
.
20.2.9.2.
Теорема Бореля (теорема об умножении
изображений). Изображение
свёртки двух оригиналов равно произведению
изображений свёртываемых оригиналов.
Док-во.
(меняем порядок интегрирования)= 
.
С помощью этой
теоремы легко находить оригиналы для
изображений вида 
.
Примеры.
Найти оригиналы, если
1. 
.
Здесь 
,
,
поэтому 
.
2. 
.
Здесь 
,
,
поэтому 
.
3. 
.
Здесь 
,
поэтому 
.
20.2.9.3. Интегралы
Дюамеля.
Запишем с помощью теоремы Бореля
оригиналы для выражения вида pF(p)G(p),
где F(p)
и G(p)
— изображения функций f(t)
и g(t).
С одной стороны,
(так как, по теореме20.2.8,
);
с другой стороны,
.
В развёрнутом виде
,
.
Каждая из этих
формул называется интегралом Дюамеля.
20.3. Таблица стандартных изображений.
Сведём в таблицу полученные ранее
изображения элементарных функций.
|
|
|
|
|
|||
|
1. |
1 |
|
9. |
|
|
|
|
2. |
|
|
10. |
|
|
|
|
3. |
|
|
11. |
|
|
|
|
4. |
|
|
12. |
|
|
|
|
5. |
|
|
13. |
|
|
|
|
6. |
|
|
14. |
|
|
|
|
7. |
|
|
15. |
|
|
|
|
8. |
|
|
16. |
|
|
20.4. Обращение преобразования Лапласа.
20.4.1.
Формула Римана-Меллина.
Если функция F(p)
— изображение функции-оригинала f(t),
то f(t)
может быть найдена по формуле
.
Это равенство
имеет место в каждой точке, в которой
f(t)
непрерывна. В точках разрыва функции
f(t)
значение правой части равно 
.
Интеграл в правой части формулы называют
интегралом Меллина; интегрирование
может вестись по любой вертикальной
прямой 
,
и интеграл понимается в смысле главного
значения:
.
Вычисление
оригинала по формуле Римана-Меллина
довольно трудоёмко, поэтому на практике
при решении задач применяют другие
методы, которые рассматриваются ниже.
20.4.2.
Элементарный метод нахождения оригинала.
Этот метод
основан на непосредственном применении
таблицы стандартных изображений 20.3 и
свойств преобразования Лапласа.
Примеры.
1. 
.
Представляя изображение в виде 
и сравнивая эти выражения с формулами
9, 10 таблицы, находим оригинал 
.
2. 
.
Наличие степеней переменной р
в знаменателе позволяет применить
теорему 20.2.5 об интегрировании оригинала:
,
,
.
Можно решить этот
пример с помощью свёртки: 
,
.
Однако проще всего представить 
в виде суммы простых дробей 
.
20.4.3. Первая
теорема разложения. Если
точка 
является нулём функции F(p),
F(p)
аналитична в окрестности этой точки и
разложение функции по степеням р
в окрестности точки 
имеет вид 
,
то функция F(p)
есть изображение функции 
.
Это выражение
получается в результате почленного
перехода к оригиналам в ряде 
:
так как 
,
то 
,
и 
.
Примеры. 1 . 
. Условия теоремы выполнены. Лорановское
разложение функции F(p)
в окрестности точки 
:
.
2. 
.
Здесь 
.
20.4.4.
Вторая теорема разложения. Пусть
функция F(p)
комплексной переменной р
аналитична во всей плоскости, за
исключением конечного числа изолированных
особых точек 
,
,
,
…, 
,
расположенных в полуплоскости
.Если
,
и F(p)
абсолютно интегрируема вдоль любой
вертикальной прямой
,
то F(p)
является изображением, и 
.
Док-во.
Сведём интеграл в формуле Римана-Меллина
к интегралу по замкнутому контуру.
Контур 
составим из отрезка ABпрямой
,
и дуги CR
окружности | p
| = R,
расположенной слева от отрезка и
содержащей внутри себя все особые точки
функции 
.
По основной теореме о вычетах 
.
,
поэтому 
.
Устремим 
.
По лемме Жордана 
;
а для второго интеграла получаем 
,
поэтому в пределе 
.
Применим эту
теорему для обращения изображения 
.
Функция 
имеет три особых точки: p
= 0 (полюс второго порядка) и 
(простые полюсы), поэтому 
.
Находим вычеты: 
;
;
;
.
Если F(p)
— несократимая дробно-рациональная
функция: 
и 
— многочлены соответствующих степеней,
и точка 
— полюс порядка 
,
т.е. точка 
— нуль порядка 
знаменателя 
,
то 
.
Производную произведения представим
по формуле Лейбница: 
,
,
поэтому
.
Если все особые
точки дробно-рациональной функции F(p)
— простые полюса, т.е простые нули
знаменателя 
,
то эта формула
существенно упрощается: 
,
и 
.
Пример: 
.
Здесь знаменатель 
имеет только простые нули, 
,
поэтому 
.
Соседние файлы в папке oper_1
- #
- #
- #
Ранее мы рассмотрели интегральное преобразование Фурье
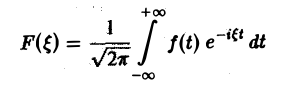
с ядром K(t, ξ) =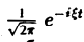 
.
Преобразование Фурье неудобно тем, что должно быть выполнено условие абсолютной интегрируемости функции f(t) на всей оси t,
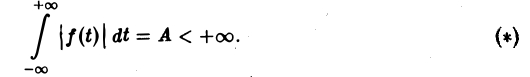
Преобразование Лапласа позволяет освободиться от этого ограничения.
Определение:
Функцией-оригиналом будем называть всякую комплекснозначную функцию f(t) действительного аргумента t, удовлетворяющую следующим условиям:
- f(t) непрерывна на всей оси t, кроме отдельных точек, в которых f(t) имеет разрыв 1-го рода, причем на каждом конечном интервале оси t таких точек может быть лишь конечное число;
- функция f(t) равна нулю при отрицательных значениях t, f(t) = 0 при t < 0;
- при возрастании t модуль f(t) возрастает не быстрее показательной функции, т. е. существуют числа М > 0 и з такие, что для всех t
Ясно, что если неравенство (1) выполняется при некотором s = s1, то оно будет выполнятся при всяком s2 > s1.
Точная нижняя грань sо всех чисел s, so = infs, для которых выполняется неравенство (1), называется показателем роста функции f(t).
Замечание:
В общем случае неравенство
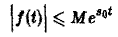
не имеет места, но справедлива оценка
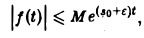
где ε > 0 — любое. Так, функция f(t) = t, t ≥ 0, имеет показатель роста so =0. Для нее неравенство |t| ≤ М ∀t ≥ 0 не выполняется, но ∀ε > О, ∀t > 0 верно неравенство 
Условие (1) гораздо менее ограничительное, чем условие (*).
Пример:
Функция
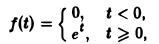
не удовлетворяет условию (*), но условие (1) выполнено при любом s ≥ 1 и М ≥ 1; показатель роста so = 1. Так что f(t) является функцией-оригиналом. С другой стороны, функция
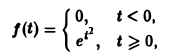
не является функцией-оригиналом: она имеет бесконечный порядок роста, sо = +∞. Простейшей функцией-оригиналом является
так называемая единичная функция
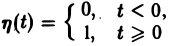
Если некоторая функция φ(t) удовлетворяет условиям 1 и 3 определения 1, но не удовлетворяет условию 2, то произведение f(t) = φ(t) η(t) уже является функцией-оригиналом.
Для простоты записи мы будем, как правило, множитель η(t) опускать, условившись, что все функции, которые мы будем рассматривать, равны нулю для отрицательных t, так что если речь идет о какой-то функции f(t) например, о sin t, cos t, et и т. д., то всегда подразумеваются следующие функции (рис. 2):
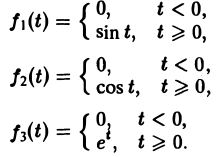
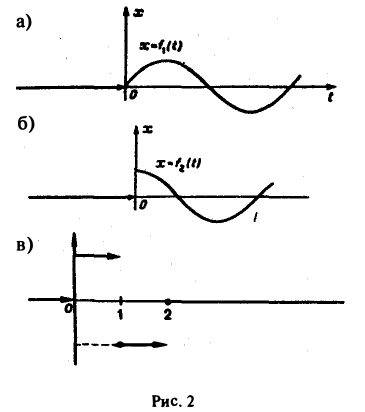
Определение:
Пусть f(t) есть функция-оригинал. Изображением функции f(t) по Лапласу называется функция F(p) комплексного переменного р = s + iσ, определяемая формулой
где интеграл берется по положительной полуоси t. Функцию F(p) называют также преобразованием Лапласа функции f(t); ядро преобразования K(t, р) = e-pt.
Тот факт, что функция f(x) имеет своим изображением F(p), будем записывать так:
Пример:
Найти изображение единичной функции η(t).
Функция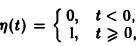 
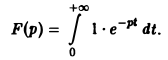
является функцией-оригиналом с показателем роста s0 = 0. В силу формулы (2) изображением функции η(t) будет функция
Если р = s + iσ, то при s > 0 интеграл в правой части последнего равенства будет сходящимся, и мы получим
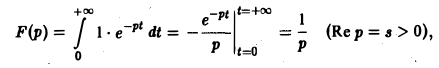
так что изображением функции η(t) будет функция 1/p. Как мы условились, будем писать, что η(t) = 1, и тогда полученный результат запишется так:
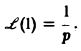
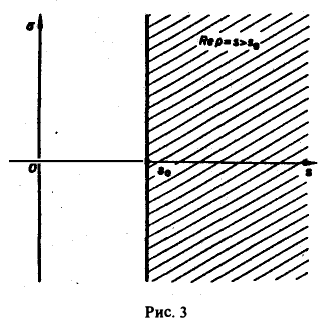
Теорема:
Для всякой функции-оригинала f(t) с показателем роста sо изображение F(p) определено в полуплоскости Re p = s > So и является в этой полуплоскости аналитической функцией (рис. 3).
Пусть
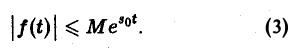
Для доказательства существования изображения F(p) в указанной полуплоскости достаточно установить, что несобственный интеграл (2) абсолютно сходится при s > so. Используя (3), получаем
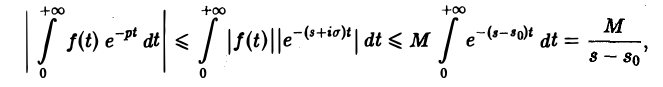
что и доказывает абсолютную сходимость интеграла (2). Одновременно мы получили оценку преобразования Лапласа F(p) в полуплоскости сходимости Re р = s > so
Дифференцируя выражение (2) формально под знаком интеграла по р, находим
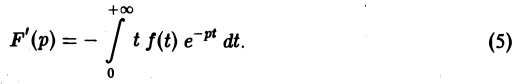
Существование интеграла (5) устанавливается так же, как было установлено существование интеграла (2).
Применяя для F'(p) интегрирование по частям, получаем оценку
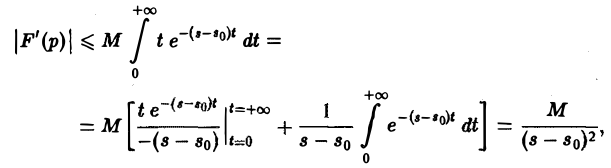
откуда следует абсолютная сходимость интеграла (5). (Внеинтегральное слагаемое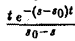 
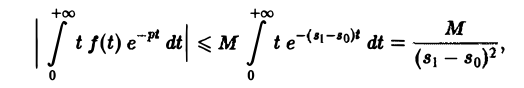
— при t → + ∞ имеет предел, равный нулю). В любой полуплоскости Re р ≥ S1 > So интеграл (5) сходится равномерно относительно р, поскольку он мажорируется сходящимся интегралом
не зависящим от р. Следовательно, дифференцированиепо р законно и равенство (5) справедливо.
Поскольку производная F'(p) существует, преобразование Лапласа F(p) всюду в полуплоскости Re p = s > sо является аналитической функцией.
Из неравенства (4) вытекает
Следствие:
Если точка р стремится к бесконечности так, что Re р = s неограниченно возрастает, то
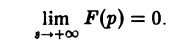
Пример:
Найдем еще изображение функции f(t) =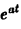
, где а = а + iβ — любое комплексное число.
Показатель роста sо функции f(t) равен а.
Считая Rep = s> а, получим
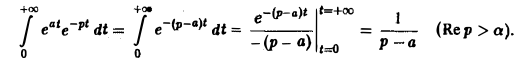
Таким образом,
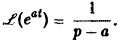
При а = 0 вновь получаем формулу
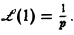
Обратим внимание на то, что изображение функции 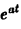является аналитической функцией аргумента р не только в полуплоскости Re p > а, но и во всех точках р, кроме точки р = а, где это изображение имеет простой полюс. В дальнейшем мы не раз встретимся с подобной ситуацией, когда изображение F(p) будет аналитической функцией во всей плоскости комплексного переменного р, за исключением изолированных особых точек. Противоречия с теоремой 1 нет. Последняя утверждает лишь, что в полуплоскости Re p > So функция F(p) не имеет особых точек: все они оказываются лежащими или левее прямой Re p = So, или на самой этой прямой.
Замечание:
В операционном исчислении иногда пользуются изображением функции f(t) по Хевисайду, определяемым равенством
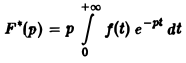
и отличаюикмся от шоСражения по Лапласу множителем р.
Свойства преобразования Лапласа
В дальнейшем через f(t), φ(t), … будем обозначать функции-оригиналы, а через F(p), Ф(р), … — их изображения по Лапласу,
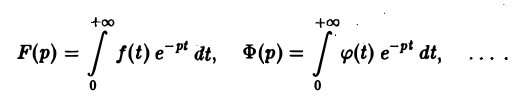
Из определения изображения следует, что если f(t) = 9 ∀t, то F(p) = 0.
Теорема единственности:
Если две непрерывные функции f(t) и φ{t) имеют одно и тоже изображение F(p), то они тождественно равны.
Теорема:
Линейность преобразования Лапласа. Если f{t) и φ{t) — функции-оригиналы, то для любых комплексных постоянных а и β
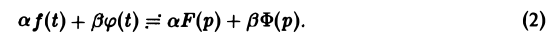
Справедливость утверждения вытекает из свойства линейности интеграла, определяющего изображение:
— показатели роста функций f(t) и φ(t) соответственно).
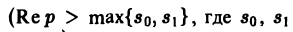
На основании этого свойства получаем
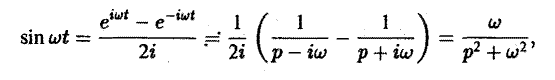
т. е. (3)
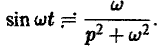
Аналогично находим, что
(4)
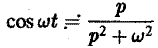
и, далее,
(5) (6)
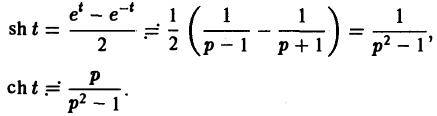
Теорема подобия:
Если f(t) — функция-оригинал и F(p) — ее изображение по Лапласу, то для любого постоянного а > 0
Полагая at = т, имеем
Пользуясь этой теоремой, из формул (5) и (6) получаем
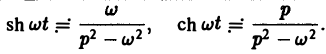
Теорема:
О дифференцировании оригинала. Пусть f(t) является функцией-оригиналом с изображением F(p) и пусть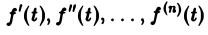 
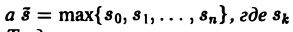
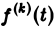
— также функции-оригиналы, 
— показатель роста функции 
(k = 0, 1,…, п). Тогда
Здесь под fk(0) (k = 0,1,… , п — 1) понимается правое предельное значение .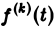
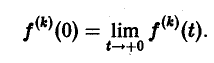
Пусть f(t) = F(p). Найдем изображение f'(t). Имеем
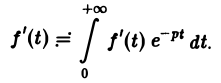
Интегрируя по частям, получаем
Внеинтегральное слагаемое в правой части (10) обращается в нуль при t → + ∞, т. к. при Re р = s >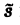 
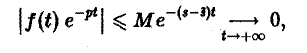
имеем
подстановка t = 0 дает -f(0).
Второе слагаемое справа в (10) равно pF(p). Таким образом, соотношение (10) принимаетвид
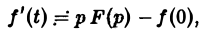
и формула (8) доказана. В частности, если f(0) = 0, то f'(t) = pF(p). Для отыскания изображения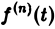 
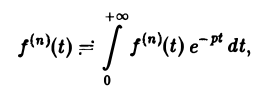
запишем
откуда, интегрируя п раз по частям, получим
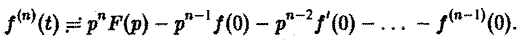
Пример:
Пользуясь теоремой о дифференцировании оригинала, найти изображение функции f(t) = sin2t.
Пусть f(t) = F(p). Тогда
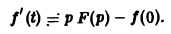
Но f(0) = О, а f'(0) = 2 sin t cos t = sin 2t =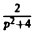 
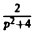
. Следовательно, = pF(p), откуда F(p) =
Теорема 5 устанавливает замечательное свойство интегрального преобразования Лапласа: оно (как и преобразование Фурье) переводит операцию дифференцирования в алгебраическую операцию умножения на р.
Формула включения. Если f(t) и f'(t) являются функциями-оригиналами, то (11)
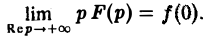
В самом деле, f'(<) = р F(p) — f(0). В силу следствия из теоремы 1, всякое изображение стремится к нулю при Rе р = s → + ∞. Значит,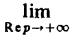 
[pF(p) — f(0)] = 0, откуда вытекает формула включения (11).
Теорема:
О дифференцировании изображения. Дифференцирование изображения сводится к умножению на (—t) оригинала,
Так как функция F(p) в полуплоскости Rep = s > so является аналитической, то ее можно дифференцировать по р. Имеем
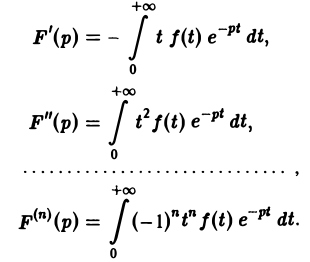
Последнее как раз и означает, что 
Пример:
Пользуясь теоремой 6, найти изображение функции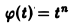 
.
Как известно, 1 = 1/p. Здесь f(t) = 1, F(p) = 1/p. Отсюда (1/p)’= (-t) • 1, или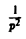 
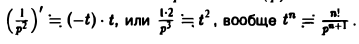
= t. Вновь применяя теорему 6, найдем
Теорема:
Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р: если f(t) = F(p), то
Положим
Нетрудно проверить, что если f(t) есть функция-оригинал, то и φ(t) будет функцией-оригиналом, причем φ(0) = 0. Пусть φ(t) = Ф(р). В силу (14)
С другой стороны, f(t) =’ F(p), откуда F(p) = рФ(р), т.е. Ф(р) =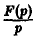
.
Последнее равносильно доказываемому соотношению (13).
Пример:
Найти изображение функции
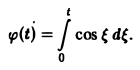
В данном случае f(t) = cos t, так что F(p) =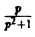 
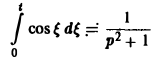
. Поэтому
Теорема:
Интегрирование изображения. Если f(t) = F(p) и интеграл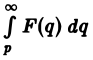 
сходится, то он служит изображением функции 
Действительно,
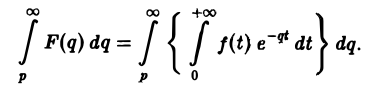
Предполагая, что путь интегрирования (р, ∞) лежит в полуплоскости Re p ≥ а> so, мы можем изменить порядок интегрирования (t > 0):
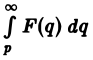
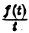
Последнее равенство означает, что является изображением функции .
Пример:
Найти изображение функции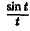 
.
Как известно, sin t =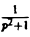 
.
Поэтому
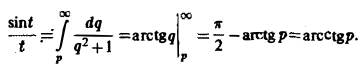
Теорема запаздывания:
Если f{t) = F(p), то для любого положительного τ («запаздывания»)
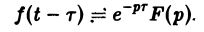
Так как
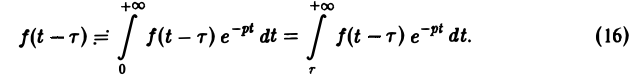
Положим ξ = t- τ. Тогда dt = d ξ. При t = τ получаем ξ = 0, при t = + ∞ имеем ξ = + ∞.
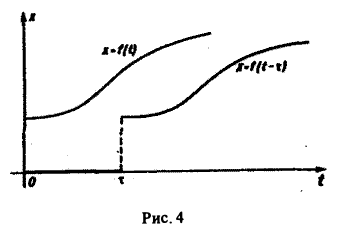
Поэтому соотношение (16) принимает вид
Пример:
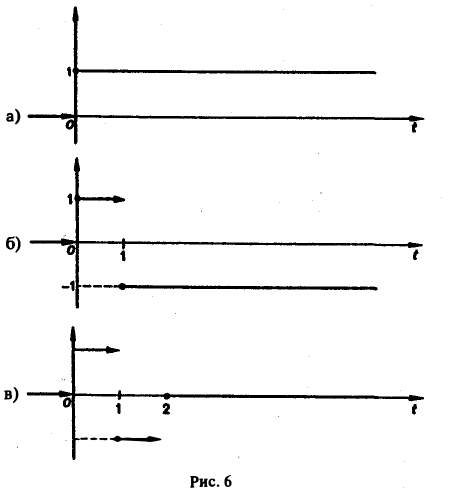
Найти изображение функции f(t), заданной графически (рис. 5).
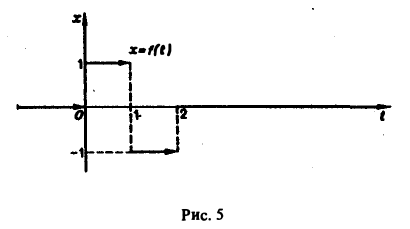
Запишем выражение для функции f(t) в следующем виде:
Это выражение можно получить так. Рассмотрим функцию f1(t) = η(t) для t ≥ 0 (рис. 6 а) и вычтем из нее функцию
Разность f(t) — h(t) будет равна единице для t ∈ [0,1) и -1 для t ≥ 1 (рис. 6 b). К полученной разности прибавим функцию
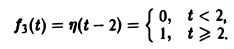
В результате получим функцию f(t) (рис. 6 в), так что
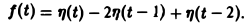
Отсюда, пользуясь теоремой запаздывания, найдем
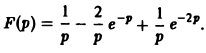
Теорема смещения:
Если f{t) = F(p) для любого комплексного числа ро
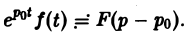
В самом деле,
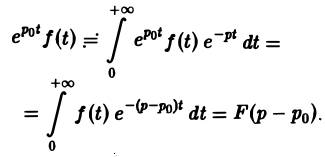
Теорема позволяет по известным изображениям функций находить изображения тех же функций, умноженных на показательную функцию 
, например,
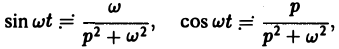
так что
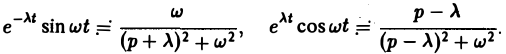
Свертка функций. Теорема умножения
Пусть функции f(t) и φ(t) определены и непрерывны для всех t. Сверткой (f *φ)(t) этих функций называется новая функция от t, определяемая равенством
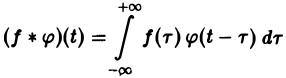
(если этот интеграл существует).
Для функций-оригиналов f(t) и φ(t) операция свертки всегда выполнима, причем
(17)
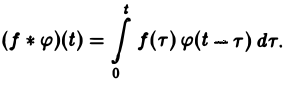
В самом деле, произведение функций-оригиналов f( τ ) φ(t — τ), как функция от τ, является финитной функцией, т.е. обращается в нуль вне некоторого конечного промежутка (в данном случае вне отрезка 0 ≤ τ ≤ t). Для финитных непрерывных функций операция свертки выполнима, и мы получаем формулу (17).
Нетрудно проверить, что операциясвертки коммутативна,
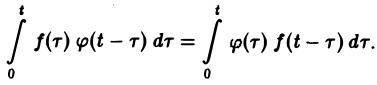
Теорема умножения:
Если f(t) = F(p), <p(t) =’Ф(р), то свертка (f * φ)(t) имеет изображение F(p) • Ф(р),
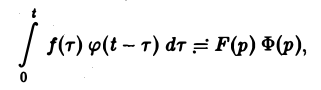
или
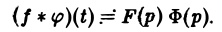
Нетрудно проверить, что свертка (f * φ)(t) функций-оригиналов есть функция-оригинал с показателем роста s* = mах{s1, s2}, где s1, s2 ~ показатели роста функций f(t) и φ(t) соответственно. Найдем изображение свертки,
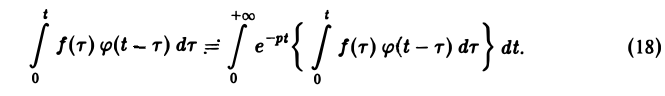
Воспользовавшись тем, что
Меняя порядок интегрирования в интеграле справа (при Re р = s > s* такая операция законна) и применяя теорему запаздывания, получим
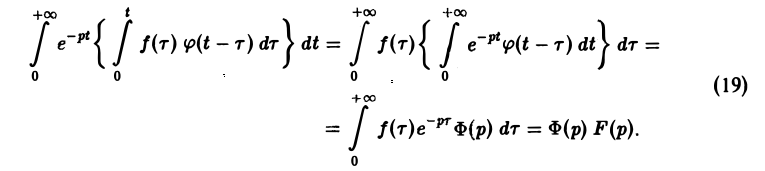
Таким образом, из (18) и (19) находим
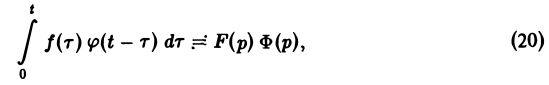
— умножению изображений отвечает свертывание оригиналов,
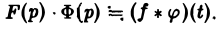
Пример:
Найти изображение функции
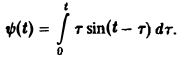
Функция ψ(t) есть свертка функций f(y) = t и φ(t) = sin t. В силу теоремы умножения
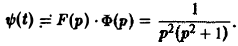
Задача:
Пусть функция f(t), периодическая с периодом Т, есть функция-оригинал. Показать, что ее изображение по Лапласу F[p) дается формулой
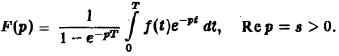
Отыскание оригинала по изображению
Задача ставится так: дана функция F(p), надо найти функцию f(t). изображением которой является F(p).
Сформулируем условия, достаточные для того, чтобы функция F(p) комплексного переменного р служила изображением.
Теорема:
Если аналитическая в полуплоскости Rep = s > so функция F(p)
1) стремится к нулю при |р| —» + ∞ в любой полуплоскости Re р = а > So равномерно относительно arg р;
2) интеграл
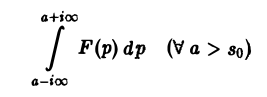
сходится абсолютно, то F(p) является изображением некоторой функции-оригинала f{t).
Задача:
Может ли функция F(p) =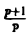 
служить изображением некоторой функции-оригинала? Укажем некоторые способы отыскания оригинала по изображению.
Отыскание оригинала с помощью таблиц изображений
Прежде всего стоит привести функцию F(p) к более простому, «табличному» виду. Например, в случае, когда F(p) — дробно-рациональная функция аргумента р,ее разлагают на элементарные дроби и пользуются подходящими свойствами преобразования Лапласа.
Пример:
Найти оригинал для
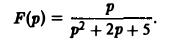
Запишем функцию F(p) в виде:
Пользуясь теоремой смещения и свойством линейности преобразования Лапласа, получаем
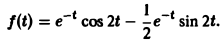
Пример:
Найти оригинал для функции
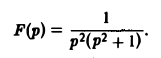
Запишем F(p) в виде
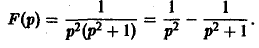
Отсюда f(t) = t — sin t.
Использование теоремы обращения и следствий из нее
Теорема обращения:
Если функция f(t) есть функция-оригинал с показателем роста so и F{p) — ее изображение, то в любой точке непрерывности функции f(t) выполняется соотношение
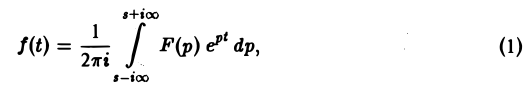
где интеграл берется вдоль любой прямой Re p = s > So и понимается в смысле главного значения, т. е. как
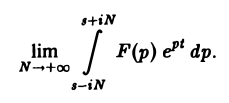
Формула (1) называется формулой обращения преобразования Лапласа, или формулой Меллина. В самом деле, пусть, например, f(t) — кусочно-гладкая на каждом конечном отрезке [0, а] функция-оригинал-с показателем роста so. Рассмотрим функцию φ(t) =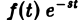 
, где s>so — любое.
Функция φ(t) удовлетворяет условиям применимости интегральной формулы Фурье, и, следовательно, справедлива формула обращения преобразования Фурье,
(φ(t) ≡ 0 при t < 0). Подставляя в (3) выражение φ(t) = f(t)
, найдем
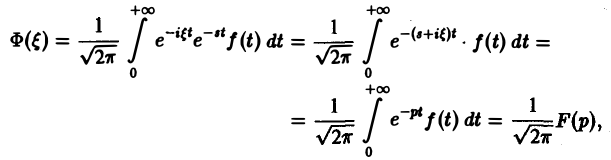
где F{p) — преобразование Лапласа функции f(t) при р = s + iξ. Формулу (2) можно переписать в виде
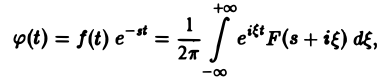
откуда получаем формулу обращения преобразования Лапласа
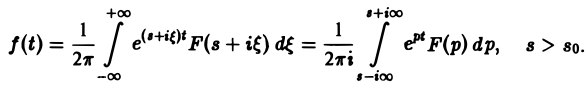
Как следствие из теоремы обращения получаем теорему единственности.
Теорема:
Две непрерывные функции f(t) и φ(t), имеющие одно и то же изображение F(p), тождественны.
Непосредственное вычисление интеграла обращения (1) обычно затруднительно. Отыскание оригинала по изображению упрощается при некоторых дополнительных ограничениях на F(p).
Теорема:
Пусть изображение F(p) — дробно-рациональная функция с полюсами р1, p2….pп. Тогда оригиналом для F(p) будет функция f(t) η(t), где
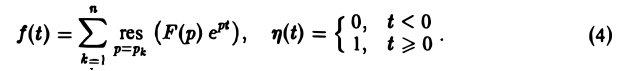
Пусть изображение F(p) — дробно-рациональная функция, F(p) =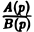 
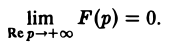
, где А(р), В(р) — многочлены относительно р (взаимно простые), причем степень числителя А(р) меньше степени знаменателя В(р), т. к. для всякого изображения должно выполняться предельное соотношение
Пусть корни знаменателя В(р), являющиеся полюсами изображения F(p), суть р1, р2, …, рп, а их кратности равны r1, r2, …, rп соответственно.
Если число s, фигурирующее в формуле (1), взять большим всех Re pk (k = 1,2,…, п), то по формуле обращения, которая в этих условиях применима, получим
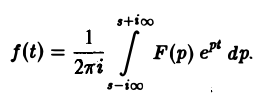
Рассмотрим замкнутый контур ГR (рис.7), состоящий из дуги CR окружности радиуса R с центром в начале координат и стягивающей ее хорды АВ (отрезка прямой Re р = s), и проходимый в положительном направлении, причем радиус R настолько велик, что все полюсы F(p) лежат внутри ГR.
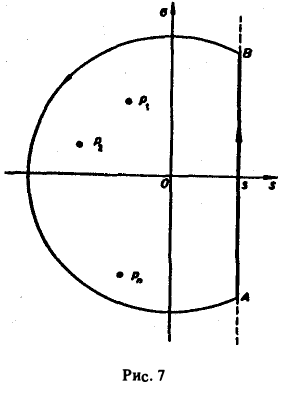
По теореме Коши о вычетах при любом R, удовлетворяющем указанному условию, будем иметь
Второе слагаемое слева в равенстве (5) стремится к нулю при R → ∞. Это следует из леммы Жордана, если в ней заменить р на iz и учесть, что F(p) → 0 при Re p → + ∞. Переходя в равенстве (5) к пределу при R → ∞, мы получим слева
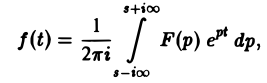
а справа — сумму вычетов по всем полюсам функции F(p)
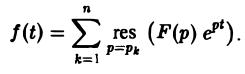
Замечание:
Воспользовавшись формулой для вычисления вычетов, найдем, что
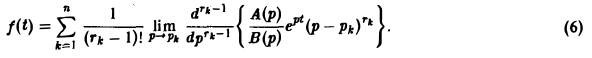
Если все полюсы p1, р2,…, рn — простые, то
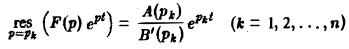
и формула (6) принимает вид
Пример:
Найти оригинал для функции
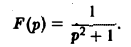
Функция F(p) имеет простые полюсы р1 = i. p2 = -i. Пользуясь формулой (7), находим
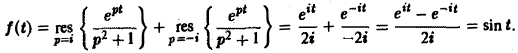
Теорема:
Пусть изображение F(p) является аналитической функцией в бесконечно удаленной точке р = ∞, причем ее разложение в окрестности |р| > R бесконечно удаленной точки имеет вид
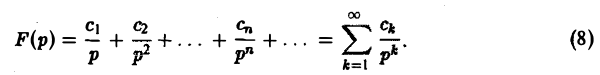
Тогда оригиналом для F(p) будет функция f(t) η{t), где
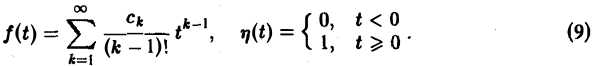
Пример:
Приложения преобразования Лапласа (операционного исчисления)
Решение линейных дифференциальных уравнений с постоянными коэффициентами
Дано линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
(1)
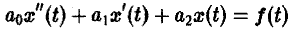
(ао, а1, а2 — действительные числа) и требуется найти решение уравнения (1) для t > 0, удовлетворяющее начальным условиям
Будем считать, что f(t) есть функция-оригинал. Тогда x(t) — также функция-оригинал. Пусть
f(t) = F(p), x(t) = X(p).
По теореме о дифференцировании оригинала имеем
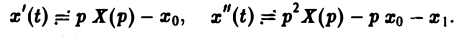
Перейдем в уравнении (1) от оригиналов к изображениям. Имеем
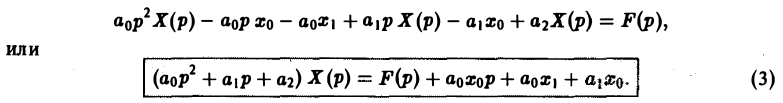
Это уже не дифференциальное, а алгебраическое уравнение относительно изображения Х(р) искомой функции. Его называют операторным уравнением. Решая его, найдем операторное решение задачи (1)-(2) —
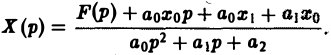
Оригинал для Х(р) будет искомым решением х(t) задачи (1)-(2).
Общий случай линейного дифференциального уравнения n-го порядка (n ≥ 1) с постоянными коэффициентами от случая п = 2 принципиально ничем не отличается.
Приведем общую схему решения задачи Коши
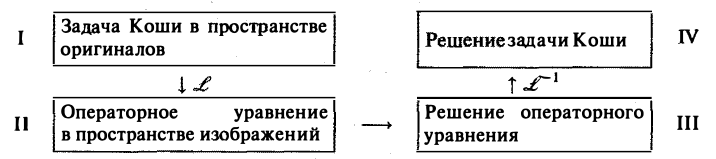
Здесь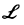 
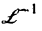
означает применение к 1 преобразование Лапласа, 
— применение к III обратного преобразования Лапласа.
Пример:
Решить задачу Коши
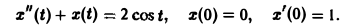
Здесь
Операторное уравнение
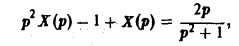
Откуда
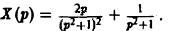
По теореме о дифференцировании изображения
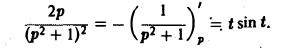
Поэтому
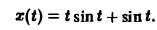
Формула Дюамеля
В приложениях операционного исчисления к решению дифференциальных уравнений часто пользуются следствием из теоремы умножения, известным под названием формулы Дюамеля.
Пусть f(t) и φt) — функции-оригиналы, причем функция f(t) непрерывна на [0, + ∞), a φ(t) — непрерывно дифференцируема на [0,+ ∞). Тогда если f(t) = F(p), φ{t) = Ф(р),то по теореме умножения получаем, что
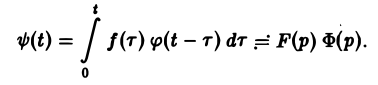
Нетрудно проверить, что функция ψ(t) непрерывно дифференцируема на [0, + ∞), причем
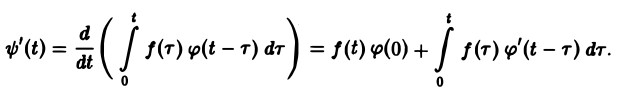
Отсюда, в силу правила дифференцирования оригиналов, учитывая, что ψ(0) = 0, получаем формулу Дюамеля
(4)
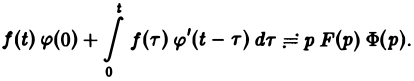
Покажем применение этой формулы.
Пусть требуется решить линейное дифференциальное уравнение n-го порядка (n ≥ 1) с постоянными коэффициентами
при нулевых начальных условиях
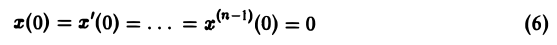
(последнее ограничение несущественно: задачу с ненулевыми начальными условиями можно свести к задаче с нулевыми условиями заменой искомой функции).
Если известно решение x(t) дифференциального уравнения с той же левой частью и правой частью, равной единице,
L[x(t)] = l (7)
при нулевых начальных условиях
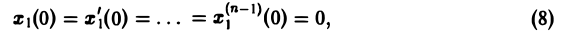
то формула Дюамеля (4) позволяет сразу получить решение исходной задачи (5)-(6).
В самом деле, операторные уравнения, отвечающие задачам (5)-(6) и (7)-(8), имеют соответственно вид
где F(p) — изображение функции f(t). Из (9) и (10) легко находи
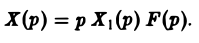
Отсюда по формуле Дюамеля
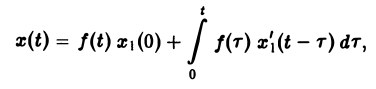
или, поскольку x1(0) = 0, (11)
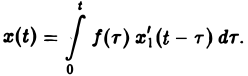
Пример:
Решить задачу Коши
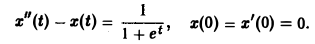
Рассмотрим вспомогательную задачу
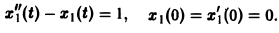
Применяя операционный метод, находим
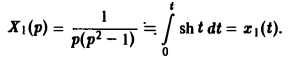
По формуле (11) получаем решение x(t) исходной задачи:
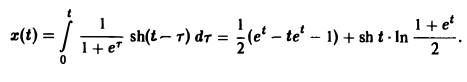
Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами
Интегрирование систем осуществляется так же, как и решение одного линейного дифференциального уравнения — путем перехода от системы дифференциальных уравнений к системе операторных уравнений. Решая последнюю как систему линейных алгебраических уравнений относительно изображений искомых функций, получаем операторное решение системы. Оригинал для негобудетрешением исходной системы дифференциальных уравнений.
Пример:
Найти решение линейной системы
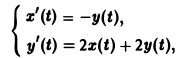
удовлетворяющее начальным условиям х(0) = у(0) = I.
Пусть х(<) = Х(р), y(t) = Y(p). Пользуясь свойством линейности преобразования Лапласа и теоремой о дифференцировании оригиналов, сводим исходную задачу Коши к операторной системе
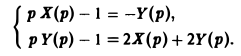
Решая последнюю относительно Х(р) и У(р), получаем
Решение исходной задачи Коши
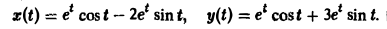
Решение интегральных уравнений
Напомним, что интегральным уравнением называют уравнение, в котором неизвестная функция входит под знак интеграла. Мы рассмотрим лишь уравнение вида (12)
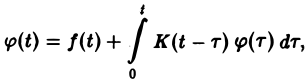
называемое линейным интегральным уравнением Вольтерра второго рода с ядром K(t — т), зависящим от разности аргументов (уравнение типа свертки). Здесь φ(t) — искомая функция, f(t) и K(t) — заданные функции.
Пусть f(t) и K(t) есть функции-оригиналы, f(t) =’ F(p), K(t) =’ K(p).
Применяя к обеим частям (12) преобразование Лапласа и, пользуясь теоремой умножения, получим
(13)
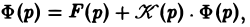
где Ф(р) = φ(t). Из (13)
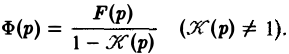
Оригинал для Ф(р) будет решением интегрального уравнения (12).
Пример:
Решить интегральное уравнение
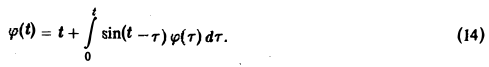
Применяя преобразование Лапласа к обеим частям (14), получим
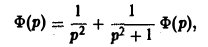
откуда
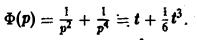
Функция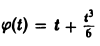 
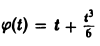
является решением уравнения (14) (подстановка в уравнение (14) обращает последнее в тождество по t).
Замечание:
Преобразование Лапласа может быть использовано также при решении некоторых задач для уравнений математической физики.
Таблица преобразования Лапласа
Дополнение к преобразованию Лапласа
Смотрите также:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Примеры решений задач по операционному исчислению (преобразованию Лапласа)
Операционное (символическое) исчисление – это один из методов математического анализа, позволяющий в
некоторых случаях свести исследование и решение дифференциальных, псевдодифференциальных, интегральных уравнений, к более простым алгебраическим задачам.
Изучая преобразование Лапласа, мы вводим оригинал функции $f(t)$ и ее изображение $F(p)$, находимое по формуле:
$$F(p) = int_0^infty f(t) e^{-pt}dt$$
Для быстроты и удобства решения задач составлена таблица изображений и оригиналов, которая, наряду с теоремами (линейности, подобия, смещения, запаздывания), свойствами и правилами дифференцирования и интегрирования изображения/оригинала, постоянно используется в решении примеров.
В этом разделе вы найдете готовые задания разного типа: восстановление оригинала или изображения функции, нахождение свертки функций, решение ДУ, систем ДУ или интегральных уравнений с помощью преобразования Лапласа и т.д.
Полезная страница? Сохрани или расскажи друзьям
Как найти изображение функции
Задача 1. Найти изображение данного оригинала, или оригинала, удовлетворяющего данному уравнению
$$f(t)=frac{e^{2t}-e^{-3t}}{t}.$$
Задача 2. Пользуясь определением, найти изображение функции $f(t)=3^t$.
Задача 3. Найти изображение функции: $int_0^t cos tau cdot e^{-3tau}dtau. $
Задача 4. Найти изображение оригинала $f(x)$ двумя способами:
1) Вычислив интеграл $F(p) = int_0^infty f(x) e^{-px}dx$;
2) Воспользовавшись таблице изображений и свойствами преобразования Лапласа.
Оригинал задается формулой (курсочно-линейная функция, см. файл).
Как найти оригинал функции
Задача 5. Найти оригинал изображения $F(p)$, где
$$F(p)=frac{2p-1}{(p^2-4p+13)^2}.$$
Задача 6. Найти оригинал изображения
$$F(p)=frac{15p^2+3p+34}{(p^2+4p+8)(p^2-6p+5)}.$$
Задача 7. Найти оригинал для функции с помощью вычетов
$$F^*(p)=frac{1}{e^{4p}-625}.$$
Как решить ДУ (систему ДУ) операционным методом
Задача 8. Найти частное решение дифференциального уравнения с заданными начальными условиями операторным методом
$$x’+x=4e^t, x(0)=2.$$
Задача 9. Найти решение задачи Коши методами операционного исчисления
$$x»+2x’+2x=te^{-t}, quad x(0)=0, x'(0)=0.$$
Задача 10. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.
$$x’=x-y,\
y’=x+y,\
x(0)=2, y(0)=1.$$
Задача 11. Методом операционного исчисления найти решение задачи Коши для ДУ 3-го порядка
$$x»’+x»-2x’-5x=5e^t, quad x(0)=0, x'(0)=1, x»(0)=2.$$
Задача 12. Решите задачу Коши для системы дифференциальных уравнений с помощью преобразования Лапласа.
$$frac{dx}{dt}=x-2y,\
frac{dy}{dt}=x+3y,\
x(0)=0, y(0)=1. $$
Задача 13. C помощью формулы Дюамеля найти решение уравнения
$$x»’+x’=tg t, quad x(0)=x'(0)=x»(0)=0.$$
Задача 14. Решить систему ДУ с помощью преобразования Лапласа
$$
x’=-y+z,\
y’=z, quad x(0)=1, \
z’=-x+z;\
y(0)=z(0)=1/2.
$$
Как решить интегральное уравнение
Задача 15. Методом операционного исчисления найти решение интегрального уравнения
$$ y(t)=cos t +int_0^t (t-tau)^2 y(tau)d tau. $$
Задача 16. Решить интегральное уравнение
$$ int_0^t ch (tau) x(t-tau)d tau = t. $$
Как найти свертку функций
Задача 17. Найти свертку функций $f(t)=1$ и $phi(t)=sin 5t$.
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей, оформление производится в Word, срок от 1 дня.
Подробнее о решении заданий с преобразованием Лапласа
Дополнительная информация
- Онлайн-помощь по математическому анализу
- Дифференциальные уравнения — задачи с решениями
- Как решать ДУ с помощью операционного исчисления
Содержание
Глава 7. Элементы операционного исчисления
Преобразование Лапласа. Оригинал и изображение
Рассмотрим функцию вещественного переменного $f(t)$ определенную на всей вещественной оси $tin R$ и интегрируемую на любом конечном промежутке. Пусть $f(t)$ удовлетворяет условиям:
1) $f(t)=0$ при $t<0$.
2) Существуют такие числа $M>0$, $sgeqslant0$, что функция $f(t)$ при любом $tin R$ удовлетворяет неравенству:
$$
|f(t)|leqslant Me^{st}.
$$
Функция $f(t)$, удовлетворяющая всем перечисленным выше условиям, называется функцией ограниченного роста, а число $s_0=mbox{inf},s$ называется показателем роста.
Первое условие можно обойти, введя функцию Хевисайда:
$$
eta(t)=left{
begin{aligned}
0,,,&t<0,\
1,,,&t geqslant0.
end{aligned}
right.
$$
В дальнейшем любую функцию $f(t)$ будем заменять на $f(t)cdoteta(t)$ и будем считать условие выполненным. Например, если мы указываем функцию $f(t)=mbox{sin}t$, то на самом деле имеем в виду функцию
$$
f(t)=mbox{sin}tcdoteta(t)=left{
begin{aligned}
0,,,&t<0,\
mbox{sin}t,,,&tgeqslant0.
end{aligned}
right.
$$
Функция комплексного переменного $pin C$, $p=s+isigma$
$$ F(p)=intlimits_0^{infty} f(t)e^{-pt}dt $$
называется изображением по Лапласу, если существует указанный несобственный интеграл. Исходная функция $f(t)$ называется оригиналом.
Обозначается: $ F(p) risingdotseq f(t), ,, mbox{или},, F(p)=L{f(t)} $.
Читается: $F(p)$ есть изображение для $f(t)$, $f(t)$ есть оригинал для $F(p)$.
П
Найти изображение для функции Хэвисайда $f(t)=eta(t)$.
Условие 1) выполнено.
Условие 2) выполнено при $M=1$, $s_0=0$.
begin{gather*}
F(p)=intlimits_0^{infty} eta(t)cdot e^{-pt}dt=intlimits_0^{infty} e^{-pt}dt=displaystylefrac{1}{p} ,,(mbox{Re}p>0).\
end{gather*}
Получили, что $eta(t)risingdotseq displaystylefrac{1}{p}$. В таблицах обычно записывают $1risingdotseq displaystylefrac{1}{p}$, имея в виду, что на самом деле мы работаем не с $f(t)=1$, а с $f(t)=eta(t)$.
Т
Теорема о существовании изображения.
Пусть функция $f(t)$ является функцией ограниченного роста с показателем роста $s_0$. Тогда в правой полуплоскости $mbox{Re},p>s_0$ существует изображение $F(p) = intlimits_0^{infty} f(t),e^{-pt}dt$, причем $F(p)$ — аналитическая функция.
Свойства преобразования Лапласа
Будем использовать следующие обозначения:
Функции действительного переменного $f(t)$, $g(t)$ являются оригиналами,
функции комплексного переменного $F(p)$, $G(p)$ являются изображениями:
$ f(t)risingdotseq F(p), ,, g(t)risingdotseq G(p).$
Свойство линейности
Пусть $alpha$, $beta in mathbb{C}$. Тогда изображение линейной комбинации функций $f(t)$ и $g(t)$ является линейной комбинацией их изображений $F(p)$ и $G(p)$:
begin{equation*}
alpha f(t)+beta g(t) risingdotseq alpha F(p)+beta G(p).
end{equation*}
П
Найти изображение для $f(t)=mbox{sin},alpha t$.
begin{equation*}
mbox{sin},alpha t=frac{e^{ialpha t}-e^{-ialpha t}}{2i} risingdotseq frac{1}{2i}left(frac{1}{p-ialpha}+frac{1}{p+ialpha}right)=frac{1}{2i}cdotfrac{2ialpha}{p^2+a^2}=frac{alpha}{p^2+alpha^2}.
end{equation*}
П
Найти изображение для $f(t)=mbox{sin}^2 t$.
begin{equation*}
begin{split}
&mbox{sin}^2 t=left(frac{e^{it}-e^{-it}}{2i}right)^2 = -frac{1}{4}e^{2it}+frac12-frac{1}{4}e^{-2it} risingdotseq \
&risingdotseq -frac14cdotfrac{1}{p-2i}+ frac{1}{2p}-frac14cdotfrac{1}{p+2i}=-frac{2p}{p^2+4}+frac{1}{2p}=frac{2}{p(p^2+4)}.
end{split}
end{equation*}
Теорема подобия
Пусть $ain R $, $a>0$.
begin{equation*}
f(at)risingdotseq displaystylefrac{1}{a}Fleft(displaystylefrac{p}{a}right).
end{equation*}
Теорема смещения
Пусть $alpha in mathbb{C}$.
begin{equation*}
e^{alpha t}cdot f(t)risingdotseq F(p-alpha).
end{equation*}
П
Найти изображение для $f_1(t)= e^{alpha t}mbox{sin},beta t, ,, f_2(t)=e^{alpha t}mbox{cos},beta t$.
begin{gather*}
mbox{sin},beta t=risingdotseq frac{beta}{p^2+beta^2},,Rightarrow e^{alpha t}mbox{sin},beta t risingdotseq frac{beta}{(p-alpha)^2+beta^2},\
mbox{cos},beta t=risingdotseq frac{p}{p^2+beta^2},,Rightarrow e^{alpha t}mbox{cos},beta t risingdotseq frac{p-alpha}{(p-alpha)^2+beta^2}.
end{gather*}
Теорема запаздывания
Пусть $tau in R$, $tau>0$.
begin{equation*}
f(t-tau) risingdotseq e^{-ptau}cdot F(p).
end{equation*}
В механике используют включение с запаздыванием для различных приборов. В математической модели таких включений удобно использовать функцию Хэвисайда, а изображения для таких функций удобно находить с помощью теоремы запаздывания.
П
Найти изображение для кусочно-непрерывной функции:
begin{equation*}
f(t)=begin{cases}
0,& t<0,\
displaystylefrac{t-a}{a},& 0leqslant t<a,\
0,& aleqslant t<2a,\
displaystylefrac{t-2a}{a},& tgeqslant2a.
end{cases}
end{equation*}
begin{equation*}
f(t)= left(frac{t}{a}-1right)eta(t)-frac{t-a}{a}eta(t-a)+frac{t-2a}{a}cdoteta(t-2a).
end{equation*}
begin{equation*}
F(p) = frac{1}{ap^2}-frac{1}{p}-frac{1}{ap^2}e^{-ap}-frac{1}{ap^2}e^{-2ap}.
end{equation*}
Дифференцирование оригинала
begin{equation*}
begin{aligned}
f'(t) & risingdotseq p,F(p)-f(0),\
f»(t)& risingdotseq p^2F(p)-p,f(0)-f'(0),\
&cdots\
f^{(n)}(t)& risingdotseq p^nF(p)-p^{n-1}f(0)-ldots -f^{(n-1)}(0).
end{aligned}
end{equation*}
П
Решить задачу Коши:
begin{equation*}
x»’+x’=1, quad x(0)=x'(0)=x»(0)=0.
end{equation*}
Запишем изображения для левой и правой частей дифференциального уравнения:
begin{equation*}
p^3,X(p)+p,X(p)=frac{1}{p}.
end{equation*}
Найдем из записанного алгебраического уравнения неизвестную функцию $X(p)$:
begin{equation*}
X(p)=frac{1}{p^2(p^2+1)}=frac{1}{p^2}-frac{1}{p^2+1}.
end{equation*}
И запишем оригинал для найденного изображения:
begin{equation*}
frac{1}{p^2}-frac{1}{p^2+1}risingdotseq t-mbox{sin},t.
end{equation*}
Получили ответ для поставленной задачи Коши:
begin{equation*}
x(t)=t-mbox{sin},t.
end{equation*}
Дифференцирование изображения
begin{equation*}
begin{aligned}
F'(p)& risingdotseq -t f(t),\
F»(p)& risingdotseq t^2 f(t),\
&cdots\
F^{(n)}(p)& risingdotseq (-1)^n t^n f(t).
end{aligned}
end{equation*}
П
Найти изображение для $f(t) = t^2e^t$.
Известно, что
$$ e^trisingdotseq frac{1}{p-1}.$$
Тогда по теореме о дифференцировании изображений
begin{equation*}
begin{aligned}
& left( frac{1}{p-1}right)’ = -frac{1}{(p-1)^2} risingdotseq t e^t,\
& left(-frac{1}{(p-1)^2}right)» = frac{2}{(p-1)^3}risingdotseq t^2 e^t.
end{aligned}
end{equation*}
Интегрирование оригинала
begin{equation*}
intlimits_0^t f(tau)dtaurisingdotseq frac{F(p)}{p}.
end{equation*}
П
Найти изображение для $f(t) = intlimits_0^t e^{tau}dtau$.
begin{equation*}
e^t risingdotseq frac{1}{p-1},, Rightarrow ,, intlimits_0^t e^{tau}dtau risingdotseq frac{1}{p(p-1)}.
end{equation*}
Интегрирование изображения
begin{equation*}
frac{f(t)}{t}risingdotseq intlimits_p^{+infty}F(p)dp.
end{equation*}
П
Найти изображение для $f(t)=frac{mbox{sin},t}{t}$.
begin{equation*}
begin{aligned}
& mbox{sin}, t risingdotseq frac{1}{p^2+1},, Rightarrow\
& frac{mbox{sin}, t}{t} risingdotseq intlimits_p^{+infty}left.frac {dp}{p^2+1} = mbox{arctg}, right|_p^{+infty}=frac{pi}{2}-mbox{arctg},p=mbox{arcctg},p.
end{aligned}
end{equation*}
Для многозначных функций берем их главные ветви.
Теоремы разложения
Первая теорема разложения
Пусть $F(p)$ — аналитическая в окрестности $z=infty$ функция и в этой окрестности раскладывается в ряд Лорана:
begin{equation*}
F(p)=sumlimits_{k=1}^{infty}displaystylefrac{c_k}{p^k}.
end{equation*}
Тогда
begin{equation*}
F(p)risingdotseq f(t)=sumlimits_{k=1}^{infty}displaystylefrac{c_k}{(k-1)!}t^{k-1}.
end{equation*}
Вторая теорема разложения
Пусть $F(p)$ — дробно-рациональная функция и $p_1, ldots p_n$ — ее полюсы (простые или кратные).
Тогда
begin{equation*}
F(p)risingdotseq f(t)=sumlimits_{k=1}^{n}mbox{res}left(F(p_k)e^{p_kt}right).
end{equation*}
Теоремы умножения. Интеграл Дюамеля
Теорема о свертке (умножение изображений)
Интеграл $intlimits_0^t,f(tau)g(t-tau),dtau$ называется свёрткой функций $f(t)$, $g(t)$ и обозначается $(fast g)(t)$:
begin{equation*}
(fast g)(t)=intlimits_0^t,f(tau)g(t-tau),dtau.
end{equation*}
Если $F(p)$ и $G(p)$ являются изображениями по Лапласу функций $f(t)$ и $g(t)$, то их произведение также является изображением, причем
begin{equation*}
F(p)cdot G(p)risingdotseq (fast g)(t)=intlimits_0^t,f(tau)g(t-tau),dtau.
end{equation*}
(произведение изображений является изображением свертки).
Свертка коммутативна:
begin{equation*}
(fast g)(t)=(gast f)(t)=intlimits_0^t,f(tau)g(t-tau),dtau=intlimits_0^t,g(tau)f(t-tau),dtau.
end{equation*}
Следствие теоремы о свёртке (интеграл Дюамеля)
begin{equation*}
pcdot F(p)cdot G(p) risingdotseq f(0)cdot g(t)+intlimits_0^t f'(tau),g(t-tau),dtau.
end{equation*}
begin{equation*}
pcdot F(p)cdot G(p) risingdotseq g(0)cdot f(t)+intlimits_0^t f(tau),g'(t-tau),dtau.
end{equation*}
Каждую из этих формул называют интеграл Дюамеля.
Теорема об умножении оригиналов
Пусть $f(t)$ и $g(t)$ удовлетворяют условиям:
1) Теорема о существовании изображения.
2) Их показатели роста равны $s_1$ и $s_2$.
3) $f(t)risingdotseq F(p)$, $ g(t) risingdotseq G(p)$.
4) Произведение $f(t)cdot g(t)$ также является оригиналом.
Тогда
begin{equation*}
f(t)cdot g(t) risingdotseq displaystylefrac{1}{2pi i}intlimits_{c-iinfty}^{c+iinfty} F(q)cdot G(p-q),dq,
end{equation*}
где $cgeqslant s_1$, $mbox{Re},p>s_2+c$, $pin mathbb{C}$, $qin mathbb{C}$.