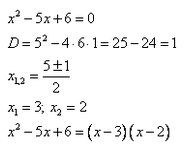Как найти какое неравенство не имеет решений - Исправление недочетов и поиск решений вместе с Examum.ru

Анастасия Коротеева

Ученик

(76),
на голосовании

7 лет назад

1) х2 + 6х — 51, больше 0.
2)х2 + 6х — 51 меньше 0.
3)х2 + 6х + 51 больше 0.
4)х2 + 6х + 51 меньше 0.

Голосование за лучший ответ

No name

Мастер

(2218)

7 лет назад

реши уравнения соответственно x2+6x-51=0 и x2+6x+51=0, напиши уравнения в виде (x-x1)(x-x2)=0 расположи корни на координатной прямой и смотри.

Несмотря на то, что решение неравенств очень напоминает решение уравнений, все-таки неравенства вызывают у школьников больше затруднений.

Ученики часто спрашивают как решать неравенства те или иные, просят оценить решение неравенства, полученное у доски в школе или помочь в решении домашнего задания с неравенством. В основном они связаны не с решением неравенства как такового, а с проблемой записи решения и с проблемой знака неравенства, которое в определенные моменты заменяется на противоположный.

Решение неравенств — это материал, который помогает выявить у экзаменуемого сразу несколько умений и навыков: умение решать уравнения, работать со знаком неравенства, оценить полученное решение с точки зрения постановки неравенства. Поэтому неравенства включены в ОГЭ (ГИА).

Как решать простейшие неравенства из ОГЭ (ГИА)

Итак, первое неравенство:

3х-4<6x-6

Решаем неравенство как уравнение — перенесем все неизвестные в левую часть, а все числа — в правую. Неизвестные — это все выражения с х: 3х и 6х.

3х уже находится слева, а вот 6х — справа, и 6х мы перенесем в левую часть нашего неравенства. Не забываем, что когда мы переносим любые выражения и числа из одной части неравенства, как и равенства, в другую, то мы обязательно меняем знак. То есть слева у нас запишется:

3х-6х.

Что будет справа? Справа останется число -6 (со знаком минус), и еще мы перенесем 4 из левой части в правую. Перед четверкой в левой части неравенства стоит знак минус, значит, при переносе мы получим четверку со знаком +. Смотрите, что получилось:

3х-6х<-6+4

Упростим левую и правую части, получим:

-3х<-2

Если бы у нас вместо неравенства было уравнение: -3х=-2, то x мы бы нашли разделив -2 на -3. Точно также поступают и в неравенстве, но, помнят одно простое правило,

если мы делим или умножаем на отрицательное число (число со знаком минус), то знак неравенства меняется на противоположный.

То есть мы запишем решение нашего неравенства вот так:

$x< frac{-2}{-3}$

Мы поменяли знак, так как делили на отрицательное число — -3. При этом знак бы не менялся, если бы мы делили отрицательное число на положительное. Знак неравенства меняется только тогда — когда отрицательным является число на которое делят или умножают.

Итак, ответ у нас будет таким:

$x> frac{2}{3}$ .

Как решать нестрогое неравенство

Нестрогим неравенством называется неравенство, у которого вместо строгого знака «больше» или «меньше», стоит знак «больше или равно» или «меньше или равно». Например, давайте решим нестрогое неравенство. Возьмем простое неравенство, чтобы вы поняли суть вопроса.

Решаем аналогично — только сначала упростим правую часть нашего неравенства. Переносим неизвестные в левую часть неравенства, а известные (числа) в правую часть неравенства:

Упрощаем правую часть:

Посчитаем, получим:

$x geqslant frac {6}{3}$

Ответ: .

Обратите внимание на запись ответа. Так как у нас неравенство нестрогое, то число 2 будет входить в решение этого неравенства, поэтому мы его включаем в ответ, отмечая квадратной скобкой.

Вот так:

Решение неравенств из сборника ОГЭ по математике ФИПИ

Неравенство 1

Укажите решение неравенства

Решение:

Перенесем неизвестные в левую часть неравенства, а известные — в правую часть неравенства:

Посчитаем:

, отсюда

искомый интервал: . Таким образом, из списка предложенных интервалов нам подходит интервал под номером 2.

Ответ 2.

Неравенство 2

Укажите множество решений неравенства:

Решение:

Как обычно, переносим неизвестные влево от знака неравенства, а известные величины — вправо:

$x leqslant frac{-3}{6}$

Обратите внимание — здесь мы делим отрицательное число. Но делим то мы его на положительное число 6. Поэтому знак неравенства остается прежним!

$x leqslant frac{-1}{2}$

или

Нам подходит вариант решения 4.

Ответ: 4.

Неравенство 3

Укажите решение неравенства

Решение:

Подходит вариант решения 2.

Ответ: 2

Неравенство 4

Укажите множество решений неравенства

Решение:

Итак, решение неравенство иллюстрируется графиком 3.

Ответ: 3.

Теперь вы знаете, как решать неравенства, которые даны в части «Алгебра» ОГЭ (ГИА).

Если перед тобой выражение, в котором есть числа, буквы и знаки неравенства, — это неравенство. Самые простые — это линейные и квадратные неравенства.

Пример:

2x+3≤100;x2+2x−4<0.

Если есть два и более неравенства и они объединены фигурной скобкой — это система неравенств.

Пример:

2x+3≤100500>10x+5x

Любое значение переменной, при котором выражение обращается в равенство, является решением неравенства.

Решить неравенство значит найти все такие числа или определить, что у неравенства нет решения. Решить систему неравенств — значит найти значения, подходящие для всех неравенств, входящих в систему.

Обрати внимание!

Любое неравенство, так же как и уравнение, можно разделить или умножить на какое-либо число. Если неравенство разделить или умножить на отрицательное число, оно изменит свой знак.

5x<120⋅(−1)−5x>−120.

Решать неравенства проще всего при помощи числовых промежутков. Решение оформляется с помощью специальных символов или самих числовых промежутков, изображённых графически.

∈ — знак принадлежности, ∉ — не принадлежит, ∪ — объединение промежутков.

Кроме того, для обозначения числовых диапазонов используются скобки разных видов, круглые и квадратные; неравенства бывают строгими и нестрогими, всё это объединяет одна система использования символов и рисунков.

Соответствие знака неравенства, скобки и графического изображения точки

1. Если в неравенстве переменная имеет первую степень — перед нами неравенство линейное. Оно имеет форму (kx>b), где (k) и (b) — любые числа, а (x) — любая переменная, имеющая первую степень, значение которой надо найти. Знак может быть любой, (<), (>), (⩽), (⩾). Многие неравенства, даже на первый взгляд не похожие на линейные, приводятся к этому типу при помощи тождественных преобразований.

Пример:

x+3<−9x;−5+9x>10x+4;12x+5≤125;4x+3(x+1)≥5(2−x).

2. Если в неравенстве после всех тождественных преобразований (раскрытие скобок, приведение подобных членов) остаётся переменная второй степени — перед нами квадратное неравенство, или неравенство второй степени, полное или неполное. В последнем примере вторая степень обязательно образуется после раскрытия скобок.

Пример:

3×2+12x+4<0;3×2+12x>0;(5x−2)(−x+3)≤0.

3. Если два и более линейных неравенств объединены фигурной скобкой, перед нами система линейных неравенств.

Пример:

2x+3≤100500>10x+5x

Справочник ОГЭ по математике. 3.2. Неравенства.

3.2.1. Числовые неравенства и их свойства.
3.2.2. Неравенство (линейное) с одной переменной. Решение неравенства.
3.2.3. Линейные неравенства с одной переменной и сводящиеся к ним.
3.2.4. Системы линейных неравенств. Совокупности неравенств.
3.2.5. Квадратные неравенства. Метод интервалов.

Вы смотрели конспект по математике «3.2. Неравенства (справочник ОГЭ)».

OСR-текст раздела (только текст)

3.2.1. Числовые неравенства и их свойства Определение. Выражения а > b и а b называются неравенствами На координатной прямой большее число а b изображается точкой, которая расположена справа от меньшего числа, а меньшее m n k число точкой, которая расположена m n k слева от большего числа Знаки > и < знаки строгих неравенств а b, m > k (а меньше b; m больше k) Знаки ≥ и ≤ знаки нестрогих неравенств p n (p меньше или равно n или p не больше n); С помощью определения неравенства можно доказывать неравенства. Пример 1. Доказать, что при любых значениях а неравенство верно: (а + 7)(а + 1) (а + 2)(а + 6). Доказательство: Найдем разность правой и левой частей неравенства: (а + 2)(а + 6) – (а + 7)(а + 1) = а2 + 6а + 2а + 12 – а2 – а – 7а – 7 = 5 > 0. Это значит, что правая часть неравенства при любых а больше левой части, что и требовалось доказать. Этим методом доказываются так называемые опорные неравенства. Пример 2. Доказать, что сумма двух положительных взаимно обратных чисел не меньше двух: а b > 2, где а > 0, b > 0. b а Доказательство: Найдем разность правой и левой частей неравенства: поскольку (а – b)2 > 0, а > 0, b > 0. Равенство достигается, если а – b. Аналогично доказывается, что среднее арифметическое двух чисел среднее геометрическое (аЬ) и среднее гармоническое положительных чисел связаны соотношением: ab , а > 0, b > 0. С помощью опорных неравенств, в свою очередь, можно доказывать ряд неравенств. Пример 3. Доказать неравенство: (а + b)^b + 1) > 4а^ если а > 0, b > 0. Доказательство: Используем опорные неравенства: а + b > у/аЪ, а > 0, b > 0. Запишем верные неравенства: а + b > у[аЕ и °b^ 1 > у[оЪ. Почленно перемножим эти неравенства, получим: что и требовалось доказать. Основные свойства числовых неравенств Свойства Примеры Если а > b, то b а; Если 10 > 2, то 2 10; если а b, то b > а если –7 –1, то –1 > –7 Свойство транзитивности: Если 10 > 1 и 1 > –4, то если а > b и b > c, то а > c 10 > –4 Если к обеим частям верного неравенства прибавить Если 20 > 3, то 20 + 1 > 3 + одно и то же число, то получим верное неравенство: + 1, т. е. 21 > 4 и 20 – 4 > если а > b, то а + c > b + c > 3 – 4, т. е. 16 > –1 Свойства Примеры Если обе части верного неравенства умножить на Если 7 > –3,1 и 5 > 0, одно и то же положительное число, то получим то 7 • 5 > –3,1 • 5, т. е. верное неравенство: 35 > –15,5 если а > b и c > 0, то ас > bc Если обе части верного неравенства умножить на Если 10 > 2 и –2 0, то одно и то же отрицательное число и знак нера– –2 • 10 2 • (–2), –20 –4 венства изменить на противоположный, то получим верное неравенство: если а > b; с 0, то ас bc или а b; с 0, то ас > bc Если почленно сложить два верных неравенства одного знака, то получим верное неравенство: + Если а, b, с и d ––– положительные числа, при– 20 > 4 чем а > b и с > d, то ас > bd, т. е. если почленно х 2 1 перемножить верные неравенства одного знака, > все члены которых ––– положительные числа, то 5 5 получим верное неравенство Если а > b и с d, то а – с > b – d Если 20 > 3 и 4 10, то 20 – 4 > 3 – 10, 16 > –6 Если а > b > 0, то 1 1 Если 7 > 3. Если а > b > 0, то для любого натурального числа Если 5 > 2, п – 6, то n верно неравенство ап > bn 56 > 26 Пример 4. Известно, что –3 a 7. Оценить: а) 2а + 7; б) 3а – 1; в) 4 – 2а; г) –——. Решение: а) –3 а 7, тогда –6 2а 14 и –6 + 7 2а + 7 14 + 7, т. е. 1 2а + 7 21; б) –3 а 7, тогда –9 3а 21, то –10 3а – 1 20; в) –3 а 7. Умножим почленно двойное числовое неравенство на –2, получим: –3 • (–2) > –2а > 7 • (–2) или –14 –2а 6. Тогда 4 – 14 4 – 2а 4 + 6, т. е. –10 4 – 2а 10; г) –3 а 7, тогда –3 • 7 –3а –3 • (–3); –21 –3а 9; 1 – 21 1 – 3а 1 + 9; on о щ п 20 1 – 3а 10 _ 1 – 3а _ _ –20 1 – 3а 10. Получим – ; –5 2,5. Пример 5. Доказать, что сумма расстояний от любой точки, лежащей внутри треугольника, до его вершин больше полупериметра этого треугольника. Решение: Пусть x, у и z — расстояния от внутренней точки M до вершин треугольника. Из получившихся трех треугольников AMB, BMC и AMC по теореме о неравенстве треугольников (сумма двух любых сторон треугольника больше третьей стороны) имеем: x + у > c 3.2.2. Неравенство (линейное) с одной переменной. Решение неравенства Линейным неравенством называется неравенство вида ax + b > 0 (или ax + b 0), где а и b — некоторые числа, x — переменная. К линейным относятся также нестрогие неравенства вида ax + b > 0 (или ax + b 0). Решением линейного неравенства с одной переменной называется такое число, при подстановке которого вместо переменной неравенство обращается в верное числовое неравенство. Например, значение x – 1 является решением неравенства 5x – 4 > 0, поскольку 5 • 1 – 4 > 0, т. е. 1 > 0 — верное числовое неравенство. Решить неравенство — значит найти все его решения или доказать, что их нет. Равносильными называют неравенства, имеющие одинаковые решения. Неравенства, не имеющие решений, также называются равносильными. Например, неравенства 4x – 8 > 0 и 3x – 6 > 0 равносильны. При решении неравенств используют следующие свойства: Свойства Примеры Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное 5x + 3x > 5 – 3 + 1 – 6 ему неравенство 8x > –3 Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство Если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак б) – 3 > 9 {» 3); x s –15 неравенства на противоположный, то получится равносильное ему неравенство Рассмотрим примеры решений линейных неравенств и способы изображения множества решений этих неравенств. Пример 1. Решить неравенство: –x + 3(–7 + 5x) > 7x + 7. Решение: Упростим левую и правую части неравенства: раскроем скобки и перенесем члены, содержащие неизвестное, в левую часть, а члены, не содержащие неизвестное, — в правую: После приведения подобных слагаемых разделим обе части неравенства на 7. Получим x > 4. Множество чисел, удовлетворяющих этому неравенству, на числовой оси изображается открытым 4 лучом (рис. 3.5). Число 4 не принадлежит этому лучу, на рисунке изображается пустой точкой, луч отмечен штриховкой. Кроме того, множество решений неравенства записывают в виде x е (4; +да>). Читают: «x принадлежит открытому числовому лучу от 4 до бесконечности» (+да> — знак, обозначающий бесконечно большие положительные числа). Аналогично множество чисел, удовлетворяющих неравенству x –3, изображается открытым лучом, –з и множество решений записывают в виде (–да; –3) рис 3.6. Число –3 не принадлежит этому лучу, поэтому оно изображено пустой точкой на числовой оси и в записи возле него ставится круглая скобка (знак «–да» читается «минус бесконечность» и означает бесконечно большие отрицательные числа). В свою очередь множество чисел, удовлетворяющих, например, неравенству x > 5, изображают на 5 числовой прямой и называют лучом, пишут: Рис. 3.7 Читают: «x принадлежит лучу от пяти до плюс бесконечности». Число 5 принадлежит этому лучу, поэтому на числовой прямой оно отмечено закрашенной точкой. В записи возле него стоит квадратная скобка. Аналогично изображается решение неравенства, например x 1 (рис. 3.8). x е (–да; 1]. Пример 2. Найти наименьшее число, являющееся решением неравенства: а) 4(x – 1) 2 + 7x; б) 6у + 1 > 2(у – 1) Решение: а) 4(x – 1) 2 + 7x; 4x – 4 2 + 7x; 4x – 7x 2 + 4; –3x 6; x > –2 (рис. 3.9). Луч (–2; +да>) — открытый, и число –2 не входит в множество решений этого неравенства. Поэтому наименьшее целое число, являющееся решением неравенства, — это число –1. б) 6у + 1 > 2(у – 1) + 3у; 6у + 1 > 2у – 2 + 3у; ____ 6у – 2у – 3у > –2 – 1; у > –3 (рис. 3.10). Луч [–3; +да>) содержит число –3, поэтому наименьшим числом, являющимся решением этого неравенства, будет число –3. Ответ: а) –1; б) –3. Пример 3. Найти наибольшее целое число, являющееся решением неравенства: а) –3x – 6 > 7x + 4; б) 6x + 1 0. Решение: а) –3x + 6 > 7x + 4; –3x – 7x > 6 + 4; –10x > 10; x –1 (рис. 3.11). Луч (–да; –1] содержит число –1, поэтому наибольшим целым числом, являющимся решением данного неравенства, будет число –1. б) 6x + 1 0; 6x –1; x –1 (рис. 3.12). Наибольшим целым числом, являющимся решением данного неравенства, будет число –1. Ответ: а) –1; б) –1. 3.2.3. Линейные неравенства с одной переменной и сводящиеся к ним Основные свойства линейных неравенств рассмотрены в предыдущем пункте. Рассмотрим более сложные неравенства, задачи на составление неравенств и линейные неравенства с параметрами. Линейные неравенства могут не иметь решений или иметь бесчисленное множество решений. Пример 1. Решить неравенства: Решение: а) Домножим все члены неравенства на общий знаменатель этих дробей, т. е. число 4 > 0. Знак неравенства не изменится. Получили верное числовое неравенство, значит, при любых значениях x неравенство верно. б) Домножим все члены неравенства на 3 > 0. Получили неверное числовое неравенство, т. е. при любых значениях x верного числового неравенства получить не сможем. Ответ: а) x — любое число; б) решений нет. Пример 2. Решим задачу на составление неравенства. Из двух пунктов, находящихся на расстоянии 30 км, отправляются одновременно навстречу друг другу велосипедист и пешеход. Скорость движения велосипедиста 12 км/ч. С какой скоростью должен двигаться пешеход, чтобы его встреча с велосипедистом произошла не позже чем через 2 ч после начала движения? Решение: Пусть скорость движения пешехода x км/ч, скорость движения велосипедиста — 12 км/ч, тогда скорость их сближения будет (x + 12) км/ч, значит, встретятся они через ч. По условию они должны встретиться не позднее чем через 2 ч после начала движения, т. е. время должно быть не больше 2 ч. Получим неравенство: Все числа по условию положительны, поэтому умножение обеих частей неравенства на x + 12 приведет к равносильному неравенству: 30 2(x + 12) или 2(x + 12) > 30; x + 12 > 15; x > 3. Ответ: скорость пешехода должна быть не меньше 3 км/ч. Пример 3. При каких значениях x значение дроби больше дроби Решение: Очевидно, что ответ на вопрос сводится к решению неравенства вида: 3 – 2x 3 – 2x 3 – 2x 3 – 2x Ответ: при x > 4 Пример 4. Найти область определения функции: а) у = 2(3x –1) – 7x + 2; б) у = 2 . Решение: а) Функция вида у – у/f (x) определена на множестве, где f(x) > 0, это множество и называют областью определения данной функции. Таким образом, необходимо решить неравенство: б) Функция у – 1 определена на множестве f(x) > 0. Решим неравенство: Ответ: а) функция определена для всех x е (–да; 0]; б) функция определена lля всех x Пример 5. Решить неравенство: а) Решение: а) Дробь положительна, если ее числитель и знаменатель одного знака, поскольку 3 > 0, то 2x – 1 > 0; x > 1. б) Дробь неположительна, если ее числитель и знаменатель имеют разные знаки, –4 0, тогда 3x – 7 > 0; 3x > 7; x > ; x > 2 . Пример 6. Найти все значения а, при которых квадратное уравнение (2a – 1)x2 + 2x – 1 = 0 имеет два действительных и различных корня. Решение: Квадратное уравнение имеет два действительных различных корня, если первый коэффициент не равен нулю и дискриминант этого уравнения положителен. Ответ: уравнение имеет два различных действительных корня при 0 а Линейное неравенство с параметром Рассмотрим схему решения неравенства вида ax > b при различных значениях а и b. x > x решений нет x ––– любое число Пример 7. Решить неравенство: а) (а – 3)x 8; б) 5x – а > ax – 3. Решение: а) Рассмотрим случаи: Ответ: 1) а) x — любое число при а – 3; б) x при а > 3; в) x > при Пример 8. В зависимости от параметра b решить неравенство: (b2 + 2b – 3)x b2 – 1. Решение: Разложим на множители коэффициент при x и правую часть неравенства: Ответ: а) x — любое число при b – 1; б) решений нет при b – –3; в) x 3.2.4. Системы линейных неравенств. Совокупности неравенств Если необходимо найти общее решение двух или более линейных неравенств с одной переменной, говорят, что нужно решить систему двух и более неравенств. Решением системы неравенств с одной переменной называется число, при подстановке которого вместо переменной в каждое из неравенств системы они становятся верными числовыми неравенствами. Решить систему неравенств — значит найти все ее решения или доказать, что их нет. Пример 1. Решить систему неравенств: Решение: Разделим первое неравенство на –2 (знак неравенства изменится на противоположный Решением этой системы являются числа, которые одновременно больше, чем –2, и не превышают 4 (рис. 3.15). Множество чисел x, удовлетворяющих этому условию, можно записать в виде двойного неравенства –2 x 4, изобразить на числовой прямой. Такое множество называется полуинтервал и записывается (–2; 4], где число –2 не принадлежит этому множеству, а число 4 принадлежит. Аналогично вводится понятие интервал, т. е. множество чисел x, удовлетворяющих условию а x b, записывается (а; b), где числа а и b не являются решениями соответствующей системы неравенств (рис. 3.16). a b Если числа а и b являются решениями соответствующей системы неравенств, то множество таких чисел x записывают а x b или [а; b]. Это множество чисел называется числовым отрезком (рис. 3.17). Отрезки, интервалы, полуинтервалы и лучи называются числовыми промежутками. Числовые промежутки могут объединяться и пересекаться. Пример 2. Найти объединение и пересечение промежутков [а; b] и [с; d], если на числовой прямой они изображаются следующим образом (рис. 3.18). Решение: Очевидно, что пересечением числовых отрезков будет отрезок [с; b], т. е. это множество чисел x, которые одновременно входят в [а; b] и [с; d]. Записывают: [с; b] = [а; b] п [с; d]. Объединением этих отрезков будет множество чисел x, которые входят хотя бы в одно из множеств [а; b] или [с; d]. Очевидно, что это будет отрезок [а; d] = = [а; b] и [с; d]. Аналогично можно пересекать и объединять другие числовые промежутки. Если числовые промежутки не имеют общих элементов, их пересечением является пустое множество 0 (рис. 3.19), например: [а; b) п (с; d) = 0. Рассмотрим примеры решения систем линейных неравенств. Пример 3. Решить систему неравенств: Решение: а) Раскроем скобки в каждом неравенстве, перенесем слагаемые с переменной в левую часть неравенства, числа — в правую, приведем подобные слагаемые: Второе неравенство системы верно для всех значений x, поэтому общим решением будет x > 1 (рис. 3.20). 1 б) Домножим первое неравенство почленно на 8, а второе — на 12 (общий знаменатель дробей). Получим пересечение лучей (рис. 3.21): x –0,5 и x > –26,5, x e (–26,5; –0,5). Пример 4. Найти все целые числа, являющиеся решениями системы неравенств: Решение: Число нуль не является решением системы. Целыми числами, которые находятся на пересечении этих лучей, будут только 1 и 2 (рис. 3.22). Ответ: 1; 2. Пример 5. Найти наименьшее целое x, удовлетворяющее системе неравенств: Решение: Общим решением будет луч | —; + * |, а наименьшим целым числом на этом множестве будет число 1 (рис. 3.23). Ответ: 1. Пример 6. Найти область определения функции: y = ((x + 7 – 3) Решение: Областью определения данной функции будет множество x, удовлетворяющих системе неравенств: Общее решение — на полуинтервале [–7; 3) (рис. 3.24). Ответ: [–7; 3). Пример 7. Решить систему неравенств: Решение: Домножим первое уравнение системы на 4, а второе — на 12. Получим: {12x + 4x – 2 > 8x – 1, {12x + 4x – 8x > –1 + 2, Множество решений полученной системы пусто (рис. 3.25). Ответ: решений нет. Рассмотрим простейшие системы линейных неравенств с параметром. Пример 8. При каких значениях а система не имеет решений? Решение: Чтобы система не имела решений, необходимо, чтобы число а – 1 находилось не правее числа 1 на числовой прямой, т. е. а – 1 1, а 2 (рис. 3.26). Ответ: при а 2 система не имеет решений. Пример 9. При каких значениях параметра а уравнение x2 – 6ax + 9а2 – 16 = 0 имеет два отрицательных корня? Решение: Чтобы квадратное уравнение имело два корня, необходимо, чтобы его дискриминант был положителен, т. е. Данное уравнение всегда имеет два корня. Уравнение — квадратное приведенное. По теореме Виета имеем: если x2 + px + q – 0, то x1 + x2 = –p, x1 ■ x2 – q, т. е. x1 + x2 = 6а, x1 • x2 = 9а2 – 16; если x1 0 и x2 0, то x1 + x2 0 и x1 • x2 > 0. Система распадается на две: система несовместна Ответ: при b – уравнение имеет два отрицательных корня. 3 Неравенства с модулем. Системы и совокупности систем неравенств Решение неравенств с модулем сводится к решению системы или совокупности неравенств. Несколько неравенств с одной переменной образуют системы неравенств, если ставится задача об отыскании таких значений переменной, которые удовлетворяют одновременно каждому из этих неравенств. Решением системы является пересечение решений неравенств. Например, [–3; 5) система решений не имеет Несколько неравенств с одной переменной образуют совокупность неравенств в том случае, если ставится задача об отыскании всех значений переменных, каждое из которых удовлетворяет по крайней мере одному из этих неравенств. Решением совокупности неравенств является объединение решений неравенств. Например, Решение простейших неравенств с модулем а) если а 0, решений нет; а) если а 0, x ––– любое число; б) если а – 0, f(x) – 0; б) если а – 0, f(x) = 0; в) если а > 0, то неравенство равно¬ в) если а > 0, неравенство равносильно системе неравенств: но совокупности неравенств: или двойному неравенству вида а) если a 0, решений нет; б) если a > 0, то неравенство равносильно системе неравенств: или двойному неравенству –a f(x) a Пример 10. Решить неравенство: а) |2x – 5| 3; а) Данное неравенство равносильно двойному неравенству: б) Неравенство равносильно двойному неравенству: в) Неравенство равносильно совокупности неравенств: г) Данное неравенство равносильно совокупности неравенств: Второе неравенство совокупности не имеет решения, поэтому рассмотрим решение первого неравенства: д) Данное неравенство равносильно системе неравенств: е) Данное неравенство равносильно совокупности неравенств: Ответ: а) (1; 4); б) Пример 11. Для каждого значения a решить неравенство: а) |x – 3| a; б) |3 – 2x| > a. Решение: а) Если a 0, решений нет; если a > 0, получим двойное неравенство –a x – 3 a или 3 – a x a + 3. б) При a 0 x — любое число. Если a > 0, получим совокупность неравенств: Ответ: а) решений нет при a 0, 3 – a x a + 3 при a > 0; 3.2.5. Квадратные неравенства. Метод интервалов Если левая часть неравенства — выражение вида ax2 + bx + c, где x — переменная, a, b и c — некоторые числа (a 0), а правая часть неравенства представлена нулем, то такое неравенство называется квадратным. Например, 5×2 0; 3×2 + 2x – 1 > 0; x2 – x > 0. Существует три метода решения квадратных неравенств: 1) метод сведения к решению систем линейных неравенств; 2) графический метод (с помощью графика квадратичной функции); 3) метод интервалов. Метод сведения к решению систем линейных неравенств Метод сводится к разложению квадратного трехчлена на множители ax2 + bx + + c – a(x – x1)(x – x2), где x1 и x2 — корни квадратного трехчлена. Далее рассматривается совокупность соответствующих систем линейных неравенств. Пример 1. Решить квадратное неравенство: а) x2 – 3x + 2 0; б) –4×2 + 3x + 1 0. Решение: а) Разложим на множители квадратный трехчлен. Корни x1 = 1, x2 = 2. Поэтому (x – 1)(x – 2) = 0. Произведение двух множителей неположительно, значит, множители имеют разные знаки: Вторая система: эта система решений не имеет б) Умножим обе части неравенства на (–1), получим: 4×2 – 3x – 1 > 0. Найдем корни трехчлена: Неравенство примет вид: 4(x – 1) ^x + 1 j > 0. Произведение множителей положительно, значит, множители одного знака: Решениями данного неравенства являются числа x > 1, а также числа x – . Ответ: а) [1; 2]; б) I–да; – 4 lu (1; + да). Решение квадратного неравенства с помощью графика квадратичной функции (графический метод) Алгоритм решения квадратного неравенства графическим методом: 1. Находим нули функции соответствующей квадратичной функции или доказываем, что их нет. 2. Определяем направление ветвей параболы (если a > 0, то ветви параболы направлены вверх, если a 0, то вниз). 3. Рисуем эскиз графика квадратичной функции. 4. По графику определяем решение неравенства. Пример 2. Решить квадратное неравенство: а) x2 – 3x – 4 > 0; г) x2 + 5x + 12 > 0; б) –2×2 + x + 1 > 0; д) –x2 – 1 0. в) x2 – 14x + 49 0; Решение: а) Корни квадратного трехчлена x1 = –1, x2 = 4. Ветви параболы направлены вверх (a = 1 > 0). Рисуем эскиз графика функции y – x2 – 3x – 4 (рис. 3.27). Определяем решения. По графику видно, что неотрицательные значения функция принимает при x –1 и x > 4, т. е. x е (–да; –1] и [4; +да>). По этому же эскизу также можно решить неравенства, отличающиеся от исходного только знаком: x2 – 3x – 4 > 0, x e (–да; –1) u (4; +да); x2 – 3x – 4 0, x e [–1; 4]; x2 – 3x – 4 0, x e (–1; 4). б) Ветви параболы направлены вниз, поскольку –2 0. Парабола пересекает ось Ox в точках: x1 = 1, x2 = –1 (рис. 3.28). Определим, где функция принимает неотрицательные значения. Очевидно, это будет при По этому же эскизу можно решить неравенства: в) Ветви параболы направлены вверх. Соответствующий квадратный трехчлен имеет один корень x – 7. По эскизу (рис. 3.29) видно, что данное неравенство имеет решение только в точке x – 7. Определим по этому эскизу решения для неравенств: x2 – 14x + 49 0, решений нет; x2 – 14x + 49 > 0, решениями являются все действительные числа; x2 – 14x + 49 > 0, x — любое число, кроме 7, т. е. x е (–да; 7) и (7; +да). г) Построим эскиз графика (рис. 3.30), ветви параболы направлены вверх, в уравнении x2 + 5x + + 12 = 0 действительных корней нет, поэтому парабола не пересекает ось Ox. Из рисунка видно, что решениями неравенства x2 + 5x + 12 > 0 (а также x2 + 5x + 12 > 0) являются все действительные числа. Для неравенств x2 + 5x + 12 0 (или x2 + 5x + 12 0) решений нет. д) Ветви параболы направлены вниз (рис. 3.31), уравнение –(x2 + 1) = 0 действительных корней не имеет. Тогда для неравенства –x2 – 1 0 (и –x2 – 1 0) решениями являются все действительные числа; –x2 – 1 > 0 (и –x2 – 1 > 0) — решений нет. Пример 3. При каких значениях параметра а неравенство (a2 – 1)x2 + 2(a – 1)x + + 1 > 0 выполняется для любого x? Рис. 3.31 Решение: Для того чтобы квадратный трехчлен y – ax2 + bx + c (а Ф 0) был положителен при всех x, необходимо и достаточно, чтобы выполнялись условия: d > 0 и D 0, где d — коэффициент при x2. Имеем: d – а2 – 1 > 0. Дискриминант = (а – 1)2 – (а2 – 1) = а2 – 2а + 1 – а2 + 1 = 2 – 2а. Получим систему неравенств: Эти неравенства одновременно выполняются при а > 1. Отметим, что при а – 1 заданный трехчлен тождественно равен 1, 1 > 0. Ответ: для а > 1 неравенство выполняется для всех x. Пример 4. Решить систему неравенств: Решение: а) Решим первое неравенство системы: построим параболу с ветвями, направленными вверх. Найдем корни квадратного уравнения x2 – 9 = 0, x1 = –3 и x2 = 3. Решение первого неравенства: x –3 и x 3 (рис. 3.32). Решение второго неравенства: x 5 (рис. 3.33). Нанесем эти решения на одну числовую прямую (рис. 3.34) и запишем общие решения: x е (–да; –3] и [3; 5). б) Решением первого неравенства является множество x: x2 + 4x – 5 = 0; x1 = 1, x2 = –5 (рис. 3.35). Для второго неравенства: x2 – 2x – 8 = 0; x1 = –2, x2 = 4 (рис. 3.36). Нанесем на одну числовую прямую общее решение (рис. 3.37): x е [–2; 1). Пример 5. Найти область определения функции: Решение: Очевидно, что нахождение области определения данной функции сводится к выполнению условий x2 – 1 > 0 и 4 – x2 > 0, т. е. решению системы: Метод интервалов Этот метод применяется для решения квадратных неравенств, неравенств высших степеней, дробно–рациональных неравенств, уравнений и неравенств с модулем и т. д. Действия согласно Пример методу интервалов f(x) > 0 x2 + 7x + 10 > 0 1. Найти корни уравнения f(x) = 0: Найдем корни уравнения 2. Нанести эти корни на числовую прямую, разбивая ее на интервалы: Наносим корни на числовую прямую, получим три интервала: 3. Если коэффициент при старшей степени f(x) положителен, то на крайнем правом интервале функция –5 2 сохраняет знак «+»; остальные знаки Коэффициент при x2 равен 1 > 0, по расставлены в порядке чередования этому на интервале x > 2 функция сохраняет знак «+», остальные знаки ставим в порядке чередования 4. В ответ записать интервалы, соответствующие знаку неравенства пишем интервалы, где сохраняется знак «+». Ответ: (–да; –5) и (2; +да>). Пример 6. Решить неравенства методом интервалов: Решение: а) Отметим на числовой прямой точки, обращающие числитель и знаменатель в нули: –5, –4, 1, 2 (рис. 3.41). Кружки в точках 1 и 2 закрасим, а –5 и –4 оставим пустыми, т. к. дробь равна нулю при условии, что числитель равен нулю, а знаменатель нулю не равен. Поэтому точки –5 и –4 исключены из решения неравенства. На интервале x > 2 дробь положительна, далее знаки чередуются. Получим решение: б) Запишем неравенство в виде: (x + 3)2(x – 2)(x –– 3) > 0. Так как (x + 3)2 > 0 при всех x Ф –3, то при переходе через точку –3 знак функции не изменится (рис. 3.42) Заметим, что для неравенства вида (x – 9)2(x + 3)(x – 2) > 0 ответ будет выглядеть так (рис. 3.43): x е (–да; 2] и [3; +да>), поскольку числа –3, 2 и 3 входят в решение неравенства. Для неравенства (x2 – 9)(x + 3)(x – 2) 0 ответ: (2; 3); для неравенства (x2 – 9)(x + 3)(x – 2) 0 ответ: {–3} u [2; 3], т. к. числа –3, 2 и 3 необходимо включить в решение. в) Разложим на множители числитель и знаменатель дроби: (x – 3)(x2 + 3x + 9) 0 (x + 2)(x2 – 2x + 4) Дискриминанты уравнений x2 + 3x + 9 = 0 и x2 – 2x + 4 = 0 отрицательны, следовательно, уравнения решений не имеют. Отсутствие решений означает, что квадратные трехчлены на множители не раскладываются, и на всем промежутке изменения x имеют постоянный знак, совпадающий со знаком старшего члена (в данном случае «+»). Умножим и разделим исходное неравенство на положительные выражения (x2 – 2x + 4) и (x2 + 3x + 9) соответственно. Получим равносильное неравенство: Разобьем числовую прямую на промежутки, в которых числитель и знаменатель обращаются в нуль, учитывая, что x – –2 не является решением неравенства. Ответ: а) x е (–да; –5) и (–4; 1] и [2; +да>); б) (–да; –3) и (–3; 2) и (3; +да>); в) x е (–2; 3]. Методом интервалов можно решать уравнения и неравенства с модулем. Пример 7. Решить уравнение с модулем: |x – 3| + 2|x + 1| = 4. Решение: 1) Находим критические точки, т. е. значения x, при которых выражения, стоящие под знаком модуля, обращаются в нуль: 2) Критические точки разбивают числовую ось на интервалы, на каждом из которых выражение под модулем сохраняет знак: 3) Раскрываем все модули на каждом интервале, решаем полученное уравнение, проверяем, принадлежит ли полученный корень рассматриваемому интервалу: а) x –1. Получим уравнение: Корень принадлежит рассматриваемому интервалу. б) –1 x 3. Уравнение –(x – 3) + 2(x + 1) = 4; –x + 3 + 2x + 2 = 4; x – –1. Этот корень не принадлежит рассматриваемому интервалу. в) x > 3. этот корень не принадлежит интервалу x > 3. Ответ: –1. Аналогично решаются неравенства с модулем. Пример 8. Решить неравенство: |x – 1| + |x + 1| 4. Решение: Критические точки x1 = 1 и x2 = –1 разбивают числовую ось на три интервала: де — 1 0 л: — 1 0 ж – 1 > О Рассмотрим решение неравенства на каждом интервале. Числовое неравенство 2 4 верно для всех x, решением является весь промежуток –1 x 1. Объединяем полученные множества решений, получим –2 x 2. Ответ: x е (–2; 2). Пример 9. Решить неравенство: |x – a 2x – 1, где a — параметр. Решение: Критическая точка x – а. Данное неравенство равносильно совокупности систем неравенств: Рассмотрим каждую систему в отдельности: x > a, Если a ,’ то расположение точек a; 1 – a и на числовой оси следующее: Тогда решение системы — множество x > 1 – a. Если a > ^, получаем: Тогда решение системы — множество x > a; x a, Объединим решения двух систем неравенств. Ответ.

Источник

Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Неравенства

Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:

> больше,

≥ больше или равно,

< меньше,

≤ меньше или равно,

то получится неравенство.

Линейные неравенства

Линейные неравенства – это неравенства вида:

a x < b a x ≤ b a x > b a x ≥ b

где a и b – любые числа, причем a ≠ 0, x – переменная.

Примеры линейных неравенств:

3 x < 5 x − 2 ≥ 0 7 − 5 x < 1 x ≤ 0

Решить линейное неравенство – получить выражение вида:

x < c x ≤ c x > c x ≥ c

где c – некоторое число.

Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.

Если знак неравенства строгий > , < , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.

Смысл выколотой точки в том, что сама точка в ответ не входит.

Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.

Смысл жирной точки в том, что сама точка входит в ответ.

Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.

Таблица числовых промежутков

Неравенство	Графическое решение	Форма записи ответа
x < c		x ∈ ( − ∞ ; c )
x ≤ c		x ∈ ( − ∞ ; c ]
x > c		x ∈ ( c ; + ∞ )
x ≥ c		x ∈ [ c ; + ∞ )

Алгоритм решения линейного неравенства

Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:

a x < b a x ≤ b a x > b a x ≥ b

Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.

Если a > 0 то неравенство приобретает вид x ≤ b a .

Если a < 0 , то знак неравенства меняется на противоположный, неравенство приобретает вид x ≥ b a .

Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.

Примеры решения линейных неравенств:

№1. Решить неравенство 3 ( 2 − x ) > 18.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6 − 3 x > 18

− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )

Делим обе части неравенства на (-3) – коэффициент, который стоит перед x. Так как − 3 < 0 , знак неравенства поменяется на противоположный. x < 12 − 3 ⇒ x < − 4 Остается записать ответ (см. таблицу числовых промежутков).

Ответ: x ∈ ( − ∞ ; − 4 )

№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6 x + 4 ≥ 3 x + 3 − 14

6 x − 3 x ≥ 3 − 14 − 4

3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на (3) – коэффициент, который стоит перед x. Так как 3 > 0, знак неравенства после деления меняться не будет.

x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).

Ответ: x ∈ [ − 5 ; + ∞ )

Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).

Примеры:

№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6 x − 1 ≤ 6 x − 1

6 x − 6 x ≤ − 1 + 1

0 ≤ 0

Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.

Ответ:

x – любое число
x ∈ ( − ∞ ; + ∞ )
x ∈ ℝ

№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

x + 6 − 9 x > − 8 x + 48

− 8 x + 8 x > 48 − 6

0 > 42

Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.

Ответ: x ∈ ∅

Квадратные неравенства

Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c < 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная.

Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.

Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).

Алгоритм решения квадратного неравенства методом интервалов

Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .

Отметить на числовой прямой корни трехчлена.

Если знак неравенства строгий > , < , точки будут выколотые.

Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).

Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение a x 2 + b x + c вместо x.

Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Выбрать подходящие интервалы (или интервал).

Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.

Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.

Записать ответ.

Примеры решения квадратных неравенств:

№1. Решить неравенство x 2 ≥ x + 12.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

x 2 ≥ x + 12

x 2 − x − 12 ≥ 0

x 2 − x − 12 = 0

a = 1, b = − 1, c = − 12

D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:

x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0

Это значит, что знак на интервале, в котором лежит точка 6 будет +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ .

Точки -3 и 4 будут в квадратных скобках, так как они жирные.

Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )

№2. Решить неравенство − 3 x − 2 ≥ x 2 .

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

− 3 x − 2 ≥ x 2

− x 2 − 3 x − 2 ≥ 0

− x 2 − 3 x − 2 = 0

a = − 1, b = − 3, c = − 2

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1

x 1 = − 2, x 2 = − 1

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:

− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 < 0

Это значит, что знак на интервале, в котором лежит точка 0 будет − .

Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +.

Точки -2 и -1 будут в квадратных скобках, так как они жирные.

Ответ: x ∈ [ − 2 ; − 1 ]

№3. Решить неравенство 4 < x 2 + 3 x .

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

4 < x 2 + 3 x

− x 2 − 3 x + 4 < 0

− x 2 − 3 x + 4 = 0

a = − 1, b = − 3, c = 4

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1

x 1 = − 4, x 2 = 1

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:

− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 < 0

Это значит, что знак на интервале, в котором лежит точка 2, будет -.

Поскольку знак неравенства < , выбираем в ответ интервалы со знаком − .

Точки -4 и 1 будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )

№4. Решить неравенство x 2 − 5 x < 6.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

x 2 − 5 x < 6

x 2 − 5 x − 6 < 0

x 2 − 5 x − 6 = 0

a = 1, b = − 5, c = − 6

D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1

x 1 = 6, x 2 = − 1

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:

x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0

Это значит, что знак на интервале, в котором лежит точка 10 будет +.

Поскольку знак неравенства < , выбираем в ответ интервал со знаком -.

Точки -1 и 6 будут в круглых скобках, так как они выколотые

Ответ: x ∈ ( − 1 ; 6 )

№5. Решить неравенство x 2 < 4.

Решение:

Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.

x 2 < 4

x 2 − 4 < 0

x 2 − 4 = 0

( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2

x 1 = 2, x 2 = − 2

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:

x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0

Это значит, что знак на интервале, в котором лежит точка 3 будет +.

Поскольку знак неравенства < , выбираем в ответ интервал со знаком − .

Точки -2 и 2 будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − 2 ; 2 )

№6. Решить неравенство x 2 + x ≥ 0.

Решение:

Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.

x 2 + x ≥ 0

x 2 + x = 0

x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1

x 1 = 0, x 2 = − 1

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:

x 2 + x = 1 2 + 1 = 2 > 0

Это значит, что знак на интервале, в котором лежит точка 1 будет +.

Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.

Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )

Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.

Дробно рациональные неравенства

Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:

f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).

Примеры дробно рациональных неравенств:

x − 1 x + 3 < 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3

Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.

Алгоритм решения дробно рациональных неравенств:

Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):

f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя.

Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя.

В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.

Нанести нули числителя и нули знаменателя на ось x.

Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые.

Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.

Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.

Расставить знаки на интервалах.

Выбрать подходящие интервалы и записать ответ.

Примеры решения дробно рациональных неравенств:

№1. Решить неравенство x − 1 x + 3 > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.

Приравниваем числитель к нулю f ( x ) = 0.

x − 1 = 0

x = 1 — это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.

Приравниваем знаменатель к нулю g ( x ) = 0.

x + 3 = 0

x = − 3 — это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,

Это значит, что знак на интервале, в котором лежит точка 2 будет +.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.

Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )

№2. Решить неравенство 3 ( x + 8 ) ≤ 5.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Привести неравенство к виду f ( x ) g ( x ) ≤ 0.

3 ( x + 8 ) ≤ 5

3 ( x + 8 ) − 5 x + 8 ≤ 0

3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 x − 40 x + 8 ≤ 0

− 5 x − 37 x + 8 ≤ 0

Приравнять числитель к нулю f ( x ) = 0.

− 5 x − 37 = 0

− 5 x = 37

x = − 37 5 = − 37 5 = − 7,4

x = − 7,4 — ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.

Приравнять знаменатель к нулю g ( x ) = 0.

x + 8 = 0

x = − 8 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :

− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 < 0

Это значит, что знак на интервале, в котором лежит точка 0 будет -.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.

В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.

Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )

№3. Решить неравенство x 2 − 1 x > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.

Приравнять числитель к нулю f ( x ) = 0.

x 2 − 1 = 0

( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1

x 1 = 1, x 2 = − 1 — нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.

Приравнять знаменатель к нулю g ( x ) = 0.

x = 0 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :

x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )

Системы неравенств

Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств — это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.

Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.

Пример системы неравенств:

{ x + 4 > 0 2 x + 3 ≤ x 2

Алгоритм решения системы неравенств

Решить первое неравенство системы, изобразить его графически на оси x.

Решить второе неравенство системы, изобразить его графически на оси x.

Нанести решения первого и второго неравенств на ось x.

Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.

Примеры решений систем неравенств:

№1. Решить систему неравенств { 2 x − 3 ≤ 5 7 − 3 x ≤ 1

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

2 x − 3 ≤ 5

2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.

x ≤ 4 ;

Графическая интерпретация:

Точка 4 на графике жирная, так как знак неравенства нестрогий.

Решаем второе неравенство системы.

7 − 3 x ≤ 1

− 3 x ≤ 1 − 7

− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 < 0, знак неравенства после деления меняется на противоположный.

x ≥ 2

Графическая интерпретация решения:

Точка 2 на графике жирная, так как знак неравенства нестрогий.

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.

Ответ: x ∈ [ 2 ; 4 ]

№2. Решить систему неравенств { 2 x − 1 ≤ 5 1 < − 3 x − 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

2 x − 1 ≤ 5

2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.

x ≤ 3

Графическая интерпретация:

Точка 3 на графике жирная, так как знак неравенства нестрогий.

Решаем второе неравенство системы.

1 < − 3 x − 2

3 x < − 1 − 2

3 x < − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется.

x < − 1

Графическая интерпретация решения:

Точка -1 на графике выколотая, так как знак неравенства строгий.

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.

Ответ: x ∈ ( − ∞ ; − 1 )

№3. Решить систему неравенств { 3 x + 1 ≤ 2 x x − 7 > 5 − x

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

3 x + 1 ≤ 2 x

3 x − 2 x ≤ − 1

x ≤ − 1

Графическая интерпретация решения:

Решаем второе неравенство системы

x − 7 > 5 − x

x + x > 5 + 7

2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.

x > 6

Графическая интерпретация решения:

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.

Ответ: x ∈ ∅

№4. Решить систему неравенств { x + 4 > 0 2 x + 3 ≤ x 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

x + 4 > 0

x > − 4

Графическая интерпретация решения первого неравенства:

Решаем второе неравенство системы

2 x + 3 ≤ x 2

− x 2 + 2 x + 3 ≤ 0

Решаем методом интервалов.

− x 2 + 2 x + 3 = 0

a = − 1, b = 2, c = 3

D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16

D > 0 — два различных действительных корня.

x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1

Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.

Графическая интерпретация решения второго неравенства:

Наносим оба решения на ось x.

Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ .

Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.

Ответ: x ∈ ( − 4 ; − 1 ] ∪ [ 3 ; + ∞ )

Скачать домашнее задание к уроку 8.

Источник

Решение неравенства изображено под номером 4.

Пересекая решения обоих неравенств, получим, что решением системы является отрезок

Можно сразу заметить, что в знаменателе первого выражения стоит квадрат числа плюс положительное число, значит, знаменатель всегда больше нуля.

3) система не имеет решений

Решением системы является отрезок, изображённый под номером 1.

Решите систему неравенств

На каком рисунке изображено множество её решений?

В ответе укажите номер правильного варианта.

Решением системы является отрезок, изображённый под номером 2.

Правильный ответ указан под номером 2.

Решите систему неравенств

Используя тот факт, что знаменатель первого неравенства всегда больше нуля, преобразуем систему неравенств:

А куда делся знаменатель в первой части? Его можно просто так выкидывать?

Никита, знаменатель в первом уравнении всегда больше ноля, поэтому мы его не учитываем.

Решите систему неравенств

На каком из рисунков изображено множество её решений?

В ответе укажите номер правильного варианта.

Правильный ответ указан под номером 3.

Найдите наибольшее значение , удовлетворяющее системе неравенств

Значит, наибольшее значение удовлетворяющее данной системе неравенств −3.

и определите, на каком рисунке изображено множество его решений.

В ответе укажите номер правильного варианта.

Решение неравенства изображено на рис. 1.

Правильный ответ указан под номером 1.

Решите систему неравенств

Преобразуем систему неравенств:

Аналоги к заданию № 338522: 341418 Все

Укажите решение системы неравенств:

Данное решение соответствует варианту 2).

Аналоги к заданию № 348461: 348486 Все

Решение какого из данных неравенств изображено на рисунке?

В ответе укажите номер правильного варианта.

Решим каждое из неравенств.

1) &nbsp — решений нет.

2) &nbsp

3) &nbsp верно для всех

4) &nbsp

На рисунке изображено решение четвёртого неравенства.

Источник

Метод интервалов, решение неравенств

О чем эта статья:

Определение квадратного неравенства

Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.

Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

Квадратное неравенство выглядит так:

где x — переменная,

Квадратное неравенство можно решить двумя способами:

графический метод;
метод интервалов.

Решение неравенства графическим методом

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.

Как дискриминант влияет на корни уравнения:

D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два корня;
D

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.

Если неравенство со знаком

Плюс или минус: как определить знаки

Можно сделать вывод о знаках по значению старшего коэффициента a:

если a > 0, последовательность знаков: +, −, +,

если a 0, последовательность знаков: +, +,

если a 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.

Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.

Когда квадратный трехчлен корней не имеет (D
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.

Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.

Разложим квадратный трехчлен на множители.

Неравенство примет вид:

Проанализируем два сомножителя:

Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 > 0.

Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.

Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.

В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.

Построим чертеж.

Рассмотрим интервалы в том же порядке, как пишем и читаем: слева направо.
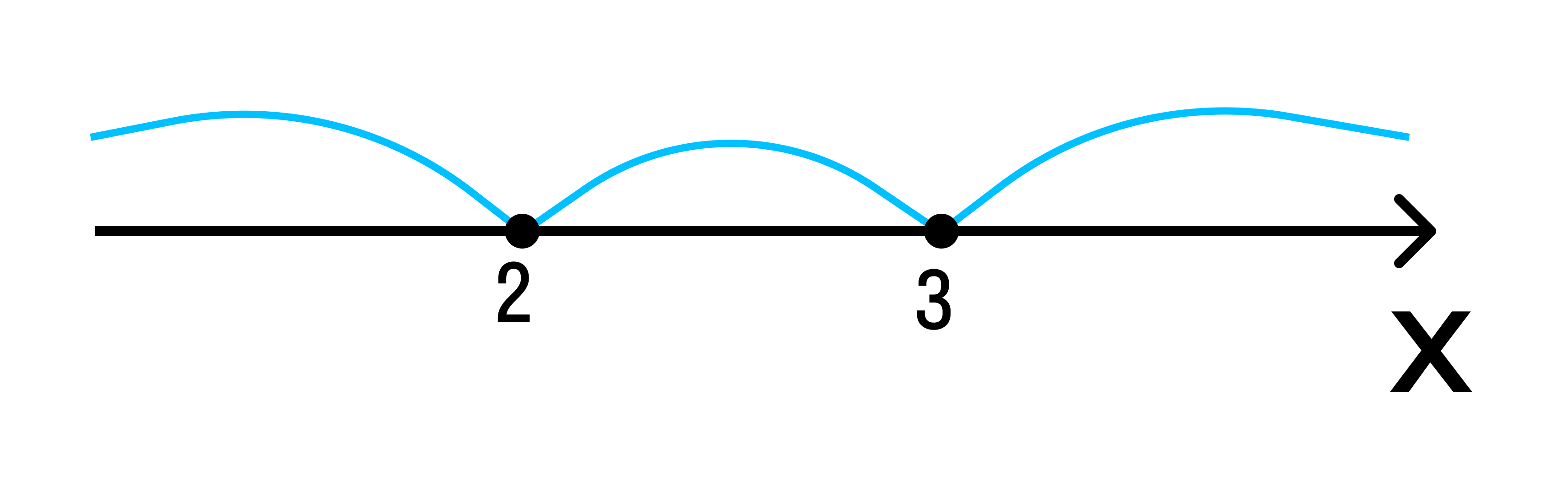
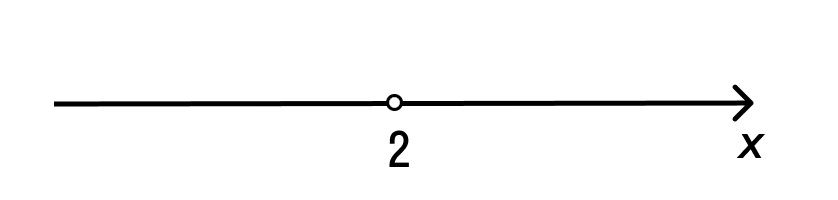
Отобразим эти данные на чертеже:

2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.

(25 — 3) (25 — 2) = 22*23 = 506 > 0

Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.

Исходное неравенство: (х — 3) * (х — 2) ≥ 0.

Если (х — 3) * (х — 2) > 0:

Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.

Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.

Пример 2. Применить метод интервалов для решения неравенства х2+4х+3

Источник

Решение линейных неравенств

О чем эта статья:

Основные понятия

Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.

Неравенство — это алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.

Линейные неравенства — это неравенства вида:

где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит сделать так, чтобы в левой части осталось только неизвестное в первой степени с коэффициентом равном единице.

Типы неравенств

Строгие — используют только больше (>) или меньше ( b — это значит, что a больше, чем b.

a > b и b > и

Линейные неравенства: свойства и правила

Вспомним свойства числовых неравенств:

Если а > b , то b а.

Если а > b и b > c, то а > c. И также если а b, то а + c > b+ c (и а – c > b – c).

Если же а b и c > d, то а + c > b + d.

Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.

Если а d, то а – c b, m — положительное число, то mа > mb и

Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).

Если же а > b, n — отрицательное число, то nа

Обе части можно умножить или разделить на одно отрицательное число, при этом знак поменять на противоположный.

Если а > b и c > d, где а, b, c, d > 0, то аc > bd.

Если а 0, то аc b, где а, b > 0, то а2 > b2, и если а b, где а, b > 0, то
b» height=»45″ src=»https://lh5.googleusercontent.com/MuRDPQeqxIZvVG_mHVaktFp6nlIEEbz8zdRs1ZW8CZbZacJrS4aKzrDyhKxXpJvc35TSAgiRpqr-63sGzL9_sPU80vFhR0ZDAmSmRFZtwEldDkWRttfSGuaJJIb7xWxZDugU3xTt»>

Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.

Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.

Свойства выше помогут нам использовать следующие правила.

Правила линейных неравенств

Любой член можно перенести из одной части в другую с противоположным знаком. Знак неравенства при этом не меняется.

2x − 3 > 6 ⇒ 2x > 6 + 3 ⇒ 2x > 9.

Обе части можно умножить или разделить на одно положительное число. Знак неравенства при этом не меняется.

Умножим обе части на пять 2x > 9 ⇒ 10x > 45.

Обе части можно умножить или разделить на одно отрицательное число. Знак неравенства при этом меняется на противоположный.

Разделим обе части на минус два 2x > 9 ⇒ 2x : –2 > 9 : -2 ⇒ x

Решение линейных неравенств

Со школьных уроков мы помним, что у неравенств нет ярко выраженных различий, поэтому рассмотрим несколько определений.

Определение 1. Линейное неравенство с неизвестной переменной x имеет вид ax + b > 0, когда вместо > используется любой знак c , где x — переменная, a, c — некоторые числа.

Мы не знаем может ли коэффициент равняться нулю, поэтому: 0 * x > c и 0 * x 0 — в первом и ax > c — во втором;

допустимость равенства нулю: a ≠ 0 — в первом, a = 0 — во втором.

Неравенства ax + b > 0 и ax > c равносильные, так как получены переносом слагаемого из одной части в другую.

Определение 3. Линейные неравенства с одной переменной x выглядят так:

где a и b — действительные числа. А на месте x может быть обычное число.

Равносильные преобразования

Для решения ax + b , ≥) нужно применить равносильные преобразования неравенства. Рассмотрим два случая: когда коэффициент равен и не равен нулю.

Алгоритм решения ax + b , ≥) является верным, когда исходное имеет решение при любом значении. Неверно тогда, когда исходное не имеет решений.

Рассмотрим пример: 0 * x + 5 > 0.

Как решаем:

Данное неравенство 0 * x + 5 > 0 может принимать любое значение x.

Получается верное числовое неравенство 5 > 0. Значит его решением может быть любое число.

Метод интервалов

Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.

Метод интервалов это:

введение функции y = ax + b;

поиск нулей для разбиения области определения на промежутки;

отметить полученные корни на координатной прямой;

определение знаков и отмечание их на интервалах.

Алгоритм решения ax + b , ≥) при a ≠ 0 с использованием метода интервалов:

найдем нули функции y = ax + b для решения уравнения ax + b = 0.

Если a ≠ 0, тогда решением будет единственный корень — х₀;

начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;

определим знаки функции y = ax + b на промежутках.

Для этого найдем значения функции в точках на промежутке;

если решение неравенства со знаками > или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если 0.

Как решаем:

В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,

Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.

Определим знаки на промежутках.

Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.

Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6 * 3 + 12 = − 6, − 6

Выполним решение со знаком >. Штриховку сделаем над положительным промежутком.

По чертежу делаем вывод, что решение имеет вид (−∞, 4) или x

Графический способ

Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.

Алгоритм решения y = ax + b графическим способом

во время решения ax + b 0 произвести определение промежутка, где график изображается выше Ох;

во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.

Рассмотрим пример: −5 * x − √3 > 0.

Как решаем

Так как коэффициент при x отрицательный, данная прямая является убывающей.

Координаты точки пересечения с Ох равны −√3 : 5.

Неравенство имеет знак >, значит нужно обратить внимание на промежуток выше оси Ох.

Поэтому открытый числовой луч (−∞, −√3 : 5) будет решением.

Ответ: (−∞, −√3 : 5) или x

Источник

Adblock
detector

Источник

где a и b — действительные числа. А на месте x может быть обычное число.

Для решения ax + b , ≥) нужно применить равносильные преобразования неравенства. Рассмотрим два случая: когда коэффициент равен и не равен нулю.

Алгоритм решения ax + b , ≥) является верным, когда исходное имеет решение при любом значении. Неверно тогда, когда исходное не имеет решений.

Рассмотрим пример: 0 * x + 5 > 0.

Как решаем:

Данное неравенство 0 * x + 5 > 0 может принимать любое значение x.
Получается верное числовое неравенство 5 > 0. Значит его решением может быть любое число.

Метод интервалов

Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.

Метод интервалов заключается в следующем:

вводим функцию y = ax + b;
ищем нули для разбиения области определения на промежутки;
отмечаем полученные корни на координатной прямой;
определяем знаки и отмечаем их на интервалах.

Алгоритм решения ax + b , ≥) при a ≠ 0 с использованием метода интервалов:

найдем нули функции y = ax + b для решения уравнения ax + b = 0.

Если a ≠ 0, тогда решением будет единственный корень — х₀;

начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;
определим знаки функции y = ax + b на промежутках.

Для этого найдем значения функции в точках на промежутке;

если решение неравенства со знаками > или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если 0.

Как решаем:

В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,

Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.

Определим знаки на промежутках.

Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.

Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6 * 3 + 12 = − 6, − 6

Графический способ

Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.

Алгоритм решения y = ax + b графическим способом

во время решения ax + b 0 определить промежуток, где график изображается выше Ох;
во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.

Рассмотрим пример: −5 * x − √3 > 0.

Как решаем

Так как коэффициент при x отрицательный, данная прямая является убывающей.
Координаты точки пересечения с Ох равны (−√3 : 5; 0).
Неравенство имеет знак >, значит нужно обратить внимание на промежуток выше оси Ох.
Поэтому открытый числовой луч (−∞, −√3 : 5) будет решением.

Ответ: (−∞, −√3 : 5) или x

Источник

Алгебра. Урок 8. Неравенства, системы неравенств.

Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Неравенства

Линейные неравенства

Неравенства

Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:

≥ больше или равно,

≤ меньше или равно,

то получится неравенство.

Линейные неравенства

Линейные неравенства – это неравенства вида:

a x b a x ≤ b a x > b a x ≥ b

где a и b – любые числа, причем a ≠ 0, x – переменная.

Примеры линейных неравенств:

3 x 5 x − 2 ≥ 0 7 − 5 x 1 x ≤ 0

Решить линейное неравенство – получить выражение вида:

x c x ≤ c x > c x ≥ c

где c – некоторое число.

Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.

Если знак неравенства строгий > , , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой .

Смысл выколотой точки в том, что сама точка в ответ не входит.

Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной .

Смысл жирной точки в том, что сама точка входит в ответ.

Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.

Таблица числовых промежутков

Алгоритм решения линейного неравенства

Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:

a x b a x ≤ b a x > b a x ≥ b

Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.

Если a > 0 то неравенство приобретает вид x ≤ b a .

Если a 0 , то знак неравенства меняется на противоположный , неравенство приобретает вид x ≥ b a .

Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.

Примеры решения линейных неравенств:

№1. Решить неравенство 3 ( 2 − x ) > 18.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )

Делим обе части неравенства на ( -3 ) – коэффициент, который стоит перед x . Так как − 3 0 , знак неравенства поменяется на противоположный . x 12 − 3 ⇒ x − 4 Остается записать ответ (см. таблицу числовых промежутков).

Ответ: x ∈ ( − ∞ ; − 4 )

№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6 x + 4 ≥ 3 x + 3 − 14

6 x − 3 x ≥ 3 − 14 − 4

3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на ( 3 ) – коэффициент, который стоит перед x . Так как 3 > 0, знак неравенства после деления меняться не будет.

x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).

Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).

№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6 x − 6 x ≤ − 1 + 1

Получили верное неравенство, которое не зависит от переменной x . Возникает вопрос, какие значения может принимать переменная x , чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.

Ответ:

x – любое число
x ∈ ( − ∞ ; + ∞ )
x ∈ ℝ

№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

x + 6 − 9 x > − 8 x + 48

− 8 x + 8 x > 48 − 6

Получили неверное равенство, которое не зависит от переменной x . Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.

Квадратные неравенства

Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная.

Алгоритм решения квадратного неравенства методом интервалов

Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .

Отметить на числовой прямой корни трехчлена.

Если знак неравенства строгий > , , точки будут выколотые.

Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).

Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A ) и подставить её значение в выражение a x 2 + b x + c вместо x .

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Выбрать подходящие интервалы (или интервал).

Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.

Если знак неравенства или ≤ в ответ выбираем интервалы со знаком -.

Примеры решения квадратных неравенств:

№1. Решить неравенство x 2 ≥ x + 12.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

a = 1, b = − 1, c = − 12

D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3

Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6 . Подставляем эту точку в исходное выражение:

x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0

Это значит, что знак на интервале, в котором лежит точка 6 будет +.

Точки -3 и 4 будут в квадратных скобках, так как они жирные.

Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )

№2. Решить неравенство − 3 x − 2 ≥ x 2 .

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

a = − 1, b = − 3, c = − 2

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1

x 1 = − 2, x 2 = − 1

Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение:

− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0

Это значит, что знак на интервале, в котором лежит точка 0 будет − .

Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +.

Точки -2 и -1 будут в квадратных скобках, так как они жирные.

Ответ: x ∈ [ − 2 ; − 1 ]

№3. Решить неравенство 4 x 2 + 3 x .

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

a = − 1, b = − 3, c = 4

D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1

Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение:

− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0

Это значит, что знак на интервале, в котором лежит точка 2 , будет -.

Поскольку знак неравенства , выбираем в ответ интервалы со знаком − .

Точки -4 и 1 будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )

№4. Решить неравенство x 2 − 5 x 6.

Решение:

Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.

a = 1, b = − 5, c = − 6

D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49

D > 0 ⇒ будет два различных действительных корня

x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1

Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:

x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0

Это значит, что знак на интервале, в котором лежит точка 10 будет +.

Поскольку знак неравенства , выбираем в ответ интервал со знаком -.

Точки -1 и 6 будут в круглых скобках, так как они выколотые

Ответ: x ∈ ( − 1 ; 6 )

№5. Решить неравенство x 2 4.

Решение:

Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.

( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2

Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3 . Подставляем эту точку в исходное выражение:

x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0

Это значит, что знак на интервале, в котором лежит точка 3 будет +.

Поскольку знак неравенства , выбираем в ответ интервал со знаком − .

Точки -2 и 2 будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − 2 ; 2 )

№6. Решить неравенство x 2 + x ≥ 0.

Решение:

Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.

x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1

Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1 . Подставляем эту точку в исходное выражение:

x 2 + x = 1 2 + 1 = 2 > 0

Это значит, что знак на интервале, в котором лежит точка 1 будет +.

Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.

Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )

Дробно рациональные неравенства

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

Примеры дробно рациональных неравенств:

x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3

Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.

Алгоритм решения дробно рациональных неравенств:

Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):

f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0

Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя .

Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя .

Нанести нули числителя и нули знаменателя на ось x .

Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые .

Если знак неравенства строгий ,
при нанесении на ось x нули числителя выколотые .

Если знак неравенства нестрогий ,
при нанесении на ось x нули числителя жирные .

Расставить знаки на интервалах.

Выбрать подходящие интервалы и записать ответ.

Примеры решения дробно рациональных неравенств:

№1. Решить неравенство x − 1 x + 3 > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.

Приравниваем числитель к нулю f ( x ) = 0.

x = 1 — это ноль числителя . Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.

Приравниваем знаменатель к нулю g ( x ) = 0.

x = − 3 — это ноль знаменателя . При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства) .

Наносим нули числителя и нули знаменателя на ось x .

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,

Это значит, что знак на интервале, в котором лежит точка 2 будет +.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.

Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )

№2. Решить неравенство 3 ( x + 8 ) ≤ 5.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Привести неравенство к виду f ( x ) g ( x ) ≤ 0.

3 ( x + 8 ) − 5 x + 8 ≤ 0

3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 ( x + 8 ) x + 8 ≤ 0

3 − 5 x − 40 x + 8 ≤ 0

− 5 x − 37 x + 8 ≤ 0

Приравнять числитель к нулю f ( x ) = 0.

x = − 37 5 = − 37 5 = − 7,4

x = − 7,4 — ноль числителя . Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.

Приравнять знаменатель к нулю g ( x ) = 0.

x = − 8 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x .

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) :

− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0

Это значит, что знак на интервале, в котором лежит точка 0 будет -.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.

Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )

№3. Решить неравенство x 2 − 1 x > 0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.

Приравнять числитель к нулю f ( x ) = 0.

( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1

x 1 = 1, x 2 = − 1 — нули числителя . Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.

Приравнять знаменатель к нулю g ( x ) = 0.

x = 0 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).

Наносим нули числителя и нули знаменателя на ось x .

Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) :

x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.

Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.

В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.

Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )

Системы неравенств

Пример системы неравенств:

Алгоритм решения системы неравенств

Решить первое неравенство системы, изобразить его графически на оси x .

Решить второе неравенство системы, изобразить его графически на оси x .

Нанести решения первого и второго неравенств на ось x .

Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.

Примеры решений систем неравенств:

№1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.

Точка 4 на графике жирная, так как знак неравенства нестрогий.

Решаем второе неравенство системы.

− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный.

Графическая интерпретация решения:

Точка 2 на графике жирная, так как знак неравенства нестрогий.

Наносим оба решения на ось x .

Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается на отрезке от 2 до 4 . Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.

№2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.

Точка 3 на графике жирная, так как знак неравенства нестрогий.

Решаем второе неравенство системы.

3 x − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется.

Графическая интерпретация решения:

Точка -1 на графике выколотая, так как знак неравенства строгий.

Наносим оба решения на ось x .

Выбираем подходящие участки и записываем ответ.

Ответ: x ∈ ( − ∞ ; − 1 )

№3. Решить систему неравенств < 3 x + 1 ≤ 2 x x − 7 >5 − x

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

Графическая интерпретация решения:

Решаем второе неравенство системы

2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.

Графическая интерпретация решения:

Выбираем подходящие участки и записываем ответ.

Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.

№4. Решить систему неравенств < x + 4 >0 2 x + 3 ≤ x 2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

Решаем первое неравенство системы.

Графическая интерпретация решения первого неравенства:

Решаем второе неравенство системы

Решаем методом интервалов.

a = − 1, b = 2, c = 3

D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16

D > 0 — два различных действительных корня.

x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1

Графическая интерпретация решения второго неравенства:

Выбираем подходящие участки и записываем ответ.

Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.

Источник

Adblock
detector

Неравенство	Графическое решение	Форма записи ответа
x c

Источник