Как найти какой треугольник по 3 сторонам - Исправление недочетов и поиск решений вместе с Examum.ru

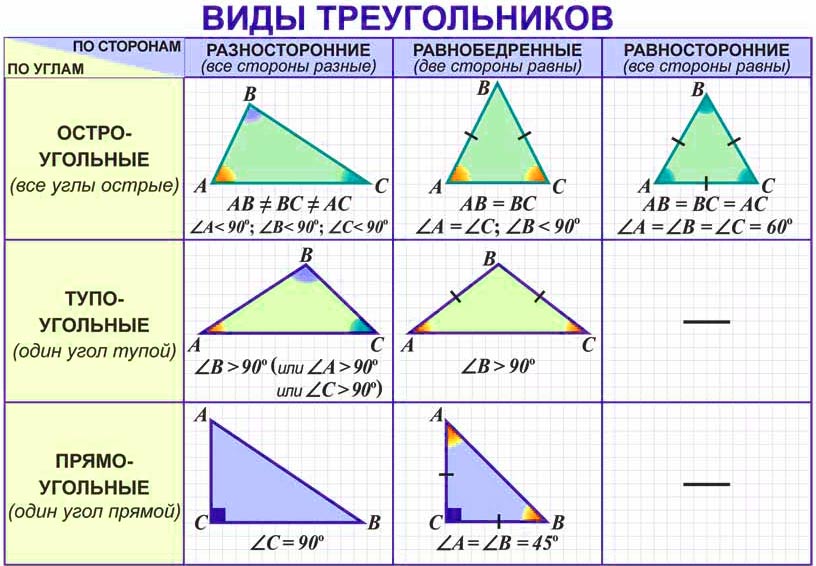
Определение вида треугольника по длинам его сторон

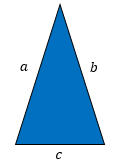
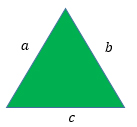
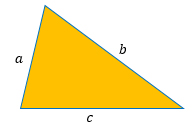
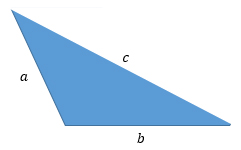
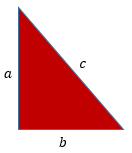
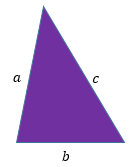
Пусть а, b и c — стороны треугольника, тогда

1) если а = b, то треугольник равнобедренный.

2) если а = b = c, то треугольник равносторонний.

3) если а ≠ b ≠ с, то треугольник разносторонний.

Пусть с — бóльшая сторона, тогда

4) если с² > a² + b², то треугольник тупоугольный.

5) если с² = a² + b², то треугольник прямоугольный.

6) если с² < a² + b², то треугольник остроугольный.

Успешной сдачи экзаменов!

С уважением, Васильева Анна.

Источник

Онлайн калькулятор поможет узнать по сторонам, является ли треугольник прямоугольным, равнобедренным, равносторонним или разносторонним.

Как определить, что треугольник прямоугольный: по Теорема Пифагора — сумма квадратов длин катетов равна квадрату длины гипотенузы
c² = a² + b²
Как определить, что треугольник равнобедренный: один из признаков равнобедренного треугольника — две стороны равны.
Как определить, что треугольник равносторонний: все стороны равны.

Принято выделять три типа треугольников:
тупоугольные — один из углов более 90 градусов,
прямоугольные — один из угол равен 90 градусов,
остроугольные — все углы менее 90 градусов.
Это классификация по типу углов.

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также

Источник

Математика, 3 класс. Урок № 61

Виды треугольников (по соотношению сторон). Закрепление

Перечень вопросов, рассматриваемых в теме:

Какие виды треугольников различают по соотношению сторон?

Как определить вид треугольника?

Глоссарий по теме:

Виды треугольников по сторонам:

равносторонние
равнобедренные
разносторонние

Равносторонний треугольник (или правильный треугольник) — это треугольник, у которого все три стороны равны.

Равнобедренный треугольник — это треугольник, у которого две стороны равны.

Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.

Отрезки равной длины на чертеже отмечают равным количеством черточек:

разносторонний треугольник

равносторонний треугольник

равнобедренный треугольник

Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника.

Основная и дополнительная литература по теме урока:

1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 73-80.

2. Волкова С. И. Карточки с математическими заданиями 3 кл. — М.: Просвещение, 2018.

3. Волкова С.И. математика. Тесты. 3 кл. — М.: Просвещение, 2018. С. 54-59.

4. Рудницкая В. Н. Математика. Дидактические материалы.ч.1 3 кл. – М. «Вентана- Граф», 2016, с. 47-53.

Теоретический материал для самостоятельного изучения

В огромном мире Математики есть очень интересная страна с красивым названием Геометрия. Эту страну населяют не числа, а различные линии и фигуры, плоские и объёмные. Сегодня, путешествуя по стране Геометрии, мы посетим город Треугольников.

Конечно, вы уже умеете отличать треугольники от других геометрических фигур. Но у жителей этого города есть, что рассказать о себе. И этих тайн так много, что вы будете их открывать все школьные годы.

Сегодня вы откроете некоторые секреты треугольников и подружитесь с жителями этого города.

Мы посетим город Треугольников.

Что вы уже знаете о жителях этого города?

Их легко отличить от других геометрических фигур по трём сторонам и трём углам.

У вас появились идеи по поводу названий этих треугольников?

Оказывается, по длине сторон все треугольники можно разделить на 3 вида:

те, у которых все стороны разные – разносторонние,

те, у которых имеются две равные стороны – равнобедренные,

а те, у которых все стороны равны – равносторонние.

Для того чтобы безошибочно определить вид треугольника по сторонам необходимо измерить все три стороны.

Теперь легко определить вид треугольника.

У первого треугольника все стороны разные, значит он разносторонний, у второго две стороны одинаковые, значит он равнобедренный, а у третьего все три стороны равны, значит он равносторонний.

Часто вид треугольника можно определить на глаз.

Попробуйте определить виды треугольников без измерений.

Проверим.

Разносторонний

– 1, 2, 4, 7

Равнобедренный

– 3 и 5

Равносторонний – 6

Сделаем вывод:

По сторонам различают 3 вида треугольников: разносторонние, равнобедренные и равносторонние.

Определить вид треугольника можно тремя способами: с помощью измерений, на глаз и по условным обозначениям.

Отрезки равной длины на чертеже отмечают равным количеством черточек:

разносторонний треугольник

равносторонний треугольник

равнобедренный треугольник

Теперь вы можете различать виды треугольников по сторонам. Эти знания необходимы в стране Геометрии.

Задания тренировочного модуля:

1. Выберите правильный ответ

Как называется треугольник, у которого все стороны равны?

a. одинаковосторонний треугольник
б. похожесторонний треугольник
в. равносторонний треугольник
г. равнодлинный треугольник

Правильные варианты ответов:

в. равносторонний треугольник

2. Закончите предложения:

Равносторонний треугольник— это треугольник, у которого ………………………….

Равнобедренный треугольник — это треугольник, у которого ………………………..

Разносторонний треугольник — треугольник, все стороны которого ………………………..

Правильные варианты ответов:

Равносторонний треугольник — это треугольник, у которого все три стороны равны.

Равнобедренный треугольник — это треугольник, у которого две стороны равны.

Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.

3. Определите вид треугольника по сторонам и выпишите номера треугольников по порядку:

Правильный вариант:

Равносторонние – 2,3
Равнобедренные – 1, 6
Разносторонние – 4, 5

4. Рассортируйте таблички по категориям.

Разносторонний треугольник	Равнобедренный треугольник	Равносторонний треугольник

9 см, 9 см, 9 см

4 см, 6 см, 4 см

5 см, 7 см, 11см

9 см, 12 см, 9 см

8 см, 3 см, 6 см

6 см, 6 см, 6 см

Правильный вариант

Разносторонний треугольник	Равнобедренный треугольник	Равносторонний треугольник
5 см, 7 см, 11 см	4 см, 6 см, 4 см	6 см, 6 см, 6 см
8 см, 3 см, 6 см	9 см, 12 см, 9 см	9 см, 9 см, 9 см

Источник

Download Article

Determining if three side lengths can make a triangle is easier than it looks. All you have to do is use the Triangle Inequality Theorem, which states that the sum of two side lengths of a triangle is always greater than the third side. If this is true for all three combinations of added side lengths, then you will have a triangle.^[1]

Steps

1
Learn the Triangle Inequality Theorem. This theorem simply states that the sum of two sides of a triangle must be greater than the third side. If this is true for all three combinations, then you will have a valid triangle. You’ll have to go through these combinations one by one to make sure that the triangle is possible. You can also think of the triangle as having the side lengths a, b, and c and the theorem being an inequality, which states: a+b > c, a+c > b, and b+c > a.^[2]
- For this example, a = 7, b = 10, and c = 5.
2

Check to see if the sum of the first two sides is greater than the third. In this case, you can add the sides a and b, or 7 + 10, to get 17, which is greater than 5. You can also think of it as 17 > 5.^[3]

Advertisement
3

Check to see if the sum of the next combination of two sides is greater than the remaining side. Now, just see if the sum of sides a and c are greater than the side b.^[4] This means you should see if 7 + 5, or 12, is greater than 10. 12 > 10, so it is.
4

Check to see if the sum of the last combination of two sides is greater than the remaining side. You need to see if the sum of side b and side c is greater than side a. To do this, you’ll need to see if 10 + 5 is greater than 7. 10 + 5 = 15, and 15 > 7, so the triangle passes on all sides.^[5]
5
Check your work. Now that you’ve checked the side combinations one by one, you can double check that the rule is true for all three combinations. If the sum of any two side lengths is greater than the third in every combination, as it is for this triangle, then you’ve determined that the triangle is valid. If the rule is invalid for even just one combination, then the triangle is invalid. Since the following statements are true, you’ve found a valid triangle:^[6]
- a + b > c = 17 > 5
- a + c > b = 12 > 10
- b + c > a = 15 > 7
6
Know how to spot an invalid triangle. Just for practice, you should make sure you can spot a triangle that doesn’t work as well.^[7] Let’s say you’re working with these three side lengths: 5, 8, and 3. Let’s see if it passes the test:
- 5 + 8 > 3 = 13 > 3, so one side passes.
- 5 + 3 > 8 = 8 > 8. Since this is invalid, you can stop right here. This triangle is not valid.

Calculator, Practice Problems, and Answers

Add New Question

Question

What if the sides are equal?

Then you have an equilateral triangle.
Question

Can three equal side lengths form a triangle?

Yes. It’s called an equilateral triangle, and it can work because two side lengths added together are bigger than the third side.
Question

What if the addition of the two sides is the same as the other side?

The resulting figure is not a triangle, because the two smaller sides must be on top of the larger side in order to connect to the larger segment’s endpoints. This figure has no area, and is a line segment, not a triangle.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

This is foolproof as long as you do the math right, and it is basic addition, so it is very simple.

Thanks for submitting a tip for review!

About This Article

Article SummaryX

To determine if 3 side lengths are a triangle, use the triangle inequality theorem, which states that the sum of 2 sides of a triangle must be greater than the third side. Therefore, all you have to do is add together each combination of 2 sides to see if it’s greater than the third side. If each combination is, the 3 side lengths are a triangle, but if one or more of them isn’t, it’s not a triangle. To see examples of how to apply the triangle equality theorem, keep reading!

Did this summary help you?

Thanks to all authors for creating a page that has been read 950,517 times.

Did this article help you?

Источник

Содержание

— Как определить остроугольный треугольник зная его стороны?
— Как доказать что треугольник прямоугольный по сторонам?
— Как определить треугольник по 3 сторонам?
— Как узнать существует ли треугольник со сторонами?
— Как определить тип треугольника по длине сторон?
— Как определить Остроугольный?
— Чему равны стороны треугольника?
— В чем заключается неравенство треугольника?

Как определить остроугольный треугольник зная его стороны?

Если квадрат максимальной стороны меньше суммы квадратов других сторон треугольника, значит, он является остроугольным.

Как доказать что треугольник прямоугольный по сторонам?

Так вот, прямоугольный треугольник обладает такими свойствами:

Сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы
Медиана прямоугольного треугольника равна половины гипотенузы
сумма двух острых углов прямоугольного треугольника равна 90 градусов

Как определить треугольник по 3 сторонам?

У треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто «лягут» на третью и треугольника не получится. Пользователь вводит длины трех сторон.

Как узнать существует ли треугольник со сторонами?

Треугольник существует только тогда, когда сумма двух его сторон больше третьей. Требуется сравнить каждую сторону с суммой двух других. Если хотя бы в одном случае сторона окажется больше либо равна сумме двух других, то треугольника с такими сторонами не существует.

Как определить тип треугольника по длине сторон?

Если выполняется теорема Пифагора: с²=a²+b² , где с — наибольшая сторона, а и b две других, – треугольник прямоугольный. Если квадрат наибольшей стороны меньше суммы квадратов двух других сторон: с² < a²+b² треугольник остроугольный.

Как определить Остроугольный?

В зависимости от углов треугольник может быть:

Прямоугольным, если один из углов равен 90 градусов;
Тупоугольный, если один из углов тупой, т. е. больше 90 градусов;
Остроугольным, если все углы треугольника острые.

Чему равны стороны треугольника?

По числу равных сторон

Равнобедренный треугольник — две стороны равны. Равносторонним треугольник или правильный треугольник — все три стороны равны.

В чем заключается неравенство треугольника?

Нера́венство треуго́льника в геометрии, функциональном анализе и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда меньше суммы длин двух его других сторон.

Интересные материалы:

Что насыпать под тротуарную плитку?
Что нужно для укладки клинкерной плитки?
Что нужно класть под тротуарную плитку чтоб не росла трава?
Что нужно стелить под тротуарную плитку?
Что подложить под плитку чтобы не росла трава?
Что подсыпают под тротуарную плитку?
Что положить под тротуарную плитку?
Что прочнее керамогранит или керамическая плитка?
Что прочнее плитка или керамогранит?
Что стелить под тротуарную плитку?

Источник