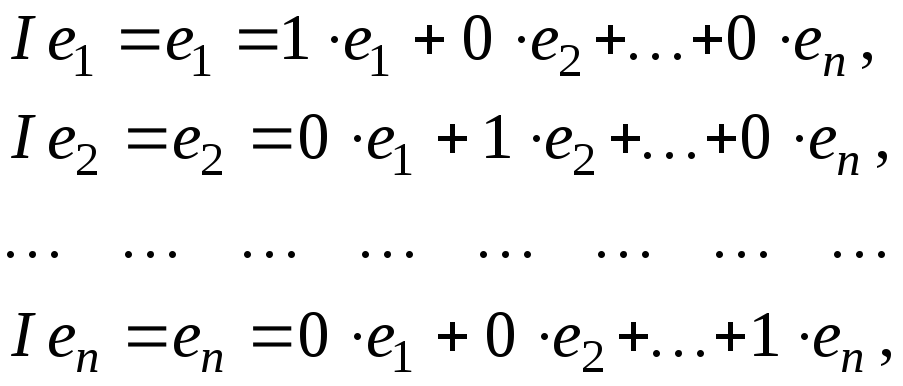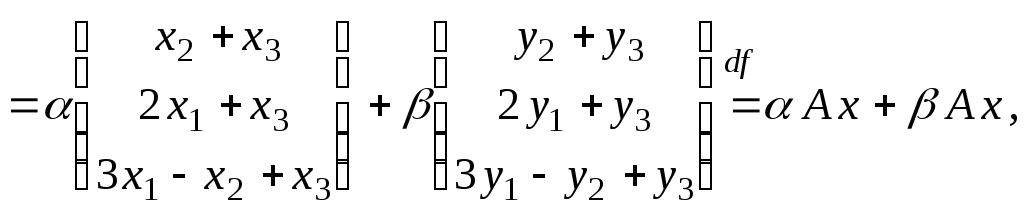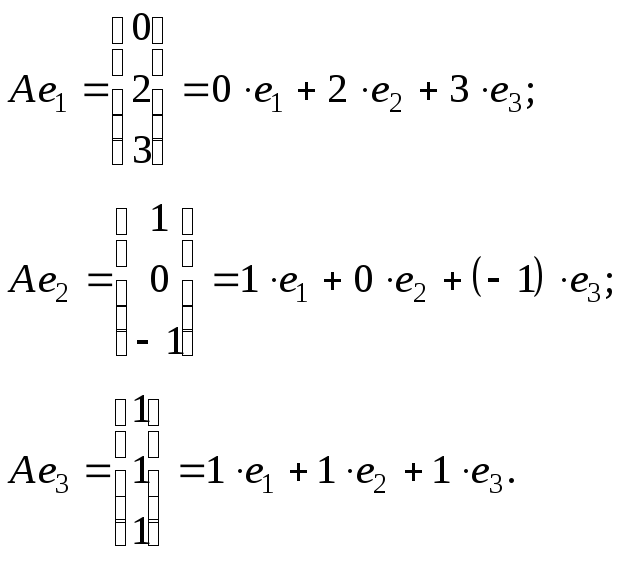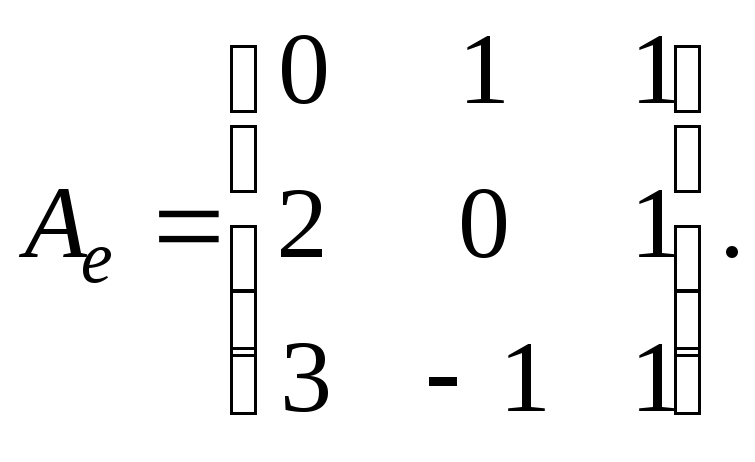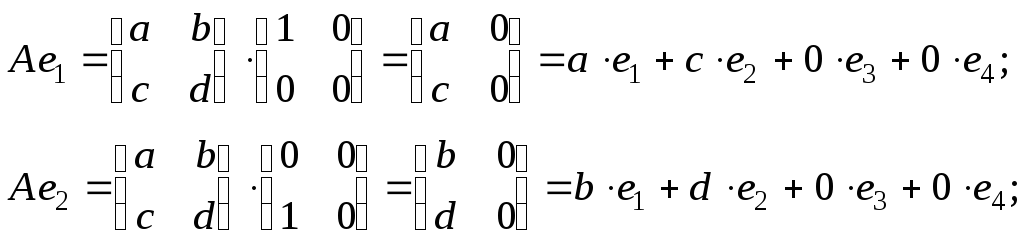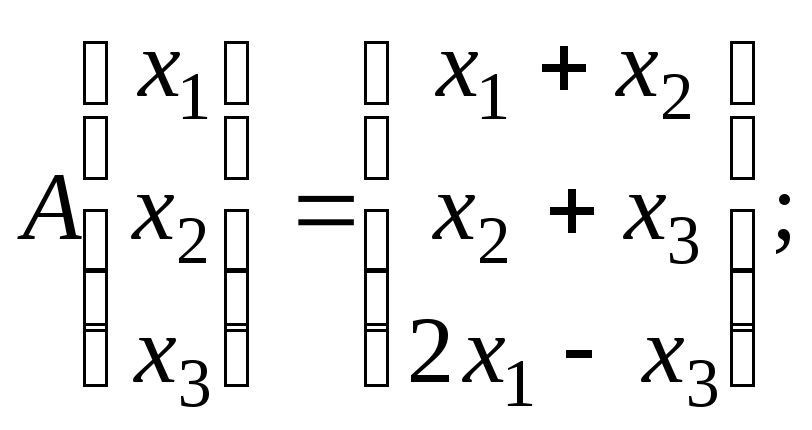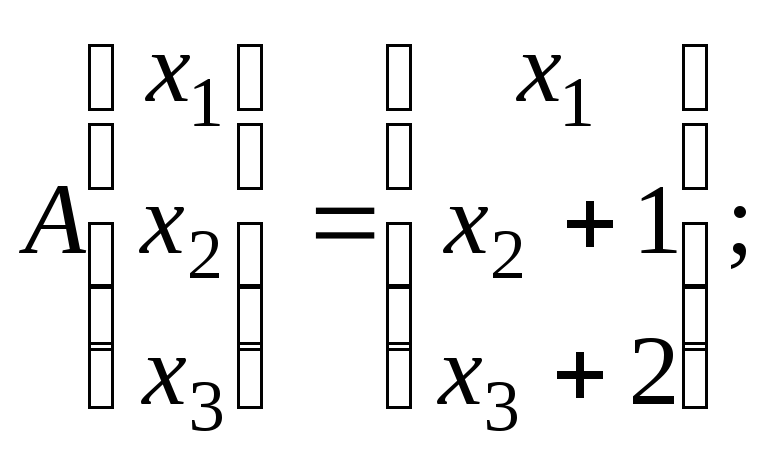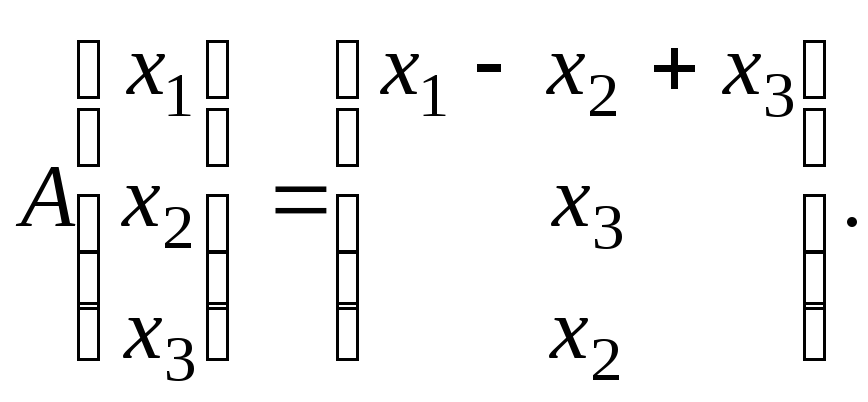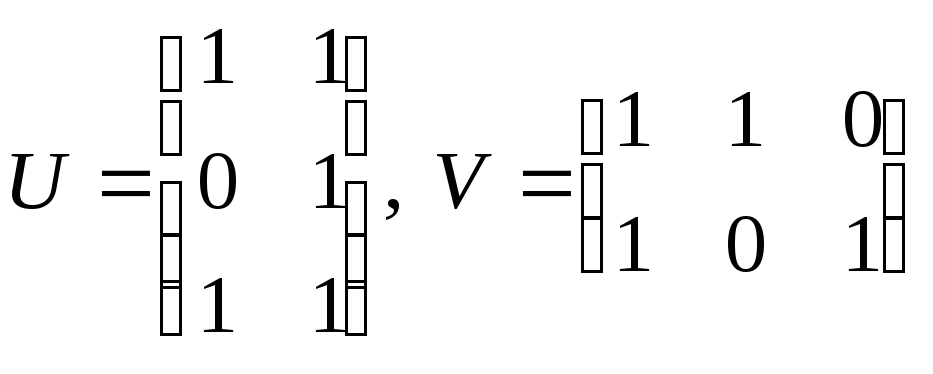Как найти канонический базис линейного оператора

Канонический вид линейного оператора (преобразования)

Матрица линейного преобразования n-мерного линейного пространства определяется относительно его базиса. Выбирая разные базисы, получаем разные матрицы одного и того же преобразования. Поэтому возникает задача приведения линейного преобразования к каноническому виду: требуется найти такой базис пространства , в котором матрица преобразования имеет наиболее простой вид. Упрощение матрицы преобразования позволяет выяснить его структуру, представить в виде композиции простых преобразований. Например, если в некотором базисе матрица преобразования оказывается диагональной, то с геометрической точки зрения это преобразование сводится к гомотетиям вдоль каждого из направлений базисных векторов. Кроме того, приведение преобразований к каноническому виду позволяет сравнивать различные преобразования. Все преобразования, которые имеют одинаковый канонический вид, эквивалентны, так как обладают одинаковыми свойствами.

Ранее были рассмотрены задачи приведения матрицы к диагональному виду и к жордановой нормальной форме при помощи преобразования подобия. В этом разделе аналогичные задачи рассматриваются для линейного преобразования.

---

Приведение линейного оператора (преобразования) к диагональному виду

Говорят, что линейное преобразование n-мерного линейного пространства приводится к диагональному виду, если существует базис, в котором матрица преобразования диагональная, т.е. , где — некоторые числа, среди которых могут быть равные. Если преобразование приводится к диагональному виду, то оно называется диагонализируемым.

Ранее было сформулировано необходимое и достаточное условие приводимости матрицы к диагональному виду. Переформулируем это условие для линейного преобразования: линейное преобразование приводится к диагональному виду тогда и только тогда, когда в пространстве существует базис из собственных векторов.

Действительно, предположим, что в базисе матрица преобразования имеет диагональный вид

Найдем образ . Умножая матрицу на координатный столбец базисного вектора , получаем . Значит, , т.е. вектор является собственным, а преобразование действует в подпространстве как гомотетия (с коэффициентом ). Аналогичный вывод можно сделать и про другие базисные векторы. Следовательно, базис пространства состоит из собственных векторов . Необходимость доказана. Достаточность доказывается путем приведения тех же рассуждений, но в обратном порядке.

Критерий диагонализируемости линейного преобразования можно сформулировать иначе.

---

Теорема (9.7) о диагонализируемости линейного преобразования (оператора)

Для того чтобы линейное преобразование (оператор) приводилось к диагональному виду, необходимо и достаточно, чтобы все корни характеристического многочлена являлись собственными значениями преобразования и геометрическая кратность каждого собственного значения была равна его алгебраической кратности.

Достаточность следует из теорем 9.5 и 9.6. Действительно, если для каждого из различных собственных значений геометрическая кратность равна алгебраической кратности, то , т.е. для всех . Поэтому в равенстве (9.9) корневые подпространства можно заменить собственными: . Выбрав в каждом собственном подпространстве базис и объединив все эти базисы в единую систему, получим базис всего пространства, составленный из собственных векторов. Достаточность доказана. Необходимость доказывается путем приведения тех же рассуждений, но в обратном порядке.

Ранее было доказано, что существование линейно независимых собственных векторов необходимо и достаточно для диагонализируемости матрицы при помощи преобразования подобия. Теорема 9.7 дает более тонкое условие диагонализируемости матрицы линейного преобразования. Отмечалось также, что не всякую матрицу можно привести к диагональному виду при помощи преобразования подобия (см. пример 7.9). Аналогичный вывод справедлив и для линейного преобразования.

Следствие 1. Если характеристическое уравнение линейного преобразования комплексного (вещественного) пространства имеет попарно различных комплексных (действительных) корней (короче говоря, преобразование имеет простой спектр), то это преобразование приводится к диагональному виду.

Действительно, в этом случае алгебраическая и геометрическая кратности каждого собственного значения равны единице.

Следствие 2. Если сумма размерностей всех собственных подпространств линейного преобразования равна размерности линейного пространства , то линейное преобразование приводится к диагональному виду.

---

Пример 9.2. Линейное преобразование в базисе имеет матрицу . Привести это преобразование к диагональному виду, т.е. найти базис , в котором матрица преобразования имеет диагональный вид, и найти эту диагональную матрицу.

Решение. Задача сводится к нахождению собственных векторов и собственных значений преобразования. Применяем для их нахождения алгоритм, рассмотренный ранее.

1. Выбираем базис , в котором задана матрица преобразования.

2-5. Собственные значения и собственные векторы этой матрицы, а также ее диагональный вид были найдены в примере 7.10:

Осталось по координатным столбцам записать искомый базис

---

Приведение линейного преобразования к каноническому виду

Говорят, что линейное преобразование n-мерного линейного пространства приводится к каноническому виду, если существует базис, в котором матрица преобразования имеет нормальную жорданову форму. Такой базис называется жордановым.

Напомним, что жордановой клеткой r-то порядка, соответствующей собственному значению , называют квадратную матрицу r-го порядка (7.35):

Жордановой матрицей называют блочно-диагональную матрицу вида (7.38):

на диагонали которой стоят жордановы клетки (9.10), причем среди собственных значений могут быть равные, порядки жордановых клеток (всех или некоторых) могут совпадать.

---

Существование и структура жорданова базиса

Пусть преобразование имеет собственный вектор , соответствующий собственному значению . Вектор , удовлетворяющий условию , называется присоединенным вектором 1-го порядка. Вектор , удовлетворяющий условию , называется присоединенным вектором 2-го порядка и т.д. Присоединенный вектор p-го порядка определяется соотношением , где — присоединенный вектор (p-l)-го порядка.

Определение присоединенных векторов можно записать эквивалентным образом, используя преобразование (характеристическое преобразование для преобразования ): вектор является присоединенным p-го порядка, если , где — собственный вектор преобразования .

Действительно, при из условия получаем , то есть . При из условия имеем . Отсюда , то есть и т.д. Заметим, что присоединенный вектор p-го порядка по определению удовлетворяет одновременно двум условиям: и , так как собственный вектор ненулевой, , поскольку .

Необходимость рассмотрения присоединенных векторов объясняется следующим свойством: жорданов базис состоит из собственных и присоединенных векторов линейного преобразования, взятых в определенном порядке.

Предположим, что в базисе пространства матрица преобразования имеет жорданову форму (9.11). Рассмотрим преобразование первых базисных векторов ( — порядок первой жордановой клетки в (9.11)). Умножая координатный столбец базисного вектора на матрицу с учетом (9.10), получаем , то есть . Следовательно, вектор — собственный. Умножая матрицу на координатный столбец базисного вектора , получаем , то есть . Следовательно, — присоединенный вектор (1-го порядка). Аналогично заключаем, что векторы также присоединенные (от второго до ()-гo порядков соответственно). Для других жордановых клеток выводы аналогичные.

Таким образом, жорданов базис составляют собственные и присоединенные векторы, взятые в следующем порядке (базисные векторы удобно обозначить иначе):

где — собственные векторы, а остальные векторы — соответственно присоединенные к ним, . Каждой из жордановых клеток в (9.11) отвечает одна группа векторов в (9.12). Количество собственных векторов в (9.12) равно количеству жордановых клеток в (9.11). Перестановке групп векторов в базисе (9.12) соответствует перестановка жордановых клеток в (9.11), при этом форма матрицы остается жордановой.

Докажем существование жорданова базиса для преобразования n-мерного линейного пространства при условии, что все корни характеристического уравнения являются собственными значениями преобразования .

Сначала рассмотрим случай, когда преобразование имеет единственное собственное значение . В этом случае в прямой сумме (9.9) имеется одно слагаемое (см. теорему 9.5), а цепочка (9.8) инвариантных подпространств имеет вид

где , а — наименьшее натуральное число, при котором . Здесь, как и ранее, — характеристическое преобразование для преобразования .

Каждое подпространство , состоит из собственных векторов (которые образуют собственное подпространство ) и присоединенных векторов первого, второго и т.д. до (p-l)-ro порядка включительно. Действительно, присоединенный вектор определяется равенством , где — собственный вектор. Тогда , то есть .

Будем строить базис корневого подпространства следующим образом. Так как не совпадает с , то существует максимальная линейно независимая над подпространством система присоединенных векторов (m-)-го порядка (которая дополняет любой базис подпространства до базиса подпространства , ). Напомним, что векторы называются линейно независимыми над подпространством , если любая нетривиальная линейная комбинация этих векторов не принадлежит .

Векторы являются присоединенными (m-2)-го порядка, принадлежат и линейно независимы над подпространством . Дополним их присоединенными векторами (m-2)-го порядка до максимальной линейно независимой над подпространством системы . Применяя к этим векторам преобразование , получаем линейно независимые над подпространством векторы

Дополняем их векторами до максимальной линейно независимой над подпространством системы. Продолжая аналогично, приходим к следующей таблице базисов:

В таблице базисов (9.13) указаны следующие базисы:

в последней строке — базис собственного подпространства ;

в двух последних строках — базис подпространства и т.д.;

вся таблица — базис корневого подпространства .

По таблице (9.13) составим базис корневого подпространства. Записываем векторы, стоящие в первом столбце, один за другим снизу вверх, начиная с собственного вектора:

К ним приписываем в таком же порядке векторы, стоящие во втором столбце, и т.д. Получим жорданов базис корневого подпространства, состоящий из собственных и присоединенных векторов, взятых в определенном порядке, как это указано в (9.12). Все клетки жордановой формы (9.11) соответствуют собственному значению . Каждому из первых столбцов таблицы (9.13) соответствует жорданова клетка m-го порядка, каждому из следующих столбцов соответствует жорданова клетка (m-1)-гo порядка и т.д. Общее число жордановых клеток равно количеству собственных векторов в последней строке таблицы (9.13).

Таким образом, доказано существование жорданова базиса в случае единственного собственного значения.

Рассмотрим теперь случай, когда имеется несколько различных собственных значений . В этом случае по теореме 9.5 пространство разлагается в прямую сумму инвариантных (корневых) подпространств . При объединении жордановых базисов корневых подпространств получаем жорданов базис всего пространства. Таким образом, справедливо следующее утверждение.

---

Теорема (9.8) о приведении линейного преобразования к каноническому виду

Если все корни характеристического уравнения являются собственными значениями преобразования, то это преобразование приводится к каноническому виду, т.е. существует базис пространства, в котором матрица преобразования имеет жорданову форму.

Из теоремы следует, что любое линейное преобразование комплексного линейного пространства приводится к каноническому виду, а преобразование вещественного линейного пространства приводится к каноническому виду только тогда, когда все корни характеристического уравнения действительные.

---

Замечания 9.5

1. По таблице (9.13) нетрудно выразить количество жордановых клеток порядка через ранги преобразований , учитывая, что . Количество жордановых клеток порядка равно количеству векторов в первой строке таблицы (9.13):

Количество жордановых клеток порядка равно количеству векторов во второй строке таблицы (9.13):

Продолжая вычисления аналогичным образом, получаем следующий результат: количество жордановых клеток порядка находится по формуле

где — наименьшее натуральное число, при котором .

2. Число в (9.14) равно кратности корня минимального многочлена матрицы линейного преобразования.

3. Из пункта 1 следует единственность жордановой формы матрицы линейного преобразования (с точностью до перестановок жордановых клеток), так как состав жордановых клеток (количество и порядки) полностью определяется по размерностям инвариантных подпространств (9.8), (9.9). От выбора базиса зависит расположение жордановых клеток на главной диагонали матрицы (9.11). Поэтому жордановы формы, отличающиеся перестановкой жордановых клеток, считаются одинаковыми.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Определение. Пусть даны два пространства и . Если по закону каждому вектору поставлен в соответствие вектор , то говорят, что задан оператор (функция, отображение), отображающий в и пишут .

Обозначение: ; – образ, – прообраз.

Определение. Если для любых и из и любых вещественных чисел и имеет место , то оператор называется линейным.

Произвольные отображения линейных пространств изучаются в курсе математического анализа. В курсе линейной алгебры изучаются лишь линейные отображения.

Пример 6. Оператор действует из в по закону , где , и – фиксированный вектор, например, . Оператор переводит вектор из в другой вектор из . Докажем, что он линейный: . Здесь воспользовались свойствами векторного произведения.

Пример 7. Линеен ли оператор , где произвольный вектор, а вектор – фиксированный?

Решение. , так как , . Следовательно, оператор – нелинейный.

Пусть даны два пространства и и оператор , действующий из в . Пусть в есть базис , а в – базис .

Подействовав оператором на базисные векторы пространства , получим векторы из , которые можно разложить по базису с коэффициентами линейных комбинаций :

Строим матрицу таким образом, чтобы в ее столбцах стояли координаты образов базисных векторов пространства относительно базисных векторов пространства :

.

Матрица называется матрицей линейного оператора , действующего из в . Таким образом, если оператор , то матрица этого оператора имеет размер , то есть у нее строк и столбцов.

Замечание. Если в и выбрать другие базисы, то в этих базисах матрица линейного оператора будет иметь другой вид.

Из определения матрицы линейного оператора следует, что, зная закон (оператор), по которому вектору сопоставляется вектор , можно построить матрицу, и наоборот, любой матрице соответствует некоторый линейный оператор.

Пример 8. Построить матрицу линейного оператора, действующего из в по закону , где векторы и заданы относительно канонического базиса.

Решение. Подействуем оператором на базисные векторы :

;

;

.

Таким, образом, – искомая матрица.

Пример 9. Пусть в выбран базис , , , а в выбран базис , . Найти матрицу линейного оператора, действующего из в по закону , где .

Решение. ; ;

; .

Пример 10. Дана матрица . Найти линейный оператор (закон, по которому действует оператор).

Решение. Матрица – это матрица линейного оператора, действующего из в . Пусть в базис , в базис . Так как в столбцах матрицы стоят координаты векторов относительно базиса , то

(1)

Пусть произвольный вектор из , где – координаты этого вектора в базисе , тогда . Действуя оператором на вектор и учитывая линейность оператора, получим: .

Учитывая (1), имеем:

.

Таким образом, оператор действует по закону

.

Зная матрицу оператора , результат его действия на вектор можно найти в матричной форме. Пусть известна матрица оператора размера с элементами . В этом случае оператор с такой матрицей действует из в . Если – любой вектор из , то результат действия оператора на вектор можно найти по формуле:

,

Где – координаты вектора .

Пример 11. Операторы и действуют в пространстве по законам , , где ; ( – скалярное произведение векторов и ). Найти координаты вектора в каноническом базисе.

Решение. Координаты вектора можно найти двумя способами:

А) найдем матрицу .

Строим матрицу в каноническом базисе:

; ;

.

.

Строим матрицу в каноническом базисе:

; ;

.

;

.

.

Этот способ решения называется матричным;

Б) операторный способ.

. Подействуем оператором на вектор :

, теперь на полученный вектор подействуем оператором :

.

Для самостоятельной работы.

1. Оператор действует по закону:

.

Найти его матрицу в каноническом базисе.

Ответ: .

2. Оператор действует в плоскости и осуществляет зеркальное отражение относительно прямой . Доказать, что он линейный и найти его матрицу в каноническом базисе.

Ответ: .

3. Дана матрица .

А) Найти оператор, матрицей которого является матрица .

Б) Найти образ вектора .

Ответ: .

< Предыдущая		Следующая >

Светлой
памяти

Чубича
Михаила Петровича

посвящается

§ 7.1. Определение линейного оператора.

Матрица линейного оператора

Пусть

и
— линейные пространства над одним и тем
же полем .
Будем говорить, что из
пространства

в пространство

действует оператор

или, что то же самое, отображение

,
преобразование
,
если каждому вектору
по какому — либо правилу поставлен в
соответствии определенный вектор
из .

Наиболее
простыми являются линейные операторы.
Отображение
называется линейным
оператором
(линейным
преобразованием),
действующим из
в ,
если оно удовлетворяет следующим двум
условиям:

;

,
.

Совокупность
условий 1 и 2 равносильна следующему
условию:

.
(7.1.1)

Обозначим
через
множество всех линейных операторов,
действующих из линейного пространства

в линейное пространство .
Два линейных оператора
и
из
называются равными,
если

.

(7.1.2)

Множество
будет линейным пространством над полем
,
если определить сумму

операторов


и произведение

оператора


на число

соотношениями

(7.1.3)

(7.1.4)

Нулевым
вектором пространства
будет нулевой
оператор
из
в,
т.е. оператор, переводящий любой вектор

линейного пространства
в нулевой вектор линейного пространства
.

В
случае, когда ,
линейный оператор

называется линейным преобразованием
пространства .

Пусть
—
оператор из ,
и пусть и
—
фиксированные базисы линейных пространств
исоответственно.
Разложим векторы
по базису :

,

,
(7.1.5)

.

Из
коэффициентов этих разложений составим
—
матрицу

.

(7.1.6)

Матрица

называется матрицей
линейного оператора

в паре базисов и
.
Заметим, что столбцами матрицы
служат столбцы координат векторов
в базисе ,
т.е. строки коэффициентов из разложений
(7.1.5).

Если

,
то при нахождении матрицы линейного
оператора фиксируются векторы одного
базиса ,
по которому раскладываются .
Записанные столбцами коэффициенты
разложений образуют квадратную матрицу

порядка .

Равные
линейные операторы в одном и том же
базисе имеют одинаковые матрицы.

Матрицей
суммы линейных операторов в фиксированных
базисах является сумма матриц слагаемых
операторов в тех же базисах.

При
умножении линейного оператора на число
его матрица умножается на то же число.

Если

и

—
соответственно,
—
и
—
мерное линейные пространства над одним
полем
,
то линейное пространство

изоморфно
линейному пространству
—
матриц с элементами из
с
операциями сложения матриц и умножения
их на числа из поля
.

Пример
1.
Оператор
называется
тождественным
(единичным)
оператором,
если

.

(7.1.7)

Покажите
линейность оператора
и постройте его матрицу в базисе .

Решение.
В силу того, что

,

убеждаемся
в линейности тождественного оператора.
Поскольку

получаем,
что

.

В
любом базисе тождественный оператор
имеет единичную матрицу.

Пример
2.
Докажите, что преобразование

пространства

линейно и найдите его матрицу в
каноническом базисе.

Решение.
Пусть

и

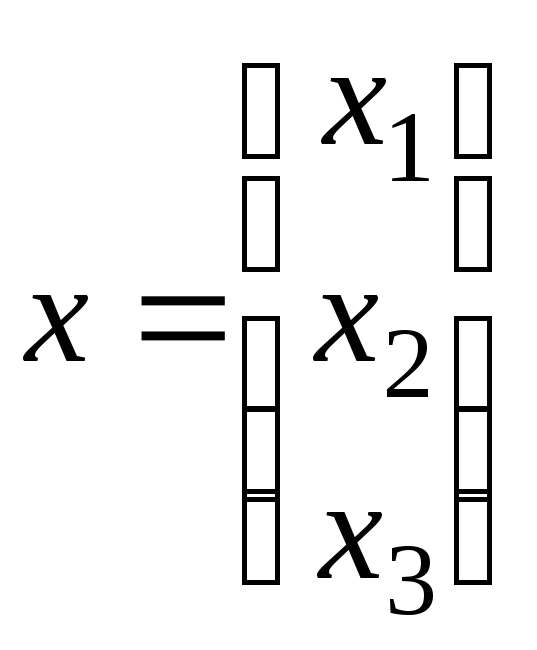
— произвольные векторы из .
Тогда

т.
е. преобразование
пространства
линейно. Канонический базис линейного
пространства
составляют векторы

.
Из определения оператора
вытекает, что

Таким
образом,

Пример
3.
Покажите, что умножение квадратных
матриц второго порядка слева на данную
матрицу
является линейным преобразованием
пространства
и найдите матрицу этого преобразования
в базисе, состоящем из матриц

Решение.
По определению преобразования
для любых матриц
и любых чисел
имеем:

.

Перейдем
к построению матрицы оператора
в данном базисе. В силу того, что

получаем:

.

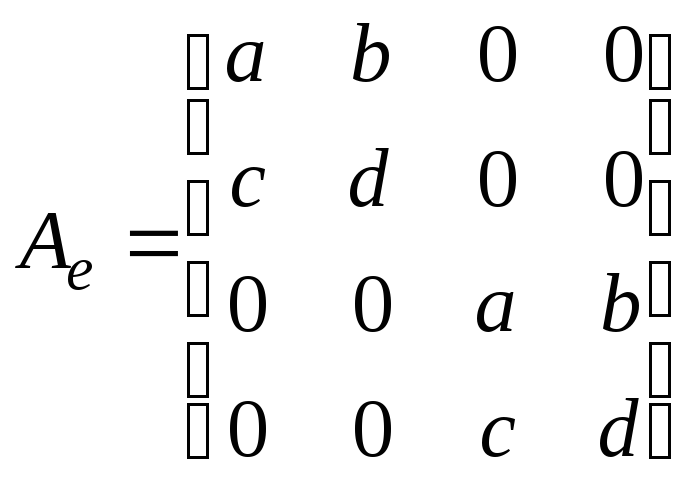
7.1.1.
Какую матрицу имеет нулевой оператор
в любых базисах пространств
и ?

7.1.2.
Линейное пространство
является прямой суммой подпространств

и .
Докажите, что оператор
пространства ,
который каждому вектору
с разложением ,
где ,
ставит в соответствие вектор
этого разложения, является линейным.
Оператор
называется оператором
проектирования
пространства
на
параллельно .

Найдите
матрицу этого оператора в базисе,
полученном объединением базисов
подпространств
и .

7.1.3.
Линейное пространство
является прямой суммой подпространств

и .
Докажите, что оператор ,
который каждому вектору
с разложением ,
где ,
ставит в соответствие вектор ,
является линейным. Оператор
называется отражением
пространства
в
параллельно .

Найдите
матрицу этого оператора в базисе,
полученном объединением базисов
подпространств
и .

7.1.4.
Докажите, что всякий линейный оператор,
действующий в одномерном пространстве,
сводится к умножению всех векторов
пространства на фиксированное (для
данного оператора) число.

7.1.5.
Верно ли, что линейный оператор переводит:

а)
линейно зависимую систему векторов в
линейно зависимую;

б)
линейно независимую систему векторов
в линейно независимую?

7.1.6.
Выясните, какие из следующих преобразований
пространства
линейны, и в случае линейности найдите
их матрицы в каноническом базисе:

а)

б)

в)

г)

7.1.7.
Укажите, какие из приведенных преобразований
пространства
являются линейными операторами, и
найдите их матрицы в базисе .
Каждое преобразование описывается
своим действием на произвольный многочлен
:

а)

б)

в)
,
где
и
— фиксированные числа, причем ;

г)

Этот оператор в дальнейшем называется
оператором
дифференцирования.

7.1.8.
Какова матрица оператора дифференцирования,
действующего в линейном пространстве
,
в базисе ,
где
— действительное число?

7.1.9.
Покажите, что умножение квадратных
матриц второго порядка справа на данную
матрицу
является линейным преобразованием
пространства ,
и найдите матрицу этого преобразования
в базисе, состоящем из матриц :

7.1.10.
Проверьте линейность оператора ,
заданного формулой ,
где
и постройте матрицу этого оператора в
базисах

и

7.1.11.
В пространстве
фиксирован базис, состоящий из матриц

(в
указанном порядке). Запишите в этом
базисе матрицу оператора транспонирования,
т.е. оператора, который каждой матрице

ставит в соответствие транспонированную
матрицу.

Как
изменится эта матрица, если в базисе
поменять местами векторы
и ?

Соседние файлы в папке Задачник-2

• #
• #
• #
• #
• #
• #