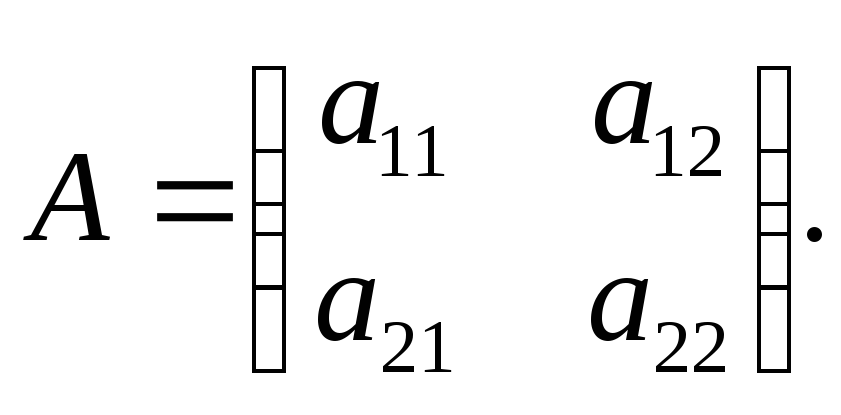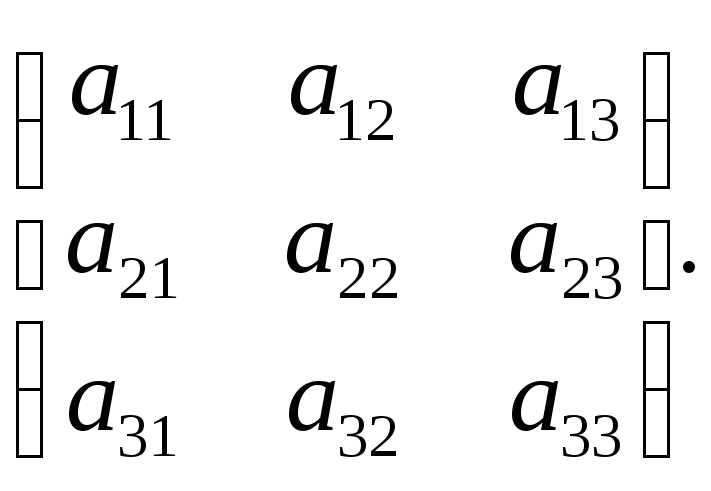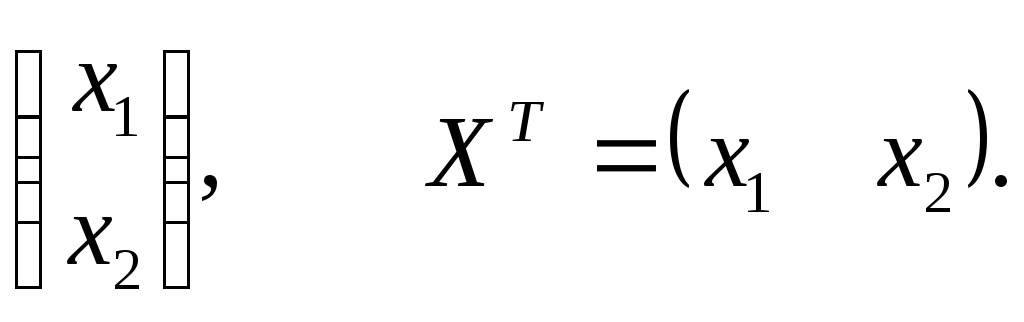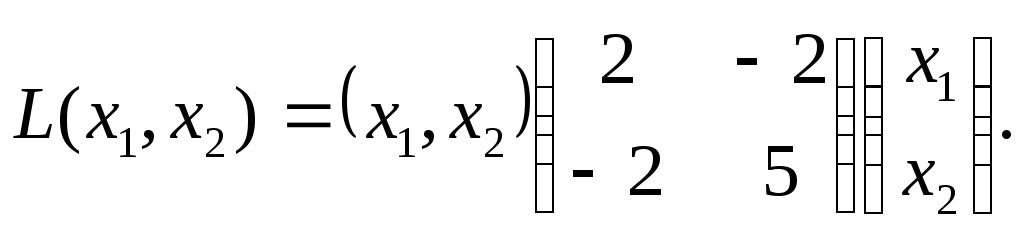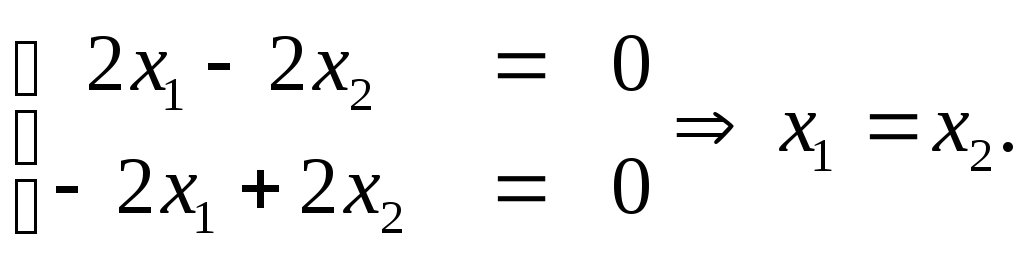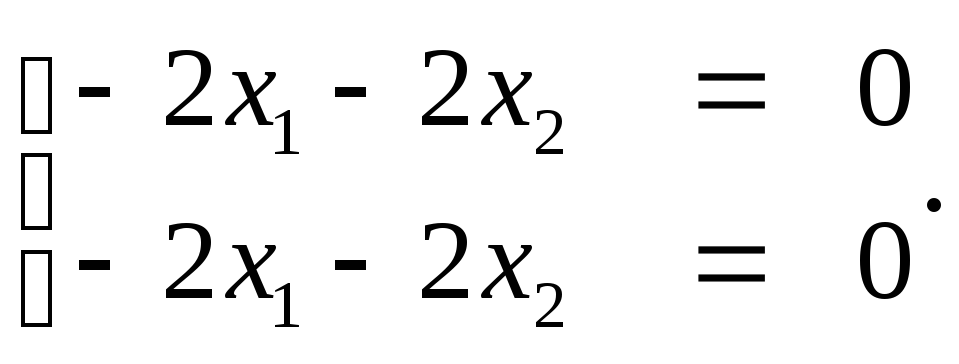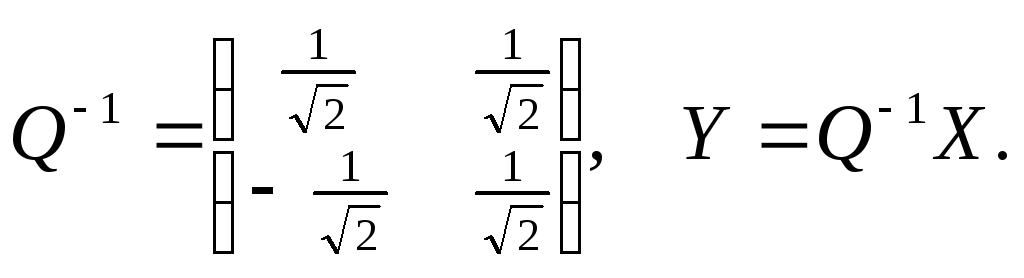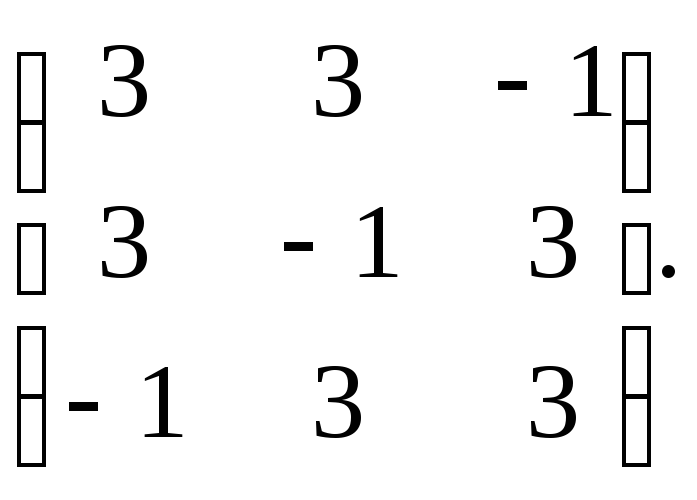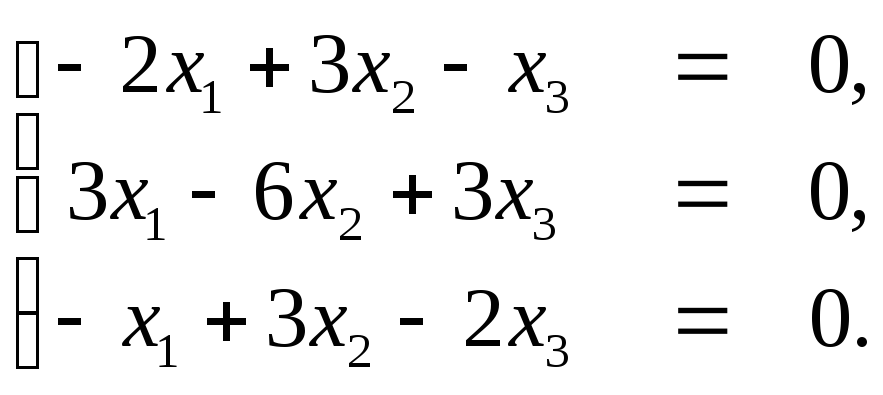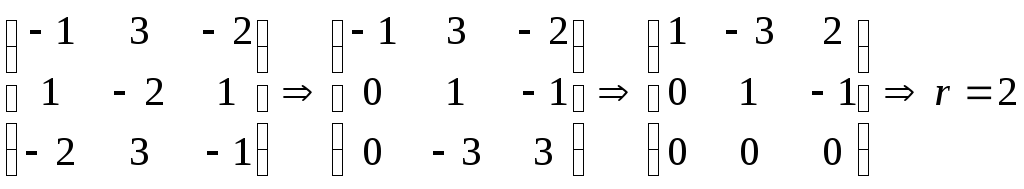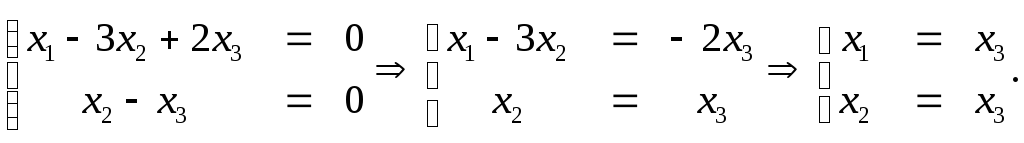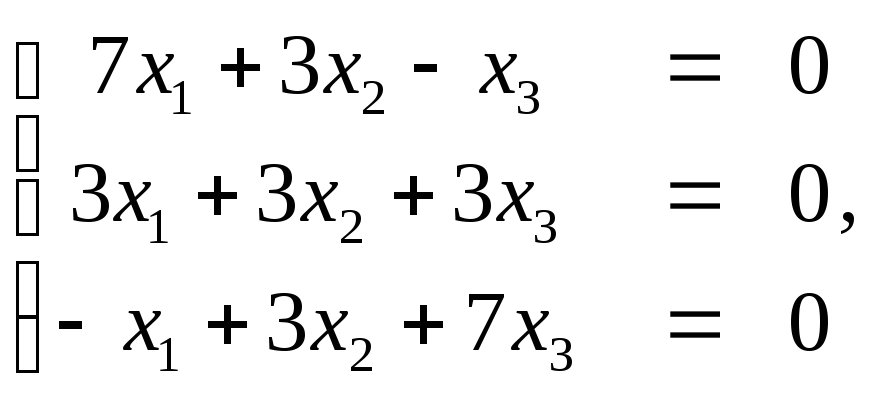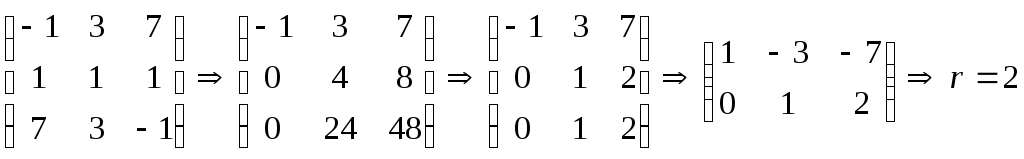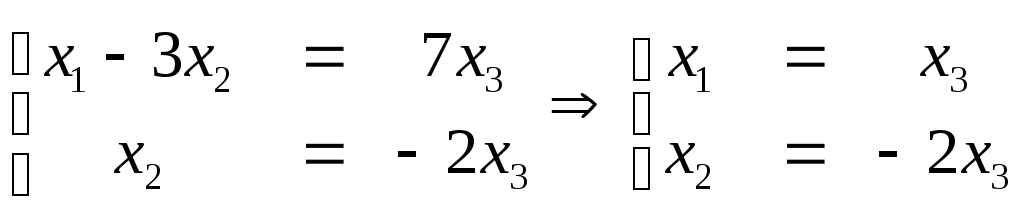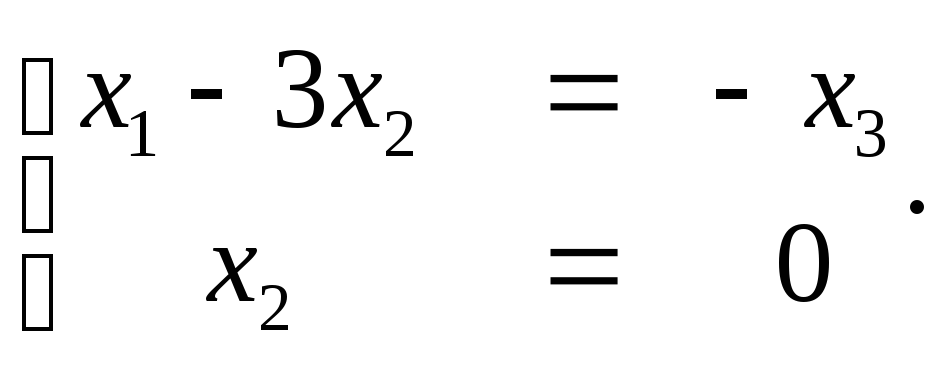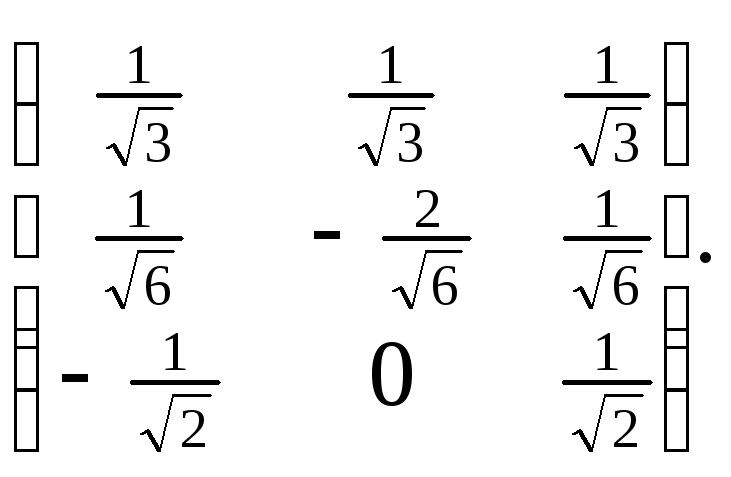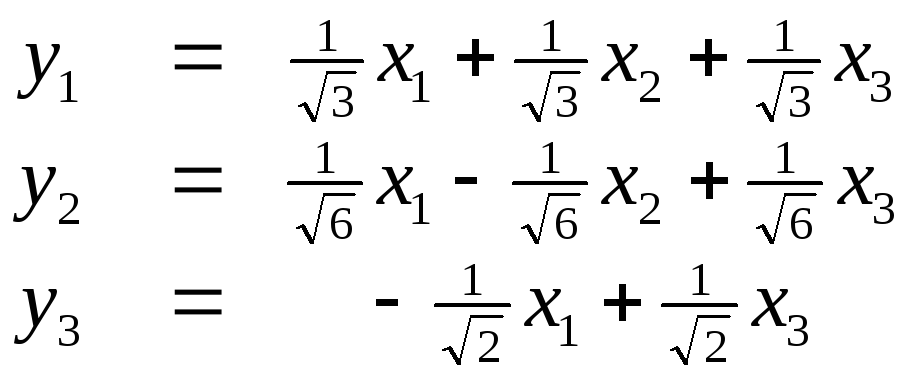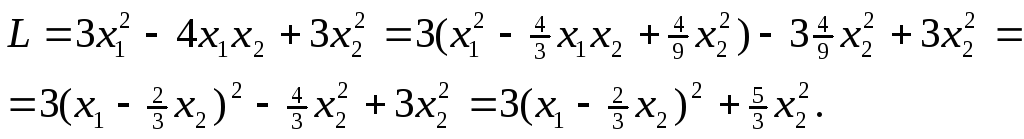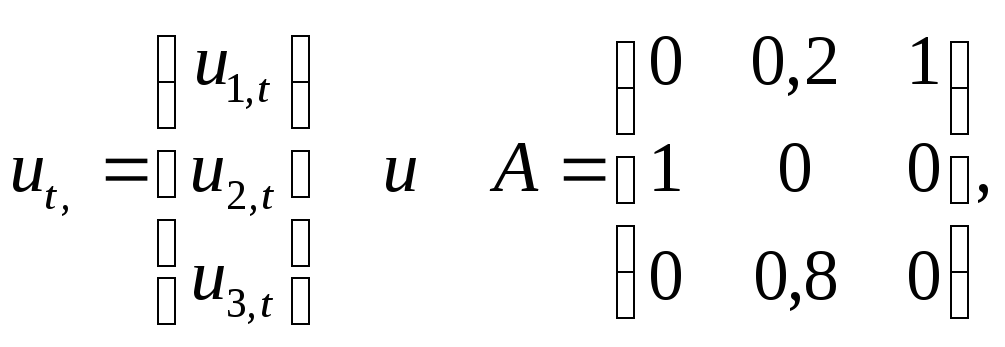-
Квадратичные формы
-
Матрица квадратичной формы
Определение.
Квадратичной формой Ĺ(х1,х2,…,хп)
от n переменных называется сумма, каждый
член которой является или квадратом
одной из переменных или произведением
двух разных переменных, взятых с
некоторыми коэффициентами – действительными
числами.
Мы будем рассматривать квадратичные
формы с двумя переменными
(5.1.1)
и с
тремя переменными
(5.1.2)
Квадратичные
формы можно записать в матричной форме,
введя в рассмотрение матрицу А квадратичной
формы. Для (5.1.1) матрица имеет вид
Для (5.1.2) матрица записывается в виде:
А=
То
есть матрица квадратичной формы является
симметрической матрицей. Для переменных
вводится матрица-столбец Х и
транспонированная
—
матрица – строка. Тогда квадратичная
форма может быть записана в виде
произведения трех матриц
( 5.1.3)
Пример.
Дана квадратичная
форма
Записать ее в матричной форме.
Решение.
Матрица квадратичной формы составляется
следующим образом: элементы главной
диагонали равны коэффициентам при
квадратах переменных, остальные элементы
равны половине коэффициента при
произведении х1х2:
А=
Матрица Х=
Таким
образом,
Пример.
Написать матрицу квадратичной формы
Решение.
На главной диагонали располагаем
элементы при квадратах переменных
а11=3,
а22=1,
а33=6,
остальные элементы а12=а21=5/2,
а13=а31=-2,
а23=а32=0.
Следовательно,
А=
Ранг матрицы квадратичной формы называют
рангом квадратичной формы. Если ранг
совпадает с числом переменных квадратичной
формы, то ее называют невырожденной.
Если ранг меньше, то квадратичная форма
– вырожденная.
Пример.
Является ли невырожденной квадратичная
форма L(х1,х2,х3
) = х21+4х1х3?
Решение.
Составим матрицу квадратичной формы
А=
Найдем ранг матрицы А. Так как величина
ранга не зависит от элементарных
преобразований матрицы, то отбрасывая
нулевую строку, найдем минор второго
порядка М2=
то есть ранг меньше трех переменных,
входящих в квадратичную форму.
Следовательно, данная квадратичная
форма вырожденная.
-
Канонический вид квадратичной формы
В
квадратичной форме
можно выполнить линейное преобразование
переменных
невырожденная
квадратная матрица n-ого порядка. Учитывая
линейное преобразование переменных,
получим равенство:
(5.2.1)
Здесь
использовано свойство
.
Новая матрица квадратичной формы
( 5.2.2)
Первоначальная квадратичная форма и
полученная из нее (5.2.1) с помощью
невырожденного линейного преобразования
называются эквивалентными квадратичными
формами.
Пример.
Дана квадратичная форма
.
Найти эквивалентную квадратичную форму
L(y1,y2),
используя линейное преобразование
переменных х1=у1-2у2,
х2=у1+у2.
Решение.
По условию матрица данной квадратичной
формы А=
Заданное линейное преобразование в
матричной форме
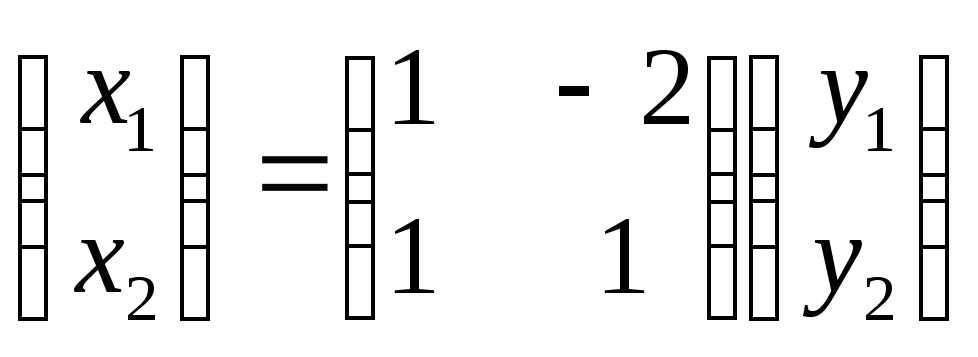
Следовательно,
матрица С=
Теперь
по формуле (5.2.2) новая матрица получается
Ответ.
Квадратичная форма, эквивалентная
данной
Определение.
Квадратичная форма имеет канонический
вид, если все коэффициенты
,
т.е.
и ее матрица является диагональной.
В примере после линейного преобразования
квадратичная форма приняла канонический
вид.
Справедливо следующее утверждение:
любая квадратичная форма с помощью
невырожденного линейного преобразования
переменных может быть приведена к
каноническому виду. Возможны два способа
приведения квадратичных форм к
каноническому виду.
Первый
способ. Идея
метода состоит в том, что путем
тождественных преобразований в
квадратичной форме последовательно
выделяются полные квадраты по всем
переменным.
Пример.
Привести к каноническому виду квадратичную
форму
Решение.
Выделим полный квадрат по переменной
х1:
Введя
новые переменные у1=х1—получим
канонический вид
Пример.
Привести к каноническому виду
квадратичную форму
Решение.
Сначала сгруппируем все слагаемые,
содержащие х1,
и затем дополним их до полного квадрата:
Теперь
полный квадрат по х1
оставляем неизменным, а среди оставшихся
слагаемых объединяем все члены, содержащие
х2,
и выделяем полный квадрат:
Обозначим
у1=х1+2х2+2х3,
у2=х2+х3,
у3=х3,
в результате
получаем канонический вид
Второй
способ. Матрица
квадратичной формы всегда симметрическая,
поэтому она имеет действительные
собственные значения и сводится к
диагональному виду с помощью линейного
ортогонального преобразования Х=QY,
где Q
– ортогональная матрица (см. пример в
4.4.1)
Если
квадратичная форма зависит от двух
переменных L=L(x1,x2)
и λ1,λ2
собственные значения ее матрицы , то
канонический вид квадратичной формы
Если
L=L(x1,x2,x3)
и ее матрица имеет собственные значения
λ1,
λ2,
λ3
, то кононический вид в новых переменных
Чтобы найти линейное преобразование
переменных, приводящих квадратичную
форму к каноническому виду, нужно найти
собственные векторы, нормировать их и
записать матрицу Q.
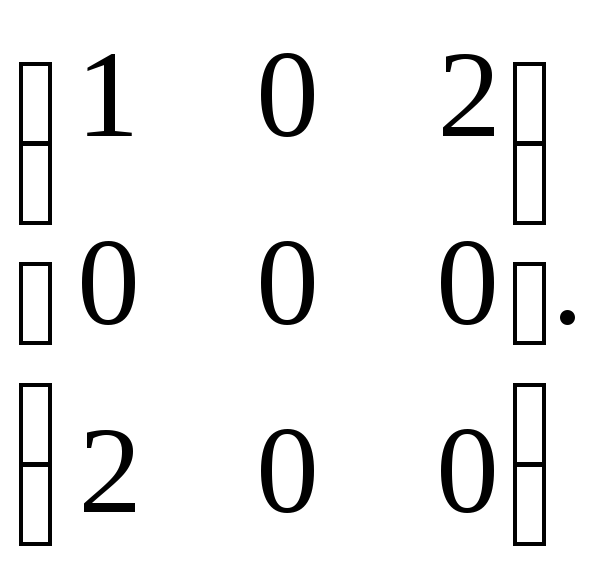
Пример.
Привести к каноническому виду квадратичную
форму
Решение.
Матрица данной квадратичной формы
А=.
Характеристическое уравнение
.
Собственные
значения λ1=1,λ2=5.
Квадратичная форма в новом базисе из
собственных векторов имеет канонический
вид
Найдем
собственные векторы. Для этого в систему
уравнений вида (4.3.2)
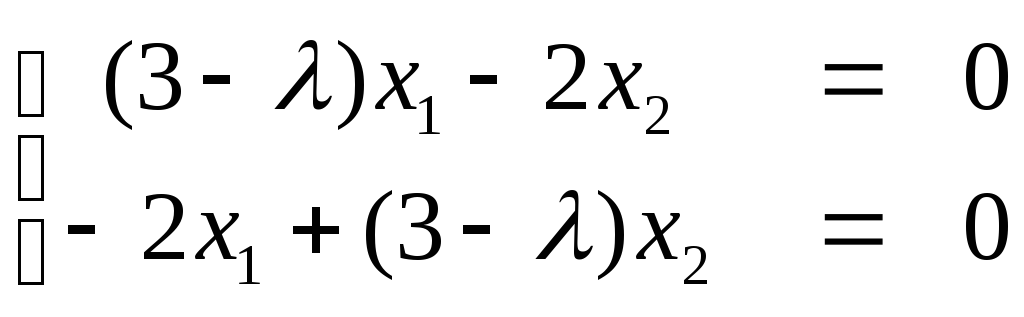
подставим собственные значения.
а)
При λ=λ1=1
получим
Пусть
х2=1
и х1=1.
Тогда е1=(1,1).
б)
При λ=λ2=5
система имеет вид
Таким
образом, х1=-х2
и за второй собственный вектор можно
взять е2=(-1,1).
Очевидно, что е1е2=0
– векторы ортогональны. Нормируя е1,
е2,
запишем ортонормированный базис:
е1=(
Матрица
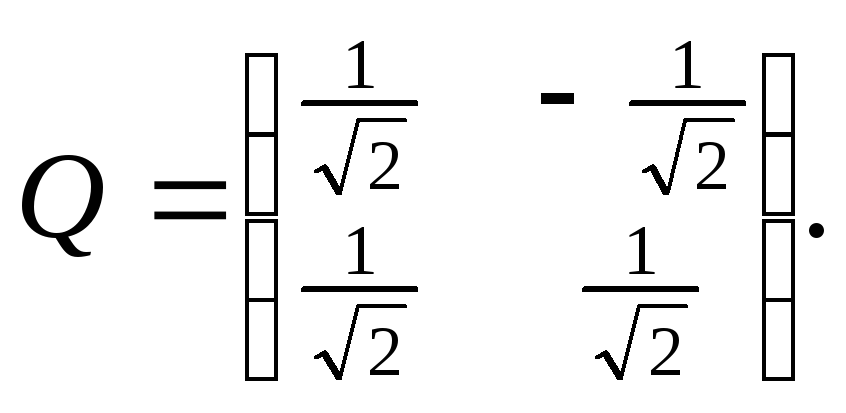
преобразование координат получено.
Заметим,
что в случае ортогональных преобразований
легко получить обратное преобразование
переменных, воспользовавшись свойством
Обратная
матрица равна
Поэтому выполняются соотношения
Ответ.
Канонический
вид
Пример.
Привести квадратичную форму к
каноническому виду и найти ортогональное
преобразование переменных, если
Решение.
Матрица квадратичной формы А=
Характеристическое уравнение
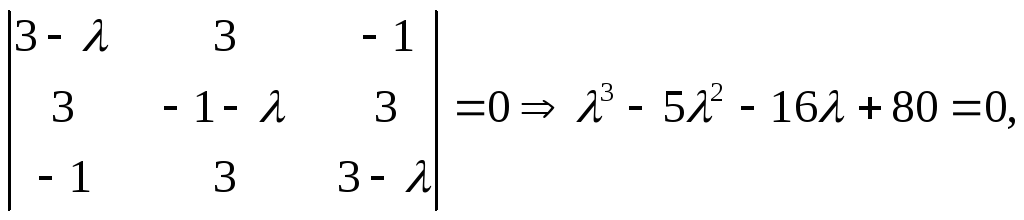
корни
которого λ1=5,
λ2=-4
, λ3=4
Тогда канонический вид квадратичной
формы
Заметим,. что нумерация собственных
значений произвольная. Например, если
взять
то
канонический вид будет
Для каждого такого
варианта обозначений меняется
соответственно расположение (нумерация)
базисных собственных векторов (то есть
система координат), а смысл квадратичной
формы не меняется.
Найдем теперь ортонормированный базис
и преобразование переменных. Составим
систему уравнений:
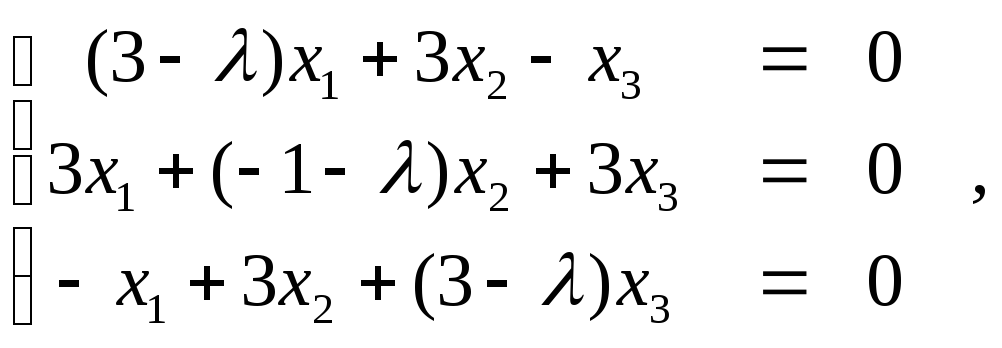
последовательно подставим собственные
значения.
а)
При λ=5 система
примет вид
Выпишем
матрицу системы и подвергнем ее
элементарным преобразованиям:
Получим систему эквивалентную исходной:
Если
х3=k
– любое число, не равное нулю, то множество
собственных векторов (k,k,k).
Пусть k=1,
тогда е1=(1,1,1).
б)
При λ=-4 имеем систему
Преобразуем
матрицу системы
По
последней матрице запишем систему
уравнений
При х3=k,
где k≠0,
множество собственных векторов (k,
-2k,
k).
Возьмем k=1,
тогда е2=(1,
-2, 1).
в)
При λ=4
получим систему уравнений
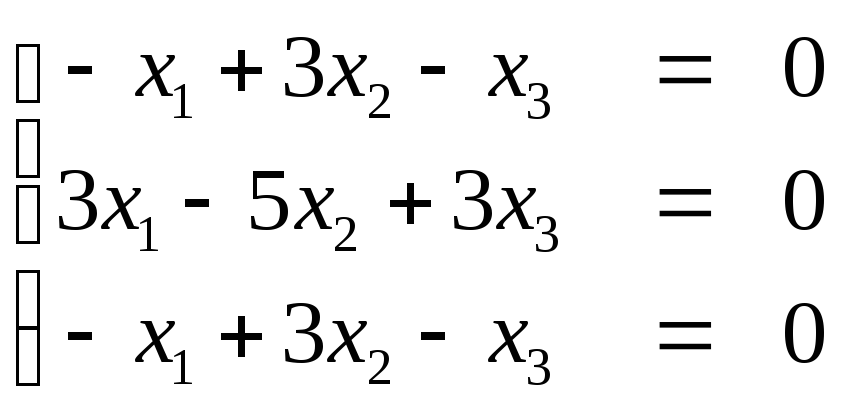
Здесь первое и третье уравнения
одинаковые, поэтому запишем матрицу
системы в виде:
Откуда следует, что
Если х3=k,
где k≠0,
то множество собственных векторов (-k,
0, k).
Пусть k=1,
тогда е3=(-1,0,1).
Получили собственные векторы е1=(1,1,1),
е2=(1,-2,1),
е3=(-1,
0, 1). Легко увидеть, что они попарно
ортогональны. Запишем ортонормированный
базис:
Ортогональная
матрица Q=
Транспонируя
матрицу Q, получим матрицу:
=
И
так как
записываем ортогональное преобразование
переменных
(*)
Ответ.
Квадратичная форма имеет канонический
вид
в базисе из собственных векторов и может
быть получена с помощью преобразования
координат в виде (*).
Отметим
некоторые свойства квадратичных форм:
-
Канонический
вид квадратичной формы не определяется
однозначно, так как зависит от выбора
системы координат (базисных векторов). -
В
каноническом виде число слагаемых с
положительными (отрицательными)
коэффициентами не зависит от способа
приведения формы к каноническому виду. -
Ранг матрицы квадратичной формы не
меняется при линейных преобразованиях
переменных. Ранг всегда равен количеству
ненулевых коэффициентов в канонической
форме. -
Квадратичная форма называется
положительно (отрицательно) определенной,
если при всех значениях переменных, из
которых хотя бы одно отлично от нуля,
выполняется
>0,
<0.
Например,положительно
определенная форма, а
отрицательно определенная.
5. Если все
собственные значения матрицы квадратичной
формы положительны, то
>0
положительно определена. Если все
собственные значения отрицательны, то
<
0- отрицательно определенная форма.
6. Знакоопределенность
квадратичной формы может быть установлена
с помощью критерия Сильвестра: если все
главные миноры матрицы квадратичной
формы положительны, то квадратичная
форма положительно определена. Если
все главные миноры матрицы нечетного
порядка положительны, то квадратичная
форма отрицательно определена.
Продемонстрируем
на примере перечисленные свойства.
Пример.
Дана квадратичная форма
Ее канонический вид
получен с помощью собственных значений
λ1=1 ,λ2=5. Приведем теперь
эту форму к каноническому виду по первому
способу с помощью выделения полных
квадратов.
Таким образом
Канонический вид квадратичной формы
зависит от выбора линейного преобразования
переменных, то есть от выбора системы
координат. Если, например, взять L=1, то
уравнения
являются уравнениями одного и того же
эллипса в разных системах координат.
Пример.
В предыдущем примере мы обратили внимание
на то, что канонический вид квадратичной
формы можно записать разными способами:
Во всех этих записях число слагаемых с
положительными и отрицательными
коэффициентами одно и то же.
Пример. Исследовать на знакоопределенность
квадратичную форму
Решение. Составим матрицу данной
квадратичной формы А=
и вычислим главные угловые миноры
М1=3>0,
М2=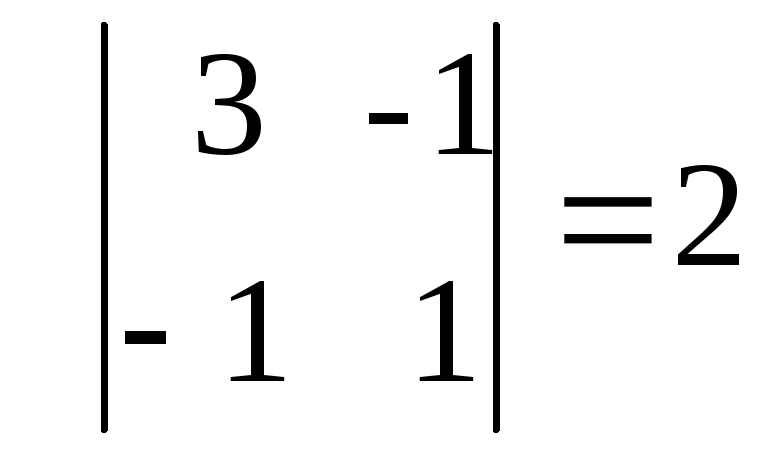
М3=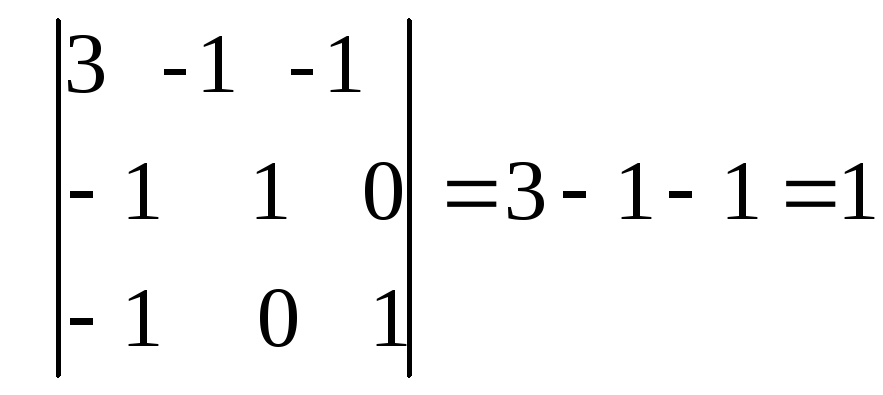
Следовательно,
по критерию Сильвестра квадратичная
форма положительно определенная.
В заключение рассмотрим экономический
смысл понятий собственного значения и
собственного вектора. Предположим, что
на некотором предприятии в начале года
заменяют 20 % оборудования, проработавшего
два года, и все оборудование, проработавшее
три года. То оборудование, которое было
в эксплуатации один год, не заменяется.
Для анализа и прогнозирования экономических
параметров работы предприятия надо
знать устойчивое, т.е. не изменяющееся
из года в год, распределение количества
единиц работающего оборудования. Введем
следующие обозначения:
количество
единиц оборудования, проработавшего i
лет к началу года t, тогда
Это равенство означает, что не заменяется
новое оборудование прошлого года,
заменяется 20 % оборудования, проработавшего
два года к началу предыдущего года и
все оборудование, проработавшее три
года к началу предыдущего года.
Это равенство означает, что два года
проработает то оборудование, которое
к началу предыдущего года эксплуатировалось
один год.
т.е. три года эксплуатируют то оборудование,
которое к началу года проработало два
сезона и не было заменено. Введем матрицы
тогда все
предыдущие рассуждения описываются
уравнением
Если нас интересует устойчивое
распределение, то
и приходится решать уравнение
Если справедливо предположение о том,
что оборудование заменяется пропорционально
количеству единиц техники, находящейся
на предприятии, то приходится искать
распределение, которое является решением
уравнения
Задача отыскания таких λ , при которых
существует ненулевое решение уравнения
и приводит к понятию собственного
вектора и собственного значения
оператора.
Упражнения для
самостоятельного решения
-
Привести
к каноническому виду квадратичную
форму L=х2—у2-4ху
путем выделения полного квадрата. Какую
кривую определяет уравнение L(x,y)=1? -
Привести
к каноническому виду квадратичную
форму, выделяя полные квадраты, L= -
Привести
к каноническому виду квадратичную
форму, определив собственные значения
ее матрицы
Ответы: 1.
2.
3.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Оглавление — Линейная алгебра
Канонический вид ортогонального преобразования евклидова пространства
Рассмотрим инвариантные подпространства ортогонального преобразования евклидова пространства. По теореме 9.4 линейное преобразование вещественного пространства имеет одномерное или двумерное инвариантное подпространство. Выясним геометрический смысл сужения ортогонального преобразования на инвариантное подпространство.
1. Пусть [math]L[/math] — одномерное инвариантное подпространство с базисом [math]boldsymbol{e}_1[/math]. Тогда [math]boldsymbol{e}_1[/math] — собственный вектор преобразования: [math]mathcal{A}(boldsymbol{e}_1)=lambda boldsymbol{e}_1[/math]. По свойству [math]lambda=pm1[/math]. Следовательно, ортогональное преобразование [math]mathcal{A}colon Lto L[/math] одномерного пространства — это либо тождественное преобразование [math]mathcal{A}(boldsymbol{e}_1)= boldsymbol{e}_1[/math] либо отражение (симметрия) [math]mathcal{A}(boldsymbol{e}_1)= -boldsymbol{e}_1[/math].
2. Пусть [math]L[/math] — двумерное инвариантное подпространство с ортонормированным базисом [math]boldsymbol{e}_1, boldsymbol{e}_2[/math]. Запишем для матрицы [math]A=begin{pmatrix} a&b\ c&d end{pmatrix}[/math] ортогонального преобразования [math]mathcal{A}colon Lto L[/math] равенство [math]A^T=A^{-1}:[/math]
[math]begin{pmatrix}a&c\ b&d end{pmatrix}= frac{1}{det{A}}! begin{pmatrix} d&-b\ -c&a end{pmatrix}!.[/math]
По свойству 6 для собственного преобразования [math]det{A}=1[/math], поэтому [math]d=a,~ c=-b,[/math] [math]det{A}=a^2+b^2=1[/math], т.е. [math]a=cosvarphi[/math] и [math]b=sinvarphi[/math], где [math]varphi[/math] — некоторый угол. Следовательно, матрица собственного ортогонального преобразования двумерного пространства совпадает с матрицей поворота на угол [math](-varphi)colon[/math] [math]A=R_{varphi}= begin{pmatrix} cosvarphi& sinvarphi\ -sinvarphi& cosvarphi end{pmatrix}[/math]. Для несобственного преобразования [math]det{A}=-1[/math] (см. свойство 6), поэтому [math]d=-a,~ c=b,[/math] [math]det{A}=-a^2-b^2=-1[/math]. Матрица [math]A=begin{pmatrix}a&b\ b&-aend{pmatrix}[/math] имеет два действительных собственных значения [math](lambda_1=1,~ lambda_2=-1)[/math], так как
[math]det(A-lambda E)= begin{vmatrix}a-lambda&b\ b&-a-lambda end{vmatrix}=(a-lambda)cdot(-a-lambda)-bcdot b= lambda^2-a^2-b^2=lambda^2-1.[/math]
Поэтому несобственное ортогональное преобразование имеет два одномерных инвариантных подпространства (см. пункт 1).
Получим канонический вид преобразования. Пусть [math]L[/math] — одномерное или двумерное инвариантное подпространство для ортогонального преобразования [math]mathcal{A}colon mathbb{E}to mathbb{E}[/math]. Представим пространство в виде прямой суммы [math]mathbb{E}= Lplus L^{perp}[/math]. Выберем в [math]L[/math] ортонормированный базис и дополним его до ортонормированного базиса всего пространства. В этом базисе матрица [math]A[/math] преобразования будет иметь блочно-диагональный вид [math]A=operatorname{diag} (A_L,A_{L^{perp}})[/math], где [math]A_{L}[/math] — матрица сужения [math]mathcal{A}_L[/math] преобразования [math]mathcal{A}[/math] на [math]L[/math], а [math]A_{L^{perp}}[/math] — матрица сужения [math]mathcal{A}_{L^{perp}}[/math] преобразования [math]mathcal{A}[/math] на [math]L^{perp}[/math]. Согласно пунктам 1, 2: [math]A_L=(1)[/math] или [math]A_L=-1[/math] при [math]dim{L}=1[/math], либо [math]A_L= R_{varphi}= begin{pmatrix} cosvarphi&sinvarphi\ -sinvarphi& cosvarphi end{pmatrix}[/math] при [math]dim{L}=2[/math]. Следовательно, в матрице [math]A=operatorname{diag} (A_L,A_{L^{perp}})[/math] ортогонального преобразования блок [math]A_L[/math] имеет один из указанных трех видов. Поскольку подпространство [math]L^{perp}[/math] инвариантно относительно ортогонального преобразования [math]mathcal{A}[/math] (см. свойство 7), то к матрице [math]A_{L^{perp}}[/math] применимы те же выводы, что и к матрице [math]A[/math]. Таким образом, справедливо следующее утверждение.
Теорема (9.9) о каноническом виде ортогонального преобразования
Для каждого ортогонального преобразования [math]mathcal{A}colon mathbb{E}to mathbb{E}[/math] n-мерного евклидова пространства [math]mathbb{E}[/math] существует ортонормированный базис, в котором матрица преобразования имеет канонический вид:
[math]mathop{A}limits_{(boldsymbol{s})}= begin{pmatrix}pm1&{}&{}&{}&{}&{}\ {}&ddots&{}&{}&O&{}\ {}&{}&pm1&{}&{}&{}\ {}&{}&{}&R_{varphi_1}&{}&{}\ {}&O&{}&{}&ddots&{}\ {}&{}&{}&{}&{}&R_{varphi_k} end{pmatrix}!.[/math]
(9.20)
На главной диагонали матрицы стоят либо числа 1 или (–1), либо блоки вида [math]R_{varphi}= begin{pmatrix}cosvarphi&sinvarphi\ -sinvarphi&cosvarphi end{pmatrix}[/math], а остальные элементы матрицы равны нулю.
Базис [math](boldsymbol{s})=(boldsymbol{s}_1,ldots,boldsymbol{s}_n)[/math], в котором матрица преобразования имеет вид (9.20), называется каноническим. Заметим, что канонический базис определяется неоднозначно.
Приведение ортогонального преобразования к каноническому виду
Задача приведения ортогонального преобразования к каноническому виду формулируется следующим образом: требуется найти базис (канонический), в котором матрица ортогонального преобразования имеет канонический вид (9.20). Для приведения ортогонального преобразования к каноническому виду нужно выполнить следующие действия.
Нахождение канонического вида ортогонального преобразования (первый этап).
1. Выбрать базис [math]boldsymbol{e}_1,ldots, boldsymbol{e}_n[/math] евклидова пространства [math]mathbb{E}[/math] и найти матрицу [math]A[/math] преобразования в этом базисе.
2. Составить характеристическое уравнение [math]det(A-lambda E)=0[/math] и найти различные его корни [math]lambda_1,ldots, lambda_k[/math] (а также их алгебраические кратности).
3. Записать блочно-диагональную матрицу (9.20) канонического вида ортогонального преобразования:
— каждый действительный корень [math]lambda_1[/math] кратности [math]n_1[/math] поместить на главной диагонали [math]n_1[/math] раз;
— для каждой пары [math]lambda=alphapmbeta i[/math] комплексных сопряженных корней кратности [math]m[/math] записать [math]m[/math] блоков вида [math]R_{varphi}= begin{pmatrix} alpha&beta\ -beta&alpha end{pmatrix}[/math] (см. доказательство свойства 8 ортогональных преобразований).
Нахождение канонического базиса (второй этап).
4. Для действительного корня [math]lambda_1[/math] кратности [math]n_1[/math] найти фундаментальную систему [math]x_1,ldots,x_{n_1}[/math] решений однородной системы [math](A-lambda_1E)x=o[/math]. Линейно независимую систему [math]boldsymbol{x}_1,ldots, boldsymbol{x}_{n_1}[/math] векторов (пространства [math]mathbb{R}^n[/math]) ортогонализировать и нормировать. Получим векторы [math]boldsymbol{s}_1,ldots, boldsymbol{s}_{n_1}[/math].
5. Для пары [math]lambda=alphapmbeta i[/math] комплексных сопряженных корней кратности [math]m[/math] найти фундаментальную систему [math]z_1,ldots,z_{m}[/math] решений однородной системы [math](A+(alpha+beta i)E)z=o[/math]. Выделяя действительные [math]x_j=operatorname{Re}z_j[/math] и мнимые части [math]y_j=operatorname{Im}z_j,[/math] [math]j=1,ldots,m[/math], комплексных столбцов [math]z_1,ldots,z_{m}[/math], получить [math]m[/math] пар ортогональных векторов [math]boldsymbol{x}_1,boldsymbol{y}_1; boldsymbol{x}_2, boldsymbol{y}_2;ldots; boldsymbol{x}_m,boldsymbol{y}_m[/math] (пространства [math]mathbb{R}^n[/math]). Эту систему векторов ортогонализировать и нормировать. Получим [math]2m[/math] векторов [math]boldsymbol{s}_1,ldots,boldsymbol{s}_{2m}[/math].
6. Выполнить пункт 4 или пункт 5 для всех различных корней характеристического уравнения. Получаемые в результате группы столбцов последовательно записать в матрицу [math]S[/math] перехода от базиса [math]boldsymbol{e}_1,ldots,boldsymbol{e}_n[/math] к искомому каноническому базису [math]boldsymbol{s}_1,ldots, boldsymbol{s}_n colon,(boldsymbol{s})= (boldsymbol{e})S[/math]. Матрица [math]S^{-1}AS[/math] преобразования [math]mathcal{A}[/math] будет иметь канонический вид (9.20), полученный в пункте 3.
Замечания 9.7
1. Собственные векторы ортогональной матрицы, принадлежащие различным собственным значениям, ортогональны.
2. Из пункта 1 следует, что для получения ортонормированного базиса достаточно ортонормировать отдельно каждую группу векторов, получаемых в пункте 4 или пункте 5 алгоритма, причем по свойству 8 столбцы [math]x_j,y_j[/math] в пункте 5 будут ортогональными.
3. Матрицу вида (9.20) можно представить в виде произведения матриц, каждая из которых есть либо матрица [math]operatorname{diag}(1,ldots,1,-1,1,ldots,1)[/math] простого отражения относительно гиперплоскости, либо матрица math]operatorname{diag}(1,ldots,1, R_{varphi},1,ldots,1)[/math] простого вращения двумерной плоскости. Поэтому любое ортогональное преобразование можно представить в виде композиции простых отражений и простых вращений.
Пример 9.5. Ортогональное преобразование [math]mathcal{A}colon Vto V[/math] в базисе [math]boldsymbol{e}_1,boldsymbol{e}_2,boldsymbol{e}_3[/math] имеет матрицу [math]A=begin{pmatrix} 2/3&-1/3&2/3\ 2/3&2/3&-1/3\ -1/3&2/3&2/3 end{pmatrix}[/math]. Привести это преобразование к каноническому виду, т.е. найти базис [math]boldsymbol{s}_1, boldsymbol{s}_2, boldsymbol{s}_3[/math], в котором матрица преобразования имеет канонический вид (9.20).
Решение. Первый этап. Нахождение канонического вида преобразования.
1. Выбираем базис [math]boldsymbol{e}_1, boldsymbol{e}_2, boldsymbol{e}_3[/math], в котором задана матрица преобразования.
2. Составляем характеристическое уравнение
[math]det(A-lambda E)= begin{vmatrix}dfrac{2}{3}-lambda&-dfrac{1}{3}&dfrac{2}{3}\[8pt] dfrac{2}{3}&dfrac{2}{3}-lambda&-dfrac{1}{3}\[8pt] -dfrac{1}{3}&dfrac{2}{3}&dfrac{2}{3}-lambda end{vmatrix}= (1-lambda)(lambda^2-lambda+1)=0.[/math]
Уравнение имеет три простых (кратности 1) корня: один действительный [math]lambda_1=1[/math] и пару комплексных сопряженных [math]lambda_{2,3}= frac{1}{2}pmfrac{sqrt{3}}{2},i,~ alpha=frac{1}{2},~ beta=frac{sqrt{3}}{2}[/math].
3. Записываем искомый канонический вид (9.20), указывая на главной диагонали действительный корень [math]lambda_1=1[/math] и блок [math]R_{varphi}= begin{pmatrix}1/2&sqrt{3}/2\ -sqrt{3}/2&1/2 end{pmatrix}!,~ varphi=frac{pi}{3}:[/math]
[math]mathop{A}limits_{(boldsymbol{s})}= operatorname{diag}(1,,R_{varphi})= operatorname{diag}!!leftlgroup 1, begin{pmatrix} dfrac{1}{2}&dfrac{sqrt{3}}{2}\[7pt] -dfrac{sqrt{3}}{2}&dfrac{1}{2} end{pmatrix}!!rightrgroup= begin{pmatrix}1&0&0\[1pt] 0&dfrac{1}{2}&dfrac{sqrt{3}}{2}\[7pt] 0&-dfrac{sqrt{3}}{2}& dfrac{1}{2} end{pmatrix}!.[/math]
Второй этап. Нахождение канонического базиса. Найдем матрицу [math]S[/math] перехода от данного базиса [math]boldsymbol{e}_1,boldsymbol{e}_2,boldsymbol{e}_3[/math] к каноническому [math]boldsymbol{s}_1, boldsymbol{s}_2, boldsymbol{s}_3[/math].
4. Для действительного корня [math]lambda_1=1[/math] кратности 1 находим фундаментальную систему решений однородной системы [math](A-lambda_1E)x=o[/math]. Приводим матрицу системы к упрощенному виду:
[math]A-lambda_1E=A-E= left(!! begin{array}{rrr}dfrac{2}{3}&-dfrac{1}{3}&dfrac{2}{3}\[9pt] dfrac{2}{3}& dfrac{2}{3}&-dfrac{1}{3}\[9pt] -dfrac{1}{3}&dfrac{2}{3}&dfrac{2}{3} end{array}!!right)- begin{pmatrix}1&0&0\[2pt] 0&1&0\[2pt] 0&0&1end{pmatrix}= left(!! begin{array}{rrr} -dfrac{1}{3}&-dfrac{1}{3}&dfrac{2}{3}\[9pt] dfrac{2}{3}&-dfrac{1}{3}&-dfrac{1}{3}\[9pt] -dfrac{1}{3}&dfrac{2}{3}& -dfrac{1}{3}end{array} !!right)sim begin{pmatrix}1&0&-1\ 0&1&-1\ 0&0&0 end{pmatrix}!.[/math]
Следовательно, фундаментальная система содержит одно решение [math]x=begin{pmatrix} 1&1&1 end{pmatrix}^T[/math]. Нормируя это решение (поделив координаты на норму [math]|x|= sqrt{1^2+1^2+1^2}=sqrt{3}[/math]), получаем столбец [math]s_1=begin{pmatrix} dfrac{sqrt{3}}{3}& dfrac{sqrt{3}}{3}& dfrac{sqrt{3}}{3}end{pmatrix}^T[/math].
5. Для пары комплексных сопряженных корней [math]lambda_{2,3}= frac{1}{2}pm frac{sqrt{3}}{2},i[/math] находим фундаментальную систему решений однородной системы [math](A-lambda_2E)z=o[/math]. Приводим матрицу системы к упрощенному виду
[math]A-left(dfrac{1}{2}+dfrac{sqrt{3}}{2},iright)!E= begin{pmatrix} dfrac{1}{6}-dfrac{sqrt{3}}{2},i&-dfrac{1}{3}&dfrac{2}{3}\[9pt] dfrac{2}{3}&dfrac{1}{6}-dfrac{sqrt{3}}{2},i&-dfrac{1}{3}\[8pt] -dfrac{1}{3}&dfrac{2}{3}&dfrac{1}{6}-dfrac{sqrt{3}}{2},i end{pmatrix}sim begin{pmatrix}1&0&dfrac{1}{2}+dfrac{sqrt{3}}{2},i\[8pt] 0&1&dfrac{1}{2}-dfrac{sqrt{3}}{2},i\[8pt] 0&0&0 end{pmatrix}!.[/math]
Следовательно, фундаментальная система содержит одно решение. Полагая [math]z_3=1[/math], получаем решение:
[math]z=begin{pmatrix}z_1&z_2&z_3 end{pmatrix}^T=begin{pmatrix}-dfrac{1}{2}-dfrac{sqrt{3}}{2},i&-dfrac{1}{2}+ dfrac{sqrt{3}}{2},i &1end{pmatrix}^T.[/math]
Выделяем действительную и мнимую части:
[math]x=operatorname{Re}z= begin{pmatrix}-dfrac{1}{2}&-dfrac{1}{2}& 1end{pmatrix}^T, quad y=operatorname{Im}z= begin{pmatrix}-dfrac{sqrt{3}}{2}& dfrac{sqrt{3}}{2}& 0 end{pmatrix}^T.[/math]
Нормируя столбцы, поделив координаты вектора [math]boldsymbol{x}[/math] на его длину
[math]|boldsymbol{x}|=sqrt{{left(-frac{1}{2}right)!}^2+ {left(-frac{1}{2}right)!}^2+1^2}= sqrt{dfrac{3}{2}},,[/math] а координаты вектора [math]boldsymbol{y}[/math] — на [math]|boldsymbol{y}|= frac{sqrt{6}}{2}[/math], получаем
[math]s_2=begin{pmatrix}-dfrac{sqrt{6}}{6}&-dfrac{sqrt{6}}{6}&dfrac{sqrt{6}}{3} end{pmatrix}^T,quad s_3=begin{pmatrix}-dfrac{sqrt{2}}{2}& dfrac{sqrt{2}}{2}& 0end{pmatrix}^T.[/math]
6. Записываем полученные в пункт 4, 5 столбцы [math]s_1,,s_2,,s_3[/math] в искомую матрицу перехода
[math]S= begin{pmatrix}s_1&s_2&s_3end{pmatrix}= begin{pmatrix}dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{6}&-dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{6}& dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{3}&0 end{pmatrix}!.[/math]
Проверим равенство [math]Smathop{A}limits_{(boldsymbol{s})}=AS[/math] (равносильное [math]mathop{A}limits_{(boldsymbol{s})}=S^{-1}AS[/math]), находя произведения
[math]begin{aligned}Scdot mathop{A}limits_{(boldsymbol{s})}&= begin{pmatrix} dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{6}&-dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{6}& dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{3}&0 end{pmatrix}!cdot! begin{pmatrix}1&0&0\[1pt] 0&dfrac{1}{2}&dfrac{sqrt{3}}{2}\[8pt] 0&-dfrac{sqrt{3}}{2}&dfrac{1}{2} end{pmatrix}= begin{pmatrix} dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{6}&-dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{3}& 0\[9pt] dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{6}& dfrac{sqrt{2}}{2}end{pmatrix}!,\[5pt] Acdot S&= left(!! begin{array}{rrr}dfrac{2}{3}&-dfrac{1}{3}&dfrac{2}{3}\[9pt] dfrac{2}{3}& dfrac{2}{3}&-dfrac{1}{3}\[9pt] -dfrac{1}{3}&dfrac{2}{3}&dfrac{2}{3} end{array}!!right)!cdot! begin{pmatrix} dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{6}&-dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{6}& dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{3}&0 end{pmatrix}= begin{pmatrix} dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{6}&-dfrac{sqrt{2}}{2}\[9pt] dfrac{sqrt{3}}{3}&-dfrac{sqrt{6}}{3}& 0\[9pt] dfrac{sqrt{3}}{3}& dfrac{sqrt{6}}{6}& dfrac{sqrt{2}}{2} end{pmatrix}!. end{aligned}[/math]
Результаты совпадают.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Как привести матрицу к каноническому виду
Матрицы — удобный инструмент для решения самых различных алгебраических задач. Знание некоторых простых правил для оперирования с ними позволяет приводить матрицы к любым удобным и необходимым в данный момент формам. Часто полезным является использование канонической формы матрицы.

Инструкция
Запомните, что канонический вид матрицы не требует, чтобы на всей главной диагонали стояли единицы. Суть определения заключается в том, что единственные ненулевые элементы матрицы в ее каноническом виде – это единицы. Если они присутствуют, то располагаются на главной диагонали. При этом их количество может варьироваться от нуля до количества строчек в матрице.
Не забывайте, что элементарные преобразования позволяют любую матрицу привести к каноническому виду. Самая большая сложность – интуитивно найти наиболее простую последовательность цепочек действий и не ошибиться в вычислениях.
Выучите основные свойства операций со строчками и столбцами в матрице. К элементарным преобразованиям относят три стандартных преобразования. Это умножение строчки матрицы на любое ненулевое число, суммирование строк (в том числе прибавление к одной другой, умноженной на какое-то число) и их перестановка. Подобные действия позволяют получить матрицу эквивалентную данной. Соответственно, вы можете выполнить такие операции и со столбцами без потери эквивалентности.
Старайтесь не выполнять одновременно сразу несколько элементарных преобразований: продвигайтесь от этапа к этапу, чтобы не допустить случайной ошибки.
Найдите ранг матрицы, чтобы определить количество единиц на главной диагонали: это подскажет вам, какой окончательный вид будет иметь искомая каноническая форма, и избавит от необходимости выполнять преобразования, если требуется просто использовать ее для решения.
Воспользуйтесь методом окаймляющих миноров для того, чтобы выполнить предыдушую рекомендацию. Вычислите минор к-ого порядка, а также все окаймляющие его миноры степени (к+1). Если они равны нулю, то ранг матрицы есть число к. Не забывайте, что минор Мij – это определитель матрицы, получаемой при вычеркивании строки i и столбца j из исходной.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание
Квадратичная форма
$ mathbb A_{} $ означает одно из множеств: $ mathbb Q_{} $ рациональных, или $ mathbb R_{} $ вещественных, или $ mathbb C_{} $ комплексных чисел.
Определение
Квадратичной формой над множеством $ mathbb A_{} $ называют однородный полином второй степени с коэффициентами из $ mathbb A_{} $; если переменные обозначить
$ x_1,dots,x_{n} $, то общий вид квадратичной формы от этих переменных:
$$
f(x_1,dots,x_{n} )= sum_{1le j le k le n} f_{jk}x_jx_k=
$$
$$begin{array}{llll}
displaystyle=
f_{11}x_1^2&+f_{12}x_1x_2&+ dots & +f_{1n}x_1x_n+ \
&+f_{22}x_2^2 &+ dots & +f_{2n}x_2x_n+ \
&+dots & & +dots + \
& & +f_{jk}x_jx_k & + dots+ \
& & &+f_{nn}x_n^2.
end{array}
$$
П
Пример. Функции
$$x_1^2-x_1x_2+x_3^2 , , quad sqrt{3}, x_2^2 — pi, x_3^2
, , quad -x_1x_2 , , quad mathbf i , x_1^2$$
являются квадратичными формами. Функции
$$x_1^2-3, x_1+1 , , quad 5, x_1^2x_2^2 , , quad frac{x_1x_3^2}{x_2}
, , quad sqrt{x_1x_2x_3x_4} $$
не являются квадратичными формами.
Заметим, что в выражении для квадратичной формы присутствуют как квадраты переменных $ x_1^2,dots,x_n^2 $ так и их смешанные произведения $ x_j x_k $. Говорят, что квадратичная форма $ f(x_1,dots,x_{n} ) $ имеет канонический вид если
$$f(x_1,dots,x_{n} )equiv f_{11}x_1^2+f_{22}x_2^2+dots+f_{nn}x_n^2 quad npu quad left{f_{jj}right}_{j=1}^n subset mathbb A , $$
т.е. все коэффициенты при смешанных произведениях переменных равны нулю; в этом случае говорят также, что форма является «суммой квадратов»1).
Оказывается, что в любой квадратичной форме можно так сгруппировать входящие в нее одночлены, что в результате получится ее (эквивалентное) представление в виде суммы квадратов.
П
Пример.
$$ 2, x_1^2+4, x_1x_2 +x_2^2 equiv 2, (x_1+x_2)^2-x_2^2 equiv -2,x_1^2 + (2,x_1+x_2)^2 ; $$
$$ x_1^2+2 mathbf i x_1x_2 — x_2^2 equiv (x_1+ mathbf i x_2)^2 ; $$
$$-x_1^2+6,x_1x_2+6,x_1x_3+2,x_2^2+4,x_2x_3+2,x_3^2equiv $$
$$
equiv (x_1+x_2+x_3)^2-2,(x_1-x_2-x_3)^2+3,(x_2+x_3)^2 equiv
$$
$$equiv -(x_1+3,x_2+3,x_3)^2+11,(x_2+x_3)^2 ; $$
$$ x_1x_2 equiv frac{1}{4} (x_1+x_2)^2- frac{1}{4} (x_1-x_2)^2 . $$
А в общем случае:
$$ f(x_1,dots,x_{n} )equiv $$
$$
begin{array}{l}
equiv a_1(c_{11}x_1+c_{12}x_2+dots+c_{1n}x_n)^2 +\
+a_2(c_{21}x_1+c_{22}x_2+dots+c_{2n}x_n)^2+ \
+dots+ \
+a_n(c_{n1}x_1+c_{n2}x_2+dots+c_{nn}x_n)^2
end{array}
$$
при $ {a_j}_{j=1}^n,{c_{jk}}_{j,k=1}^n $ — константах. Такое представление оказывается достаточно удобным для анализа квадратичной формы — например, в случае вещественных форм, при проверке выполнимости неравенства вида $ f(x_1,dots,x_{n} ) ge 0 $. Приведенные выше примеры показывают неоднозначность представления в виде суммы квадратов: вид квадратов и даже их количество для одной и той же формы могут быть различными. С целью обеспечения частичной унификации установим некоторое дополнительное ограничение, а именно, потребуем, чтобы линейные однородные формы
$$ c_{11}x_1+c_{12}x_2+dots+c_{1n}x_n, c_{21}x_1+c_{22}x_2+dots+c_{2n}x_n,dots, c_{n1}x_1+c_{n2}x_2+dots+c_{nn}x_n $$
были линейно независимыми. При таком ограничении любое представление квадратичной формы в виде суммы квадратов называется каноническим видом квадратичной формы.
Задача. Для произвольной квадратичной формы $ f(x_1,dots,x_{n} ) $ построить (хотя бы один) ее канонический вид.
Поставленная задача имеет существенное значение для анализа
-
геометрии линий второго порядка на плоскости и поверхностей второго порядка в пространстве; например, по набору коэффициентов уравнения, задающего кривую
$$ x^2 -2,xy+3,y^2+x-4,y-15=0 $$
определить к какому типу (эллипс, гипербола, парабола,…) она относится.
Метод Лагранжа приведения квадратичной формы к каноническому виду
Существует универсальный алгоритм, приводящий произвольную квадратичную форму к каноническому виду.
Метод Лагранжа
1.
Пусть $ f_{11}ne 0 $. Выделим в $ f(x_1,dots, x_n)_{} $ все слагаемые, содержащие $ x_{1} $:
$$
f_{11}x_1^2+f_{12}x_1x_2+ dots +f_{1n}x_1x_n+ sum_{2le jle k le n} f_{jk}x_jx_k
=
$$
$$
= f_{11}left(x_1^2+frac{f_{12}}{f_{11}}x_1x_2+dots+
frac{f_{1n}}{f_{11}}x_1x_n right)+dots=
$$
$$
=f_{11}left[ left(x_1+frac{f_{12}}{2f_{11}}x_2+dots+
frac{f_{1n}}{2f_{11}}x_n right)^2-left(frac{f_{12}}{2f_{11}}x_2+dots+
frac{f_{1n}}{2f_{11}}x_n right)^2 right]+dots=
$$
$$
=f_{11} left(x_1+frac{f_{12}}{2f_{11}}x_2+dots+ frac{f_{1n}}{2f_{11}}x_n
right)^2 —
f_{11}left(frac{f_{12}}{2f_{11}}x_2+dots+
frac{f_{1n}}{2f_{11}}x_n right)^2 +dots
$$
В последнем представлении первое слагаемое представляет собой квадрат линейной формы по переменным $ x_{1},x_2,dots,x_n $; все оставшиеся слагаемые не зависят от $ x_{1} $, т.е. составляют квадратичную форму от переменных $ x_{2},dots,x_n $. Таким образом, исходная задача для формы $ n_{} $ переменных оказывается сведенной к случаю формы $ (n-1)_{} $-й переменной; последняя преобразуется по аналогичному принципу.
2.
Если $ f_{11}=0 $, но $ exists k: f_{kk}ne 0 $, т.е. при хотя бы одном квадрате переменной коэффициент отличен от нуля. Алгоритм модифицируется таким образом, что выделение полного квадрата начинается с переменной $ x_{k} $ вместо $ x_{1} $ — первая ничем не лучше (и не хуже) $ k_{} $-й!
3.
Совсем исключительный случай: квадраты переменных вообще отсутствуют, т.е. $ f_{11}=dots=f_{nn}=0 $. Выбираем один из ненулевых коэффициентов при смешанных произведениях переменных: пусть $ f_{jk}ne 0 $. Представляем $ x_k=(x_j+x_k)-x_j $ и заменяем все вхождения переменной $ x_{k} $ на $ X_k-x_j $ при вспомогательной переменной $ X_k=x_j+x_k $. В новой квадратичной форме уже присутствует квадрат переменной $ x_{j} $ с ненулевым коэффициентом. Тем самым этот случай сводится к предыдущему. После приведения новой формы к сумме квадратов возвращаемся к «старой» переменной $ x_{k} $.
П
Пример. Привести форму
$$ f=4,x_1^2+2,x_2^2+x_3^2+x_4^2-4,x_1x_2-4,x_1x_3+4,x_1x_4+4,x_2x_3-4,x_3x_4 $$
к каноническому виду.
Решение.
$$
begin{array}{ccl}
f&=&4left(x_1^2-x_1x_2-x_1x_3+x_1x_4right)+2x_2^2+x_3^2+x_4^2+4x_2x_3-4x_3x_4=\
&=&4bigg[
left(x_1-frac{1}{2}, x_2-frac{1}{2},x_3+ frac{1}{2},x_4, right)^2-
left(-frac{1}{2}, x_2-frac{1}{2}, x_3+frac{1}{2}, x_4right)^2 bigg] + \
&+&2,x_2^2+x_3^2+x_4^2+4,x_2x_3-4,x_3x_4= \
&=&4,left(x_1-frac{1}{2}, x_2-frac{1}{2},x_3+ frac{1}{2},x_4, right)^2+\
& & + Big[left(x_2+x_3+x_4, right)^2- left(x_3+x_4 right)^2Big]-2,x_3x_4 = \
&=&4,left(x_1-frac{1}{2}, x_2-frac{1}{2},x_3+ frac{1}{2},x_4, right)^2+
left(x_2+x_3+x_4, right)^2- \
&&-x_3^2-4,x_3x_4-x_4^2= \
&& 4,left(x_1-frac{1}{2}, x_2-frac{1}{2},x_3+ frac{1}{2},x_4, right)^2+
left(x_2+x_3+x_4, right)^2- \
&&-Big[
left(x_3+ 2, x_4, right)^2-4, x_4^2Big] -x_4^2 = \
&=&4,left(x_1-frac{1}{2}, x_2-frac{1}{2},x_3+ frac{1}{2},x_4, right)^2+
left(x_2+x_3+x_4, right)^2-left(x_3+ 2, x_4, right)^2+3,x_4^2
end{array}
$$
Ответ. $ fequiv 4,left(x_1-frac{1}{2}, x_2-frac{1}{2},x_3+ frac{1}{2},x_4, right)^2+
left(x_2+x_3+x_4, right)^2-left(x_3+ 2, x_4, right)^2+3,x_4^2 $.
П
Пример. Привести форму
$$ f=x_1^2+x_2^2-4,x_3^2+2,x_1x_2+6,x_1x_3+4,x_2x_3 $$
к каноническому виду.
Решение.
$$
fequiv (x_1+x_2+3,x_3)^2-(x_2+3,x_3)^2+x_2^2-4,x_3^2+4,x_2x_3 equiv
$$
$$
equiv (x_1+x_2+3,x_3)^2-2,x_2x_3 -13,x_3^2 equiv
$$
В соответствии с алгоритмом, на следующем шаге нужно выделять слагаемые, содержащие переменную $ x_{2} $, но коэффициент при $ x_2^2 $ в правой части формулы обратился в нуль. Поэтому — в соответствии с пунктом
2
метода —
приходится выделять квадрат на основе переменной $ x_{3} $:
$$ (x_1+x_2+3,x_3)^2-13, left(x_3-frac{1}{13}x_2right)^2+13cdot frac{1}{13^2}x_2^2 . $$
Ответ. $ (x_1+x_2+3,x_3)^2-13, left(x_3-frac{1}{13}x_2right)^2+ frac{1}{13}x_2^2 $.
П
Пример. Привести форму
$$ f=x_1x_2-3,x_1x_3+2,x_2x_3 $$
к каноническому виду.
Решение. Коэффициенты при квадратах переменных все равны нулю. Действуем в соответствии с пунктом
3
метода Лагранжа. Поскольку коэффициент при $ x_1x_2 $ отличен от нуля, делаем замену переменной $ x_2=X_2-x_1 $ при $ X_2=x_1+x_2 $:
$$ fequiv -x_1^2+x_1X_2-5,x_1x_3+2,X_2x_3 . $$
Дальнейший ход решения — в соответствии с пунктом
1
метода Лагранжа:
$$
-left(x_1-frac{1}{2}X_2+frac{5}{2}x_3right)^2+left(-frac{1}{2}X_2+frac{5}{2}x_3right)^2+2,X_2x_3 equiv
$$
$$
equiv -left(x_1-frac{1}{2}X_2+frac{5}{2}x_3right)^2+frac{1}{4}X_2^2-frac{1}{2}X_2x_3+frac{25}{4}x_3^2 equiv
$$
$$
equiv -left(x_1-frac{1}{2}X_2+frac{5}{2}x_3right)^2+frac{1}{4}left(X_2-x_3 right)^2+6,x_3^2
$$
Получили сумму квадратов форм от переменных $ x_1,X_2,x_3 $. Возвращаемся к переменной $ x_{2} $:
Ответ. $ -(frac{1}{2}x_1-frac{1}{2}x_2+frac{5}{2}x_3)^2+frac{1}{4}(x_1+x_2-x_3)^2+6,x_3^2 $.
Метод Лагранжа позволяет получить канонический вид квадратичной формы над тем же множеством $ mathbb A_{} $, над которым рассматривается исходная форма — например, если коэффициенты формы $ f_{} $ являются рациональными, то и коэффициенты ее канонического вида (т.е. числа $ {a_j}_{j=1}^n,{c_{jk}}_{j,k=1}^n $) будут также рациональными.
Матричная форма записи квадратичной формы
В этом и последующих пунктах существенно потребуется знание ключевых понятий ТЕОРИИ МАТРИЦ и ОПРЕДЕЛИТЕЛЕЙ.
Задача. Установить правило формирования коэффициентов канонического вида квадратичной формы, получающегося применением метода Лагранжа.
Прежде всего, соберем все переменные в один вектор, а вернее — в два вектора:
$$
{}_{.} mbox{ столбец переменных } X=
left(begin{array}{l} x_1 \ vdots \ x_n end{array} right) quad mbox{ и строку переменных }
X^{top} = (x_1,dots,x_n) ;
$$
здесь $ {}^{top} $ означает транспонирование. Не очень принципиально, что обозначать через $ X_{} $ — столбец или строку; и хотя сокращение $ f(x_1,dots,x_n)=f(X) $ кажется не вполне корректным с точки зрения только что введенного обозначения, тем не менее не будем навешивать в правую часть дополнительные
значки…
Если определить верхнетреугольную матрицу $ mathbf F $ равенством:
$$
{mathbf F}= left(
begin{array}{cccc}
f_{11}&f_{12}&dots &f_{1n} \
&f_{22}& dots & f_{2n} \
mathbb O & &ddots & vdots \
& & & f_{nn}
end{array} right),
$$
то квадратичную форму можно записать в виде произведения трех матриц
$$ {}_{.} mbox{ строка переменных } times mbox{ матрица } times mbox{ столбец переменных } $$
$$ f(X)=X^{top} {mathbf F}X .$$
Более того, можно написать бесконечно много подобных представлений для одной и той же квадратичной формы $ f_{} $, подбирая разные матрицы
П
Пример. $ f=x_1^2+x_2^2-4,x_3^2+2,x_1x_2+6,x_1x_3+4,x_2x_3 equiv $
$$
equiv (x_1,x_2,x_3)
left(
begin{array}{rrr}
1 & 2 & 6 \
0 & 1 & 4 \
0 & 0 & -4
end{array}
right)
left(
begin{array}{l}
x_1 \ x_2 \ x_3
end{array}
right)
equiv (x_1,x_2,x_3)
left(
begin{array}{rrr}
1 & 0 & 3 \
2 & 1 & 4 \
3 & 0 & -4
end{array}
right)
left(
begin{array}{l}
x_1 \ x_2 \ x_3
end{array}
right)equiv
$$
$$
equiv (x_1,x_2,x_3)
left(
begin{array}{rrr}
1 & 1 & 3 \
1 & 1 & 2 \
3 & 2 & -4
end{array}
right)
left(
begin{array}{l}
x_1 \ x_2 \ x_3
end{array}
right)equiv dots
$$
Из всего этого бесконечного множества представлений выделим одно. Рассмотрим матрицу
$${mathbf A}=frac{{mathbf F}+{mathbf F}^{top}}{2}=
left(
begin{array}{cccc}
f_{11}& 1/2 f_{12}&dots & 1/2 f_{1n} \
1/2 f_{12} &f_{22}& dots & 1/2 f_{2n} \
dots & & & dots \
1/2 f_{1n} & 1/2 f_{2n} & dots & f_{nn}
end{array} right),
$$
которая, очевидно, симметрична: $ {mathbf A}^{top}={mathbf A} $. Тогда
$$
f(X)=sum_{1le j,k le n} a_{jk}x_jx_k=X^{top}{mathbf A}X .
$$
Это представление называют правильной записью квадратичной формы; матрицу $ {mathbf A} $ называют матрицей квадратичной формы $ f_{} $, а $ det mathbf A $ — дискриминантом квадратичной формы:
$$ det A = {mathcal D} (f) . $$
В случае, когда дискриминант равен нулю квадратичная форма называется вырожденной, в противном случае — невырожденной.
П
Пример. Для приведенной выше квадратичной формы
$$ f=x_1^2+x_2^2-4,x_3^2+2,x_1x_2+6,x_1x_3+4,x_2x_3 $$
ее правильной записью будет именно последняя:
$$
fequiv
(x_1,x_2,x_3)
left(
begin{array}{rrr}
1 & 1 & 3 \
1 & 1 & 2 \
3 & 2 & -4
end{array}
right)
left(
begin{array}{l}
x_1 \ x_2 \ x_3
end{array}
right)
$$
Правило формирования матрицы довольно просты: на диагонали ставятся коэффициенты при квадратах, а внедиагональные элементы получаются располовиниванием коэффициентов при смешанных произведениях переменных.
| $ x_{1} $ | $ x_{2} $ | $ x_{3} $ | |
|---|---|---|---|
| $ x_{1} $ | $ f_{11} $ | $ frac{1}{2}f_{12} $ | $ frac{1}{2}f_{13} $ |
| $ x_{2} $ | $ frac{1}{2}f_{12} $ | $ f_{22} $ | $ frac{1}{2}f_{23} $ |
| $ x_{3} $ | $ frac{1}{2}f_{13} $ | $ frac{1}{2}f_{23} $ | $ f_{33} $ |
П
Пример. Для
$$ f(x_1,x_2)=a_{11}x_1^2+2, a_{12}x_1x_2+a_{22}x_2^2 $$
имеем:
$$ {mathbf A} =
left(
begin{array}{ll}
a_{11} & a_{12} \
a_{12} & a_{22}
end{array}
right) ; {mathcal D} (f)=a_{11}a_{22}-a_{12}^2 ; $$
последнее выражение вполне напоминает дискриминант квадратного трехчлена $ a_{11}x^2+2, a_{12}x+a_{22} $ и это обстоятельство оправдывает использование слова дискриминант для нового объекта…
Матрица квадратичной формы совпадает с половиной матрицы Гессе этой формы: $ mathbf A = 1/2 H(f) $.
Причина, по которой из бесконечного многообразия матричных представлений квадратичной формы выделяется именно то, что использует симметричную матрицу, остается пока непонятной. Отложив ненадолго обсуждение этой причины, попробуем переписать в матричных терминах приведение квадратичной формы к каноническому виду.
Рассмотрим замены переменных в квадратичной форме, т.е. переход от переменных $ x_{1},dots,x_{n} $ к новым переменным $ y_{1},dots,y_{n} $. Ограничимся только линейными заменами вида
$$
left{ begin{array}{ccc}
x_1&=&c_{11}y_1+c_{12}y_2+dots+c_{1n}y_n, \
x_2&=&c_{21}y_1+c_{22}y_2+dots+c_{2n}y_n, \
dots & & dots \
x_n&=&c_{n1}y_1+c_{n2}y_2+dots+c_{nn}y_n.
end{array}
right.
$$
Результатом такой замены переменных будет новая квадратичная форма относительно новых переменных. Установим по какому закону формируются ее коэффициенты. С этой целью введем в рассмотрение матрицу замены переменных
$$
C=
left( begin{array}{llcl}
c_{11} & c_{12} & dots & c_{1n} \
c_{21} & c_{22} & dots & c_{2n} \
dots & & & dots \
c_{n1} & c_{n2} & dots & c_{nn} \
end{array}
right) ;
$$
которая позволяет переписать саму замену переменных в матричном виде
$$
left(begin{array}{l} x_1 \ x_2 \ vdots \ x_n end{array} right)=
left( begin{array}{llcl}
c_{11} & c_{12} & dots & c_{1n} \
c_{21} & c_{22} & dots & c_{2n} \
dots & & & dots \
c_{n1} & c_{n2} & dots & c_{nn} \
end{array}
right)
left(begin{array}{l} y_1 \ y_2 \ vdots \ y_n end{array} right) qquad iff qquad
X=CY .
$$
Тогда формальная подстановка последнего варианта в правильную запись квадратичной формы приведет к следующей цепочке
$$
f(X)=X^{top}{mathbf A}X= (CY)^{top}{mathbf A} (CY)=Y^{top} C^{top}{mathbf A}C Y=tilde f (Y) ,
$$
(здесь использовались некоторые свойства операции транспонирования ) и, если обозначить матрицу
$$
mathbf B =C^{top}{mathbf A}C ,
$$
то мы получаем правило формирования матрицы квадратичной формы, получившейся в результате замены переменных, с помощью операции произведения матриц. Обратим внимание на еще один факт — матрица $ mathbf B $ является симметричной:
$$
mathbf B^{top} =(C^{top}{mathbf A}C)^{top}= C^{top}{mathbf A}^{top}left(C^{top} right)^{top} =
C^{top}{mathbf A}C= mathbf B ,
$$
т.е. выбор в качестве матричной записи квадратичной формы именно того варианта, что основан на симметричной матрице, позволяет сохранить это свойство при любой линейной замене переменных.
Задача о нахождении канонического вида квадратичной формы $ X^{top}{mathbf A}X $ может быть также переформулирована в терминах замены переменных: требуется найти такую матрицу $ C_{} $, чтобы матрица
$ mathbf B= C^{top}{mathbf A}C $ оказалась диагональной:
$$
mathbf B=
left(
begin{array}{cccc}
a_{1} & & & \
& a_{2} & & {mathbb O} \
{mathbb O} & & ddots & \
& & & a_{n}
end{array}
right) ;
$$
при этом дополнительным условием ставится невырожденность (неособенность) матрицы $ C_{} $:
$$ det C ne 0 . $$
Пока не вполне понятна существенность последнего условия: почему оно накладывается? С одной стороны, оно обеспечивает обратимость замены переменных $ (x_1,dots,x_n) leftrightarrow
(y_1,dots,y_n) $ — не происходит «потери информации». В самом деле, наличие какого-то ограничения на все возможные замены переменных, довольно очевидно: если бы разрешалось использовать, например, нулевую матрицу $ C = {mathbb O}_{n} $, то канонический вид у любой квадратичной формы был бы нулевым.. . Геометрический смысл условия $ det C ne 0 $ обсудим
☟
НИЖЕ.
Т
Теорема. Для любой квадратичной формы над $ mathbb A $ существует невырожденная линейная замена
переменных $ X=CY $ такая, что преобразованная квадратичная форма $ widetilde f(Y) $ имеет канонический вид.
Вернемся к примерам предыдущего пункта, перепишем их на матричном языке.
П
Пример. Для формы
$$ f(x_1,x_2,x_3,x_4)= $$
$$=4,x_1^2+2,x_2^2+x_3^2+x_4^2-4,x_1x_2-4,x_1x_3+4,x_1x_4+4,x_2x_3-4,x_3x_4 $$
замена переменных осуществляется формулами
$$
begin{array}{crrrr}
y_1=& x_1 &-frac{1}{2}, x_2&-frac{1}{2},x_3&+ frac{1}{2},x_4, \
y_2=& & x_2&+x_3&+x_4, \
y_3=& & & x_3 &+ 2, x_4,\
y_4=& &&& x_4,
end{array}
$$
т.е. матрица замены переменных
$$
C=
left(
begin{array}{cccc}
1 & -frac{1}{2} & -frac{1}{2} & frac{1}{2} \
0 & 1 & 1 & 1 \
0 & 0 & 1 & 2 \
0 & 0 & 0 & 1
end{array}
right)
$$
имеет верхнетреугольный вид. Канонический вид в новых переменных записывается
$$ f(x_1,x_2,x_3,x_4) equiv 4,y_1^2+y_2^2-y_3^2+3,y_4^2 . $$
Для формы
$$ f(x_1,x_2,x_3)=x_1^2+x_2^2-4,x_3^2+2,x_1x_2+6,x_1x_3+4,x_2x_3 $$
замена переменных уже не имеет треугольного вида:
$$
begin{array}{crrr}
y_1=& x_1 &+ x_2&+3,x_3 \
y_2=& & -frac{1}{13}x_2&+x_3 \
y_3=& & frac{1}{13}x_2 &
end{array}
qquad iff qquad
C=
left(
begin{array}{rrr}
1 & 1 & 3 \
0 & -frac{1}{13} & 1 \
0 & frac{1}{13} & 0
end{array}
right) .
$$
Для формы
$$ f(x_1,x_2,x_3)=x_1x_2-3,x_1x_3+2,x_2x_3 $$
получили:
$$
begin{array}{crrr}
y_1=& frac{1}{2}x_1 &-frac{1}{2}x_2&+frac{5}{2}x_3 \
y_2=& x_1&+x_2&-x_3 \
y_3=& & & x_3
end{array}
qquad iff qquad
C=
left(
begin{array}{rrr}
frac{1}{2} & -frac{1}{2} & frac{5}{2} \
1 & 1 & -1 \
0 & 1 & 1
end{array}
right) ,
$$
т.е. замена переменных также не имеет треугольного вида.
♦
Поставленную в начале пункта задачу об установлении структуры канонического вида квадратичной формы попытаемся решить сначала для случая когда замену переменных можно подобрать именно в треугольном виде.
Метод Лагранжа и метод Гаусса
В этом и последующих пунктах существенно потребуется знание МЕТОДА ГАУССА преобразования систем линейных уравнений.
П
Пример. Рассмотрим матрицу квадратичной формы
$$ f(x_1,x_2,x_3,x_4)=$$
$$ =4,x_1^2+2,x_2^2+x_3^2+x_4^2-4,x_1x_2-4,x_1x_3+4,x_1x_4+4,x_2x_3-4,x_3x_4 $$
из предыдущих пунктов, и, временно выходя из
круга поставленных в настоящем разделе задач, попробуем применить к ней метод Гаусса
приведения к треугольному виду:
$$
left(
begin{array}{rrrr}
4 & -2 & -2 & 2 \
-2 & 2 & 2 & 0 \
-2 & 2 & 1 & -2 \
2 & 0 & -2 & 1
end{array}
right)
rightarrow
left(
begin{array}{rrrr}
4 & -2 & -2 & 2 \
0 & 1 & 1 & 1 \
0 & 1 & 0 & -1 \
0 & 1 & -1 & 0
end{array}
right)
rightarrow
$$
$$
rightarrow
left(
begin{array}{rrrr}
4 & -2 & -2 & 2 \
0 & 1 & 1 & 1 \
0 & 0 & -1 & -2 \
0 & 0 & -2 & -1
end{array}
right)
rightarrow
left(
begin{array}{rrrr}
4 & -2 & -2 & 2 \
0 & 1 & 1 & 1 \
0 & 0 & -1 & -2 \
0 & 0 & 0 & 3
end{array}
right) .
$$
Обратим внимание на два обстоятельства: диагональные элементы последней матрицы
совпадают с коэффициентами канонического вида квадратичной формы, а коэффициенты
замены переменных, приводящей к этому каноническому виду, совпадают с
элементами строк этой матрицы, если их разделить на соответствующие диагональные
элементы. Возникает подозрение , что метод Лагранжа является «замаскированной»
версией метода Гаусса.
♦
Для того, чтобы выяснить аналитический смысл преобразований по методу Лагранжа найдем
правило формирования коэффициентов в первом шаге приведения квадратичной формы к каноническому виду.
Пусть исходная квадратичная форма записана в виде
$$
f(x_1,dots,x_{n} )=sum_{1le j,k le n} a_{jk}x_jx_k=
$$
$$
begin{array}{llll}
=
a_{11}x_1^2&+2a_{12}x_1x_2&+ dots & +2a_{1n}x_1x_n+ \
&+a_{22}x_2^2 &+ dots & +2a_{2n}x_2x_n+ \
& & +dots & + \
& & &+a_{nn}x_n^2,
end{array}
$$
т.е. коэффициенты при смешанных произведениях переменных записаны с выделением множителя $ 2_{} $.
После выделения полного квадрата, содержащего переменные $ x_1,x_2,dots,x_n $:
$$ f(x_1,x_2,dots,x_n)equiv a_{11}
left(x_1+frac{a_{12}}{a_{11}}x_2+dots+ frac{a_{1n}}{a_{11}}x_n
right)^2 + f_2(x_2,dots,x_n)
$$
в правой части тождества образовалась квадратичная форма $ f_{2} $, не содержащая $ x_{1} $. Она равна
$$
f_2 =sum_{2le j,k le n} a_{jk}x_jx_k-
a_{11}left(frac{a_{12}}{a_{11}}x_2+dots+
frac{a_{1n}}{a_{11}}x_n right)^2=
$$
$$
=sum_{2le j,k le n} a_{jk}x_jx_k-a_{11}sum_{2le j,k le n}
frac{a_{1j}a_{1k}}{a_{11}^2}x_jx_k=
sum_{2le j,k le n}left( a_{jk}-frac{a_{1j}}{a_{11}}a_{1k} right)
x_jx_k .
$$
Если теперь выписать матрицу этой квадратичной формы (она имеет порядок $ n_{}-1 $), то ее элементы образуются по точно такому же правилу, как и коэффициенты матрицы, получающейся из матрицы $ mathbf A_{} $ в результате первого шага метода Гаусса.
Т
Теорема. Метод Лагранжа приведения квадратичной формы $ X^{top}{mathbf A}X $ к каноническому виду эквивалентен методу Гаусса приведения матрицы $ {mathbf A} $ к треугольному виду.
Доказательство. Действительно, первый шаг прямого хода метода исключения переменных
Гаусса преобразует матрицу $ mathbf A $ следующим образом:
$$
left( begin{array}{ccccc}
a_{11}& a_{12}& a_{13}& dots & a_{1n} \
a_{12}& a_{22}& a_{23}& dots & a_{2n} \
& dots & & dots & \
a_{1n}& a_{2n}& a_{3n}& dots & a_{nn}
end{array}
right)
rightarrow
left(begin{array}{llll}
a_{11}&a_{12}&dots&a_{1n}\
0&a_{22}^{[1]}& dots &a_{2n}^{[1]}\
&dots & & dots \
0&a_{n2}^{[1]}&dots &a_{nn}^{[1]}
end{array} right) ;
$$
здесь
$$a_{jk}^{[1]} = a_{jk} — frac{a_{j1}a_{1k}}{a_{11}} ,$$
и предполагается, что $ a_{11}ne 0 $. Видим, что формула формирования
элементов матрицы
$$
left(begin{array}{llll}
a_{22}^{[1]}& dots&a_{2n}^{[1]}\
dots & & dots & \
a_{n2}^{[1]}&dots &a_{nn}^{[1]}
end{array} right)_{(n-1)times (n-1)}
$$
точно такая же, как и матрицы квадратичной формы $ f_2 $. Более того,
поскольку матрица $ {mathbf A} $ симметрична ($ a_{jk}=a_{kj} $), то
и только что полученная матрица оказывается симметричной.
Если $ a_{22}^{[1]} ne 0 $, то к этой новой матрице можно снова применить
ту же процедуру, и т.д., и в конце концов придем к матрице первого порядка.
Собирая все промежуточные результаты в одну матрицу, получим ее в треугольном
виде
$$
left(begin{array}{lllll}
a_{11}&a_{12}&dots&a_{1,n-1} &a_{1n}\
0&a_{22}^{[1]}& dots&a_{2,n-1}^{[1]} &a_{2n}^{[1]}\
& & ddots & & dots \
0 &0 & &a_{n-1,n-1}^{[n-2]}&a_{n-1,n}^{[n-2]} \
0 &0 &dots & 0 &a_{nn}^{[n-1]}
end{array} right)
$$
при условии, что ни одно из чисел на диагонали не обратилось в нуль:
$$a_{11} ne 0, a_{22}^{[1]} ne 0, dots, a_{n-1,n-1}^{[n-2]} ne 0, a_{nn}^{[n-1]} ne 0
.$$
Если теперь обратиться к методу Лагранжа, то увидим, что полученная матрица как раз и определяет
замену переменных
$$
left{begin{array}{lrrrrr}
y_1=&displaystyle x_1+&frac{a_{12}}{a_{11}}x_2+&dots+&frac{a_{1,n-1}}{a_{11}}x_{n-1}+&
frac{a_{1n}}{a_{11}}x_n \
y_2=&displaystyle &x_2+&dots + &frac{a_{2,n-1}^{[1]}}{a_{22}^{[1]}}x_{n-1}+&
frac{a_{2n}^{[1]}}{a_{22}^{[1]}}x_{n} \
vdots & & & ddots & dots & \
y_{n-1}=&displaystyle & & &x_{n-1}+ &frac{a_{n-1,n}^{[n-2]}}{a_{n-1,n-1}^{[n-2]}}x_n \
y_n=&&&&&x_n
end{array} right. ,
$$
приводящую квадратичную форму к каноническому виду:
$$
a_{11}y_1^2 + a_{22}^{[1]} y_2^2 + dots +a_{n-1,n-1}^{[n-2]} y_{n-1}^2 +
a_{nn}^{[n-1]} y_n^2 .
$$
♦
Именно выбор представления квадратичной формы посредством симметричной матрицы позволил установить взаимосвязь между двумя такими разными задачами как решение системы линейных уравнений и представление квадратичной формы в каноническом виде. Фактически весь дальнейший анализ квадратичной формы сведется к исследованию свойств ее матрицы $ mathbf A $. В теории линейных пространств для подобных соответствий, устанавливаемых между объектами разной природы, вводится понятие изоморфизма.
Явное выражение коэффициентов из последних формул, а также необходимые и достаточные условия существования такой
замены — в терминах миноров матрицы $ mathbf A $ — даются в следующем
☟
ПУНКТЕ
Формула Якоби
Т
Теорема [Якоби]. Квадратичная форма $ f(X)=X^{top}{mathbf A}X $ с симметричной матрицей $ {mathbf A} $, ранг которой равен $ mathfrak r_{} $, а главные миноры $ {det mathbf A_j }_{j=1}^{mathfrak r} $ отличны от нуля, приводится к следующему каноническому виду (формула Якоби3)):
$$
frac{z_1^2}{1 cdot det mathbf A_1} +frac{z_2^2}{det mathbf A_1 cdot det mathbf A_2}
+frac{z_3^2}{det mathbf A_2 cdot det mathbf A_3} +dots+frac{z_{mathfrak r}^2}{det mathbf A_{{mathfrak r}-1} cdot det mathbf A_{mathfrak r}}
$$
Здесь
$$
z_1 =frac{1}{2} partial f / partial x_1, z_2=
frac{1}{2}
left|
begin{array}{ll}
a_{11} & partial f / partial x_1 \
a_{12} & partial f / partial x_2
end{array}
right|,
z_3=
frac{1}{2}
left|
begin{array}{lll}
a_{11} & a_{12} & partial f / partial x_1 \
a_{12} & a_{22} & partial f / partial x_2 \
a_{13} & a_{23} & partial f / partial x_3
end{array}
right|, dots ,
$$
$$
qquad qquad
z_{mathfrak r}=
frac{1}{2}
left|
begin{array}{lllll}
a_{11} & a_{12} & dots & a_{1,mathfrak r-1} & partial f / partial x_1 \
a_{12} & a_{22} & dots & a_{2,mathfrak r-1} & partial f / partial x_2 \
dots & & & dots & dots \
a_{1,mathfrak r } & a_{2,mathfrak r } & dots & a_{mathfrak r-1,mathfrak r } & partial f / partial x_{mathfrak r}
end{array}
right|
$$
Доказательство
☞
ЗДЕСЬ.
П
Пример. Для квадратичной формы
$$ f(x_1,x_2,x_3,x_4)=
$$
$$
=4,x_1^2+2,x_2^2+x_3^2+x_4^2-4,x_1x_2-4,x_1x_3+4,x_1x_4+4,x_2x_3-4,x_3x_4
$$
имеем:
$$
mathbf A=
left(
begin{array}{rrrr}
4 & -2 & -2 & 2 \
-2 & 2 & 2 & 0 \
-2 & 2 & 1 & -2 \
2 & 0 & -2 & 1
end{array}
right) quad , left{det mathbf A_jright}_{j=1}^4=left{4,4,-4,-12right}
$$
и
$$z_1=frac{1}{2} (8,x_1-4,x_2-4,x_3+4,x_4)=4,x_1-2,x_2-2,x_3+2,x_4 ; $$
$$z_2=frac{1}{2}
left|
begin{array}{rl}
4 & 8,x_1-4,x_2-4,x_3+4,x_4 \
-2 & -4,x_1+4,x_2+4,x_3
end{array}
right|=4,x_2+4,x_3+4,x_4 ;
$$
$$
z_3=
frac{1}{2} left|
begin{array}{rrl}
4 & -2 & 8,x_1-4,x_2-4,x_3+4,x_4 \
-2 & 2 & -4,x_1+4,x_2+4,x_3
\
-2 & 2 & -4,x_1+4,x_2+2,x_3-4,x_4
end{array}
right|=-4,x_3-8,x_4 ;
$$
$$
z_4=
frac{1}{2}
left|
begin{array}{rrrl}
4 & -2 & -2 & 8,x_1-4,x_2-4,x_3+4,x_4 \
-2 & 2 & 2 & -4,x_1+4,x_2+4,x_3 \
-2 & 2 & 1 & -4,x_1+4,x_2+2,x_3-4,x_4
\
2 & 0 & -2 & 4,x_1-4,x_3+2,x_4
end{array}
right|= -12,x_4 .
$$
$$ fequiv frac{(4,x_1-2,x_2-2,x_3+2,x_4)^2 }{1cdot 4}+frac{(4,x_2+4,x_3+4,x_4)^2 }{4cdot 4}+frac{(-4,x_3-8,x_4)^2 }{4cdot (-4)}+
$$
$$
+frac{(-12,x_4 )^2 }{(-4)cdot (-12)} .
$$
Обратим внимание, что замена переменных в настоящем примере имеет треугольный вид:
$$
left(
begin{array}{l}
z_1 \ z_2 \ z_3 \ z_4
end{array}
right)
=
left(begin{array}{rrrr}
4 & -2 & -2 & 2 \
& 4 & 4 & 4 \
& & -4 & -8 \
& & & -12
end{array}
right)
left(
begin{array}{l}
x_1 \ x_2 \ x_3 \ x_4
end{array}
right) , .
$$
♦
Легко убедиться, что это — проявление общего правила. Выражение для
$$
z_{k}=
frac{1}{2}
left|
begin{array}{lllll}
a_{11} & a_{12} & dots & a_{1,k-1} & partial f / partial x_1 \
a_{12} & a_{22} & dots & a_{2,k-1} & partial f / partial x_2 \
dots & & & dots & dots \
a_{k1 } & a_{k2 } & dots & a_{k,k-1 } & partial f / partial x_{k}
end{array}
right|
$$
при $ k in {1,dots, mathfrak r} $ преобразуем следующим образом: из последнего столбца определителя
$$
=
left|
begin{array}{lllll}
a_{11} & a_{12} & dots & a_{1,k-1} & a_{11}x_1+a_{12}x_2+dots+ a_{1,k-1} x_{k-1}+a_{1k}x_k+dots+a_{1n}x_n \
a_{12} & a_{22} & dots & a_{2,k-1} & a_{21}x_1+a_{22}x_2+dots+ a_{2,k-1} x_{k-1}+a_{2k}x_k+dots+a_{2n}x_n \
dots & & & dots & dots \
a_{k1 } & a_{k2 } & dots & a_{k,k-1 } & a_{k1}x_1+a_{k2}x_2+dots+ a_{k,k-1} x_{k-1}+a_{kk}x_k+dots+a_{kn}x_n
end{array}
right|
$$
вычтем первый, домноженный на $ x_1 $, второй, домноженный на $ x_2 $, и т.д., $ (k-1) $-й, домноженный на $ x_{k-1} $. В результате получим линейную форму
$$
z_k=
left|
begin{array}{lllll}
a_{11} & a_{12} & dots & a_{1,k-1} & a_{1k} \
a_{12} & a_{22} & dots & a_{2,k-1} & a_{2k} \
dots & & & dots & dots \
a_{k1 } & a_{k2 } & dots & a_{k,k-1 } & a_{kk}
end{array}
right|x_k + dots +
left|
begin{array}{lllll}
a_{11} & a_{12} & dots & a_{1,k-1} & a_{1n} \
a_{12} & a_{22} & dots & a_{2,k-1} & a_{2n} \
dots & & & dots & dots \
a_{k1 } & a_{k2 } & dots & a_{k,k-1 } & a_{kn}
end{array}
right|x_n , ,
$$
не зависящую от $ x_1,dots, x_{k-1} $. Коэффициент же при $ x_k $ равен $ det mathbf A_k $ и отличен от нуля по условию теоремы. Если его вынести за пределы формы, то получим еще альтернативный вариант формулы Якоби.
=>
Квадратичная форма $ f(X)=X^{top}{mathbf A}X $ с симметричной матрицей $ {mathbf A} $, ранг которой равен $ mathfrak r_{} $, а главные миноры $ {det mathbf A_j }_{j=1}^{mathfrak r} $ отличны от нуля, приводится к следующему каноническому виду:
$$
y_1^2 det mathbf A_1 + y_2^2frac{det mathbf A_2}{ det mathbf A_1}
+y_3^2frac{det mathbf A_3}{det mathbf A_2} +dots+y_{mathfrak r}^2 frac{det mathbf A_{mathfrak r}}{det mathbf A_{mathfrak r-1}} ;
$$
при этом линейные относительно переменных $ x_1,dots,x_n $ формы $ {y_j }_{j=1}^{mathfrak r} $ выражаются по формулам
$$
left{
begin{array}{lrrrrrr}
y_1=&displaystyle x_1+&tilde c_{12}x_2& &+dots+&tilde c_{1,n-1}x_{n-1}+&tilde c_{1n}x_n \
y_2=&displaystyle &x_2+& & dots + &tilde c_{2,n-1}x_{n-1}+&tilde c_{2n}x_{n} \
vdots & & & ddots & & dots & \
y_{mathfrak r}=&displaystyle & & &x_{mathfrak r}+ & dots + & tilde c_{mathfrak r n}x_n
end{array}
right.
$$
Здесь
$$
tilde c_{1j}=a_{1j}/a_{11}, tilde c_{kj}=left|
begin{array}{lllll}
a_{11} & a_{12} & dots & a_{1,k-1} & a_{1j} \
a_{12} & a_{22} & dots & a_{2,k-1} & a_{2j} \
dots & & & dots & dots \
a_{k1 } & a_{k2 } & dots & a_{k,k-1 } & a_{kj}
end{array}
right| Bigg/ det mathbf A_j , .
$$
При $ mathfrak r = n $ матрица $ tilde C_{} $ из предыдущей формулы становится верхнетреугольной:
$$
Y=tilde C X , ;
$$
при этом на главной диагонали будут стоять $ 1 $. Обратная к матрице такого вида имеет ту же структуру — и матрица $ C=tilde C^{-1} $ является матрицей, которая встретилась нам в предыдущем ПУНКТЕ.
T
Теорема. Квадратичная форма $ f(X)=X^{top}{mathbf A}X $ при симметричной неособенной матрице $ {mathbf A} $ приводится к каноническому виду заменой переменных, задаваемой верхней унитреугольной матрицей
$$
X=CY quad npu C=
left(
begin{array}{llll}
1& c_{12}& dots & c_{1n} \
& 1& dots & c_{2n} \
mathbb O & & ddots & vdots \
& & & 1
end{array}
right)
$$
тогда и только тогда, когда все главные миноры матрицы $ {mathbf A} $ отличны от нуля. Этот канонический вид представлен формулой Якоби
$$
y_1^2 det mathbf A_1 + y_2^2frac{det mathbf A_2}{ det mathbf A_1}
+dots+y_{n}^2 frac{det mathbf A_{n}}{det mathbf A_{n-1}} .
$$
Доказательство достаточности условия теоремы уже произведено, необходимость доказывается в пункте
☞
LDU-разложение матрицы.
Закон инерции для квадратичных форм
Для заданной квадратичной формы канонические виды, т.е. представления
в виде сумм квадратов, можно построить разными способами. Выясним, какие характеристики являются общими (инвариантными) для этих представлений.
Ранг квадратичной формы
Предположим, что с помощью какой-либо невырожденной замены переменных мы привели квадратичную форму к каноническому виду:
$$widetilde f(Y)=alpha_1y_1^2+dots+alpha_n y_n^2 .$$
Может так случиться, что часть коэффициентов $ {alpha_j }_{j=1}^n $ обратится в нуль.
Рангом квадратичной формы называется ранг ее матрицы:
$$operatorname{rank} ( f ) = operatorname{rank} ( {mathbf A} ) .$$
Т
Теорема. Ранг квадратичной формы не меняется при невырожденных заменах переменных:
$$ operatorname{rank} (f) = operatorname{rank}( C^{top}{mathbf A}C ) quad npu quad forall C,
det C ne 0 .$$
Доказательство основано на следствии к теореме $ 2 $, приведенной
☞
ЗДЕСЬ: ранг матрицы не меняется при домножении ее на произвольную неособенную.
=>
Ранг квадратичной формы равен числу ненулевых коэффициентов в ее каноническом виде.
Закон инерции
Начиная с этого момента рассматриваем только вещественные квадратичные формы.
Число положительных (или отрицательных) коэффициентов в каноническом виде квадратичной формы $ f_{}(X) $ называется ее положительным (соответственно, отрицательным) индексом инерции. Буду обозначать эти индексы4)
$$n_{+}(f) quad mbox{ и } quad n_{-}(f) . $$
Разность5)
$$sigma (f) = n_{+}(f)-n_{-}(f)$$
называется сигнатурой квадратичной формы (а также сигнатурой соответствующей ей симметричной матрицы).
Т
Теорема [закон инерции]. Индексы инерции не зависят от способа приведения квадратичной формы к каноническому виду.
Эта теорема часто формулируется в виде: «ранг и сигнатура квадратичной формы не зависят…». Эквивалентность этой формулировки исходной очевидно следует из формул
$$ operatorname{rank} (f) = n_{+}(f)+n_{-}(f), sigma (f) = n_{+}(f)-n_{-}(f) . $$
Доказательство
☞
ЗДЕСЬ.
П
Пример. Найти ранг и сигнатуру квадратичной формы $ f(x_1,x_2,x_3)=x_1x_2-x_2x_3 $.
Решение. Приводим квадратичную форму к каноническому виду по методу Лагранжа:
$$f=frac{1}{4} ,(x_1+x_2-x_3)^2 — frac{1}{4} ,(x_1-x_2-x_3)^2 .$$
Ответ. $ operatorname{rank} (f) = 2,, sigma (f)=0 $.
=>
В предположении, что ранг матрицы $ mathbf A_{} $ равен $ mathfrak r_{} $, а ее главные миноры $ { det {mathbf A}_j }_{j=1}^{mathfrak r} $ отличны от нуля, имеем:
$$
n_{+}(f)={mathcal P}(1,det {mathbf A}_1,dots, det {mathbf A}_{mathfrak r}),
n_{-}(f)={mathcal V}(1,det {mathbf A}_1,dots, det {mathbf A}_{mathfrak r}) .
$$
Здесь $ {mathcal P}_{} $ — число знакопостоянств, а $ {mathcal V}_{} $ — число число знакоперемен в последовательности.
Для сигнатуры квадратичой формы также справедлива и формула
$$ sigma (f)= sum_{j=1}^{mathfrak r} operatorname{sign} (det (mathbf A_{j-1}) cdot det (mathbf A_{j}) ) quad npu quad det (mathbf A_{0})=1 $$
и операции $ operatorname{sign} $ определения знака, введенной
☞
ЗДЕСЬ.
Доказательство следует из формулы Якоби.
§
Правило вычисления сигнатуры из предыдущей теоремы остается справедливым и в случае, если в последовательности главных миноров $ { det {mathbf A}_j }_{j=1}^{mathfrak r} $ имеются нулевые, но не подряд идущие, и $ det {mathbf A}_{mathfrak r} ne 0 $. Если, например,
$$ det (mathbf A_{j}) = 0, det (mathbf A_{j-1}) ne 0, det (mathbf A_{j+1}) ne 0 quad npu quad jin{1,dots, {mathfrak r}-1} ,$$
то сумма
$$ operatorname{sign} (det (mathbf A_{j-1}) cdot det (mathbf A_{j}) )+ operatorname{sign} (det (mathbf A_{j}) cdot det (mathbf A_{j+1}) ) $$
считается равной нулю. (Можно также доказать, что в этом случае главные миноры $ det (mathbf A_{j-1}) $ и $ det (mathbf A_{j+1}) $ имеют противоположные знаки.)
П
Пример. Найти ранг и сигнатуру квадратичной формы
$$f_{{color{Red} alpha }}(x_1,x_2,x_3)=3,x_1^2 -4,x_1x_2-2,x_1x_3 + {color{Red} alpha } , x_2^2 +6, x_2x_3 $$
в зависимости от значений параметра $ {color{Red} alpha } $.
Решение. Сначала пробуем применить формулу из последнего следствия:
$$det {mathbf A}_1=3, det {mathbf A}_2=3, {color{Red} alpha } -4, det {mathbf A}_3=
det {mathbf A}=- {color{Red} alpha } -15 .$$
При $ {color{Red} alpha } notin {4/3,, -15 } $ формула применима при
$ {mathfrak r}=3 $:
$$n_{+}(f)=left{ begin{array}{llr}
2 & npu & {color{Red} alpha } >4/3 ;\
2 & npu & -15<{color{Red} alpha } <4/3 ;\
1 & npu & {color{Red} alpha } < -15 .
end{array} right.
$$
При $ {color{Red} alpha }=4/3 $, по-прежнему, $ {mathfrak r}=3 $, но формула следствия к закону инерции
неприменима. В этом случае приходится действовать по методу Лагранжа:
$$f_{4/3}(x_1,x_2,x_3)=3, left(x_1-frac{2}{3}, x_2 -frac{1}{3}, x_3right)^2-
frac{1}{3}, (x_3-7, x_2)^2+frac{49}{3}x_2^2 .$$
Следовательно, $ n_{+}(f)=2 $. Осталось рассмотреть случай $ {color{Red} alpha } =-15 $,
когда $ {mathfrak r}=2 $. Поскольку условия следствия выполняются, то формула из него применима: $ n_{+}(f)=1 $.
Во всех случаях отрицательный индекс инерции вычисляется по формуле $ n_{-}(f)={mathfrak r}-n_{+}(f) $.
Ответ.
$$
begin{array}{c|c|c}
{color{Red} alpha } & operatorname{rank} (f) & sigma (f) \
hline
< -15 & 3 & -1 \
hline
=-15 & 2 & 0 \
hline
> -15 & 3 & 1
end{array}
$$
Рассмотренный только что пример относится к общей задаче оценки влияния параметров на характеристики квадратичной формы:
Как меняются ранг и сигнатура при непрерывном изменении параметров?
Пусть квадратичная форма зависит от параметров $ alpha, beta, dots $, причем эта зависимость — полиномиальная. Пусть при некотором наборе вещественных значений параметров все главные миноры матрицы квадратичной формы отличны от нуля. Тогда ранг и сигнатура квадратичной формы могут быть вполне определены знаками этих миноров посредством формулы из следствия к закону инерции. Поскольку элементы миноров полиномиально зависят от параметров, то мы получаем систему неравенств, которую (при необходимости домножением некоторых неравенств на $ (-1) $) можно переписать в виде
$$ G_1(alpha,beta,dots) > 0, dots, G_n(alpha,beta,dots) > 0 . $$
Здесь $ G_1,dots, G_n $ — полиномы от $ alpha,beta,dots $. Если при некотором наборе значений $ alpha=alpha_0, beta=beta_0, dots $ эта система удовлетворена, при непрерывной вариации этих параметров $ alpha_0+delta_{alpha}, beta_0 + delta_{beta},dots $ какое из неравенств системы нарушится в первую очередь, т.е. раньше остальных? Иными словами: какое из неравенств системы самое важное? — Оказывается, последнее.
Т
Теорема[2]. Пусть $ f_{{color{Red} alpha }}(x_1,dots,x_n) $ — квадратичная форма, зависящая от параметра $ {color{Red} alpha } $ линейным образом:
$$ f_{{color{Red} alpha }}(x_1,dots,x_n) equiv (1-{color{Red} alpha }) f_{0}(x_1,dots,x_n)+ {color{Red} alpha } f_{1}(x_1,dots,x_n) . $$
Если $ operatorname{rank} (f_{{color{Red} alpha }})=n $ при $ 0 le {color{Red} alpha } le 1 $, то $ n_{+} (f_{0})= n_{+} (f_{1}) $.
Справедливо и более общее утверждение.
Т
Теорема[1,5]. Если при непрерывном изменении коэффициентов формы $ f_{} $ ее ранг $ {mathfrak r}_{} $ остается неизменным, то не изменяется и ее сигнатура $ sigma_{}(f) $.
В случае, когда главные миноры матрицы $ mathbf A $ обращаются в нуль, к анализу канонического вида квадратичной формы приходится привлекать «тяжелую артиллерию» в виде ведущих миноров. Но, по крайней мере, один теоретический результат можно сформулировать немедленно.
Т
Теорема. В произвольной квадратичной форме $ f(X) $ ранга $ mathfrak rge 1 $ можно так перенумеровать переменные, чтобы в матрице получившейся квадратичной формы $ tilde f(Y) $ в последовательности главных миноров
$$ det widetilde{mathbf A}_1, dots, det widetilde{mathbf A}_{ mathfrak r} $$
не было двух подряд идущих нулевых и $ det widetilde{mathbf A}_{ mathfrak r} ne 0 $.
Конгруэнтность квадратичных форм
Матрицы $ {mathbf A} $ и $ {mathbf B} $, связанные соотношением
$ {mathbf B}=C^{top}{mathbf A}C $ при некоторой неособенной матрице $ C $, называются
конгруэнтными: $ {mathbf A} cong {mathbf B} $. Если, вдобавок, матрицы
$ {mathbf A} $ и $ {mathbf B} $ симметричны, то конгруэнтными называются
и соответствующие им квадратичные формы $ X^{top}{mathbf A}X $ и $ X^{top}{mathbf B}X $.
Т
Теорема. Квадратичные формы $ X^{top}{mathbf A}X $ и $ X^{top}{mathbf B}X $
конгруэнтны тогда и только тогда, когда совпадают их индексы инерции, или, что то же, равны их ранги и сигнатуры.
Из всего разнообразия канонических видов квадратичной формы
выберем самый простой, именно тот, коэффициенты которого равны $ +1 $ или $ (-1) $. Например, если квадратичная форма $ f(X) $ уже приведена к каноническому виду
$$widetilde f(Y)=alpha_1y_1^2+dots+alpha_{mathfrak r} y_{mathfrak r}^2 .$$
то преобразование
$$y_j=frac{z_j}{sqrt{alpha_j}} npu jin {1,dots, {mathfrak r}} ,
y_j=z_j npu jin {{mathfrak r}+1,dots, n }
$$
приводит эту форму к виду
$$
z_1^2+dots + z_{n_{+}(A)}^2 -z_{n_{+}(A)+1}^2 — dots — z_{{mathfrak r}}^2
,
$$
который называется нормальным видом квадратичной формы.
Множество всех квадратичных форм с вещественными коэффициентами можно разбить на классы эквивалентности,
в каждом из которых будут находиться только конгруэнтные между собой формы.
Каждый из классов полностью описывается каким-то из своих представителей. Таким
представителем можно взять нормальный вид.
Какое преобразование квадратичной формы оставляет ее инвариантной?
Т
Теорема [Эрмит]. Квадратичная форма $ X^{top}{mathbf A}X $ переходит в себя при преобразовании
$$ X= ({mathbf A}+S)^{-1}({mathbf A}-S) Y $$
где $ S $ означает произвольную кососимметричную матрицу порядка $ n $.
Доказательство. Обозначим
$$ R=({mathbf A}+S)^{-1}({mathbf A}-S) $$
и докажем, что $ R^{top}{mathbf A}R= {mathbf A} $. Используя равенства $ {mathbf A}^{top}={mathbf A} $ ,
$ S^{top}=-S $, получим:
$$ R^{top}{mathbf A}R=({mathbf A}-S)^{top} left(({mathbf A}+S)^{-1}right)^{top}{mathbf A} ({mathbf A}+S)^{-1}({mathbf A}-S)=
$$
$$
=({mathbf A}+S)left(({mathbf A}+S)^{top}right)^{-1} {mathbf A}
({mathbf A}+S)^{-1}({mathbf A}-S)=
$$
$$
=({mathbf A}+S)({mathbf A}-S)^{-1}left[frac{1}{2}({mathbf A}-S)+ frac{1}{2}({mathbf A}+S)right]({mathbf A}+S)^{-1}({mathbf A}-S)=
$$
$$
=frac{1}{2}({mathbf A}+S)({mathbf A}-S)^{-1}({mathbf A}-S)({mathbf A}+S)^{-1}({mathbf A}-S)+frac{1}{2}({mathbf A}+S)({mathbf A}-S)^{-1}({mathbf A}+S)({mathbf A}+S)^{-1}({mathbf A}-S)=
$$
$$
=frac{1}{2}({mathbf A}-S)+
frac{1}{2}({mathbf A}+S)={mathbf A} , .
$$
♦
Знакоопределенность
Здесь рассматриваются только вещественные квадратичные формы.
Квадратичная форма $ f_{}(X) $ называется
а) неотрицательной если $ f(X)ge 0 $ для любого $ Xin mathbb R^n $;
б) положительно определенной, если она неотрицательна и $ f(X)= 0 $ только при $ X=mathbb O_{} $;
в) неопределенной или знакопеременной, если существуют $ {X_1,X_2} subset mathbb R^n $ такие что числа $ f(X_1) $ и $ f(X_2) $ имеют разные знаки: $ f(X_1)f(X_2)<0 $.
По аналогии с пунктами а) и б) определяются неположительные и отрицательно определенные квадратичные формы. Иногда неотрицательные или неположительные формы называют полуопределенными.
П
Пример. При $ n_{}=3 $ квадратичная форма
а) $ x_1^2+3x_2^2+4x_3^2 $ является положительно определенной;
б) $ x_1^2+x_3^{2} $ (или $ (x_1+{sqrt 2} x_2-x_3)^{2} $) является неотрицательной, но не положительно определенной;
в) $ -x_1^2 $ является неположительной, но не отрицательно определенной;
г) $ -x_1^2-2,x_2^2-4,x_3^{2} $ является отрицательно определенной;
д) $ x_1x_{2}+x_2x_3 $ является неопределенной.
Какой смысл имеет свойство неотрицательности и положительной определенности с точки зрения математического анализа? — Неотрицательность формы $ f_{}(X) $ означает, что в точке $ X=mathbb O $ эта функция достигает своего минимального значения: $ f(X)ge 0 = f(mathbb O) $; подчеркнем, что этот минимум будет глобальным. В случае положительной определенности точка $ X=mathbb O $ будет единственной точкой пространства $ mathbb R^{n} $, в которой $ f_{}(X) $ достигает своего минимального значения. Однако если свойство положительной определенности будет нарушено: $ f(X_1) =0 $ при $ X_1 ne mathbb O $, то вследствие однородности формы $ f_{}(X) $ будет выполнено
$$ f(tX_1)=t^2f(X_1)= 0 quad npu quad forall t in mathbb R . $$
Иными словами, свое минимальное значение $ 0_{} $ неотрицательная, но не положительно определенная, форма $ f_{} (X) $ будет принимать на всей прямой, проходящей через точки $ mathbb O $ и $ mathbb X_1 $. Точка $ X=mathbb O $ перестает быть изолированной точкой минимума: в любой ее окрестности находятся другие точки минимума. С точки зрения здравого смысла, подобная ситуация может считаться исключительным, вырожденным случаем. Интуиция подтверждается аналитикой: как увидим впоследствии вероятность того, что случайным образом выбранная квадратичная форма, обладающая свойством неотрицательности, не будет, вдобавок, положительно определенной, равна $ 0_{} $.
Событие теоретически возможно, но практически немыслимо.
Какой смысл имеет свойство положительной определенности с точки зрения геометрии? — Рассмотрим вещественную квадратичную форму от трех переменных: $ f(x,y,z) $. Поставим задачу определения типа поверхности второго порядка
$$ f(x,y,z)=C $$
при произвольной константе $ Cin mathbb R $. Если $ f $ положительно определена, то это уравнение не имеет вещественных решений при $ C<0 $. При $ C=0 $ уравнение определяет единственную точку в $ mathbb R^3 $, а именно — начало координат. При $ C>0 $
уравнение определяет эллипсоид с центром в начале координат. От всех остальных поверхностей второго порядка эллипсоид отличает его замкнутость (и, как следствие, ограниченность).
Оказывается условие положительной определенности формы $ f $ является необходимым и достаточным для обеспечения подобного свойства в произвольном пространстве $ mathbb R^n $. И это утверждение верно не только для квадратичной формы, но и для однородного полинома (формы) произвольного порядка.
§
Задача об условных экстремумах квадратичной формы $ f_{}(X) $ на сфере $ x_1^2+dots+x_n^2 =1 $ решается
☞
ЗДЕСЬ.
П
Пример. В произвольном евклидовом пространстве $ mathbb E $ квадратичная форма с матрицей Грама произвольной системы векторов $ {X_1,dots,X_m} subset mathbb E $
$$ G(X_1,dots,X_m)=
left(
begin{array}{cccc}
langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \
langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \
dots & & & dots \
langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle
end{array}
right)
$$
будет неотрицательной; эта квадратичная форма будет положительно определенной тогда и только тогда, когда система $ {X_1,dots,X_m} $ линейно независима.
Задача.
Найти условия неотрицательности и положительной определенности квадратичной формы в терминах ее коэффициентов.
Очевидны необходимые условия неотрицательности квадратичной формы
$$ f(X)=displaystyle sum_{1le j le k le n} f_{jk}x_jx_k : $$
все коэффициенты при квадратах переменных должны быть неотрицательными:
$$ f_{11}ge 0, dots , f_{nn}ge 0 . $$
Также очевидно, что эти условия будут и достаточными, если все остальные коэффициенты $ f_{jk}^{} $ при $ jne k $
равны нулю. Если же последнее условие не выполняется, то имеет смысл предварительно преобразовать квадратичную форму к сумме квадратов, т.е.
исследовать ее канонический вид.
Т
Теорема. Ненулевая квадратичная форма, представленная в правильном виде
$$ f(X)=X^{top}{mathbf A}X , , $$
будет неотрицательной тогда и только тогда, когда ее отрицательный индекс инерции равен нулю:
$$ n_{-} ({mathbf A})=0 qquad iff qquad qquad sigma (
{mathbf A})=operatorname{rank} {mathbf A} .$$
Если это условие выполнено, то для положительной определенности формы необходимо и достаточно чтобы она была невырождена: $ det {mathbf A} ne 0 $.
Доказательство
☞
ЗДЕСЬ.
К счастью, явное представление канонического вида квадратичной формы уже имеется — как правило, он задается формулой Якоби. Индексы инерции
вычисляются через знаки главных миноров матрицы квадратичной формы.
Т
Теорема [Сильвестр]. Квадратичная форма
$$
f(X)=X^{top}{mathbf A}X
$$
будет положительно определенной тогда и только тогда, когда все главные миноры ее матрицы положительны:
$$
a_{11}>0, left| begin{array}{cc}
a_{11} & a_{12} \
a_{12} & a_{22}
end{array} right| >0, left| begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{12} & a_{22} & a_{23} \
a_{13} & a_{23} & a_{33}
end{array} right| >0, dots, det {mathbf A} >0 .
$$
Доказательство
☞
ЗДЕСЬ.
=>
Квадратичная форма будет отрицательно определенной тогда и только тогда, когда знаки главных миноров ее матрицы будут чередоваться следующим образом:
$$
a_{11}<0, left| begin{array}{cc}
a_{11} & a_{12} \
a_{12} & a_{22}
end{array} right| >0, left| begin{array}{ccc}
a_{11} & a_{12} & a_{13} \
a_{12} & a_{22} & a_{23} \
a_{13} & a_{23} & a_{33}
end{array} right| <0, dots, (-1)^ndet {mathbf A} >0 .
$$
В настоящем ресурсе я буду часто говорить об определенности или неопределенности вещественной симметричной матрицы, имея в виду соответствующее свойство порождаемой ею квадратичной формы. Имеется одна особенность в определении симметричной матрицы, задающей неотрицательную квадратичную форму, не являющуюся положительно определенной. Такую матрицу НЕ называют неотрицательной (этот термин закреплен за другим понятием теории матриц); такую матрицу называют положительно полуопределенной6).
П
Пример. Найти все значения параметра $ {color{Red} alpha } $, при которых
квадратичная форма
$$2, x_1^2+2, x_2^2+x_3^2+ 2, {color{Red}{ alpha} } , x_1x_2+6, x_1x_3 +2,x_2x_3 $$
будет положительно определенной.
Решение. Значения главных миноров:
$$det {mathbf A}_1=2, det {mathbf A}_2=4- {color{Red} alpha }^2, det {mathbf A}_3=-{color{Red} alpha }^2+
6, {color{Red} alpha } -16 . $$
Последнее выражение будет отрицательно при любых $ {color{Red} alpha } in mathbb R $.
Ответ. Таких значений нет: $ {color{Red} alpha } in varnothing $.
Можно ли получить условия неотрицательности квадратичной формы:
$$ f(X) ge 0 npu forall X in {mathbb R}^n $$
превращением всех неравенств из критерия Сильвестра в нестрогие: $ > to {color{Red}{ to} } ge $
?
— Вообще говоря, нет.
П
Пример.
Квадратичная форма
$$f(x_1,x_2,x_3,x_4)=x_1^2+2x_1x_3+2x_2x_4+x_4^2=
X^{top} left(
begin{array}{cccc}
1&0&1 &0 \
0&0&0&1 \
1&0&0&0 \
0&1&0&1
end{array} right)X
$$
— неопределенная, т.к. $ f(1,0,-1,0)=-1_{}<0 $, а $ f(1,0,0,0)=1_{}>0 $. Тем не менее, все главные миноры ее матрицы неотрицательны.
♦
Имеются ли конструктивные необходимые и достаточные условия неотрицательности квадратичной формы?
Т
Теорема. Для неотрицательности квадратичной формы $ X^{top} mathbf A X $ необходимо и достаточно, чтобы все ведущие миноры матрицы $ mathbf A $, т.е. миноры, стоящие на пересечении строк и столбцов матрицы с одинаковыми номерами
$$
Aleft(
begin{array}{lll}
j_1 & dots & j_k \
j_1 & dots & j_k
end{array}
right) , j_1<j_2<dots < j_k
$$
были неотрицательны.
П
Пример. При любой матрице $ A in mathbb R^{mtimes n} $ матрицы
$$ A^{top} A quad mbox{ и } quad A A^{top} $$
являются положительно полуопределенными.
Знакоопределенность на подпространстве
Будем говорить, что квадратичная форма $ f(X) $ положительно определена на подпространстве $ mathbb V_1 $ пространства $ mathbb R^{n} $ если $ f(X)>0 $ при всех $ Xin mathbb V_1, X ne mathbb O $.
Т
Теорема. Пусть линейное подпространство задано системой линейных однородных уравнений
$$
left{ begin{array}{cccc}
h_{11}x_1 & + dots & + h_{1n}x_n&=0, \
dots & & & dots \
h_{k1}x_1 & + dots & + h_{kn}x_n&=0, \
end{array}
right. qquad iff qquad
underbrace{left(
begin{array}{lll}
h_{11} & dots & h_{1n} \
dots & & dots \
h_{k1} & dots & h_{kn}
end{array}
right)}_{=H}X=mathbb O
$$
Здесь $ k<n $ и предполагается, что минор, образованный первыми $ k_{} $ столбцами матрицы $ H_{} $ отличен от нуля, (т.е. $ operatorname{rank} (H)=k $). Тогда необходимым и достаточным условием положительной определенности квадратичной формы $ X^{top} mathbf A X $ на этом подпространстве является то, что все главные миноры матрицы
$$
(-1)^k
left( begin{array}{cc}
mathbb O_{ktimes k} & H \
H^{top} & mathbf A
end{array}
right)_{(n+k)times (n+k)}
$$
порядков $ 2k+1, 2k+2, dots, n+k $ положительны.
Результат приведен в [3] со ссылкой на статью [4], однако у меня есть основания считать, что он был известен еще Борхардту.
Приведение квадратичной формы к каноническому виду с помощью ортогональной замены переменных
В этом пункте рассматриваются только вещественные квадратичные формы.
Существенно используются материалы из раздела СИММЕТРИЧНАЯ МАТРИЦА и начальный пункт раздела ОРТОГОНАЛЬНАЯ МАТРИЦА.
Т
Теорема. Cуществует замена переменных
$$ X=PY , $$
c ортогональной матрицей $ P_{} $, приводящая квадратичную форму $ f(X)=X^{top} mathbf A X $ к каноническому виду
$$ lambda_1 y_1^2 + lambda_2 y_2^2+ dots + lambda_n y_n^2 ; $$
при этом коэффициентами канонического вида являются собственные числа матрицы $ mathbf A $ (более точно: набор $ { lambda_1,dots, lambda_n } $ составляет спектр матрицы $ mathbf A $).
Доказательство
☞
ЗДЕСЬ.
П
Пример. Найти ортогональную замену переменных, приводящую квадратичную форму
$$ X^{top} mathbf A X quad
npu quad
{mathbf A}=left(begin{array}{rrr}
2 & 2 & -1 \
2 & -1 & 2 \
-1& 2 & 2
end{array}
right)
$$
к каноническому виду.
Решение. Характеристический полином $ det (mathbf A- lambda E)=-(lambda-3)^2(lambda+3) $.
Простому собственному числу $ lambda=-3 $ соответствует собственный вектор
$ {mathfrak X}_1=[1,-2,1]^{^{top}} $, а собственному числу $ lambda=3 $ второй кратности соответствуют
два линейно-независимых собственных вектора $ {mathfrak X}_2=[2,1,0]^{^{top}} $ и
$ {mathfrak X}_3=[-1,0,1]^{^{top}} $. Очевидно, что
$ langle {mathfrak X}_1, {mathfrak X}_2rangle=0 , langle {mathfrak X}_1, {mathfrak X}_3 rangle =0 $, но
$ langle {mathfrak X}_2, {mathfrak X}_3 rangle ne 0 $. Ортогонализуем систему
векторов $ left{{mathfrak X}_2,{mathfrak X}_3right} $:
$${mathfrak Y}_2={mathfrak X}_2, {mathfrak Y}_3={mathfrak X}_3+ {color{Red} alpha } {mathfrak Y}_2
quad mbox{ и } langle {mathfrak Y}_2,{mathfrak Y}_3rangle =0
Longrightarrow {color{Red} alpha }=-frac{langle {mathfrak X}_2,{mathfrak X}_3rangle}
{langle {mathfrak X}_2,{mathfrak X}_2rangle}=frac{2}{5}
$$
и $ {mathfrak Y}_3=left[-1/5, 2/5, 1 right]^{^{top}} $.
После нормирования, получаем ортогональную матрицу
$$
P=left(begin{array}{rrr}
1/sqrt{6} & 2/sqrt{5} & -1/sqrt{30} \
-2/sqrt{6} & 1/sqrt{5} & 2/sqrt{30} \
1/sqrt{6} & 0 & 5/sqrt{30}
end{array}
right) .
$$
Замена переменных $ X=PY $ приводит квадратичную форму $ X^{top} mathbf A X $ к каноническому виду
$$
(y_1,y_2,y_3)
left(begin{array}{rrr}
-3 & 0 & 0 \
0 & 3 & 0 \
0& 0 & 3
end{array}
right)
left(
begin{array}{c}
y_1 \ y_2 \ y_3
end{array}
right)=-3,y_1^2+3,y_2^2+3,y_3^2 .
$$
Поскольку фундаментальную систему решений системы уравнений $ (mathbf A — lambda_j E)X= mathbb O $ для кратного собственного числа $ lambda_j $ можно строить разными способами, то у последней задачи имеется бесконечное
множество ответов. Так, например, в качестве еще одной ортогональной
матрицы можно взять
$$P=left(begin{array}{rrr}
1/sqrt{6} & -1/sqrt{2} & 1/sqrt{3} \
-2/sqrt{6} & 0 & 1/sqrt{3} \
1/sqrt{6}& 1/{sqrt 2} & 1/sqrt{3}
end{array}
right).
$$
Т
Теорема. Если известны коэффициенты характеристического полинома матрицы квадратичной формы $ f(X)=X^{top}mathbf A X $:
$$ det (mathbf A- lambda E) equiv (-1)^n left(lambda^n+a_{1}lambda^{n-1}+ dots + a_n right) , ,$$
то
$$ operatorname{rank} (f(X))={mathfrak r} iff
a_{n}=a_{n-1}=dots=a_{{mathfrak r}+1}=0,a_{{mathfrak r}}ne 0 , . $$
В этом случае будет также выполнено
$$ n_{+} (f(X))={mathcal V}(1,a_1,dots,a_{{mathfrak r}}),quad
n_{-} (f(X))={mathcal P}(1,a_1,dots,a_{mathfrak r}) , , $$
$$ sigma(f(X))=sum_{j=1}^{mathfrak r} operatorname{sign} (a_{j-1}a_j) quad npu quad a_0=1 , . $$
Доказательство основано на правиле знаков Декарта.
Геометрия замен переменных
В предыдущих пунктах мы рассмотрели два подхода к построению канонического вида квадратичной формы. Очевидно, что подход, основанный на ортогональной замене переменных более дорогостоящий в построении по сравнению с методом Лагранжа. В самом деле, он требует нахождения собственных чисел симметричной матрицы, т.е. решения алгебраического уравнения $ det (mathbf A — lambda E)=0 $. В случае матриц порядка $ n> 4 $ корни этого уравнения, как правило, на находятся в виде «хорошей» комбинации коэффициентов, и могут быть определены разве лишь приближенно. Метод же Лагранжа принципиально безошибочен: коэффициенты канонического вида определяются в виде рациональных функций от коэффициентов квадратичной формы.
П
Пример. Уравнение $ 1/3x_1^2-x_1x_2+x_2^2=1 $ задает на плоскости эллипс:

Преобразование
$$
y_1=x_1-3/2x_2, y_2=x_2
$$
приводит уравнение к виду
$$ 1/3 y_1^2+1/4 y_2^2=1 ; $$
в новых координатах кривая имеет вид на рисунке слева. С другой стороны, преобразование
$$
begin{array}{ll}
z_1&= sqrt{1/2+1/sqrt{13}},x_1+sqrt{1/2-1/sqrt{13}},x_2,\
z_2&= sqrt{-1/2-1/sqrt{13}},x_1+sqrt{1/2+1/sqrt{13}}x_2
end{array}
$$
приводит уравнение к виду
$$frac{4-sqrt{13}}{6}z_1^2+frac{4+sqrt{13}}{6}z_2^2=1 . $$
В этих координатах кривая имеет вид на рисунке справа.
Оба преобразования координат не изменяют типа кривой: эллипс остается эллипсом. Но второе преобразование дает нечто большее: оно сохраняет размеры. Фактически, оно сводится к повороту исходного эллипса.
Вывод. Метод Лагранжа «дешевле» метода ортогональных преобразований при решении задачи классификации алгебраических многообразий, заданных уравнением вида $ X^{top} mathbf A X=1 $. Иными словами, он позволяет «дешевле» определить тип поверхности с точностью до ее формы: например, в $ mathbb R^3 $ является ли эта поверхность эллипсоидом или гиперболоидом (и каким именно — однополостным или двуполостным)? Но если нас интересуют истинные размеры этой поверхности: например, размеры посылочного ящика, в который эллипсоид, заданный уравнением $ X^{top} mathbf A X=1 $, можно было бы поместить — то здесь без собственных векторов и чисел матрицы $ mathbf A $ не обойтись!
Здесь уместно вспомнить замечание о невырожденности замены переменных, приводящей квадратичную форму к каноническому виду.
В чем заключается его геометрический смыcл? Для ответа на вопрос обратимся к приведенному выше примеру.
Сделаем в квадратичной форме замену переменных зависящей от параметра:
$$ x_1=t_1+alpha t_2, x_2=t_1+t_2 , . $$
На рисунке изображены получаемые в результате такой замены кривые при различных значениях параметра. И если при значениях $ alpha=0.4 $ и $ alpha=0.7 $ мы еще можем визуально распознать эллипс, то значение $ alpha=0.9 $ заставляет подозревать, что соответствующая кривая при сильном растяжении разрывается на два куска, близкие к прямым. Именно это и происходит при $ alpha=1 $. Вместо двух существенных переменных $ x_1 $ и $ x_2 $, у нас остается, фактически, одна, а именно $ t_1 + t_2 $, а нелинейная кривая выродилась в две прямые линии.
Билинейные формы
Задачи
Источники
[1]. Гантмахер Ф.Р. Теория матриц. 4-е изд. М.Наука. 1988.
[2]. Knuth D.E. A permanent inequality. American Math. Monthly, v. 88, N 10, 1981, p.731–740
[3]. Шилов Г.Е. Математический анализ. Конечномерные линейные пространства. М.Наука.1969, с.243
[4]. Шостак Р.Я. О признаке условной определённости квадратичной формы n переменных, подчинённых линейным связям, и о достаточном признаке условного экстремума функций n переменных, УМН, 9:2(60) (1954), 199–206
[5]. Иохвидов И.С. Ганкелевы и теплицевы матрицы и формы. М. Наука. 1974.
[6]. Turnbull H.W. The Theory of Determinants, Matrices and Invariants. Blackie & Sons Ltd. 1929.