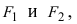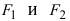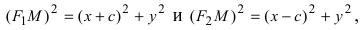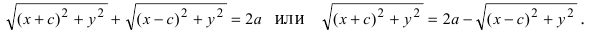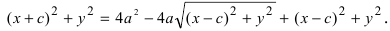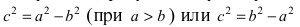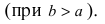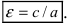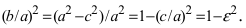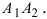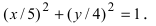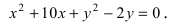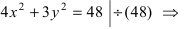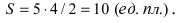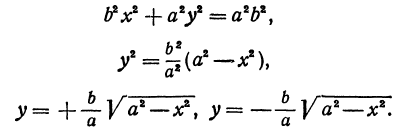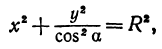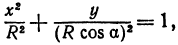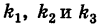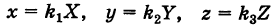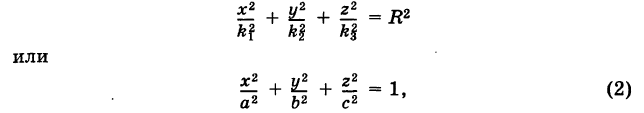-
Определение эллипса.
Начать изучение
-
Фокусы, эксценриситет и директрисы эллипса.
Начать изучение
-
Уравнение касательной к эллипсу.
Начать изучение
Определение эллипса.
Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1label{ref1}
$$
при условии (a geq b > 0).
Из уравнения eqref{ref1} следует, что для всех точек эллипса (|x| leq a) и (|y| leq b). Значит, эллипс лежит в прямоугольнике со сторонами (2a) и (2b).
Точки пересечения эллипса с осями канонической системы координат, имеющие координаты ((a, 0)), ((-a, 0)), ((0, b)) и ((0, -b)), называются вершинами эллипса. Числа (a) и (b) называются соответственно большой и малой полуосями эллипса.
В каноническое уравнение входят только квадраты координат. Поэтому, если координаты ((x, y)) какой-либо точки /(M) ему удовлетворяют, то ему удовлетворяют и координаты ((-x, y)), ((x, -y)) и ((-x, -y)) точек (M_{1}), (M_{2}) и (M_{3}) (рис. 8.1). Следовательно, справедливо следующее утверждение.
Утверждение 1.
Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.
Внешний вид эллипса проще всего описать сравнением с окружностью радиуса (a) с центром в центре эллипса: (x^{2}+y^{2}=a^{2}). При каждом (x) таком, что (|x| < a), найдутся две точки эллипса с ординатами (pm b sqrt{1-x^{2}/a^{2}}) и две точки окружности с ординатами (pm a sqrt{1-x^{2}/a^{2}}). Пусть точке эллипса соответствует точка окружности с ординатой того же знака. Тогда отношение ординат соответствующих точек равно (b/a). Итак, эллипс получается из окружности таким сжатием ее к оси абсцисс, при котором ординаты всех точек уменьшаются в одном и том же отношении (b/a) (рис. 8.2).
Фокусы, эксценриситет и директрисы эллипса.
У эллипса есть две замечательные точки, которые называются его фокусами.
Определение.
Пусть по определению
$$
c^{2}=a^{2}-b^{2}label{ref2}
$$
и (c geq 0).
Фокусами называются точки (F_{1}) и (F_{2}) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат (рис. 8.3).
Для окружности (c=0), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.
Определение.
Отношение
$$
varepsilon=frac{c}{a}label{ref3}
$$
называется эксцентриситетом эллипса.
Отметим, что (varepsilon < 1).
Утверждение 2.
Расстояние от произвольной точки (M(x, y)), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы (x):
$$
r_{1}=|F_{1}M|=a-varepsilon x, r_{2}=|F_{2}M|=a+varepsilon x.label{ref4}
$$
Доказательство.
Очевидно, что (r_{1}^{2}=(x-c)^{2}+y^{2}). Подставим сюда выражение для (y^{2}), найденное из уравнения эллипса. Мы получим
$$
r_{1}^{2}=x^{2}-2cx+c^{2}+b^{2}-frac{b^{2}x^{2}}{a^{2}}.nonumber
$$
Учитывая равенство eqref{ref2}, это можно преобразовать к виду
$$
r_{1}^{2}=a^{2}-2cx+frac{c^{2}x^{2}}{a^{2}}=(a-varepsilon x)^{2}.nonumber
$$
Так как (x leq a) и (varepsilon < 1), отсюда следует, что справедливо первое из равенств eqref{ref4}: (r_{1}=a-varepsilon x). Второе равенство доказывается аналогично.
Утверждение 3.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса (2a).
Доказательство.
Необходимость. Если мы сложим равенства eqref{ref4} почленно, то увидим, что
$$
r_{1}+r_{2}=2a.label{ref5}
$$
Достаточность. Пусть для точки (M(x, y)) выполнено условие eqref{ref5}, то есть
$$
sqrt{(x-c)^{2}+y^{2}}=2a-sqrt{(x+c)^{2}+y^{2}}.nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^{2}=asqrt{(x+c)^{2}+y^{2}}.label{ref6}
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение eqref{ref2}. Мы придем к (b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2}), равносильному уравнению эллипса eqref{ref1}.
С эллипсом связаны две замечательные прямые, называемые его директрисами. Их уравнения в канонической системе координат (рис. 8.4)
$$
x=frac{a}{varepsilon},\ x=-frac{a}{varepsilon}.label{ref7}
$$
Директрису и фокус, которые лежат по одну сторону от центра, будем считать соответствующими друг другу.
Утверждение 4.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса (varepsilon).
Доказательство.
Докажем это предложение для фокуса (F_{2}(-c, 0)). Пусть (M(x, y)) — произвольная точка эллипса. Расстояние от (M) до директрисы с уравнением (x=-a/varepsilon) по формуле (9) §3 гл. II равно
$$
d_{2}=|x+frac{a}{varepsilon}|=frac{1}{varepsilon}(varepsilon x+a).nonumber
$$
Из формулы eqref{ref4} мы видим теперь, что (r_{2}/d_{2}=varepsilon).
Обратно, пусть для какой-то точки плоскости (r_{2}/d_{2}=varepsilon), то есть
$$
sqrt{(x+c)^{2}+y^{2}}=varepsilon left(x+frac{a}{varepsilon}right).nonumber
$$
Так как (varepsilon=c/a), это равенство легко приводится к виду eqref{ref6}, из которого, как мы знаем, следует уравнение эллипса.
Уравнение касательной к эллипсу.
Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть (M_{0}(x_{0}, y_{0})) — точка на эллипсе и (y_{0} neq 0). Через (M_{0}) проходит график некоторой функции (y=f(x)), который целиком лежит на эллипсе. (Для (y_{0} > 0) это график (f_{1}(x)=bsqrt{1-x^{2}/a^{2}}), для (y_{0} < 0) — график (f_{2}(x)=-bsqrt{1-x^{2}/a^{2}}). Не уточняя знака (y_{0}), обозначим подходящую функцию (f(x)).) Для нее выполнено тождество
$$
frac{x^{2}}{a^{2}}+frac{(f(x))^{2}}{b^{2}}=1.nonumber
$$
Дифференцируем его по (x):
$$
frac{2x}{a^{2}}+frac{2ff’}{b^{2}}=0.nonumber
$$
Подставляя (x=x_{0}) и (f(x_{0}=y_{0})), находим производную от (f) в точке (x_{0}), равную угловому коэффициенту касательной:
$$
f'(x_{0})=frac{b^{2}}{a^{2}} frac{x_{0}}{y_{0}}.nonumber
$$
Теперь мы можем написать уравнение касательной:
$$
y-y_{0}=-frac{b^{2}}{a^{2}} frac{x_{0}}{y_{0}}(x-x_{0}).nonumber
$$
Упрощая это уравнение, учтем, что (b^{2}x_{0}^{2}+a^{2}y_{0}^{2}=a^{2}b^{2}), так как (M_{0}) лежит на эллипсе. Результату можно придать вид
$$
frac{xx_{0}}{a^{2}}+frac{yy_{0}}{b^{2}}=1.label{ref8}
$$
При выводе уравнения eqref{ref8} мы исключили вершины эллипса ((a, 0)) и ((-a, 0)), положив (y_{0} neq 0). Для этих точек оно превращается, соответственно, в уравнения (x=a) и (x=-a). Эти уравнения определяют касательные в вершинах. Проверить это можно, заметив, что в вершинах ж как функция от у достигает экстремума. Предоставим читателю проделать это подробно и показать тем самым, что уравнение eqref{ref8} определяет касательную для любой точки (M_{0}(x_{0}, y_{0})) на эллипсе.
Утверждение 5.
Касательная к эллипсу в точке (M_{0}(x_{0}, y_{0})) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.
Доказательство.
Нам надо сравнить углы (varphi_{1}) и (varphi_{2}), составленные векторами (overrightarrow{F_{1}M_{0}}) и (overrightarrow{F_{2}M_{0}}) с вектором (boldsymbol{n}), перпендикулярным касательной (рис. 8.5). Из уравнения eqref{ref8} находим, что (boldsymbol{n}(x_{0}/a^{2}, y_{0}/b^{2})), и потому
$$
(overrightarrow{F_{1}M_{0}}, boldsymbol{n})=frac{x_{0}}{a^{2}}(x_{0}-c)+frac{y_{0}}{b^{2}}y_{0}=1-frac{x_{0}c}{a^{2}}=frac{a-varepsilon x_{0}}{a}.nonumber
$$
Используя eqref{ref4}, мы получаем отсюда, что (cos varphi_{1}=1/(a|boldsymbol{n}|)). Аналогично находим (cos varphi_{2}=1/(a|boldsymbol{n}|)). Утверждение доказано.
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 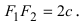
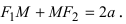
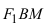
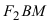
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 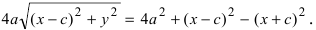
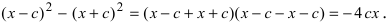
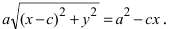
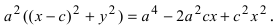
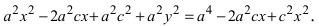
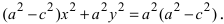
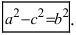
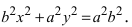
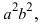
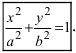
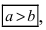
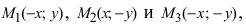
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 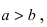
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 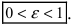
Если 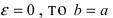
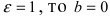
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 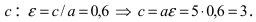
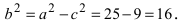
Пример:
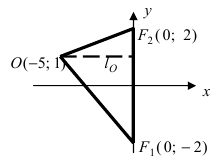
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 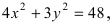
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
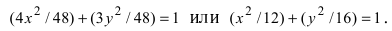
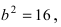
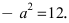
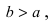
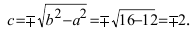
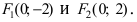
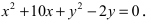
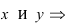
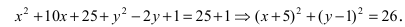
Построим в декартовой системе координат треугольник 
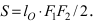
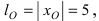
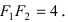
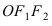
Эллипс в высшей математике
Рассмотрим уравнение
где 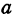
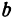
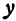
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 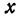
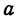
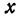
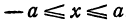
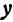
При 
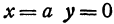
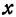

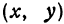
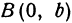
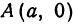
Полученная линия называется эллипсом. Число 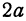
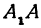
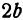
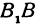
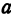
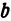
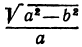
Пример:
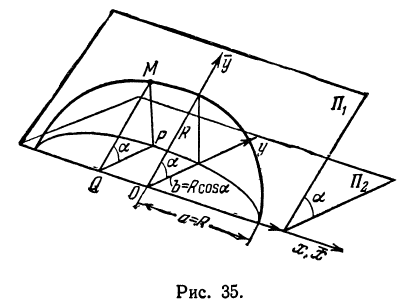
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 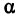
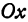
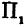
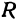
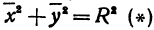
Пусть точка 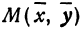
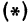
Обозначим проекцию точки 
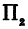
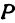
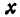
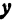
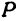

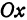
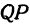
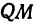
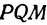
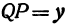
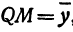
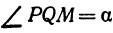
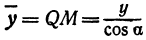

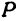
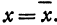
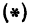
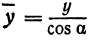
или
а это есть уравнение эллипса с полуосями 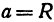
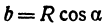
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 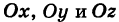
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 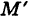
(рис. 206). Отсюда
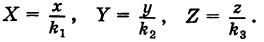
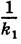
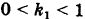
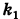
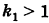
Подставляя эти формулы в уравнение (1), будем иметь
где 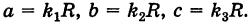
Величины 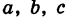
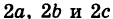
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
Определение.
Пусть на плоскости заданы две точки F1
и F2,
расстояние между которыми равно 2c.
Пусть, кроме того, задано число a,
большее c.
Эллипсом
называется множество точек той же
плоскости, для каждой из которых сумма
расстояний до точек F1
и F2,
называемых фокусами
эллипса,
есть число постоянное, равное 2а.
Вывод канонического уравнения
Для вывода
канонического уравнения эллипса выберем
на плоскости следующую прямоугольную
декартову систему координат: ось
проведем через фокусы эллипса, а ось
–
перпендикулярно ей через середину
отрезка F1F2
(рис. 3.4). По определению эллипсу
удовлетворяют те, и только те точки М
плоскости, для которых
.
(1)
Ч
получить уравнение эллипса следует
записать равенство (1) в координатах. В
выбранной системе координат фокусы
эллипса имеют следующие координаты: F1
(–c;
0); F2
(c;
0). Произвольную (или текущую) точку
множества опять обозначаем M(x;
y).
Так как
,
,
то уравнение (1)
равносильно следующему:
,
(2)
которое, в свою
очередь, равносильно
Рис. 3.4
уравнению:
.
(3)
Оба эти уравнения
являются уравнениями эллипса, но мы
преобразуем их к более простому виду.
Проведем следующую цепочку преобразований:
(3)
.
Учитывая, что
,
разделив последнее уравнение на
,
получаем:
.
(4′)
Так как
,
то
,
поэтому найдется такое положительное
число
,
что
.
Теперь уравнение (4′) примет вид:
.
(4)
Мы доказали: если
точка принадлежит эллипсу, то её
координаты удовлетворяют уравнению
(3) или (4).
Докажем обратное:
если координаты точки удовлетворяют
уравнению (4) или (3), то она принадлежит
эллипсу. Итак,
{M
(x;
y)
удовлетворяет (4)}
.
(5)
Аналогично получаем:
.
(6)
Находим сумму
расстояний:
[(4)
]
=
.
Таким образом, (4)
– уравнение эллипса, которое и называется
его каноническим
уравнением.
Исследование формы эллипса по его каноническому уравнению
1. Из (4)
вытекает: если точка M(x;
y)
принадлежит эллипсу, то
,
т.е. эллипс полностью лежит внутри этого
прямоугольника.
2
Так же как и гипербола, эллипс симметричен
относительно обеих координатных осей
и относительно начала координат. Оси
симметрии эллипса называются осями
эллипса,
центр симметрии – его центром.
3
x
. Если y
= 0, то из (1) следует, что x
= a,
если же x
= 0, то y
= b.
Таким образом, эллипс
пересекает обе координатные оси: ось
в точках A1(–a;
0), A2(a;
0), а ось
Рис. 3.5.
–
в точках B1(0;
–b),
B2(0;
b).
Эти точки называются вершинами эллипса
Числа а
и b
называются полуосями эллипса, большой
и малой соответственно.
4
y
. В силу симметрии эллипса его можно
вначале нарисовать только в первой
четверти, а затем продолжить по симметрии.
Если
,
то из (4) получаем:
.
Найдем производную:
y
.
при
,
поэтому функция убывает на отрезке
.
Так как
и
,
то в точке пересечения эллипса с осью
он имеет горизонтальную касательную,
а в точке пересечения с осью
– вертикальную. Так же, как и у гиперболы,
фокусы эллипса находятся в точках F1
(–c;
0) F2
(c;
0). Теперь уже можно эллипс изобразить
(см. рис. 3.5).
Замечание.
Уравнение (4) задаёт эллипс, фокусы
которого лежат на оси абсцисс при
,
и лежат на оси ординат при
.
Если же
,
то (4) – уравнение окружности радиуса
с центром в начале координат. В этом
случае c
= 0. Таким
образом, окружность –
это частный случай эллипса с совпадающими
фокусами.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
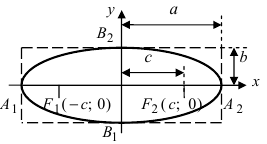
Эллипсом называют плоскую кривую, состоящую из точек, сумма расстояний которых от двух определённых точек плоскости является неизменной, строго заданной величиной, равной суммарной длине двух больших его полуосей (2a). Эти две точки называются фокусами эллипса.
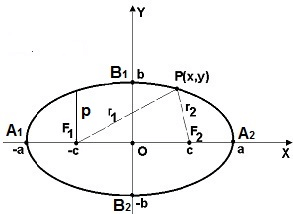
F1 и F2 – фокусы эллипса;
а – большая полуось;
b – малая полуось
с – фокусное расстояние
Теорема
Фокусное расстояние эллипса и его полуоси связаны между собой соотношением [boldsymbol{a^{2}=b^{2}+c^{2}}]
Доказательство:
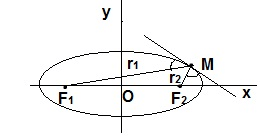
Когда точка M на линии эллипса находится на его пересечении с вертикальной осью, из теоремы Пифагора выходит, что
r1 + r2 = 2*√(b2 + c2)
Когда точка M пересекает горизонтальную ось
r1 + r2 = а – c + а + c
По определению эллипса r1 + r 2 = const
Это позволяет после приравнивания получить
a² = b² + c²
r1 + r2 = 2а
Что и требовалось доказать.
Уравнение эллипса
Каноническим уравнением эллипса называют уравнение [boldsymbol{1=left(x^{2} / a^{2}right)+left(y^{2} / b^{2}right)}]
Доказательство уравнения:
Введём прямоугольную декартову систему координат.
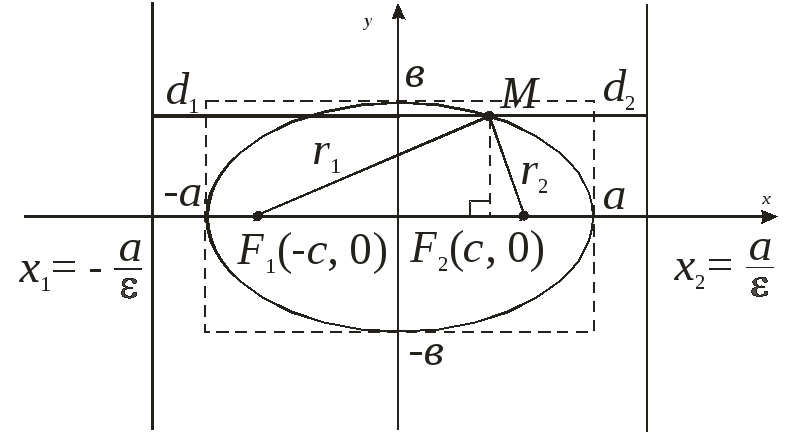
Сначала докажем, что координаты любой из точек на эллипсе удовлетворяют приведённому каноническому уравнению. Затем покажем, что любое из решений уравнения является координатами точки, лежащей на линии эллипса. Из этого будет следовать удовлетворение каноническому уравнению только тех точек, которые лежат на поверхности эллипса. Опираясь на этот факт и на определение эллипса можно будет однозначно сделать вывод, что написанное нами уравнением является каноническим уравнением или, как ещё говорят, основной формулой эллипса.
- Пусть М(х, у) будет точкой эллипса, т.е. сумму её фокальных радиусов примем равной 2а, т. е. r1 + r2 = 2a.
С помощью формулы расстояния, разделяющего две точки на координатной плоскости, можно легко найти фокальные радиусы точки M.r1 = √[(x + c)2 + y2]
r2 = √[(x — c)2 + y2]Из этих уравнений получаем √[(x + c)2 + y2] + √[(x — c)2 + y2] = 2a
Если один из корней перенести в правую часть и возвести всё в квадрат, то придём к выражению
(x + c)2 + y2 = 4a2 – 4a√[(x — c)2 + y2] + (x – c)2 + y2После сокращения приходим к 2xc = 4a2 – 4a√[(x-c)2 + y2] – 2xc
После приведения подобных членов, сокращения на 4 и уединения радикала будем иметь
a√[(x-c)2 + y2] = a2 – xcВозведём это выражение в квадрат
a2(x-c)2 + a2 y2 = a4 – 2a2xc + x2c2Если раскрыть скобки и сократить на -2a2 xc, то a2x2 + a2c2 + a2y2 = a4 + x2c2
Отсюда легко получить (a2 – c2)x2 + a2y2 = a2(a2 – c2)
Из этого следует, что b2x2 +a2y2 = a2b2 - Пусть некоторые числа (x, y) полностью удовлетворяют каноническому уравнению
1 = (x2/a2) + (y2/b2)
Пусть нам дана точка M(x,y) на координатной плоскости 0xy
Из канонического уравнения следует, что Y2 = b2(1- x2/a2)
Если это равенство подставить в выражение для фокальных радиусов, которые имеет точка M, то можно получить
r1 = √[(x + c)2 +y2] = √[x2 +2xc + c2 +b2 – b2x2/a2] = √[x2(1 – b2/a2) + 2xc +c2 +b2] =
= √[x2(a2 – b2)/a2 + 2xc + (c2 + b2)] = √[x2 (c2/a2) + 2xc +a2] = √[x(c/a) +a]2 = |a +xε|
т. е. r1 = |a +xε|
Отношение 2с/2a = c/a = ε называется эксцентриситетом эллипса. Оно у него всегда меньше 1.
То же самое просчитываем для r2.
Т. к. x2/a2 больше или равно 1 или x больше или равно большой полуоси (a), то можно сделать вывод о справедливости неравенства a≥|x|> |x|* ε = |xε|
Отсюда явно следует, что a+-|xε|>0 или a+-xε > 0 и r1 = a + xε, r2 = a — xε
Из полученных равенств выходит, что r1 + r2 = 2a, это значит, что точка M однозначно является точкой эллипса. Это нам и нужно было доказать.
Свойства эллипса
- У эллипса имеются две взаимно перпендикулярные оси симметрии.
Доказательство:
Переменные x и y в уравнение эллипса входят лишь во второй степени. Это означает, что если точка M с координатами (x,y) ему принадлежит, то и точки М1 (-x, y) и M2 (x, -y) тоже принадлежат ему. Легко проверить, что указанные координаты удовлетворяют каноническому уравнению эллипса. M1 симметрична по отношению к оси X, а M2 по отношению к оси Y. Получается, что у эллипса есть две взаимно перпендикулярные точки симметрии. - У эллипса есть центр симметрии.
Доказательство:
Если координаты точки М(x,y) будут удовлетворять уравнению эллипса, то и точка
N (–x; –y) ему тоже будет удовлетворять. M и N симметричны по отношению к началу координат. Это как раз и означает, что у эллипса имеется центр симметрии. - Эллипс пересекает каждую из осей в двух точках.
Доказательство:
Возьмём произвольную точку эллипса M(x,y). Расстояние этой точки до фокусов будетr1 = √[(x + c)2 + y2]
r2 = √[(x — c)2 + y2]Теперь давайте рассмотрим выражение
(x+-c)2 + y2 = x2 +- 2xc + c2+ y2 =
= x2 +- 2xc + a2 – b2 +y2 = x2 +- 2xc+ a2 — b2 + b2(1-x2/a2) =
= (a2 – b2)*x2/a2 +-2xc +a2 = c2*x2/a2+-2xa(c/a) + a2 = (a +c*x/a)2Эксцентриситет эллипса, как сказано ранее, меньше 1. Т. к. |x|≤ a, то a – εx > 0. Поэтому
F1M = a + εx и F2M = a – εx. Напомним, что ε – это эксцентриситет эллипса.
А теперь несколько свойств эллипса без доказательств.
- Эллипс можно получить, сжав окружность.
- Если через эллипс проходят две прямые, то отрезок, концами которого являются середины отрезков созданных при пересечении прямых, обязательно пересекает середину, центр эллипса.
- Угол, созданный касательной к эллипсу и его радиусом, проходящем через фокусы указанной геометрической фигуры, в любых случаях пересекает середину эллипса.
- Уравнение касательной к эллипсу в точке М, имеющей координаты xM и yM
1 = (x*xM)/a2 + (y*yM)/b2 - Эволюта эллипса представляет собой астероиду, растянутую вдоль его малой оси.
- Угол между касательной к эллипсу и одним его фокальным радиусом (r1) имеет ту же величину, что и угол, разделяющий касательную и другой фокальный радиус (r2) фигуры.
Как построить эллипс
Расскажем, как построить эллипс по его большой и малой полуосям и с помощью циркуля.
Построение эллипса по его большой и малой осям
Считается самым простым, не требующим серьёзных навыков.
Проведите две перпендикулярные оси;
От места пересечения осей на вертикальной отложите верх и вниз отрезки. Они будут составлять малую ось эллипса. На горизонтальной отложите отрезки вправо и влево. Из них будет состоять большая ось;
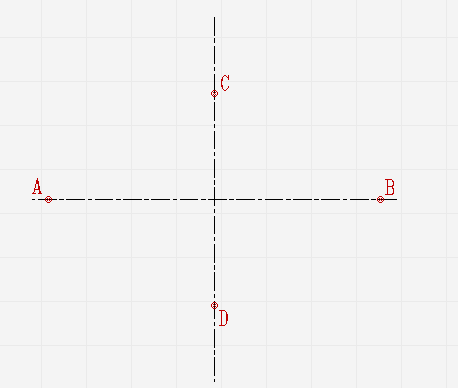
Проведите две концентрические окружности. Одну диаметром AB, диаметром CD;
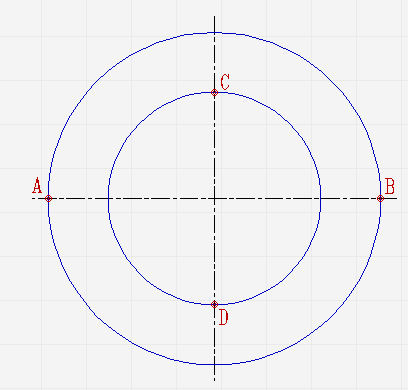
Проведите ещё диаметры в различных направлениях;
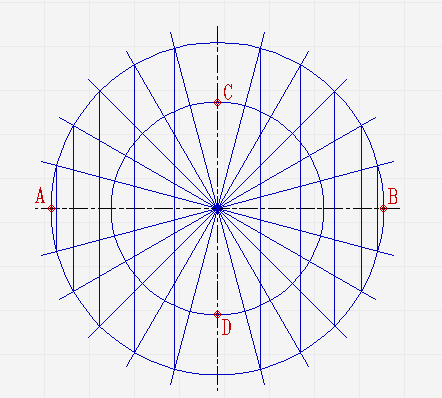
В местах, где лучи соприкасаются с окружностями, проведите линии параллельные малой и большой осям эллипса, пока они не пересекутся в точках, которые принадлежат эллипсу;
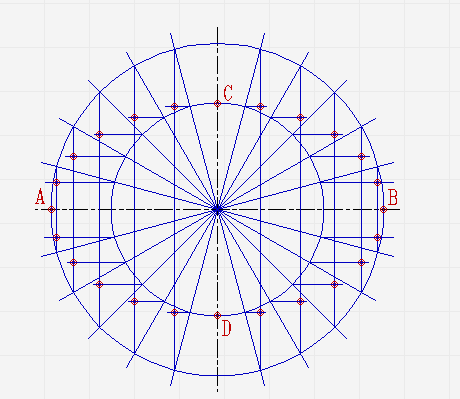
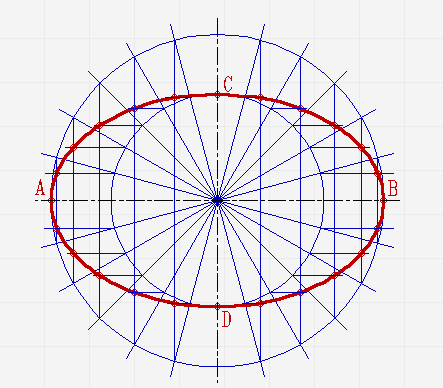
Соедините полученные точки плавной линией.
Нет времени решать самому?
Наши эксперты помогут!
Как построить эллипс с помощью циркуля
Во многом здесь всё аналогично предыдущему способу, поэтому перегружать текст иллюстрациями не будем.
Порядок действий следующий:
- Проведите две перпендикулярные линии. Они будут осями эллипса, а точка их пересечения центром геометрической фигуры;
- Определитесь с величиной большой и малой полуосей, если их значения не заданы в условии задачи;
- Установите раствор циркуля на длину большой полуоси (a). Поместите циркуль в точку O и отметьте на одной из линий две точки, P1 и P2. Установите раствор циркуля на длину малой полуоси. Опять поместите его в точку O и отметьте на другой из линий ещё две точки, обозначьте их как Q1 и Q2. Отрезки P1P2 и Q1Q2 будут большой и малой полуосями будущего эллипса;
- Установите раствор циркуля на величину a. Поместите циркуль в точке Q1 или Q2. После этого обозначьте циркулем на отрезке P1P2 точки F1 и F2. Это будут фокусы фигуры.
- Отметьте на P1P2 любую точку и обозначьте её T. Поставьте в этой точке циркуль и измерьте этим инструментом расстояние до P1. Затем начертите окружность данного радиуса из фокуса F1. После этого нужно сделать ещё одну окружность с радиусом величиной с расстояние от T до P2, но уже с центром из F2;
- Отметьте точки, в которых пересекаются обе окружности. Повторяйте процедуру, описанную в предыдущем пункте с новыми точками, отмечаемыми на отрезке P1P2;
- Соедините точки пересечения окружностей сплошной линией, когда построите их достаточное количество. Так у вас получится построить фигуру эллипс с помощью циркуля.
Примеры решения задач
Задача 1
Эллипс задан уравнением 16x2 + 25y2 = 400. Требуется найти большую и малую полуоси эллипса, координаты его фокусов и эксцентриситет.
Решение:
Разделим полученное уравнение на 400. Этим мы приведём его к виду
(x2/25) + (y2/16) =1. Большая полуось равна 5, корню квадратному из 25, а малая 4, корню квадратному из 16.
Из соотношения a² = b² + c² находим фокусное расстояние. Оно равно
c=+-√(a2 – b2) = +-√(25-16) = +-3, а значит координаты фокусов будут
F1(-3,0) и F2 (3,0). Эксцентриситет ε = с/a = 3/5.
Ответ: a = 5, b = 4, ε = 3/5.
Задача 2
Выяснить, является ли эллипсом линия, заданная как
9x2 + 25y2 – 225 = 0
Преобразуем данное нам уравнение к каноническому виду. Для этого:
Перенесём 225 в правую сторону
9x2 + 25y2 = 225
Поделим обе части этого уравнения на 225
(9x2/225) + (25y2/225) = 1
Сократим дроби и получим
(x2/25) + (y2/9) = 1
Как видим, нам удалось получить каноническое уравнение эллипса в чистом виде, т. е. исходное уравнение представляет собой эллипс, что и требовалось выяснить.
Ответ: 9x2 + 25y2 – 225 = 0 является уравнением эллипса.
Задача 3
Составить каноническое уравнение эллипса если расстояние между фокусами равно 8, а большая ось 10.
Решение:
Если большая ось равняется 10, значит полуось будет 5.
Если фокусное расстояние равно 8, то число c из координат фокусов будет 4.
Далее нужно подставить и вычислить
4 = √(25-b2)
Возведём это уравнение в квадрат
16 = 25 – b2
Перенесём b2 влево, а 16 вправо
b2 = 25 – 16 =9
В результате этих не сложных преобразований и вычислений получим каноническое уравнение
(x2/25) + (y2/9) = 1
Ответ: (x2/25) + (y2/9) = 1.
Задача 4
Получить каноническое уравнение эллипса, если его эксцентриситет равен 12/13, а большая полуось равна 26.
Решение:
Из уравнения эксцентриситета ε = с/a находим, что a = 13, а величина с = 12. Далее нужно вычислить квадрат длины меньшей полуоси
c = √(169 – b2)
Возведём обе части уравнения в квадрат
c2 = 169 – b2
Отсюда
b2 = 169 – 144 = 25
Далее остаётся лишь составить каноническое уравнение
(x2/169) + (y2/25) = 1
Ответ: (x2/169) + (y2/25) = 1
Задача 5
Найти фокусы у эллипса, который задан уравнением (x2/25) + (y2/16) = 1
Решение:
Нам нужно найти число с, которое определяет первые координаты фокусов
c = √(25-16) =3
Фокусы заданного эллипса будут равны
F1(-3,0) и F2(3,0).
Ответ: F1(-3,0) и F2(3,0).