11.3.1. Классификация поверхностей второго порядка
Алгебраической поверхностью
второго порядка называется
геометрическое место точек пространства,
которое в какой-либо аффинной системе
координат
может быть задано уравнением вида
,
где старшие коэффициенты
,
,
,
,
,
не равны нулю одновременно. Без ограничения
общности можно считать, что система
координат, в которой задано уравнение
поверхности второго порядка, прямоугольная.
Для каждой поверхности второго порядка
существует прямоугольная система
координат
,
в которой уравнение принимает наиболее
простой (канонический) вид. Она
называется канонической, а
уравнение – каноническим.
Канонические уравнения поверхностей второго порядка
1.
– уравнение эллипсоида;
2.
–
уравнение мнимого эллипсоида;
3.
–
уравнение мнимого конуса;
4.
–
уравнение однополостного
гиперболоида;
5.
–
уравнение двуполостного
гиперболоида;
6.
–
уравнение конуса;
7.
–
уравнение эллиптического
параболоида;
8.
–
уравнение гиперболического
параболоида;
9.
–
уравнение эллиптического
цилиндра;
10.
–
уравнение мнимого
эллиптического цилиндра;
11.
– уравнение пары мнимых
пересекающихся плоскостей;
1
2.
– уравнение гиперболического
цилиндра;
13.
– уравнение пары пересекающихся
плоскостей;
14.
– уравнение параболического
цилиндра;
15.
– уравнение пары параллельных
плоскостей;
16.
– уравнение пары мнимых
параллельных плоскостей;
17.
– уравнение пары совпадающих
плоскостей.
В этих уравнениях
,
,
,
,
причем
в уравнениях п.1–3;
в уравнениях п.4–7,9–11.
Поверхности (1),(4)–(9), (12)–(15),(17) называются
вещественными (действительными),
а поверхности (2),(3),(10),(11),(16) – мнимыми.
Вещественные поверхности изображены
в канонических системах координат.
Изображения мнимых поверхностей даются
штриховыми линиями только для иллюстрации.
Поверхность второго порядка называется
центральной, если она имеет
единственный центр (симметрии). В
противном случае, если центр отсутствует
или не является единственным, поверхность
называется нецентральной. К
центральным поверхностям относятся
эллипсоиды (вещественный и мнимый),
гиперболоиды (однополостный и
двуполостный), конусы (вещественный и
мнимый). Остальные поверхности –
нецентральные.
Алгоритм составления канонического уравнения поверхности второго порядка
Пусть в прямоугольной системе координат
поверхность второго порядка описывается
уравнением
.
Требуется определить ее название и
составить каноническое уравнение. Для
этого нужно выполнить следующие действия:
1. Вычислить ортогональные инварианты
,
,
,
.
Если
,
то вычислить семиинвариант
.
Если
и
,
то вычислить семиинвариант
.
2. По табл. 11.1 определить название
поверхности, а по названию –каноническое
уравнение поверхности второго порядка.
3. Составить характеристическое уравнение
,
используя коэффициенты, вычисленные в
п.1, либо разлагая определитель
.
Найти корни
,
,
(с учетом кратности) характеристического
уравнения.
4. Занумеровать корни
,
,
характеристического уравнения в
соответствии с правилами:
а) если поверхность эллиптического
типа, то
;
б) если поверхность гиперболического
типа, то обозначить через
и
корни одного знака так, чтобы
,
а через
– корень противоположного знака;
в) если поверхность параболического
типа, то
– если нулевой корень двойной, то
и
;
– если нулевой корень простой, а
ненулевые корни одного знака, то
и
;
– если нулевой корень простой, а
ненулевые корни разных знаков, то
и либо
,
если
или
,
либо
,
если
и
.
5. Вычислить коэффициенты канонического
уравнения и записать его в канонической
системе координат
:
а) для поверхностей эллиптического
типа:
(1) – при
– уравнение эллипсоида
с коэффициентами
,
,
;
Таблица
11.1. Классификация
поверхностей второго порядка
|
Признаки |
Название |
№ |
||||
|
Центральные |
|
Эллиптический тип |
|
|
Эллипсоид |
1 |
|
|
Мнимый эллипсоид |
2 |
||||
|
|
Мнимый конус |
3 |
||||
|
Гиперболический тип |
|
Однополостный |
4 |
|||
|
Двуполостный |
5 |
|||||
|
Конус |
6 |
|||||
|
Нецентральные |
|
Параболический |
|
Эллиптический |
7 |
|
|
Гиперболический |
8 |
|||||
|
|
|
|
Эллиптический |
9 |
||
|
|
Мнимый эллиптический цилиндр |
10 |
||||
|
|
Пара мнимых |
11 |
||||
|
|
|
Гиперболический |
12 |
|||
|
Пара пересекающихся плоскостей |
13 |
|||||
|
|
Параболический |
14 |
||||
|
|
Пара параллельных плоскостей |
15 |
||||
|
|
Пара мнимых плоскостей |
16 |
||||
|
|
Пара совпадающих плоскостей |
17 |
(2) при
– уравнение мнимого эллипсоида
с коэффициентами
,
,
;
(3) при
– уравнение мнимого конуса
с коэффициентами
,
,
;
б) для поверхностей гиперболического
типа:
(4) при
– уравнение однополостного гиперболоида
с коэффициентами
,
,
;
(5) при
– уравнение двуполостного гиперболоида
с коэффициентами
,
,
;
(6) при
– уравнение конуса
с коэффициентами
,
,
;
в) для поверхностей параболического
типа:
(7) при
– уравнение эллиптического параболоида
с коэффициентами
,
;
(8) при
– уравнение гиперболического
параболоида
с коэффициентами
,
;
(9) при
,
,
– уравнение эллиптического цилиндра
с коэффициентами
,
;
(10) при
,
,
– уравнение мнимого эллиптического
цилиндра
с коэффициентами
,
;
(11) при
,
,
– уравнение пары мнимых пересекающихся
плоскостей
с коэффициентами
,
;
(12) при
,
,
– уравнение гиперболического цилиндра
с коэффициентами
,
;
(13) при
,
,
– уравнение пары пересекающихся
плоскостей
с коэффициентами
,
;
(14) при
,
,
– уравнение параболического цилиндра
с коэффициентом
;
(15) при
,
,
,
– уравнение пары параллельных
плоскостей
с коэффициентом
;
(16) при
,
,
,
– уравнение пары мнимых параллельных
плоскостей
с коэффициентом
;
(17) при
,
,
,
– уравнение пары совпадающих плоскостей
.
Пример 11.10. Определить названия и
составить канонические уравнения
алгебраических поверхностей второго
порядка, заданных в прямоугольной
системе координат
уравнениями:
а)
;
б)
при
,
или
;
в)
;
г)
;
д)
;
е)
при
или
;
ж)
;
з)
;
и)
.
а)
Определяем коэффициенты уравнения:
,
,
,
,
,
,
,
,
,
.
1. Вычисляем инварианты:
,
,
,
.
2. По табл. 11.1 определяем, что уравнение
задает эллипсоид, так как
,
,
.
3. Составляем характеристическое
уравнение
и находим его корни:
(двойной корень),
(простой корень).
4. Поскольку поверхность эллиптического
типа, то корни уравнения обозначим
,
,
чтобы выполнялось условие
.
5. Вычисляем коэффициенты канонического
уравнения эллипсоида:
,
,
.
Таким образом, каноническое уравнение
(1) заданной поверхности имеет вид
.
б) Определяем коэффициенты уравнения:
,
,
,
,
,
,
,
,
.
1. Вычисляем инварианты:
,
,
,
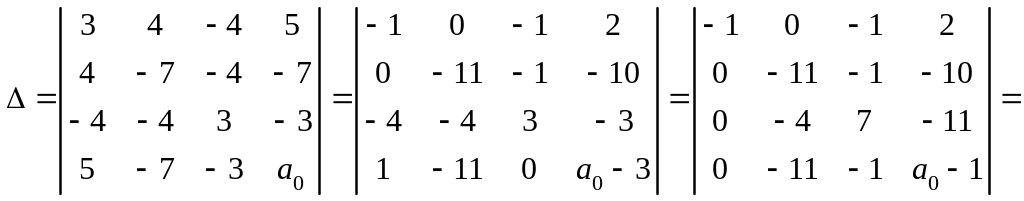
.
2. По табл. 11.1 определяем, что уравнение
задает поверхность гиперболического
типа, так как
.
При
получаем уравнение однополостного
гиперболоида, так как
,
при
– уравнение конуса, так как
,
при
– уравнение двуполостного гиперболоида,
так как
.
3. Составляем характеристическое
уравнение
и находим его корни:
,
,
(все корни простые).
4. Поскольку поверхность гиперболического
типа, то корни уравнения обозначим
,
,
т.е.
и
корни одного знака, причем
,
а
– корень противоположного знака.
5. Вычисляем коэффициенты канонического
уравнения:
– однополостного гиперболоида (при
):
,
,
,
следовательно, каноническое уравнение
(4) имеет вид
;
– конуса (при
):
,
,
;
следовательно, каноническое уравнение
(6) имеет вид
;
– двуполостного гиперболоида (при
):
,
,
;
следовательно, каноническое уравнение
(5) имеет вид
.
в) Определяем коэффициенты уравнения:
,
,
,
,
,
,
,
,
,
.
1. Вычисляем инварианты:
,
,
,
.
2. По табл. 11.1 определяем, что уравнение
задает эллиптический параболоид,
так как
,
.
3. Составляем характеристическое
уравнение
и находим его корни:
(двойной корень),
(простой корень).
4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:
– единственный нулевой корень; так как
ненулевые корни одного знака, то
,
чтобы выполнялось условие
.
5. Вычисляем коэффициенты канонического
уравнения эллиптического параболоида:
,
.
Таким образом, каноническое уравнение
(7) заданной поверхности имеет вид
.
г) Определяем коэффициенты уравнения:
,
,
,
,
,
,
,
,
,
.
1. Вычисляем инварианты:
,
,
,

.
2. По табл. 11.1 определяем, что уравнение
задает гиперболический параболоид,
так как
,
.
3. Составляем характеристическое
уравнение
и находим его корни:
,
,
(все корни простые).
4. Поскольку поверхность параболического
типа, то корни характеристического
уравнения обозначим следующим образом:
– единственный нулевой корень; так как
ненулевые корни разных знаков и
,
то
,
тогда
.
5. Вычисляем коэффициенты канонического
уравнения гиперболического параболоида:
,
.
Таким образом, каноническое уравнение
(8) заданной поверхности имеет вид
.
д) Определяем коэффициенты уравнения:
,
,
,
,
,
,
,
,
,
.
1. Вычисляем инварианты:
,
,
,
.
Так как
,
то вычисляем семиинвариант:
.
2. По табл. 11.1 определяем, что уравнение
задает эллиптический цилиндр, так
как
,
,
,
.
3. Составляем характеристическое
уравнение
и находим его корни:
,
,
(все корни простые).
4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:
– единственный нулевой корень; так как
ненулевые корни одного знака, то
,
,
чтобы выполнялось условие
.
5. Вычисляем коэффициенты канонического
уравнения эллиптического цилиндра:
,
.
Таким образом, каноническое уравнение
(9) заданной поверхности имеет вид
.
е) Определяем коэффициенты уравнения:
,
,
,
,
,
,
,
,
.
1. Вычисляем инварианты:
,
,
,
.
Так как
,
то вычисляем семиинвариант:
.
2. По табл. 11.1 определяем, что уравнение
задает поверхность параболического
типа, так как
.
При
получаем уравнение гиперболического
цилиндра, так как
,
,
;
при
– уравнение пары пересекающихся
плоскостей, так как
,
,
.
3. Составляем характеристическое
уравнение
и находим его корни:
,
,
(все корни простые).
4. Поскольку поверхность параболического
типа, то корни характеристического
уравнения обозначим следующим образом:
– единственный нулевой корень; так как
ненулевые корни разных знаков и
,
то
,
тогда
(при
имеем
и
,
а при
имеем
).
5. Вычисляем коэффициенты канонического
уравнения:
– гиперболического цилиндра (при
):
,
;
следовательно,
каноническое уравнение (12) имеет вид
;
– пары пересекающихся плоскостей (при
):
,
;
следовательно, каноническое уравнение
(13) имеет вид
.
ж) Определяем коэффициенты уравнения:
,
,
,
,
,
,
,
,
,
.
1. Вычисляем инварианты:
,
,
,
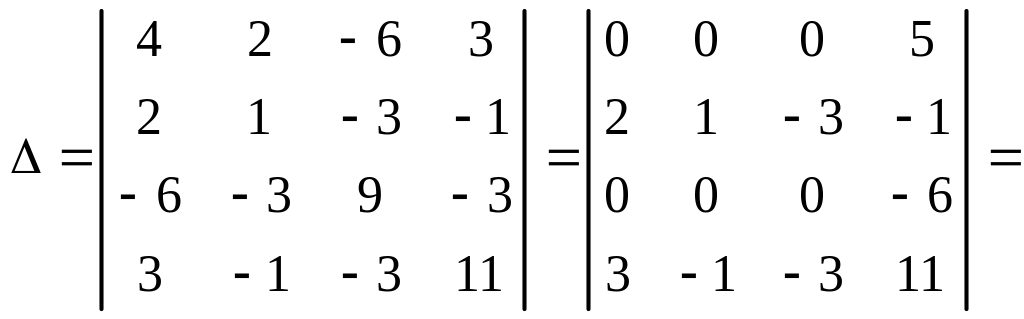
.
Так как
,
то вычисляем
.
2. По табл. 11.1 определяем, что уравнение
задает параболический цилиндр, так
как
,
,
,
.
3. Составляем характеристическое
уравнение
и находим его корни:
(двойной корень),
(простой корень).
4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:
– двойной нулевой корень, а
– ненулевой корень.
5. Вычисляем коэффициент канонического
уравнения параболического цилиндра:
.
Таким образом, каноническое уравнение
(14) заданной поверхности имеет вид
.
з) Определяем коэффициенты уравнения:
,
,
,
,
,
,
,
,
,
.
1. Вычисляем инварианты:
,
,
,
.
Так как
,
то вычисляем
.
Так как
и
,
то вычисляем
.
2. По табл. 11.1 определяем, что уравнение
задает пару параллельных плоскостей,
так как
,
,
,
,
.
3. Составляем характеристическое
уравнение
и находим его корни:
(двойной корень),
(простой корень).
4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:
– двойной нулевой корень, а
– ненулевой корень.
5. Вычисляем коэффициент канонического
уравнения пары параллельных плоскостей:
.
Таким образом, каноническое уравнение
(15) заданной поверхности имеет вид
.
и) Определяем коэффициенты уравнения:
,
,
,
,
,
,
,
,
,
.
1. Вычисляем инварианты:
,
,
,
.
Так как
,
то вычисляем
.
Так как
и
,
то вычисляем
.
2. По табл. 11.1 определяем, что уравнение
задает пару совпадающих плоскостей,
так как
,
,
,
,
.
3. Составляем характеристическое
уравнение
и находим его корни:
(двойной корень),
(простой корень).
4. Поскольку поверхность параболического
типа, то корни уравнения обозначим
следующим образом:
– двойной нулевой корень, а
– ненулевой корень.
5. Записываем каноническое уравнение
(17) пары совпадающих плоскостей:
.
Канонические уравнения поверхностей второго порядка
Рассмотрим задачу приведения уравнения поверхности второго порядка к наиболее простому (каноническому) виду.
Напомним, что алгебраической поверхностью второго порядка называется геометрическое место точек плоскости, которое в какой-либо аффинной системе координат может быть задано уравнением вида
(4.41)
где левая часть — многочлен трех переменных второй степени. Коэффициенты при первых степенях переменных
, а также при их произведениях
взяты удвоенными просто для удобства дальнейших преобразований.
Уравнение (4.41) можно записать в матричном виде: где
— матрица квадратичной формы,
— столбец коэффициентов линейной формы (см. пункты 5,6, замечаний 4.1).
Требуется найти прямоугольную систему координат , в которой уравнение поверхности приняло бы наиболее простой вид.
Результатом решения поставленной задачи является следующая основная теорема.
Классификация алгебраических поверхностей второго порядка
Теорема 4.3. Для любой алгебраической поверхности второго порядка существует прямоугольная система координат , в которой уравнение этой поверхности принимает один из следующих семнадцати канонических видов:
В этих уравнениях , причем
в уравнениях 1,2;
в уравнениях 3,4,5,6,7,9,10.
Теорема 4.3 дает аналитические определения поверхностей второго порядка. Согласно п.2 замечаний 4.1, поверхности (1),(4),(5),(6),(7),(8),(9), (12),(13),(14),(15),(17) называются вещественными (действительными), а поверхности (2),(3),(10),(11),(16) — мнимыми.
Поясним доказательство теоремы. Оно аналогично доказательству теоремы 3.3 и фактически содержит алгоритм решения поставленной задачи.
Без ограничения общности можно предполагать, что уравнение поверхности второго порядка задано в прямоугольной системе координат. В противном случае можно перейти от непрямоугольной системы координат к прямоугольной
, при этом уравнение линии будет иметь тот же вид и ту же степень согласно теореме 4.1.
Пусть в прямоугольной системе координат алгебраическая поверхность второго порядка задана уравнением (4.41), в котором хотя бы один из старших коэффициентов ап,
отличен от нуля,n поскольку левая часть уравнения — многочлен трех переменных
второй степени.
Упрощение общего уравнения (4.41) производится в два этапа. На первом этапе при помощи однородного ортогонального преобразования координат «уничтожаются» члены с произведением неизвестных, как и в случае уравнения линии второго порядка, при этом достаточно сделать три поворота (см. углы Эйлера).
Докажем, что существует однородная ортогональная замена переменных
(4.42)
где — столбцы старых и новых переменных,
— ортогональная матрица
, при которой квадратичная форма
приводится к каноническому виду
для которого матрица квадратичной формы диагональная:
Действительно, подставляя в квадратичную форму
, получаем
т.е. при однородной ортогональной замене переменных (4.42) матрица квадратичной формы преобразуется по закону
(4.43)
Составим характеристическое уравнение для матрицы (см. пункт 3 замечаний 3.12):
Так как это уравнение третьей степени, то оно имеет хотя бы один действительный корень. Обозначим его . Однородная система уравнений
или
определитель которой равен нулю, имеет бесконечно много ненулевых решений. Обозначим через вектор, координатный столбец которого совпадает с ненулевым решением
системы, удовлетворяющим условию нормировки
. Дополним этот единичный вектор
векторами
до ортонормированного базиса
пространства. Координатные столбцы
векторов
удовлетворяют условиям
(4.44)
кроме того столбец удовлетворяет равенству
или, что то же самое,
. Из координатных столбцов
базисных векторов составим матрицу
, которая в силу (4.44) является ортогональной, так как
и, следовательно, . Сделаем в квадратичной форме
замену переменных
с ортогональной матрицей
. По закону (4.43) находим
Последний столбец этой матрицы, учитывая равенство и ортогональность
, имеет вид
Следовательно, в матрице элементы
и
. Поэтому квадратичная форма имеет вид
Как показано при доказательстве теоремы 3.3, многочлен двух переменных при помощи поворота системы координат
можно привести к виду
. Этот поворот соответствует повороту найденной системы координат
вокруг оси аппликат.
Таким образом, существует преобразование прямоугольной системы координат, приводящее квадратичную форму к каноническому виду. При этом уравнение (4.41) не содержит членов с произведением неизвестных:
(4.45)
На втором этапе, при помощи параллельного переноса «уничтожаются» один, два или все три члена первой степени. В результате всех преобразований получаем систему координат , в которой уравнение (4.45) становится приведенным (одного из следующих пяти типов):
Уравнения (I), (II), (II) совпадают с приведенными уравнениями линии второго порядка, поскольку не зависят от неизвестной . В разделе показано, что они сводятся к каноническим уравнениям эллипсов, гиперболы, параболы или пар прямых. Поэтому уравнения (I), (II), (III) соответственно сводятся к каноническим уравнениям цилиндров (9), (10), (12), (14): эллиптического, гиперболического, параболического, или пар плоскостей (11), (13), (15), (16), (17).
Уравнение (IV) в зависимости от знаков коэффициентов сводится к каноническим уравнениям параболоидов (7) или (8). Например, если все коэффициенты положительны, то, перенося линейный член
в правую часть и разделив обе части уравнения на
, получим
. Обозначим положительные величины
и изменим направление оси аппликат, т.е. сделаем замену:
,
,
. В результате получим уравнение эллиптического параболоида (7):
Если окажется, что
, то переименуем координатные оси:
Уравнение (V) в зависимости от знаков коэффициентов сводится к каноническим уравнениям эллипсоидов (1),(2), гиперболоидов (4),(5) или конусов (3),(6).
Замечания 4.7.
1. Система координат, в которой уравнение алгебраической поверхности второго порядка имеет канонический вид, называется канонической. Каноническая система координат определяется неоднозначно. Например, изменяя направление оси ординат на противоположное, снова получаем каноническую систему координат, так как замена переменной на
не изменяет уравнений (1)–(17).
2. Поверхности второго порядка, приведенные в формулировке теоремы 4.3, изображены в канонической системе координат. Изображение мнимых поверхностей дается штриховыми линиями только для иллюстрации.
3. В случаях (11),(13),(15)-(17) поверхности называются распадающимися, поскольку соответствующие им многочлены второй степени разлагаются в произведение многочленов первой степени.
4. Напомним, что ненулевой столбец , удовлетворяющий равенству
, называется собственным вектором матрицы
, а число
— собственным значением этой матрицы. Говорят, что собственный вектор
соответствует (принадлежит) собственному значению
.
Как показано при доказательстве теоремы 4.3, при помощи однородной ортогональной замены переменных (4.42) или, что то же самое, при помощи поворотов прямоугольной системы координат
вокруг ее начала
, квадратичную форму
можно привести к каноническому виду
где — собственные числа матрицы
квадратичной формы, т.е. корни характеристического уравнения:
, а матрица
замены переменных составлена из попарно ортогональных единичных собственных векторов
матрицы
, соответствующих собственным значениям
. Другими словами, для любой квадратичной формы
(трех переменных) существует ортонормированный базис
, составленный из собственных векторов матрицы
, в котором квадратичная форма имеет канонический вид.
5. При ортогональном преобразовании координат собственные векторы матрицы квадратичной формы не изменяются, а именно, если
собственный вектор матрицы
(соответствующий собственному значению
), то вектор
является собственным для матрицы
, где
— ортогональная матрица.
Действительно, учитывая, что и
, получаем
т.е. . Следовательно,
— собственный вектор, соответствующий собственному значению
.
6. При однородной невырожденной замене переменных линейная форма
меняется следующим образом
, т.е. столбец коэффициентов линейной формы изменяется по закону
. Свободный член квадратичной функции при однородной замене переменных
не изменяется.
Продолжение Порядок приведения уравнения поверхности второго порядка к каноническому виду
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Поверхности второго порядка: их виды, уравнения, примеры
Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат
Общее уравнение поверхности второго порядка имеет вид
Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты — это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:
Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:
В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.
Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому
I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:
,
где λ 1 , λ 2 , λ 3 — корни характеристического уравнения
.
В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.
Эллипсоид
Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.
После решения характеристического уравнения общее уравнение можно переписать в следующем виде:
.
Тогда полуоси эллипсоида будут
, , .
Поэтому каноническое уравнение эллипсоида имеет вид
.
Мнимый эллипсоид
Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.
После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:
,
, , .
Мнимый конус
Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.
После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:
,
, , .
Однополостный гиперболоид
Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.
Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:
.
, , ,
то каноническое уравнение однополостного гиперболоида будет иметь вид
.
Двуполостный гиперболоид
Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.
Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:
.
Последняя запись и есть каноническое уравнение двуполостного гиперболоида.
Конус
Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.
Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:
,
известном как каноническое уравнение конуса.
II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:
,
где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.
Эллиптический параболоид
Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.
Общее уравнение можно переписать в виде:
.
Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая
,
,
получим каноническое уравнение эллиптического параболоида:
.
Гиперболический параболоид
Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.
Обозначая через λ 1 положительный корень, а через λ 2 — отрицательный и беря перед корнем знак минус, переписываем уравнение в виде:
.
, ,
получим каноническое уравнение гиперболического параболоида:
.
III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:
,
где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.
Эллиптический цилиндр
Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:
.
, ,
получим каноническое уравнение эллиптического цилиндра:
.
Мнимый эллиптический цилиндр
Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:
.
Последняя запись — каноническое уравнение мнимого эллиптического цилиндра.
Мнимые пересекающиеся плоскости
Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:
.
, ,
получим каноническое уравнение мнимых пересекающихся плоскостей:
.
Гиперболический цилиндр
Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:
,
, .
Таким образом, каноническое уравнение гиперболического цилиндра:
.
Пересекающиеся плоскости
Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:
,
, .
Таким образом, пересекающихся плоскостей:
.
IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:
,
где λ 1 = I 1 — отличный от нуля корень характеристического уравнения.
Параболический цилиндр
Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:
,
.
Это уравнение параболического цилиндра, в каноническом виде оно записывается так:
.
V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:
,
.
Параллельные плоскости
Если K 2 , то общее уравнение поверхности второго порядка определяет две параллельные плоскости.
,
перепишем его в виде
.
Мнимые параллельные плоскости
Если K 2 > 0 , то общее уравнение поверхности второго порядка определяет две мнимые параллельные плоскости.
,
перепишем его в виде
.
Совпадающие плоскости
Если K 2 = 0 , то общее уравнение поверхности второго порядка определяет две совпадающие плоскости:
.
Решение примеров на определение вида поверхности второго порядка
Пример 1. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Решение. Найдём I 3 :
(как вычислить определитель).
I 1 = 1 + 5 + 1 = 7 ,
Следовательно, данная поверхность — однополостный гиперболоид.
.
Составляем и решаем характеристическое уравнение:
;
.
,
, , .
Пример 2. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Решение. Найдём I 3 :
.
.
Следовательно, общее уравнение определяет эллиптический параболоид.
.
I 1 = 2 + 2 + 3 = 7 .
Решаем характеристическое уравнение:
.
.
,
, .
Пример 3. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
,
,
,
I 1 = 5 + 2 + 5 = 12 .
Так как I 3 = К 4 = 0 , I 2 > 0 , I 1 K 3 , то данное общее уравнение определяет эллиптический цилиндр.
.
.
Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение
Пример 4. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Кривые и поверхности второго порядка в математике с примерами решения и образцами выполнения
Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида.
Кривые второго порядка используются при решении задач по аналитической геометрии, кривые других порядков используются при решении задач математического анализа в разделе вычисления кратных, криволинейных и поверхностных интегралов.
Кривые и поверхности второго порядка
Преобразование координат на плоскости
Пусть на плоскости заданы две прямоугольные декартовы системы координат, Оху и О’х’у’ (рис. 1). Произвольная точка М относительно одной из этих координатных систем определяется парой чисел х и у, а относительно другой — парой чисел x’ и у’. Ясно, что между парами (х,у) и (x’, у’) имеется связь. Найдем ее.
Параллельный перенос
Предположим, что соответствующие координатные оси параллельны и сонаправлены, а точки начала отсчета различны. Это означает, что орты координатных осей соответственно равны (рис. 2).
Пусть г и г’ — радиусы-векторы точки М, т.е.
и а, β — координаты точки О’ относительно системы координат Оху, т. е.
Поворот
Предположим, что координатные оси одной системы координат получаются из координатных осей другой системы поворотом на угол φ, а начальные точки совпадают (рис.4). Координатами единичного вектора i’ являются косинусы углов φ и , образованных этим вектором с осями Ох и Оу:
а координатами единичного вектора j’ служат косинусы углов и φ:
(рис. 5). Так как радиус-векторы
произвольной точки М в рассматриваемом случае равны,
то, заменяя векторы i’ и j’ их выражениями, получаем, что
Зеркальное отражение
В случае, когда оси абсцисс Ох и Ох’ координатных систем совпадают, а оси ординат Оу и Оу’ направлены противоположно, координаты (х, у) и (х’,у’) произвольной точки М связаны равенствами
Справедливо следующее утверждение.
Любое преобразование прямоугольных декартовых координат (с сохранением масштаба) можно представить в виде последовательного выполнения переноса, поворота и <если необходимо) зеркального отражения.
Кривые второго порядка
Пусть на плоскости задана прямоугольная декартова система координат Оху. Множество точек плоскости, координаты х и у которых удовлетворяют равенству
F(x, у) = 0,
где F(x, у) — некоторая функция двух переменных, называется плоской кривой, или плоской линией само равенство называется уравнением данной линии (кривой).
Например, равенство х — у = 0 есть уравнение прямой — биссектрисы первого и третьего координатных углов (рис. 7). Равенство x 2 + y 2 — 1 = 0 — уравнение окружности единичного радиуса с центром в начале координат (рис. 8).
Рассмотрим многочлен второй степени от двух переменных х и у:
F(x,y) = 0
будем называть уравнением линии (кривой) второго порядка.
Если линиями первого порядка являются именно прямые и только они, то множество кривых второго порядка заметно разнообразней. Поэтому исследованию общего уравнения кривой второго порядка естественно предпослать изучение некоторых частных, но важных случаев.
Эллипс
Эллипсом называется кривая, уравнение которой в некоторой прямоугольной декартовой системе координат Оху имеет вид (1)
Система координат Оху, в которой уравнение эллипса имеет вид (1), называется канонической (для данного эллипса); само уравнение (!) называется каноническим уравнением эллипса. Окружность
является частным случаем эллипса (при а = b). Это позволяет несложным способом определить форму эллипса: эллипс (1) получается из окружности (2) путем ее равномерного сжатия» к оси Ох (с коэффициентом), т.е. заменой в уравнении x 2 + y 2 = a 2 координаты у на (рис.9).
Свойства эллипса
- Эллипс (I) содержится в прямоугольнике
В этом легко убедиться, заметив, что, если точка М(х, у) принадлежит эллипсу (1), то (рис. 10)
Точки (±а, 0), (0, ±b) называются вершинами эллипса.
2. Координатные оси Ох и Оу канонической системы являются осями симметрии эллипса, а начало координат О — его центром симметрии. Это означает, что если точка Мо(хo, yо) принадлежит эллипсу, то точки (-хо, yо), (-xо, -yо) и (хо, -yо) также ему принадлежат (рис. 11).
3. Если эллипс не является окружностью, то координатные оси канонической системы — единственные оси симметрии.
Положим с = . Ясно, что с 0 называется преобразование, переводящее произвольную точку М(х, у) окружности в точку М’ ().
Пусть сначала М(х, у) — произвольная точка эллипса
Вычислим ее расстояния от фокусов эллипса (рис. 12). Имеем
Заменяя y 2 его выражением
после несложных преобразований получаем, что
Последнее равенство вытекает из того, что
Легко убедиться в том, что
Доказательство того, что точки, обладающие указанным свойством, принадлежат эллипсу, было проведено ранее (см. раздел «Простейшие задачи аналитической геометрии» Введения, задача 2).
называется эксцентриситетом эллипса (I). Ясно, что 0
называются директрисами эллипса. У каждого эллипса две директрисы — левая и правая (рис. 13).
5. Эллипс есть множество точек плоскости, отношение расстояний от которых до данной точки (фокуса эллипса) и доданной прямой (одноименной с фокусом директрисы эллипса) постоянно (равно эксцентриситету эллипса).
Пусть сначала М(х,у) — произвольная точка эллипса (1). Вычислим расстояния от нее до правого фокуса и до правой директрисы (рис. 14). Имеем соответственно
Откуда легко получаем требуемое
Аналогично проверяется, что
Рассмотрим теперь на плоскости точку (с, 0) и прямую х =(с = ае). Возьмем произвольную точку М(х, у) и вычислим расстояния от нее до выбранной точки (с, 0) —
— и до выбранной прямой —
Возведем обе части последнего соотношения в квадрат и, положив и учтя равенство с = ае, после простых преобразований получим
Тем самым, точка М(х,у) лежит на эллипсе (1).
Гипербола
Гиперболой называется кривая, уравнение которой в некоторой прямоугольной системе координат Оху имеет вид (1)
Система координат Оху, в которой уравнение гиперболы имеет вид (1), называется канонической (для данной гиперболы); само уравнение (1) называется каноническим уравнением гиперболы.
Свойства гиперболы
- Гипербола (1) лежит вне полосы |x|
и, значит, |x| ≥ а (рис. 15).
Точки (±а, 0) называются вершинами гиперболы.
2. Гипербола (1) лежит в вертикальных углах, образованных прямыми у = ±х и содержащих точки оси Ох (рис. 16).
вытекает, что если точка М(х, у) лежит на гиперболе (1), то
Таким образом, гипербола состоит из двух частей — ветвей гиперболы, левой и правой. Прямые
называются асимптотами гиперболы.
3, На гиперболе лежат точки, сколь угодно далекие от начала координат O(0, 0).
Пусть, например, точка М(х, у) лежит на гиперболе (1) и у = n, где n — произвольное положительное число (рис. 17).
Возьмем в первой четверти две точки: точку гиперболы (1) и точку ее асимптоты = 0 с одинаковой абсциссой х > а —
соответственно — и вычислим расстояние между ними. Имеем
Умножив и разделив полученное выражение на сумму х +и перейдя затем к пределу при получим
Тем самым, установлен следующий факт.
4. Если текущая точка асимптоты неограниченно удаляется от начала координат, т.е. х —» + ∞, то на гиперболе можно указать соответствующую ей точку так, чтобы расстояние между ними стремилось к нулю (рис. 18).
Верно и обратное.
стремится к нулю.
6. Оси канонической координатной системы являются осями симметрии гиперболы, а начало координат — ее центром симметрии (рис. 19).
Координатные оси канонической системы — единственные оси симметрии гиперболы.
Положим с = . Ясно, что с > 0. .Точки (-с, 0) и (с, 0) называются фокусами гиперболы, 2с — фокусное расстояние.
Гипербола есть множество точек, абсолютная величина разности расстояний от которых до двух данных точек (фокусов гиперболы) постоянна (равна заданному числу).
Доказательство этого свойства проводится так же, как и доказательство свойства 4 эллипса. Покажем, например, что каждая точка гиперболы обладает указанным свойством. Если М(х, у) — точка гиперболы (1), то расстояния от нее до фокусов соответственно равны
(рис. 20). Так как > 1, то
Отсюда нетрудно вычислить, что
называется эксцентриситетом гиперболы (1). Ясно, что е > 1. Прямые
называются директрисами гиперболы (рис. 21). У каждой гиперболы две директрисы — левая и правая.
Практически также, как и для эллипса, доказывается следующий факт.
8. Гипербола есть множество точек, отношение расстояний от которых до данной точки (фокуса гиперболы) и доданной прямой (одноименной с фокусом директрисы) постоянно (равно эксцентриситету гиперболы) (рис. 22).
Гипербола (2)
называется сопряженной гиперболе (1). Взаимное расположение гипербол (1) и (2) указано на рис. 23.
Парабола
Параболой называется кривая, уравнение которой в некоторой прямоугольной декартовой системе координат Оху имеет вид (1)
Система координат Оху, в которой уравнение параболы имеет вид (1), называется канонической (для данной параболы); уравнение (]) называется каноническим уравнением параболы.
Свойства параболы
- Все точки параболы лежат в правой полуплоскости: х ≥ 0 (рис. 25). Точка 0(0, 0) лежит на параболе и называется ее вершиной.
- На параболе лежат точки, сколь угодно далеко расположенные от начала координат О(0, 0).
- Ось абсцисс канонической координатной системы является (единственной) осью симметрии параболы (рис. 26).
Ось симметрии параболы называется осью параболы. Число р называется фокальным параметром параболы; точка (; 0) — фокус параболы; прямая х = — директриса параболы.
4. Парабола есть множество точек, равноудаленных отданной точки (фокуса параболы) и от данной прямой (директрисы параболы) (рис. 27).
Пусть точка М(х, у) лежит на параболе (1). Вычислим расстояния от нее до фокуса (;0)
и до директрисы х = —
Заменяя у 2 его выражением 2рх, легко убеждаемся в том, что
Верно и обратное. Если для некоторой точки М(х, у) расстояния от нее до точки (; 0) и до прямой х = — равны —
то, возводя в квадрат, после простых преобразований получаем, что эта точка лежит на параболе:
Оптическое свойство кривых второго порядка
Касательные к эллипсу и гиперболе
Если кривая задана уравнением
y = f(x)
то уравнение касательной к ней, проходящей через точку (хо,у0)> где Уо = f(xо), можно записать в следующем виде
Пусть Мо(хо, yо) — точка эллипса
Предположим для определенности, что точка М0 лежит в первой четверти, т. е. хо > 0, yо > 0. Тогда часть эллипса, лежащую в первой четверти, можно описать уравнением
Пользуясь формулой (1), получаем уравнение касательной к эллипсу в точке Мо
а так как точка (х0, у о) лежит на эллипсе, то
Полученное соотношение после несложных преобразований можно записать так:
Отсюда с учетом тождества
приходим к уравнению
(рис. 28). Полученное соотношение является уравнением касательной к эллипсу, проходящей через его точку (х0, yо), и в общем случае ее произвольного расположения, т. е. при любых знаках хо и уо.
Уравнение касательной к гиперболе выводится аналогично и имеет следующий вид
Подчеркнем, что точка (хо, yо) лежит на гиперболе.
Касательные к параболе
Если кривая задана уравнением
х = g(у),
то уравнение касательной к ней, проходящей через точку (хo,уo), где х0 = g (уо), можно записать в следующем виде
Пусть М0(х0, у0) — точка параболы. Пользуясь формулой (I), получаем уравнение касательной к параболе
Отсюда в силу равенства приходим к уравнению касательной вида
Замечание:
Сопоставляя канонические уравнения эллипса, гиперболы и параболы с уравнениями касательных к этим кривым, нетрудно заметить, что для получения последних не требуется специальных вычислений. В самом деле, заменяя у 2 на уу 0 , а х 2 на хх 0 (в случае параболы 2х нужно заменить на x + х 0 ). приходим к уравнению соответствующей касательной. Еще раз отметим, что сказанное справедливо лишь в том случае, когда точка (x 0 . y 0 ) лежит на кривой.
Оптическое свойство эллипса
Пусть М 0 — произвольная точка эллипса
Как уже отмечалось, расстояния от нее до фокусов Fл и F n — фокальные радиусы — равны соответственно
Проведем через точку М 0 касательную к эллипсу,
и вычислим, на каком расстоянии от этой касательной лежат фокусы Fл (-c, 0) и Fn (c; 0) (напомним, что для этого следует воспользоваться формулой (10).
— нормирующий множитель (рис. 29). Нетрудно проверить, что
Обратившись к рис.29, заметим, что вычисленные отношения равны синусам углов, образованных касательной и фокальными радиусами точки касания. Из того, что синусы этих углов равны, вытекает равенство и самих углов. Тем самым доказано оптическое свойство эллипса: касательная к эллипсу образует равные углы с фокальными радиусами точки касания.
Это свойство называется оптическим по следующей причине: если поместить в один из фокусов эллипса с зеркальной «поверхностью» точечный источник света, то все лучи после отражения от «поверхности» эллипса сойдутся в другом его фокусе (рис. 30).
Оптическое свойство гиперболы
Устанавливается аналогичными выкладками и заключается в следующем.
Если поместить в один из фокусов гиперболы точечный источник света, то каждый луч после отражения от зеркальной «поверхности» гиперболы видится исходящим из другого фокуса (рис. 31).
Оптическое свойство параболы
Если в фокус параболы помещен точечный источник света, то все лучи, отраженные от зеркальной «поверхности» параболы, будут направлены параллельно оси параболы (рис. 32).
Классификация кривых второго порядка
Многочлены второй степени на плоскости
Теорема:
Пусть на плоскости введена прямоугольная декартова система координат Оху и пусть
— многочлен второй степени от переменных х и у.
Тогда на плоскости можно построить прямоугольную дека ртов у систему координат O’XY так, что после замены переменных х и у на переменные X и Y исходный многочлен f(x, у) приведется к многочлену F(X, Y) одного из следующих трех видов:
1-й шаг. Поворотом координатных осей на подходящим образом выбранный угол всегда можно добиться того, чтобы коэффициент при произведении разноименных координат обратился в нуль.
Пусть b ≠ 0 (при 6 = 0 этот шаг не нужен). Повернем оси координат вокруг точки О. Эта операция описывается следующими формулами
При этом координатные оси исходной системы Оху поворачиваются на угол φ (рис.33).
Заменим переменные х и у в формуле (1) их выражениями (2) через x’ и у’ и вычислим коэффициент 2b’ при произведении х’у’. Он равен
и обращается в нуль, если
Так как полученное уравнение разрешимо относительно φ, то указанным преобразованием всегда можно добиться обращения в нуль нужного коэффициента.
Приступая ко второму этапу преобразования, будем считать, что исходный многочлен f(x,у) уже имеет вид
где а 2 + с 2 >0. Для определенности положим с ≠ 0 (это не ограничивает общности наших рассуждений, так как заменой х, у в случае необходимости этого всегда можно добиться).
2-й шаг. Переносом начала координат можно достичь дальнейшего упрощения вида многочлена f(x,y). Эта операция описывается следующими формулами:
координатные оси новой системы O’XY получаются из координатных осей исходной системы Оху параллельным переносом в точку (-а, — β) (рис. 34).
Укажем конкретные значения а и β. Возможны три случая
I. а ≠ 0, с ≠ 0. Тогда, полагая
где А = а, В = с, С = g —
II. а = 0, d ≠ 0. Тогда, полагая
III. а = d = 0. Тогда, полагая
где В = с, Е = g —
Канонические уравнения кривых второго порядка
Если многочлен второй степени F(X, У) приравнять к нулю, то получим уравнение линии второго порядка
F(X, У) = 0.
Рассмотрим каждый из трех полученных выше случаев I, II, III отдельно.
I.
Э. А • В > 0. Домножением обеих частей уравнения на — 1 и заменой X на У, а У на X (в случае необходимости) всегда можно добиться того, чтобы В ≥ А > 0.
-
С
(мнимый эллипс)2). На действительной плоскости нет ни одной точки (X, Y), координаты которой обращали бы это уравнение в тождество.
Точка (0, 0) является единственной точкой плоскости, координаты которой удовлетворяют этому уравнению; точку (0,0) можно мыслить как действительную точку пересечения двух мнимых пересекающихся прямых 3).
Г. А • В 0, В
— пару пересекающихся прямых:
2) Название можно объяснить некоторым сходством этого уравнения с уравнением эллипса.
3) Название можно объяснить некоторым сходством этого уравнения с уравнением пары пересекающихся
прямых.
II. BY 2 + 2DX = О, В • D ≠ 0.
Всегда можно добиться того, чтобы В • D
III. BY 2 + Е = 0, В ≠ 0. Можно считать, что В > 0.
1. Е
Y 2 — с 2 = 0, с > 0
— пару параллельных прямых.
Y 2 — с 2 = 0, с 2 = 0
— пара совпадающих прямых.
Чтобы определить тип кривой второго порядка, не обязательно проводить все указанные выше преобразования. Достаточно вычислить знаки некоторых выражений, составленных из коэффициентов уравнения.
— уравнение линии второго порядка. Введем следующие обозначения
Числа D и ∆ не зависят от выбора системы координат на плоскости и называются инвариантами. Из приводимой таблицы видно, какому сочетанию знаков определителей D и ∆ соответствует та или иная линия второго порядка.
Задача:
Убедитесь в том, что D и ∆ при рассмотренных преобразованиях системы координат действительно остаются неизменными.
4) Название можно объяснить некоторым сходством этого уравнения с уравнением пары параллельных прямых.
Поверхности второго порядка
Пусть в пространстве задана прямоугольная декартова система координат Oxyz. Множество точек пространства, координаты х, у и z которых удовлетворяют равенству
F(x, у, z) = О,
называется поверхностью; равенство (*) называется уравнением этой поверхности.
Пример:
— уравнение сферы радиуса о с центром в точке (0,0,0) (рис. 35).
Рассмотрим многочлен второй степени от трех переменных х, у и z
Уравнение
F(x, y, z) = 0
будем называть уравнением поверхности второго порядка.
Исследование общего уравнения поверхностей второго порядка оказывается зна-чительноболее сложным, чем исследование общего уравнения кривых второго порядка, требует разработки соответствующего математического аппарата и будет проведено в конце главы VI.
В оставшихся параграфах этой главы мы сначала остановимся на изучении геометрических свойств некоторых важных классов общих поверхностей; затем используем их для рассмотрения канонических уравнений основных поверхностей второго порядка и исследования структуры этих поверхностей.
Некоторые классы поверхностей
Поверхности вращения
Рассмотрим на плоскости Oxz кривую γ, заданную уравнением
г = f(x), х ≥ 0
(рис. 36). При вращении кривой γ вокруг оси Oz она будет заметать некоторую поверхность, называемую поверхностью вращения (рис. 37). Найдем уравнение этой поверхности, т. е. равенство, которому должны удовлетворять координаты точек построенной поверхности и только они.
Тем самым, координаты х, у и z0 любой точки М этой окружности связаны следующим равенством
В силу произвольности выбора точки М0 на кривой γ искомое уравнение полученной поверхности вращения имеет вид
Цилиндрические поверхности
Через каждую точку некоторой заданной кривой γ проведем прямую l параллельно заданной прямой l0. Множество точек, лежащих на так построенных прямых, назовем цилиндрической поверхностью (рис. 39); кривая γ называется направляющей цилиндрической поверхности, а прямая l — ее образующей.
Найдем уравнение, описывающее цилиндрическую поверхность.
Возьмем произвольную точку О и проведем через нее плоскость П, перпендикулярную образующей I. Построим в пространстве прямоугольную координатную систему Oxyz, взяв за ось Oz прямую, перпендикулярную плоскости П. Тогда плоскость П будет координатной плоскостью Оху (рис.40). Плоскость П пересекает цилиндрическую поверхность по направляющей γ0.
F(x,y) = 0
— уравнение этой направляющей. Убедимся в том, что последнее соотношение можно считать уравнением искомой цилиндрической поверхности.
самом деле, пусть (х, у, z) — точка цилиндрической поверхности (рис. 41). Тогда точка (х, у, 0) лежит на γ0 и, значит, удовлетворяет уравнению
F(x,y)=0.
Но координаты точки (х, у, z) также обращают это уравнение в тождество. Последнее обстоятельство и позволяет считать соотношение F(x,y) = 0 искомым уравнением.
Пример:
Введем в пространстве прямоугольные декартовы координаты Охуz. Соотношение
является уравнением цилиндрической поверхности (эллиптического цилиндра) (рис. 42).
Замечание:
F(y, z) = 0
описывает цилиндрическую поверхность с образующей, параллельной координатной оси Оx, а уравнение
F(x,z) = 0
— цилиндрическую поверхность с образующей, параллельной оси Oy.
Конические поверхности
Пусть γ — произвольная кривая и О — точка вне eе. Через каждую точку кривой γ и точку О проведем прямую l. Множество точек, лежащих на построенных таким образом прямых, называется конической поверхностью (рис.43); кривая γ — направляющая конической поверхности, l — ее образующая, точка О — вершина. Рассмотрим функцию
F (x, у, z)
переменных х, у и z. Функция F(x, у, z) называется однородной функцией степени q, если для любого t > 0 выполняется равенство
Покажем, что если F(x, у, z) однородная функция, то F
является уравнением конической поверхности.
В самом деле, пусть
т.е. точка М0(xo, уо, zо) лежит на этой поверхности. Будем считать, что . Проведем через эту точку и точку 0(0,0, 0) (считая, что F(0,0, 0) = 0) прямую I (рис. 44). Ее параметрические уравнения имеют вид
Подставляя полученные выражения для х, у и z в функцию F(x, у, z), видим, что
Это означает, что вся прямая l лежит на поверхности, определяемой уравнением F(x,y,z) = 0, которое, следовательно, и описывает коническую поверхность.
Пример:
является однородной функцией второй степени:
— уравнение конической поверхности (конуса второго порядка) (рис.45).
Воспользуемся теперь полученными выше результатами для исследования геометрической формы поверхностей второго порядка.
Эллипсоид. Гиперболоиды. Параболоиды. Цилиндры и конус второго порядка
Эллипсоид
Эллипсоидом называется поверхность, уравнение которой в некоторой прямоугольной декартовой системе координат Oxyz имеет вид
где а ≥ b ≥ с > 0. Для того, чтобы выяснить, как выглядит эллипсоид, поступим следующим образом. Возьмем на плоскости Oxz эллипс
и будем вращать его вокруг оси Oz (рис. 46).
— эллипсоид вращения — уже дает представление о том, как устроен эллипсоид общего вида. Чтобы получить его уравнение, достаточно равномерно сжать эллипсоид вращения . вдоль оси Оу с коэффициентом — ≤ 1, т. с. заменить в его уравнении у на y 5).
Гиперболоиды
вокруг оси Oz (рис. 47), получим поверхность, называемую однополостным гиперболоидом вращения. Его уравнение имеет вид
получается тем же способом, что и в случае эллипсоида вращения.
5) Эллипсоид вращения («) можно получить равномерным сжатием сферы х 2 + у 2 + z 2 = а 2 вдоль оси Оz с коэффициентом — ≤ 1.
Путем равномерного сжатия этой поверхности вдоль оси Оу с коэффициентом ≤ 1 получим однополостный гиперболоид общего вида. Его уравнение
получается тем же способом, что и в разобранном выше случае эллипсоида. Путем вращения вокруг оси Oz сопряженной гиперболы
получим двуполостный гиперболоид вращения (рис.48). Его уравнение
Путем равномерного сжатия этой поверхности вдоль оси Оу с коэффициентом ≤ 1 приходим к двуполостному гиперболоиду общего вида. Заменой у на у получаем его уравнение
Эллиптический параболоид
вокруг оси Oz (рис.49), получаем параболоид вращения. Его уравнение имеет вид
Путем сжатия параболоида вращения вдоль оси Оу с коэффициентом получаем эллиптический параболоид. Его уравнение
получается из уравнения параболоида вращения
путем замены у на . Если р Гиперболический параболоид
Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой прямоугольной декартовой системе координат Oxyz имеет вид
где р > 0, q > 0. Вид этой поверхности определим, применив так называемый метод сечений, который заключается в следующем: параллельно координатным плоскостям проводятся плоскости, пересекающие исследуемую поверхность, и по изменению конфигурации возникающих в результате плоских кривых делается вывод о структуре самой поверхности.
Начнем с сечений плоскостями z = h = const, параллельными координатной плоскости Оху. При h > 0 получаем гиперболы
при h
при h = 0 — пару пересекающихся прямых
Заметим, что эти прямые являются асимптотами для всех гипербол (т. е. при любом h ≠ 0). Спроектируем получаемые кривые на плоскость Ох у. Получим следующую картину (рис. 51). Уже это рассмотрение позволяет сделать заключение о седлообразном строении рассматриваемой поверхности (рис. 52).
Рассмотрим теперь сечения плоскостями
у = h.
Заменяя в уравнении поверхности у на h, получаем уравнения парабол (рис.53).
Аналогичная картина возникает при рассечении заданной поверхности плоскостями
х = h.
В этом случае также получаются параболы
ветви которых направлены вниз (а не вверх, как для сечения плоскостями у = h) (рис. 54).
Используя последние два типа сечений, приходим к заключению, что гиперболический параболоид можно получить путем параллельного переноса параболы х2 = 2pz вдоль параболы у2 = -2qz, или наоборот (рис. 55).
Замечание:
Методом сeчeний можно разобраться в строении и всех ранее рассмотренных поверхностей второго порядка. Однако путем вращения кривых второго порядка и последующего равномерного сжатия к пониманию их структуры можно прийти проще и значительно быстрее.
Оставшиеся поверхности второго порядка по существу уже рассмотрены ранее. Это цилиндры:
представление о котором можно получить либо путем вращения пары пересекающихся прямых
вокруг оси Oz и последующего сжатия, либо методом сечений. Конечно, в обоих случаях получим, что исследуемая поверхность имеет вид, указанный на рис. 59.
Дополнение к поверхностям второго порядка
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Как найти каноническое уравнение поверхности второго порядка
С помощью векторов мы ввели понятие пространства и его размерности, в частности трехмерного. Рассмотрим в нем поверхности, которые «похожи» на поверхности, образованные вращением кривой второго порядка вокруг ее оси симметрии. Например, сфера может быть получена вращением окружности вокруг диаметра. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d. Наряду с такими поверхностями мы встретимся и с более сложными случаями.
Пусть в пространстве задана прямоугольная декартова система координат.
Поверхность второго порядка – геометрическое место точек, декартовы прямоугольные координаты которых, удовлетворяют уравнению вида
в котором хотя бы один из коэффициентов отличен от нуля. Уравнение (2.48) называется общим уравнением поверхности второго порядка.
Уравнение (2.48) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую поверхность второго порядка. В зависимости от значений коэффициентов общего уравнения (2.48) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из канонических видов, каждому из которых соответствует определённый класс поверхностей второго порядка. Среди них выделяют пять основных классов поверхностей: эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры. Для каждой из этих поверхностей существует декартова прямоугольная система координат, в которой поверхность задается простым уравнением, называемым каноническим уравнением.
Перечисленные поверхности второго порядка относятся к так называемым нераспадающимся поверхностям второго порядка. Можно говорить о случаях вырождения – распадающихся поверхностях второго порядка, к которым относятся: пары пересекающихся плоскостей, пары мнимых пересекающихся плоскостей, пары параллельных плоскостей, пары мнимых параллельных плоскостей, пары совпадающих плоскостей.
Наша цель – указать канонические уравнения для поверхностей второго порядка и показать, как выглядят эти поверхности.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется эллипсоидом (рис. 2.22) .
1. Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует, что .
2. Эллипсоид обладает
· центральной симметрией относительно начала координат,
· осевой симметрией относительно координатных осей,
· плоскостной симметрией относительно начала координат.
3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс (см. рис. 2.22).
Так же, как для эллипса, точки пересечения эллипсоида с координатными осями называются вершинами эллипсоида, центр симметрии – центром эллипсоида. Числа а, b , с называются полуосями. Если полуоси попарно различны, то эллипсоид называется трехосным.
Если две полуоси равны друг другу, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей.
Примечание. Сфера является частным случаем эллипсоида при а= b =с. Тогда все равные полуоси обозначают R и уравнение (2.49) после умножения на R 2 принимает вид .
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется эллиптическим параболоидом (рис. 2.23) .
1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.
2. Эллиптический параболоид обладает
· осевой симметрией относительно оси 0z ,
· плоскостной симметрией относительно координатных осей 0xz и 0yz .
3. В сечении эллиптического параболоида плоскостью, ортогональной оси 0z , получается эллипс, а плоскостями, ортогональными осям 0x и 0y –парабола. (см. рис. 2.23).
Можно получить эллиптический параболоид симметричный относительно оси 0х или 0у, для чего нужно в уравнении (2.50) поменять между собой переменные х и z или у и z соответственно.
Если полуоси равны a = b , то параболоид называется параболоидом вращения и может быть получен вращением параболы вокруг ее оси симметрии. При этом в сечении параболоида вращения плоскостью, перпендикулярной оси 0z , получается окружность.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется гиперболическим параболоидом (рис . 2.24).
Свойства гиперболического параболоида.
1. Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
2. Гиперболический параболоид обладает
· осевой симметрией относительно оси 0z ,
· плоскостной симметрией относительно координатных плоскостей 0xz и 0yz .
4. Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.
5. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется однополостным гиперболоидом (рис. 2.25) .
Свойства однополостного гиперболоида.
1. Однополостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
2. Однополостный гиперболоид обладает
· центральной симметрией относительно начала координат,
· осевой симметрией относительно всех координатных осей,
· плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат 0z , получается эллипс, а плоскостями, ортогональными осям 0x и 0y, – гипербола (см. рис. 2.25).
Если в уравнении (2.52) a = b , то сечения однополостного гиперболоида плоскостями, параллельными плоскости х0у, являются окружностями. В этом случае поверхность называется однополостным гиперболоидом вращения.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
называется двуполостным гиперболоидом (рис. 2.26) .
1. Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что | z |≥ c и неограничен сверху.
2. Двуполостный гиперболоид обладает
· центральной симметрией относительно начала координат,
· осевой симметрией относительно всех координатных осей,
· плоскостной симметрией относительно всех координатных плоскостей.
3. В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат 0z , при | z |> c получается эллипс, при | z |= c – точка, а в сечении плоскостями, перпендикулярными осям 0x и 0y , – гипербола (см. рис. 2.26).
Если в уравнении (2.53) a = b , то сечения двуполостного гиперболоида плоскостями, параллельными плоскости х0у, являются окружностями. В этом случае поверхность называется двуполостным гиперболоидом вращения.
Примечание. Если уравнение поверхности в прямоугольной системе координат имеет вид: F ( x 2 + y 2 ; z )=0, то эта поверхность – поверхность вращения с осью вращения 0z. Аналогично: F ( x 2 + z 2 ; y )=0 – поверхность вращения с осью вращения 0у, F ( z 2 + y 2 ; x )=0 – с осью вращения 0х
С учетом данного примечания могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси 0х или 0у.
Цилиндрическая поверхность образуется движением прямой линии, скользящей по некоторой неподвижной замкнутой или незамкнутой кривой и остающейся параллельной своему исходному положению. Множество прямолинейных образующих представляет собой непрерывный каркас цилиндрической поверхности. Через каждую точку поверхности проходит одна прямолинейная образующая. Неподвижная кривая, по которой скользит образующая, называется направляющей. Если направляющая линия является кривой второго порядка, то и цилиндрическая поверхность – второго порядка.
Если уравнение поверхности не содержит в явном виде какой–либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение.
Достаточно нарисовать на плоскости х0у направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси 0z. Для наглядности следует построить также одно–два сечения плоскостями, параллельными плоскости х0у. В каждом таком сечении получим такую же кривую, как и исходная направляющая. Аналогично поступают, рассматривая направляющую в плоскости х0z или у0z.
Цилиндрическая поверхность является бесконечной в направлении своих образующих. Часть замкнутой цилиндрической поверхности, заключенная между двумя плоскими параллельными сечениями, называется цилиндром, а фигуры сечения – его основаниями. Сечение цилиндрической поверхности плоскостью, перпендикулярной ее образующим, называется нормальным. В зависимости от формы нормального сечения цилиндры бывают:
1) эллиптические – нормальное сечение представляет собой эллипс (рис. 2.27а), каноническое уравнение
2) круговые – нормальное сечение круг, при a = b = r уравнение
3) гиперболические – нормальное сечение гипербола (рис. 2.27б), каноническое уравнение
4) параболические – нормальное сечение парабола (рис. 2.27в), каноническое уравнение
5) общего вида – нормальное сечение кривая случайного вида.
Если за основание цилиндра принимается его нормальное сечение, цилиндр называют прямым (рис. 2.27). Если за основание цилиндра принимается одно из косых сечений, цилиндр называют наклонным. Например, наклонные сечения прямого кругового цилиндра являются эллипсами. Наклонные сечения прямого эллиптического цилиндра в общем случае – эллипсы. Однако его всегда можно пересечь плоскостью, наклонной к его образующим, таким образом, что в сечении получится круг.
Конической поверхностью называется поверхность, производимая движением прямой, перемещающейся в пространстве так, что она при этом постоянно проходит через неподвижную точку и пересекает данную линию. Данная прямая называется образующей, линия – направляющей, а точка – вершиной конической поверхности (рис. 2.28).
Конусом называется тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины, и плоскостью, пересекающей все образующие по ту же сторону от вершины. Часть конической поверхности, ограниченная этой плоскостью, называется боковой поверхностью, а часть плоскости, отсекаемая боковой поверхностью, – основанием конуса. Перпендикуляр, опущенный из вершины на плоскость основания, называется высотой конуса.
Конус называется прямым круговым, если его основание есть круг, а высота проходит через центр основания. Такой конус можно рассматривать как тело, происходящее от вращения прямоугольного треугольника, вокруг катета как оси. При этом гипотенуза описывает боковую поверхность, а катет – основание конуса.
В курсе геометрии общеобразовательной школы рассматривается только прямой круговой конус, который для краткости называется просто конусом.
Если вершина конуса расположена в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат, то уравнение эллиптического конуса имеет вид:
( a >0, b >0, c >0). (2.58)
При а = b конус становится круговым.
Примечание. По аналогии с коническими сечениями (аналогично теореме 2.1) существуют и вырожденные поверхности второго порядка. Так, уравнением второго порядка x 2 = 0 описывается пара совпадающих плоскостей, уравнением x 2 = 1 – пара параллельных плоскостей, уравнением x 2 – y 2 = 0 – пара пересекающихся плоскостей. Уравнение x 2 + y 2 + z 2 = 0 описывает точку с координатами (0;0;0). Существуют и другие вырожденные случаи. Полная теория поверхностей второго порядка рассматривается в курсе аналитической геометрии
http://lfirmal.com/poverhnosti-vtorogo-poryadka/
http://www.sites.google.com/site/vyssaamatem/kupit-ucastok/ii-10-poverhnosti-vtorogo-poradka
Содержание
- Понятие о поверхности второго порядка
- Общее уравнение поверхности второго порядка, основные определения
- Цилиндрические и конические поверхности
- Исследование формы поверхностей второго порядка методом сечений
- Поверхности второго порядка
- Сфера и ее уравнение
- Цилиндрические поверхности
- Цилиндры второго порядка
- Эллипсоид
- Гиперболоиды
- Параболоиды
- Конические поверхности
- Поверхность вращения
- Как построить график функции
- Трехмерные графики функции
- Принципы и способы построения графика функции
Понятие о поверхности второго порядка
Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению.
Общее уравнение поверхности второго порядка, основные определения
Поверхностью второго порядка называется множество точек пространства 


где 



Уравнение (10.27) называют общим уравнением поверхности второго порядка. Вид поверхности и ее расположение относительно координатных плоскостей зависит от значений параметров в (10.27).
Если не существует ни одной точки 
Поверхность называется вырожденной, если ее общее уравнение описывает точку, одну или две плоскости. К примеру:
уравнение точки в
уравнения двух плоскостей, параллельных
уравнения двух биссекторных плоскостей.
При изучении поверхностей второго порядка решаются две взаимно обратные основные задачи:
- по известным геометрическим свойствам точек поверхности составить уравнение соответствующей поверхности;
- по известным уравнением поверхности установить геометрические свойства ее точек.
Примером решения первой основной задачи является построение уравнения сферы (9.2). Уравнение других важнейших поверхностей рассматриваются ниже.
Цилиндрические и конические поверхности
Цилиндрической поверхностью, или просто цилиндром, называется поверхность, образованная движением прямой, перемещается параллельно самой себе вдоль фиксированной линии (кривой). Подвижную прямую называют образующей, а фиксированную кривую — направляющей цилиндрической поверхности. Направляющей может быть любая сомкнутая или разомкнутая линия.
Цилиндром второго порядка называется цилиндрическая поверхность, направляющей которой является кривая второго порядка: эллипс (круг), гипербола, парабола. Название цилиндра определяется названием его направляющей. Если образующая параллельна одной из координатных осей, а направляющая лежит в плоскости, перпендикулярной этой оси, то уравнение цилиндра совпадает с уравнением направляющей. При геометрической интерпретации изображается, как правило, часть поверхности между двумя плоскостями, перпендикулярными образующей.
К примеру:
уравнения эллиптического цилиндра (рис. 10.9 а)
уравнения гиперболического цилиндра (рис. 10.9 б)
уравнения параболического цилиндра (рис. 10.9 в).
Рис. 10.9
Отсутствие переменной 
в уравнениях следует считать равными нулю. Например, уравнение параболического цилиндра можно записать в виде: 
Если в уравнениях эллипса и гиперболы положить 
Конической поверхностью, или конусом, называется поверхность, образованная движением прямой, проходящей через заданную точку, вдоль фиксированной кривой. Подвижную прямую называют образующей, заданную точку — вершиной, а фиксированную кривую — направляющей конуса. Если образующей является кривая второго порядка, то поверхность называется конусом второго порядка.
На рис. 10.10 изображен конус второго порядка, определяется уравнением
Рис. 10.10
с вершиной в начале координат, направляющей которого является эллипс

Поверхность симметрична относительно начала координат, а координатные плоскости является ее плоскостями симметрии. Множество точек поверхности с неотъемлемыми (неположительные) аппликатами называется верхней (нижней) полостью конуса.
Если направляющей конуса является круг 
Эллипс, парабола, гипербола — кривые второго порядка — можно получить сечением прямого кругового конуса плоскостями, которые не проходят через его вершину (рис. 10.11).
А именно:
- если плоскость пересекает только одну полость конуса и непараллельных одной из его образующих, то кривой сечения является эллипс;
- в частном случае — круг;
- если секущая плоскость параллельна одной из образующих конуса, то результат сечения — парабола;
- если плоскость сечения пересекает обе полости конуса, то кривой сечения является гипербола.
Рис. 10.11
Исследование формы поверхностей второго порядка методом сечений
Приведенные выше уравнения поверхностей второго порядка складывались по геометрическим свойствам их точек в соответствии с определений поверхностей. Для решения обратной задачи (по данным уравнением поверхности определить ее вид) применяется метод сечений, суть которого заключается в следующем:
- анализируют поверхность, устанавливая за ее уравнением линии пересечения (сечения) данной поверхности координатными плоскостями параллельными им;
- синтезируют определенные на предыдущем шаге геометрические свойства поверхности, что позволяет представить вид поверхности и изобразить ее.
Продемонстрируем применение метода сечений к исследованию уравнения эллиптического параболоида:
Если:






то есть сечением поверхности плоскостями, параллельными 
(рис. 10.12);
- установим линию пересечения поверхности с плоскостью
:
Это уравнение параболы, расположенной в плоскости 

Рис. 10.12
Аналогично осуществляется построение параболоида 

Поверхностью вращения называется поверхность, для которой каждый из ее сечений плоскостью, перпендикулярной одной из координатных осей или произвольной оси 
прямой, проходящей через начало координат, а цилиндр — прямой, параллельной оси 
Уравнения поверхностей, симметричные относительно координатных осей или / и координатных плоскостей, называют каноническими, или стандартными.
В заключение отметим, что приведенные сведения используются при изучении интегрирования функций двух переменных и является фундаментом для более глубокого изучения теории поверхностей второго порядка.
Далее в таблице 10.1 приводятся канонические уравнения и изображения важнейших поверхностей второго порядка.
Важнейшие поверхности второго порядка Таблица 10.1
Поверхности второго порядка
Определение. Поверхности второго порядка называют геометрическое место точек пространства, декартовые координаты которых удовлетворяют уравнению второй степени.
Сфера и ее уравнение
Сферой называют геометрическое место точек пространства, равноудаленное от заданной точки — центра сферы.
- Если центром сферы является точка
а радиус
тогда уравнение сферы будет:
- Если центр сферы находится в начале координат
и радиус
тогда уравнение сферы будет:
Цилиндрические поверхности
Поверхность называется цилиндрической, если она образуется прямой (образующая), параллельно к заданной прямой
и которая проходит через заданную линию
(направляющая линия). Пример цилиндрической линии изображен на рис. 2.24
Если образующая цилиндрической поверхности параллельна оси 



Уравнение 


Цилиндры второго порядка
- Эллиптичным цилиндром называется поверхность (рис. 2.25), каноничное уравнение которой имеет вид:
Если 
- Гиперболичным цилиндром называется поверхность, уравнение которой имеет вид (рис. 2.26):
- Параболическим цилиндром называется поверхность, каноничное уравнение которой имеет вид (рис. 2.27):
Эллипсоид
Эллипсоидом называется поверхность, каноничное уравнение которой имеет вид (рис. 2.28):
Отрезки
— называются полуосями эллипсоида.
Гиперболоиды
- Однополосным гиперболоидом (рис. 2.29) называется поверхность, каноническое уравнение которой имеет вид :
- Двуполостный гиперболоид. Двуполостным гиперболоидом (рис. 2.30) называется поверхность, каноничное уравнение которой имеет вид:
Параболоиды
Конические поверхности
конической поверхностью называется поверхность, которая описана прямой, что проходит через точку — вершину конуса — и что
пересекает заданную линию — направляющую конуса.
Уравнение конуса (рис. 2.33) второго порядка имеет вид:
Поверхность вращения
Пусть в плоскости 

Тогда чтобы получить уравнение поверхности, что образована вращением линии 




Аналогично правила будут иметь место и по отношению к поверхностям, которые образуют обращение плоских линий около других координатных осей.
Примеры:
Примеры решения задач:
Задача 2.126
Обозначить координаты центра сферы и ее радиус:
Решение. Предоставим заданное уравнение в виде (2.43), для этого:
- объединяем в группы члены, которые содержат одноименные координаты;
- выделим в группах полные квадраты. Получим:
Соизмеряя с (2.43), получим
Следует, центр сферы — точка 
Задача 2.127
Эллипс с полуосями 5 и 3 вращается около своей большей оси. которая совпадает с началом координат. Сложить уравнение поверхности, что описывает эллипс при вращении.
Решение. Сложим каноническое уравнение эллипса с центром в начале координат, который размещен в плоскости
чтобы получить уравнение поверхности, которая образована вращением в плоскости 
необходимо в уравнении эллипса заменить 
Получим эллипсоид вращения, который протянул вдоль оси
или
Задача 2.128
Сложим уравнение конуса с вершиной в начале координат и направляющей:
Решение. Канонические уравнения образующих, что проходят через вершину 

Исключим 







или
Задача 2.129
Какие поверхности обозначаются уравнениями:
Решение. Каждое из уравнений содержит только две переменные 


- круг,
- эллипс,
- параболу,
- гиперболу.
В пространстве же каждое из них обозначается цилиндрическую поверхность с образующими, что параллельны оси 

— уравнение прямого углового цилиндра;
— уравнение эллиптического цилиндра;
— уравнение параболического цилиндра;
— уравнение гиперболичного цилиндра.
Задача 2.130
Гипербола с полуосями 3 и 4 вращается около своей мнимой оси, которая совпадает с осью
Центры гиперболы совпадает с началом координат. Сложить уравнение поверхности, которое получим при вращении гиперболы.
Решение. Сложим каноничное уравнение гиперболы с центром в начале координат, что находятся в плоскости
Чтобы сложить уравнение поверхности, образованной вращением гиперболы, что находится в уравнение гиперболы вместо
подставить
или
Следует, получим однополосный гиперболоид вращения:
Как построить график функции
Трехмерные графики функции
Построить графики (в том числе и трехмерные) можно также, используя следующий сервис. Например, построить график функцииcosx + esinx+x3. Записываем как cos(x)+exp((sin(x)+x^3)) и нажимаем кнопку Построить график.
Чтобы построит два графика в одних координатах, например, y=3x-1, y=x2-2x+5, указываем: 3*x-1,x^2-2*x+5. Также можно задать пределы отображения по оси X (ось абсцисс).
Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3).
f(x)=Пределы по x = ..
Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3).
Также можно начертить график по точкам. Необходимо вставить данные для X (первый столбец) и Y (второй и последующие столбцы). <текстареа name=»TEXTEXCEL» rows=»10″ class=»form-control»>
Построение графика функции в Excel осуществляется в два этапа:
- На первом этапе при заданном интервале [a;b] и шаге h рассчитываются значения функции y=f(x).
- На втором этапе с помощью инструмента ExcelМастер диаграмм строится визуализация рассчитанных значений.
Чтобы построить трехмерный график в Excel, необходимо указать функцию f(x,y), пределы по x и y и шаг сетки h.
f(x,y)=x= .. y= .. h=
Принципы и способы построения графика функции
График любой функции можно построить прямыми вычислениями значения функции y=f(x) и методом дифференциального исчисления.
- При прямом вычислении значений функции y=f(x) необходимо задать интервал [a;b] вычислений и шаг h. Получается таблица, по которой можно построить график.
Например, определим для функции y=x*e2x/3+4 интервал [-3;7], на котором будем отображать найденные точки. Чем меньше шаг h, тем точнее график функции (другими словами, тем точнее аппроксимация). Например, при h=2 количество точек для построения равно N=(7-(-3))/2+1=6 (-3; -1; 1; 3; 5; 7), а при h=0.1 уже N=(7-(-3))/0.1+1=101. - Построение графика функции методом дифференциального исчисления предполагает схематичное построение, используя свойства функции.



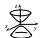




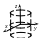
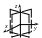
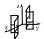




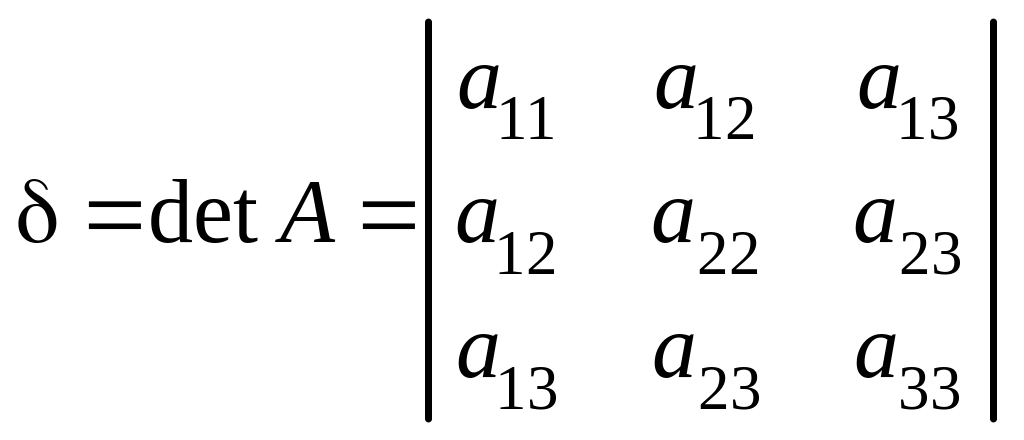
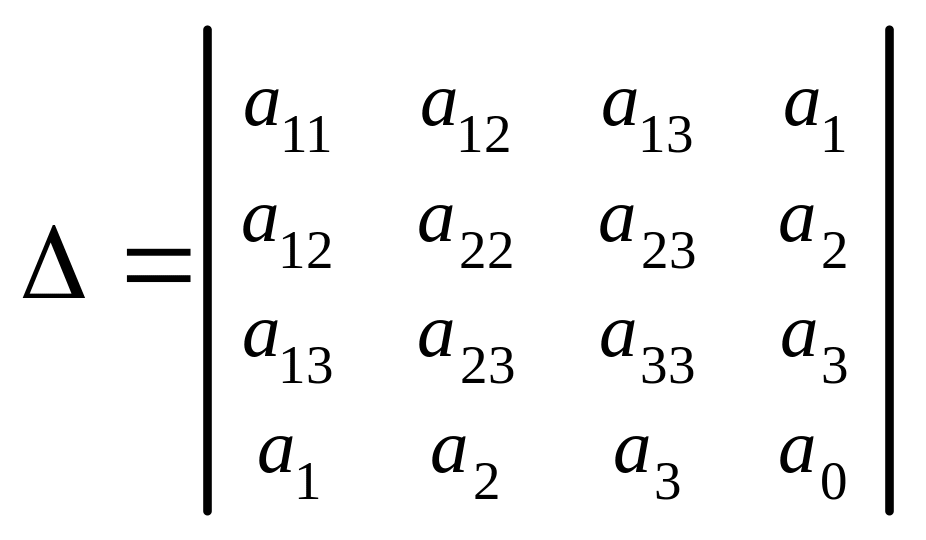
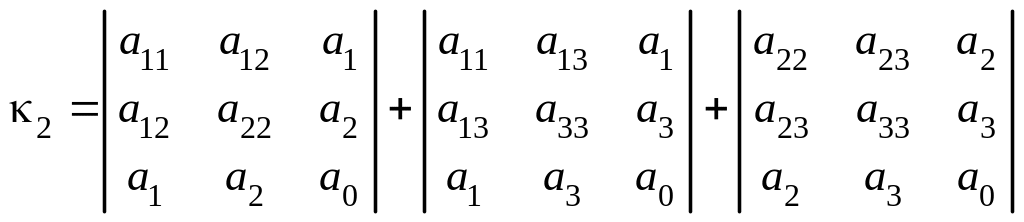
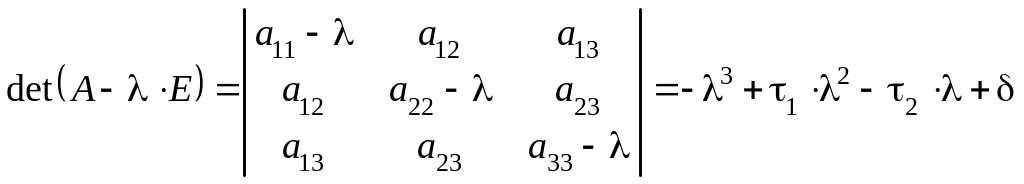
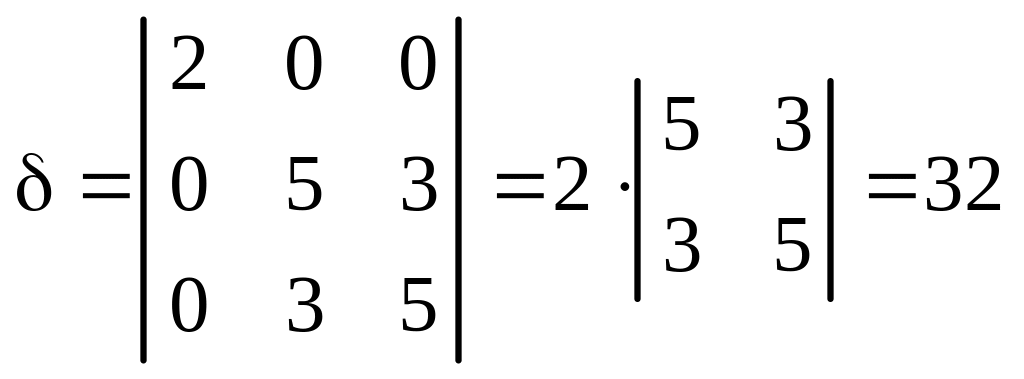
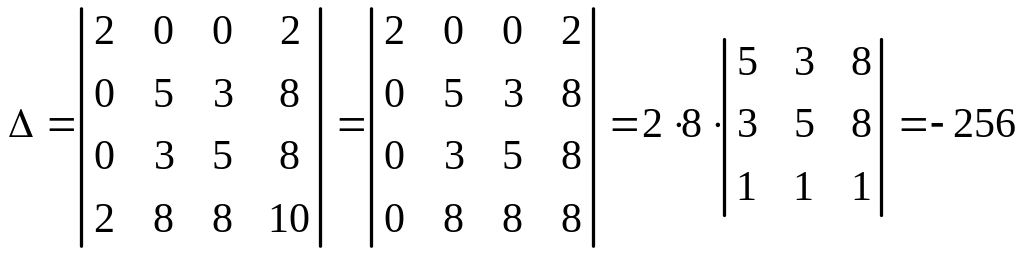
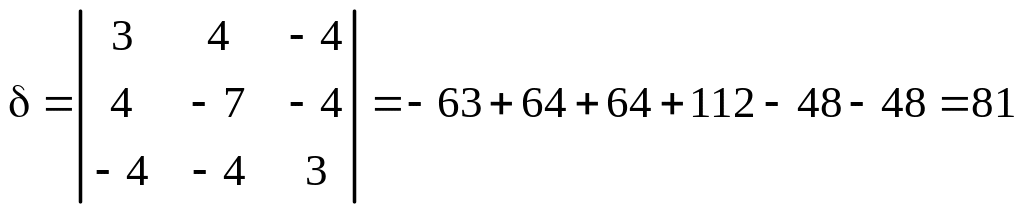

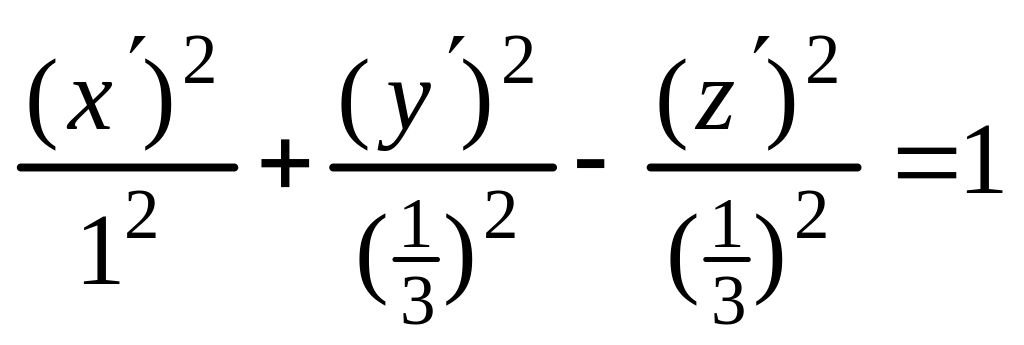
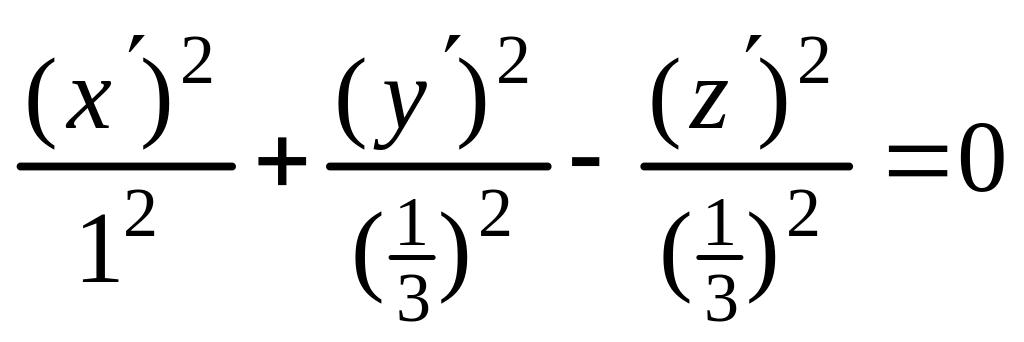
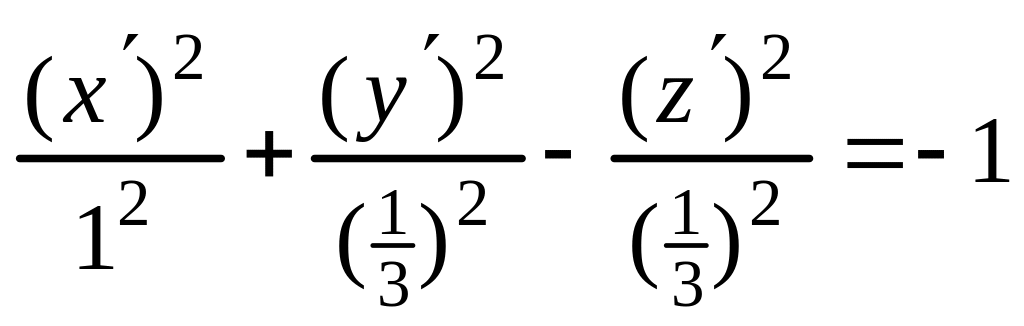
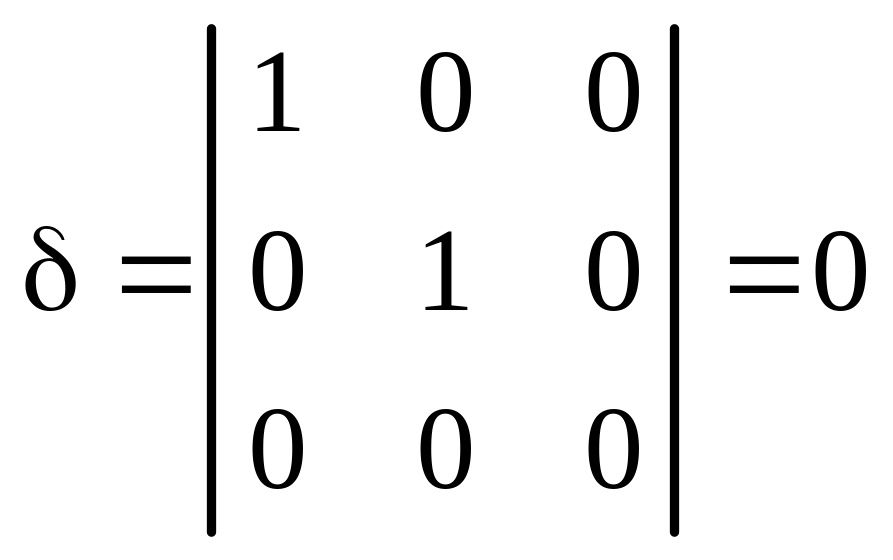



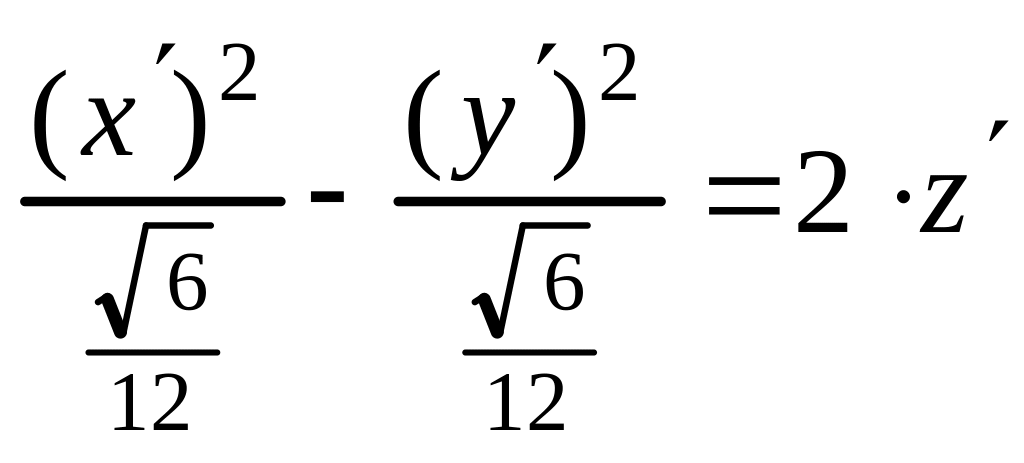
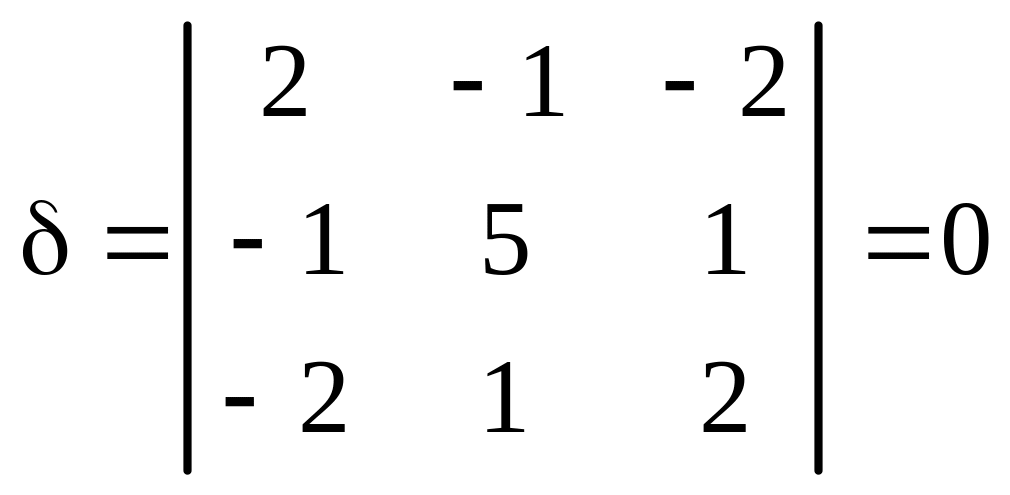


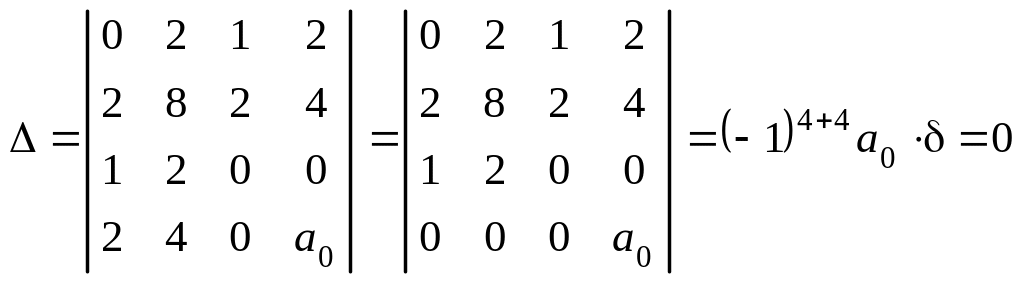
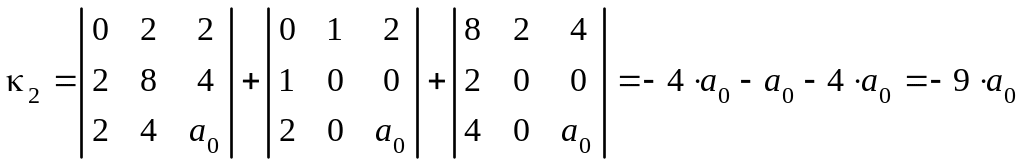


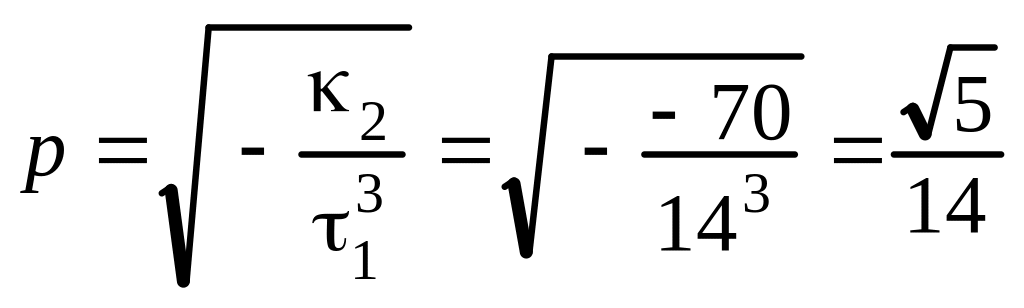
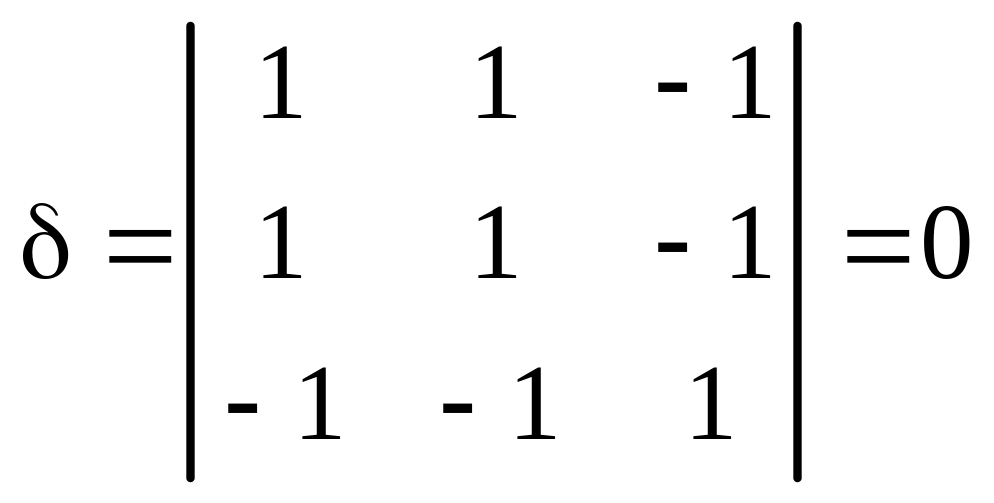
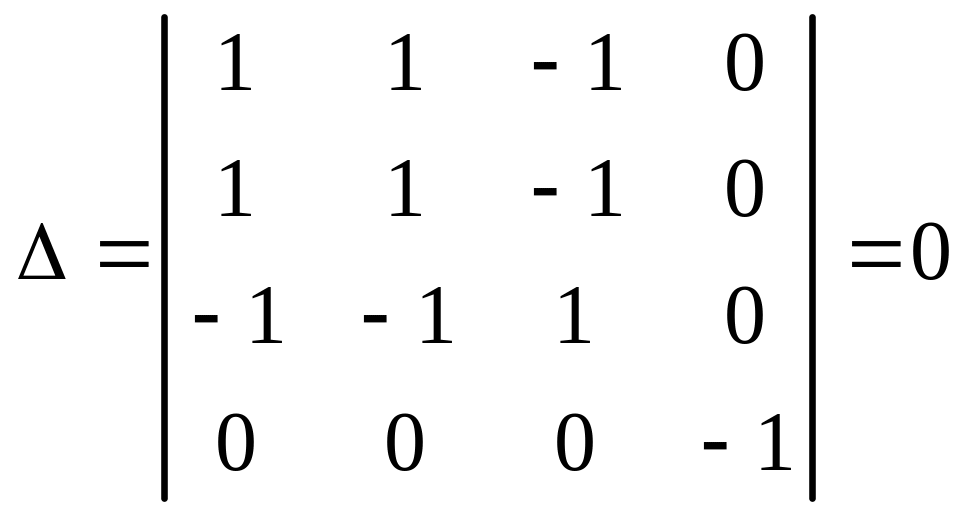
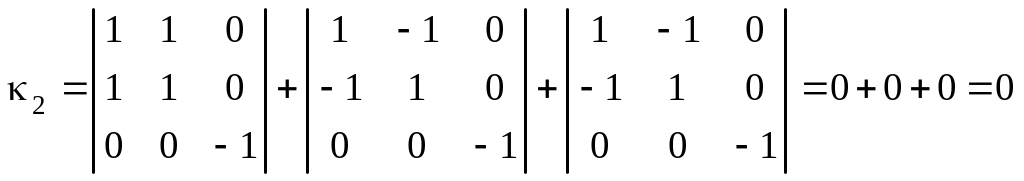
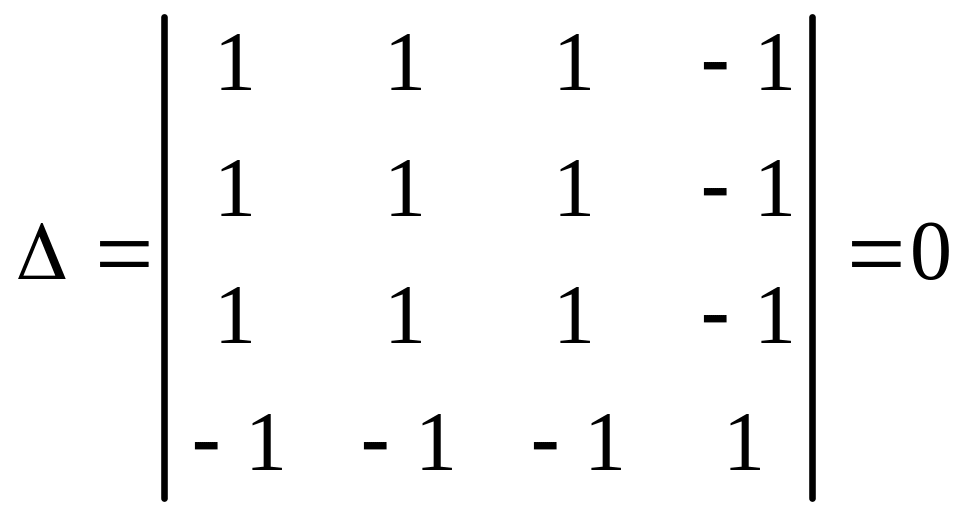
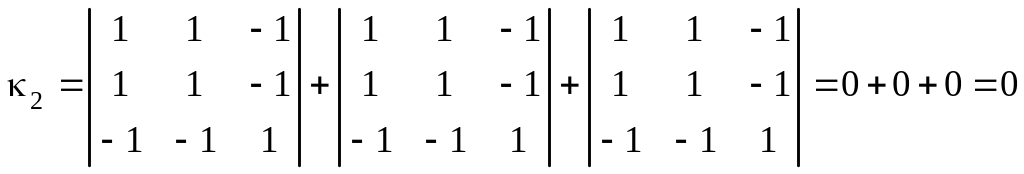




















 :
:



 а радиус
а радиус  тогда уравнение сферы будет:
тогда уравнение сферы будет:
 и радиус
и радиус  тогда уравнение сферы будет:
тогда уравнение сферы будет: 













 — называются полуосями эллипсоида.
— называются полуосями эллипсоида.




































