Как найти карманы в excel

Гистограмма распределения — это инструмент, позволяющий визуально оценить величину и характер разброса данных. Создадим гистограмму для непрерывной случайной величины с помощью встроенных средств MS EXCEL из надстройки Пакет анализа и в ручную с помощью функции

ЧАСТОТА()

и диаграммы.

Гистограмма (frequency histogram) – это

столбиковая диаграмма MS EXCEL

, в каждый столбик представляет собой интервал значений (корзину, карман, class interval, bin, cell), а его высота пропорциональна количеству значений в ней (частоте наблюдений).

Гистограмма поможет визуально оценить распределение набора данных, если:

• в наборе данных как минимум 50 значений;
• ширина интервалов одинакова.

Построим гистограмму для набора данных, в котором содержатся значения

непрерывной случайной величины

. Набор данных (50 значений), а также рассмотренные примеры, можно взять на листе

Гистограмма AT

в

файле примера.

Данные содержатся в диапазоне

А8:А57

.

Примечание

: Для удобства написания формул для диапазона

А8:А57

создан

Именованный диапазон

Исходные_данные.

Построение гистограммы с помощью надстройки

Пакет анализа

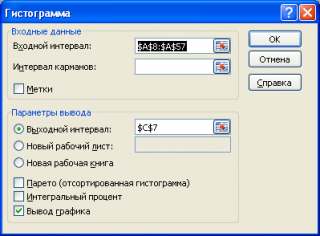
Вызвав диалоговое окно

надстройки Пакет анализа

, выберите пункт

Гистограмма

и нажмите ОК.

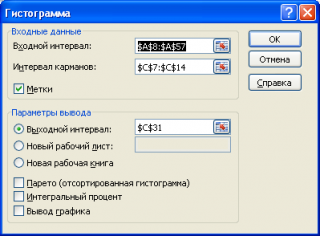
В появившемся окне необходимо как минимум указать:

входной интервал

и левую верхнюю ячейку

выходного интервала

. После нажатия кнопки

ОК

будут:

• автоматически рассчитаны интервалы значений (карманы);
• подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
• если поставлена галочка напротив пункта
  
  Вывод графика
  
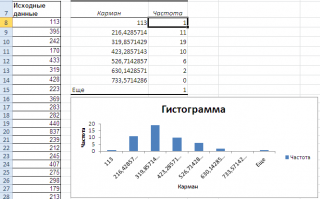
  , то вместе с таблицей частот будет выведена гистограмма.

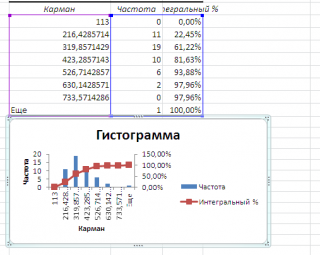
Перед тем как анализировать полученный результат —

отсортируйте исходный массив данных

.

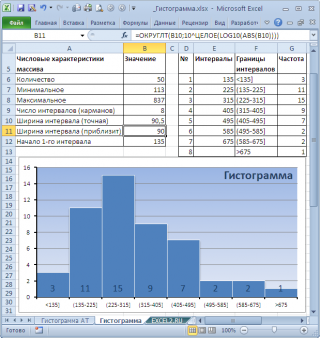
Как видно из рисунка, первый интервал включает только одно минимальное значение 113 (точнее, включены все значения меньшие или равные минимальному). Если бы в массиве было 2 или более значения 113, то в первый интервал попало бы соответствующее количество чисел (2 или более).

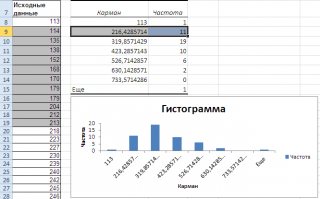
Второй интервал (отмечен на картинке серым) включает значения больше 113 и меньше или равные 216,428571428571. Можно проверить, что таких значений 11. Предпоследний интервал, от 630,142857142857 (не включая) до 733,571428571429 (включая) содержит 0 значений, т.к. в этом диапазоне значений нет. Последний интервал (со странным названием

Еще

) содержит значения больше 733,571428571429 (не включая). Таких значений всего одно — максимальное значение в массиве (837).

Размеры карманов одинаковы и равны 103,428571428571. Это значение можно получить так:

=(МАКС(

Исходные_данные

)-МИН(

Исходные_данные

))/7

где

Исходные_данные –

именованный диапазон

, содержащий наши данные.

Почему 7? Дело в том, что количество интервалов гистограммы (карманов) зависит от количества данных и для его определения часто используется формула √n, где n – это количество данных в выборке. В нашем случае √n=√50=7,07 (всего 7 полноценных карманов, т.к. первый карман включает только значения равные минимальному).

Примечание

:

Похоже, что инструмент

Гистограмма

для подсчета общего количества интервалов (с учетом первого) использует формулу

=ЦЕЛОЕ(КОРЕНЬ(СЧЕТ(

Исходные_данные

)))+1

Попробуйте, например, сравнить количество интервалов для диапазонов длиной 35 и 36 значений – оно будет отличаться на 1, а у 36 и 48 – будет одинаковым, т.к. функция

ЦЕЛОЕ()

округляет до ближайшего меньшего целого

(ЦЕЛОЕ(КОРЕНЬ(35))=5

, а

ЦЕЛОЕ(КОРЕНЬ(36))=6)

.

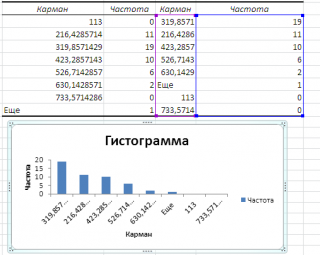
Если установить галочку напротив поля

Парето (отсортированная гистограмма)

, то к таблице с частотами будет добавлена таблица с отсортированными по убыванию частотами.

Если установить галочку напротив поля

Интегральный процент

, то к таблице с частотами будет добавлен столбец с

нарастающим итогом

в % от общего количества значений в массиве.

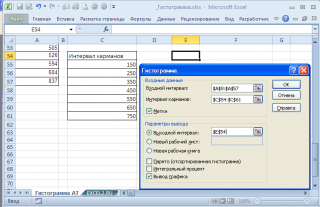
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов (если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля

Метка

).

Для нашего набора данных установим размер кармана равным 100 и первый карман возьмем равным 150.

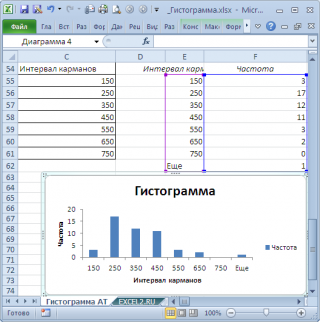
В результате получим практически такую же по форме

гистограмму

, что и раньше, но с более красивыми границами интервалов.

Как видно из рисунков выше, надстройка

Пакет анализа

не осуществляет никакого

дополнительного форматирования диаграммы

. Соответственно, вид такой гистограммы оставляет желать лучшего (столбцы диаграммы обычно располагают вплотную для непрерывных величин, кроме того подписи интервалов не информативны). О том, как придать диаграмме более презентабельный вид, покажем в следующем разделе при построении

гистограммы

с помощью функции

ЧАСТОТА()

без использовании надстройки

Пакет анализа

.

Построение гистограммы распределения без использования надстройки Пакет анализа

Порядок действий при построении гистограммы в этом случае следующий:

• определить количество интервалов у гистограммы;
• определить ширину интервала (с учетом округления);
• определить границу первого интервала;
• сформировать таблицу интервалов и рассчитать количество значений, попадающих в каждый интервал (частоту);
• построить гистограмму.

СОВЕТ

: Часто рекомендуют, чтобы границы интервала были на один порядок точнее самих данных и оканчивались на 5. Например, если данные в массиве определены с точностью до десятых: 1,2; 2,3; 5,0; 6,1; 2,1, …, то границы интервалов должны быть округлены до сотых: 1,25-1,35; 1,35-1,45; … Для небольших наборов данных вид гистограммы сильно зависит количества интервалов и их ширины. Это приводит к тому, что сам метод гистограмм, как инструмент

описательной статистики

, может быть применен только для наборов данных состоящих, как минимум, из 50, а лучше из 100 значений.

В наших расчетах для определения количества интервалов мы будем пользоваться формулой

=ЦЕЛОЕ(КОРЕНЬ(n))+1

.

Примечание

: Кроме использованного выше правила (число карманов = √n), используется ряд других эмпирических правил, например, правило Стёрджеса (Sturges): число карманов =1+log2(n). Это обусловлено тем, что например, для n=5000, количество интервалов по формуле √n будет равно 70, а правило Стёрджеса рекомендует более приемлемое количество — 13.

Расчет ширины интервала и таблица интервалов приведены в

файле примера на листе Гистограмма

. Для вычисления количества значений, попадающих в каждый интервал, использована

формула массива

на основе функции

ЧАСТОТА()

. О вводе этой функции см. статью

Функция ЧАСТОТА() — Подсчет ЧИСЛОвых значений в MS EXCEL

.

В MS EXCEL имеется диаграмма типа

Гистограмма с группировкой

, которая обычно используется для построения

Гистограмм распределения

.

В итоге можно добиться вот такого результата.

Примечание

: О построении и настройке макета диаграмм см. статью

Основы построения диаграмм в MS EXCEL

.

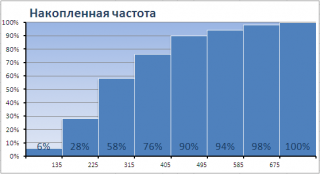
Одной из разновидностей гистограмм является

график накопленной частоты

(cumulative frequency plot).

На этом графике каждый столбец представляет собой число значений исходного массива, меньших или равных правой границе соответствующего интервала. Это очень удобно, т.к., например, из графика сразу видно, что 90% значений (45 из 50) меньше чем 495.

СОВЕТ

: О построении

двумерной гистограммы

см. статью

Двумерная гистограмма в MS EXCEL

.

Примечание

: Альтернативой

графику накопленной частоты

может служить

Кривая процентилей

, которая рассмотрена в

статье про Процентили

.

Примечание

: Когда количество значений в выборке недостаточно для построения полноценной

гистограммы

может быть полезна

Блочная диаграмма

(иногда она называется

Диаграмма размаха

или

Ящик с усами

).

При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы «от и до» (в статистике их называют «карманы»). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:

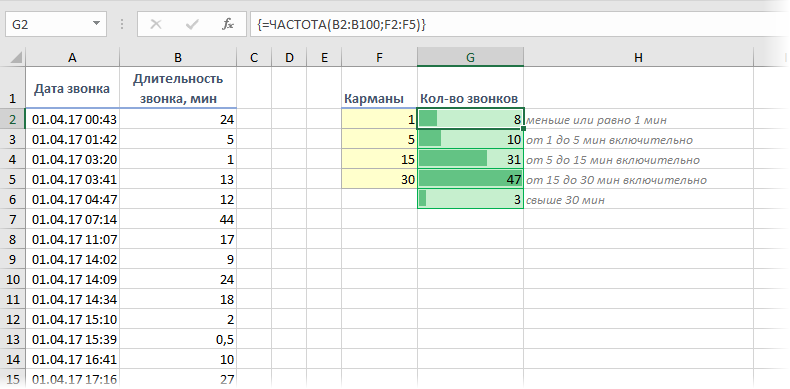
Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY). Ее синтаксис прост:

=ЧАСТОТА(Данные; Карманы)

где

• Карманы — диапазон с границами интервалов, попадание в которые нас интересует
• Данные — диапазон с исходными числовыми значениями, которые мы анализируем

Обратите внимание, что эта функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.

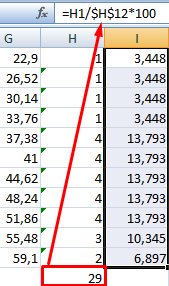
Для использования функции ЧАСТОТА нужно:

1. заранее подготовить ячейки с интересующими нас интервалами-карманами (желтые F2:F5 в нашем примере)
2. выделить пустой диапазон ячеек (G2:G6) по размеру на одну ячейку больший, чем диапазон карманов (F2:F5) 
3. ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива

Во всех предварительно выделенных ячейках посчитается количество попаданий в заданные интервалы. Само-собой, для реализации подобной задачи можно использовать и другие способы (функцию СЧЁТЕСЛИ, сводные таблицы и т.д.), но этот вариант весьма хорош.

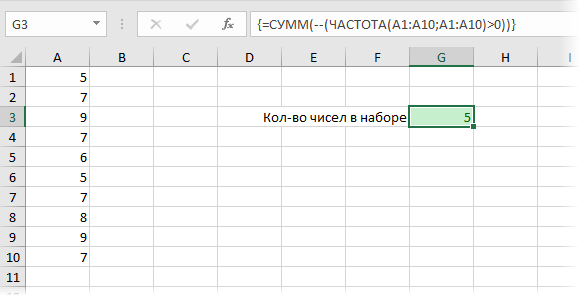
Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:

Ссылки по теме

• Как подсчитать количество уникальных элементов в списке
• Как сделать список без повторений
• Частотный анализ данных с помощью сводных таблиц и формул

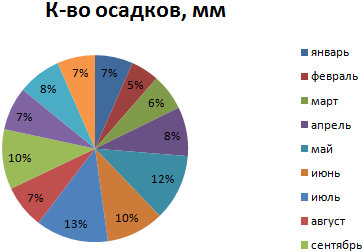
Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.

Как построить диаграмму распределения в Excel

График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.

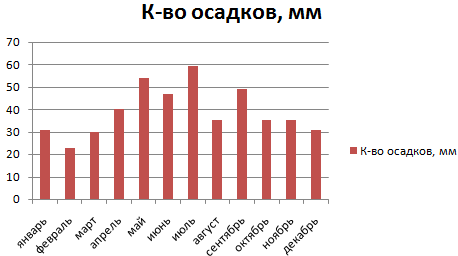
Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.

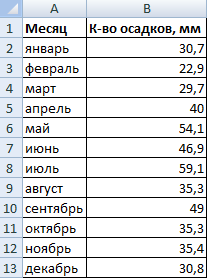
Имеются следующие данные о количестве выпавших осадков:

Первый способ. Открываем меню инструмента «Анализ данных» на вкладке «Данные» (если у Вас не подключен данный аналитический инструмент, тогда читайте как его подключить в настройках Excel):

Выбираем «Гистограмма»:

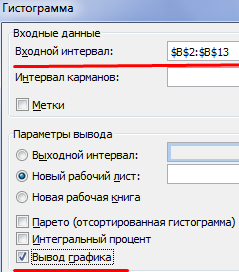
Задаем входной интервал (столбец с числовыми значениями). Поле «Интервалы карманов» оставляем пустым: Excel сгенерирует автоматически. Ставим птичку около записи «Вывод графика»:

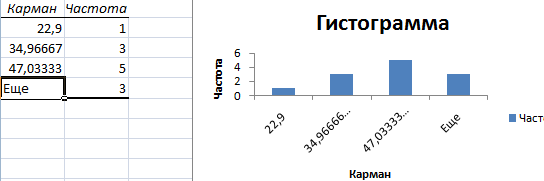
После нажатия ОК получаем такой график с таблицей:

В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.



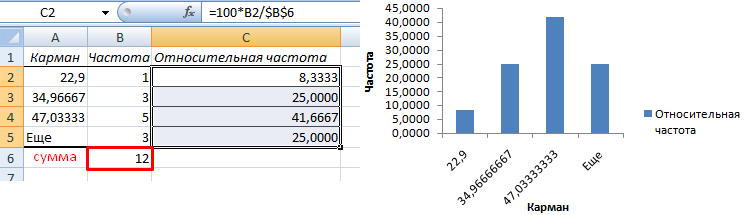
Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.

Найдем сумму всех абсолютных частот (с помощью функции СУММ). Сделаем дополнительный столбец «Относительная частота». В первую ячейку введем формулу:

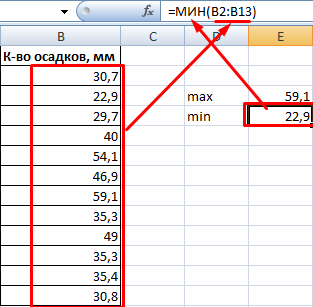
Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.

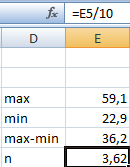
Чтобы найти интервал карманов, нужно разность максимального и минимального значений массива разделить на количество интервалов. Получим «ширину кармана».

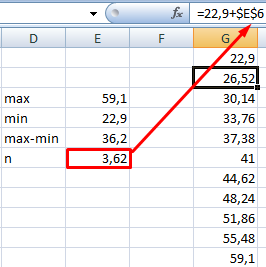
Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.

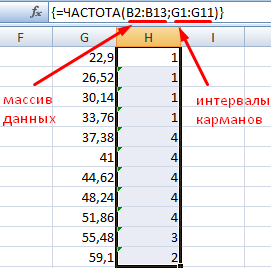
Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:

Вычислим относительные частоты (как в предыдущем способе).

Построим столбчатую диаграмму распределения осадков в Excel с помощью стандартного инструмента «Диаграммы».

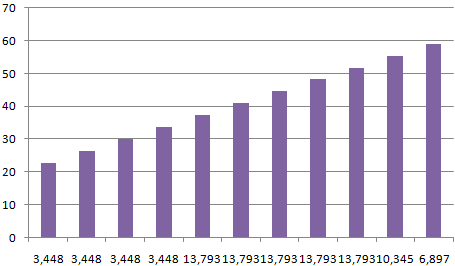
Частота распределения заданных значений:

Круговые диаграммы для иллюстрации распределения

С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.

С помощью любой круговой диаграммы можно показать распределение в том случае, если

• имеется только один ряд данных;
• все значения положительные;
• практически все значения выше нуля;
• не более семи категорий;
• каждая категория соответствует сегменту круга.

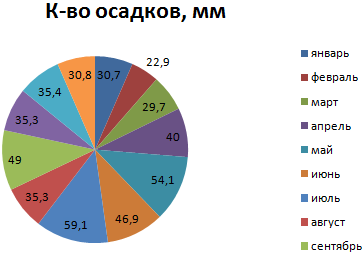
На основании имеющихся данных о количестве осадков построим круговую диаграмму.

Доля «каждого месяца» в общем количестве осадков за год:

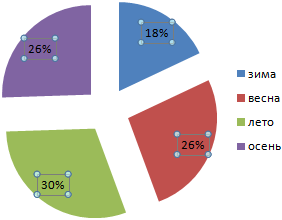
Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:

Получили количество выпавших осадков в процентном выражении по сезонам.

Частотный анализ по интервалам функцией ЧАСТОТА (FREQUENCY)

При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы «от и до» (в статистике их называют «карманы»). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:

Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY) . Ее синтаксис прост:

=ЧАСТОТА( Данные ; Карманы )

• Карманы — диапазон с границами интервалов, попадание в которые нас интересует
• Данные — диапазон с исходными числовыми значениями, которые мы анализируем

Обратите внимание, что эта функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.

Для использования функции ЧАСТОТА нужно:

1. заранее подготовить ячейки с интересующими нас интервалами-карманами (желтые F2:F5 в нашем примере)
2. выделить пустой диапазон ячеек (G2:G6) по размеру на одну ячейку больший, чем диапазон карманов (F2:F5)
3. ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива

Во всех предварительно выделенных ячейках посчитается количество попаданий в заданные интервалы. Само-собой, для реализации подобной задачи можно использовать и другие способы (функцию СЧЁТЕСЛИ, сводные таблицы и т.д.), но этот вариант весьма хорош.

Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:

Сведение и группировка статистических данных

Цель работы – получить навыки группировки данных в MS Excel.

Задание – сгруппировать статистические данные с помощью надстройки Excel “Анализ данных”

Сведение и группировка статистической информации целесообразно проводить с помощью модуля “Гистограмма” пристройки “Анализ”.

Режим “Гистограмма” служит для вычисления частот попадания данных в указанные границы интервалов, и так же для построения гистограммы интервального вариационного ряда распределения.

В диалоговом окне этого режима

задаются следующие параметры:

1. Входной интервал – вводятся ссылки на ячейки, которые содержат данные для анализа.

2. “Интервал карманов” (необязательный параметр) – вводится ссылки на ячейки, которые содержат набор граничных значений, которые определяют интервалы (карманы). Эти значения должны быть введены в возрастающем порядке. В MS Excel вычисляется число попаданий данных в сформированные интервал, при этом границы интервалов являются строгими нижними границами и нестрогими верхними.

Если диапазон карманов не был введен, то набор интервалов, равномерно распределенных между минимальными и максимальными значениями данных, будет создан автоматически.

3. Метки устанавливаются в активное положение, если первый ряд или столбец во входном диапазоне содержит заголовки. Если заголовки отсутствуют, флажок нужно деактивировать. В этом случае будут автоматически созданы стандартные названия данных выходного диапазона.

4. Выходной интервал/Новый рабочий лист/Новая рабочая книга – активируется поле, в которое необходимо ввести ссылку на левую верхнюю ячейку выходного диапазона.

5. Парето (отсортированная гистограмма) – устанавливается в активное положение, если нужно представить данные в порядке убывания частоты. Если флажок снят, то данные в выходном диапазоне будут приведены в порядке следования интервалов.

6. Интегральный процент – устанавливается в активное положение для расчета выраженных в процентах накопленных частот (накопленных частностей) и включения в гистограмму графика кумуляты.

7. Вывод графика – устанавливается в активное положение для автоматического создания встроенной диаграммы на листе, который содержит выходной диапазон.

Пример анализа статистических данных в Excel

Объем экспорта по регионам Украины за 2009 год приведен ниже.