было в ЕГЭ
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 120 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
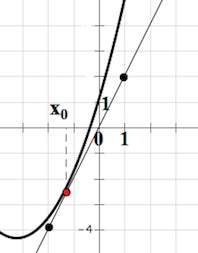
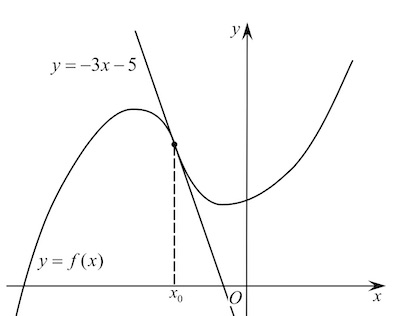
Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
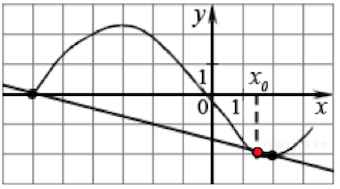
Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
Прямая параллельна касательной к графику функции
Найдите абсциссу точки касания.
Прямая является касательной к графику функции
Найдите абсциссу точки касания.
Прямая является касательной к графику функции
Найдите абсциссу точки касания.
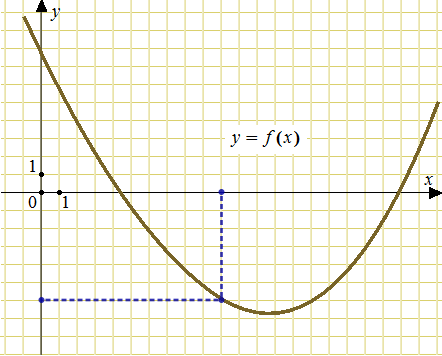
На рисунке изображен график функции y=f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 12 или совпадает с ней.
На рисунке изображен график производной функции f(x), определенной на интервале (−9; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −x − 12 или совпадает с ней.
На рисунке изображен график производной функции f(x), определенной на интервале (−9; 3). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = 2x − 19 или совпадает с ней.
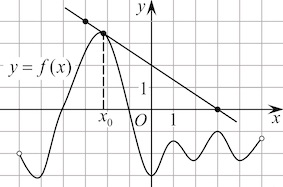
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке
Всего: 120 1–20 | 21–40 | 41–60 | 61–80 …
Геометрический смысл производной
Если плохо разбираешься в производной, то вот тебе полноценный гид по ней, с текстом, примерами и вебинарами: «Производная функции – геометрический смысл и правила дифференцирования»!
Рассмотрим график какой-то функции ( y=fleft( x right)):
Выберем на линии графика некую точку ( A). Пусть ее абсцисса ( {{x}_{0}}), тогда ордината равна ( fleft( {{x}_{0}} right)).
Затем выберем близкую к точке ( A) точку ( B) с абсциссой ( {{x}_{0}}+Delta x); ее ордината – это ( fleft( {{x}_{0}}+Delta x right)):
Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).
Обозначим угол наклона прямой к оси ( Ox) как ( alpha ).
Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.
Какие значения может принимать угол ( alpha )?
Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – ( 180{}^circ ), а минимально возможный – ( 0{}^circ ).
Значит, ( alpha in left[ 0{}^circ ;180{}^circ right)). Угол ( 180{}^circ ) не включается, поскольку положение прямой в этом случае в точности совпадает с ( 0{}^circ ), а логичнее выбирать меньший угол.
Возьмем на рисунке такую точку ( C), чтобы прямая ( AC) была параллельна оси абсцисс, а ( BC) – ординат:
По рисунку видно, что ( AC=Delta x), а ( BC=Delta f).
Тогда отношение приращений:
( frac{Delta f}{Delta x}=frac{BC}{AC}={tg}alpha )
(так как ( angle C=90{}^circ ), то ( triangle ABC) – прямоугольный).
Давай теперь уменьшать ( Delta x).
Тогда точка ( B) будет приближаться к точке ( A). Когда ( Delta x) станет бесконечно малым ( left( Delta xto 0 right)), отношение ( frac{Delta f}{Delta x}) станет равно производной функции в точке ( {{x}_{0}}).
Что же при этом станет с секущей?
Точка ( B) будет бесконечно близка к точке ( A), так что их можно будет считать одной и той же точкой.
Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки ( A), но этого достаточно).
Говорят, что при этом секущая занимает предельное положение.
Угол наклона секущей к оси ( displaystyle Ox) назовем ( varphi ). Тогда получится, что производная
( {f}’left( {{x}_{0}} right)underset{Delta xto 0}{mathop{=}},frac{Delta f}{Delta x}= {tg}varphi ),
то есть
Производная равна тангенсу угла наклона касательной к графику функции в данной точке
Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:
( y=kx+b).
За что отвечает коэффициент ( displaystyle k)? За наклон прямой. Он так и называется: угловой коэффициент.
Что это значит? А то, что равен он тангенсу угла между прямой и осью ( displaystyle Ox)!
То есть вот что получается:
( {f}’left( {{x}_{0}} right)= {tg}varphi =k).
Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?
Посмотрим: Теперь углы ( alpha ) и ( displaystyle varphi ) тупые. А приращение функции ( Delta f) – отрицательное.
Снова рассмотрим ( triangle ABC): ( angle B=180{}^circ -alpha text{ }Rightarrow text{ } {tg}angle B=- {tg}alpha ).
С другой стороны, ( {tg}angle B=frac{AC}{BC}=frac{-Delta f}{Delta x}).
Получаем: ( frac{-Delta f}{Delta x}=- {tg}alpha text{ }Rightarrow text{ }frac{Delta f}{Delta x}= {tg}alpha ), то есть все, как и в прошлый раз.
Снова устремим точку ( displaystyle B) к точке ( displaystyle A), и секущая ( displaystyle AB) примет предельное положение, то есть превратится в касательную к графику функции в точке ( displaystyle A).
Итак, сформулируем окончательно полученное правило:
Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:
( {f}’left( {{x}_{0}} right)= {tg}varphi =k)
Это и есть геометрический смысл производной.
Окей, все это интересно, но зачем оно нам? Вот пример:
На рисунке изображен график функции ( displaystyle y=mathsf{f}left( x right)) и касательная к нему в точке с абсциссой ( {{x}_{0}}).
Найдите значение производной функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}).
Решение.
Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:
( displaystyle f’left( x right)=k= {tg}varphi).
Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной.
На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!
Угол наклона касательной к оси ( displaystyle Ox) – это ( displaystyle angle BAC). Найдем тангенс этого угла:
( displaystyle {tg}angle BAC=frac{BC}{AC}=frac{6}{5}=1,2).
Таким образом, производная функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}) равна ( displaystyle 1,2).
Ответ: ( displaystyle 1,2).
Теперь попробуй сам.
Уравнение касательной к графику функций
А сейчас сосредоточимся на произвольных касательных.
Предположим, у нас есть какая-то функция, например, ( fleft( x right)=left( {{x}^{2}}+2 right)). Мы нарисовали ее график и хотим провести касательную к нему в какой-нибудь точке ( {{x}_{0}}). Например, в точке ( {{x}_{0}}=2).
Берем линейку, пристраиваем ее к графику и чертим:
Что мы знаем об этой прямой? Что самое важное нужно знать о прямой на координатной плоскости?
Поскольку прямая – это изображение линейной функции, очень удобно было бы знать ее уравнение. То есть коэффициенты ( k) и ( b) в уравнении
( y=kx+b).
Но ведь ( k) мы уже знаем! Это угловой коэффициент касательной, который равен производной функции в этой точке:
( k={f}’left( {{x}_{0}} right)).
В нашем примере будет так:
( {f}’left( x right)={{left( {{x}^{2}}+2 right)}^{prime }}=2x;)
( k={f}’left( {{x}_{0}} right)={f}’left( 2 right)=2cdot 2=4.)
Теперь остается найти ( b) . Это проще простого: ведь ( b) – значение ( y) при ( displaystyle x=0).
Графически ( b) – это координата пересечения прямой с осью ординат (ведь ( displaystyle x=0) во всех точках оси ( displaystyle Oy)):
Проведём ( BCparallel Ox) (так, что ( triangle ABC) – прямоугольный).
Тогда ( angle ABC=alpha )(тому самому углу между касательной и осью абсцисс). Чему равны ( displaystyle AC) и ( displaystyle BC)?
По рисунку явно видно, что ( BC={{x}_{0}}), а ( AC=fleft( {{x}_{0}} right)-b). Тогда получаем:
( {f}’left( {{x}_{0}} right)= {tg}alpha =frac{AC}{BC}=frac{fleft( {{x}_{0}} right)-b}{{{x}_{0}}}text{ }Rightarrow text{ }b=fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right)).
Соединяем все полученные формулы в уравнение прямой:
( y=kx+b={f}’left( {{x}_{0}} right)cdot x+fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right);)
( y={f}’left( {{x}_{0}} right)cdot left( x-{{x}_{0}} right)+fleft( {{x}_{0}} right))
Это и есть уравнение касательной к графику функции ( fleft( x right)) в точке ( {{x}_{0}}).
Пример:
Найди уравнение касательной к графику функции ( fleft( x right)={{x}^{2}}-2x+3) в точке ( {{x}_{0}}=3).
Решение:
На этом примере выработаем простой…
Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике
ЕГЭ №7. Производная функции — геометрический смысл, дифференцирование
На этом видео мы вспомним, что такое функция и её график, научимся искать производную некоторых функций, например, такой: y = 2×3 – 3×2 + x + 5.
Мы разберём от А до Я все 7 типов задач, которые могут попасться в задаче №7 из ЕГЭ. Узнаем, на какие 3 фразы в условии задачи нужно обратить особое внимание, чтобы с лёгкостью решить задачу и не потерять баллы на ровном месте.
Разберём все возможные ошибки, которые можно допустить в этих задачах. Мы поймём, что многие из этих задач решаются обычным подсчётом клеточек на графике! Главное – не перепутать, что нужно считать.
P.S. Не забудьте потом посмотреть родственную тему: «Интегралы на ЕГЭ. Первообразные элементарных функций».
16 января 2014
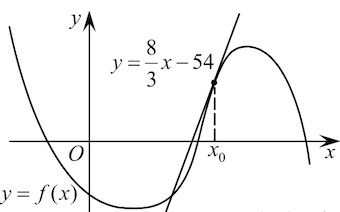
Существует целый класс задач 6 из профильного ЕГЭ, в которых вообще не дается график функции. Все, что известно — это уравнение функции и касательной. И сегодня мы будем учиться решать именно такие задачи.
В этой короткой серии уроков мы разберем непростые задачи, которые не так часто встречаются в настоящем ЕГЭ по математике. Однако если встречаются, то у многих учеников вызывают серьезные затруднения. Речь идет о касательных, заданных уравнением, функция которого также задана своим уравнением. Никаких графиков в этих задачах нет. Более того, отдельные два видеоурока будут посвящены примерам, содержащие параметры. И хотя, на первый взгляд, может показаться, что параметры — это очень сложно, на самом деле, такие задания решаются буквально в несколько строчек.
Решаем реальный пример
Итак, первая задача:
Прямая[y˜=16x-38]является касательной к графику функции:
[y={{x}^{3}}-3{{x}^{2}}+7x-11]
Найдите абсциссу точки касания.
Прежде всего, давайте вообще вспомним, что такое касательная к графику функции. Итак, у нас есть некий график, а также прямая, которая касается этого графика, т. е. пересекает график только в одной точке, причем угол ее пересечения с осью $Ox$, точнее, тангенс этого угла равен значению производной в этой точке:
[tglambda ={f}’left( {{x}_{0}} right)]
Теперь переведем формальное определение на понятный человеку язык. Во-первых, поскольку наша прямая, заданная уравнением, является касательной, то эти уравнения обязательно имеют общую точку, т. е. они имеют общее решение. Следовательно, мы можем приравнять их правые части, т. е.:
[16x-38={{x}^{3}}-3{{x}^{2}}+7x-11]
С другой стороны, поскольку речь идет о касательной к графику, а не о произвольной секущей, мы вправе потребовать, чтобы равны были не только сами функции, но еще и их производные, т. е.:
[{{left( 16x-38 right)}^{prime }}={{left( {{x}^{3}}-3{{x}^{2}}-11 right)}^{prime }}]
Давайте займемся первым выражением:
[16x-38={{x}^{3}}-3{{x}^{2}}+7x-11]
[{{x}^{3}}-3{{x}^{2}}+7x-11-16x+38=0]
[{{x}^{3}}-3{{x}^{2}}+9x+27=0]
Вот мы получили первую конструкцию. Это уравнение третьей степени. Для его решения можно попробовать разложить этот многочлен на множители, и, действительно, после определенных преобразований и нескольких строчек вычислений мы получим несколько кандидатов на ответ. Однако вспомним, что речь идет о простой задаче из ЕГЭ по математике, причем задача из части В. Следовательно, она должна решаться гораздо проще без всяких разложений. И именно для этого нам дано второе уравнение. Мы уже приравняли производные, а теперь давайте посчитаем их:
[{{left( 16x-38 right)}^{prime }}={{left( {{x}^{3}}-3{{x}^{2}}=7x-11 right)}^{prime }}]
[16=3{{x}^{2}}-6x+7]
[3{{x}^{2}}-6x+7-16=0]
[3{{x}^{2}}-6x-9=0]
[{{x}^{2}}-2x-3=0]
Мы получили уравнение второй степени. Данное тождество легко решается и через дискриминант, и по формулам Виета. Давайте решим его по формуле Виета:
[left( -3 right)left( +1 right)=0]
[{{}_{1}}=3]
[{{}_{2}}=-1]
Вот мы и получили два корня, это два кандидата на ответ, т. е. те абсциссы, в которых производная нашей касательной к графику функции равна производной. Теперь возвращаемся к нашей исходной конструкции и вспоминаем, что помимо производных сами функции тоже должны быть равны, т. е. из полученных нами иксов нужно выбрать те, которые удовлетворяют уравнению. Давайте подставим[=3]:
[27-27-27+27=0]
[0=0]
Очевидно, что[=3]является корней обоих выражений — и нашего исходного, и производной. На этом можно было бы закончить решение, но давайте для надежности мы подставим и[=-1]:
[-1-3cdot 1-9cdot left( -1 right)+27=0]
[-text{ }4+9+27=0]
[32ne 0]
Очевидно, что данное выражение не является равенством. Следовательно,[=-1]не является корнем нашего тождества. Отсюда заключаем, что единственным корнем, удовлетворяющим все требования, является[=3]. Это и является ответом к задаче. Мы нашли абсциссу точки касания к графику.
Ключевые моменты
В заключении давайте еще раз пробежимся по ключевым шагам решения.
В первую очередь, что значит, что прямая является касательной графику функции? Это значит, что данная прямая и $fleft( x right)$ имеют общее решение. Следовательно, мы можем приравнять $y$ из выражений. Мы получим первое тождество.
Однако после его преобразования, мы получим уравнение третьей степени, а поскольку такая конструкция вообще решается довольно сложно и к тому же имеет несколько корней, мы записываем вспомогательное равенство, вспоминая о том, что речь идет именно о касательных к графику функции, т. е. помимо самих $fleft( x right)$ равными должны быть еще и их производные. В нашем случае производные легко считаются. Итого у нас получилось простое квадратное равенство, которое затем легко решается, и получается два корня.
Возникает вопрос: какой из этих корней является правильным ответом? Чтобы найти правильный ответ, достаточно каждое из этих чисел подставить в наше уравнение, которое мы получили в самом начале. Здесь мы и получим, что один из корней нас полностью устраивает, а второй корень — нет, т. е. он точно не является решением.
С точки зрения геометрии происходит следующее. Допустим, что у нас есть вот такая функция:
У нее есть точка максимума и точка минимума. В обоих случаях производная равна нулю, и, следовательно, касательная, проведенная через каждую из этих точек, тоже имеет производную, равную 0, т. е. она горизонтальна. Однако, как мы видим, не существует такой касательной к графику функции. Если касательная проходит сверху, то она никак не сможет пересечь кривую в нижнем значении. И, наоборот, если мы рассматриваем касательную в нижней точке, то она никак не сможет пересечь нашу кривую в верхнем значении. Этим и объясняется, что хотя производная функции равна производной касательной в двух точках, в итоге в нашем уравнении нас удовлетворяет лишь одна из них.
Задачи B9 такого типа действительно встречаются на ЕГЭ. Как правило, в процессе решения таких задач возникают целые системы уравнений, которые надо уметь решать. В этом и следующих видеоуроках мы последовательно рассмотрим такие «нестандартные» задачи — от самых простых (как сегодня) до действительно серьезных — с параметром и квадратичной функцией.
Смотрите также:
- ЕГЭ 2022, задание 6. Касательная к графику функции
- Профильный ЕГЭ-2022, задание 6. Геометрический смысл производной
- Сложение и вычитание дробей
- Сводный тест по задачам B15 (1 вариант)
- Однородные тригонометрические уравнения: общая схема решения
- Задача B4: тарифы на сотовую связь
09
Авг 2013
Категория: 07 Производная, ПО
07. Геометрический смысл производной. Касательная
2013-08-09
2022-09-11
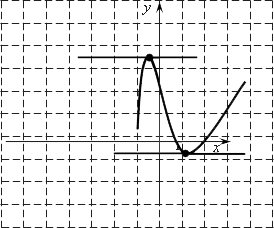
Задача 1. Прямая параллельна касательной к графику функции
. Найдите абсциссу точки касания.
Решение: + показать
Задача 2. Прямая является касательной к графику функции
. Найдите абсциссу точки касания.
Решение: + показать
 Замечание.
Замечание.
Немного облечим себе задачу на будущее. Хотя вполне можно решать задачи способом, показанным выше (задача 2).
Сформулируем условие касания графика функции и прямой
в точке (точках)
.
+ показать
Задача 3. Прямая является касательной к графику функции
Найдите
Решение: + показать
Задача 4. Прямая является касательной к графику функции
. Найдите
, учитывая, что абсцисса точки касания больше
.
Решение: + показать
Задача 5. На рисунке изображён график функции и касательная к нему в точке с абсциссой
. Найдите значение производной функции
в точке
.
Решение: + показать
Задача 6. На рисунке изображён график функции и касательная к нему в точке с абсциссой
. Найдите значение производной функции
в точке
.
Решение: + показать
Задача 7. На рисунке изображен график функции . Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 10. Найдите значение производной функции в точке
.
Решение: + показать
Задача 8. На рисунке изображены график функции и касательная к этому графику, проведённая в точке
. Найдите значение производной функции
в точке
.
Решение: + показать
Задача 9. На рисунке изображены график функции и касательная к этому графику, проведённая в точке
. Уравнение касательной показано на рисунке. Найдите значение производной функции
в точке
.
Решение: + показать
Задача 10. На рисунке изображены график функции и касательная к этому графику, проведённая в точке
. Уравнение касательной показано на рисунке. Найдите значение функции
в точке
.
Решение: + показать
Вы можете пройти тест по задачам, аналогичным разобранным, здесь.
Автор: egeMax |
комментариев 14
В этой статье мы разберем все типы задач на нахождение уравнения касательной.
Вспомним геометрический смысл производной: если к графику функции 



Возьмем на касательной произвольную точку с координатами 
И рассмотрим прямоугольный треугольник 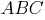
В этом треугольнике
Отсюда
Или
Это и есть уравнение касательной, проведенной к графику функции 

Чтобы написать уравнение касательной, нам достаточно знать уравнение функции и точку, в которой проведена касательная. Тогда мы сможем найти 

Есть три основных типа задач на составление уравнения касательной.
1. Дана точка касания
2. Дан коэффициент наклона касательной, то есть значение производной функции 

3. Даны координаты точки, через которую проведена касательная, но которая не является точкой касания.
Рассмотрим каждый тип задач.
1. Написать уравнение касательной к графику функции 

а) Найдем значение функции в точке 

б) Найдем значение производной в точке 
Подставим найденные значения в уравнение касательной:
Раскроем скобки в правой части уравнения. Получим:
Ответ: 
2. Найти абсциссы точек, в которых касательные к графику функции 
Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси 

а) Найдем производную функции 
б) Приравняем производную к нулю и найдем значения 

Приравняем каждый множитель к нулю, получим:
Ответ: 0;3;5
3. Написать уравнения касательных к графику функции 

Касательная параллельна прямой 
Это второй тип задач на нахождение уравнения касательной.
Итак, у нас дана функция 
а) Найдем точки, в которых производная функции 
Сначала найдем уравнение производной.
Нам нужно найти производную дроби.
Приравняем производную к числу -1.


б) Найдем уравнение касательной к графику функции 

Найдем значение функции в точке 

Подставим эти значения в уравнение касательной:

б) Найдем уравнение касательной к графику функции 

Найдем значение функции в точке 

Подставим эти значения в уравнение касательной:

Ответ:
4. Написать уравнение касательной к кривой 
Сначала проверим, не является ли точка 



Это последний тип задач на нахождение уравнения касательной. Первым делом нам нужно найти абсциссу точки касания.
Найдем значение 
Пусть 



Значение функции 


Найдем значение производной функции 

Сначала найдем производную функции 
Производная в точке 

Подставим выражения для 


Решим это уравнение.
Сократим числитель и знаменатель дроби на 2:
Приведем правую часть уравнения к общему знаменателю. Получим:
Упростим числитель дроби и умножим обе части на 
Получим уравнение
Это иррациональное уравнение.
Решим его. Для этого возведем обе части в квадрат и перейдем к системе.
Решим первое уравнение.
Решим квадратное уравнение, получим

Второй корень не удовлетворяет условию 

Напишем уравнение касательной к кривой 



Получим:
Ответ:
И.В. Фельдман, репетитор по математике.

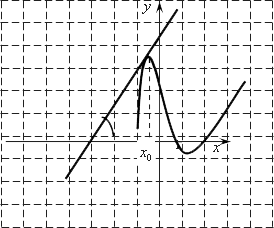
 Замечание.
Замечание.