Как найти касательную к кругу - Исправление недочетов и поиск решений вместе с Examum.ru

Что такое касательная к окружности

8 июля 2018

Домашняя работа
Ответы и решения

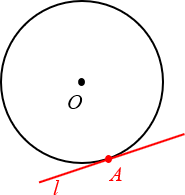
Определение. Касательная к окружности — это прямая на плоскости, имеющая ровно одну общую точку с окружностью.

Вот парочка примеров:

Окружность с центром O касается прямой l в точке A

Из любой точки M за пределами окружности можно провести ровно две касательных

Различие между касательной l, секущей BC и прямой m, не имеющей общих точек с окружностью

На этом можно было бы закончить, однако практика показывает, что недостаточно просто зазубрить определение — нужно научиться видеть касательные на чертежах, знать их свойства и вдобавок как следует попрактиковаться в применении этих свойств, решая реальные задачи. Всем этим всем мы сегодня и займёмся.

Основные свойства касательных

Для того, чтобы решать любые задачи, нужно знать четыре ключевых свойства. Два из них описаны в любом справочнике / учебнике, а вот последние два — про них как-то забывают, а зря.

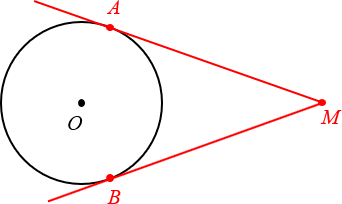
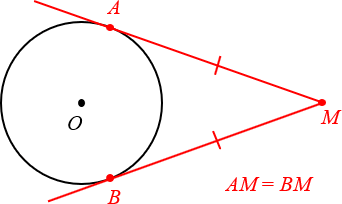
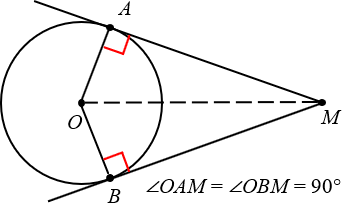
1. Отрезки касательных, проведённых из одной точки, равны

Чуть выше мы уже говорили про две касательных, проведённых из одной точки M. Так вот:

Отрезки касательных к окружности, проведённых из одной точки, равны.

Отрезки AM и BM равны

2. Касательная перпендикулярна радиусу, проведённому в точку касания

Ещё раз посмотрим на картинку, представленную выше. Проведём радиусы OAи OB, после чего обнаружим, что углы OAMи OBM — прямые.

Радиус, проведённый в точку касания, перпендикулярен касательной.

Этот факт можно использовать без доказательства в любой задаче:

Радиусы, проведённые в точку касания, перпендикулярны касательным

Кстати, заметьте: если провести отрезок OM, то мы получим два равных треугольника: OAM и OBM.

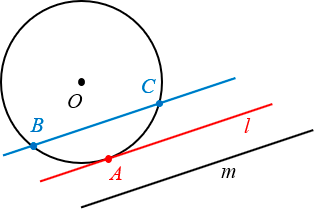
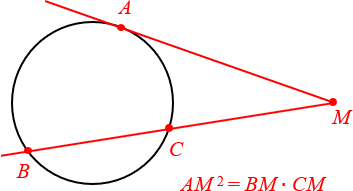
3. Соотношение между касательной и секущей

А вот это уже факт посерьёзнее, и большинство школьников его не знают. Рассмотрим касательную и секущую, которые проходят через одну и ту же общую точку M. Естественно, секущая даст нам два отрезка: внутри окружности (отрезок BC — его ещё называют хордой) и снаружи (его так и называют — внешняя часть MC).

Произведение всей секущей на её внешнюю часть равно квадрату отрезка касательной

Соотношение между секущей и касательной

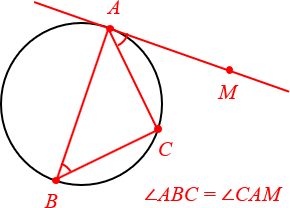
4. Угол между касательной и хордой

Ещё более продвинутый факт, который часто используется для решения сложных задач. Очень рекомендую взять на вооружение.

Угол между касательной и хордой равен вписанному углу, опирающемуся на эту хорду.

Откуда берётся точка B? В реальных задачах она обычно «всплывает» где-то в условии. Поэтому важно научиться распознавать данную конфигурацию на чертежах.

Иногда всё-таки касается

Смотрите также:

Вписанный угол в геометрии
Задачи B12, сводящиеся к линейным уравнениям
Геометрическая вероятность
Задача 18: метод симметричных корней
Задача B2 про комиссию в терминале
Значение тригонометрических функций

Источник

Наталья Игоревна Восковская

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Понятие касательной к окружности

Окружность имеет три возможных взаимных расположений относительно прямой:

Если расстояние от центра окружности до прямой меньше радиуса, то прямая имеет две точки пересечения с окружностью.
Если расстояние от центра окружности до прямой равно радиусу, то прямая имеет две точки пересечения с окружностью.
Если расстояние от центра окружности до прямой больше радиуса, то прямая имеет две точки пересечения с окружностью.

Введем теперь понятие касательной прямой к окружности.

Определение 1

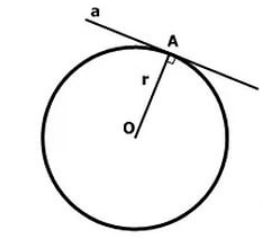
Касательной к окружности называется прямая, которая имеет с ней одну точку пересечения.

Общая точка окружности и касательной называется точкой касания (рис 1).

Рисунок 1. Касательная к окружности

Теоремы, связанные с понятием касательной к окружности

Теорема о свойстве касательной: касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Доказательство.

Рассмотрим окружность с центром $O$. Проведем в точке $A$ касательную $a$. $OA=r$ (Рис. 2).

Докажем, что $abot r$

Будем доказывать теорему методом «от противного». Предположим, что касательная $a$ не перпендикулярна радиусу окружности.

Рисунок 2. Иллюстрация теоремы 1

То есть $OA$ — наклонная к касательной. Так как перпендикуляр к прямой $a$ всегда меньше наклонной к этой же прямой, то расстояние от центра окружности до прямой меньше радиуса. Как нам известно, в этом случае прямая имеет две точки пересечения с окружностью. Что противоречит определению касательной.

«Касательная к окружности» 👇

Следовательно, касательная перпендикулярна к радиусу окружности.

Теорема доказана.

Теорема 2

Обратная теореме о свойстве касательной: Если прямая, проходящая через конец радиуса какой-либо окружности перпендикулярна радиусу, то данная прямая является касательной к этой окружности.

Доказательство.

По условию задачи мы имеем, что радиус — перпендикуляр, проведенный из центра окружности к данной прямой. Следовательно, расстояние от центра окружности до прямой равняется длине радиуса. Как мы знаем, в этом случае окружность имеет только одну точку пересечения с этой прямой. По определению 1 и получаем, что данная прямая — касательная к окружности.

Теорема доказана.

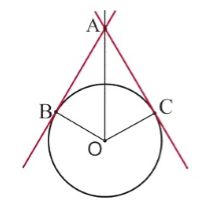
Теорема 3

Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Доказательство.

Пусть дана окружность с центром в точке $O$. Из точки $A$ (лежащей все окружности) проведены две различные касательные. Из точки касания соответственно $B$ и $C$ (Рис. 3).

Докажем, что $angle BAO=angle CAO$ и что $AB=AC$.

Рисунок 3. Иллюстрация теоремы 3

По теореме 1, имеем:

Следовательно, треугольники $ABO$ и $ACO$ — прямоугольные. Так как$OB=OC=r$, а гипотенуза $OA$ — общая, то эти треугольники равны по гипотенузе и катету.

Отсюда и получаем, что $angle BAO=angle CAO$ и $AB=AC$.

Теорема доказана.

Пример задачи на понятие касательной к окружности

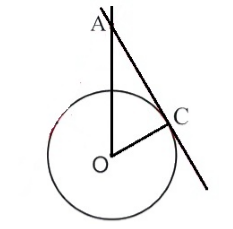
Пример 1

Дана окружность с центром в точке $O$ и радиусом $r=3 см$. Касательная $AC$ имеет точку касания $C$. $AO=4 см$. Найти $AC$.

Решение.

Изобразим вначале все на рисунке (Рис. 4).

Рисунок 4.

Так как $AC$ касательная, а $OC$ радиус, то по теореме 1, получаем, что$angle ACO={90}^{{}^circ }$. Получили, что треугольник $ACO$ — прямоугольный, значит, по теореме Пифагора, имеем:

[{AC}^2={AO}^2+r^2] [{AC}^2=16+9] [{AC}^2=25] [AC=5]

Ответ: $5$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Угол между касательной и хордой

Угол между касательной и хордой равен половине градусной меры дуги, которая находится внутри угла.

Прежде всего: как это понимать? Подробнее о том, что такое «градусная мера дуги», написано в теме «Окружность. Вписанный угол».

Здесь напомним только, что в дуге столько же градусов, сколько в центральном угле, заключающем эту дугу.

То есть «градусная мера дуги» – это «сколько градусов в центральном угле» – и всё!

Ну вот, как говорит Карлсон, продолжаем разговор. Рисуем ещё раз теорему об угле между касательной и хордой.

Смотри, хорда ( displaystyle AB) разбила окружность на две дуги. Одна дуга находится ВНУТРИ угла ( displaystyle BAC), а другая дуга – внутри угла ( displaystyle BAD).

И теорема об угле между касательной и хордой говорит, что ( displaystyle angle CAB) равен ПОЛОВИНЕ угла ( displaystyle AOB), ( displaystyle angle DAB) равен ПОЛОВИНЕ большего (на рисунке — зеленого) угла ( displaystyle AOB).

При чем же тут тот факт, что радиус, проведенный в точку касания, перпендикулярен касательной?

Сейчас и увидим. ( displaystyle OA) – радиус, ( displaystyle AC) – касательная.

Значит, ( displaystyle angle OAC=90{}^circ ).

Поэтому:( displaystyle angle 1=90{}^circ -angle 4).

Но ( displaystyle angle 2=angle 1) (( displaystyle OA) и ( displaystyle OB) – радиусы)( displaystyle angle 2=90{}^circ -angle 4).

И осталось вспомнить, что сумма углов треугольника ( displaystyle AOB) равна ( displaystyle 180{}^circ ).

Пишем:

Короче:

ugol mezhdu kasatelnoj i hordoj i tsentralnyj ugol

Здорово, правда? И самым главным оказалось то, что ( displaystyle angle OAC=90{}^circ ).

Равенство отрезков касательных

Задумывался ли ты над вопросом «а сколько касательных можно провести из одной точки к одной окружности»? Вот, представь себе, ровно две! Вот так:

А ещё более удивительный факт состоит в том, что:

Отрезки касательных, проведённых из одной точки к одной окружности, равны.

То есть, на нашем рисунке, ( displaystyle AB=AC).

И для этого факта тоже самым главным является то, что радиус, проведённый в точку касания, перпендикулярен касательной.

Вот, убедись.

Проведём радиусы ( displaystyle OB) и ( displaystyle OC) и соединим ( displaystyle O) и ( displaystyle A).

( displaystyle OB) – радиус.

( displaystyle AB) – касательная, значит, ( displaystyle OBbot AB).
Ну, и так же ( displaystyle OCbot AC).

Получилось два прямоугольных треугольника ( displaystyle AOB) и ( displaystyle AOC), у которых:

( displaystyle OB=OC) — равные катеты
( displaystyle OA) — общая гипотенуза

( displaystyle Rightarrow Delta AOB = Delta AOC)

(заглядываем в тему «Прямоугольный треугольник«, если не помним, когда бывают равны прямоугольные треугольники).

Но раз ( displaystyle Delta AOB=Delta AOC,) то( displaystyle AB=AC). УРА!

И ещё раз повторим – этот факт тоже очень важный:

Отрезки касательных, проведённых из одной точки, – равны.

И есть ещё один факт, который мы здесь не будем доказывать, но он может оказаться тебе полезен при решении задач.

Для любой прямой ( displaystyle AD), пересекающей окружность,( displaystyle ADcdot AC=A{{B}^{2}}), где ( displaystyle AB) – отрезок касательной.

Хитроумными словами об этом говорят так:

«Квадрат длины отрезка касательной равен произведению секущей на её внешнюю часть».

Страшно? Не бойся, помни только, что в буквах это:

Источник

Касательная к окружности

Содержание:

Касательная к окружности
- Свойство №1
- Свойство №2
- Свойство №3
- Свойство №4
Теоремы и доказательства

Касательная к окружности

Определение

Касательная к окружности — в геометрии это прямая, которая имеет с окружностью одну общую точку. Такая точка называется точкой касания.

У этой прямой есть ряд свойств.

Свойство №1

Отрезки линий касательных, проведенных из одной точки, равны.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

На чертеже это выглядит таким образом:

Свойство №1

Свойство №2

Касательная линия перпендикулярна радиусу, проведенному в точку касания.

Свойство №2

При этом, если провести отрезок из центра окружности до начальной точки прямых (OM), мы получим два равных прямоугольных треугольника (OAM=OBM).

Свойство №3

Соотношение между касательной и секущей.

Графическое изображение этого утверждения выглядит так:

Свойство №3

Это утверждение о касательной и секущей, которые проходят через общую точку (M). Секущая дает нам два отрезка: BC (внутренний отрезок, хорда) и CM (внешняя часть секущей). Произведение всей секущей BM на ее внешнюю часть CM равно квадрату отрезка касательной. Формула выглядит так:

(AM^2=BMcdot CM.)

Свойство №4

Угол между касательной и хордой.

Это утверждение относится к продвинутому уровню и используется для решения сложных задач. Звучит оно так: угол между касательной и хордой равен вписанному углу, который опирается на эту хорду.

Рисунок к этому правилу:

Свойство №4

Точка B обычно задается в условии задачи, поэтому ученику нужно лишь уметь распознавать эту конфигурацию в заданиях и уметь применять правило при решении.

Теоремы и доказательства

Теорема №1

Отрезки касательных, проведенных из одной точки, равны и формируют равные углы с прямой, проходящей через эту точку и центр окружности.

Доказательство

Дано: AB и AC — касательные к окружности с центром O. B и C — точки касания.

Теорема №1

Доказать: (AB=AC, a angle3=angle4.)

Доказательство: (angle1=angle2=90^circ), так как (OВperp АВ), (ОСperp АС) согласно теореме о свойстве касательной, поэтому (triangle ABO) и (triangle ACO) — прямоугольные. OB и OC — радиусы, OB=OC, AO — общая сторона. Значит, (triangle ABO = triangle ACO) по гипотенузе и катету. Следовательно, уравнения AB=AC и (angle3=angle4) верны (по равенству треугольников). Ч.Т.Д.

Теорема №2

Касательная перпендикулярна радиусу, проведенному в точку касания.

Доказательство

Дано: a — касательная к кругу с центром O. Она пересекает круг в точке H.

Теорема №2

Доказать: (OHperp a).

Доказательство: воспользуемся методом от противного. Предположим, что OH не перпендикулярна a. В этом случае радиус OH — наклонная к прямой a. Перпендикуляр, проведенный из точки O к a, меньше наклонной OH. Тогда расстояние от центра O до прямой a меньше радиуса. Значит, у прямой a и окружности есть две общие точки, что противоречит условию, в котором прямая a — касательная. Следовательно, предположение неверно и (Hperp a). Ч.Т.Д.

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Касательная к окружности

Касательная к окружности — прямая, имеющая с окружностью единственную общую точку.

Расскажем подробнее, что такое касательная и секущая.

Напомним, что расстояние от точки до прямой — это длина перпендикуляра, опущенного из точки на прямую.

Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая является касательной к окружности. В этом случае она имеет с окружностью ровно одну общую точку. Такую прямую называют касательной к окружности.

Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая пересекает окружность в двух точках. Такую прямую называют секущей.

Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая не имеет с окружностью общих точек.

Запишем основные теоремы о касательных. Они помогут нам при решении задач ЕГЭ и ОГЭ.

Теорема 1.

Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

На рисунке радиус OA перпендикулярен прямой m.

Теорема 2. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Доказательство:

Дана окружность с центром O.

Прямые AB и AC — касательные, точки B и C — точки касания. Докажем, что
AB = AC и

Проведем радиусы OB и OC в точки касания.

По свойству касательной, и .

В прямоугольных треугольниках AOB и AOC катеты OB и OC равны как радиусы одной окружности, AO — общая гипотенуза. Следовательно, треугольники AOB и AOC равны по гипотенузе и катету. Отсюда AB = AC и

Теорема 3. Отрезки касательных, проведенных к окружности из одной точки, равны.

Доказательство:

Пусть из точки A к окружности проведены касательные AB и AC. Соединим точку A с центром окружности точкой O. Треугольники AOB и AOC равны по гипотенузе и катету, следовательно, AB = AC.

Теорема 4. Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

Угол ACМ на рисунке равен половине угловой величины дуги AC.

Доказательство теоремы здесь.

Теорема 5, о секущей и касательной.

Если из одной точки к окружности проведены секущая и касательная, то произведение всей секущей на ее внешнюю часть равно квадрату отрезка касательной.

Доказательство теоремы смотрите здесь.

Разберем задачи ЕГЭ и ОГЭ по теме: Касательная к окружности.

Задача 1.

Угол ACO равен $28^{circ}$ , где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Решение:

Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Значит, угол CAO — прямой. Из треугольника ACO получим, что угол AOC равен 62 градуса. Bеличина центрального угла равна угловой величине дуги, на которую он опирается, значит, величина дуги AB— тоже 62 градуса.

Ответ: 62.

Задача 2.

Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна $116^{circ}$ . Ответ дайте в градусах.

Решение:

Это чуть более сложная задача. Центральный угол AOD опирается на дугу AD, следовательно, он равен 116 градусов. Тогда угол AOC равен $180^{circ}-116^{circ}=64^{circ}.$ Касательная перпендикулярна радиусу, проведенному в точку касания, значит, угол OAC — прямой. Тогда угол ACO равен $90^{circ}-64^{circ}=26^{circ}.$

Ответ: 26.

Задача 3.

Хорда AB стягивает дугу окружности в $92^{circ}.$ Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

Решение:

Проведем радиус OB в точку касания, а также радиус OA. Угол OBC равен $90^{circ}.$ Треугольник BOA — равнобедренный. Нетрудно найти, что угол OBA равен 44 градуса, и тогда угол CBA равен 46 градусов, то есть половине угловой величины дуги AB.

Мы могли также воспользоваться теоремой: Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

Задача 4.

К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.

Решение:

Вспомним еще одно важное свойство касательных к окружности:
Отрезки касательных, проведенных из одной точки, равны.
Периметр треугольника — это сумма всех его сторон. Обратите внимание на точки на нашем чертеже, являющиеся вершинами шестиугольника. Из каждой такой точки проведены два отрезка касательных к окружности. Отметьте на чертеже такие равные отрезки. Еще лучше, если одинаковые отрезки вы будете отмечать одним цветом. Постарайтесь увидеть, как периметр треугольника ABC складывается из периметров отсеченных треугольников.

Ответ: 24.

Вот более сложная задача из вариантов ЕГЭ:

Задача 5.

Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.

Решение:

Обратите внимание — в условии даже не сказано, сколько сторон у этого многоугольника. Видимо, это неважно. Пусть их будет пять, как на рисунке.
Окружность касается всех сторон многоугольника. Отметьте центр окружности — точку O — и проведите перпендикулярные сторонам радиусы в точки касания.

Соедините точку O с вершинами A, B, C, D, E. Получились треугольники AOB, BOC, COD, DOE и EOA.

Очевидно, что площадь многоугольника $S=S_{AOB} + S_{BOC}+S_{COD}+S_{DOE}+S_{EOA}.$

Треугольники АОВ, ВОС, COD, DOE и ЕОА имеют равные высоты, причем все эти высоты равны радиусу окружности.

$S_{ABCD}=S_{vartriangle AOB}+S_{vartriangle BOC}+S_{vartriangle COD}+S_{vartriangle DOE}+S_{vartriangle EOA}=$

$=displaystyle frac{1}{2}ABcdot r+displaystyle frac{1}{2}BCcdot r+displaystyle frac{1}{2}CDcdot r+displaystyle frac{1}{2}DEcdot r+displaystyle frac{1}{2}AEcdot r=$

$=displaystyle frac{1}{2}cdot rcdot left(AB+BC+CD+DE+EAright)=displaystyle frac{1}{2}Pcdot r=pcdot r,$ где p — полупериметр многоугольника.

По условию, P = 10, S = 5, тогда $r=displaystyle frac{S}{p}=displaystyle frac{5}{5}=1.$

Ответ: 1

Задачи ЕГЭ

1. Угол ACO равен ${27}^circ$ , где O — центр окружности. Его сторона CA касается окружности. Сторона CO пересекает окружность в точке B . Найдите величину меньшей дуги AB окружности. Ответ дайте в градусах.

Решение:

По условию, CA — касательная, A — точка касания.

. Треугольник ACO — прямоугольный, $angle AOC=90{}^circ -angle ACO=90{}^circ -27{}^circ =63{}^circ$ .

Угол — центральный, и он равен угловой величине дуги AB, на которую опирается. Значит, градусная мера дуги AB равна $63{}^circ$ . Это меньшая дуга AB, а большая — с другой стороны от точек A и B, и она больше 180 градусов.

Ответ: 63.

2. Через концы A и B дуги окружности с центром O проведены касательные AC и BC. Меньшая дуга AB равна ${58}^circ$ . Найдите угол ACB. Ответ дайте в градусах.

Решение:

Центральный угол AOB равен угловой величине дуги, на которую он опирается, то есть $58{}^circ .$

AC и BC — касательные, поэтому $angle OAC=angle OBC=90{}^circ$ , поскольку касательная перпендикулярна радиусу, проведенному в точку касания.

Сумма углов четырехугольника ACBO равна $360{}^circ .$

$angle ACB=360{}^circ -90{}^circ -90{}^circ -58{}^circ =122{}^circ$

Ответ: 122.

3. Хорда AB стягивает дугу окружности в ${92}^circ$ . Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

Решение:

Применим теорему об угле между касательной и хордой.

Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.

Значит, угол ABC равен $46{}^circ$ .

Ответ: 46.

4. Через концы A и B дуги окружности с центром О проведены касательные AC и BC. Угол CAB равен $32{}^circ$ . Найдите угол AOB. Ответ дайте в градусах.

Угол между касательной и хордой равен половине угловой величины дуги, заключённой между ними.

Поэтому меньшая дуга AB окружности равна $64{}^circ$ . Центральный угол равен угловой величине дуги, на которую он опирается, значит, угол AOB равен $64{}^circ$ .

Мы могли бы решить задачу и по-другому, рассматривая четырехугольник ACBO, как в задаче 2.

Ответ: 64.

5. Через концы A, B дуги окружности в ${62}^circ$ проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

Решение:

Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними. В треугольнике ABC:

$angle ACB=180{}^circ -left(angle BAC+angle CBAright)=$

$=180{}^circ -cup AB=180{}^circ -62{}^circ =118{}^circ$

Ответ: 118.

6. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, сторона CO пересекает окружность в точках B и D, а дуга AD окружности, заключенная внутри этого угла, равна $116{}^circ$ . Ответ дайте в градусах.

Решение:

По условию, DB — диаметр окружности, поэтому дуга AВ, не содержащая точки D, равна $180{}^circ - 116{}^circ = 64{}^circ$ . На эту дугу опирается центральный угол AOB, он равен $64{}^circ$ . Треугольник AOC прямоугольный, так как касательная CA перпендикулярна радиусу ОA, проведенному в точку касания.

$angle ACO=90{}^circ -angle COA=90{}^circ -64{}^circ =26{}^circ .$

Ответ: 26.

Задачи ОГЭ по теме: Касательная к окружности

1. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.

Решение:

Отрезок OB — радиус, проведённый в точку касания, поэтому AB и OB перпендикулярны, треугольник AOB — прямоугольный. По теореме Пифагора:

${OB}^2={AO}^2-{AB}^2$

${{OB}^2=13}^2-{12}^2=169-144=25;; OB=5$

Ответ: 5.

2. Прямая касается окружности в точке K. Точка O — центр окружности. Хорда KM образует с касательной угол, равный ${83}^circ$ . Найдите величину угла OMK. Ответ дайте в градусах.

Решение:

Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому угол OКD — прямой. Тогда $angle OKM = 90{}^circ - 83{}^circ = 7{}^circ .$ Треугольник OMK — равнобедренный, его стороны OК и OМ являются радиусами окружности, поэтому $angle OMK =angle OKM= 7{}^circ$

Ответ: 7.

3. Отрезок AB = 40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

Решение:

Касательная перпендикулярна радиусу, проведенному в точку касания, значит, треугольник AOB — прямоугольный. Из прямоугольного треугольника AOB по теореме Пифагора найдём AO:

$AO=sqrt{{AB}^2+{OB}^2}=sqrt{{40}^2+{75}^2}=sqrt{5^2left(8^2+{15}^2right)}=$

Ответ: 10.

4. На отрезке AB выбрана точка C так, что AC = 75 и BC = 10. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.

Решение:

Проведём радиус AH в точку касания. Касательная перпендикулярна радиусу, проведенному в точку касания, поэтому треугольник ABН — прямоугольный. Из прямоугольного треугольника ABH по теореме Пифагора найдём BH:

$BH=sqrt{{AB}^2-{AH}^2}=sqrt{{left(AC+CBright)}^2-{AH}^2}=sqrt{{85}^2-{75}^2}=$

$=sqrt{5^2left({17}^2-{15}^2right)}=40$

Ответ: 40.

5. Касательные в точках A и B к окружности с центром O пересекаются под углом ${72}^circ$ . Найдите угол ABO. Ответ дайте в градусах.

Решение:

Касательные, проведённые к окружности из одной точки, равны, поэтому AC=BC и треугольник ABC — равнобедренный.

$angle CAB=angle CBA=displaystyle frac{180{}^circ -angle ACB}{2}=54{}^circ$

Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними, значит, дуга AB равна ${108}^circ$ . Угол AOB — центральный, он равен дуге, на которую опирается, то есть ${108}^circ$ . Треугольник AOB равнобедренный,

$angle OAB=angle ABO=displaystyle frac{180{}^circ -108{}^circ }{2}=36{}^circ$

Ответ: 36.

6. Из точки A проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен ${60}^circ$ , а расстояние от точки A до точки O равно 8.

Решение:

Проведём радиусы OB и OC в точки касания. Треугольники AOB и AOC — прямоугольные. Эти треугольники равны по катету и гипотенузе.

OB — OC как радиусы окружности, гипотенуза общая. Значит,

$angle BAO=angle OAC=displaystyle frac{60{}^circ }{2}=30{}^circ$

Из треугольника AOB найдём OB, то есть радиус окружности.

$OB=AOcdot {sin 30{}^circ }=8cdot displaystyle frac{1}{2}=4$

Ответ: 4.

7. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB = 2, AC = 8. Найдите AK.

Решение:

По теореме о секущей и касательной, ${AK}^2=ABcdot AC,$

Ответ: 4.

8. На окружности отмечены точки A и B так, что меньшая дуга AB равна ${72}^circ$ . Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

Решение:

Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними.

$angle ABC = 72{}^circ : 2 = 36{}^circ .$

Ответ: 36.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Касательная к окружности» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник