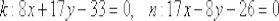Как найти уравнение касательной и уравнение нормали, если функция задана неявно?
Формулы касательной и нормали остаются прежними, но меняется техника решения:
Пример 6
Найти уравнения касательной и нормали к кривой 

Решение: судя по уравнению, это какая-то линия 3-го порядка, какая именно – нас сейчас совершенно не интересует.
В уравнении присутствует зловред 

Но этого и не требуется! Есть куда более остроумное решение. Уравнение касательной составим по той же формуле

Из условия известны значения 
Получено верное равенство, значит, с точкой 
Осталось вычислить 
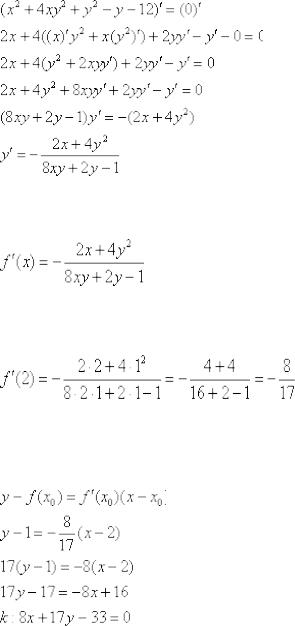
Перепишем результат с более подходящим для нашей задачи обозначением:
На 2-м шаге в найденное выражение производной подставим 
Вот так-то!
Осталось аккуратно разобраться с уравнением:
Составим уравнение нормали:

Ответ:
Готово! А поначалу представлялось всё непросто. Хотя производная здесь, конечно, – место уязвимое. Миниатюра для самостоятельного решения:
Пример 7
Найти уравнение нормали к линии 
Хватит уже вымучивать касательную =)
В данном случае легко выяснить, что это окружность 


заданной функции на порядок легче! Она тут чуть ли не самая примитивная.
Краткое решение и ответ в конце урока.

Как найти уравнение касательной и уравнение нормали, если функция задана параметрически?
Ещё проще. Но для этого нужно потренироваться в нахождении
производной от параметрически заданной функции. А так – почти халява:
Пример 8
Составить уравнения касательной и нормали к циклоиде 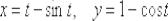

Чертёж циклоиды можно найти на странице S и V, если линия задана параметрически (так получилось, что эта статья была создана раньше). Там даже изображена точка касания.
Решение: абсцисса и ордината точки касания рассчитываются непосредственно из параметрических уравнений кривой:
Найдём 1-ую производную от параметрически заданной функции:
И вычислим её значение при 

Уравнение касательной составим по обычной формуле с поправкой на несколько другие обозначения:
Уравнение нормали:
Ответ: 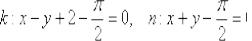

линией: Пример 9
Составить уравнение нормали к полукубической параболе 
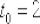
Это пример для самостоятельного решения. Напоминаю, что графики параметрически заданных функций можно построить, например, с помощью моего расчётного геометрического макета.
Ну а наш урок подошёл к концу, и я надеюсь, что изложенный материал прошёл для вас не по касательной, а нормально =)
Спасибо за внимание и успехов!
Решения и ответы:
Пример 2: Решение: уравнение касательной составим по формуле:
В данном случае:
Таким образом:

Уравнение нормали составим по формуле 
Ответ:
Пример 4: Решение: уравнение касательной составим по формуле:
В данной задаче:
Таким образом:

В точке 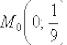

Ответ:
Пример 7: Решение: в данной задаче: 
Или:
Подставим в выражение производной 
Искомое уравнение нормали:

Ответ: 
Найдём производную и вычислим её значение при 
Уравнение нормали:
Ответ:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уравнение касательной и уравнение нормали к графику функции
Как получить уравнение касательной и уравнение нормали
Касательная — это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.
Уравнение касательной выводится из уравнения прямой.
Выведем уравнение касательной, а затем — уравнение нормали к графику функции.
В нём k — угловой коэффициент.
Отсюда получаем следующую запись:
Значение производной f ‘(x 0 ) функции y = f(x) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M 0 (x 0 , y 0 ) , где y 0 = f(x 0 ) . В этом состоит геометрический смысл производной.
Таким образом, можем заменить k на f ‘(x 0 ) и получить следующее уравнение касательной к графику функции:
В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде. Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.
Теперь об уравнении нормали. Нормаль — это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали:
Переходим к примерам. Для решений потребуется таблица производных (откроется в новом окне).
Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».
Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1) .
Решаем задачи вместе
Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции (функция представляет собой многочлен и её производную можно найти по формулам 1, 2 и 3 в таблице производных):
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем
В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:
На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.
Следующий пример — тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг — приведение уравнения к общему виду.
Пример 2. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Найдём производную функции:
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:
Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):
Составляем уравнение нормали:
Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Находим уравнение касательной:
Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:
Составляем уравнение нормали:
Решить задачи самостоятельно, а затем посмотреть решения
Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Снова решаем задачи вместе
Пример 6. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Распространённая ошибка при составлении уравнений касательной и нормали — не заметить, что функция, данная в примере, — сложная и вычислять её производную как производную простой функции. Следующие примеры — уже со сложными функциями (соответствующий урок откроется в новом окне).
Пример 7. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Внимание! Данная функция — сложная, так как аргумент тангенса ( 2x ) сам является функцией. Поэтому найдём производную функции как производную сложной функции (потребуется формула 9 в таблице производных сложной функции):
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Получаем уравнение касательной:
Приводим уравнение к общему виду:
Составляем уравнение нормали:
Пример 8. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .
Решение. Найдём ординату точки касания:
.
Как и в предыдущем примере, данная функция — сложная, так как степень () сама является функцией. Поэтому найдём производную функции как производную сложной функции (используя формулу 1 в таблице производных сложной функции):
.
Найдём значение производной в точке касания, то есть угловой коэффициент касательной:
.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Уравнение прямой касательной к графику функции в заданной точке
Эта математическая программа находит уравнение касательной к графику функции ( f(x) ) в заданной пользователем точке ( x_0 ).
Программа не только выводит уравнение касательной, но и отображает процесс решения задачи.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Статью из энциклопедии о касательной прямой вы можете посмотреть здесь (статья из Википедии).
Если вам нужно найти производную функции, то для этого у нас есть задача Найти производную.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> Введите выражение функции ( f(x)) и число (x_0) — абсциссу точки в которой нужно построить касательную Найти уравнение касательной
Немного теории.
Угловой коэффициент прямой
Напомним, что графиком линейной функции ( y=kx+b) является прямая. Число (k=tg alpha ) называют угловым коэффициентом прямой, а угол ( alpha ) — углом между этой прямой и осью Ox
Уравнение касательной к графику функции
Если точка М(а; f(a)) принадлежит графику функции у = f(x) и если в этой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то из геометрического смысла производной следует, что угловой коэффициент касательной равен f'(a). Далее мы выработаем алгоритм составления уравнения касательной к графику любой функции.
Пусть даны функция у = f(x) и точка М(а; f(a)) на графике этой функции; пусть известно, что существует f'(a). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид y = kx + b, поэтому задача состоит в нахождении значений коэффициентов k и b.
С угловым коэффициентом k все понятно: известно, что k = f'(a). Для вычисления значения b воспользуемся тем, что искомая прямая проходит через точку М(а; f(a)). Это значит, что если подставить координаты точки М в уравнение прямой, получим верное равенство: (f(a)=ka+b ), т.е. ( b = f(a) — ka ).
Осталось подставить найденные значения коэффициентов k и b в уравнение прямой:
Нами получено уравнение касательной к графику функции ( y = f(x) ) в точке ( x=a ).
Алгоритм нахождения уравнения касательной к графику функции ( y=f(x) )
1. Обозначить абсциссу точки касания буквой ( a )
2. Вычислить ( f(a) )
3. Найти (f'(x) ) и вычислить (f'(a) )
4. Подставить найденные числа ( a, f(a), f'(a) ) в формулу ( y=f(a)+ f'(a)(x-a) )
Касательная и нормаль к графику функции
Основные формулы
Пусть на некотором интервале X задана функция . Нас интересуют геометрические характеристики графика этой функции в некоторой заданной точке при значении аргумента , где . Пусть функция имеет в производную, которую будем обозначать как . Тогда через точку мы можем провести касательную к графику. Тангенс угла α между осью абсцисс x и касательной равен производной функции в точке :
(1) .
А само уравнение касательной имеет вид:
(2) .
В аналитической геометрии тангенс угла между прямой и осью абсцисс называют угловым коэффициентом прямой. Таким образом производная равна угловому коэффициенту касательной в .
См. Геометрический смысл производной
Прямая, перпендикулярная касательной, проведенной через точку , называется нормалью к графику функции в этой точке. Уравнение нормали имеет вид:
(3) .
См. Уравнение прямой с угловым коэффициентом ⇓
Пусть две кривые и пересекаются в точке . Тогда угол φ между касательными к этим кривым в точке называется углом между кривыми. Он определяется по формуле:
(4) , где .
Отсюда .
при .
Вывод формулы ⇓
Определения
Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.
Определение касательной приводится здесь. Уравнение касательной:
.
Касательная TM0, нормаль M0N, подкасательная TP, поднормаль PN. Нормалью к графику функции в точке называется прямая, перпендикулярная касательной, проведенной через эту точку. Уравнение нормали:
.
Отрезком касательной называют отрезок между точкой пересечения касательной с осью абсцисс и точкой .
.
Отрезком нормали называют отрезок между точкой пересечения нормали с осью абсцисс и точкой .
.
Подкасательной называют отрезок между точкой пересечения касательной с осью абсцисс и проекции точки на эту ось.
.
Поднормалью называют отрезок между точкой пересечения нормали с осью абсцисс и проекции точки на эту ось.
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым, проведенных через точку .
Полезные формулы из аналитической геометрии
Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.
Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.
Умножив это уравнение на , получим уравнение прямой в другом виде:
.
Здесь – вектор нормали прямой. Тогда само уравнение означает равенство нулю скалярного произведения векторов и .
Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :
Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.
Уравнение прямой с угловым коэффициентом k , проходящей через точку :
.
Угол α между прямой и осью x определяется по формуле:
.
Если две прямые взаимно перпендикулярны, то их угловые коэффициенты и связаны соотношением:
.
Уравнение прямой в отрезках, пересекающей оси координат в точках :
.
Примеры решения задач
Все примеры Ниже рассмотрены примеры решений следующих задач.
1. Найти уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали. Решение ⇓
2. Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде
, проведенных в точке . Решение ⇓
3. Заданной в неявном виде . Решение ⇓
4. Найти угол между кривыми и Решение ⇓
Пример 1
Составить уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали.
Находим значение функции при :
.
Находим производную:
.
Находим производную в точке :
;
.
Находим уравнение касательной по формуле (2):
;
;
;
– уравнение касательной.
Строим касательную на графике. Поскольку касательная – это прямая, то нам нужно знать положения двух ее точек, и провести через них прямую.
При ;
при .
Проводим касательную через точки и .
Касательная и нормаль к графику функции y=x 2 в точке M0(1;1).
Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.
Находим уравнение нормали по формуле (3):
;
;
;
;
;
– уравнение нормали.
Строим нормаль по двум точкам.
При ;
при .
Проводим нормаль через точки и .
Находим длину отрезка касательной . Из прямоугольника имеем:
.
Поясним использованную формулу. Поскольку , то . Тогда
.
Подставляем :
.
Находим длину отрезка подкасательной . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка нормали . Поскольку и , то треугольники и подобны. Тогда . Из прямоугольника имеем:
.
Подставляем :
.
Находим длину отрезка поднормали . Из прямоугольника имеем:
.
Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.
Уравнение касательной: ; уравнение нормали: ;
длина отрезка касательной: ; длина отрезка нормали: ; длина подкасательной: ; длина поднормали: .
Пример 2
Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде , проведенных в точке .
Находим значения переменных при .
;
.
Обозначим эту точку как .
Находим производные переменных x и y по параметру t .
;
;
;
;
.
Подставляя , находим производную y по x в точке .
.
Касательная и нормаль к циссоиде в точке (2;2).
Применяя формулу (2), находим уравнение касательной к циссоиде, проходящей через точку .
;
;
;
.
Применяя формулу (3), находим уравнение нормали к циссоиде в точке .
;
;
;
.
Уравнение касательной: .
Уравнение нормали: .
Пример 3
Составить уравнения касательной и нормали к циссоиде, заданной в неявном виде:
(П3) ,
проведенных в точке .
Для получения уравнение касательной и нормали, нам нужно знать значение производной функции в заданной точке. Функция (П3) задана неявно. Поэтому применяем правило дифференцирования неявной функции. Для этого дифференцируем (П3) по x , считая, что y является функцией от x .
;
;
;
.
Отсюда
.
Находим производную в заданной точке, подставляя .
;
.
Находим уравнение касательной по формуле (2).
;
;
;
.
Находим уравнение нормали по формуле (3).
;
;
;
.
Касательная и нормаль к циссоиде изображены на рисунке ⇑.
Уравнение касательной: .
Уравнение нормали: .
Пример 4
Найти угол между кривыми и .
Найдем множество точек пересечения кривых, решая систему уравнений.
Левые части равны. Приравниваем правые части и выполняем преобразования.
;
(П4) .
Поскольку функция строго монотонна, то уравнение (П4) имеет один корень:
.
При . Кривые пересекаются в единственной точке . Обозначим ее как , где .
Введем обозначения для функций, с помощью которых заданы кривые:
.
Найдем их производные.
;
.
Найдем значения производных в точке , подставляя .
;
.
Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.
Вывод формулы для угла между кривыми
Изложим вывод формулы (4). Для иллюстрации используем только что рассмотренный пример ⇑, в котором .
Рассмотрим две кривые, заданные уравнениями и , и пересекающиеся в некоторой точке . Докажем, что угол между кривыми определяется по формуле (4):
, где .
Или ;
при .
Проведем касательные к графикам функций в точке . Углы, которые образуют касательные с осью x обозначим как и . За положительное направление выберем направление против часовой стрелки. На рисунке . Считаем, что значения углов принадлежат интервалам . Согласно геометрическому смыслу производной,
.
В аналитической геометрии принято, что угол φ между прямыми равен наименьшему значению угла между ними.
Если , то ;
если , то .
Таким образом величина угла φ между касательными может находиться только в пределах
(Ф2) .
На рисунке угол между лучами и больше 90°, а между лучами и – меньше. Поэтому .
При доказательстве мы будем использовать соотношение:
, которое выполняется при .
Тогда в силу (Ф2),
.
Случай мы рассмотрим отдельно.
1) Пусть .
Тогда угол между прямыми . И мы имеем:
.
В конце мы подставили (Ф1).
2) Пусть .
Тогда ; . Поэтому . Это можно записать так: . Также применим формулу: . В результате получаем:
.
Этот случай изображен на рисунке ⇑.
3) Пусть .
При этом касательные взаимно перпендикулярны, . В этом случае , что указано в (4).
Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.
Автор: Олег Одинцов . Опубликовано: 30-06-2021
http://www.math-solution.ru/math-task/equation-tangent
http://1cov-edu.ru/mat-analiz/proizvodnaya/kasatelnaya-i-normal-k-grafiku-funktsii/
3. Аналитическая геометрия на плоскости
3.9 Касательные
Пусть на плоскости задана кривая уравнением $F(x,y)=0$ (т.е. неявным образом). Пусть точка $(x_0, y_0)$ принадлежит этой кривой. Выпишем уравнение касательной к кривой в этой точке.
Напомним, что если кривая задана уравнением $y=f(x)$, то, как известно из курса дифференциального исчисления, угловой коэффициент касательной в точке $(x_0,y_0)$, лежащей на кривой, равен значению производной $f(x)$ в этой точке, т.е. $k=f'(x_0)$. Таким образом, уравнение касательной (уравнение прямой с заданным угловым коэффициентом, проходящей через заданную точку) имеет вид:
[
y-y_0=f'(x_0)(x-x_0).
]
Если кривая задана неявно, то производная $f'(x_0)$ вычисляется согласно соотношению
[
f'(x_0)=-frac{frac{partial F}{partial x}}{frac{partial F}{partial y}}|_{x_0, y_0}.
]
Подставляя в уравнение касательной, получаем уравнение касательной в окончательном виде:
begin{equation}
(y-y_0)cdot frac{partial F}{partial y}(x_0, y_0)+(x-x_0)cdot frac{partial F}{partial x}(x_0, y_0)=0. (26)
label{kasat}
end{equation}
Рассмотрим с помощью этого соотношения касательные к кривым второго порядка.
1. Касательная к эллипсу.
Исходное уравнение
[
frac{x^2}{a^2}+frac{y^2}{b^2}=1,
]
так что $frac{partial F}{partial x}=frac{2x}{a^2}$, $frac{partial F}{partial y}=frac{2y}{b^2}$. При этом уравнение (26) принимает вид
[
frac{2(x-x_0)x_0}{a^2}+frac{2(y-y_0)y_0}{b^2}=0.
]
Сокращая на 2 и учитывая, что точка $(x_0,y_0)$ лежит на эллипсе, получаем уравнение касательной эллипса, проходящей через эту точку:
begin{equation}
frac{xx_0}{a^2}+frac{yy_0}{b^2}=1. (27)
label{kasell}
end{equation}
2. Касательная к гиперболе.
Исходное уравнение
[
frac{x^2}{a^2}-frac{y^2}{b^2}=1,
]
так что $frac{partial F}{partial x}=frac{2x}{a^2}$, $frac{partial F}{partial y}=-frac{2y}{b^2}$. При этом уравнение (26) принимает вид
[
frac{2(x-x_0)x_0}{a^2}-frac{2(y-y_0)y_0}{b^2}=0.
]
Сокращая на 2 и учитывая, что точка $(x_0,y_0)$ лежит на гиперболе, получаем уравнение касательной гиперболы, проходящей через эту точку:
begin{equation}
frac{xx_0}{a^2}-frac{yy_0}{b^2}=1. (28)
label{kashyp}
end{equation}
3. Касательная к параболе.
Исходное уравнение
[
y^2-2px=0,
]
так что $frac{partial F}{partial x}=-2p$, $frac{partial F}{partial y}=2y$. При этом уравнение (26) принимает вид
[
-2p(x-x_0)+2(y-y_0)y_0=0.
]
Сокращая на 2 и учитывая, что точка $(x_0,y_0)$ лежит на параболе, получаем уравнение касательной параболы, проходящей через эту точку:
begin{equation}
yy_0=p(x+x_0). (29)
label{kaspar}
end{equation}
Пример.
Задачи.