Как найти касательную составляющую ускорения

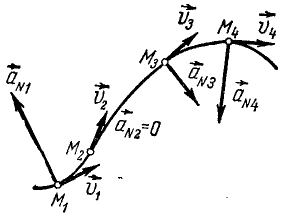
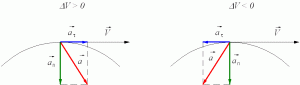
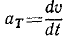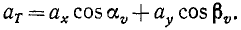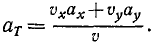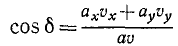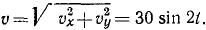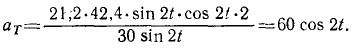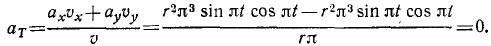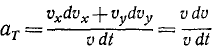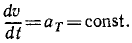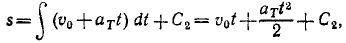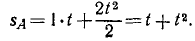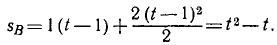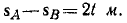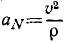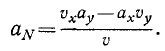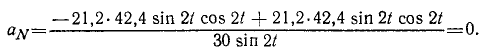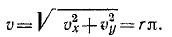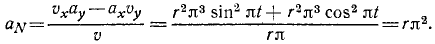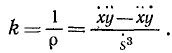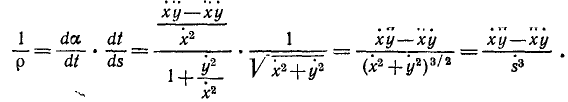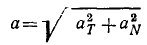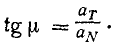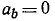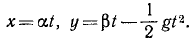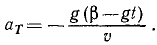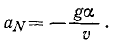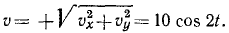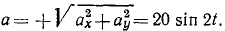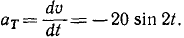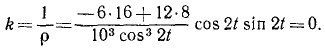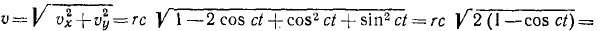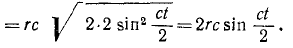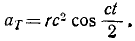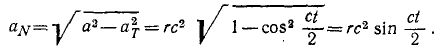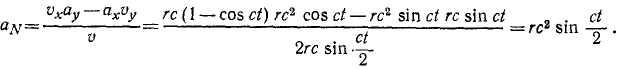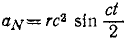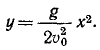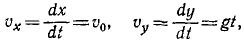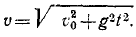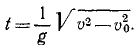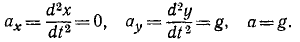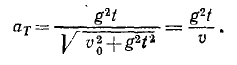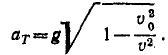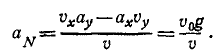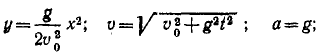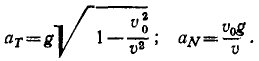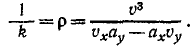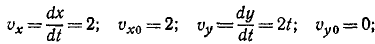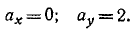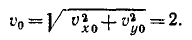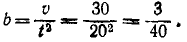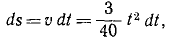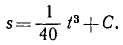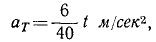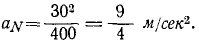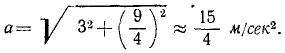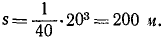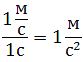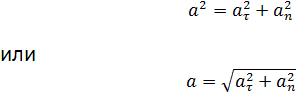Касательное и нормальное ускорения точки

Касательное ускорение характеризует изменение в данное мгновение вектора скорости по величине, а нормальное — по направлению

Проекция ускорения на касательную и на нормаль

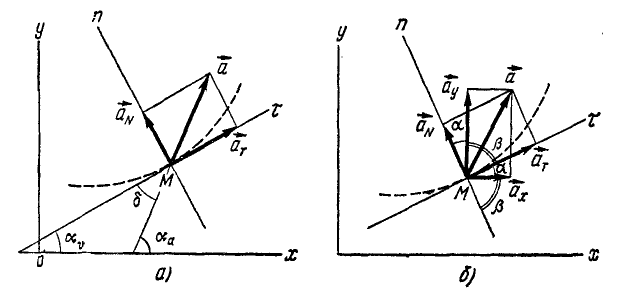
Если движение точки задано в векторной или в координатной форме, то часто встречается необходимость определить проекции ускорения на касательную и главную нормаль к траектории точки в том ‘ месте, где в данное мгновение находится точка (рис. 91, а).

При естественной форме определения движения точки сначала определяют проекции ускорения на касательную и на нормаль, а затем уже по этим проекциям находят величину и направление полного ускорения точки.

 Проекцию ускорения точки на касательную к ее траектории называют касательным ускорением, или тангенциальным ускорением (от латинского слова tangens—касающийся), и обозначают a_N.

Проекцию ускорения на нормаль называют нормальным ускорением и обозначают a_r.
Часто касательное и нормальное ускорения рассматривают не как проекции, а как составляющие полного ускорения, т. е. как векторные величины. В таком случае над а_r и a_N ставят стрелку, указывающую на их векторный характер.

Разложение ускорения по касательной и нормали имеет физический смысл: касательная составляющая ускорения направлена по касательной (как и скорость), а потому не может повлиять на направление скорости, но влияет на ее величину; составляющая ускорения по нормали направлена перпендикулярно к скорости, а потому не может повлиять на величину скорости, но влияет на ее направление.

Касательное ускорение равно первой производной от величины скорости по времени:

Касательное ускорение

Пусть точка M движется по траектории, расположенной в плоскости хОу.
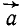
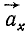
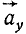
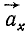
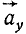
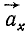
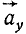
Проведем касательную и нормаль к кривой в точке M (рис. 91, б), нанесем на чертеж вектор ускорения точки M и его составляющие и по координатным осям. Чтобы определить касательное ускорение, надо спроецировать на касательную вектор полного ускорения или найти алгебраическую сумму проекций на касательную составляющих и полного ускорения по осям координат. Воспользовавшись вторым из этих способов, спроецируем и на касательную:

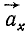
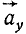
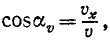
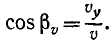
Составляющие ускорения и направлены по координатным осям, а направление касательной совпадает с направлением скорости, поэтому косинусы углов а и β равны направляющим косинусам скорости:

   (62′)

   (62»)

Подставляя значения направляющих косинусов, получаем

По формуле (68) удобно вычислять касательное ускорение точки, если ее движение задано в координатной форме уравнениями (58′) и (58″).

Можно дать еще другой изящный вывод формулы (68) тангенциального ускорения, для чего спроецировать на касательную вектор полного ускорения, не раскладывая его предварительно по осям декартовых координат. В самом деле, тангенциальное ускорение равно проекции полного ускорения на касательную (рис. 91, а):

a_r = a cos δ,
но угол δ, как внутренний угол треугольника, равен внешнему α_а без другого внутреннего α_υ, поэтому:

cos δ = cos (α_а—a_υ) = cos α_а cos a_υ + sin α_а sin a_υ

или, так как α_а = 90°- β_a и a_υ = 90°-β_υ, 

cos δ = cos α_а cos a_υ + cos β_a cos β_υ .

Подставляя сюда вместо направляющих косинусов их выражения (67) n (62′), получим

Напомним, что в числителе этой формулы проекции имеют свой знак, а знаменатель определяется по (64), т. е. существенно положителен.

Задача №1

Движение точки задано в декартовых координатах уравнениями:

x=21,2 sin² t,   y=21,2 cos² t

Определить касательное ускорение точки (см. задачу № 36, стр. 132).

Решение. Дифференцируя уравнения движения, найдем υ_x = 21,2 sin 2t, υ_y = -21,2 sin 2t. Определим теперь полную скорость:

Дифференцируя уравнения движения вторично, найдем

α_x = 42,2 cos 2t, α_y = -42,4 cos 2t.

Касательное ускорение определим по формуле (68):

Ответ. Касательное ускорение равно 60 cos 2t.

Задача №2

Точка M движется в системе координат хОу согласно уравнениям x=r cos πt, y=r sin πt. Найти касательное ускорение точки М.

Решение. Проекции скорости и ускорения на оси координат, а также и полная скорость точки M были уже нами получены при решении задачи № 44 (см. стр. 142). Для определения касательного ускорения точки M нам остается только подставить эти величины в формулу (68):

Ответ. Касательное ускорение равняется нулю.

Для случая задания движения в естественной форме преобразуем формулу (68) следующим образом:

и, сокращая на υ, найдем касательное ускорение

   (69)

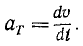
Принимая во внимание (53), можно придать этой формуле несколько иной вид:

   (69′)

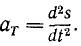
Итак, касательное ускорение—это проекция ускорения точки на касательную к траектории, равная первой производной от величины скорости по времени. Чтобы получить касательное ускорение в векторном выражении, нужно его умножить на единичный вектор касательной:

   (69»)

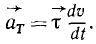
Как уже было сказано, касательное ускорение не может изменить направления скорости, оно характеризует быстроту изменения величины скорости, т. е. соответствует изменению вектора скорости вдоль его направления.

Если с течением времени величина скорости увеличивается, то касательное ускорение направлено в ту же сторону, что и скорость. Такое движение называют ускоренным.

Если же величина скорости уменьшается, то касательное ускорение направлено в сторону, противоположную скорости. Такое движение называют замедленным.

Каждое из этих движений называют переменным движением.

Если величина скорости точки постоянна, то производная 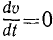, а потому равно нулю и касательное ускорение. Движение точки с постоянной по величине скоростью по любой траектории называют равномерным. Следовательно, при равномерном движении точки касательное ускорение равно нулю.

Обратное заключение можно сделать лишь с некоторой оговоркой: если касательное ускорение постоянно равняется нулю, то, следовательно, величина скорости постоянна и движение равномерно; если же касательное ускорение точки равняется нулю не в течение всего рассматриваемого промежутка времени, а только в какое-то мгновение, то движение точки не является равномерным, и равенство 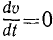означает, что в это мгновение величина скорости достигла экстремального (максимального или минимального) значения.

При равномерном движении точки по любой траектории

   (70)

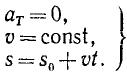
Формулы (70) справедливы только для равномерного движения точки и неприменимы при других движениях.

Равнопеременное движение точки

Из переменных движений точки в задачах наиболее часто встречается равнопеременное движение — такое движение, при котором касательное ускорение остается постоянным.

При равнопеременном движении точки по любой траектории
   (71)

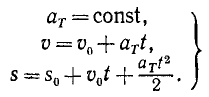
Формулы (71) справедливы только для равнопеременного движения и неприменимы при других движениях. Они даны здесь без вывода и известны из элементарной физики. Вывод этих формул приведен в решении задачи № 48.

Задача №3

Точка А начала двигаться с начальной скоростью υ₀= 1 м/сек и с ускорением a_T =2 м/сек². Через одну секунду следом за точкой А по той же траектории с такой же начальной скоростью и с таким же касательным ускорением стала двигаться точка В. Определить расстояние (по траектории) между точками А и В через t сек после выхода первой точки. Построить графики движения точек.

Решение. Определим сначала уравнение движения точек. Нам дано, что

Разделяя переменные и интегрируя, получим

υ = a_Tt + C₁

Постоянную C₁ определим из начальных данных:

υ₀ = a_T  ^. 0 + C₁;    C₁=υ₀

Следовательно, 

υ = υ_0  + a_Tt.

Написав υ по (53), разделяя переменные и интегрируя, найдем

где

С₂ = s₀ = 0.

Подставляя вместо υ₀ и а_T заданные величины, найдем расстояние (в м), пройденное точкой А за время t:

В то же мгновение t расстояние, пройденное точкой В, будет меньше, так как точка В будет находиться в пути лишь t—1 сек. Для точки В

Расстояние между A и B найдем как разность пройденных ими путей:

Это расстояние растет пропорционально времени, хотя точка В во времени не отстает от точки А и каждую точку траектории проходит через 1 сек после того, как через нее прошла точка А.

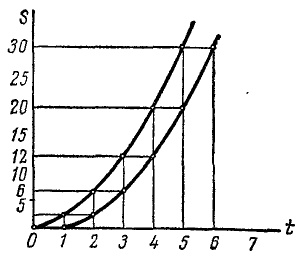
Графики движения точек А и В изображаются одинаковыми параболами (рис. 92), но парабола, представляющая движение точки В, смещена по оси времени относительно параболы, представляющей движение точки А, на 1 сек вправо. Чтобы определить расстояние (в м) между А и В в какое-либо мгновение, надо восставить перпендикуляр к оси времени в точке, соответствующей этому мгновению, и измерить расстояние по вертикали между параболами. Чтобы определить интервал времени (в сек) между прохождениями точками А и В какой-либо точки К траектории, надо восставить перпендикуляр к оси расстояний в точке, соответствующей расстоянию точки К от начала отсчета, и измерить расстояние по горизонтали между параболами. Графики наглядно показывают, что точка В отстает от точки А по расстоянию, так как А В непрерывно увеличивается, но не отстает по времени, и точка В проходит каждый отрезок траектории за такое же время, как и точка А.

Рис. 92

Ответ. S_A— S_B = 2t м.

Нормальное ускорение равно отношению квадрата скорости точки к радиусу кривизны траектории:

Нормальное ускорение

Чтобы получить формулы нормального ускорения, мы опять воспользуемся тем, что проекция вектора на ось равна сумме проекций его составляющих на ту же ось, и определим a_N как алгебраическую сумму проекций составляющих ax и ay на нормаль к траектории точки. Выберем за положительное направление нормали то, которое получается от поворота положительного направления касательной на прямой угол против хода часов (см. рис. 91) в сторону вогнутости кривой.
Как видно из чертежа (см. рис. 91, б)

a_N = a_y cos  α_υ—a_x cos β_υ.

Подставляем значения (62) направляющих косинусов:

   (72)

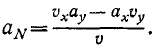
По этой формуле удобно вычислять нормальное ускорение точки, если ее движение задано в координатной форме уравнениями (58′) и (58″).

Эту же формулу (72) можно получить, спроецировав полное ускорение а на нормаль M_n (рис. 91, а):

a_N = a sin δ = a sin (α_α—α_υ)

или

a_N=a (sinα_α cos α_υ -cos α_α sin α_υ).

Подставляя эти значения и сокращая на а, получим:

Задача №4

Движение точки задано уравнениями X= 21,2 sin² t, у= 212 cos² t. Определить нормальное ускорение точки.

Решение. Дифференцируя эти же уравнения движения при решении задачи № 36 (см. стр. 132), мы уже определили нужные нам величины: υ_x, υ_y,  υ, a_x, а_у. Подставляя их в формулу (72), найдем

Ответ. Нормальное ускорение равно нулю.

Задача №5

Точка M движется согласно уравнениям x= r cos πt, y= r sin πt. Найти нормальное ускорение точки М.
Решение. Дифференцируя при решении задачи № 44 (см. стр. 142) эти уравнения движения, мы уже нашли проекции скорости и проекции ускорения. Полную скорость определим по ее проекциям согласно (64):

Подставляя все эти величины в формулу (72), найдем

Ответ. Нормальное ускорение равно rπ².

Чтобы преобразовать формулу (72) для случая, когда движение точки задано в естественной форме, припомним из курса высшей математики выражение кривизны плоской кривой, представленной в параметрической форме уравнениями (58′) и (58″),

Если параметр t означает время, то эту геометрическую формулу можно переписать в обозначениях кинематики:
   (73)

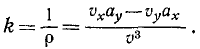
Сравнивая равенства (72) и (73), находим

   (74)

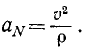
Мы получили положительное значение проекции, следовательно, нормальное ускорение направлено от точки M в положительном направлении оси M_n (см. рис. 91), т. е. в ту сторону от касательной, по которую лежит траектория точки.

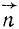
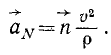
Чтобы получить нормальное ускорение в векторном выражении, надо (74) умножить на единичный вектор нормали:

      (74^/)

Как уже было сказано, нормальное ускорение не влияет на величину скорости, потому что оно направлено перпендикулярно к скорости. Оно влияет на направление скорости.

Итак, нормальное ускорение—это проекция ускорения точки на нормаль к траектории, направленная в сторону вогнутости, равная квадрату скорости, деленному на радиус кривизны траектории.
Если движение точки прямолинейное, то радиус кривизны траектории (прямой линии) равен бесконечности, а нормальное ускорение равно нулю.

Обратное заключение можно сделать лишь с некоторой оговоркой: если в каждое мгновение данного промежутка времени нормальное ускорение движущейся точки равняется нулю, то точка движется по прямой; если же нормальное ускорение точки не постоянно равно нулю, а только в какое-либо мгновение, то движение точки не а потому

является прямолинейным и равенство 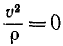означает, что в это мгновение положение точки совпадает с точкой перегиба траектории или же направление скорости меняется на обратное. На чертеже (рис. 93) изображено нормальное ускорение точки в различных местах траектории при равномерном движении.

Рис. 93

Величина ускорения точки равна квадратному корню из суммы квадратов касательного и нормального ускорений:

Ускорение при естественном способе задания движения

Если движение точки задано в естественной форме, то проекции ускорения на нормаль и на касательную можно определить по формулам (69) и (74) и по проекциям определить величину полного ускорения точки (см. рис. 91):

   (75)

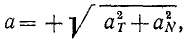
или

      (75^/)

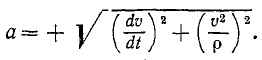
Перед радикалом стоит знак « + », потому что величина ускорения существенно положительна.

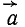
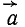
Вектор полного ускорения направлен по диагонали прямоугольника, построенного на векторах касательного и нормального ускорений. Можно точно установить направление ускорения по тангенсу угла, составляемого им с нормалью к траектории:

Касательное ускорение направлено по касательной к траектории, а нормальное к центру кривизны траектории, поэтому вектор полного ускорения лежит с той стороны от касательной, с которой расположена траектория точки.

При криволинейном ускоренном движений точки полное ускорение составляет со скоростью  острый угол, а при замедленном—тупой.

Вектор ускорения лежит в соприкасающейся плоскости, и проекция ускорения на бинормаль равна нулю:

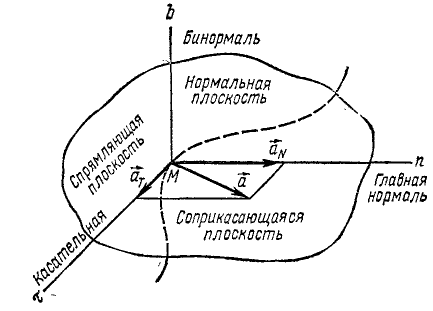
Разложение ускорения при движении точки по кривой двоякой кривизны. Если кривая не лежит в одной плоскости, то ее называют пространственной кривой, или кривой двоякой кривизны. В каждой точке к кривой можно провести только одну касательную и бесчисленное множество нормалей, расположенных в плоскости, перпендикулярной к касательной и называемой нормальной плоскостью (рис. 94).

рис. 94

Пусть в мгновение t точка занимает на кривой двоякой кривизны положение М. В это мгновение скорость точки направлена по касательной к кривой в точке М. Через эту касательную и через близкую точку M₁ (не показанную на чертеже)., в которую движущаяся точка придет в мгновение t + Δt, проведем плоскость и будем стремить Δt к нулю. Тогда точка M₁ будет стремиться к точке М. При этом плоскость будет поворачиваться около касательной, проведенной в точке М и стремиться к некоторому определенному положению, в котором она называется соприкасающейся плоскостью. Следовательно, в соприкасающейся плоскости находится вектор скорости движущейся точки в то мгновение, когда эта точка совпадает с точкой М, а также когда она занимает положение, предельно близкое к точке M. А так как ускорение характеризует изменение скорости в данное мгновение, то вектор ускорения тоже находится в соприкасающейся плоскости.

Плоскость, проведенную через точку M перпендикулярно к соприкасающейся и к нормальной плоскостям, называют спрямляющей плоскостью.

Нормаль, лежащую в спрямляющей плоскости, называют бинормалью, а нормаль, лежащую в соприкасающейся плоскости,—главной нормалью (главную нормаль плоской кривой обычно называют просто нормалью).

Касательная Mτ главная нормаль M_n и бинормаль M_b пересекаются в точке M под прямыми углами. Эти три взаимно перпендикулярные прямые в механике часто принимают в качестве координатных осей и называют естественными осями, или осями натурального триэдра. По мере движения точки по траектории естественные оси движутся вместе с ней, поворачиваются относительно основных (неподвижных) осей xOyz.

Положительные направления на естественных осях примем такими, чтобы трехгранный угол τMnb можно было привести в совпадение с углом xОyz. Касательная Mτ играет роль оси Ох, главная нормаль Mn— оси Oy и бинормаль Mb— оси Oz.

Так как вектор ускорения лежит в соприкасающейся плоскости τМn, а бинормаль Mb перпендикулярна к соприкасающейся плоскости, то проекция ускорения на бинормаль всегда равна нулю (α_b = 0), и при проецировании ускорения на три естественные оси мы имеем только две проекции: касательное ускорение и нормальное ускорение.

Таким образом, мы установили, что формулы (69), (69′) и (69″) касательного ускорения, формулы (74) и (74′) нормального ускорения, а также формулы (75) и (75′) полного ускорения, выведенные нами в предположении, что точка движется по плоской траектории, остаются справедливыми для любого движения точки.

Именно потому, что проекция ускорения на бинормаль всегда равна нулю, в формуле (75) величина полного ускорения определяется по двум проекциям, а не по трем, как это имеет место в формуле (66). Приравнивая выражение (66) модуля полного ускорения точки через проекции на неподвижные оси координат его же выражению (75) через проекции на естественные оси, получим для движения точки по любой траектории соотношение

   (76)

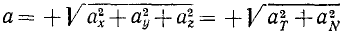
или

      (76^/)

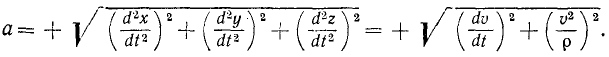
Эти равенства часто бывают полезны при решении задач.

Задача №6

Найти касательное и нормальное ускорения точки, движение которой выражается уравнениями:

Решение. Найдем проекции скорости и ускорения на оси координат:

x=υ_x=α, χ=a_x=0, y = υ_y = β-gt,  y= — g.

Подставляя найденные величины в (68), найдем касательное ускорение

Подставляя те же величины в формулу (72), найдем нормальное ускорение

Нормальное ускорение всегда направлено во внутрь траектории, отрицательный знак получился потому, что в этой задаче естественные оси взяты по левой системе, (ось М,— вправо, ось M_n — вниз), а неподвижные — по правой.

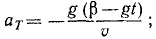
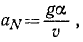
Ответ.   где υ — скорость точки.

Задача №7

Найти скорость, полное, касательное и нормальное ускорения точки, описывающей фигуру Лиссажу, по уравнениям движения точки, заданным в координатной форме:

х= 3 sin 2t, у = 4 sin 2t.

Решение. Найдем сначала проекции скорости:

υ_χ = 6 cos 2t, υ_y = 8 cos 2t.

Затем определим величину полной скорости точки:

Для определения касательного и нормального ускорений определим проекции ускорения на декартовы оси координат, затем найдем полное ускорение и разложим его на касательное и нормальное. Имеем

a_x= —12 sin 2t, a_y =—16 sin 2t, 

Найдем сначала касательное ускорение, для чего продифференцируем по времени полную скорость или воспользуемся формулой (68):

Мы видим, что полное ускорение по величине равно касательному ускорению, т. е. что нормальное ускорение равно нулю. Это возможно только в случае, если траектория — прямая линия. Для проверки можно определить кривизну траектории или найти уравнение траектории. По первому способу имеем

По второму способу найдем 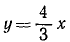(прямая).

Ответ. υ=10 cos 2t; α = 20 sin 2t; а_т= —20sin 2t; α_N = 0.

Задача №8

Точка обода колеса, катящегося без скольжения и без буксования по прямолинейному рельсу, движется согласно уравнениям x=r (ct-sin сt), y=r(l — cos ct). Найти нормальное ускорение точки.
Решение. Для решения задачи можно наметить следующий путь: найти проекции скорости, величину полной скорости, проекции ускорения и полное ускорение; затем, продифференцировав по времени величину полной скорости, найти касательное ускорение и, вычитая его геометрически из полного, найти нормальное.

Дифференцируя уравнения движения, найдем

υ_x= rc (1 —cos ct), υ_y = rc sin ct.

Далее получаем

Дифференцируя проекции скорости, найдем

a_x = rc² sin ct, a_y = rc² cos ct

полое ускорение 

а = rs²

Дифференцируя υ, найдем касательное ускорение:

Вектор aτ перпендикулярен вектору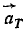 и в сумме с ним равняется вектору полного ускорения, поэтому

Задачи такого типа быстрее и короче решать с применением формулы (72). По этой формуле непосредственно получаем:

Ответ: 

Задача №9

Тяжелое тело, размерами которого можно пренебречь, брошено с большой высоты с горизонтальной скоростью υ₀ и движется согласно уравнениям x-υ₀t, 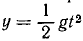. Найти траекторию, скорость, касательное и нормальное ускорения в любом положении, выразив их через скорость тела в этом положении.

Решение. Определяя из первого уравнения t и подставляя во второе, найдем уравнение траектории:

Траектория—парабола (рис. 95). Дифференцируя уравнения движения по времени, найдем проекции скорости и по ним полную скорость:

В начальное мгновение (t = 0), скорость точки υ = υ_o, а затем с течением времени величина скорости непрерывно возрастает. Из полученного равенства определим время t, в течение которого тело приобретает скорость у:

Вторично дифференцируя уравнения движения точки, найдем проекции ускорения на оси координат и полное ускорение:

В данном случае тело движется с постоянным по модулю и направлению ускорением, параллельным оси Оу.
Обращаем внимание на то, что, хотя здесь a = const, движение точки не является равнопеременным, так как условием равнопеременного движения является не условие a = const, а условие a_т= const. В данном же случае, как мы сейчас увидим, а_т непостоянно.

Дифференцируя величину полной скорости по времени или непосредственно по (68), получим касательное ускорение

Подставляя вместо t найденное нами значение, выразим касательное ускорение a_т через скорость υ:

Отсюда следует, что в начальное мгновение, когда υ = υ₀, a_т=0. Затем с увеличением υ величина а_т растет и в пределе стремится к полному ускорению g.
Для нахождения нормального ускорения обратимся к (72). Имеем

В начальное мгновение (при t = 0 и υ=v₀) a_N=g, а затем с увеличением υ а_N убывает, стремясь в пределе к нулю.
Ответ. Парабола

Задача №10

Определить радиус кривизны траектории точки в начале движения, если уравнения ее движения имеют вид: x = 2t, y = t² (t— в cек; х, у— в м).
Решение. Из формулы кривизны (73) имеем

Для получения проекций скорости и ускорения в начальное мгновение продифференцируем уравнения движения и подставим t = 0:

Полную скорость в начальное мгновение определяем по ее проекциям:

Подставляя эти величины в формулу (73), получим ответ.
Ответ. р = 2 м

Задача №11

Через 20 сек после начала движения автомобиль, двигаясь иа закруглении радиуса 400 м, приобрел скорость 108 км/ч. Считая, что величина скорости автомобиля пропорциональна квадрату времени, определить полное ускорение автомобиля в конце 20-й секунды н пройденное за это время расстояние.
Решение. За единицы принимаем метр и секунду. Траектория задана—дорога с закруглением радиуса 400 м, и для решения задачи необходимо определить Уравнение движения автомобиля по траектории. (Применять формулы (71) здесь нельзя, так как при равиоперемениом движении величина скорости пропорциональна времени, а в данной задаче она пропорциональна квадрату времени.)
В условии дано

υ=bt².

Найдем коэффициент пропорциональности

Выражая скорость по (53) и разделяя переменные, получим

откуда, интегрируя, получаем

Постоянную C определим из начальных данных: в начальное мгновение (t = 0) автомобиль не прошел еще никакого расстояния, а потому C = 0. Дважды дифференцируя по времени полученное уравнение, найдем касательное ускорение

или в конце 20-й секунды

α_т=3 м/ceκ².

Скорость в конце 20-й секунды была 30 м/сек, и по (74)

Полное ускорение в конце 20-й секунды было

Чтобы определить расстояние, пройденное автомобилем за 20 сек, положим в уравнении движения t = 20 сек:

Ответ. а = 3,75 м/сек², s = 200 м.

Ускорение и его составляющие

В случае неравномерного движения важно
знать, как быстро изменяется скорость
с течением времени. Физической величиной,
характеризующей быстроту изменения
скорости по модулю и направлению,
является ускорение.

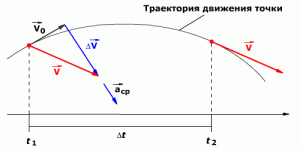
Рассмотрим плоское движение, т.е.
движение, при котором все участки
траектории точки лежат в одной плоскости.
Пусть вектор v задает скорость точки А
в момент времени t.
За время t
движущаяся точка перешла в положение
В и приобрела скорость, отличную от
v как по модулю, так и
направлению и равную v₁
= v + v.
Перенесем вектор v₁
в точку А и найдем v
(рис. 4).

Средним ускорением неравномерного
движения в интервале от t
до t + t
называется векторная величина, равная
отношению изменения скорости v
к интервалу вре­мени t

Мгновенным ускорением а (ускорением)
материальной точки в момент време­ни
t будет предел среднего
ускорения:

Таким образом, ускорение a
есть векторная величина, равная первой
производной скорости по времени.

Разложим вектор v
на две составляющие. Для этого из точки
А (рис. 4) по направлению скорости v
отложим вектор

,
по модулю равный v₁.
Очевидно, что вектор

,
равный

,
определяет изменение скорости за время
t
по моду­лю:

.
Вторая же составляющая

вектора v
характеризует изменение ско­рости
за время t
по направлению.

1. Тангенциальное и нормальное ускорение.

Тангенциа́льное
ускоре́ние
— компонента ускорения, направленная
по касательной к траектории движения.
Совпадает с направлением вектора
скорости при ускоренном движении и
противоположно направлено при замедленном.
Характеризует изменение модуля скорости.
Обозначается обычно или (, итд в
соответствии с тем, какая буква выбрана
для обозначения ускорения вообще в
данном тексте).

Иногда
под тангенциальным ускорением понимают
проекцию вектора тангенциального
ускорения — как он определен выше — на
единичный вектор касательной к траектории,
что совпадает с проекцией (полного)
вектора ускорения на единичный вектор
касательной то есть соответствующий
коэффициент разложения по сопутствующему
базису. В этом случае используется не
векторное обозначение, а «скалярное»
— как обычно для проекции или координаты
вектора —

.

Величину
тангенциального ускорения — в смысле
проекции вектора ускорения на единичный
касательный вектор траектории — можно
выразить так:

где

— путевая скорость вдоль траектории,
совпадающая с абсолютной величиной
мгновенной скорости в данный момент.

Если
использовать для единичного касательного
вектора обозначение

,
то можно записать тангенциальное
ускорение в векторном виде:

Вывод

Выражение
для тангенциального ускорения можно
найти, продифференцировав по времени
вектор скорости, представленный в виде

через единичный вектор касательной

:

где
первое слагаемое — тангенциальное
ускорение, а второе — нормальное
ускорение.

Здесь
использовано обозначение

для единичного вектора нормали к
траектории и

— для текущей длины траектории (
);
в последнем переходе также использовано
очевидное

и,
из геометрических соображений,

Центростремительное
ускорение(нормальное) —
часть полного ускорения точки,
обусловленного кривизной траектории
и скоростью движения по ней материальной
точки. Такое ускорение направлено к
центру кривизны траектории, чем и
обусловлен термин. Формально и по
существу термин центростремительное
ускорение в целом совпадает с термином
нормальное ускорение, различаясь скорее
лишь стилистически (иногда исторически).

Особенно
часто о центростремительном ускорении
говорят, когда речь идет о равномерном
движении по окружности или при движении,
более или менее приближенном к этому
частному случаю.

Элементарная
формула

или

где

— нормальное (центростремительное)
ускорение,

— (мгновенная) линейная скорость движения
по траектории,

— (мгновенная) угловая скорость этого
движения относительно центра кривизны
траектории,

— радиус кривизны траектории в данной
точке. (Cвязь между первой формулой и
второй очевидна, учитывая ).

Выражения
выше включают абсолютные величины. Их
легко записать в векторном виде, домножив
на — единичный вектор от центра кривизны
траектории к данной ее точки:

Эти
формулы равно применимы к случаю движения
с постоянной (по абсолютной величине)
скоростью, так и к произвольному случаю.
Однако во втором надо иметь в виду, что
центростремительное ускорение не есть
полный вектор ускорения, а лишь его
составляющая, перпендикулярная траектории
(или, что то же, перпендикулярная вектору
мгновенной скорости); в полный же вектор
ускорения тогда входит еще и тангенциальная
составляющая (тангенциальное ускорение)

,
по направлению совпадающее с касательной
к траектории (или, что то же, с мгновенной
скоростью).

вывод

То,
что разложение вектора ускорения на
компоненты — одну вдоль касательного
к траектории вектора (тангенциальное
ускорение) и другую ортогональную ему
(нормальное ускорение) — может быть
удобным и полезным, довольно очевидно
само по себе. Это усугубляется тем, что
при движении с постоянной по величине
скоростью тангенциальная составляющая
будет равной нулю, то есть в этом важном
частном случае остается только нормальная
составляющая. Кроме того, как можно
увидеть ниже, каждая из этих составляющих
имеет ярко выраженные собственные
свойства и структуру, и нормальное
ускорение содержит в структуре своей
формулы достаточно важное и нетривиальное
геометрическое наполнение. Не говоря
уже о важном частном случае движения
по окружности (который, к тому же,
практически без изменения может быть
обобщен и на общий случай).

Формальный
вывод

Разложение
ускорения на тангенциальную и нормальную
компоненты (вторая из которых и есть
центростремительное или нормальное
ускорение) можно найти, продифференцировав
по времени вектор скорости, представленнный
в виде

через единичный вектор касательной

.

Где
первое слагаемое — тангенциальное
ускорение, а второе — нормальное
ускорение.

Здесь
использовано обозначение

для единичного вектора нормали к
траектории и —

для

текущей
длины траектории (
);
в последнем переходе также использовано
очевидное

.

Далее
можно просто формально назвать член

—

нормальным
(центростремительным) ускорением. При
этом его смысл, смысл входящих в него
объектов, а также доказательство того
факта, что он действительно ортогонален
касательному вектору (то есть что —
действительно вектор нормали) — будет
следовать из геометрических соображений
(впрочем, то, что производная любого
вектора постоянной длины по времени
перпендикулярна самому этому вектору,
— достаточно простой факт; в данном
случае мы применяем это утверждение
для ).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).

Среднее ускорение

Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с², то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

v2 > v1

а направление вектора ускорения совпадает с вектором скорости 

Если скорость тела по модулю уменьшается, то есть

v2 < v1

то направление вектора ускорения противоположно направлению вектора скорости  Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.

Рис. 1.9. Мгновенное ускорение.

При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).

Тангенциальное ускорение

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения  (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов: