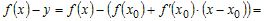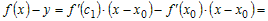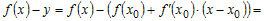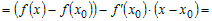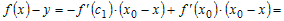Опр.Точка
графика функции
называетсяточкой перегибаэтого
графика, если существует такая окрестность
точкисоси абсцисс, в пределах
которой график функции
слева и справа отсимеет разные
направления выпуклости.
Иногда при определении точки перегиба
графика функции
дополнительно требуют, чтобы этот график
всюду в пределах достаточно малой
окрестности точки с оси абсцисс слева
и справа от с лежал по разные стороны
от касательной к этому графику в точке
.
Точки отделяющие выпуклую вверх часть
кривой от выпуклой вниз (или наоборот)
называются точками перегиба, в точках
перегиба касательная пересекает кривую.
Th. Если ф-яy=f(x)
во всех точках (a;b)
имеет отрицательную вторую производную
т.е.f II
<0, то график ф-ии на этом интервале
выпуклый вверх. Еслиf
II >0, то
он выпуклый вниз.
Достаточное условие существования
точек перегиба.
Если f II(x)
при переходе черезx0в которой она равна 0 или не существует,
меняет знак то точка графика с абсциссойx0есть точка перегиба.
ПРИМЕР:
y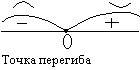
yI=5x
4-1
yII=20x3
20x3=0
x=0
График выпуклый
вверх в интервале (-;0),
график вогнутый на (0; +),
(0;5) – точка перегиба.
Th.
(необх. усл-е сущ-е точки перегиба). Если
в точке есть перегиб у дважды дифф-й
ф-ции, тоf”(c)=0/
f”(c)-не
полож-е, не отриц-е, значит 0
f(x)=x4
c=0
f”(x)=12x2
f”(c)-усл-е
необх-е, но не дост-е.
(дост.
усл. т. перегиба) Если ф-ция дважды дифф-ма
в окр т.с, то с-точка перегиба, меняет
знак.
38. Вертикальные и наклонные асимптоты графика функции.
Определение
наклонной асимптоты к графику функции.
Опр.Говорят, что прямая
(1)
является наклонной асимптотойграфика функциипри
,
если функцияf(x)
представима в виде
,
где
(2)
Опр. Говорят, что прямая x
= a является
вертикальной асимптотой графика функции
,
если хотя бы одно из предельных значений
или
равно + или
—.
Опр.
Часть графика называется бесконечной
ветвью если при движении точки по этой
части, расстояние между ей и началом
координат стремится к бесконечности.
Опр.Прямая называется асимптотой бесконечной
ветви графика функции, если при удалении
точки от начала координат по этой ветви,
расстояние до данной прямой стремится
к нулю.
Теорема
1:x=a(вертикальная прямая) – является
асимптотой для бесконечно вертикальной
ветви графика функцииy=f(x),
тогда когдаf(x),
приxa.
Т
2:Критерий существования
наклонной асимптоты прямаяy=kx+bявляется асимптотой для правой (левой)
ветви графика функции тогда, когда
существует предел при :
Док-во:ТочкаM0(x0,y0)
и прямая
L:Ax+By+Cz=0,
то расстояние
П
асимптота
=>
d(M,l)0=>
kx-f(x)+b0
тогда
f(x)-kxb
при
x+
существует
предел:
Теорема:
Необходимый признак существования
наклонной асимптоты.Если прямаяl:y=kx+b
наклонная
асимп. для правой наклонной ветви, то:
Док-во:
Пример:
x=1
– верт. Асимптота, т.к.
f(x),
когдаx1
Вывод:y=0y+1
– наклонная асимптота для левой и правой
ветви.
Для отыскания вертикальной асимптоты
нужно найти х вблизи которого функция
f(x) возрастает
по модулю. Обычно это точки разрыва
второго рода.
Если хотя бы один из этих
пределов не существует, то кривая
асимптоты не имеет. Если k=0,bимеет конечное значение,
то асимптота наз-ся горизонтальной.
График функции y=f(x) называется выпуклым на интервале (a;
b), если он расположен ниже любой своей касательной на
этом интервале.
График функции y=f(x) называется вогнутым на интервале (a;
b), если он расположен выше любой своей касательной на
этом интервале.
На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).
Примеры.
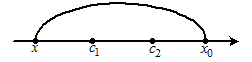
- Полуокружность
выпукла на [–1; 1].
- Парабола y = x2 вогнута на интервале (-∞; +∞).
- График функции в одних интервалах может быть
выпуклым, а в других вогнутым. Так график функции y = sin x на
[0,2; π], выпуклый в интервале (0; π) и вогнутый в (π;
2π).
Рассмотрим достаточный признак, позволяющий установить,
будет ли график функции в данном интервале выпуклым или вогнутым.
Теорема. Пусть y=f(x) дифференцируема на (a;
b). Если во всех точках интервала (a;
b) вторая производная функции y = f(x) отрицательная, т.е. f »(x) < 0, то график функции
на этом интервале выпуклый, если же f»(x) > 0 – вогнутый.
Доказательство.
Предположим для определенности, что f»(x) < 0 и докажем, что график функции будет выпуклым.
Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.
Итак, уравнение кривой имеет вид y
= f(x). Обозначим ординату касательной,
соответствующую абсциссе x. Тогда . Следовательно, разность ординат кривой и касательной при
одном и том же значении x будет .
Разность f(x)
– f(x0) преобразуем по теореме
Лагранжа , где c между x и x0.
Таким образом,
.
К выражению, стоящему в квадратных скобках
снова применим теорему Лагранжа: , где c1 между c0 и x0. По условию теоремы f »(x) < 0. Определим знак
произведения второго и третьего сомножителей.
- Предположим, что x>x0. Тогда x0<c1<c<x,
следовательно,(x – x0)
> 0 и (c – x0) > 0. Поэтому.
- Пусть x<x0, следовательно, x < c
< c1 < x0 и (x – x0)
< 0, (c – x0) < 0. Поэтому вновь.
Таким образом, любая
точка кривой лежит ниже касательной к кривой при всех значениях x и x0 Î
(a; b), а это значит, что кривая
выпукла. Вторая часть теоремы доказывается аналогично.
Примеры.
- Установить интервалы
выпуклости и вогнутости кривой y = 2 – x2.Найдем y » и определим, где вторая
производная положительна и где отрицательна. y‘ = –2x, y» = –2 < 0 на (–∞; +∞), следовательно, функция всюду
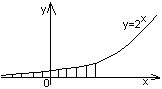
выпукла. - y = ex. Так как y» = ex
> 0 при любых x, то кривая всюду вогнута. - y = x3. Так как y» = 6x, то y» < 0 при x
< 0 и y» > 0 при x
> 0. Следовательно, при x < 0 кривая выпукла, а
при x > 0 вогнута.
Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной
стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.
Определим достаточные
условия того, что данная точка кривой является точкой перегиба.
Теорема. Пусть кривая определяется
уравнением y = f(x). Если f »(x0) = 0 или f »(x0) не существует и при переходе
через значение x = x0 производная f »(x) меняет знак, то точка
графика функции с абсциссой x = x0 есть точка перегиба.
Доказательство. Пусть
f »(x) < 0 при x
< x0 и f
»(x) > 0 при x
> x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с
абсциссой x0 есть точка перегиба. Аналогично можно
рассматривать второй случай, когда f
»(x) > 0 при x
< x0 и f
»(x) < 0 при x
> x0.
Таким образом, точки перегиба следует искать только
среди таких точек, где вторая производная обращается в нуль или не существует.
Примеры. Найти точки перегиба и определить интервалы
выпуклости и вогнутости кривых.
Найдем производные
заданной функции до второго порядка..
. Вторая производная не существует при x =
1. Исследуем эту точку на возможный перегиб.Итак, точка
перегиба x = 1. Функция выпукла на (1; +∞), вогнута на (–∞;
1).Возможные точки
перегиба найдем, решив уравнение 2x2 – 1 = 0. Отсюда.
Точки перегиба
. Функция выпукла на
и вогнута на
.
- y = ln (1 – x2). Область определения функции D(y) = (-1; 1).
.
при всех x из
(–1; 1).Следовательно,
f(x) выпуклая на (–1; 1).
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
При исследовании функции
важно установить форму ее графика при неограниченном удалении точки графика от
начала координат.
Особый интерес
представляет случай, когда график функции при удалении его переменной точки в
бесконечность неограниченно приближается к некоторой
прямой.
Прямая называется асимптотой графика функции y = f(x), если расстояние от
переменной точки M графика до этой прямой при удалении точки M в
бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении
в бесконечность должна неограниченно приближаться к асимптоте.
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от
нее или с разных сторон, бесконечное множество раз пересекая асимптоту и
переходя с одной ее стороны на другую.
Если обозначим
через d расстояние от точки M
кривой до асимптоты, то ясно, что d стремится к нулю при
удалении точки M в бесконечность.
Будем в дальнейшем различать асимптоты вертикальные и наклонные.
ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ
Пусть при x→ x0 с какой-либо стороны функция y = f(x)неограниченно возрастает по абсолютной
величине, т.е. или
или
. Тогда из определения асимптоты следует, что прямая x = x0 является асимптотой. Очевидно и обратное,
если прямая x = x0 является асимптотой, т. о. .
Таким образом, вертикальной
асимптотой графика функции y = f(x)
называется прямая, если f(x) → ∞ хотя бы при одном из условий x→
x0 – 0 или x → x0 + 0, x = x0
Следовательно,
для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x0, при которых функция обращается в бесконечность (терпит бесконечный
разрыв). Тогда вертикальная асимптота имеет уравнение x = x0.
Примеры.
- Найти вертикальные асимптоты графика функции
.
Так как
, то прямая x =
2 является вертикальной асимптотой. .
Прямая x = 0 – вертикальная асимптота.
НАКЛОННЫЕ АСИМПТОТЫ
Поскольку
асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту,
то ее уравнение будет y = kx + b. Наша задача найти
коэффициенты k и b.
Теорема. Прямая y = kx + b служит наклонной
асимптотой при x → +∞
для графика функции y
= f(x) тогда и только тогда,
когда . Аналогичное утверждение верно и при x → –∞.
Доказательство. Пусть MP –
длина отрезка, равного расстоянию от точки M до асимптоты. По условию . Обозначим через φ угол наклона асимптоты к
оси Ox. Тогда из ΔMNP
следует, что . Так как φ постоянный угол (φ ≠ π/2), то
, но
MN = MK – NK = y — yас = f(x) — (kx+b).
Следовательно, мы можем
записать следующее равенство .
Так как x → +∞, то должно
выполняться равенство . Но при постоянных k и b
и
. Следовательно,
, т.е.
.
Если число k
уже известно, то , поэтому
.
Для
доказательства в случае x → –∞ все рассуждения аналогичны.
Докажем обратное
утверждение. Предположим, что существуют пределы, определяющие числа k и b.
Тогда несложно заметить, что выполняется равенство . Действительно
Следовательно,
прямая y = kx + b
есть асимптота. Теорема полностью доказана.
Сделаем несколько замечаний.
Замечание 1. Теорема
показывает, что для нахождения асимптот достаточно найти два указанных предела.
Причем, если хотя бы один из пределов не существует или обращается в бесконечность,
то кривая асимптот не имеет.
Замечание 2. В случае,
когда k = 0 асимптота y = b
называется горизонтальной асимптотой. Наличие горизонтальной асимптоты
означает, что существуют пределы
.
Замечание 3. Пределы для отыскания k и b могут
быть различны при x
→ +∞ и x
→ – ∞ и, следовательно, график функции может иметь две различные
асимптоты при x → +∞ и x → –∞.
Примеры. Найти асимптоты кривых.
.
- Вертикальные:
x = 0 – вертикальная асимптота.
- Наклонные:
.
При x → — ∞ получим те
же значения k и b. Следовательно, прямая
y = x + 2 является наклонной асимптотой.
- Вертикальные:
- y = e–x sin x + x.
- Функция определена и непрерывна на всей числовой прямой, следовательно,
вертикальных асимптот нет. -
а)
.
Итак, при x
→ +∞ наклонная асимптота у=
х.б)
, т. к.
, поэтому при x
→ — ∞ наклонных асимптот нет.
- Функция определена и непрерывна на всей числовой прямой, следовательно,
- y = x – 2arctg x.
- Вертикальных асимптот нет.
-
а)
.
. Наклонная асимптота y = x – π
при.
б)
при
.
1) Возьмем произвольную точку 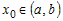
функции в этой точке имеет вид:
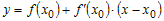
Покажем, что в любой точке 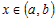
этой касательной.
Рассмотрим любую точку 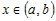
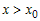
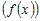
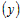
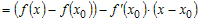
Поскольку функция 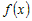
промежутке 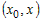
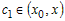
равенство
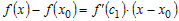
Учитывая это, разность ординат функции и касательной в точке 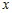
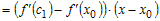
Производная 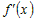
промежутке 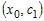
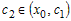
равенство
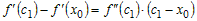
Учитывая это, разность ординат функции и касательной в точке 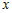
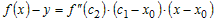
Так как 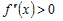
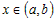
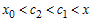
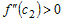
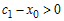
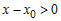
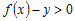
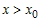
касательной.
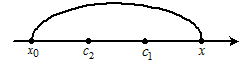 |
| Рис. 18 |
2) Рассмотрим любую точку 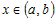
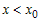
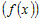
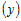
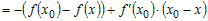
Поскольку функция 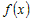
промежутке 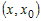
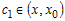
равенство
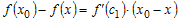
Учитывая это, разность ординат функции и касательной в точке 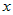
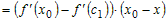
Производная 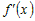
промежутке 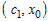
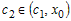
равенство
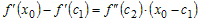
Учитывая это, разность ординат функции и касательной в точке 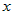
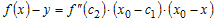
Так как 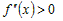
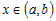
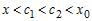
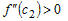
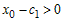
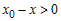
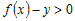
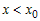
касательной.
 |
| Рис. 19. |



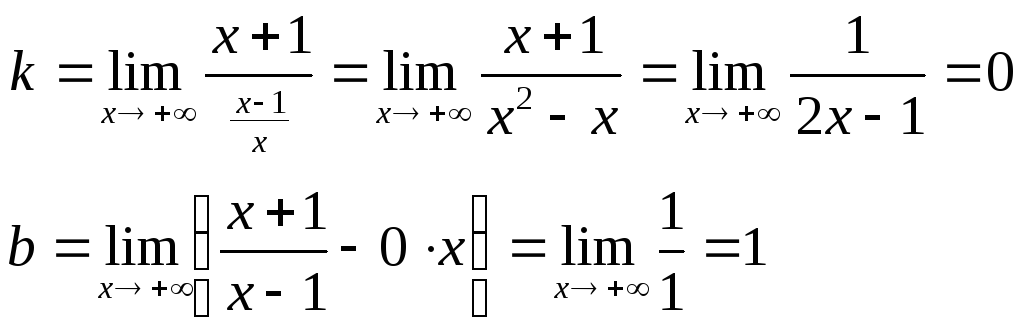











 при всех x из
при всех x из




 .
. .
. , т. к.
, т. к. , поэтому при x
, поэтому при x