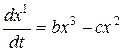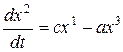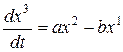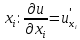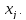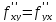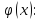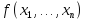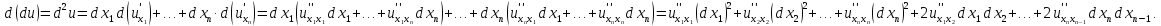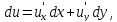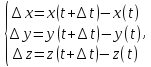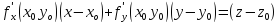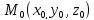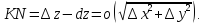Как найти касательный вектор к кривой - Исправление недочетов и поиск решений вместе с Examum.ru

VMath

Инструменты сайта

Основное

Информация

Действия

Содержание

Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Краткие теоретические сведения

Кривая в пространстве

Рассмотрим в пространстве гладкую кривую $gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end

Пусть в точке $M$ $ vec(t_0)neqvec<0>$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.

Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).

Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x»(t_0) & y»(t_0) & z»(t_0) \ end right|=0 end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:

Уравнение в каноническом виде распишите самостоятельно.

Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ vec<tau>=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec<beta>=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec<nu>=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$

Правая тройка векторов $vec<tau>$, $vec<nu>$, $vec<beta>$ называется репером Френе.

Решение задач

Задача 1

Кривая $gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end

begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end

begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec<tau>$, $vec<nu>$, $vec<beta>$ не будет правой (по определению векторного произведения вектор $vec<tau>timesvec<beta>$ направлен так, что тройка векторов $vec<tau>$, $vec<beta>$, $vec<nu>=vec<tau>timesvec<beta>$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $vec<tau>$, $vec<nu>$, $vec<tilde<beta>>$ образует репер Френе для кривой $gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac<2>,,, z=frac<3>, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end

begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.

Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_<01>=2,, t_<02>=-frac25. end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end

Касательный вектор и касательное пространство к многообразию

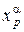
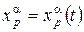
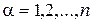
Пусть на многообразии M задана кривая x = x(t) , a £ t £ b , где x – точка многообразия. Пока кривая находится в области U_p действия локальных координат , уравнения кривой можно записать в виде

В этих координатах имеем вектор скорости кривой

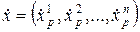
В области действия двух координатных систем U_p и U_q имеем две записи для уравнения кривой

и ,

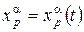
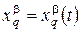
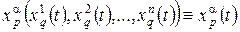
Дифференцируя это равенство получаем

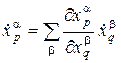
На основании этой формулы вводится следующее определение.

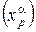
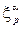
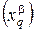
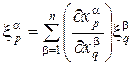
Определение 1. Касательным вектором к многообразию M в произвольной точке x называется вектор, записываемый в системе локальных координат набором чисел , который при переходе к другой системе координат преобразуется по закону

Касательные векторы к n-мерному многообразию M в данной точке x образуют n-мерное линейное пространство T_x = T_xM — касательное пространство.

В частности, вектор скорости любой гладкой кривой является касательным вектором.

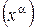
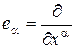
Выбор локальных координат в окрестности точки x задает базис в касательном пространстве T_x .

Гладкое отображение f многообразия M в многообразие N определяет индуцированное линейное отображение касательных пространств

При этом вектор скорости кривой x = x(t) на многообразии M переходит в вектор скорости кривой f(x(t)) на многообразии N.

В локальных координатах (x a ) в окрестности точки x и локальных координатах (y b ) в окрестности точки f(x) отображение f имеет вид

y b = f b (x 1 ,x 2 ,…,x n ), b = 1, 2, …, m ,

тогда индуцированное отображение f_* касательных пространств задается матрицей Якоби:

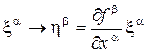
Векторное поле

Определение 1. Если в каждой точке x многообразия M определен вектор из соответствующего касательного пространства T_x, то говорят, что на многообразии задано векторное поле.

Для уточнения этого понятия отметим, что на множестве TM всех касательных пространств к многообразию M естественным образом вводится структура многообразия, картами которого служат прямые суммы карт многообразия M и касательных пространств к M в соответствующих точках многообразия M. Получаемое таким образом многообразие называется векторным расслоением многообразия M .Теперь векторное поле на многообразии M можно определить как отображение

такое, что y(x) Î T_xM для каждого x Î M.

Определение 2. Векторное поле называется гладким (класса C ¥ ), если отображение y является гладким.

В локальных координатах многообразия TM векторное поле имеет вид

. (2)

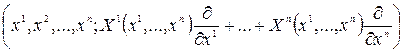
Определение 3. Векторной линией называется такая линия многообразия, в каждой точке которой вектор поля касается этой линии. Векторные линии также называются орбитами и интегральными кривыми векторного поля.

В локальных координатах векторная линия описывается следующей системой дифференциальных уравнений:

, i = 1,2,…,n ,

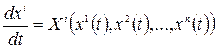
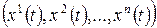
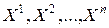
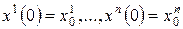
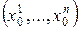
где — координатное задание искомой линии, а — координаты векторной части векторного поля. Граничным условием здесь является , где — координаты точки x_o.

Пример 1. В трехмерном евклидовом пространстве рассмотрим векторное поле

X 1 = bx 3 – cx 2 , X 2 = cx 1 — ax 3 , X 3 = ax 2 — bx 1 .

Система дифференциальных уравнений для нахождения векторной линии принимает вид

Умножим эти уравнения на x i соответственно и, сложив, получим

x 1 dx 1 + x 2 dx 2 + x 3 dx 3 = 0 dt = 0. (3)

Аналогично, умножая эти уравнения на a, b и c и складывая получим

adx 1 + bdx 2 + cdx 3 = 0. (4)

Интегрируя уравнения (3) и (4) получаем следующую систему уравнений

(5)

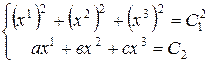
Из этой системы следует, что векторные линии рассматриваемого векторного поля получаются в результате пересечения всевозможных концентрических сфер с центрами в начале координат со всевозможными плоскостями перпендикулярными вектору (a,b,c), то есть, векторные линии данного векторного поля являются окружностями с центрами на прямой, проходящей через начало координат и имеющей направляющим вектором вектор (a,b,c) и лежащими в плоскостях перпендикулярных этой прямой.

Отметим, что рассмотренное векторное поле является полем скоростей точек твердого тела, вращающегося вокруг описанной выше прямой с постоянной угловой скоростью.

Касательная и нормаль к графику функции

Основные формулы

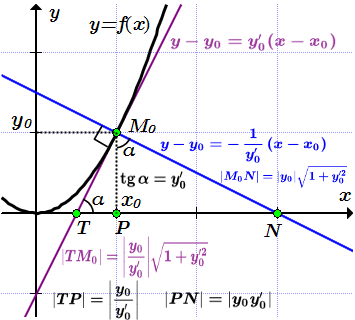
Пусть на некотором интервале X задана функция . Нас интересуют геометрические характеристики графика этой функции в некоторой заданной точке при значении аргумента , где . Пусть функция имеет в производную, которую будем обозначать как . Тогда через точку мы можем провести касательную к графику. Тангенс угла α между осью абсцисс x и касательной равен производной функции в точке :
(1) .
А само уравнение касательной имеет вид:
(2) .
В аналитической геометрии тангенс угла между прямой и осью абсцисс называют угловым коэффициентом прямой. Таким образом производная равна угловому коэффициенту касательной в .
См. Геометрический смысл производной

Прямая, перпендикулярная касательной, проведенной через точку , называется нормалью к графику функции в этой точке. Уравнение нормали имеет вид:
(3) .
См. Уравнение прямой с угловым коэффициентом ⇓

Пусть две кривые и пересекаются в точке . Тогда угол φ между касательными к этим кривым в точке называется углом между кривыми. Он определяется по формуле:
(4) , где .
Отсюда .
при .
Вывод формулы ⇓

Определения

Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.

Определение касательной приводится здесь. Уравнение касательной:
.

Касательная TM₀, нормаль M₀N, подкасательная TP, поднормаль PN. Нормалью к графику функции в точке называется прямая, перпендикулярная касательной, проведенной через эту точку. Уравнение нормали:
.
Отрезком касательной называют отрезок между точкой пересечения касательной с осью абсцисс и точкой .
.
Отрезком нормали называют отрезок между точкой пересечения нормали с осью абсцисс и точкой .
.
Подкасательной называют отрезок между точкой пересечения касательной с осью абсцисс и проекции точки на эту ось.
.
Поднормалью называют отрезок между точкой пересечения нормали с осью абсцисс и проекции точки на эту ось.
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым, проведенных через точку .

Полезные формулы из аналитической геометрии

Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.

Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.

Умножив это уравнение на , получим уравнение прямой в другом виде:
.
Здесь – вектор нормали прямой. Тогда само уравнение означает равенство нулю скалярного произведения векторов и .

Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :

Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.

Уравнение прямой с угловым коэффициентом k , проходящей через точку :
.
Угол α между прямой и осью x определяется по формуле:
.
Если две прямые взаимно перпендикулярны, то их угловые коэффициенты и связаны соотношением:
.

Уравнение прямой в отрезках, пересекающей оси координат в точках :
.

Примеры решения задач

Все примеры Ниже рассмотрены примеры решений следующих задач.
1. Найти уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали. Решение ⇓
2. Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде
, проведенных в точке . Решение ⇓
3. Заданной в неявном виде . Решение ⇓
4. Найти угол между кривыми и Решение ⇓

Пример 1

Составить уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали.

Находим значение функции при :
.

Находим производную:
.
Находим производную в точке :
;
.

Находим уравнение касательной по формуле (2):
;
;
;
– уравнение касательной.
Строим касательную на графике. Поскольку касательная – это прямая, то нам нужно знать положения двух ее точек, и провести через них прямую.
При ;
при .
Проводим касательную через точки и .

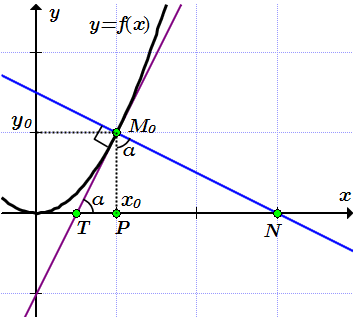
Касательная и нормаль к графику функции y=x 2 в точке M₀(1;1).

Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.

Находим уравнение нормали по формуле (3):
;
;
;
;
;
– уравнение нормали.
Строим нормаль по двум точкам.
При ;
при .
Проводим нормаль через точки и .

Находим длину отрезка касательной . Из прямоугольника имеем:
.
Поясним использованную формулу. Поскольку , то . Тогда
.
Подставляем :
.

Находим длину отрезка подкасательной . Из прямоугольника имеем:
.
Подставляем :
.

Находим длину отрезка нормали . Поскольку и , то треугольники и подобны. Тогда . Из прямоугольника имеем:
.
Подставляем :
.

Находим длину отрезка поднормали . Из прямоугольника имеем:
.

Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.

Уравнение касательной: ; уравнение нормали: ;
длина отрезка касательной: ; длина отрезка нормали: ; длина подкасательной: ; длина поднормали: .

Пример 2

Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде , проведенных в точке .

Находим значения переменных при .
;
.
Обозначим эту точку как .

Находим производные переменных x и y по параметру t .
;
;
;
;
.

Подставляя , находим производную y по x в точке .
.

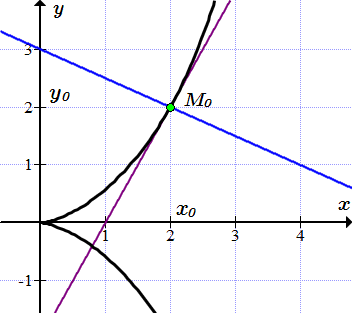
Касательная и нормаль к циссоиде в точке (2;2).

Применяя формулу (2), находим уравнение касательной к циссоиде, проходящей через точку .
;
;
;
.

Применяя формулу (3), находим уравнение нормали к циссоиде в точке .
;
;
;
.

Уравнение касательной: .
Уравнение нормали: .

Пример 3

Составить уравнения касательной и нормали к циссоиде, заданной в неявном виде:
(П3) ,
проведенных в точке .

Для получения уравнение касательной и нормали, нам нужно знать значение производной функции в заданной точке. Функция (П3) задана неявно. Поэтому применяем правило дифференцирования неявной функции. Для этого дифференцируем (П3) по x , считая, что y является функцией от x .
;
;
;
.
Отсюда
.

Находим производную в заданной точке, подставляя .
;
.

Находим уравнение касательной по формуле (2).
;
;
;
.

Находим уравнение нормали по формуле (3).
;
;
;
.

Касательная и нормаль к циссоиде изображены на рисунке ⇑.

Уравнение касательной: .
Уравнение нормали: .

Пример 4

Найти угол между кривыми и .

Найдем множество точек пересечения кривых, решая систему уравнений.

Левые части равны. Приравниваем правые части и выполняем преобразования.
;
(П4) .
Поскольку функция строго монотонна, то уравнение (П4) имеет один корень:
.
При . Кривые пересекаются в единственной точке . Обозначим ее как , где .

Введем обозначения для функций, с помощью которых заданы кривые:
.
Найдем их производные.
;
.
Найдем значения производных в точке , подставляя .
;
.

Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.

Вывод формулы для угла между кривыми

Изложим вывод формулы (4). Для иллюстрации используем только что рассмотренный пример ⇑, в котором .

Рассмотрим две кривые, заданные уравнениями и , и пересекающиеся в некоторой точке . Докажем, что угол между кривыми определяется по формуле (4):
, где .
Или ;
при .

Проведем касательные к графикам функций в точке . Углы, которые образуют касательные с осью x обозначим как и . За положительное направление выберем направление против часовой стрелки. На рисунке . Считаем, что значения углов принадлежат интервалам . Согласно геометрическому смыслу производной,
.

В аналитической геометрии принято, что угол φ между прямыми равен наименьшему значению угла между ними.
Если , то ;
если , то .
Таким образом величина угла φ между касательными может находиться только в пределах
(Ф2) .

На рисунке угол между лучами и больше 90°, а между лучами и – меньше. Поэтому .

При доказательстве мы будем использовать соотношение:
, которое выполняется при .
Тогда в силу (Ф2),
.
Случай мы рассмотрим отдельно.

1) Пусть .
Тогда угол между прямыми . И мы имеем:
.
В конце мы подставили (Ф1).

2) Пусть .
Тогда ; . Поэтому . Это можно записать так: . Также применим формулу: . В результате получаем:

Этот случай изображен на рисунке ⇑.

3) Пусть .
При этом касательные взаимно перпендикулярны, . В этом случае , что указано в (4).

Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.

Автор: Олег Одинцов . Опубликовано: 30-06-2021

источники:

http://helpiks.org/8-24441.html

http://1cov-edu.ru/mat-analiz/proizvodnaya/kasatelnaya-i-normal-k-grafiku-funktsii/

Источник

From Wikipedia, the free encyclopedia

For a more general, but more technical, treatment of tangent vectors, see Tangent space.

In mathematics, a tangent vector is a vector that is tangent to a curve or surface at a given point. Tangent vectors are described in the differential geometry of curves in the context of curves in Rⁿ. More generally, tangent vectors are elements of a tangent space of a differentiable manifold. Tangent vectors can also be described in terms of germs. Formally, a tangent vector at the point is a linear derivation of the algebra defined by the set of germs at .

Motivation[edit]

Before proceeding to a general definition of the tangent vector, we discuss its use in calculus and its tensor properties.

Calculus[edit]

Let be a parametric smooth curve. The tangent vector is given by , where we have used a prime instead of the usual dot to indicate differentiation with respect to parameter t.^[1] The unit tangent vector is given by

${displaystyle mathbf {T} (t)={frac {mathbf {r} '(t)}{|mathbf {r} '(t)|}},.}$

Example[edit]

Given the curve

${displaystyle mathbf {r} (t)=left{left(1+t^{2},e^{2t},cos {t}right)mid tin mathbb {R} right}}$

in $mathbb{R} ^{3}$ , the unit tangent vector at t=0 is given by

${displaystyle mathbf {T} (0)={frac {mathbf {r} '(0)}{|mathbf {r} '(0)|}}=left.{frac {(2t,2e^{2t},-sin {t})}{sqrt {4t^{2}+4e^{4t}+sin ^{2}{t}}}}right|_{t=0}=(0,1,0),.}$

Contravariance[edit]

If is given parametrically in the n-dimensional coordinate system xⁱ (here we have used superscripts as an index instead of the usual subscript) by ${displaystyle mathbf {r} (t)=(x^{1}(t),x^{2}(t),ldots ,x^{n}(t))}$ or

${displaystyle mathbf {r} =x^{i}=x^{i}(t),quad aleq tleq b,,}$

then the tangent vector field ${displaystyle mathbf {T} =T^{i}}$ is given by

${displaystyle T^{i}={frac {dx^{i}}{dt}},.}$

Under a change of coordinates

${displaystyle u^{i}=u^{i}(x^{1},x^{2},ldots ,x^{n}),quad 1leq ileq n}$

the tangent vector ${displaystyle {bar {mathbf {T} }}={bar {T}}^{i}}$ in the uⁱ-coordinate system is given by

${displaystyle {bar {T}}^{i}={frac {du^{i}}{dt}}={frac {partial u^{i}}{partial x^{s}}}{frac {dx^{s}}{dt}}=T^{s}{frac {partial u^{i}}{partial x^{s}}}}$

where we have used the Einstein summation convention. Therefore, a tangent vector of a smooth curve will transform as a contravariant tensor of order one under a change of coordinates.^[2]

Definition[edit]

Let ${displaystyle f:mathbb {R} ^{n}to mathbb {R} }$ be a differentiable function and let be a vector in $mathbb {R} ^{n}$ . We define the directional derivative in the direction at a point ${displaystyle mathbf {x} in mathbb {R} ^{n}}$ by

${displaystyle nabla _{mathbf {v} }f(mathbf {x} )=left.{frac {d}{dt}}f(mathbf {x} +tmathbf {v} )right|_{t=0}=sum _{i=1}^{n}v_{i}{frac {partial f}{partial x_{i}}}(mathbf {x} ),.}$

The tangent vector at the point may then be defined^[3] as

${displaystyle mathbf {v} (f(mathbf {x} ))equiv (nabla _{mathbf {v} }(f))(mathbf {x} ),.}$

Properties[edit]

Let ${displaystyle f,g:mathbb {R} ^{n}to mathbb {R} }$ be differentiable functions, let be tangent vectors in $mathbb {R} ^{n}$ at ${mathbf {x}}in {mathbb {R}}^{n}$ , and let . Then

Tangent vector on manifolds[edit]

Let be a differentiable manifold and let A(M) be the algebra of real-valued differentiable functions on . Then the tangent vector to at a point in the manifold is given by the derivation $D_{v}:A(M)rightarrow {mathbb {R}}$ which shall be linear — i.e., for any and we have

$D_{v}(af+bg)=aD_{v}(f)+bD_{v}(g),.$

Note that the derivation will by definition have the Leibniz property

${displaystyle D_{v}(fcdot g)(x)=D_{v}(f)(x)cdot g(x)+f(x)cdot D_{v}(g)(x),.}$

References[edit]

^ J. Stewart (2001)
^ D. Kay (1988)
^ A. Gray (1993)

Bibliography[edit]

Gray, Alfred (1993), Modern Differential Geometry of Curves and Surfaces, Boca Raton: CRC Press.
Stewart, James (2001), Calculus: Concepts and Contexts, Australia: Thomson/Brooks/Cole.
Kay, David (1988), Schaums Outline of Theory and Problems of Tensor Calculus, New York: McGraw-Hill.

Источник

Лекция 3

Дифференцируемость
функции многих переменных.

Производные и
дифференциалы высших порядков.

Геометрические
приложения частных производных.

Геометрический
смысл первого дифференциала

П.1. Производные
высших порядков.

Теорема о
равенстве смешанных производных

Пусть дана
дифференцируемая функция n
переменных
u(.
Пусть также вычислена производная
первого порядка по переменной

. Эта функция тоже зависит от переменных
.

Возьмем от

производную по переменной
:

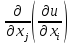
Функция

называется
частной производной второго порядка
от функции u(по
переменным

Таким же образом
можно определить производные и третьего
порядка .

Таким образом,
справедлива рекуррентная формула

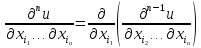
Производная

называется смешанной, если среди
переменных
есть несовпадающие.

Пример.
Рассмотрим функцию двух переменных

. Производные
,

являются несмешанными производными,
,
—
смешанными производными.

Теорема (о
равенстве смешанных производных).

Пусть

1)
функция

определена в некоторой окрестности
точки
;

2)
существуют частные производные
,
,
,

в этой окрестности;

2)
производные второго порядка
,

непрерывны в точке
.

Тогда

в точке
.

Доказательство.

Рассмотрим
вспомогательное выражение:

Здесь
h,k
-достаточно малые чтобы оставаться в
пределах окрестности из пунктов 1)-2).

Введем вспомогательную
функцию

(*).

Очевидно,

Но

непрерывна в точке
.

Пусть
.
Тогда
.

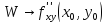
Рассмотрим
выражение, аналогичное предложенному
выше:

где

Аналогично
получаем, что при

выполнено
.

Следовательно,

▲

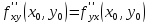
Справедлива
следующая общая теорема.

Теорема
( без доказательства).

Пусть
функция

определена в области
.
Пусть существуют и непрерывны все
частные производные до k
-го порядка включительно в области.
Тогда смешанные производные до -го
порядка не зависят от порядка
дифференцирования.

Пример.
Рассмотрим
функцию двух переменных, у которой
смешанные производные второго порядка
существуют, но не равны в точке (0,0):

Имеем:

Видим,
что

П.2. Дифференциалы
высших порядков.

Неинвариантность
дифференциалов порядка выше первого

Рассмотрим
дифференцируемую функцию n
переменных
.
Вычислим ее первый дифференциал:

В правой части
этого равенства стоит функция от
переменных
,

— некоторые фиксированные постоянные.
Возьмем дифференциал от левой и правой
частей:

Формально можно
записать:

Аналогично,

Вообще, справедлива
формула:

Рассмотрим
функцию двух переменных
.
Запишем формулы первого, второго и
третьего дифференциалов этой функции:

Исследуем,
является ли дифференциал порядка выше
первого инвариантной величиной. Пусть
функция

является сложной функцией переменных

x=x(u,v),
y=y(u,v);

Справедлива
формула второго дифференциала:

(*)

Докажем, что
нельзя записать, как это мы делали для
первого дифференциала, что
то есть форма второго дифференциала
зависит от того, являются ли используемые
переменные зависимыми или нет.

Имеем:

{так как первый
дифференциал инвариантен}=

Если
бы

были независимыми переменными, то была
бы справедлива формула, аналогичная
формуле (*). Но в нашем случае, когда

являются в свою очередь некоторыми
функциями, видим, что форма второго
дифференциала меняется, появляются два
новых слагаемых

и

. Видим, что форма второго дифференциала
неинвариантна.

Однако, существует
частный случай, когда можно говорить,
что форма второго дифференциала
инвариантна. Это случай линейной замены
переменных:

Отсюда в случае
линейной замены переменных действительно
получаем

П.3. Геометрические
приложения частных производных.

Касательный
вектор к кривой. Нормаль к поверхности.

Касательная
плоскость

1)
Касательный
вектор.
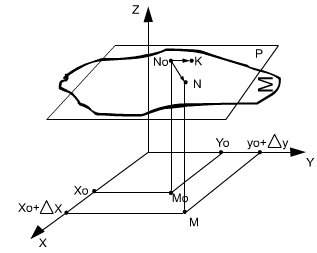
Рассмотрим кривую L
в пространстве, заданную параметрическими
уравнениями:

Фиксируем некоторое
значение
,
тем самым фиксируем некоторую точку M
на кривой L
:

Придадим переменной t
некоторое приращение
,
получим точку

Рассмотрим вектор

Пусть
.
Тогда из рисунка мы видим, что вектор

направлен по касательной к кривой
,
в пределе можно записать формулу

Вектор

является
касательным вектором к кривой L.

2)
Касательная
плоскость к поверхности
.

Пусть задана
поверхность

Пусть
точка

— произвольная точка на поверхности
то
есть ее координаты удовлетворяют
уравнению поверхности

.

Проведем через
точку M кривую L,
целиком лежащую на поверхности
:
.

Строим
—
касательный вектор к кривой L
в точке M.
Пусть кривая L
имеет следующие параметрические
уравнения:

Но

Функция

одной переменной
t
тождественно равна 0 на отрезке [a,b]

Здесь мы ввели
вектор

— градиент функции

Вектор

перпендикулярен касательному вектору
ко кривой L
в точке M.

Соотношение
(
верно для любой кривой L,
проходящей через точку M
целиком лежащей на поверхности
.
Таким образом, вектор

направлен вдоль нормали к поверхности
S
в точке M.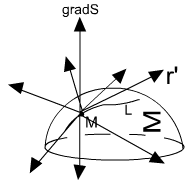

Учитывая этот
факт, получаем, что касательная
плоскость к поверхности

в
точке

имеет
уравнение:

Рассмотрим L
— нормаль к поверхности

в точке
.
Вектор

является направляющим вектором этой
прямой, отсюда выписываем уравнение
нормали к поверхности

в точке
:

—
уравнение нормали к поверхности.

Замечания.

1)
Пусть поверхность

задана явно:

этом случае
уравнение касательной плоскости к
поверхности

имеет вид:

Нормаль
к поверхности

имеет
уравнение:

2)
Если в точке

выполнено

или хотя бы одна из частных производных
не существует в этой точке, то касательная
плоскость в точке

не существует.

Рассмотрим
геометрический
смысл первого дифференциала.
Используем
результаты, полученные выше.

Рассмотрим функцию
двух переменны
.
Пусть точка

принадлежит области определения функции
z.
Тогда точка
лежит на
поверхности
Фиксируем
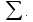
приращения
.
Имеем:

_точка_N_{лежит на поверхности, точка}_M_{лежит на плоскости, касающейся поверхности

в точке}:

Пусть Pкасательная
плоскость к поверхности

в точке

Пусть точка
,
где координата

удовлетворяет уравнению плоскости P.

_Имеем:

Отсюда
получаем геометрический смысл первого
дифференциала:

первый
дифференциал
геометрически
равен приращению аппликаты точкиприращению
аппликаты точки касательной плоскости,
если переменным

приданы
приращения

Если функция z
дифференцируема
в точке,
то верно соотношение ( точки K
и N
имеют совпадающие проекции на плоскость
OXY
)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Для более общей, но более технической обработки касательных векторов см. Касательное пространство .

В математике , А касательный вектор представляет собой вектор , который является касательной к кривой или поверхности в данной точке. Касательные векторы описываются в дифференциальной геометрии кривых в контексте кривых в R ⁿ . В более общем смысле , касательные векторы являются элементами касательного пространства в виде дифференцируемого многообразия . Касательные векторы также можно описать в терминах ростков . Формально касательный вектор в точке является линейным производным алгебры, определяемой множеством ростков в точке .
Икс Икс

Мотивация

Прежде чем перейти к общему определению касательного вектора, мы обсудим его использование в исчислении и его тензорные свойства.

Исчисление

Позвольте быть параметрической гладкой кривой . Касательный вектор задается как , где мы использовали штрих вместо обычной точки для обозначения дифференцирования по параметру t . Единичный касательный вектор задается формулой
${ mathbf {r}} ^ { prime} (т)$

${ mathbf {T}} (t) = { frac {{ mathbf {r}} ^ { prime} (t)} {| { mathbf {r}} ^ { prime} (t) |} } ,.$

Пример

Учитывая кривую

${ displaystyle mathbf {r} (t) = {(1 + t ^ {2}, e ^ {2t}, cos {t}) | t in mathbb {R} }}$

в единичный касательный вектор в задается формулой
$mathbb {R} ^ {3}$ t = 0

${ Displaystyle mathbf {T} (0) = { frac { mathbf {r} ^ { prime} (0)} { | mathbf {r} ^ { prime} (0) |}} = left. { frac {(2t, 2e ^ {2t}, - sin {t})} { sqrt {4t ^ {2} + 4e ^ {4t} + sin ^ {2} {t }}}} right | _ {t = 0} = (0,1,0) ,.}$

Контравариантность

Если задано параметрически в n -мерной системе координат x ⁱ (здесь мы использовали верхние индексы в качестве индекса вместо обычного нижнего индекса) посредством или
${ mathbf {r}} (t) = (x ^ {1} (t), x ^ {2} (t), ldots, x ^ {n} (t))$

${ mathbf {r}} = x ^ {i} = x ^ {i} (t), quad a leq t leq b ,,$

то касательное векторное поле задается формулой
${ mathbf {T}} = T ^ {i}$

$T ^ {i} = { frac {dx ^ {i}} {dt}} ,.$

При смене координат

$u ^ {i} = u ^ {i} (x ^ {1}, x ^ {2}, ldots, x ^ {n}), quad 1 leq i leq n$

касательный вектор в u ⁱ -системе координат задается формулой
${ bar {{ mathbf {T}}}} = { bar {T}} ^ {i}$

${ bar {T}} ^ {i} = { frac {du ^ {i}} {dt}} = { frac { partial u ^ {i}} { partial x ^ {s}}} { frac {dx ^ {s}} {dt}} = T ^ {s} { frac { partial u ^ {i}} { partial x ^ {s}}}$

где мы использовали соглашение Эйнштейна о суммировании . Следовательно, касательный вектор гладкой кривой при изменении координат преобразуется в контравариантный тензор первого порядка.

Определение

Позвольте быть дифференцируемой функцией и пусть быть вектором в . Определим производную по направлению в точке как
$е: { mathbb {R}} ^ {n} rightarrow { mathbb {R}}$ $mathbb {R} ^ {n}$ ${ mathbf {x}} in { mathbb {R}} ^ {n}$

$D _ {{ mathbf {v}}} f ({ mathbf {x}}) = left. { Frac {d} {dt}} f ({ mathbf {x}} + t { mathbf {v }}) right | _ {{t = 0}} = sum _ {{i = 1}} ^ {{n}} v_ {i} { frac { partial f} { partial x_ {i} }} ({ mathbf {x}}) ,.$

Касательный вектор в точке может быть определен как

${ Displaystyle mathbf {v} (е ( mathbf {x})) Equiv (D _ { mathbf {v}} (f)) ( mathbf {x}) ,.}$

Характеристики

Позвольте быть дифференцируемыми функциями, пусть быть касательными векторами в at , и пусть . потом
${ displaystyle f, g: mathbb {R} ^ {n} to mathbb {R}}$ $mathbb {R} ^ {n}$ ${ mathbf {x}} in { mathbb {R}} ^ {n}$

Касательный вектор на многообразиях

Пусть — дифференцируемое многообразие и пусть — алгебра вещественнозначных дифференцируемых функций на . Тогда касательный вектор к в точке на многообразии задается дифференцированием, которое должно быть линейным, т. Е. Для любого, и мы имеем
Икс $D_ {v}: A (M) rightarrow { mathbb {R}}$

$D_ {v} (af + bg) = aD_ {v} (f) + bD_ {v} (g) ,.$

Обратите внимание, что вывод по определению будет обладать свойством Лейбница

${ Displaystyle D_ {v} (е cdot g) (x) = D_ {v} (f) (x) cdot g (x) + f (x) cdot D_ {v} (g) (x) ,.}$

Смотрите также

Дифференцируемая поверхность # Касательная плоскость и вектор нормали

использованная литература

^ Дж. Стюарт (2001)
↑ Д. Кей (1988)
↑ А. Грей (1993)

Библиография

Грей, Альфред (1993), Современная дифференциальная геометрия кривых и поверхностей , Бока-Ратон: CRC Press.
Стюарт, Джеймс (2001), Исчисление: концепции и контексты , Австралия: Томсон / Брукс / Коул.
Кей, Дэвид (1988), Обзор теории и проблем тензорного исчисления Шаумсом , Нью-Йорк: МакГроу-Хилл.

Источник

1 Найти годограф вектор-функции

Решение. Параметрические уравнения годографа есть

, , .

Из первых двух уравнений исключаем параметр :

Следовательно, годографом вектор-функции является окружность

, ,

Из которой исключена точка .

При изменении от до точка на годографе движется от точки против часовой стрелки (если наблюдать из точки, расположенной выше плоскости ). При этом

, .

2 Вычислить , если .

Решение. Согласно определению

3 Найти единичный касательный вектор годографа вектор-функции

При .

Решение. Параметрические уравнения годографа есть

, , .

Найдем координаты направляющего вектора касательной к кривой :

В частности в точке

Тогда единичный вектор годографа имеет вид

4 Найти производную скалярного произведения векторов

и .

Решение. Согласно свойствам дифференцируемых векторных функций, имеем

==.

5 Дано уравнение движения . Определить траекторию и скорость движения.

Решение. Параметрические уравнения годографа есть

, , .

Из первого уравнения исключим параметр

И подставим во второе

Отсюда уравнение траектории движения

, .

Вектор скорости движения есть

6 Написать уравнения касательной и нормальной плоскости к кривой

В точке .

Решение. Данной точке соответствует значение параметра .

Имеем

, , .

Подставляя значение , получаем

, , .

Тогда уравнение касательной:

Уравнение нормальной плоскости:

Или .

7 Найти скорость и ускорение материальной точки , движущейся с постоянной угловой скоростью по окружности

Решение. Пусть – произвольная точка окружности. Обозначим через угол между радиус-вектором точки и положительным направлением оси . По условию

Где – время движения.

Выразим координаты точки как функции времени (рисунок 9.8):

Следовательно, радиус-вектор точки

Скорость движения точки

Модуль скорости

Рисунок 9.8 – Геометрическая интерпретация задачи 7.

Скалярное произведение векторов и есть:

Т. е. векторы и перпендикулярны.

Отсюда следует, что вектор направлен по касательной к окружности, по которой движется точка .

Найдем ускорение :

Значит, векторы и имеют противоположные направления.

Таким образом, ускорение материальной точки, движущейся с постоянной угловой скоростью по окружности, в каждый момент времени направлено к центру этой окружности.

8 К годографу винтовой линии (рисунок 9.9)