Все формулы для радиуса вписанной окружности
Радиус вписанной окружности в треугольник
a , b , c — стороны треугольника
p — полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
r — радиус вписанной окружности
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Как найти катеты через вписанную окружность
Радиус вписанной окружности в прямоугольный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в прямоугольный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Открыть онлайн калькулятор
1. Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
Пусть известны катеты a и b прямоугольного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
Радиус вписанной в треугольник окружности, если известна площадь треугольника S и полупериметр p вычисляется из следующей формулы (статья Радиус вписанной в треугольник окружности, формула (5)):
| ( small r= frac , ) | (1) |
| ( small p= frac . ) | (2) |
Площадь прямоугольного треугольника по катетам вычисляется из формулы:
| ( small S= large frac small cdot a cdot b. ) | (3) |
Подставляя (2) и (3) в (1) получим формулу вписанной в прямоугольный треугольник окружности:
| ( small r= large frac ab> (a+b+c)> ) ( small = large frac, ) | (4) |
| ( small c= sqrt . ) | (5) |
Из формулы (4) выведем другую эквивалентную формулу. Умножим числитель и знаменатель формулы (4) на ( small a+b-c ):
| ( small r= frac ) ( small = frac ) ( small = frac ) | (6) |
Учитывая (5), формулу (6) можно переписать так:
( small r= frac ) ( small = frac .)
Таким образом другая формула вычисления радиуса вписанной в треугольник окружности имеет вид:
| ( small r= frac ,) | (7) |
где c вычисляется из (5).
Пример 1. Известны катеты прямоугольного треугольника a=17 и b=5. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (4) и (7). Вычислим, сначала, гипотенузу прямоугольного треугольника из формулы (5):
Подставим значения ( small a=17, ; b=5; c=17.720045 ) в (7):
Ответ:
2. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
Пусть известны катет a прямоугольного треугольника и прилежащий к нему угол β(Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
( small frac =frac .)
Учитывая, что ( small alpha=90°-beta ) и ( small sin (90°-beta)=cos beta ), получим:
| ( small frac =frac ) ( small =frac =frac .) | (8) |
Тогда из (8) получим:
| ( small b=frac . ) | (9) |
Далее, из теоремы синусов:
( small frac =frac ) ( small =frac =frac .)
| ( small c=frac .) | (10) |
Чтобы получить формулу радиуса вписанной в прямоугольный треугольник окружности через катет и прилежащий к нему угол, подставим значения ( small b ) и ( small c ) из (9) и (10) в (7):
Пример 2. Известны катет ( small a=21 ) и прилежащий к нему угол ( small beta=30° ) прямоугольного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Подставим значения ( small a=21 ) ( small beta=30° ) в (11):
Ответ:
3. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
Пусть известны катет a прямоугольного треугольника и противолежащий угол ( small alpha; ) (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
В предыдущем параграфе мы вывели формулу вписанной в прямоугольный треугольник окружности по катету и прилежащему углу (формула (11)). Учитывая, что в прямоугольном треугольнике сумма острых углов равна 90°, имеем:
( small alpha+beta=90°) ( small beta=90°-alpha )
Тогда (11) можно преобразовать так (подробнее на странице Формулы приведения тригонометрических функций:
Пример 3. Известны катет ( small a=6 ) прямоугольного треугольника и противолежащий угол ( small alpha=53°. ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (12). Подставим значение ( small a=6, ; alpha=53° ) в (12):
Ответ:
Треугольник вписанный в окружность
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = frac ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Узнать ещё
Знание — сила. Познавательная информация
Окружность, вписанная в прямоугольный треугольник
Если в задаче дана окружность, вписанная в прямоугольный треугольник, то ее решение может быть связано со свойством отрезков касательных, проведенных из одной точки, и теоремой Пифагора.
Кроме того, следует учесть, что радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле
где a и b — длины катетов, c — гипотенузы.
Рассмотрим две задачи на вписанную в прямоугольный треугольник окружность.
Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки 4 см и 6 см. Найти периметр и площадь треугольника и радиус окружности.
Дано: ∆ ABC, ∠C=90º,
окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
1) По свойству отрезков касательных, проведенных из одной точки,
AK=AM=6 см,
2) AB=AM+BM=6+4=10 см,
3) По теореме Пифагора:
Второй корень не подходит по смыслу задачи. Значит, CK+CF=2 см, AC=8 см, BC=6 см.
Ответ: 24 см, 24 см², 2 см.
Найти площадь прямоугольного треугольника, гипотенуза которого равна 26 см, а радиус вписанной окружности — 4 см.
Дано:∆ ABC, ∠C=90º,
окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
1) Проведем отрезки OK и OF.
(как радиусы, проведенные в точки касания).
Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые).
А так как OK=OF (как радиусы), то OKCF — квадрат.
2) По свойству касательных, проведенных из одной точки,
3) AC=AK+KC=(x+4) см, BC=BF+CF=26-x+4=(30-x) см.
Радиус вписанной окружности в прямоугольный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в прямоугольный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Открыть онлайн калькулятор
1. Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
Пусть известны катеты a и b прямоугольного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
Радиус вписанной в треугольник окружности, если известна площадь треугольника S и полупериметр p вычисляется из следующей формулы (статья Радиус вписанной в треугольник окружности, формула (5)):
| ( small r= frac<large S><large p>, ) | (1) |
| ( small p= frac<large a+b+c><large 2>. ) | (2) |
Площадь прямоугольного треугольника по катетам вычисляется из формулы:
| ( small S= large frac<1> <2>small cdot a cdot b. ) | (3) |
Подставляя (2) и (3) в (1) получим формулу вписанной в прямоугольный треугольник окружности:
| ( small r= large frac<frac<1><2>ab><frac<1><2>(a+b+c)> ) ( small = large frac, ) | (4) |
| ( small c= sqrt< a^2+b^2>. ) | (5) |
Из формулы (4) выведем другую эквивалентную формулу. Умножим числитель и знаменатель формулы (4) на ( small a+b-c ):
| ( small r= frac<large ab(a+b-c)> <large (a+b+c)(a+b-c)>) ( small = frac<large ab(a+b-c)> <large (a+b)^2-c^2>) ( small = frac<large ab(a+b-c)> <large a^2+2ab+b^2-c^2>) | (6) |
Учитывая (5), формулу (6) можно переписать так:
( small r= frac<large ab(a+b-c)> <large 2ab>) ( small = frac<large a+b-c> <large 2>.)
Таким образом другая формула вычисления радиуса вписанной в треугольник окружности имеет вид:
| ( small r= frac<large a+b-c> <large 2>,) | (7) |
где c вычисляется из (5).
Пример 1. Известны катеты прямоугольного треугольника a=17 и b=5. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (4) и (7). Вычислим, сначала, гипотенузу прямоугольного треугольника из формулы (5):
Подставим значения ( small a=17, ; b=5; c=17.720045 ) в (7):
Ответ:
2. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
Пусть известны катет a прямоугольного треугольника и прилежащий к нему угол β(Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
( small frac<large a><large sin alpha>=frac<large b> <large sin beta>.)
Учитывая, что ( small alpha=90°-beta ) и ( small sin (90°-beta)=cos beta ), получим:
| ( small frac<large a><large sin alpha>=frac<large a> <large sin (90°-beta)>) ( small =frac<large a><large cos beta>=frac<large b> <large sin beta>.) | (8) |
Тогда из (8) получим:
| ( small b=frac<large a cdot sin beta><large cos beta>. ) | (9) |
Далее, из теоремы синусов:
( small frac<large a><large sin alpha>=frac<large a> <large sin (90°-beta)>) ( small =frac<large a><large cos beta>=frac<large c> <large sin 90°>.)
| ( small c=frac<large a> <large cos beta>.) | (10) |
Чтобы получить формулу радиуса вписанной в прямоугольный треугольник окружности через катет и прилежащий к нему угол, подставим значения ( small b ) и ( small c ) из (9) и (10) в (7):
Пример 2. Известны катет ( small a=21 ) и прилежащий к нему угол ( small beta=30° ) прямоугольного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Подставим значения ( small a=21 ) ( small beta=30° ) в (11):
Ответ:
3. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
Пусть известны катет a прямоугольного треугольника и противолежащий угол ( small alpha; ) (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
В предыдущем параграфе мы вывели формулу вписанной в прямоугольный треугольник окружности по катету и прилежащему углу (формула (11)). Учитывая, что в прямоугольном треугольнике сумма острых углов равна 90°, имеем:
( small alpha+beta=90°) ( small beta=90°-alpha )
Тогда (11) можно преобразовать так (подробнее на странице Формулы приведения тригонометрических функций:
Пример 3. Известны катет ( small a=6 ) прямоугольного треугольника и противолежащий угол ( small alpha=53°. ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (12). Подставим значение ( small a=6, ; alpha=53° ) в (12):
Ответ:
http://b4.cooksy.ru/articles/kak-nayti-katety-cherez-vpisannuyu-okruzhnost
http://matworld.ru/geometry/radius-vpisannoj-okruzhnosti-v-pryamougolnyj-treugolnik.php
Если в задаче дана окружность, вписанная в прямоугольный треугольник, то ее решение может быть связано со свойством отрезков касательных, проведенных из одной точки, и теоремой Пифагора.
Кроме того, следует учесть, что радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле
где a и b — длины катетов, c — гипотенузы.
Рассмотрим две задачи на вписанную в прямоугольный треугольник окружность.
Задача 1.
Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки 4 см и 6 см. Найти периметр и площадь треугольника и радиус окружности.

окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
BM=4 см, AM=6 см.
Найти:
Решение:
1) По свойству отрезков касательных, проведенных из одной точки,

BF=BM=4 см,
CK=CF=x см.
2) AB=AM+BM=6+4=10 см,
AC=AK+CK=(6+x) см,
BC=BF+CF=(4+x) см.
3) По теореме Пифагора:
По теореме Виета,
Второй корень не подходит по смыслу задачи. Значит, CK+CF=2 см, AC=8 см, BC=6 см.
4)
Ответ: 24 см, 24 см², 2 см.
Задача 2.
Найти площадь прямоугольного треугольника, гипотенуза которого равна 26 см, а радиус вписанной окружности — 4 см.

окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
AB=26 см, r=4 см.
Найти:
Решение:
1) Проведем отрезки OK и OF.
(как радиусы, проведенные в точки касания).
Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые).
А так как OK=OF (как радиусы), то OKCF — квадрат.
2) По свойству касательных, проведенных из одной точки,
AM=AK=x см,
BF=BM=(26-x) см,
CF=CK=r=4 см.
3) AC=AK+KC=(x+4) см, BC=BF+CF=26-x+4=(30-x) см.
По теореме Пифагора,
Если AM=20 см, то AC=24 см, BC=10 см.
Если AM=6 см, то AC=10 см, BC=24 см.
Ответ: 120 см².
ВИДЕОУРОК
Вписанная окружность
прямоугольного треугольника.
Радиус окружности,
вписанной в прямоугольный треугольник,
можно найти по формуле:
где r –
искомый радиус, а и b – катеты,
с – гипотенуза треугольника.
Радиус вписанной в
прямоугольный треугольник окружности
равен произведению катетов, делённому на сумму
катетов и гипотенузы,
где r –
искомый радиус, а и b – катеты,
с – гипотенуза треугольника.
Радиус вписанной в
прямоугольный треугольник окружности равен площади этого треугольника, делённой
на полупериметр:
где р – полупериметр
ЗАДАЧА:
Точка касания окружности, вписанной в прямоугольный треугольник,
делит один из катетов на отрезки 2 см и 8 см,
отсчитывая от вершины прямого угла. Найдите периметр треугольника.
РЕШЕНИЕ:
Начертим чертёж:
ВМ
= ВN = х.
(2 + х)2 + (2 + 
+ х)2,
х2 + 4х + 4
+ 100 =
= х2 + 16х + 64,
12х = 40,
х =
10/3 (см).
Р = (2 + 
ЗАДАЧА:
Вписанная окружность прямоугольного треугольника АВС касается гипотенузы АВ в точке
К. Найдите радиус
вписанной окружности, если АК = 4 см, ВК
= 6 см.
РЕШЕНИЕ:
За свойством касательных имеем:
АК = АМ = 4 см,
ВК = ВN = 6 см.
Обозначим радиус вписанной окружности
через х:
СN = СM = NО = МО = х.
Тогда
АС =
(4 + х) см.
ВС = (6 + х) см,
АВ =
4 см +
6 см =
10 см.
По теореме Пифагора для треугольника АВС
можно записать соотношение:
(4 + х)2 + (6 + х)2 = 102.
Решим это квадратное уравнение:
16 + 8x + x2
+ 36 + 12x + x2 = 100,
2x2 + 20x + 52 – 100 = 0,
2x2 + 20x – 48 = 0,
x2 + 10x – 24 = 0,
x1 = 2, x2 = –10.
x2 не
удовлетворяет условию задачи.
ОТВЕТ: 2 см.
ЗАДАЧА:
Точка касания окружности, вписанной в прямоугольный треугольник,
делить гипотенузу на отрезки 8 см и 12
см. Найдите периметр треугольника.
РЕШЕНИЕ:
Начертим чертёж:
(8 + 12)2
= (8 + х)2 + (12 + х)2,
400 = 64 + 16x + x2
+ x2 + 24x + 144,
2x2 + 40x – 192 = 0,
x2 + 20x – 96 = 0,
x1 = 4, x2 = –24.
x2 не
подходит.
Р
= 8 + 12 + 12 + 4 + 4 + 8 = 48 (см).
ОТВЕТ: 48 см.
Описанная окружность
прямоугольного треугольника.
Центром окружности, описанной
вокруг прямоугольного треугольника, будет середина его гипотенузы.
Диаметр окружности,
описанной вокруг прямоугольного треугольника, равен его гипотенузе.
Медиана прямоугольного
треугольника, проведённая к его гипотенузе, равна половине гипотенузы и
является радиусом окружности, описанной около этого треугольника.
ОА = ОВ = ОС = R
Радиус описанной окружности равен половине
гипотенузы:
ЗАДАЧА:
Отрезок ВС – диаметр окружности, изображённой на рисунку.
Угол АВС = 55°.
Найдите
величину
угла АСВ
?
РЕШЕНИЕ:
ВС – диаметр,
поэтому ∠ ВАС = 90°,
∠ АСВ = 180° – (90° + 55°) = 35°.
ЗАДАЧА:
Перпендикуляр,
опущенный из точки окружности на его диаметр, делит диаметр на отрезки, разность
между которыми равна 5 см. Найдите радиус окружности, если длина перпендикуляра равна 6 см.
РЕШЕНИЕ:
Пусть АВ – диаметр окружности с
центром в точке О, СD ⊥ АВ,
где С – точка окружности,
СD = 6 см, АD = х см,
ВD – АD = 5 см.
Тогда
DВ = (х + 5) см.
Треугольник АСВ – прямоугольный (угол С прямой, так как
он вписанный и опирается на диаметр).
СD – перпендикуляр, проведений из вершины прямого угла на
гипотенузу. Тогда:
АD ∙ DВ = СD2,
х(х + 5) = 62,
х2
+ 5х – 36 = 0,
x1 = –9, x2 = 4.
x1 не подходит.
Поэтому, АD = 4 см,
DВ = 4 + 5 = 9 (см).
АВ
= АD
+ DВ
=
=
4
+ 9 = 13 (см).
Тогда
r = АВ :
2 = 13 : 2 = 6,5 (см).
ОТВЕТ: 6,5 см
ЗАДАЧА:
Из точки на окружности проведены две перпендикулярные
хорды, разность между которыми равна 4 см. Найдите эти хорды, если радиус окружности равен 10
см.
РЕШЕНИЕ:
Пусть задана окружность радиуса R,
в
которой
проведены
хорды АВ и
АС (АВ ⊥ АС),
R = АО = ВО = СО =
10 см,
АС – АВ =
4
см.
Пусть АВ = х см, тогда
АС = (4
+ х) см.
Так как ∠ А = 90°, то треугольник
ВАС –
прямоугольный,
в
котором
ВС = 2ОВ= 2 ∙ 10 = 20 см.
Из
прямоугольного треугольника ВАС имеем:
АВ2 + АС2
= ВС2,
х2 + (4 + х)2
= 202,
х2 + 16 + 8х
+ х2 = 400,
х2 + 4х –
192 = 0,
х1 = 12,
х2
= –16 – не подходит.
Поэтому,
АВ = 12 см,
АС
= 4 + 12 = 16 (см).
ОТВЕТ: 12
см, 16 см
ЗАДАЧА:
Угол между биссектрисой и
медианой прямоугольного треугольника, проведёнными из вершины прямого угла,
равен 14°.
Найдите меньший угол этого треугольника.
РЕШЕНИЕ:
Начертим чертёж.
Так как треугольник
прямоугольный и медиана ВМ иcходит
из прямого угла В, то точка М является центром
описанной окружности вокруг треугольника
АВС.
Следовательно,
АМ
= МС = МВ = R,
где R –
радиус описанной окружности.
Найдём сначала угол МВС.
Учитывая, что BD – биссектриса, то
∠ DВС = 90/2 = 45°. Тогда
∠ МВС = ∠ МВD + ∠ DВС,
∠ МВС = 14° + 45° = 59°.
Рассмотрим
равнобедренный треугольник МВС со сторонами
МВ = МС,
в
котором углы при основании ВС равны, то есть
∠ С = ∠ МВС
= 59°.
Так
как сумма острых углов в прямоугольном треугольнике равна 90°, то
∠ А + ∠ С = 90°,
∠ А = 90° – ∠ С =
= 90° – 59° = 31°.
ЗАДАЧА:
Периметр
прямоугольного треугольника равен 72 м, а радиус вписанной в него окружности – 6 м. Найдите диаметр описанной окружности.
РЕШЕНИЕ:
DO = OF = OE = r = 6 м.
Поэтому AD =
AF =
6 м.
FC = EC, BD = BE (отрезки касательных, проведённых из
одной точки)
Пусть
BD = BE = x,
FC = EC = y,
Тогда
AB
= x + 6, AC = y + 6,
BC = x + y.
AB + AC + BC =
= x + 6 + y + 6
+ x + y = 72.
2x + 2y + 12 = 72,
2x + 2y = 60,
x + y = 30.
(x + y) – гипотенуза, или диаметр описанной окружности.
ОТВЕТ: 30 м.
ЗАДАЧА:
В окружности на расстоянии 6
см от его центра проведена хорда длинной 16
см. Найдите радиус окружности.
РЕШЕНИЕ:
Начертим чертёж:
Пользуясь теоремой
Пифагора, находим радиус.
ЗАДАЧА:
Две окружности, радиусы которых равны 4 см и 9 см, имеют внешнее касание. Найдите расстояние между
точками касания данных окружностей с их общей внешней касательной.
РЕШЕНИЕ:
ВК ⊥ АD, АК = 9 – 4 = 5 см.
Из ∆ ВКА:
Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:
- Найти все стороны треугольника.
- Найти все углы треугольника.
- Найти площадь (S) и периметр (P) треугольника.
- Найти радиус (r) вписанной окружности.
- Найти радиус (R) описанной окружности.
- Найти высоту (h) треугольника.
Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.
Как найти длину стороны треугольника?
Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
Для прямоугольного треугольника:
1) Найти катет через гипотенузу и другой катет
где a и b — катеты, с — гипотенуза.
2) Найти гипотенузу по двум катетам
где a и b — катеты, с — гипотенуза.
3) Найти катет по гипотенузе и противолежащему углу
где a и b — катеты, с — гипотенуза,α° и β° — углы напротив катетов.
4) Найти гипотенузу через катет и противолежащий угол
где a и b — катеты, с — гипотенуза,α° и β°- углы напротив катетов.
Для равнобедренного треугольника:
1) Найти основание через боковые стороны и угол между ними
где a — искомое основание, b — известная боковая сторона,α° — угол между боковыми сторонами.
2) Найти основание через боковые стороны и угол при основании
где a — искомое основание,b — известная боковая сторона,β° — угол при осноавнии.
3) Найти боковые стороны по углу между ними
где b — искомая боковая сторона, a — основание,α° — угол между боковыми сторонами.
4) Найти боковые стороны по углу при основании
где b — искомая боковая сторона, a — основание,β° — угол при осноавнии.
Для равностороннего треугольника:
1) Найти сторону через площадь
где a — искомая сторона, S — площадь треугольника.
2) Найти сторону через высоту
где a — искомая сторона,h — высота треугольника.
3) Найти сторону через радиус вписанной окружности
где a — искомая сторона,r — радиус вписанной окружности.
4) Найти сторону через радиус описанной окружности
где a — искомая сторона,R — радиус описанной окружности.
Для произвольного треугольника:
1) Найти сторону через две известные стороны и один угол (теорема косинусов)
где a — искомая сторона, b и с — известные стороны, α° — угол напротив неизвестной стороны.
2) Найти сторону через одну известную сторону и два угла (теорема синусов)
где a — искомая сторона, b — известная сторона, α° и β° известные углы.
Скачать все формулы в формате Word
Утверждение.
Радиус вписанной в прямоугольный треугольник окружности равен
где a и b — катеты, c — гипотенуза.
Доказательство:
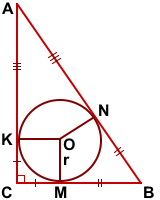
Проведём радиусы OK, OM, ON к сторонам треугольника.
(как радиусы, проведённые в точку касания).
(как отрезки касательных, проведённых из одной точки).
Отсюда следует, что четырёхугольник CKOM — квадрат, стороны которого равны радиусу вписанной в треугольник ABC окружности: CK=CM=OM=OK=r.
Следовательно,
то есть
Таким образом, формула радиуса вписанной в прямоугольный треугольник окружности
Что и требовалось доказать.














































