Как найти катеты равностороннего треугольника по гипотенузе

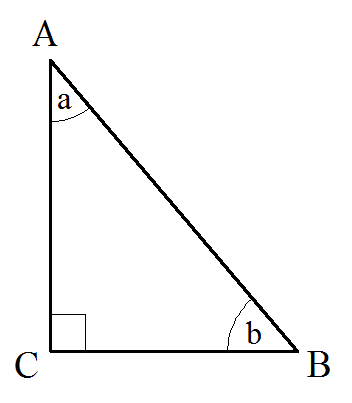
Как найти стороны прямоугольного треугольника

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для гипотенузы (с):
  • длины катетов a и b
  • длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• для катета:
  • длину гипотенузы (с) и длину одного из катетов
  • длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
  • длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
  • длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Формула

следовательно: c = √ a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

Формула

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу по двум углам

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √ 5² — 4² = √ 25 — 16 = √ 9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

Формула

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

Расчёт катетов по гипотенузе и углу

Прямоугольный треугольник это треугольник у которого один из углов равен 90 градусов.

Прямой угол это угол 90 градусов.

Гипотенуза это противолежащая прямому углу сторона, самая длинная сторона прямоугольного треугольника.

Катеты это стороны прямоугольного треугольника прилежащие к прямому углу.

Сумма внутренних углов треугольника равна 180 градусам.

Синусом называется отношение противолежащего катета к гипотенузе.

Косинусом называется отношение прилежащего катета к гипотенузе.

Расчет катета треугольника

Катет треугольника — это одна из двух сторон прямоугольного треугольника, образующая между собой прямой угол.

Формула расчета катета:

a = √(c 2 — b 2 ), где

a — катет;
b — катет;
c — гипотенуза.

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета катета прямоугольного треугольника, если известен его другой катет и гипотенуза. С помощью этой программы вы в один клик сможете рассчитать катет треугольника.

Катеты равнобедренного прямоугольного треугольника по гипотенузе Калькулятор

Search
Дом	математика ↺
математика	Геометрия ↺
Геометрия	2D геометрия ↺
2D геометрия	Треугольник ↺
Треугольник	Равнобедренный прямоугольный треугольник ↺
Равнобедренный прямоугольный треугольник	Сторона равнобедренного прямоугольного треугольника ↺

Катеты равнобедренного прямоугольного треугольника по гипотенузе Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Гипотенуза равнобедренного прямоугольного треугольника: 11 метр —> 11 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

7.77817459305202 метр —> Конверсия не требуется

7 Сторона равнобедренного прямоугольного треугольника Калькуляторы

Катеты равнобедренного прямоугольного треугольника по гипотенузе формула

Катеты равнобедренного прямоугольного треугольника = Гипотенуза равнобедренного прямоугольного треугольника/sqrt(2)

S_Legs = H/sqrt(2)

Что такое равнобедренный прямоугольный треугольник?

Равнобедренный прямоугольный треугольник – это прямоугольный треугольник, состоящий из двух катетов одинаковой длины. Поскольку две стороны прямоугольного треугольника равны по длине, соответствующие углы также будут равны. Таким образом, в равнобедренном прямоугольном треугольнике две стороны и два острых угла равны.

Что такое гипотенуза?

В геометрии гипотенуза — это самая длинная сторона прямоугольного треугольника, сторона, противоположная прямому углу.

Расчёт катетов по гипотенузе и углу

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

1. Найти все стороны треугольника.
2. Найти все углы треугольника.
3. Найти площадь (S) и периметр (P) треугольника.
4. Найти радиус (r) вписанной окружности.
5. Найти радиус (R) описанной окружности.
6. Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
 

Сторона треугольника (или длина сторон) может быть найдена различными методами. 
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

Для прямоугольного треугольника:

1) Найти катет через гипотенузу и другой катет

где a и b — катеты, с — гипотенуза.

2) Найти гипотенузу по двум катетам

где a и b — катеты, с — гипотенуза.

3) Найти катет по гипотенузе и противолежащему углу

где a и b — катеты, с — гипотенуза,α° и β° — углы напротив катетов.

4) Найти гипотенузу через катет и противолежащий угол

где a и b — катеты, с — гипотенуза,α° и β°- углы напротив катетов.

Для равнобедренного треугольника:

1) Найти основание через боковые стороны и угол между ними

где a — искомое основание, b — известная боковая сторона,α° — угол между боковыми сторонами.

2) Найти основание через боковые стороны и угол при основании

где a — искомое основание,b — известная боковая сторона,β° — угол при осноавнии.

3) Найти боковые стороны по углу между ними

где b — искомая боковая сторона, a — основание,α° — угол между боковыми сторонами.

4) Найти боковые стороны по углу при основании

где b — искомая боковая сторона, a — основание,β° — угол при осноавнии.

​​​​​Для равностороннего треугольника:

1) Найти сторону через площадь

где a — искомая сторона, S — площадь треугольника.

2) Найти сторону через высоту

где a — искомая сторона,h — высота треугольника.

3) Найти сторону через радиус вписанной окружности

где a — искомая сторона,r — радиус вписанной окружности.

4) Найти сторону через радиус описанной окружности

где a — искомая сторона,R — радиус описанной окружности.

​​​​​Для произвольного треугольника:

1) Найти сторону через две известные стороны и один угол (теорема косинусов)

где a — искомая сторона, b и с — известные стороны, α° — угол напротив неизвестной стороны.

2) Найти сторону через одну известную сторону и два угла (теорема синусов)

где a — искомая сторона, b — известная сторона, α° и β° известные углы.

Скачать все формулы в формате Word

• 
  
  
• 0
•