Как найти каждый угол правильного десятиугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Вася Иванов

Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.

Источник

В последнее время я не раз убеждался в том, что при решении подобного рода задач первым делом необходимо отыскать в литературе полную информацию о свойствах той или иной геометрической фигуры — треугольника или квадрата, круга или того же десятиугольника. Если под рукой не окажется бумажного справочника, обратитесь хотя бы к Википедии. Если не все, то большинство важных свойств она вам покажет непременно. Честно говоря, я чаще всего именно с неё и начинаю. А уже потом, если не нашёл ничего подходящего, могу покопаться в других источниках информации. Но, по-моему, на сей раз долго искать не придётся. Упомянутая энциклопедия выдала мне следующие сведения о десятиугольниках:

Я с вами согласен — очень мелко. Только, может быть, оно и к лучшему? Из всего, что там написано, в нашем случае особую важность составляет только одно трёхзначное число — 144. А всё потому, что:

При этом хотелось бы обратить внимание на то, что в задании у нас спрашивается об угле ∠BCE, а в прилагаемой иллюстрации выделен треугольник ∆CDE. И именно в этом треугольнике явно тупой угол и составляет 144°. Но сам треугольник нам пригодится. Ведь, как известно, сумма углов в треугольнике равна 180°. Кроме того, если «у правильного десятиугольника все стороны равной длины», то этот маленький треугольник ∆CDE является равнобедренным, потому что CD = DE. Но при таком раскладе мы можем вычислить и оставшиеся углы, которые равны между собой:

∠DCE = ∠DEC = (180° — 144°) / 2 = 36° / 2 = 18°

Пусть так, но что нам даёт знание величины этих углов? Ведь вычислить нужно совсем другой угол — ∠BCE. Чтобы разобраться, я предлагаю пририсовать ещё один треугольник, в котором нам и следует вычислить тупой угол:

Мы с вами знаем, что ∠CDE = 144°. Нам также известно, что и другой угол десятиугольника ∠BCD = 144°. Но чем при этом ∠BCD отличается от искомого ∠BCE? Так ведь он больше на те самые 18°, которые мы вычислили выше. И тогда:

∠BCE = ∠BCD — ∠DCE = 144° — 18° = 126°

Источник

Чему равен каждый угол правильного десятиугольника

Полиект

6 января, 12:41

0

Сумма углов правильного n — угольника=180 * (n-2);

один угол α (n) = 180° (n-2) / n

при n=10 α (10) = 180° (10-2) / 10=18*8=144° — это ответ.
- Комментировать
- Жалоба
- Ссылка

Найди верный ответ на вопрос ✅ «Чему равен каждый угол правильного десятиугольника …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Новые вопросы по математике

Источник

Предмет: Математика,

автор: kdsk02

Чему равен каждый угол правильного десятиугольника

Ответы

Автор ответа: Аноним

Сумма углов правильного n — угольника=180*(n-2);
один угол α(n)=180°(n-2)/n
при n=10 α(10)=180°(10-2)/10=18*8=144° — это ответ.

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Английский язык,
автор: LOX1717

английский задание 6,спасибо!

4 года назад

Предмет: Математика,
автор: lunevtaya

Задана система уравнений. Выясните, какая пара чисел является верным решением системы.
Выберите верный ответ:
а) (2;20)
б) (0;18)
в) (18;18)
Г) (5;63)
ПОМОГИТЕ ПОЖАЛУЙСТА

4 года назад

Предмет: Русский язык,
автор: adjacenko3

Оле нравится Мамина профессия. синтаксический разбор .пожалуйста помогите

4 года назад

Предмет: Литература,
автор: bak2104

Как вы понимаете слова Евгения Шварца они-то спаслись, но ты помни: человек, который понапрасну теряет время, сам не замечает, как стареет

7 лет назад

Предмет: Математика,
автор: lapteva3

Раскройте скобки, приведите подобные слагаемые:
(3x + y) — (-x — 4y)
(x + 6y) — (8x — 7y)
(m + n) — ( m — n)
( m + 3) — (6m +5) — (m -1)
(x — y) + (x — y) — (2x + y)
(0,2x — 3) — ( x — 2) — (0,4x — 1)

7 лет назад

Источник

From Wikipedia, the free encyclopedia

Regular decagon
A regular decagon
Type	Regular polygon
Edges and vertices	10
Schläfli symbol	{10}, t{5}
Coxeter–Dynkin diagrams
Symmetry group	Dihedral (D₁₀), order 2×10
Internal angle (degrees)	144°
Properties	Convex, cyclic, equilateral, isogonal, isotoxal
Dual polygon	Self

In geometry, a decagon (from the Greek δέκα déka and γωνία gonía, «ten angles») is a ten-sided polygon or 10-gon.^[1] The total sum of the interior angles of a simple decagon is 1440°.

Regular decagon[edit]

A regular decagon has all sides of equal length and each internal angle will always be equal to 144°.^[1] Its Schläfli symbol is {10} ^[2] and can also be constructed as a truncated pentagon, t{5}, a quasiregular decagon alternating two types of edges.

Side length[edit]

The picture shows a regular decagon with side length and radius of the circumscribed circle.

So the regular decagon can be constructed with ruler and compass.

Further conclusions

${displaystyle ;R={frac {2a}{{sqrt {5}}-1}}={frac {a}{2}}({sqrt {5}}+1);}$ and the base height of ${displaystyle Delta ,E_{10}E_{1}M,}$ (i.e. the length of ) is ${displaystyle h={sqrt {R^{2}-(a/2)^{2}}}={frac {a}{2}}{sqrt {5+2{sqrt {5}}}};}$ and the triangle has the area: ${displaystyle A_{Delta }={frac {a}{2}}cdot h={frac {a^{2}}{4}}{sqrt {5+2{sqrt {5}}}}}$ .

Area[edit]

The area of a regular decagon of side length a is given by:^[3]

${displaystyle A={frac {5}{2}}a^{2}cot left({frac {pi }{10}}right)={frac {5}{2}}a^{2}{sqrt {5+2{sqrt {5}}}}simeq 7.694208843,a^{2}}$

In terms of the apothem r (see also inscribed figure), the area is:

${displaystyle A=10tan left({frac {pi }{10}}right)r^{2}=2r^{2}{sqrt {5left(5-2{sqrt {5}}right)}}simeq 3.249196962,r^{2}}$

In terms of the circumradius R, the area is:

${displaystyle A=5sin left({frac {pi }{5}}right)R^{2}={frac {5}{2}}R^{2}{sqrt {frac {5-{sqrt {5}}}{2}}}simeq 2.938926261,R^{2}}$

An alternative formula is where d is the distance between parallel sides, or the height when the decagon stands on one side as base, or the diameter of the decagon’s inscribed circle.
By simple trigonometry,

${displaystyle d=2aleft(cos {tfrac {3pi }{10}}+cos {tfrac {pi }{10}}right),}$

and it can be written algebraically as

{displaystyle d=a{sqrt {5+2{sqrt {5}}}}.}

Sides[edit]

A regular decagon has 10 sides and is equilateral. It has 35 diagonals

Construction[edit]

As 10 = 2 × 5, a power of two times a Fermat prime, it follows that a regular decagon is constructible using compass and straightedge, or by an edge-bisection of a regular pentagon.^[4]

Construction of decagon

Construction of pentagon

An alternative (but similar) method is as follows:

Construct a pentagon in a circle by one of the methods shown in constructing a pentagon.
Extend a line from each vertex of the pentagon through the center of the circle to the opposite side of that same circle. Where each line cuts the circle is a vertex of the decagon. In other words, the image of a regular pentagon under a point reflection with respect of its center is a concentric congruent pentagon, and the two pentagons have in total the vertices of a concentric regular decagon.
The five corners of the pentagon constitute alternate corners of the decagon. Join these points to the adjacent new points to form the decagon.

Nonconvex regular decagon[edit]

The length ratio of two inequal edges of a golden triangle is the golden ratio, denoted by Phi , or its multiplicative inverse:

${displaystyle Phi -1={frac {1}{Phi }}=2,cos 72,^{circ }={frac {1}{,2,cos 36,^{circ }}}={frac {,{sqrt {5}}-1,}{2}}{text{.}}}$

So we can get the properties of a regular decagonal star, through a tiling by golden triangles that fills this star polygon.

The golden ratio in decagon[edit]

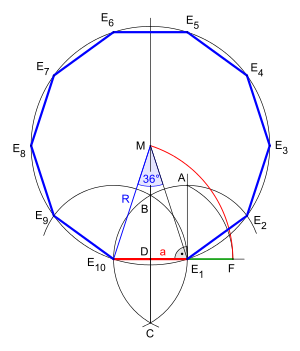
Both in the construction with given circumcircle^[5] as well as with given side length is the golden ratio dividing a line segment by exterior division the
determining construction element.

In the construction with given circumcircle the circular arc around G with radius GE₃ produces the segment AH, whose division corresponds to the golden ratio.

${displaystyle {frac {overline {AM}}{overline {MH}}}={frac {overline {AH}}{overline {AM}}}={frac {1+{sqrt {5}}}{2}}=Phi approx 1.618{text{.}}}$

In the construction with given side length^[6] the circular arc around D with radius DA produces the segment E₁₀F, whose division corresponds to the golden ratio.

${displaystyle {frac {overline {E_{1}E_{10}}}{overline {E_{1}F}}}={frac {overline {E_{10}F}}{overline {E_{1}E_{10}}}}={frac {R}{a}}={frac {1+{sqrt {5}}}{2}}=Phi approx 1.618{text{.}}}$

Decagon with given circumcircle,^[5] animation

Decagon with a given side length,^[6] animation

Symmetry[edit]

Symmetries of a regular decagon. Vertices are colored by their symmetry positions. Blue mirrors are drawn through vertices, and purple mirrors are drawn through edges. Gyration orders are given in the center.

The regular decagon has Dih₁₀ symmetry, order 20. There are 3 subgroup dihedral symmetries: Dih₅, Dih₂, and Dih₁, and 4 cyclic group symmetries: Z₁₀, Z₅, Z₂, and Z₁.

These 8 symmetries can be seen in 10 distinct symmetries on the decagon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway labels these by a letter and group order.^[7] Full symmetry of the regular form is r20 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries in the middle column are labeled as g for their central gyration orders.

Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g10 subgroup has no degrees of freedom but can seen as directed edges.

The highest symmetry irregular decagons are d10, an isogonal decagon constructed by five mirrors which can alternate long and short edges, and p10, an isotoxal decagon, constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular decagon.

Dissection[edit]

10-cube projection	40 rhomb dissection

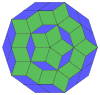
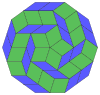
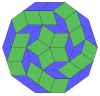
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms.^[8]
In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular decagon, m=5, and it can be divided into 10 rhombs, with examples shown below. This decomposition can be seen as 10 of 80 faces in a Petrie polygon projection plane of the 5-cube. A dissection is based on 10 of 30 faces of the rhombic triacontahedron. The list OEIS: A006245 defines the number of solutions as 62, with 2 orientations for the first symmetric form, and 10 orientations for the other 6.

Regular decagon dissected into 10 rhombi

5-cube

Skew decagon[edit]

3 regular skew zig-zag decagons

{5}#{ }	{5/2}#{ }	{5/3}#{ }

A regular skew decagon is seen as zig-zagging edges of a pentagonal antiprism, a pentagrammic antiprism, and a pentagrammic crossed-antiprism.

A skew decagon is a skew polygon with 10 vertices and edges but not existing on the same plane. The interior of such an decagon is not generally defined. A skew zig-zag decagon has vertices alternating between two parallel planes.

A regular skew decagon is vertex-transitive with equal edge lengths. In 3-dimensions it will be a zig-zag skew decagon and can be seen in the vertices and side edges of a pentagonal antiprism, pentagrammic antiprism, and pentagrammic crossed-antiprism with the same D_5d, [2⁺,10] symmetry, order 20.

These can also be seen in these 4 convex polyhedra with icosahedral symmetry. The polygons on the perimeter of these projections are regular skew decagons.

Orthogonal projections of polyhedra on 5-fold axes

Dodecahedron

Icosahedron

Icosidodecahedron

Rhombic triacontahedron

Petrie polygons[edit]

The regular skew decagon is the Petrie polygon for many higher-dimensional polytopes, shown in these orthogonal projections in various Coxeter planes:^[9] The number of sides in the Petrie polygon is equal to the Coxeter number, h, for each symmetry family.

A₉	D₆	B₅
9-simplex	4₁₁	1₃₁	5-orthoplex	5-cube

References[edit]

^ ^a ^b Sidebotham, Thomas H. (2003), The A to Z of Mathematics: A Basic Guide, John Wiley & Sons, p. 146, ISBN 9780471461630.
^ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 9, ISBN 9780521098595.
^ The elements of plane and spherical trigonometry, Society for Promoting Christian Knowledge, 1850, p. 59. Note that this source uses a as the edge length and gives the argument of the cotangent as an angle in degrees rather than in radians.
^ Ludlow, Henry H. (1904), Geometric Construction of the Regular Decagon and Pentagon Inscribed in a Circle, The Open Court Publishing Co..
^ ^a ^b Green, Henry (1861), Euclid’s Plane Geometry, Books III–VI, Practically Applied, or Gradations in Euclid, Part II, London: Simpkin, Marshall,& CO., p. 116. Retrieved 10 February 2016.
^ ^a ^b Köller, Jürgen (2005), Regelmäßiges Zehneck, → 3. Section «Formeln, Ist die Seite a gegeben …» (in German). Retrieved 10 February 2016.
^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
^ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
^ Coxeter, Regular polytopes, 12.4 Petrie polygon, pp. 223-226.

External links[edit]

Weisstein, Eric W. «Decagon». MathWorld.
Definition and properties of a decagon With interactive animation

Источник

Чему равен каждый угол правильного десятиугольника

Чему равен каждый угол правильного десятиугольника

Ответы

Regular decagon[edit]

Side length[edit]

Area[edit]

Sides[edit]

Construction[edit]

Nonconvex regular decagon[edit]

The golden ratio in decagon[edit]

Symmetry[edit]

Dissection[edit]

Skew decagon[edit]

Petrie polygons[edit]

See also[edit]

References[edit]

External links[edit]