Как найти кенетическую энергию - Исправление недочетов и поиск решений вместе с Examum.ru

Энергию, которой обладают только движущиеся тела, называют кинетической энергией.

Если тело находится в состоянии покоя, его кинетическая энергия равна нулю.

Кинетическая энергия тела (Eкин) зависит от массы тела (m) и от скорости его движения (v).

Кинетическая энергия прямо пропорциональна массе тела и квадрату его скорости.

Определяют кинетическую энергию по формуле:

Чтобы рассчитать массу или скорость, формулу преобразуют следующим образом:

С увеличением массы тела в линейной зависимости увеличивается также и его кинетическая энергия.

Если масса увеличивается в (2) раза, тогда кинетическая энергия увеличивается также в (2) раза.

Зависимость кинетической энергии от массы можно отобразить на данном графике, если принять скорость тела постоянной и равной (2 м/с).

Рис. (1). График, зависимость кинетической энергии от массы

С увеличением скорости движения тела увеличивается также и его кинетическая энергия в квадратичной зависимости.

Если скорость увеличивается в (2) раза, тогда кинетическая энергия увеличивается в (4) раза.

Зависимость кинетической энергии от скорости движения можно отобразить на данном графике, если принять массу тела постоянной и равной (2 кг).

Рис. (2). График, зависимость кинетической энергии от скорости движения

Пример:

Автомобиль, масса которого (1400 кг), из состояния покоя развивает скорость до значения (5 м/с).

Какова кинетическая энергия автомобиля на конечном этапе движения?

Eкин=m⋅v22=1400⋅522=17500Дж

Источники:

Рис. 1. График, зависимость кинетической энергии от массы. © ЯКласс.
Рис. 2. График, зависимость кинетической энергии от скорости движения. © ЯКласс.

Источник

Загрузить PDF

Существует два вида энергии: потенциальная и кинетическая. Потенциальная энергия — это энергия одного объекта по отношению к другому, которая зависит от их взаимного расположения.^[1] Например, если вы стоите на вершине холма, то ваша потенциальная энергия будет отличаться от той, которой вы обладали бы у подножия этого холма. Кинетическая энергия — это энергия движущегося объекта.^[2] Кинетическая энергия возникает при колебаниях, вращении и поступательном движении (перемещении тела из одного места в другое).^[3] Кинетическую энергию любого объекта легко вычислить, если известны его масса и скорость.^[4]

1
Запомните формулу для вычисления кинетической энергии. Формула для нахождения кинетической энергии (КЕ) имеет следующий вид: KE = 0,5 x mv². Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.^[5]
- Ответ должен быть выражен в стандартных единицах измерения кинетической энергии, джоулях (Дж). Один джоуль эквивалентен 1 кг * м²/с².
2
Определите массу объекта. Если в исходном условии не дана масса, ее придется определить самостоятельно. Для этого можно взвесить предмет и найти массу в килограммах (кг).
- Настройте весы. Прежде чем взвешивать предмет, необходимо выставить на весах ноль. Это называется тарировкой весов.^[6]
- Положите объект на весы. Осторожно положите предмет на весы и запишите его массу в килограммах.
- При необходимости переведите граммы в килограммы. В конечную формулу необходимо подставить значение массы в килограммах.
3
Найдите скорость объекта. Часто в условии задачи дается скорость объекта. Если скорость не дана, ее можно найти по пройденному расстоянию и затраченному для этого времени.^[7] Скорость измеряется в метрах в секунду (м/с).
- Чтобы определить скорость, необходимо расстояние поделить на время: V = d/t. Скорость является векторной величиной, то есть имеет абсолютное значение и направление. Абсолютное значение соответствует величине скорости, а направление указывает на то, куда движется объект.
- Например, скорость объекта может составлять 80 м/с или –80 м/с, в зависимости от направления движения.
- Чтобы вычислить скорость, просто поделите пройденное расстояние на затраченное время.
Реклама

1
Запишите формулу. Кинетическая энергия (KE) вычисляется по следующей формуле: KE = 0,5 x mv². Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.^[8]
- Ответ записывается в джоулях (Дж). Это стандартная единица измерения кинетической энергии. Один джоуль эквивалентен 1 кг * м²/с².
2
Подставьте в формулу массу и скорость. Если в условии задачи не дана масса или скорость, необходимо найти их. Предположим, что заданы обе эти величины, и необходимо решить следующую задачу: Найдите кинетическую энергию женщины массой 55 кг, которая бежит со скоростью 3,87 м/с. В условии даны масса и скорость, поэтому их можно сразу подставить в формулу:^[9]
- KE = 0,5 x mv²
- KE = 0,5 x 55 x (3,87)²
3
Проведите вычисления. После подстановки массы и скорости можно рассчитать кинетическую энергию (KE). Возведите скорость в квадрат и умножьте полученное значение на массу и на 0,5. Помните, что ответ должен получиться в джоулях (Дж).^[10]
- KE = 0,5 x 55 x (3,87)²
- KE = 0,5 x 55 x 14,97
- KE = 411,675 Дж
Реклама

1
Запишите формулу. Кинетическая энергия (KE) вычисляется по следующей формуле: KE = 0,5 x mv². Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.^[11]
- Ответ записывается в джоулях (Дж). Это стандартная единица измерения кинетической энергии. Один джоуль эквивалентен 1 кг * м²/с².
2
Подставьте в формулу известные значения. В некоторых задачах дается кинетическая энергия и масса, или кинетическая энергия и скорость. Сначала необходимо подставить в формулу все известные величины.
- Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
  - KE = 0,5 x mv²
  - 500 Дж = 0,5 x 30 x v²
- Пример 2: чему равна масса предмета, если его кинетическая энергия составляет 100 Дж, и он движется со скоростью 5 м/с?
  - KE = 0,5 x mv²
  - 100 Дж = 0,5 x m x 5²
3
Преобразуйте уравнение, чтобы найти неизвестную величину. Путем алгебраических преобразований перенесите искомую величину по одну, а все известные величины — по другую сторону знака равенства.
- Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
  - KE = 0,5 x mv²
  - 500 Дж = 0,5 x 30 x v²
  - Умножим массу на 0,5: 0,5 x 30 = 15
  - Поделим кинетическую энергию на получившееся значение: 500/15 = 33,33
  - Извлечем квадратный корень, чтобы найти скорость: 5,77 м/с
- Пример 2: чему равна масса предмета, если его кинетическая энергия составляет 100 Дж, и он движется со скоростью 5 м/с?
  - KE = 0,5 x mv²
  - 100 Дж = 0,5 x m x 5²
  - Возведем скорость в квадрат: 5² = 25
  - Умножим полученное значение на 0,5: 0,5 x 25 = 12,5
  - Поделим кинетическую энергию на эту величину: 100/12,5 = 8 кг
Реклама

Об этой статье

Эту страницу просматривали 29 609 раз.

Была ли эта статья полезной?

Источник

Download Article

There are two basic forms of energy: potential and kinetic energy. Potential energy is the energy an object has relative to the position of another object.^[1] For example, if you are at the top of a hill, you have more potential energy than if you are at the bottom of the hill. Kinetic energy is the energy an object has when it is in motion.^[2] Kinetic energy can be due to vibration, rotation, or translation (movement from one place to another).^[3] The kinetic energy of an object can easily be determined by an equation using the mass and velocity of that object.^[4]

1
Know the formula for calculating kinetic energy. The formula for calculating kinetic energy (KE) is KE = 0.5 x mv². Here m stands for mass, the measure of how much matter is in an object, and v stands for the velocity of the object, or the rate at which the object changes its position.^[5]
- Your answer should always be stated in joules (J), which is the standard unit of measurement for kinetic energy. It is equivalent to 1 kg * m²/s².
2
Determine the mass of an object. If you are solving a problem where the mass isn’t given, you will have to determine the mass yourself. This can be done by weighing the object on a balance and obtaining the mass in kilograms (kg).
- Tare the balance. Before you weigh your object, you must set it to zero. Zeroing out the scale is called taring.^[6]
- Place your object in the balance. Gently, place the object on the balance and record its mass in kilograms.
- If necessary, convert grams to kilograms. For the final calculation, the mass must be in kilograms.
Advertisement
3
Calculate the velocity of the object. Oftentimes, the problem will give you the velocity of the object. If this is not the case, you can determine the velocity by using the distance an object travels and how long it takes to cover that distance.^[7] The units for velocity are meters per second (m/s).
- Velocity is defined by the equation, displacement divided by time: V = d/t. Velocity is a vector quantity, meaning it has both a magnitude and a direction. Magnitude is the number value that quantifies the speed, while the direction is the direction in which the speed takes place during motion.
- For example, an object’s velocity can be 80 m/s or -80 m/s depending on the direction of travel.
- To calculate velocity, simply divide the distance the object traveled by the time it took to travel that distance.

1
Write the equation. The formula for calculating kinetic energy (KE) is KE = 0.5 x mv². Here m stands for mass, the measure of how much matter is in an object, and v stands for velocity of the object, or the rate at which the object changes its position.^[8]
- Your answer should always be stated in joules (J), which is the standard unit of measurement for kinetic energy. It is equivalent to 1 kg * m²/s².
2
Plug the mass and velocity into the equation. If you don’t know the mass or velocity of the object, then you’ll have to calculate it. But let’s say that you do know both quantities and are working to solve the following problem: Determine the kinetic energy of a 55 kg woman running with a velocity of 3.87m/s. Since you know the mass and velocity of the woman, you can plug it into the equation:^[9]
- KE = 0.5 x mv²
- KE = 0.5 x 55 x (3.87)²
3
Solve the equation. Once you’ve plugged in the mass and velocity, you can solve for kinetic energy (KE). Square the velocity and then multiply all of the variables together. Remember to state your answer in joules (J). ^[10]
- KE = 0.5 x 55 x (3.87)²
- KE = 0.5 x 55 x 14.97
- KE = 411.675 J

1
Write the equation. The formula for calculating kinetic energy (KE) is KE = 0.5 x mv². Here m stands for mass, the measure of how much matter is in an object, and v stands for velocity of the object, or the rate at which the object changes its position.^[11]
- Your answer should always be stated in joules (J), which is the standard unit of measurement for kinetic energy. It is equivalent to 1 kg * m²/s².
2
Plug in the known variables. In some problems, you may know the kinetic energy and the mass or kinetic energy and velocity. The first step to solving this problem is to plug in all of the variables that are known.
- Example 1: What is the velocity of an object with a mass of 30 kg and a kinetic energy of 500 J?
  - KE = 0.5 x mv²
  - 500 J = 0.5 x 30 x v²
- Example 2: What is the mass of an object with a kinetic energy of 100 J and a velocity of 5 m/s?
  - KE = 0.5 x mv²
  - 100 J = 0.5 x m x 5²
3
Rearrange the equation to solve for the unknown variable. Using algebra, you can solve for the unknown variable by rearranging all of the known variables to one side of the equation.
- Example 1: What is the velocity of an object with a mass of 30 kg and a kinetic energy of 500 J?
  - KE = 0.5 x mv²
  - 500 J = 0.5 x 30 x v²
  - Multiply mass by 0.5: 0.5 x 30 = 15
  - Divide kinetic energy by the product: 500/15 = 33.33
  - Square root to find velocity: 5.77 m/s
- Example 2: What is the mass of an object with a kinetic energy of 100 J and a velocity of 5 m/s?
  - KE = 0.5 x mv²
  - 100 J = 0.5 x m x 5²
  - Square the velocity: 5² = 25
  - Multiply by 0.5: 0.5 x 25 = 12.5
  - Divide kinetic energy by product: 100/12.5 = 8 kg

Calculator, Practice Problems, and Answers

Add New Question

Question

What is the kinetic energy possessed by a car having a mass of 1500 kg and travelling at a velocity of 50 km/h?

Recalulate 50 km/h into m/s which is 13.889 m/s; then apply the formula:

KE = 0.5 * 1500kg * (13.889 m/s)^2 = 144678 J => appr. 145 kJ
Question

If mass and velocity of body is doubled how can I figure out the change in kinetic energy?

The formula given for K.E. is K.E. = 0.5m(v^2). Doubling mass gives m = 2m. Doubling velocity gives v^2 = (2v)^2 =4v^2. Which makes K.E. 4 x 2 = 8 times bigger in total.
Question

What if the amount is in grams?

Electric gears

Community Answer

If it’s in grams, you’ll have to convert it to kilograms by dividing it by 1000. For example, 100g becomes 0.1kg, and 3g becomes 0.003kg.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

Thanks for submitting a tip for review!

About This Article

Article SummaryX

To calculate kinetic energy, write out a formula where kinetic energy is equal to 0.5 times mass times velocity squared. Add in the value for the mass of the object, then the velocity with which it is moving. Solve for the unknown variable. Your answer should be stated in joules, or J. If you want to learn how to solve velocity or mass using kinetic energy, keep reading the article!

Did this summary help you?

Thanks to all authors for creating a page that has been read 1,064,800 times.

Did this article help you?

Источник

Энергия — важнейшее понятие и термин в механике. Что такое энергия, и что она значит? Существует множество определений, и вот одно из них.

Что такое энергия?

Энергия в физике — это способность тела совершать работу.

Кинетическая энергия

Что такое кинетическая энергия?

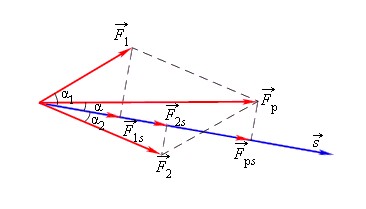
Рассмотрим тело, которое двигалось под действием каких-то сил, изменило свою скорость с v1→ до v2→. В этом случае силы, действующие на тело, совершили определенную работу A.

Работа всех сил, действующих на тело, равна работе равнодействующей силы.

Fр→=F1→+F2→

A=F1·s·cosα1+F2·s·cosα2=Fрcosα.

Как находить связь между изменением скорости тела и работой, совершенной действующими на тело силами. Для простоты будем считать, что на тело действует одна сила F→, направленная вдоль прямой линии. Под действием этой силы тело движется равноускоренно и прямолинейно. В этом случае векторы F→, v→, a→, s→ совпадают по направлению и их можно рассматривать как алгебраические величины.

Работа силы F→ равна A=Fs. Перемещение тела выражается формулой s=v22-v122a. Отсюда:

A=Fs=F·v22-v122a=ma·v22-v122a

A=mv22-mv122=mv222-mv122.

Если вычислять, то работа, совершенная силой, пропорционально изменению квадрата скорости тела.

Определение. Кинетическая энергия

Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости. Вот как выглядит формула кинетической энергии:

EK=mv22.

Кинетическая энергия — это энергия движения тела. При нулевой скорости она равна нулю.

Теорема о кинетической энергии

Вновь будем работать с рассмотренным примером и сформулируем теорему о кинетической энергии тела.

Теорема о кинетической энергии

Работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы.

A=EK2-EK1.

Таким образом, кинетическая энергия тела массы m, движущегося со скоростью v→, будет измеряться (при измерении) и равна работе, которую сила должна совершить, чтобы разогнать тело до этой скорости.

A=mv22=EK.

Чтобы остановить тело, нужно совершить работу

A=-mv22=-EK

Потенциальная энергия

Что будет означать или обозначать кинетическая энергия?

Кинетическая энергия — это энергия движения. Наряду с кинетической энергией есть еще такой вид энергии как потенциальная энергия, то есть энергия взаимодействия тел, которая будет вычисляться и зависеть от их положения. Кинетическая и потенциальная энергии рассматриваются параллельно.

Формула потенциальной энергии:

E пот = m * g * h

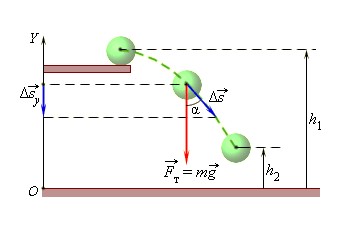
Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциал-я энергия. Когда тело движется и падает вниз под действием силы тяжести (притяжения), эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.

Важно!

Вообще о потенциально энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.

Примеры консервативных сил: сила тяжести, сила упругости.

Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу.

Рассмотрим вычисление на примере, когда шар переместился из точки с высотой h1 в точку с высотой h2.

При этом сила тяжести совершила работу, равную

A=-mg(h2-h1)=-(mgh2-mgh1).

Эта работа равна изменению величины mgh, взятому с противоположным знаком.

Величина ЕП=mgh — потенциальна энергия в поле силы тяжести. На нулевом уровне (на земле) потенциальную энергию тела можно не рассчитывать: она равна нулю.

Определение. Потенциальная энергия

Потенциальная энергия — часть полной механической энергии системы, с нахождением в поле консервативных сил. Потенциальная энергия зависит от положения точек, составляющих систему. Механическая энергия — это сумма потенциальной и кинетической энергий, которые есть в компонентах механической системы.

Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины (пружинной энергии) и т.д.

Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.

A=-(EП2-EП1).

Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.

При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.

EП=-GmMr.

Здесь G — гравитационная постоянная, M — масса Земли.

Потенциальная энергия пружины

Представим, что в первом случае мы взяли пружину и удлинили ее на величину x. Во втором случае мы сначала удлинили пружину на 2x, а затем уменьшили на x. В обоих случаях пружина оказалась растянута на x, но это было сделано разными способами.

При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна

Aупр=-A=-kx22.

Величина Eупр=kx22 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.

Если перед вами часто поднимается вопрос определения и характеристики энергии, как явления, вам стоит подумать о сохранении описанной выше информации.

Источник

Содержание:

Определение и формула кинетической энергии
Кинетическая энергия материальной точки и тела
Единицы измерения кинетической энергии
Теорема Кенига
Примеры решения задач

Определение и формула кинетической энергии

Определение

Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.

Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.

Встречаются следующие обозначения кинетической энергии: E_k,W_k,T.

Работу, которую производят над телом (A’) можно связать с изменением его кинетической энергии:

$$A^{prime}=E_{k 2}-E_{k 1}(1)$$

Кинетическая энергия материальной точки и тела

Кинетическая энергия материальной точки равна:

$$E_{k}=frac{m v^{2}}{2}=frac{p^{2}}{2 m}=frac{p v}{2}(2)$$

где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной.

Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:

$$E_{k}=frac{1}{2} int_{m} v^{2} d m=frac{1}{2} int_{m} rho v^{2} d V(3)$$

где dm – элементарный участок тела, который можно считать материальной точкой, dV – объем выделенного элементарного участка тела,
v – скорость перемещения рассматриваемого элемента, $rho$ — плотность участка, m–масса всего рассматриваемого тела, V – объем тела.

В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом.

При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:

$$E_{k}=frac{J omega^{2}}{2}=frac{omega^{2}}{2} int_{m} r^{2} d m=frac{L^{2}}{2 J}=frac{L omega}{2}(4)$$

где J – момент инерции тела по отношению к оси вращения, ?–модуль угловой скорости вращения тела,
r – расстояние от элементарного участка тела до оси вращения,
L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение.

Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:

$$E_{k}=frac{bar{L} bar{omega}}{2}(5)$$

$bar{L}$ – момент импульса рассматриваемого тела относительно точки О.

Единицы измерения кинетической энергии

Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:

[E_k]=Дж (джоуль),

в системе СГС –[E_k]= эрг.

При этом: 1 дж= 10⁷ эрг.

Теорема Кенига

Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой,
кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения
системы со скоростью центра масс (v_c) и кинетической энергии
(E’_k) системы при ее относительном движении к поступательному перемещению системы отсчета.
При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:

$$E_{k}=sum_{i=1}^{n} frac{m_{i} v_{i}^{2}}{2}=frac{m v_{c}^{2}}{2}+E_{k}^{prime}$$

где $mathrm{E}_{k}^{prime}=sum_{i=1}^{n} frac{m_{i} v_{i}^{prime 2}}{2}, v_{i}^{prime}=v_{i}-v_{c}, m=sum_{i=1}^{n} m_{i}$ –суммарная масса системы материальных точек.

Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:

$$E_{k}=frac{m v_{c}^{2}}{2}+frac{J_{c} omega^{2}}{2}(7)$$

где J_c — момент инерции тела по отношению к оси вращения, проходящей через центр масс. В частности, при плоском движении
J_c=const.В общем случае, ось (она называется мгновенной) перемещается в теле, тогда момент инерции является переменным во времени.

Примеры решения задач

Пример

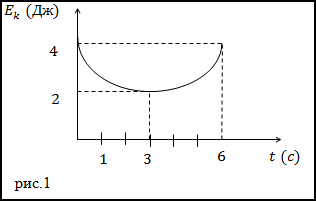
Задание. Какова работа, которая производится над телом за t=3 c (с начала отсчета времени),
при силовом взаимодействии, если изменение кинетической энергии исследуемого тела задано графиком (рис.1)?

Решение. По определению изменение кинетической энергии равно работе (A’),
которая производится над телом при силовом взаимодействии, то есть можно записать, что:

$$A^{prime}=Delta E_{k}(1.1)$$

Исследуя график, приведенный на рис.1 мы видим, что за время t=3 c кинетическая энергия тела изменяется от 4 Дж до 2 Дж, следовательно:

$A^{prime}=2-4=-2$ (Дж)

Ответ. A’=-2 Дж.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Материальная точка движется по окружности, радиус которой равен R. Кинетическая
энергия частицы связана c величиной пути (s), пройденного ей в соответствии с формулой:
$E_{k}=alpha s^{2}(alpha=$const$)$. Какое уравнение связывает силу (F), действующую на точку и путь s?

Решение. В качестве основы для решения задачи используем формулу, определяющую кинетическую энергию материальной точки:

$$E_{k}=frac{m v^{2}}{2}(2.1)$$

Но по условию задачи:

$$E_{k}=alpha s^{2}(2.2)$$

Следовательно, можно приравнять правые части выражений (2.1) и (2.2), и получить:

$$frac{m v^{2}}{2}=alpha s^{2} rightarrow v^{2}=frac{2 alpha s^{2}}{m} rightarrow v=s sqrt{frac{2 alpha}{m}}(2.3)$$

Из второго закона Ньютона нам известно, что сила, действующая на частицу, будет равна:

$$bar{F}=m bar{a}(2.4)$$

где

$$a=sqrt{a_{n}^{2}+a_{tau}^{2}}(2.5)$$

При этом нормальное ускорение частицы (a_n), перемещающейся по окружности найдем как:

$$a_{n}=frac{v^{2}}{R}=frac{2 alpha s^{2}}{R m}(2.6)$$

Тангенциальную составляющую ускорения (a_т)используя определение тангенциального ускорения, определение скорости
($v=frac{d s}{d t}$) и выражение v(s) (2.3) вычислим как:

$$a_{tau}=frac{d v}{d t}=frac{d v}{d s} cdot frac{d s}{d t}=sqrt{frac{2 a}{m}} cdot v=s frac{2 a}{m}(2.7)$$

Используем выражения: (2.5), (2.6), (2.7), окончательно получаем для модуля силы:

$$F=m a=m sqrt{frac{4 alpha^{2} s^{4}}{R^{2} m^{2}}+s^{2} frac{4 alpha^{2}}{m^{2}}}=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$$

Ответ. $F=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$

Читать дальше: Формула массы тела.

Источник