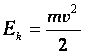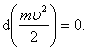Загрузить PDF
Загрузить PDF
Когда на движущееся тело не действуют противодействующие силы, оно двигается с постоянной скоростью — это следует из первого закона Ньютона. Однако если на движущееся тело действует сила, направление которой совпадает с направлением движения тела, оно будет ускоряться в соответствии со вторым законом Ньютона 
-
1
Запишите формулу, связывающую работу и энергию. Работа, выполненная над телом, равна изменению его кинетической энергии.
-
2
Вместо работы подставьте в формулу интеграл. То есть в формуле замените работу на интеграл произведения силы и перемещения тела.
-
3
Вместо силы подставьте произведение массы и ускорения. Теперь вместо ускорения подставьте изменение скорости, деленное на изменение времени. Обратите внимание, что масса является скалярной величиной, поэтому ее можно вынести за интеграл.
-
4
Избавьтесь от перемещения и времени. Обратите внимание, что перемещение, деленное на изменение времени, равно скорости. Поэтому перепишите формулу так:
-
5
Возьмите интеграл по изменению скорости. Как правило, начальная скорость
равна 0.
Реклама
-
1
Запишите формулу, связывающую работу и энергию. Работа, выполненная над телом, равна изменению его кинетической энергии.
-
2
Вместо работы подставьте в формулу произведение силы и перемещения тела. Теперь силу замените произведением массы и ускорения. Так как мы используем обычные математические операции (а не интегралы), здесь ускорение считается постоянным (то есть не меняется).
-
3
Запишите формулу для вычисления скорости по начальной скорости, ускорению и перемещению. Есть формулы, которые включают время, перемещение, скорость и ускорение, но ниже приведена формула, в которой времени нет.
-
4
На основании предыдущей формулы выведите формулу для вычисления ускорения. Помните, что начальная скорость равна 0.
-
5
Подставьте выражение для нахождения ускорения в исходную формулу, а затем упростите ее.
Реклама
Об этой статье
Эту страницу просматривали 25 860 раз.
Была ли эта статья полезной?
Содержание:
Кинетическая энергия:
Иногда значение работы можно найти, не используя понятия силы и перемещения, на основании характеристики изменения энергии тела.
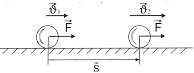
Рассмотрим тело массой m, на которое действует сила F. Направление действия силы совпадает с направлением перемещения. Работа, которую выполняет эта сила,
A = Fs.
Согласно второму закону механики Ньютона значение силы
Как известно, модуль перемещения равен:
Поэтому
Как известно, выражение 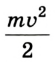
Физическая величина, описывающая состояние движущегося тела и изменение которой определяет работу, называется кинетической энергией.
Для измерения энергии, как и работы, используется единица джоуль (Дж), названная в честь английского ученого Д. Джоуля.
Кинетической энергией обладает тело, движущееся в данной системе отсчета с определенной скоростью:
Скорость тела, измеренная в разных системах отсчета, будет иметь разное значение, т. е. она является относительной величиной. Поэтому кинетическая энергия тела постоянной массы тоже величина относительная и в разных системах отсчета имеет разное значение.
Рассмотрим, например, два железнодорожных вагона, массы которых составляют по 2 • 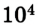
Если же систему отсчета связать со вторым вагоном, то первый будет двигаться со скоростью 5 м/с , а второй — со скоростью v = 0. В этом случае
Следовательно, при расчетах в разных инерциальных системах отсчета следует учитывать, что кинетическая энергия в случае перехода из одной системы в другую будет изменяться.
Что такое кинетическая энергия
Кинетическая энергия (от греческого слова кинетикос — тот, что приводит в движение) — это энергия, которой тело обладает вследствие собственного движения.
Кинетической энергией обладает ветер, её используют для сообщения движения ветряным двигателям. Движущиеся массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и заставляют их вращаться. На рисунке 175, а изображена ветряная мельница, в которой за счёт энергии ветра мелют зерно. Современные довольно мощные ветряные двигатели (рис. 175, б) используют для того, чтобы вырабатывать электроэнергию, качать из скважин воду и подавать её в водонапорные башни.
Движущаяся вода или нагретый пар, вращая турбины электростанции, теряет часть своей кинетической энергии и выполняет работу. Самолёт, летящий высоко в небе, кроме потенциальной обладает и кинетическуй энергией. Если тело находится в состоянии покоя, т. е. его скорость относительно Земли равна нулю, то и его кинетическая энергия относительно Земли будет равна нулю.
Опытами установлено, что чем больше масса тела и скорость, с которой оно движется, тем больше его кинетическая энергия. Выявленная зависимость математически выражается такой формулой:
где 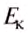
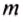
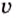
Определение кинетической энергии
Наблюдения явлений природы показывают, что работа может выполняться при движении тел. Так, движущийся тепловоз, стыкуясь с вагоном, перемещает его на некоторое расстояние. Выполняется работа и в том случае, когда брошенный камень разбивает лед. Выстреленная из ружья пуля пробивает доску и т. п. Если потенциальной энергией обладают тела, на которые действует сила, то в упомянутых выше случаях работа выполняется потому, что они осуществляли перемещение, двигались.
Какой энергией обладают движущиеся тела
Энергию движущегося тела называют кинетической энергией.
Кинетическая энергия является физической величиной ее значение можно рассчитывать. Для этого необходимо знать, от каких физических величин она зависит.
Как рассчитывают кинетическую энергию
Поставим желоб под некоторым углом к поверхности стола. На некотором расстоянии от его нижнего конца поставим брусок. На средней части желоба разместим маленький стальной шарик и отпустим его. Скатившись по желобу, шарик ударится о брусок и переместит его на некоторое расстояние. Отметим расстояние, на которое сместился брусок.
Поместим шарик в верхней части желоба и отпустим его. В этом случае, скатившись желобом к основе, шарик приобрел большую скорость, чем раньше. Ударившись в брусок, он переместит его на большее расстояние, чем в предыдущем опыте, соответственно выполнив большую работу.
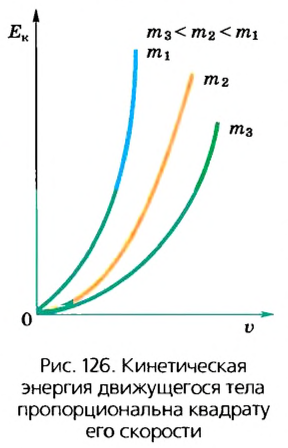
Таким образом, кинетическая энергия тела зависит от его скорости. Эта зависимость нелинейная, что заметно на графике зависимости кинетической энергии тела от его скорости. График имеет вид кривой линии (рис. 126).
Кинетическая энергия тела относительна
Как известно, скорость тела является относительной величиной и зависит от выбора тела отсчета. Поэтому и кинетическая энергия является величиной относительной. Если артиллерийский снаряд, попав в стену, причиняет значительные разрушения, то снаряд, посланный вдогонку сверхзвуковому самолету, не причинит ему существенных повреждений, поскольку скорость снаряда относительно самолета будет небольшой.
Последствия столкновения автомобилей в случае их движения навстречу друг другу будут всегда более ощутимы, чем тогда, когда один автомобиль догоняет другой.
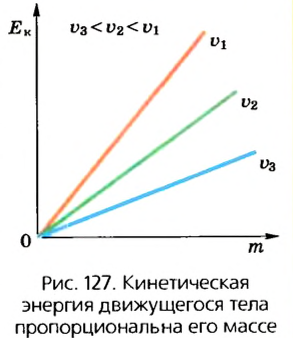
Кинетическая энергия зависит и от массы тела. Если повторим предыдущие опыты с шариком большей массы, то увидим, что перемещения бруска в этом случае будет большим. Эта зависимость линейная, поэтому можно сказать, что кинетическая энергия тела пропорциональна его массе (рис. 127).
Как рассчитать кинетическую энергию
Чтобы рассчитать кинетическую энергию, используют формулу:
где 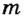
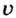
Кинетическая энергия разных физических тел используется для выполнения механической работы. Так, опытные водители автомобилей время от времени отсоединяют двигатель от колес, выключая сцепление, и этим экономят топливо. Работа по преодолению сил трения выполняется за счет кинетической энергии автомобиля. Конструкторы работают над моделью городского автобуса, который начинает движение за счет энергии раскрученного во время стоянки большого маховика. Это дает возможность существенно уменьшить выбросы вредных газов в атмосферу и экономить топливо.
В южных областях Украины, в частности на Крымском полуострове, используют ветряные электростанции, которые работают за счет кинетической энергии потоков воздуха — ветра (рис. 128).
- Заказать решение задач по физике
Кинетическая энергия тела
Рассмотрим движение тела массой т под действием нескольких сил, например движение санок (см. рис. 124). Предположим также, что сила натяжения веревок постоянна, а следовательно, постоянной будет и результирующая сила 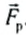
Рассмотрим случай, когда проекция результирующей силы на направление движения положительна, т. е. санки движутся равноускоренно с ускорением а, которое находится из второго закона Ньютона:
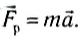
Работа результирующей силы:
A = Fp△r, (2)
где △r— модуль перемещения тела за некоторый промежуток времени. Подставим выражение (1) в (2). В результате получим:
A = ma△r. (3)
При равноускоренном одномерном движении модуль перемещения △r и изменение скорости связаны соотношением:
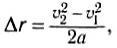
где 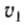
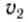
Соотношение (3) с учетом (4) примет вид:
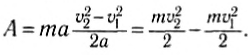
Полученная формула связывает работу результирующей силы, действующей на тело, с изменением величины 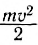
Кинетическая энергия тела — это энергия движения. Она равна половине произведения массы тела на квадрат его скорости:
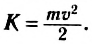
Тогда формула (5) примет вид:
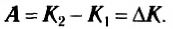
Итак, работа результирующей силы, действующей на тело, равна изменению кинетической энергии тела. Как вы уже знаете, изменение какой-то величины равно разности конечного значения и начального. Из формулы (7) очевидно следует, что кинетическая энергия выражается в тех же единицах, что и работа, т. е. в СИ в джоулях.
Когда результирующая сила действует по направлению движения тела и, следовательно, совершает положительную работу, то K2>K1. Это означает, что кинетическая энергия тела увеличивается. Понятно, что, если результирующая сила направлена в сторону, противоположную движению, она совершает отрицательную работу, и кинетическая энергия тела уменьшается. Следует отметить, что, хотя мы получили формулу (7) для частного случая равноускоренного и прямолинейного движения, она справедлива и в случае изменяющейся во времени результирующей силы. Поэтому формулу (7) часто называют теоремой о кинетической энергии.
Итак, любое движущееся тело (рис. 127, 128) обладает кинетической энергией. Поскольку скорость тела зависит от выбора инерциальной системы отсчета, то и кинетическая энергия также зависит от выбора системы отсчета. Очевидно, что, как и работа, кинетическая энергия является скалярной физической величиной. Она не зависит от направления движения тела, а определяется его массой и квадратом скорости.
Главные выводы:
- Кинетическая энергия тела — это энергия движения. Она равна половине произведения массы тела на квадрат его скорости и зависит от выбора системы отсчета.
- Изменение кинетической энергии равно работе всех сил, действующих на тело.
- Кинетическая энергия измеряется в тех же единицах, что и работа.
- Закон сохранения и превращения механической энергии
- Работа, мощность и энергия
- Движение и силы
- Давление в физике
- Взаимодействие тел
- Механическая энергия и работа
- Золотое правило механики
- Потенциальная энергия
|
Энергия. Виды механической энергии. Работа и энергия. |
|
|
Энергия — физическая величина, характеризующая состояние тела или системы тел по их движению и взаимодействию. В механике энергия тела или системы тел определяется взаимным положением тел или системы тел и их скоростями. При изменении состояния тела (изменении энергии) совершается механическая работа. Т.о. изменение энергии при переходе системы из одного состояния в другое равно работе внешних сил. Механическая работа — мера изменения энергии тела. |
|
|
В механике выделяют два вида энергии: кинетическую энергию и потенциальную энергию. |
|
|
Кинетическая энергия. Кинетическая энергия — энергия движущегося тела.(От греческого слова kinema — движение). По определению кинетическая энергия покоящегося в данной системе отсчета тела обращается в ноль. |
|
|
Пусть тело движется под действием постоянной силы Тогда: Т.к. Т.к. движение равноускоренное, то: |
|
|
Следовательно: |
|
|
|
[Ek]=Дж. |
|
Кинетическая энергия — величина относительная, зависящая от выбора СО, т.к. скорость тела зависит от выбора СО. |
|
|
Т.о. |
|
|
Эта теорема справедлива для любого движения и для сил любой природы. Если тело разгоняется из состояния покоя, то Ek1=0. Тогда A = Ek2. Следовательно, кинетическая энергия численно равна работе, которую необходимо совершить, чтобы разогнать тело из состояния покоя до данной скорости. |
|
|
Вывод: Работа силы равна изменению кинетической энергии тела, т.е. A = ΔEk. Причем, A>0, если Ekувеличивается, и А<0, если Ek<0. |
A = ΔEk |
Уравнение
движения тела под действием внешней
силы имеет вид
или,
в проекции на направление движения,
Умножив
обе части равенства на ,
получим
.
Левая
часть равенства есть полный дифференциал
некоторой функции:

Если
система замкнута, то иFτ = 0.
Тогда и
Если полный дифференциал некоторой
функции, описывающей поведение системы,
равен нулю, то эта функция может служить
характеристикой состояния данной
системы.
Функция состояния системы, определяемая
только скоростью ее движения,
называется кинетической
энергией.
Кинетическая
энергия системы есть функция состояния
движения этой системы. K –
аддитивная величина:
K –
относительная величина, её значение
зависит от выбора системы координат
(так же как и –
относительная величина).
Энергия измеряется в СИ в единицах
произведения силы на расстояние, т.е. в
ньютонах на метр. 1 Н·м = 1 Дж.
Кроме
того, в качестве единицы измерения
энергии используется внесистемная
единица – электрон-вольт (эВ). 1 эВ =
1,6·1019 Дж.
При
решении задач полезна формула, связывающая
кинетическую энергию с импульсом p.
Получим её:
отсюда
Теперь рассмотрим связь кинетической
энергии с работой.
Если постоянная сила действует на тело,
то оно будет двигаться в направлении
силы. Тогда элементарная работа по
перемещению тела из точки 1 в точку 2,
будет равна произведению силы F на
перемещение dr :
dA = F dr,
отсюда ,
Окончательно
получаем:
Следовательно, работа силы,
приложенной к телу на пути r,
численно равна изменению кинетической
энергии этого тела:
Или изменение
кинетической энергии dK равно
работе внешних сил:
dK = dA.
Работа, так же как и кинетическая
энергия, измеряется в джоулях.
Скорость совершения работы (передачи
энергии) называется мощность.
Мощность
есть работа, совершаемая в единицу
времени.
Мгновенная
мощность
,
или
Средняя
мощность
Измеряется мощность в ваттах. 1 Вт = 1
Дж/с.
11. Законы сохранения в механике
Кинетическая энергия тела
массой m,
движущегося со скоростью :
.
Потенциальная энергия тела
массой m,
находящегося на высоте h,
в поле сил тяжести с ускорением свободного
падения :
.
Энергия
пружины с
коэффициентом жесткости k,
сжатой или растянутой на :
.
Импульс тела массой m,
движущегося со скоростью :
.
Закон сохранения энергии:
В замкнутых системах
полная энергия (потенциальная +
кинетическая + тепловая) системы тел
сохраняется.
.
Если при этом можно пренебречь
переходом механической энергии
(потенциальная + кинетическая) втепловую,
то сохраняется механическая энергия
системы.
Абсолютно
упругим ударом называется
такое кратковременное взаимодействие
тел, после которого тела полностью
восстанавливают свою форму, а их суммарная
кинетическая энергия не изменяется.
При абсолютно упругом ударе
выполняются закон сохранения импульса
и закон сохранения механической энергии.
Абсолютно неупругим
ударом называется
такое кратковременное взаимодействие
тел, после которого соударяющиеся тела
образуют единое тело, движущееся с
определенной скоростью, а суммарная
кинетическая энергия тел уменьшается.
При абсолютно неупругом ударе выполняется
закон сохранения импульса, а механическая
энергия не сохраняется, часть ее
превращается во внутреннюю энергию
тел.
Закон сохранения импульса:
Полный импульс замкнутой
системы тел остается постоянным.
.
Работа постоянной
силы :
,
где s –
модуль перемещения, а — угол между
векторами силы
и перемещения
.
Работа так же может быть
найдена по следующей формуле:
.
Мощность –
работа A совершенная
за единицу времени:
.
Силы:
—
сила упругости.
—
сила тяжести.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
12.02.201524.81 Mб14Физиология растений Н. И. Якушкина.pdf
- #
Содержание:
- Определение и формула кинетической энергии
- Кинетическая энергия материальной точки и тела
- Единицы измерения кинетической энергии
- Теорема Кенига
- Примеры решения задач
Определение и формула кинетической энергии
Определение
Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.
Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.
Встречаются следующие обозначения кинетической энергии: Ek,Wk,T.
Работу, которую производят над телом (A’) можно связать с изменением его кинетической энергии:
$$A^{prime}=E_{k 2}-E_{k 1}(1)$$
Кинетическая энергия материальной точки и тела
Кинетическая энергия материальной точки равна:
$$E_{k}=frac{m v^{2}}{2}=frac{p^{2}}{2 m}=frac{p v}{2}(2)$$
где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной.
Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:
$$E_{k}=frac{1}{2} int_{m} v^{2} d m=frac{1}{2} int_{m} rho v^{2} d V(3)$$
где dm – элементарный участок тела, который можно считать материальной точкой, dV – объем выделенного элементарного участка тела,
v – скорость перемещения рассматриваемого элемента, $rho$ — плотность участка, m–масса всего рассматриваемого тела, V – объем тела.
В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом.
При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:
$$E_{k}=frac{J omega^{2}}{2}=frac{omega^{2}}{2} int_{m} r^{2} d m=frac{L^{2}}{2 J}=frac{L omega}{2}(4)$$
где J – момент инерции тела по отношению к оси вращения, ?–модуль угловой скорости вращения тела,
r – расстояние от элементарного участка тела до оси вращения,
L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение.
Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:
$$E_{k}=frac{bar{L} bar{omega}}{2}(5)$$
$bar{L}$ – момент импульса рассматриваемого тела относительно точки О.
Единицы измерения кинетической энергии
Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:
[Ek]=Дж (джоуль),
в системе СГС –[Ek]= эрг.
При этом: 1 дж= 107 эрг.
Теорема Кенига
Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой,
кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения
системы со скоростью центра масс (vc) и кинетической энергии
(E’k) системы при ее относительном движении к поступательному перемещению системы отсчета.
При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:
$$E_{k}=sum_{i=1}^{n} frac{m_{i} v_{i}^{2}}{2}=frac{m v_{c}^{2}}{2}+E_{k}^{prime}$$
где $mathrm{E}_{k}^{prime}=sum_{i=1}^{n} frac{m_{i} v_{i}^{prime 2}}{2}, v_{i}^{prime}=v_{i}-v_{c}, m=sum_{i=1}^{n} m_{i}$ –суммарная масса системы материальных точек.
Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:
$$E_{k}=frac{m v_{c}^{2}}{2}+frac{J_{c} omega^{2}}{2}(7)$$
где Jc — момент инерции тела по отношению к оси вращения, проходящей через центр масс. В частности, при плоском движении
Jc=const.В общем случае, ось (она называется мгновенной) перемещается в теле, тогда момент инерции является переменным во времени.
Примеры решения задач
Пример
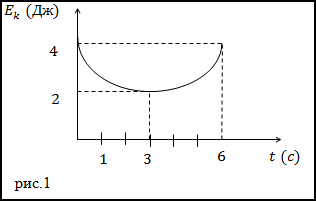
Задание. Какова работа, которая производится над телом за t=3 c (с начала отсчета времени),
при силовом взаимодействии, если изменение кинетической энергии исследуемого тела задано графиком (рис.1)?
Решение. По определению изменение кинетической энергии равно работе (A’),
которая производится над телом при силовом взаимодействии, то есть можно записать, что:
$$A^{prime}=Delta E_{k}(1.1)$$
Исследуя график, приведенный на рис.1 мы видим, что за время t=3 c кинетическая энергия тела изменяется от 4 Дж до 2 Дж, следовательно:
$A^{prime}=2-4=-2$ (Дж)
Ответ. A’=-2 Дж.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Материальная точка движется по окружности, радиус которой равен R. Кинетическая
энергия частицы связана c величиной пути (s), пройденного ей в соответствии с формулой:
$E_{k}=alpha s^{2}(alpha=$const$)$. Какое уравнение связывает силу (F), действующую на точку и путь s?
Решение. В качестве основы для решения задачи используем формулу, определяющую кинетическую энергию материальной точки:
$$E_{k}=frac{m v^{2}}{2}(2.1)$$
Но по условию задачи:
$$E_{k}=alpha s^{2}(2.2)$$
Следовательно, можно приравнять правые части выражений (2.1) и (2.2), и получить:
$$frac{m v^{2}}{2}=alpha s^{2} rightarrow v^{2}=frac{2 alpha s^{2}}{m} rightarrow v=s sqrt{frac{2 alpha}{m}}(2.3)$$
Из второго закона Ньютона нам известно, что сила, действующая на частицу, будет равна:
$$bar{F}=m bar{a}(2.4)$$
где
$$a=sqrt{a_{n}^{2}+a_{tau}^{2}}(2.5)$$
При этом нормальное ускорение частицы (an), перемещающейся по окружности найдем как:
$$a_{n}=frac{v^{2}}{R}=frac{2 alpha s^{2}}{R m}(2.6)$$
Тангенциальную составляющую ускорения (aт)используя определение тангенциального ускорения, определение скорости
($v=frac{d s}{d t}$) и выражение v(s) (2.3) вычислим как:
$$a_{tau}=frac{d v}{d t}=frac{d v}{d s} cdot frac{d s}{d t}=sqrt{frac{2 a}{m}} cdot v=s frac{2 a}{m}(2.7)$$
Используем выражения: (2.5), (2.6), (2.7), окончательно получаем для модуля силы:
$$F=m a=m sqrt{frac{4 alpha^{2} s^{4}}{R^{2} m^{2}}+s^{2} frac{4 alpha^{2}}{m^{2}}}=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$$
Ответ. $F=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$
Читать дальше: Формула массы тела.









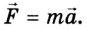
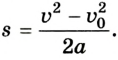
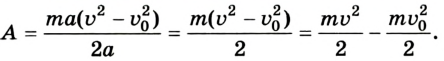
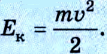
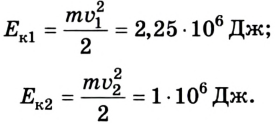
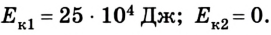
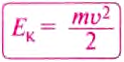


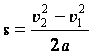 .
.
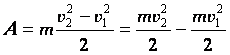 .
.