Как найти кинетическую энергию груза маятника

Кинетическая энергия

Например, движущийся автомобиль невозможно остановить мгновенно. Для остановки необходимо затратить энергию трения тормозных колодок о тормозные диски колес и шин об асфальт.

В некоторых физических системах происходят циклические преобразования потенциальной (запасенной) энергии в кинетическую и обратно. Такие системы называются маятниками. Например, для груза, подвешенного на нити, потенциальная энергия максимальна, когда он отклонен на максимальный угол от вертикали. Мгновенная скорость груза в этот момент равна нулю и, следовательно, нулю равна и кинетическая энергия. По мере движения вниз под действием силы тяжести, скорость груза нарастает и достигает максимума в нижней точке, после чего снова начинает запасаться по мере движения вверх.

Проще всего изучать переход кинетической и потенциальной энергий друг в друга на примере пружинного маятника, где действует, если пренебречь силой трения, лишь сила упругости. Когда пружину сжимают, энергия запасается. Когда отпускают — потенциальная энергия, сохраненная в кристаллической решетке материала, высвобождается и превращается в кинетическую, разгоняя груз. Когда скорость груза достигает максимума, он продолжает движение по инерции, растягивая пружину в противоположном направлении, вновь запасая энергию и снижая скорость. Характеристики такого колебательного движения зависят только от материала пружины, толщины проволоки, из которой она намотана, диаметра и количества витков. Все эти факторы описываются единым параметром — коэффициентом упругости.

Максимальная кинетическая энергия груза

Для простого пружинного маятника полную энергию груза в любой момент времени можно выразить как

$E = E_p + E_k = frac{m cdot v^2}{2} + frac{k cdot x^2}{2}$, где:

• $E_p$ — потенциальная энергия,
• $E_k$ — кинетическая энергия,
• $m$ — масса,
• $v$ — моментальная скорость,
• $k$ — коэффициент упругости,
• $x$ — приращение длины пружины в данный момент.

«Максимальная кинетическая энергия груза: формула» 👇

Максимальную кинетическую энергию можно вычислить как

$(E_k)_{max} = frac{m cdot v_{max}^2}{2}$,

где $v_{max}$ — максимальная скорость груза. Однако измерить ее на практике сложно. Проще, опираясь на постоянство суммы кинетической и потенциальной энергий, определить максимальную потенциальную (когда кинетическая равна нулю). Поскольку справедливо и обратное, можно записать:

$(E_k)_{max} = (E_p)_{max} = frac{k cdot x_{max}^2}{2}$,

где $x_{max}$ — максимальное приращение растяжения пружины. Его легко измерить, а коэффициент упругости посмотреть в справочнике.

Формулы пружинного маятника в физике

Формулы пружинного маятника

Определение и формулы пружинного маятника

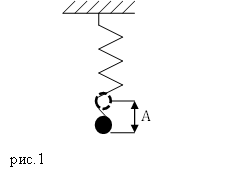
Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.

Уравнения колебаний пружинного маятника

Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:

[ddot{x}+{omega }^2_0x=0left(1right),]

где ${щu}^2_0=frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(2right),]

где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(omega }_0t+varphi )$ — фаза колебаний; $varphi $ и ${varphi }_1$ — начальные фазы колебаний.

В экспоненциальном виде колебания пружинного маятника можно записать как:

[Re tilde{x}=Releft(Acdot exp left(ileft({omega }_0t+varphi right)right)right)left(3right).]

Формулы периода и частоты колебаний пружинного маятника

Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы:

[T=2pi sqrt{frac{m}{k}}left(4right).]

Так как частота колебаний ($nu $) — величина обратная к периоду, то:

[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{k}{m}}left(5right).]

Формулы амплитуды и начальной фазы пружинного маятника

Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $).

Амплитуду можно найти как:

[A=sqrt{x^2_0+frac{v^2_0}{{omega }^2_0}}left(6right),]

начальная фаза при этом:

[tg varphi =-frac{v_0}{x_0{omega }_0}left(7right),]

где $v_0$ — скорость груза при $t=0 c$, когда координата груза равна $x_0$.

Энергия колебаний пружинного маятника

При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.

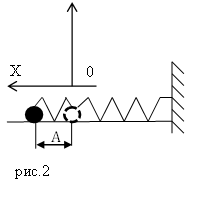
Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:

[E_p=-frac{dF}{dx}(8)]

учитывая, что для пружинного маятника $F=-kx$,

тогда потенциальная энергия ($E_p$) пружинного маятника равна:

[E_p=frac{kx^2}{2}=frac{m{{omega }_0}^2x^2}{2}left(9right).]

Закон сохранения энергии для пружинного маятника запишем как:

[frac{m{dot{x}}^2}{2}+frac{m{{omega }_0}^2x^2}{2}=const left(10right),]

где $dot{x}=v$ — скорость движения груза; $E_k=frac{m{dot{x}}^2}{2}$ — кинетическая энергия маятника.

Из формулы (10) можно сделать следующие выводы:

• Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
• Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.

Примеры задач с решением

Читать дальше: формулы равноускоренного прямолинейного движения.

Рассмотрим процесс превращения энергии при колебательном движении идеального горизонтального пружинного маятника (рис. (1)).

Рис. (1). Колебания горизонтального пружинного маятника

Будем считать, что в системе сил трения и сил сопротивления нет.

Когда эта система находится в равновесии и никакого колебания не происходит, скорость тела равна нулю и отсутствует деформация пружины (рис. (2)) В этом случае энергии у данного маятника нет.

Рис. (2). Положение пружинного маятника в равновесии

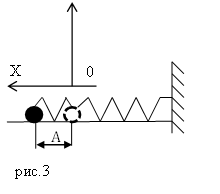
Когда тело выводится из положения равновесия, например пружина сжимается на некоторую величину (рис. (3)) телу сообщается некоторый запас потенциальной энергии:

Рис. (3). Положение пружинного маятника при сжатой пружине

Если теперь отпустить груз, не удерживать его, то он начнёт своё движение к положению равновесия, пружина начнёт выпрямляться, и деформация пружины будет уменьшаться (рис. (4)) Следовательно, будет уменьшаться и её потенциальная энергия.

Скорость же тела будет увеличиваться, и по закону сохранения энергии потенциальная энергия пружины будет превращаться в кинетическую энергию движения тела:

Рис. (4). Движение груза к положению равновесия

В момент прохождения те­лом положения равновесия (рис. (5)) его по­тенциальная энергия равна нулю, а кинетическая будет максимальна.

Рис.(5). Прохождение грузом положения равновесия

Потом вступает в действие явление инерции. Тело, которое обладает некоторой массой, по инерции проходит точку равновесия (рис. (6)). Скорость тела начинает уменьшаться, а деформация, удлинение пружины, увеличивается. Следовательно, кине­тическая энергия тела убывает, а потенциальная, наоборот, возрастает.

Рис. (6). Положение пружинного маятника при удлинении пружины

В точке максимального отклонения тела его кинетическая энергия равна нулю, а потенциальная — максимальна (рис. (7)).

Рис. (7). Положение пружинного маятника в точке максимального отклонения тела

Таким образом, при колебаниях периодически проис­ходит переход потенциальной энергии в кинетическую и обрат­но.

Рис. (8). Колебания вертикального пружинного маятника

Если для вертикального пружинного маятника выбрать систему отсчёта таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю, то всё описанное выше для горизонтального маятника можно применить для данного маятника.

Математический маят­ник — это материальная точка, подвешенная на невесомой и нерас­тяжимой нити, находящейся в поле тяжести Земли. Математический маятник — это идеализированная модель, правильно описывающая реальный маятник лишь при определенных условиях. Реальный ма­ятник можно считать математическим, если длина нити  много больше размеров подвешенного на ней тела, масса нити ничтожна мала по сравнению с массой тела, а деформации нити настолько малы, что ими вообще можно пренебречь.

Колебательную систему в данном случае образуют нить, присо­единенное к ней тело и Земля, без которой эта система не могла бы служить маятником. , где ахускорение, g– ускорение свободного падения, х – смещение, l – длина нити маятника.

Это уравнение называется урав­нением свободных колебаний математического маятника.  Оно правильно описывает рассматриваемые колебания лишь тогда, когда выполнены следующие предположения:

1)  будем считать, что силы трения, действующие на тело, пре­небрежимо малы и потому, их можно не учитывать; 2)   рассматриваются лишь малые колебания маятника с небольшим углом размаха.

Свободные колебания любых систем во всех слу­чаях описываются аналогичными уравнениями. Причинами свободных колебаний математическо­го маятника являются:

1.  Действие на маятник силы натяжения и силы тяжести, пре­пятствующей его смещению из положения равновесия и заставляю­щей его снова опускаться. 2. Инертность маятника, благодаря которой он, сохраняя свою скорость, не останавливается в положении равновесия, а проходит через него дальше.

None Период свободных колебаний математического маятника не за­висит от его массы, а определяется лишь длиной нити и ускорением свободного падения в том месте, где находится маятник.

Превращение энергии при гармонических колебаниях

При гармонических колебаниях пружинного маятника проис­ходят превращения потенциальной энергии упруго деформированного телав его кинетическую энергию, гдеkкоэффициент упругости,х – модуль смещения маятника из поло­жения равновесия,m– масса маятника,v– его скорость. В соот­ветствии с уравнением гармонических колебаний:

,.

Полная энергия пружинного маятника: .

Полная энергия для математического маятника:

В случае математического маятника Превращения энергии при колебаниях пружинного маятника происходи в соответствии с законом сохранения механической энергии (). При движении маятника вниз или вверх от положения равновесия его потенциальная энергия увеличивается, а кинетическая – уменьшается. Когда маятник проходит положение равно­весия (х = 0), его потенциальная энергия равна нулю и кинетическая энергия маятника имеет наибольшее значение, равное его полной энергии.

Таким образом, в процессе свободных колебаний маятника его потенциальная энергия превращается в кинетическую, кинетическая в потенциальную, потенциальная затем снова в кинетическую и т. д. Но полная механическая энергия при этом остается неизменной.

Вынужденные колебания. Резонанс.

Колебания, происходящие под действием внеш­ней периодической силы, называются вынужден­ными колебаниями. Внешняя периодическая си­ла, называемая вынуждающей, сообщает колеба­тельной системе дополнительную энергию, которая идет на восполнение энергетических потерь, проис­ходящих из-за трения. Если вынуждающая сила изменяется во времени по закону синуса или коси­нуса, то вынужденные колебания будут гармониче­скими и незатухающими.

В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из со­стояния равновесия), в случае вынужден­ных колебаний система поглощает эту энергию от источника внешней периоди­ческой силы непрерывно. Эта энергия восполняет потери, расходуемые на пре­одоление трения, и потому полная энергия колебательной системы no-прежнему ос­тается неизменной.

Частота вынужденных колебаний равна часто­те вынуждающей силы. В случае, когда частота вынуждающей силы υсовпадает с собственной ча­стотой колебательной системы υ,происходит рез­кое возрастание амплитуды вынужденных колеба­ний — резонансРезонанс возникает из-за того, что при υ =υ₀  внешняя сила, действуя в такт со свободными колебаниями, все время сонаправлена со скоростью колеблющегося тела и совершает по­ложительную работу: энергия колеблющегося те­ла увеличивается, и амплитуда его колебаний ста­новится большой. График зависимости амплитуды вынужденных колебаний А_тот частоты вынужда­ющей силы υпредставлен на рисунке, этот график называется резонансной кривой:

Явление резонанса играет большую роль в ря­де природных, научных и производственных про­цессов. Например, необходимо учитывать явление резонанса при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае при определенных условиях эти сооружения могут быть разрушены.

Онлайн калькуляторыНа нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

СправочникОсновные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решениеНе можете решить контрольную?! Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Рис.1. Математический маятник Математический маятник – это модель системы, совершающей гармонические колебания. Свободные колебания математического маятника при малых углах отклонения описываются уравнением гармонических колебаний.

В положении равновесия сила тяжести и сила упругости нити уравновешивают друг друга, и материальная точка находится в покое. При отклонении материальной точки от положения равновесия на малый угол на тело будет действовать возвращающая сила , которая является тангенциальной составляющей силы тяжести:

Эта сила сообщает материальной точке тангенциальное ускорение, направленное по касательной к траектории, и материальная точка начинает двигаться к положению равновесия с возрастающей скоростью. По мере приближения к положению равновесия возвращающая сила, а следовательно, и тангенциальное ускорение точки, уменьшаются. В момент прохождения положения равновесия угол отклонения , тангенциальное ускорение также равно нулю, а скорость материальной точки максимальна. Далее материальная точка проходит по инерции положение равновесия и, двигаясь в направлении, противоположном силе , сбавляет скорость. В крайнем положении материальная точка останавливается, и затем начинает двигаться в обратном направлении.

[custom_ads_shortcode1]

Период колебаний математического маятника

Период колебаний математического маятника не зависит от массы груза и амплитуды колебаний.

[custom_ads_shortcode2]

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Механическая система, которая состоит из материальной точки (тела), висящей на нерастяжимой невесомой нити (ее масса ничтожно мала по сравнению с весом тела) в однородном поле тяжести, называется математическим маятником (другое название – осциллятор). Бывают и другие виды этого устройства. Вместо нити может быть использован невесомый стержень.

Математический маятник может наглядно раскрыть суть многих интересных явлений. При малой амплитуде колебания его движение называется гармоническим.

[custom_ads_shortcode3]

Общие сведения о механической системе

Формула периода колебания этого маятника была выведена голландским ученым Гюйгенсом (1629-1695 гг. ). Этот современник И.

Ньютона очень увлекался данной механической системой. В 1656 г. он создал первые часы с маятниковым механизмом.

Они измеряли время с исключительной для тех времен точностью. Это изобретение стало важнейшим этапом в развитии физических экспериментов и практической деятельности.

Если маятник находится в положении равновесия (висит отвесно), то сила тяжести будет уравновешиваться силой натяжения нити. Плоский маятник на нерастяжимой нити является системой с двумя степенями свободы со связью. При смене всего одного компонента меняются характеристики всех ее частей.

Так, если нитку заменить на стержень, то у данной механической системы будет всего 1 степень свободы. Какими же свойствами обладает математический маятник? В этой простейшей системе под воздействием периодического возмущения возникает хаос.

В том случае, когда точка подвеса не двигается, а совершает колебания, у маятника появляется новое положение равновесия. При быстрых колебаниях вверх-вниз эта механическая система приобретает устойчивое положение «вверх тормашками». У нее есть и свое название.

Математический маятник имеет очень интересные свойства. Все они подтверждаются известными физическими законами. Период колебаний любого другого маятника зависит от разных обстоятельств, таких как размер и форма тела, расстояние между точкой подвеса и центром тяжести, распределение массы относительно данной точки.

Именно поэтому определение периода висящего тела является довольно сложной задачей. Намного легче вычисляется период математического маятника, формула которого будет приведена ниже. В результате наблюдений над подобными механическими системами можно установить такие закономерности:

• Если, сохраняя одинаковую длину маятника, подвешивать различные грузы, то период их колебаний получится одинаковым, хотя их массы будут сильно различаться. Следовательно, период такого маятника не зависит от массы груза.

• Если при запуске системы отклонять маятник на не слишком большие, но разные углы, то он станет колебаться с одинаковым периодом, но по разным амплитудам. Пока отклонения от центра равновесия не слишком велики, колебания по своей форме будут достаточно близки гармоническим. Период такого маятника никак не зависит от колебательной амплитуды. Это свойство данной механической системы называется изохронизмом (в переводе с греческого «хронос» – время, «изос» – равный).

None T = 2π√L/gПериод малых собственных колебаний ни в какой мере не зависит от массы маятника и амплитуды колебаний. В этом случае маятник двигается как математический с приведенной длиной.

[custom_ads_shortcode1]

Колебания математического маятника

[custom_ads_shortcode2]

Математический маятник совершает колебания, которые можно описать простым дифференциальным уравнением:

x + ω2 sin x = 0,где х (t) – неизвестная функция (это угол отклонения от нижнего положения равновесия в момент t, выраженный в радианах); ω – положительная константа, которая определяется из параметров маятника (ω = √g/L, где g – это ускорение свободного падения, а L – длина математического маятника (подвес).

Уравнение малых колебаний вблизи положення равновесия (гармоническое уравнение) выглядит так: x + ω2 sin x = 0.

[custom_ads_shortcode3]

Колебательные движения маятника

Математический маятник, который совершает малые колебания, двигается по синусоиде. Дифференциальное уравнение второго порядка отвечает всем требованиям и параметрам такого движения. Для определения траектории необходимо задать скорость и координату, из которых потом определяются независимые константы:

x = A sin (θ + ωt),где θ0 – начальная фаза, A – амплитуда колебания, ω – циклическая частота, определяемая из уравнения движения.

[custom_ads_shortcode1]

Математический маятник (формулы для больших амплитуд)

Данная механическая система, совершающая свои колебания со значительной амплитудой, подчиняется более сложным законам движения. Для такого маятника они рассчитываются по формуле: sin x/2 = u * sn(ωt/u),где sn – синус Якоби, который для u < 1 является периодической функцией, а при малых u он совпадает с простым тригонометрическим синусом. Значение u определяют следующим выражением:

None Определение периода колебания нелинейного маятника осуществляется по формуле:

T = 2π/Ω,где Ω = π/2 * ω/2K(u), K – эллиптический интеграл, π3,14.

[custom_ads_shortcode2]

[custom_ads_shortcode3]

Движение маятника по сепаратрисе

Сепаратрисой называют траекторию динамической системы, у которой двумерное фазовое пространство. Математический маятник движется по ней непериодически. В бесконечно дальнем моменте времени он падает из крайнего верхнего положения в сторону с нулевой скоростью, затем постепенно набирает ее. В конечном итоге он останавливается, вернувшись в исходное положение.

Если амплитуда колебаний маятника приближается к числу π, это говорит о том, что движение на фазовой плоскости приближается к сепаратрисе. В этом случае под действием малой вынуждающей периодической силы механическая система проявляет хаотическое поведение.

При отклонении математического маятника от положения равновесия с некоторым углом φ возникает касательная силы тяжести Fτ = –mg sin φ. Знак «минус» означает, что эта касательная составляющая направляется в противоположную от отклонения маятника сторону. При обозначении через x смещения маятника по дуге окружности с радиусом L его угловое смещение равняется φ = x/L. Второй закон Исаака Ньютона, предназначенный для проекций вектора ускорения и силы, даст искомое значение:

mg τ = Fτ = –mg sin x/LИсходя из этого соотношения, видно, что этот маятник представляет собой нелинейную систему, поскольку сила, которая стремится вернуть его в положение равновесия, всегда пропорциональна не смещению x, а sin x/L.

Только тогда, когда математический маятник осуществляет малые колебания, он является гармоническим осциллятором. Иными словами, он становится механической системой, способной выполнять гармонические колебания. Такое приближение практически справедливо для углов в 15–20°. Колебания маятника с большими амплитудами не является гармоническим.

[custom_ads_shortcode1]

Закон Ньютона для малых колебаний маятника

Если данная механическая система выполняет малые колебания, 2-й закон Ньютона будет выглядеть таким образом: mg τ = Fτ = –m* g/L* x.

Исходя из этого, можно заключить, что тангенциальное ускорение математического маятника пропорционально его смещению со знаком «минус». Это и является условием, благодаря которому система становится гармоническим осциллятором. Модуль коэффициента пропорциональности между смещением и ускорением равняется квадрату круговой частоты:

ω02 = g/L; ω0 = √ g/L. Эта формула отражает собственную частоту малых колебаний этого вида маятника. Исходя из этого,T = 2π/ ω0 = 2π√ g/L.

[custom_ads_shortcode2]

Вычисления на основе закона сохранения энергии

None E = mg∆h = mgL(1 – cos α) = mgL2sin2 α/2Полная механическая энергия равняется кинетической или максимальной потенциальной: Epmax = Ekmsx = EПосле того как будет записан закон сохранения энергии, берут производную от правой и левой частей уравнения:

None Ep’ = (mg/L*x2/2)’ = mg/2L*2x*x’ = mg/L*v + Ek’ = (mv2/2) = m/2(v2)’ = m/2*2v*v’ = mv* α,следовательно:

Mg/L*xv + mva = v (mg/L*x + m α) = 0. Исходя из последней формулы находим: α = – g/L*x.

[custom_ads_shortcode3]

Практическое применение математического маятника

Ускорение свободного падения изменяется с географической широтой, поскольку плотность земной коры по всей планете не одинакова. Там, где залегают породы с большей плотностью, оно будет несколько выше. Ускорение математического маятника нередко применяют для геологоразведки. В его помощью ищут различные полезные ископаемые. Просто подсчитав количество колебаний маятника, можно обнаружить в недрах Земли каменный уголь или руду. Это связано с тем, что такие ископаемые имеют плотность и массу больше, чем лежащие под ними рыхлые горные породы.

Математическим маятником пользовались такие выдающиеся ученые, как Сократ, Аристотель, Платон, Плутарх, Архимед. Многие из них верили в то, что эта механическая система может влиять на судьбу и жизнь человека. Архимед использовал математический маятник при своих вычислениях. В наше время многие оккультисты и экстрасенсы пользуются этой механической системой для осуществления своих пророчеств или поиска пропавших людей.

Известный французский астроном и естествоиспытатель К. Фламмарион для своих исследований также использовал математический маятник. Он утверждал, что с его помощью ему удалось предсказать открытие новой планеты, появление Тунгусского метеорита и другие важные события.

Во время Второй мировой войны в Германии (г. Берлин) работал специализированный Институт маятника. В наши дни подобными исследованиями занят Мюнхенский институт парапсихологии.

ОпределениеМатематический маятник – это колебательная система, являющаяся частным случаем физического маятника, вся масса которого сосредоточена в одной точке, центре масс маятника.

Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.

Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

[custom_ads_shortcode1]

Уравнение движения математического маятника

Математический маятник – классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением: [ddot{varphi }+{omega }^2_0varphi =0 left(1right),] где $varphi $ – угол отклонения нити (подвеса) от положения равновесия.

Решением уравнения (1) является функция $varphi (t):$ [varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }] где $alpha $ – начальная фаза колебаний; ${varphi }_0$ – амплитуда колебаний; ${omega }_0$ – циклическая частота.

Колебания гармонического осциллятора – это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.

[custom_ads_shortcode2]

Циклическая частота и период колебаний математического маятника

Циклическая частота математического маятника зависит только от длины его подвеса: [ {omega }_0=sqrt{frac{g}{l}}left(3right).] Период колебаний математического маятника ($T$) в этом случае равен:

[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).] Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.

[custom_ads_shortcode3]

Уравнение энергии для математического маятника

При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:

[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),] где $E_k$ – кинетическая энергия маятника; $E_p$ – потенциальная энергия маятника; $v$ – скорость движения маятника; $x$ – линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол – смещение связан с $x$ как:

None [E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;] Максимальная величина кинетической энергии:

[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),] где $h_m$ – максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ – максимальная скорость.

[custom_ads_shortcode1]

Примеры задач с решением

None Решение. Сделаем рисунок.

Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:

[frac{mv^2}{2}=mgh left(1.1right).] Из уравнения (1.1) найдем искомую высоту:

[h=frac{v^2}{2g}.] Ответ. $h=frac{v^2}{2g}$Пример 2Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:

None [g=frac{4{pi }^2l}{T^2} .] Проведем вычисления ускорения силы тяжести:

[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).] Ответ. $g=9,87 frac{м}{с^2}$Читать дальше: формулы пружинного маятника.

Источники:

• studfiles.net
• ru.solverbook.com
• fb.ru
• www.webmath.ru

тела
совершающего гармонические колебания

Выражение для
потенциальной энергии тела при
гармонических колебаниях следует из
определения потенциальной энергии

или
.
В рассматриваемом случае имеем:
,
а
.
Поэтому

.

Полагая, что в
состоянии равновесия ()
потенциальная энергия тела, совершающего
колебания, равна нулю, имеем:

.

Кинетическая
энергия тела при гармонических колебаниях
определяется скоростью его движения
(
) и определяется величиной:

.

Полная энергия
тела, совершающего гармонические
колебания, равна сумме полученных
выражений для потенциальной и кинетической
энергий:

.

Выражения
представленные выше показывают, что
при колебательном движении кинетическая
энергия преобразуется в потенциальную
и наоборот. При этом полная энергия
колебаний, не зависит от времени
(замкнутая система) и пропорциональна
квадрату амплитуды и квадрату частоты.

3.3. Пружинный, математический, физический и крутильный маятники

Пружинный
маятник

Пружинный
маятник представляет собой систему,
состоящую из пружины и тела, подвешенного
на этой пружине, систему, способную
совершать колебательное движение в
поле действия гравитационных сил или
сил инерции.

Уравнение,
описывающее движение пружинного маятника
в поле тяжести Земли имеет вид (см. рис.
3.1):

Преобразуем
это уравнение к виду:

и,
сделав замену переменных:
,
получим:

.

Как
было показано выше, решением этого
уравнения являются гармонические
колебания

Возвращаясь
к переменной
,
получаем:

или,
с учетом собственной длины пружины
,
имеем:

.

На
рисунке, представленном ниже,
.

Следует отметить,
что в колебательном процессе участвует
не только тело массой,
подвешенное на пружине, но и сама пружина.
Таким образом, возникает вопрос о влиянии
массы пружины ()
на частоту колебаний пружинного маятника.
Заметим, что если тело массой

в полной мере участвует в колебательном
движении, то различные части пружины
имеют различную амплитуду колебаний.
Таким образом, следует ожидать, что в
выражении для частоты колебаний войдет
не вся
,
а только ее часть. Расчеты показывают,
что это действительно так, и в этом
случае выражение для частоты колебаний
пружинного маятника имеет вид:

Математический
маятник

Математический
маятник состоит из подвешенной на
невесомой нерастяжимой нити материальной
точки, которая может совершать
колебательное движение в поле действия
гравитационных сил или в поле действия
сил инерции.

Для того, что бы
реализовать эту модель на практике
должны выполняться следующие условия:

1. размер
   тела должен быть много меньше длины
   нити
   ,

2. масса
   тела должна быть много больше массы
   нити
   ,

3. происходящее
   во время колебаний изменение длины
   нити должно быть много меньше длины
   самой нити
   .
   Остановимся на последнем более подробно.

При максимальном
отклонении маятника от состояния
равновесия сила натяжения нити
,
где

— угол максимального отклонения. При
прохождении телом положения равновесия
сила натяжения нити определяется как
силой тяжести, так и центробежной силой
,
где величина центробежной силы может
быть найдена следующим образом. Согласно
закону сохранения энергии запишем

,

откуда
следует:

.

Итак, величина
определяет
значение
,
которое должно быть много меньше
.
Расчет показывает, что это условие
выполняется, когда

.

Из полученного
выражения следует, что подбором амплитуды
колебаний (угла максимального отклонения)
это условие может быть всегда выполнено.

Теперь
рассмотрим движение самого маятника.
Возвращающая сила, действующая вдоль
оси «х» определяется силой натяжения
нити
,
где
,
а

-угол отклонения
.
Воспользуемся законом сохранения
энергии и получим выражение для
центростремительной силы

,

где

соответствует отклонению маятника на
максимальный угол
,
а
.

После
подстановки соответствующих величин
в выражение для
получим:

Если угол отклонения
маятника настолько мал, что
,
то

Сравнивая
это выражение с выражением для силы,
определяющей гармонические колебания,
видим, что частота колебаний математического
маятника

,

а
период колебаний составляет величину:

.

Период
колебаний математического маятника
зависит от его длины и от характеристики
поля, в котором он находится.

Физический
маятник

Физическим
маятником называется твердое тело,
способное совершать колебательное
движение в поле действия гравитационных
сил или сил инерции (см. рис. 3.3).

Ранее было показано,
что законы вращательного движения тела
формально не отличаются от законов
движения материальной точки, с той
разницей, что производится замена
величин
,
,
.

В данном случае
(см. рисунок) момент силы действующий
на физический маятник равен:

.

Если
амплитуда колебаний мала, то и углы
отклонения маятника от состояния
равновесия ()
малы, поэтому
.
В этом случае можем записать:
.
Видим, что
~
и что в рассматриваемом случае роль
коэффициента жесткости играет величина
.

По
аналогии с выражением

можно написать выражение для частоты
колебаний физического маятника в виде:

.

Замечание.
Если в полученное выражение для частоты
колебания физического маятника подставить
значение момента инерции, соответствующее
материальной точке находящейся на
расстоянии

от точки подвеса (),
то полученное выражение будет
соответствовать частоте колебаний
математического маятника, длиной
.

Сравнивая
формулу для частоты колебаний физического
маятника, с соответствующей формулой
для математического маятника
,
мы видим, что частота колебаний физического
маятника будет равна частоте колебаний
математического, если его длина будет
составлять величину

.

Это,
так называемая, приведенная
длина физического маятника.
Так как
,
где

— момент инерции тела относительно оси,
проходящей через центр инерции
,
выражение для приведенной длины мы
можем записать в виде:

.

Из
этого выражения следует, что периоды
колебаний физического маятника,
подвешенного на параллельных осях,
отстоящих друг от друга на расстояние

равны. В самом деле, отложим на прямой
ОС отрезок
.
Подвесим маятник на ось, проходящую
через точку
.
Тогда приведенная длина будет
,
где
.
Но
.
Подставим это в выражение для
и
получим:

.

Итак:
приведенные длины, а значит и периоды
(частоты) колебаний физических маятников,
подвешенных на параллельных осях,
отстоящих друг от друга на величину
равную приведенной длине равны.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #