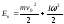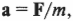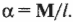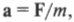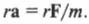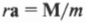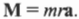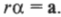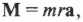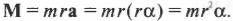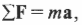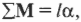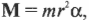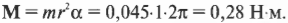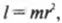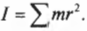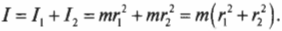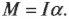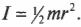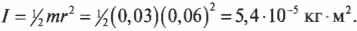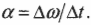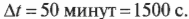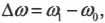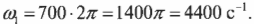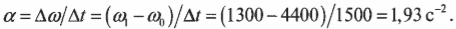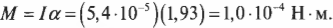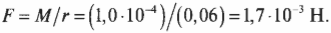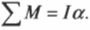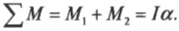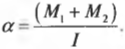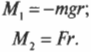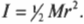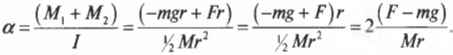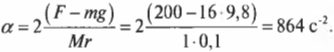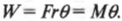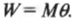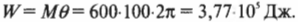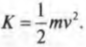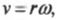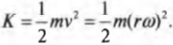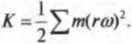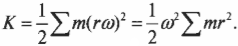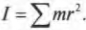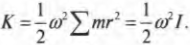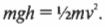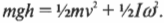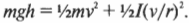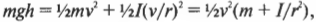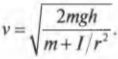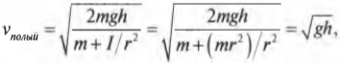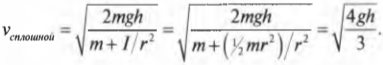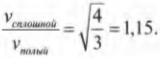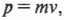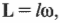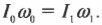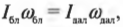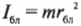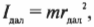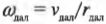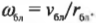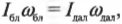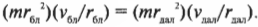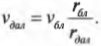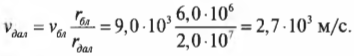§ 4.1. Кинетическая энергия вращающегося и катящегося тел
1. Найдем кинетическую энергию тела,
вращающегося относительно неподвижной
оси. Используем модель а.т.т. как сумму
м.т. (рис.16). Все точки тела движутся по
окружностям, траектория одной из них
массой mi,
движущейся по окружности радиусом ri
со скоростью υi.
указана на рисунке. Кинетическая
энергия этой точки

Найдем кинетическую энергию тела как
сумму кинетических энергий образующих
его точек:
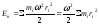
Полученный результат показывает, что
кинетическая энергия вращающегося
тела определяется двумя величинами:
его угловой скоростью и еще одной
индивидуальной характеристикой тела,
зависящей от распределения его массы
относительно оси вращения:

Ее называют моментом инерции тела
относительно оси:
I =miri2
(4.1.1)
Формула кинетической энергии
вращающегося тела имеет вид:
(4.1.2)
2. В § 1.4 мы отмечали, что произвольное
движение твердого тела можно представить
как сумму двух движений: поступательного
и вращательного. На практике часто
встречается качение твердого тела
– это вид плоского движения, т.е. такого
движения, когда все точки тела перемещаются
в параллельных плоскостях. Кинетическая
энергия катящегося тела складывается
из двух частей:
(4.1.3)
Здесь v0
— скорость поступательного
движения центра инерции, I0
– момент инерции тела относительно
оси, проходящей через центр инерции
тела перпендикулярно плоскостям
перемещения его точек.
§ 4.2. Момент инерции
1. Из формул (4.1.2) и (4.1.3) следует, что
момент инерции тела при вращательном
движении является аналогом массы при
его поступательном движении, а именно,
служит мерой инертности тела, т.е. его
способности сопротивляться изменению
скорости: чем больше инертность тела,
тем труднее изменить его скорость. Из
определения момента инерции (см. формулу
4.1.1) следует, что инертность тела при
вращении зависит от распределения его
массы относительно оси вращения. Это
означает, что одно и то же тело относительно
разных осей вращения имеет разные
моменты инерции. Это нам хорошо известно
из опыта: чем дальше вращающаяся масса
от оси вращения, тем труднее ускорить
или замедлить ее вращение. Момент
инерции, как и масса, скалярная величина,
его единица измерения в СИ обозначается
кг.м2.
Для сплошного однородного тела,
рассматриваемого как совокупность
м.т., с точки зрения математики удобно
суммирование свести к интегрированию.
Пусть dm – масса
физически малого элемента объема dV
1,
находящегося на расстоянии r
от оси вращения, плотность вещества
тела — (кг/м3),
тогда dm=
dV , и момент инерции
этого элемента массы dI
= r2dm
= r2
dV . Формула для
вычисления момента инерции сплошного
тела примет вид:
(4.2.1)
Интегрирование
проводят по всему объему тела, это
обозначено ниже знака интеграла.
2. Приведем формулы моментов инерции
некоторых тел, часто встречающихся в
практике.
а) Обруч
или тонкостенный цилиндр массой m
и радиусом R ,
вращающийся относительно своей оси
симметрии. Учитывая, что все элементы
массы m
находятся на одинаковом расстоянии
от оси, получаем по формуле (4.1.1):
I =miri2
= R2mi
= m
R2
(4.2.2)
б) Диск или
сплошной цилиндр массой m
и радиусом R ,
вращающийся относительно своей оси
симметрии. Используем формулу (4.2.1), для
этого диск разобьем на кольцевые слои.
Один такой слой толщиной dr,
высотой диска h и
объемом dV=2rhdr
показан на рис. 17. Момент инерции такого
элементарного слоя в виде кольца dI=
r2
dV= r2
2rhdr=2hr3dr.
Заметим, что в этом примере интегрирование
по объему тела свелось к интегрированию
по расстоянию r от
оси до внешней поверхности цилиндра,
так что

Учитывая, что объем цилиндра V=Sh=R2h,
а его масса m=V,
получили: 
(4.2.3)
Используя
изложенный в этой главе материал,
объясните, одновременно ли достигнут
конца спуска два цилиндра одинаковых
размеров, если один из них сплошной, а
другой пустотелый, и они одновременно
начали скатываться с вершины наклонной
плоскости (вспомните лекционную
демонстрацию).
в) Шар,
вращающийся относительно своей оси
(эту формулу нетрудно получить
интегрированием, перейдя в сферическую
систему координат):
(4.2.4)
г) Стержень
длиной l, вращающийся
относительно перпендикулярной к нему
оси, проходящей через его середину
(получите эту формулу самостоятельно):
(4.2.5)
д) Теорема
Штейнера позволяет найти момент
инерции тела относительно любой оси,
если известен его момент инерции
относительно параллельной оси, проходящей
через центр инерции тела:
I=I0+mb2
(4.2.6)
Здесь I
– момент инерции тела относительно
рассматриваемой оси, I0
— момент инерции этого же тела
относительно оси, проходящей через
центр инерции и параллельной
рассматриваемой, b
– расстояние между этими осями.
Обратите внимание, что момент инерции
тела относительно любых параллельных
осей наименьший в случае, когда ось
проходит через центр инерции.
Самостоятельно получите формулу для
момента инерции стержня, если ось
вращения проходит через его конец и
перпендикулярна стержню.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кинетическая энергия диска катящегося по окружности
«Физика — 10 класс»
Почему для увеличения угловой скорости вращения фигурист вытягивается вдоль оси вращения.
Должен ли вращаться вертолёт при вращении его винта?
Заданные вопросы наводят на мысль о том, что если на тело не действуют внешние силы или действие их скомпенсировано и одна часть тела начинает вращение в одну сторону, то другая часть должна вращаться в другую сторону, подобно тому как при выбросе горючего из ракеты сама ракета движется в противоположную сторону.
Момент импульса.
Если рассмотреть вращающийся диск, то становится очевидным, что суммарный импульс диска равен нулю, так как любой частице тела соответствует частица, движущаяся с равной по модулю скоростью, но в противоположном направлении (рис. 6.9).
Но диск движется, угловая скорость вращения всех частиц одинакова. Однако ясно, что чем дальше находится частица от оси вращения, тем больше её импульс. Следовательно, для вращательного движения надо ввести ещё одну характеристику, подобную импульсу, — момент импульса.
Моментом импульса частицы, движущейся по окружности, называют произведение импульса частицы на расстояние от неё до оси вращения (рис. 6.10):
Линейная и угловая скорости связаны соотношением v = ωr, тогда
Все точки твёрдого дела движутся относительно неподвижной оси вращения с одинаковой угловой скоростью. Твёрдое тело можно представить как совокупность материальных точек.
Момент импульса твёрдого тела равен произведению момента инерции на угловую скорость вращения:
Момент импульса — векторная величина, согласно формуле (6.3) момент импульса направлен так же, как и угловая скорость.
Основное уравнение динамики вращательного движения в импульсной форме.
Угловое ускорение тела равно изменению угловой скорости, делённому на промежуток времени, в течение которого это изменение произошло: Подставим это выражение в основное уравнение динамики вращательного движения отсюда I(ω2 — ω1) = MΔt, или IΔω = MΔt.
Изменение момента импульса равно произведению суммарного момента сил, действующих на тело или систему, на время действия этих сил.
Закон сохранения момента импульса:
Если суммарный момент сил, действующих на тело или систему тел, имеющих неподвижную ось вращения, равен нулю, то изменение момента импульса также равно нулю, т. е. момент импульса системы остаётся постоянным.
Изменение импульса системы равно суммарному импульсу сил, действующих на систему.
Вращающийся фигурист разводит в стороны руки, тем самым увеличивает момент инерции, чтобы уменьшить угловую скорость вращения.
Закон сохранения момента импульса можно продемонстрировать с помощью следующего опыта, называемого «опыт со скамьёй Жуковского». На скамью, имеющую вертикальную ось вращения, проходящую через её центр, встаёт человек. Человек держит в руках гантели. Если скамью заставить вращаться, то человек может изменять скорость вращения, прижимая гантели к груди или опуская руки, а затем разводя их. Разводя руки, он увеличивает момент инерции, и угловая скорость вращения уменьшается (рис. 6.11, а), опуская руки, он уменьшает момент инерции, и угловая скорость вращения скамьи увеличивается (рис. 6.11, б).
Человек может также заставить вращаться скамью, если пойдёт вдоль её края. При этом скамья будет вращаться в противоположном направлении, так как суммарный момент импульса должен остаться равным нулю.
На законе сохранения момента импульса основан принцип действия приборов, называемых гироскопами. Основное свойство гироскопа — это сохранение направления оси вращения, если на эту ось не действуют внешние силы. В XIX в. гироскопы использовались мореплавателями для ориентации в море.
Кинетическая энергия вращающегося твёрдого тела.
Кинетическая энергия вращающегося твёрдого тела равна сумме кинетических энергий отдельных его частиц. Разделим тело на малые элементы, каждый из которых можно считать материальной точкой. Тогда кинетическая энергия тела равна сумме кинетических энергий материальных точек, из которых оно состоит:
Угловая скорость вращения всех точек тела одинакова, следовательно,
Величина в скобках, как мы уже знаем, это момент инерции твёрдого тела. Окончательно формула для кинетической энергии твёрдого тела, имеющего неподвижную ось вращения, имеет вид
В общем случае движения твёрдого тела, когда ось вращения свободна, его кинетическая энергия равна сумме энергий поступательного и вращательного движений. Так, кинетическая энергия колеса, масса которого сосредоточена в ободе, катящегося по дороге с постоянной скоростью, равна
В таблице сопоставлены формулы механики поступательного движения материальной точки с аналогичными формулами вращательного движения твёрдого тела.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика
Оформление и защита курсовых работ
Шар массой m = 1 кг, катящийся без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку υ = 10 см/с, после удара 8 см/с. Найти количество тепла Q, выделившееся при ударе.
Кинетическая энергия катящегося тела равна:
Ek = + . (12)
Момент инерции шара I = ,
угловая скорость вращения w = .
Подставляем эти величины в формулу (12):
Ek = + = m υ 2.
Количество тепла, выделившегося при ударе, равно разнице его кинетических энергий до и после удара:
Q = Ek1 – Ek2 = m υ12 — m υ22 = m(υ12 — υ22).
Подставив числовые значения, получим:
а = ∙1(100∙10-4 – 64.10-4) = 10-4 = 2,25∙10-3 Дж = 2,52 МДж.
Найти кинетическую энергию велосипеда, едущего со скоростью υ = 9 км/ч. Масса велосипедиста вместе с велосипедом m = 78 кг, причем на колеса приходится масса m1 = 3 кг. Колеса считать тонкими обручами.
Кинетическая энергия велосипеда складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения колес.
Ek = + .
Момент инерции колес, представляющих собой тонкие обручи, равен I = , а угловая скорость вращения w = .
Подставляем эти значения в выражение для кинетической энергии: Ek = + = .
Скорость надо перевести в м/с: υ = 2,5 м/с.
Подстановка числовых значений дает: Ek =253 Дж.
Однородный стержень длиной 85см подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую наименьшую скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
Чтобы стержень смог сделать полный оборот вокруг оси, он должен подняться до вертикального положения В.
Если отсчитывать потенциальную энергию стержня от начального положения А, то в положении В центр масс его поднят на
высоту С2-С1=l – длина стержня. Стержень приобретает потенциальную энергию Еn = mgℓ за счет кинетической энергии,
В которую ему сообщили в положении А. Если
υ – наименьшая скорость нижнего конца, при которой он сможет сделать полный оборот, то
угловая скорость стержня w = .
Момент инерции стержня относительно оси, проходящей через его конец, определятся по теореме Штейнера:
I = m l2 = m = m l2,
где ml2–момент инерции стержня относительно перпендикулярной к нему оси, проходящей через центр масс, – расстояние от центра масс до требуемой оси.
Кинетическая энергия вращательного движения:
Ek = =.= .
По закону сохранения энергии, кинетическая энергия стержня в положении А равна его потенциальной энергии в положении В:
= mgl ,
отсюда υ = .
Подставляем числовые значения: υ = » 7 м/с.
Человек массой m1 = 60 кг находится на неподвижной платформе массой m = 100 кг. Какое число оборотов в минуту будет делать платформа, если человек будет двигаться по окружности радиуса 5 м вокруг оси вращения? Скорость движения человека относительно платформы равна 4 км/ч. Радиус платформы 10 м. Считать платформу однородным диском, а человека – точечной массой.
Первоначально платформа с человеком покоилась,
момент импульса этой системы был равен нулю. Когда человек начнет двигаться по платформе, платформа будет вращаться в противоположном направлении. Если расстояние от человека до оси вращения платформы r, в месте нахождения человека u = w r. Таким образом, если человек движется относительно платформы со скоростью
υ, то относительно земли он будет двигаться со скоростью υ – w r, его момент импульса относительно оси платформы L1 = m1(υ – w r)r. Момент импульса платформы относительно ее оси:
где I – момент инерции платформы.
Поскольку платформа представляет собой однородный диск, то ее момент инерции относительно оси, проходящей через центр:
I = mR2.
Запишем закон сохранения момента импульса для данной системы:
O = L1 + L = m1(υ – w r) r – mR2 w ,
отсюда можно определить угловую скорость вращения платформы:
w = .
Число оборотов платформы в минуту определится из соотношения:
n = 60 = .
Подстановка числового значений дает:
n = = 0,49 об/мин.
Знание этой зависимости позволяет найти разность теплоемкостей при постоянном давлении и постоянном объеме по уравнению (2.6), то есть технически важную характеристику термодинамических объектов.
Если переменными являются другие параметры, то термодинамическое уравнение состояния для внутренней энергии может быть записано просто по аналогии. Например, из уравнения (7.1) можно получить зависимость внутренней энергии аккумулятора от его заряда при разных температурах. Поскольку работа, совершаемая аккумулятором при перемещении по электрической цепи заряда q, равна произведению электродвижущей силы источника тока E(ЭДС) на величину заряда, то элементарная работа имеет вид dA = Edq. Сравнивая работу газа и работу источника тока, то-есть dA = PdV и dA = Edq, мы видим, что здесь заряд играет роль объема, а ЭДС источника – роль давления. Теперь по аналогии с уравнением (7.1) можно получить зависимость внутренней энергии аккумулятора от заряда через температурную зависимость ЭДС аккумулятора
Поскольку температурная зависимость ЭДС при постоянном заряде легко находится опытным путем, то это уравнение приобретает прямую практическую значимость.
Термодинамическое тождество позволяет также получить уравнение, связывающее изменение энтальпии с термодинамическими параметрами. Поскольку H = U + PV, и значит dU = dH — PdV — VdP, а дифференциал энтальпии как функции температуры Т и давления Р имеет вид
то термодинамическое тождество (5.4) после замены dU и dH дает
В то же время дифференциал энтропии как функции температуры Т и давления Р
и, следовательно,
Из равенства перекрестных производных
получаем
откуда, после раскрытия скобок, окончательно имеем
Это — термодинамическое уравнение состояния для энтальпии (как функции давления при постоянной температуре), где правая часть легко определяется опытным путем.
Глава 11. Раскручиваем объекты: момент инерции
- Переходим от динамики поступательного движения к динамике вращательного движения
- Вычисляем момент инерции
- Определяем работу вращательного движения
- Находим связь между работой и изменением кинетической энергии
- Изучаем закон сохранения момента импульса
Эта глава посвящена динамике вращательного движения, т.е. описанию сил и их влияния на характер вращательного движения. Здесь рассматриваются основные законы динамики вращательного движения по аналогии с законами динамики поступательного движения. Например, описывается аналог второго закона Ньютона (см. главу 5), представлено новое понятие “момент инерции”, исследуется связь между работой и кинетической энергией и т.п.
Применяем второй закон Ньютона для вращательного движения
Согласно второму закону Ньютона (см. главу 5), ускорение объекта под действием силы пропорционально величине силы и обратно пропорционально массе объекта:
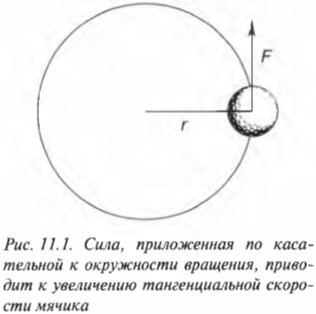
Рассмотрим простой пример. Пусть привязанный нитью мячик для игры в гольф вращается по окружности, как показано на рис. 11.1. Допустим, что к мячику приложена направленная по касательной к окружности тангенциальная сила, которая приводит к увеличению тангенциальной скорости мячика. (Обратите внимание, что речь идет не о нормальной силе, направленной вдоль радиуса окружности вращения. Более подробно нормальная и тангенциальная скорости, а также нормальное и тангенциальное ускорения рассматриваются в главе 10.)
то, умножая обе части этой формулы на радиус окружности ( r ) , получим:
Поскольку ( rmathbf=mathbf ) то
Таким образом, частично совершен переход от второго закона Ньютона для поступательного движения к его аналогу для вращательного движения. (Следует отметить, что это выражение справедливо для материальной точки, т.е. объекта, размерами которого можно пренебречь по сравнению с величиной радиуса окружности ( r ) . Для протяженного объекта следует использовать другие формулы, которые описываются далее в этой главе. — Примеч. ред.)
Преобразуем тангенциальное ускорение в угловое
Чтобы полностью перейти от описания поступательного движения к описанию вращательного движения, необходимо использовать связь между угловым ускорением ( alpha ) и тангенциальным ускорением ( mathbf ) . Как нам уже известно из главы 10, они связаны следующим соотношением:
Подставляя это выражение в приведенную выше формулу
Итак, мы получили связь момента силы, действующей на материальную точку, и ее углового ускорения. Коэффициент пропорциональности между ними, ( l=mr^2 ) , называется моментом инерции материальной точки. Таким образом, мы получили эквивалент второго закона Ньютона для вращательного движения, где роль силы играет момент силы, роль ускорения — угловое ускорение, а роль массы — момент инерции.
Пример: вычисляем момент силы для обеспечения углового ускорения
Если на объект действует несколько сил, то второй закон Ньютона имеет следующий вид:
где ( mathbf <sum!F>) обозначает векторную сумму всех сил, действующих на объект.
Аналогично, если на объект действует несколько моментов сил, то второй закон Ньютона имеет вид:
где ( mathbf <sum! M>) обозначает векторную сумму всех моментов сил, действующих на объект. Аналог массы, т.е. момент инерции, измеряется в кг·м 2 .
Помните, что аналогом второго закона Ньютона при описании вращательного движения является формула ( mathbf<sum! M>=lalpha ) , т.е. угловое ускорение прямо пропорционально сумме всех моментов сил, действующих на вращающийся точечный объект, и обратно пропорционально моменту инерции.
Пусть мячик из предыдущего примера (см. рис. 11.1) имеет массу 45 г, а длина нити равна 1 м. Какой момент сил необходимо приложить, чтобы обеспечить угловое ускорение — ( 2pi с^ <-2>) ? Подставляя значения в уже известную нам формулу
Как видите, для решения этой задачи достаточно было поступить, как при определении силы, необходимой для обеспечения ускорения поступательного движения (где нужно было бы умножить массу на ускорение), т.е. умножить угловое ускорение на момент инерции.
Вычисляем момент инерции протяженного объекта
Момент инерции легко вычисляется для очень маленького (точечного) объекта, если все точки объекта расположены на одинаковом расстоянии от точки вращения. Например в предыдущем примере, если считать, что мячик для игры в гольф гораздо меньше длины нити, то все его точки находятся на одинаковом расстоянии от точки вращения, равном радиусу окружности вращения ( r ) . В таком случае момент инерции имеет знакомый вид:
где ( r ) — это расстояние, на котором сосредоточена вся масса мячика ( m ) .
Однако такая идеальная ситуация имеет место далеко не всегда. А чему равен момент инерции протяженного объекта, например стержня, вращающегося относительно одного из своих концов? Ведь его масса сосредоточена не в одной точке, а распределена по всей длине. Вообще говоря, для определения момента инерции протяженного объекта нужно просуммировать моменты инерции всех материальных точек объекта:
Например, момент инерции ( l ) системы из двух “точечных” мячиков для игры в гольф с одинаковой массой ( m ) на расстояниях ( r_1 ) и ( r_2 ) равен сумме их отдельных моментов инерции ( l_1=mr_1^2 ) и ( l_2=mr_2^2 ) :
А как определить момент инерции диска, вращающегося относительно своего центра? Нужно мысленно разбить диск на множество материальных точек, вычислить момент инерции каждой такой точки и просуммировать полученные моменты инерции. Физики научились вычислять моменты инерции для многих объектов со стандартной формой. Некоторые из них приведены в табл. 11.1.
Попробуем вычислить моменты инерции нескольких предметов с простой геометрией.
Пример: замедление вращения компакт-диска
Компакт-диски могут вращаться с разными угловыми скоростями. Это необходимо для обеспечения одинаковой линейной скорости считывания информации на участках, находящихся на разных расстояниях от центра вращения. Пусть диск массой 30 г и диаметром 12 см сначала вращается со скоростью 700 оборотов в секунду, а спустя 50 минут — со скоростью 200 оборотов в секунду. Какой средний момент сил действует на компакт-диск при таком уменьшении скорости? Связь момента сил и углового ускорения имеет вид:
Момент инерции диска с радиусом ( r ) , вращающегося относительно своего центра в плоскости диска, выражается формулой:
Подставляя значения, получим:
Теперь нужно определить угловое ускорение, которое определяется следующей формулой:
Изменение угловой скорости ( Deltaomega ) произошло за промежуток времени:
В данном примере изменение угловой скорости:
где ( omega_1 ) — конечная, а ( omega_0 ) — начальная угловая скорость компакт-диска.
Чему они равны? Начальная скорость 700 оборотов в секунду означает, что диск за секунду 700 раз проходит ( 2pi ) радиан:
Аналогично, конечная скорость 200 оборотов в секунду означает, что диск за секунду 200 раз проходит ( 2pi ) радиан:
Подставляя значения в формулу углового ускорения, получим:
Подставляя значения момента инерции и углового ускорения в итоговую формулу момента силы, получим:
Итак, средний момент равен 10 -4 Н·м, а чему будет равна сила для создания такого момента, если она приложена к краю диска? Ее величину легко вычислить по следующей формуле:
Оказывается, для такого замедления компакт-диска нужно приложить не такую уж и большую силу.
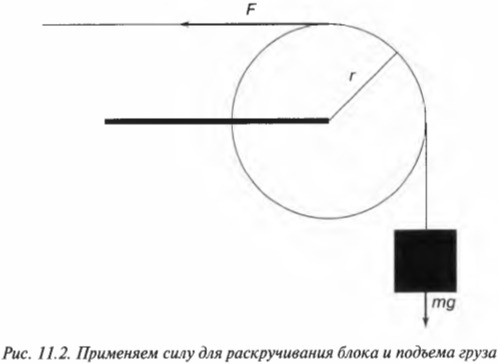
Еще один пример: поднимаем груз
Вращательное движение порой внешне выглядит не так очевидно, как вращение ком- пакт-диска. Например подъем груза с помощью блока также является примером вращательного движения. Хотя канат и груз движутся поступательно, но сам блок вращается (рис. 11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока.
В данном примере нужно вычислить сумму всех моментов сил ( mathbf <sum! M>) , которые действуют на веревку:
В данном примере на веревку действует два момента сил: один ( M_1 ) со стороны груза весом ( mg ) , а другой ( M_2 ) — со стороны горизонтальной силы ( F ) :
Отсюда получаем формулу для углового ускорения:
Эти моменты ( M_1 ) и ( M_2 ) имеют одинаковое плечо, равное радиусу блока ( r ) , поэтому:
Поскольку блок имеет форму диска, то из табл. 11.1 находим его момент инерции:
Подставляя выражения для ( l ) , ( M_1 ) и ( M_2 ) в формулу для углового ускорения, получим:
Подставляя значения, получим:
Вычисляем энергию и работу при вращательном движении
При изучении поступательного движения в главе 8 мы познакомились с понятием работа. Она равна произведению силы на перемещение под действием этой силы. Можно ли выразить работу при вращательном движении на основе его характеристик? Конечно можно, и для этого потребуется преобразовать силу в момент силы, а перемещение — в угол. В этом разделе демонстрируется такое преобразование, а также связь работы с изменением энергии.
Работа при вращательном движении
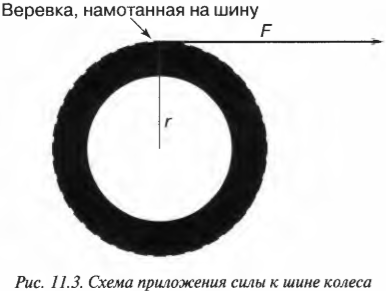
Допустим, что инженеру в области автомобилестроения необходимо рассчитать параметры революционно новой шины колеса. Для начала он решил оценить работу, которую необходимо выполнить для ускоренного раскручивания этой шины. Как связать работу при поступательном движении и работу при вращательном движении? Инженер предложил простую, как все гениальное, идею: “связать” шину веревкой. Точнее говоря, он предложил намотать веревку на шину, потянуть за веревку с помощью внешней силы и раскрутить шину. Так, приравнивая работу внешней силы при поступательном движении веревки и работу ускорения вращательного движения шины, можно, образно говоря, “связать” их веревкой.
Пусть шина имеет радиус ( r ) и для ее вращения используется сила ( F ) , как показано на рис. 11.3.
Чему равна работа этой силы? Применим знакомую нам формулу:
где ( s ) — это перемещение веревки под действием этой силы. В данном примере перемещение ( s ) равно произведению радиуса ( r ) на угол поворота шины ( theta ) :
Подставляя это выражение в формулу работы, получим:
Поскольку момент ( M ) , создаваемой этой силой, равен:
то получаем для работы:
Таким образом, работа при вращательном движении равна произведению момента силы и угла поворота. Она измеряется в тех же единицах, что и работа при поступательном движении, т.е. в джоулях.
Учтите, что для описания вращательного движения в этих формулах работы угол нужно указывать в радианах.
Вот еще один пример. Пусть пропеллер самолета совершает 100 поворотов с постоянным моментом силы 600 Н·м. Какую работу выполняет двигатель самолета? Для ответа на этот вопрос начнем с уже известной нам формулы:
Полный оборот соответствует повороту на угол ( 2pi ) . Подставляя значения в формулу, получим:
Что происходит с выполненной таким образом работой? Она преобразуется в кинетическую энергию вращательного движения.
Изучаем кинетическую энергию вращательного движения
Из главы 8 нам уже известно, что объект массы ( m ) , движущийся поступательно со скоростью ( v ) , обладает кинетической энергией:
А как получить формулу кинетической энергии для вращающегося объекта? Нужно применить данную формулу для всех его частичек.
При описании вращательного движения аналогом массы является момент инерции, а аналогом скорости — угловая скорость.
Как известно (см. главу 10), тангенциальная скорость ( v ) и угловая скорость ( omega ) связаны соотношением:
где ( r ) — это радиус окружности вращения.
Подставляя это соотношение в предыдущую формулу, получим:
Однако эта формула справедлива только для бесконечно малой материальной точки. Чтобы определить кинетическую энергию протяженного объекта, нужно просуммировать кинетические энергии всех его мельчайших материальных точек, т.е. вычислить сумму:
Как можно было бы упростить эту формулу? Предположим, что все составляющие частички протяженного объекта вращаются с одинаковой угловой скоростью. Тогда угловую скорость можно вынести за знак суммирования и получим:
Здесь начинается самое интересное. Ранее в этой главе уже приводилась формула момента инерции:
Теперь совсем нетрудно сделать подстановку в предыдущей формуле кинетической энергии:
Итак, кинетическая энергия вращательного движения вычисляется аналогично кинетической энергии поступательного движения, если вместо массы использовать момент инерции, а вместо тангенциальной скорости — угловую скорость. Примеры кинетической энергии вращательного движения окружают повсюду. Спутник на космической орбите и бочка пива, которую скатывают по наклонной плоскости, обладают определенной кинетической энергией вращательного движения. Особенности вращательного движения бочки пива более подробно описываются в следующем разделе.
Измеряем кинетическую энергию бочки, катящейся по наклонной плоскости
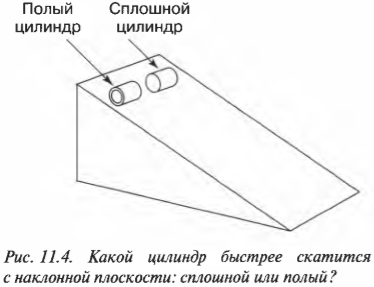
Итак, нам уже известно, что объекты могут двигаться поступательно и вращательно, причем двигаться так, что без знания строгих законов физики порой трудно понять их поведение. Да ну? Действительно, если бочка скользит вниз по наклонной плоскости, то ее потенциальная энергия превращается в кинетическую энергию поступательного движения (см. главу 8). А если бочка скатывается вниз по наклонной плоскости, то ее потенциальная энергия превращается не только в кинетическую энергию поступательного движения, но и в кинетическую энергию вращательного движения.
На рис. 11.4 показан случай, когда с наклонной плоскости высотой ( h ) скатываются сплошной и полый цилиндры с одинаковой массой ( m ) . Какой цилиндр достигнет нижнего конца наклонной плоскости?
Иначе говоря: какой цилиндр будет обладать большей скоростью в конце наклонной плоскости? Поскольку действующие на цилиндры силы постоянны, то постоянны и их ускорения, а значит, большая скорость в конце пути означает меньшее время его прохождения. В случае только поступательного движения цилиндра и при отсутствии трения уменьшение потенциальной энергии ( mgh ) преобразуется в увеличение кинетической энергии только поступательного движения ( <>^1!/!_2mv^2 ) , т.е.:
Однако в данном примере эта формула не годится, потому что цилиндры скатываются без проскальзывания. Это значит, что часть уменьшения потенциальной энергии будет преобразовываться в увеличение кинетической энергии поступательного движения ( <>^1!/!_2mv^2 ) , а часть — в кинетическую энергию вращательного движения ( <>^1!/!_2Iomega ^2 ) . Тогда предыдущее равенство принимает следующий вид:
Сделаем подстановку ( omega=v/r ) и получим:
Путем несложных алгебраических преобразований получим:
откуда легко получить выражение для скорости цилиндра:
Для обоих цилиндров все параметры одинаковы, кроме момента инерции ( I ) . Как это повлияет на скорость цилиндров? Согласно данным из табл. 11.1, полый цилиндр имеет момент инерции ( mr^2 ) , а сплошной — ( <>^1!/!_2mr^2 ) .
Итак, для полого цилиндра получим:
а для сплошного цилиндра:
А их отношение равно:
Как видите, скорость сплошного цилиндра в 1,15 раза больше скорости полого цилиндра, а значит, сплошной цилиндр быстрее достигнет конца наклонной плоскости.
Как на пальцах объяснить полученный результат? Все очень просто. В полом цилиндре вся масса сосредоточена на расстоянии радиуса цилиндра, а в сплошном цилиндре значительная часть масса распределена ближе радиуса. Это значит, что при одинаковой угловой скорости в полом цилиндре больше материала будет обладать большей тангенциальной скоростью, а для этого потребуется потратить больше энергии.
Не можем остановиться: момент импульса
Допустим, нам нужно остановить космический корабль с массой 40 т, который находится на околоземной орбите. Для этого потребуется затратить немалые усилия. Почему? Все дело во вращательном импульсе космического корабля.
В главе 9 подробно описывается понятие импульс материальной точки, который выражается следующей формулой:
где ( m ) — это масса, a ( v ) — скорость материальной точки.
По аналогии, при описании вращательного движения физики используют понятие вращательный импульс (который в русскоязычной научной литературе чаще называют моментом импульса материальной точки. — Примеч. ред.):
где ( l ) — это момент инерции, а ( omega ) — угловая скорость материальной точки.
Следует помнить, что момент импульса (или вращательный импульс) является вектором, направление которого совпадает с направлением вектора угловой скорости.
Момент импульса в системе СИ измеряется в кг·м 2 ·с -1 (более подробно системы единиц измерения описываются в главе 2). Одним из наиболее важных свойств момента импульса является закон сохранения момента импульса.
Сохраняем момент импульса
Закон сохранения момента импульса гласит: момент импульса сохраняется, если равна нулю сумма всех моментов внешних сил. Этот закон проявляется во многих обыденных ситуациях. Например часто приходится видеть, как мастера фигурного катания на льду вращаются с широко разведенными в стороны руками, а затем резко приближают их к своему телу и сильно ускоряют свое вращение. Дело в том, что таким образом они уменьшают свой момент инерции и, согласно закону сохранения момента импульса, увеличивают свою угловую скорость. Зная начальную угловую скорость вращения фигуриста ( omega_0 ) и его моменты инерции в позе с разведенными руками ( I_0 ) и в позе с сомкнутыми руками ( I_1 ) , легко найти конечную угловую скорость ( omega_1 ) по формуле:
Однако этот закон удобно использовать не только в таких простых ситуациях. Возвращаясь к примеру с космическим кораблем на околоземной орбите, следует отметить, что его орбита далеко не всегда является строго круглой. Чаще всего орбиты спутников Земли и других планет имеют эллиптическую форму. Поэтому без закона сохранения момента импульса было бы гораздо сложнее определять параметры их орбитального движения.
Пример закона сохранения момента импульса: вычисляем скорость спутника
Предположим, что космический корабль вращается на эллиптической орбите вокруг Плутона. Причем в самой близкой к Плутону точке орбиты спутник находится на расстоянии 6·10 6 м от центра Плутона и имеет скорость 9·10 3 м/с. Вопрос: какой будет скорость спутника в самой далекой точке эллиптической орбиты на расстоянии 2·10 7 м от центра Плутона?
Для ответа на этот вопрос нужно воспользоваться законом сохранения момента импульса, поскольку на спутник не действуют никакие внешние моменты сил (сила гравитационного притяжения направлена параллельно радиусу и не создает момента). Однако закон сохранения момента импульса нужно преобразовать так, чтобы вместо угловых скоростей в его формулировке фигурировали тангенциальные скорости.
Итак, рассмотрим формулу закона сохранения момента импульса:
где ( I_ <бл>) — это момент инерции спутника в самой близкой точке, ( I_ <дал>) — это момент инерции спутника в самой далекой точке, ( omega_ <бл>) — угловая скорость спутника в самой близкой точке, а ( omega_ <дал>) — угловая скорость спутника в самой далекой точке.
Предположим, что размеры спутника гораздо меньше расстояния до центра Плутона и спутник можно считать материальной точкой. Тогда его моменты инерции равны:
где ( r_ <бл>) — это расстояние от спутника до центра Плутона в самой близкой точке эллиптической орбиты, а ( r_ <дал>) — это расстояние от спутника до центра Плутона в самой далекой точке эллиптической орбиты.
Подставляя все перечисленные соотношения в формулу закона сохранения момента импульса
Отсюда путем несложных алгебраических преобразований, получим:
Подставляя значения, получим:
Итак, в ближайшей к Плутону точке орбиты спутник будет иметь скорость 9000 м/с, а в самой дальней — 2700 м/с. Этот результат мы легко получили только благодаря знанию закона сохранения момента импульса.
http://loveisflowers.ru/lectures/fazper40.htm
Основные формулы
Мерой инертности твердого тела при вращательном движении является момент инерции:
I = Σ Mi∙ Ri2,
Где Mi – элементарная масса I – го кусочка тела, Ri – расстояние этого кусочка от оси вращения.
Моменты инерции некоторых твердых тел относительно оси, проходящей через их центры масс:
Полый цилиндр I = M ( R12 + R22).
Тонкий обруч I = MR2.
Сплошной цилиндр I = mR2.
Шар I = mR2.
Тонкий стержень I = Ml2.
Если ось вращения не проходит через центр масс, для расчета момента инерции используют теорему Штейнера:
I = I0 + Ma2,
Где I – момент инерции тела относительно данной оси, I0 – момент инерции этого тела относительно оси, параллельной данной, и проходящей через центр масс, M – масса тела, А – расстояние между осями.
Основное уравнение динамики вращательного движения твердого тела: I e = M,
Где I – момент инерции твердого тела, относительно оси вращения, e – его угловое ускорение, М – суммарный момент сил, действующий на тело относительно данной оси.
Момент силы F равен: M = F L,
Где L – расстояние от линии, вдоль которой действует сила, до оси вращения.
Момент импульса твердого тела относительно неподвижной оси: L = I ω,
Где I – момент инерции твердого тела относительно данной оси, ω – угловая скорость его вращения.
Момент импульса материальной точки относительно неподвижной оси: L = M υ R,
Где M – масса частицы, υ – ее скорость, R – расстояние от линии, вдоль которой движется частица, до данной оси.
В замкнутой системе частиц полный момент импульса не меняется: ΣLi = const.
Кинетическая энергия вращающегося тела:
EK = ,
Где I – момент инерции тела, ω – его угловая скорость.
Кинетическая энергия катящегося тела:
EK = 

Где M – масса тела, υ0 – скорость поступательного движения центра масс, I0 – момент инерции тела относительно оси, проходящей через центр масс, ω – угловая скорость вращения тела.
Примеры решения задач
Задача 13
Прямой круглый однородный конус имеет массу M и радиус основания R. Найти момент инерции конуса относительно его оси.
Решение

Dm = rpR2Dr,
Где ρ – плотность материала, из которого изготовлен конус. Момент инерции этого слоя
DI = Dm.R2.
Момент инерции всего конуса складывается из моментов инерции всех слоёв:
I = =
ρπ R 4 Dr =
ρR5.
Остаётся выразить его через массу всего цилиндра:
M = 

R3,
Отсюда ρ = ,
I = 
mR2.
Задача 14
Маховое колесо, имеющее момент инерции 245 кг∙м2, вращается с частотой 20 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти: 1) момент сил трения; 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.
Решение
При торможении угловое ускорение отрицательно. Найдём его модуль из кинематического соотношения для угловой скорости.
ω 0 = 2 π ν0, ω = 0,
0 = 2 π ν0 — ε T,
Отсюда ε = 
Это ускорение обусловлено действием момента сил трения
MТр = I ε = 
Полный угол поворота при равнозамедленном движении находится из соотношения:
φ = ω0 T— ,
φ =2π N, ω 0 = 2 π ν0, ε = 
Перепишем соотношения для угла в виде:
2π N = 2 π ν0 T — = 2 π ν0 T —


Для нахождения числа оборотов получим:
N = .
Подставив числовые значения, найдём:
MТр = 
N = 
Задача 15
На барабан радиусом R = 20 см, момент инерции которого равен I = 0,1 кг∙м2, намотан шнур, к которому привязан груз массой M = 0,5 кг. До начала вращения высота груза над полом равна H1 = 1 м. Найти: 1) через какое время груз опустился до пола; 2) кинетическую энергию груза в момент удара о пол; 3) натяжение нити. Трением пренебречь.
Решение

Барабан вращается вокруг неподвижной оси. Его уравнение движения M = I ε,
Где М – момент силы натяжения шнура, М = TR, I – момент инерции барабана, ε = – его угловое ускорение.
TR = I .
Выражаем отсюда силу натяжения шнура:
T = I (10)
И подставляем ее в уравнение движения груза:
Mg = A(M + ) = Am(1 + ).
Получаем ускорение груза:
A = 
Время движения груза можно найти из уравнения:
H1 = ,
T = 

В момент удара о пол груз имел скорость:
υ = At = 
Следовательно, его кинетическая энергия:
EK = =

Подставив выражение для ускорения (11) в формулу (10), получим: T =


Подставив числовые значения, определим искомые величины:
T = 
EK = 
T = 
Задача 16
Шар массой M = 1 кг, катящийся без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку υ = 10 см/с, после удара 8 см/с. Найти количество тепла Q, выделившееся при ударе.
Решение
Кинетическая энергия катящегося тела равна:
EK = +
. (12)
Момент инерции шара I = ,
Угловая скорость вращения w = .
Подставляем эти величины в формулу (12):
EK = +

M υ 2.
Количество тепла, выделившегося при ударе, равно разнице его кинетических энергий до и после удара:
Q = EK1 – EK2 = M υ12 —
M υ22 =
M(υ12 — υ22).
Подставив числовые значения, получим:
а = ∙1(100∙10-4 – 64.10-4) =
10-4 = 2,25∙10-3 Дж = 2,52 МДж.
Задача 17
Найти кинетическую энергию велосипеда, едущего со скоростью υ = 9 км/ч. Масса велосипедиста вместе с велосипедом M = 78 кг, причем на колеса приходится масса M1 = 3 кг. Колеса считать тонкими обручами.
Решение
Кинетическая энергия велосипеда складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения колес.
EK = +
.
Момент инерции колес, представляющих собой тонкие обручи, равен I = , а угловая скорость вращения w = .
Подставляем эти значения в выражение для кинетической энергии: EK = +


Скорость надо перевести в м/с: υ = 2,5 м/с.
Подстановка числовых значений дает: EK =253 Дж.
Задача 18
Однородный стержень длиной 85см подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую наименьшую скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
Решение
Чтобы стержень смог сделать полный оборот вокруг оси, он должен подняться до вертикального положения В.
Если отсчитывать потенциальную энергию стержня от начального положения А, то в положении В центр масс его поднят на
Высоту С2-С1=L – длина стержня. Стержень приобретает потенциальную энергию ЕN = Mgℓ за счет кинетической энергии,

υ – наименьшая скорость нижнего конца, при которой он сможет сделать полный оборот, то
угловая скорость стержня w = .
Момент инерции стержня относительно оси, проходящей через его конец, определятся по теореме Штейнера:
I = M L2 = M
=
M L2,
Где Ml2–момент инерции стержня относительно перпендикулярной к нему оси, проходящей через центр масс,
– расстояние от центра масс до требуемой оси.
Кинетическая энергия вращательного движения:
EK = =



По закону сохранения энергии, кинетическая энергия стержня в положении А равна его потенциальной энергии в положении В:

Отсюда υ = .
Подставляем числовые значения: υ = »7 м/с.
Задача 19
Человек массой M1 = 60 кг находится на неподвижной платформе массой M = 100 кг. Какое число оборотов в минуту будет делать платформа, если человек будет двигаться по окружности радиуса 5 м вокруг оси вращения? Скорость движения человека относительно платформы равна 4 км/ч. Радиус платформы 10 м. Считать платформу однородным диском, а человека – точечной массой.
Решение

Момент импульса этой системы был равен нулю. Когда человек начнет двигаться по платформе, платформа будет вращаться в противоположном направлении. Если расстояние от человека до оси вращения платформы R, в месте нахождения человека U = w R. Таким образом, если человек движется относительно платформы со скоростью
υ, то относительно земли он будет двигаться со скоростью υ – w R, его момент импульса относительно оси платформы L1 = M1(υ – wR)R. Момент импульса платформы относительно ее оси:
L = – IW,
где I – момент инерции платформы.
Поскольку платформа представляет собой однородный диск, то ее момент инерции относительно оси, проходящей через центр:
I = MR2.
Запишем закон сохранения момента импульса для данной системы:
O = L1 + L = M1(υ – w R) R – MR2w,
Отсюда можно определить угловую скорость вращения платформы:
W = 
Число оборотов платформы в минуту определится из соотношения:
N = 60 =

Подстановка числового значений дает:
N =

Кинетическая энергия, теория и онлайн калькуляторы
Кинетическая энергия
Понятие энергии — это одно из основных понятий в физике. Закон сохранения энергии является важнейшим законом природы. Его используют для объяснения множества механических, тепловых и электрических явлений. Понятие «энергия» встречается в большом числе технических задач, так как важная задача техники заключается в получении, передаче и использовании энергии.
Общее понятие энергии можно получить, применяя идеи теории относительности.
Релятивистское определение кинетической энергии
Определение
Кинетической энергией тела ($E_k$) называют разность между его полной энергией ($W$) и энергией покоя ($E_0$):
[E_k=W-E_0=mc^2left(G-1right)left(1right),]
где $W$ — полная энергия изолированного тела.
[W=Gmc^{2 }left(2right),]
$c$- скорость света; $G=frac{1}{sqrt{1-frac{v^2}{c^2}}}$ ($v-$скорость движения тела по отношению к избранной инерциальной системе отсчета); $m$ — масса покоя тела.
Кинетическая энергия тела зависит от скорости, с которой тело перемещается относительно системы отсчета.
Для вычислений кинетической энергии используют ее определение в другом виде. Чтобы его получить умножим выражение (1) на $frac{G+1}{G+1}$:
[E_k=mc^2left(G-1right)frac{G+1}{G+1}=frac{mc^2(G^2-1)}{G+1}=frac{mc^2(1-frac{1}{G^2})}{frac{1}{G}+frac{1}{G^2}}=frac{mv^2}{frac{1}{G}+frac{1}{G^2}}.]
И так, мы получили, что при скорости движения тела близкой к скорости света:
[E_k=frac{mv^2}{frac{1}{G}+frac{1}{G^2}}(3).]
Кинетическая энергия тела в механике Ньютона
В механике Ньютона скорость движения тела по отношению к некоторой системе отсчета много меньше скорости света ($vll c$), тогда отношение $frac{v^2}{c^2}ll 1$, это означает, что:
[frac{1}{G}=sqrt{1-frac{v^2}{c^2}}approx 1left(4right).]
Тогда из (3) и (4) следует:
[E_k=frac{mv^2}{2}=frac{p^2}{2m}left(5right),]
где $p$ — импульс тела. Формула (5) является приближенной, но в практических расчетах она дает достаточную точность. Так, при скоростях в сотни километров вычисления по формуле (5) дают погрешность (в сравнении с вычислениями по (3)) в десятитысячную долю процента.
Если тело движеtextbf{т}ся со скоростью много меньше, чем скорость света, то кинетическая энергия существенно меньше энергии покоя.
[frac{E_k}{E_0}=frac{v^2}{2c^2}ll 1.]
При скоростях близких к скорости света почти вся энергия тела сводится к его кинетической энергии, в этом случае энергия покоя значительно меньше кинетической. Для ультрарелятивистских скоростей можно пользоваться выражением:
[E_kapprox W=Gmc^2left(6right).]
«Классическое» определение кинетической энергии
Определение
Кинетическая энергия — это скалярная физическая величина, которая является мерой движения тела (материальной точки),
которая зависит от его массы и скорости движения.
Это часть полной энергии тела, которая обусловлена его движением. При отсутствии движения кинетическая энергия тела равна нулю.
Для изолированной системы кинетическая энергия является интегралом движения.
[dleft(frac{mv^2}{2}right)=overline{F}doverline{s}left(7right),]
где $overline{F}$ — сила; $doverline{s}$ — перемещение, которое вызвано действием силы $overline{F}$.
Единицей измерения кинетической энергии является джоуль:
[left[E_kright]=Дж=Нcdot м.]
Свойства кинетической энергии
Кинетическая энергия — это аддитивная величина. Кинетическая энергия системы равна сумме кинетических энергий ее частей.
Кинетическая энергия не зависит от положения тела в пространстве.
Кинетическая энергия инвариантна к преобразованиям Галилея.
Если материальная точка перемещается, на нее действуют некоторые силы, то работа ($A$) этих сил равна изменению кинетической энергии данной точки:
[A=E_{k2}-E_{k1}left(8right).]
Для вычисления кинетической энергии вращающегося тела используют формулу:
[E_k=frac{J{omega }^2}{2}left(9right),]
где $J$ — момент инерции тела относительно оси вращения; $omega $ — угловая скорость.
Кинетическую энергию тела, которое катится без скольжения, можно найти:
[E_k=frac{mv^2}{2}+frac{J{omega }^2}{2}left(10right),]
где $v$ — скорость поступательного движения центра инерции тела.
Примеры задач с решением
Пример 1
Задание. Какова кинетическая энергия тела, которое упало на Землю в момент его удара, если тело бросили с некоторой высоты в горизонтальном направлении? Начальная скорость тела $v_0$, его масса $m$. Тело упало через время $t’$ после начала движения. Сопротивление воздуха не учитывать.
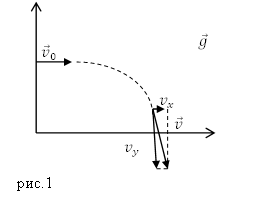
Решение. Сделаем рисунок.
Тело движется в поле тяжести Земли, его ускорение равно ускорению свободного падения ($overline{g}$). Запишем кинематическое уравнение движения тела:
[overline{v}={overline{v}}_0+overline{g}t left(1.1right).]
В проекциях на оси X и Y уравнения (1.1) имеем:
[X: v_x=v_0left(1.2right).]
[Y:v_y=-gt left(1.3right).]
Тогда модуль скорости тела при $t=t’$равен:
[v(t)=sqrt{v^2_x+v^2_y}to v(t’)=sqrt{v^2_0+g^2t^{‘2}}left(1.4right).]
Кинетическую энергию тела найдем как:
[E_k=frac{mv^2}{2}=frac{m}{2}left(v^2_0+g^2t^{‘2}right).]
Ответ. $E_k=frac{m}{2}left(v^2_0+g^2t^{‘2}right)$
Пример 2
Задание. Какова кинетическая энергия электрона, который движется со скоростью равной $v=0,9 c frac{м}{с}$ ($c$ — скорость света в вакууме)?
Решение. Кинетическую энергию релятивистской частицы найдем как:
[E_k=W-E_0=mc^2left(frac{1}{sqrt{1-frac{v^2}{c^2}}}-1right)left(2.1right).]
Подставим данные из условий задачи, учтем, что масса покоя электрона равна $m=9,1cdot {10}^{-31}кг;;$ скорость света в вакууме: $c=3cdot {10}^8frac{м}{с}$:
[E_k=9,1cdot {10}^{-31}{left(3cdot {10}^8right)}^2left(frac{1}{sqrt{1-frac{{0,9}^2c^2}{c^2}}}-1right)=1,06cdot {10}^{-13}left(Джright).]
Ответ. $E_k=1,06cdot {10}^{-13}Дж$
Читать дальше: математический маятник.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!