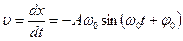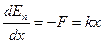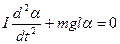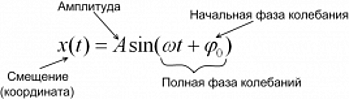Алексей Алексеевич Ивахно
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Колебания — это самая общая форма движения динамических систем около положения равновесия. При малых отклонениях от положения равновесия колебания обычно являются гармоническими. В этом заключается их особенная значимость.
Уравнение вида:
$frac{d^2x}{dt^2}+omega^2x=0 (1),$
где $omega^2$ — циклическая частота колебаний; $x$ -расстояние положения равновесия
называют уравнением механических гармонических колебания. Колебания происходят вдоль оси $X$.
Решением уравнения (1) можно считать функции:
$x=Asin (omega t+varphi)$ или
$x=Acos (omega t+varphi_1)$,
где $A$ — амплитуда колебаний.
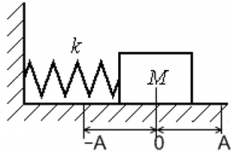
Систему, которая реализует данные малые колебания, называют линейным или гармоническим осциллятором. Примером гармонического осциллятора может служить
- малое тело, подвешенное на упругую пружину (Пружинный маятник);
- физический маятник (Тело, которое совершает колебания относительно точки (или оси, проходящей через точку тела), не являющейся его центром масс);
- математический маятник; (Малое тело, совершающее колебания на длинном, нерастяжимом, невесомом подвесе).
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 1
Собственными называют колебания системы под воздействием только внутренних сил при отсутствии внешних воздействий.
В полной механической энергии гармонического осциллятора выделяют:
- потенциальную энергию;
- и кинетическую энергию.
Потенциальная энергия
Говорить о потенциальной энергии можно только, если действующие силы потенциальны. Если колебательные движения между двумя точками являются одномерным, то автоматически обеспечивается условие потенциальности и всякую силу, зависящую только от координат, можно считать потенциальной.
Если рассматривается линейный осциллятор, то обычно считают, что потенциальная энергия точки равна нулю в положении равновесия. Считая, что осциллятор заставляет совершать колебания сила упругости;
$F=-kx(2)$
и зная, как связана потенциальная энергия и потенциальная сила, (для одномерного случая: $F=-frac{dU}{dx}$), потенциальную энергию линейного осциллятора определим как:
«Энергия гармонических колебаний» 👇
$U(x)=frac{kx^2}{2}=frac{momega^2x^2}{2}=frac{mA^2omega_0^2}{2}cos^2 (omega t+varphi)= frac{mA^2omega_0^2}{4}(1+cos 2(omega t +varphi)) (3).$
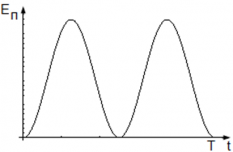
Из формулы (3) видно, что потенциальная энергия при колебаниях изменяется с течением времени, так как изменяется $x$. Частота колебаний потенциальной энергии $2omega$.
Кинетическая энергия.
Кинетическая энергия тела – это энергия движения, она зависит от скорости перемещения материальной точки, задается выражением:
$E_k=frac{mv^2}{2}=frac{mdot{x}^2}{2}=frac{mA^2omega_0^2}{2}sin^2 (omega t+varphi) =frac{mA^2omega_0^2}{4}(1-cos 2(omega t +varphi)) (4).$
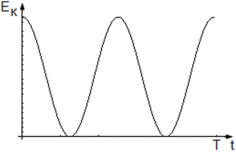
Кинетическая энергия является переменной во времени физической величиной. Колебания ее происходят с частотой $2omega$ (эта частота в два раза больше, чем частота колебаний $x$)
Закон сохранения энергии при гармонических колебаниях
Как было отмечено, кинетическая энергия и потенциальная энергия являются переменными во времени величинами, однако, их сумма у гармонического осциллятора, выполняющего свободные колебания, не изменяется:
$frac{mdot{x}^2}{2}+frac{momega^2x^2}{2}=frac{momega^2A^2}{2}=const$.
Полная энергия системы ($E$) не изменяется, поскольку при гармонических колебаниях выполняется закон сохранения механической энергии, так как сила упругости является консервативной.
Закон сохранения энергии позволяет сделать два существенных вывода
Вывод первый. Наибольшая кинетическая энергия осциллятора равна его наибольшей энергии потенциальной энергии.
Данный вывод очевиден, так как потенциальная энергия осциллятора максимальна при смещении точки выполняющей колебания на максимально возможное расстояние, при этом скорость, а соответственно и кинетическая энергия осциллятора равна нулю.
Наибольшую кинетическую энергию колебательная система имеет тогда, когда она проходит положение равновесия ($x=0$), то есть потенциальная энергия равна нулю.
$frac{mV^2}{2}=frac{momega^2A^2}{2}(5),$
где $V$ — максимальная скорость.
Вывод второй. Средняя кинетическая энергия осциллятора равна его средней потенциальной энергии.
Средняя кинетическая энергия.
Пусть параметр $f$ функция времени, тогда средняя ее величина на отрезке времени от $t_1$ до $t_2$ равна:
$f_{sr}=frac{1}{t_2-t_1}int_1^2f(t)dt (6),$
где пределы интегрирования обозначают 1 — время $t_1$; 2 — $t_2$.
Если функцию $f(t)$ изобразить на графике (рис.1), то ее среднее значение будет соответствовать высоте прямоугольника, площадь которого ограничивают функция $f$ и ось $t$ на заданном отрезке времени.
Замечание 1
Площадь под осью $t$ считают отрицательной.
Рисунок 1. График. Автор24 — интернет-биржа студенческих работ
Запишем закон движения осциллятора как:
$x(t)=Acos (omega t+varphi) (7)$,
его скорость равна:
$dot{x}=-Aomegasin (omega t+varphi) (8).$
Выражение для потенциальной энергии представим как:
$U(t) = frac{omega^2A^2}{2}cos^2 (omega t+varphi) (9)$.
Кинетическую энергию представит выражение:
$E_k=frac{omega^2A^2}{2}sin^2 (omega t+varphi) $
Отрезком времени, на котором будем брать среднее, станет период колебаний, вернее одного колебания. Нахождение средних значений кинетической и потенциальной энергии сводят к поиску средних от $cos^2 (omega t+varphi)$ и $sin^2 (omega t+varphi)$:
$(sin^2 (omega t+varphi))_{sr}=frac{1}{T}int_0^T cos^2 (omega t+varphi)dt=frac{1}{T}int_0^Tfrac{1}{2}(1-cos 2(omega t+varphi)dt)=frac{1}{2},$
где $T$ — период колебаний; $omega T=2pi.$
По аналогии получаем:
$sin^2 (omega t+varphi)_sr=frac{1}{2}.$
В результате имеем:
-
средняя по времени потенциальная энергия гармонического колебания за один период равна:
$U_{sr}=frac{momega^2A^2}{4}(10),$
-
средняя по времени кинетическая энергия составила:
$E_{k,sr}=frac{momega^2A^2}{4}(11)$.
Сравнивая (10) и (11) мы видим, что:
$U_{sr}= E_{k,sr}=frac {1}{2}E$,
где $E$ — полная механическая энергия гармонических колебаний.
то есть средняя по времени кинетическая энергия осциллятора равна средней по времени потенциальной энергии.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Кинетическую энергию
материальной точки, колеблющейся по
гармоническому закону, можно вычислить
по известной формуле,
используя выражение (5.12):

Потенциальную
энергию колебательного движения
найдем, исходя из общей формулы для
потенциальной энергии упругойдеформации
и
используя выражение (5.8):
(5.25)
Суладывая кинетическую
(5.24) и потенциальную (5.25) энергии, получаем
полную механическую энергию материальной
точки, колеблющейся по гармоническому
закону:

При отсутствии сил трения полная
механическая энергия системы
не изменяется:
(5.27)
Графически
зависимости кинетической, потенциальной
и полной механической энергий
колеблющейся системы от времени показаны
на рис. 5.8.
5.3. Сложение гармонических колебаний
Материальная точка
может одновременно участвовать в
нескольких колебаниях. В этом
случае, чтобы найти уравнение и траекторию
результирующего движения, следует
сложить колебания. Наиболее
просто выполняется сложение гармонических
колебаний. Рассмотрим
две такие задачи.
Сложение гармонических
колебаний, направленных по одной
прямой. Пусть материальная точка
одновременно участвует в двух
колебаниях, происходящих вдоль одной
линии. Аналитически такие колебания
выражаются следующими уравнениями:
Допустим, что
частоты складываемых
колебаний одинаковы
тогда результирующее
смещение точки
Выполним такое сложение
с помощью векторной диаграммы.
Изобразим положение
векторов
и
в начальный
момент времени (рис.
5.9), углы между этими векторами и осью
ОХ равны
начальным фазам слагаемых колебаний
01
и 02.
Вектор
— амплитуда
результирующего колебания. Так как
и
вращаютсяс одинаковой угловой
скоростью, то и сумма их — вектор
— будет вращаться с той же угловой
скоростью, т. е.
результирующее движение является
гармоническим с круговой частотой
(5.29)
Выразим амплитуду
А
этого колебания и начальную фазу 1
через заданные значения
Применяя теорему косинусов
к треугольнику, заштрихованному на рис.
5.9, получаем
Так
как–cos= -cos[- (02
— 01)]
= cos
(02
— 01),
то
(5.30)
Как
видно из рис. 5.9, tg
равен отношению проекции
на ось
OY
к
проекции
на
ось ОХ,
т. е. Ау
/Ах.
Учитывая,
что проекция
суммы равна сумме проекций, имеем

Таким образом,
поставленная задача решена: по формулам
(5.30) и (5.31) можно найти амплитуду и
начальную фазу результирующего
колебания. Из выражения (5.30) вытекают
следующие частные случаи:
и тогда
т. е. амплитуда результирующего
колебания равна сумме амплитуд
слагаемых колебаний, если разность
начальных фаз равна четному числу(рис. 5.10, а);
тогда
т. е. амплитуда
результирующего колебания равна разности
амплитуд слагаемых
колебаний, если разность начальных фаз
равна нечетному числу
(рис. 5.10, б). В
частности, при A1
= A2
имеем А
= О, т. е. колебания нет (рис. 5.10,в).
Это достаточно очевидно: если материальная
точка участвует одновременно в двух
колебаниях, имеющих одинаковую
амплитуду и совершающихся в противофазе,
то точка неподвижна. Если частоты
складываемых колебаний не
одинаковы, то сложное колебание уже не
будет гармоническим.
И
случай, когда частотыслагаемых
колебаний мало отличаются друг от
друга:
Результирующее
колебание при этом подобно
гармоническому, но с медленно
изменяющейся амплитудой (амплитудная
модуляция). Такие колебанияназываются
биениями (рис. 5.11).
Сложение
взаимно перпендикулярных гармонических
колебаний. Пусть материальная
точка одновременно участвует вдвух
колебаниях: одно направлено вдоль оси
ОХ, другое — вдоль оси
OY.
Колебания
заданы следующими уравнениями:
(5.34)
Допустим,
что частоты колебаний одинаковы, т. е.тогда
(5.35)
Уравнения (5.35) задают
траекторию движения материальной точки
в параметрической форме. Если в эти
уравнения подставлять разные значенияt, то можно определить
координатых иу, а совокупность
координат и есть траектория. Более
наглядно траекторию можно представить
в виде зависимостиу = f(x),
для получения которой
следует исключить время из уравнений
(5.35). Произведя
математические преобразования,
получим уравнение эллипса:
(5.36)
Таким образом, при
одновременном участии в двух взаимно
перпендикулярных гармонических
колебаниях одинаковой частоты
материальная точка движется по
эллиптической траектории
(рис. 5.12).
Из выражения (5.36)
вытекают
некоторые частные случаи:
Это каноническая
форма уравнения эллипса, соответствующая
симметричному расположению его
относительно осей координат (рис.
5.13, а). Из
(5.37) при А1
= А2
= R
(рис. 5.13, б)
получаем
уравнение
окружности радиусом R:
(5.38)
тогда
(5.39)
и после
преобразований
(5.40)
Это уравнение прямой
линии, в которую
вырождается эллипс [рис. 5.14, а
соответствует знаку « + » в уравнении
(5.40);рис. 5.14, б—
знаку «-»].
При сложении взаимно
перпендикулярных колебаний разных
частот получаются различные траектории
материальной точки, названные
фигурами
Лиссажу.
Вид фигур Лиссажу
зависит как от соотношения амплитуд А1
и
А2,
так и от отношения частот 1/2
и разности
начальных фаз 01
—
02
слагаемых колебаний (рис. 5.15):
Соседние файлы в папке lektsii_fizika
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кинетическая, потенциальная и полная энергии гармонических колебаний
Лекция 5. Механические колебания
План лекции
5.1. Основные характеристики колебательного движения.
5.2. Кинетическая, потенциальная и полная энергии гармонических колебаний.
5.3. Уравнение гармонических колебаний. Маятники.
5.4. Затухание колебания.
5.5. Вынужденные колебания. Резонанс.
5.6. Явление резонанса в строительстве.
Основные характеристики колебательного движения
Процессы точно или приблизительно повторяющиеся через одинаковые промежутки времени называются колебаниями.В зависимости от физической природы различают механические, электромагнитные и другие виды колебаний. Несмотря на разную природу колебаний, в них обнаруживаются одни и те же физические закономерности, они описываются одними и теми же математическими уравнениями и исследуются общими методами, разработка и применение которых составляют задачу теории колебаний.
В данном курсе физики мы будем изучать два наиболее распространенных класса колебаний: механические и электрические.
Среди разнообразных колебаний основную и существенную роль играют так называемые гармонические колебания, то есть такие, при которых колеблющаяся величина изменяется с течением времени по закону синуса или косинуса.
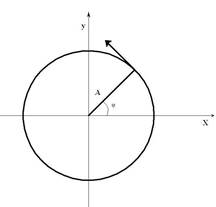
Рассмотрим гармонические колебания на примере колеблющейся точки.
Пусть точка вращается по окружности радиуса А с угловой скоростью ω0 (рис.5.1).
Рис.5.1.
Если точку спроецировать на оси X и Y, то ее проекции будут совершать колебания и удовлетворяют следующим уравнениям соответственно
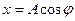
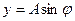
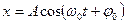
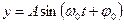
где х и y – смещения колеблющейся точки от положения равновесия;
А – амплитуда колебания (максимальное смещение);
ω0 – круговая (циклическая) частота колебаний.
Точка совершает одно полное колебание за время Τ, называемое периодом колебания. Частота колебаний ν (число колебаний в единицу времени) есть 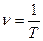
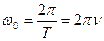
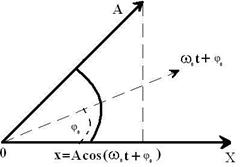
Геометрический смысл параметров уравнений (5.2) можно объяснить с помощью векторных диаграмм. Выберем на оси Х точку О и из этой точки под углом φ0 проведем вектор А. Будем вращать вектор А с угловой скоростью ω0 и тогда его проекция на ось будет смещаться на величину x (рис. 5.2).
Рис.5.2.
Колеблющаяся точка обладает скоростью и ускорением. Скорость материальной точки
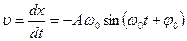
Ускорение материальной точки
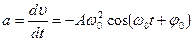
С учетом формулы (5.2) получим
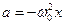
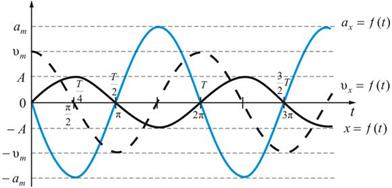
Сравнивая уравнения (5.2), (5.4) и (5.5) замечаем, что скорость опережает смещение на π/2. Фазы ускорения и смещения различаются на π (изменяются в противофазе). Графические зависимости смещения, скорости и ускорения от времени показаны на рис.5.3.
Умножив обе части равенства уравнения (5.6) на массу m материальной точки получим
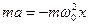
Используя II закон Ньютона, получаем
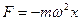
Рис.5.3.
Таким образом, чтобы совершались гармонические колебания на материальную точку должна действовать сила F, пропорциональная смещению x, которая возвращает ее в положение равновесия
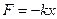
где, k – некоторый коэффициент (зависящий от свойств колеблющейся системы) и называемой жесткостью.
Из уравнения (5.7) и (5.8) видно, что 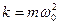
Кинетическая, потенциальная и полная энергии гармонических колебаний
Полная энергия Е колеблющейся материальной точки равна сумме кинетической Ек и потенциальной Еп энергий
Кинетическую энергию можно найти, зная массу m и скорость u
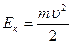
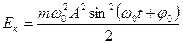
Выражение для потенциальной энергии можно найти из соотношений между потенциальной энергией и силой.
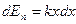
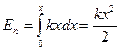
Учитывая, что 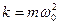
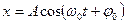
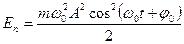
Полную энергию получим сложив (5.12) и (5.15)
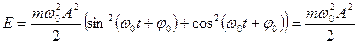
Таким образом, полная энергия пропорциональна квадрату амплитуды колебаний.
Из формул (5.12) и (5.15) видно, что когда 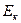
5.3. Уравнение гармонических колебаний.
Маятники
На колеблющуюся материальную точку массой m действует возвращающая сила F = — kx. Эта сила вызывает ускорение 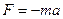
где, k – жесткость системы, 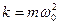
Сделав соответствующие подстановки в (5.17), получим
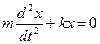
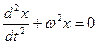
Уравнение (5.18) представляет собой дифференциальное уравнение второго порядка незатухающих гармонических колебаний материальной точки.
Решением этого дифференциального уравнения как раз и является уравнение (5.2): 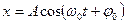
Колебания любого гармонического осциллятора (или гармонического вибратора) описываются дифференциальным уравнением второго порядка
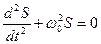
Решением этого уравнения является
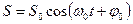
где S0 – амплитудное (максимальное) значение параметра S.
Примерами гармонических осцилляторов являются маятники, колебательный контур.
В качестве примера малых колебаний рассмотрим колебания маятников.
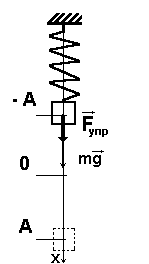
Пружинный маятник
Груз массой m, подвешенный на упругой пружине представляет собой пружинный маятник (рис.5.4). Если груз оттянуть вниз и отпустить, то под действием силы F = -kx маятник будет совершать колебания; k – коэффициент жесткости (в данном случае коэффициент упругости).
Рис.5.4.
Уравнение движения маятника имеет вид
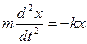
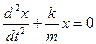
Его решением является
Это значит, что пружинный маятник совершает гармонические колебания с циклической частотой ω0
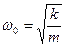
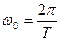
Период колебаний пружинного маятника
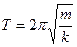
Физический маятник
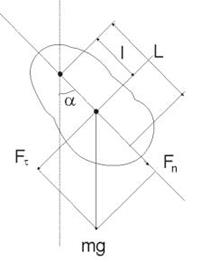
Физическим маятником называется твердое тело, которое может колебаться под действием силы тяжести вокруг оси, не проходящей через центр масс. При отклонении маятника относительно оси О угол α, на него действует М – момент возвращающей силы 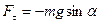
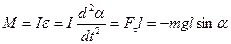
где, I – момент инерции относительно оси О;
l – плечо силы Fτ; при малых углах 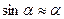
Рис.5.5.
Из (5.22) получаем дифференциальное уравнение
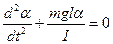
Сравнив уравнение (5.23) с уравнением гармонического осциллятора (5.19), получим
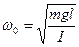
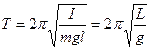
где, 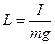
От точки подвеса О на линии ОС на расстоянии L находится точка О1, называемая центром качения. Точки О и О1 обладает свойством взаимозаменяемости.
Энергия гармонических колебаний
Введём энергию колебания.
Колебательная система движется со скоростью , тогда его кинетическая энергия должна быть равна:
- где
- — кинетическая энергия системы
- — масса колеблющегося тела
- — скорость тела в данный момент
Вспомним зависимость скорости от времени при гармоническом колебании:
- где
- — амплитуда (максимальное значение) колебания
- — циклическая частота колебания
- — начальная фаза колебания
- — время от начала колебания
Подставим (2) в (1) при условии (для упрощения):
Тогда максимальная кинетическая энергия данной системы:
т.к. максимальное значение .
С другой стороны для пружинного маятника можем записать потенциальную энергию деформации:
- где
- — потенциальная энергия деформации
- — жёсткость пружины
Вспомним зависимость координаты от времени при гармоническом колебании:
Подставим (5) в (4) при условии (для упрощения):
Тогда максимальная потенциальная энергия данной системы:
т.к. максимальное значение .
Вывод: задачи школьной физики чаще всего связаны именно с максимальным значением энергии колебания. Её можно рассчитать и как кинетическую энергию в положении равновесия (4), и как потенциальную энергию в точке максимального отклонения (8).
17. Механика Читать 0 мин.
17.547. Механические колебания
Колебания ― это процесс, при котором состояние системы изменяется, повторяясь во времени, и смещаясь то в одну, то в другую сторону относительно состояния равновесия.
Период ― это время, через которое повторяются показатели системы, т. е. система совершает одно полное колебание. Период изменяется в секундах.
Частота ― величина обратная периоду: число полных колебаний за единицу времени. Частота измеряется в герцах [Гц] = [c-1]. Частота равна v = $frac<1>$ , где
Если известно, что тело совершает N колебаний за время t, то частоту его колебаний можно определить как v = $frac$ , где
N ― количество колебаний;
Для описания колебательных систем, совершающих круговые процессы, удобно использовать круговую (циклическую) частоту. Циклическая частота показывает количество полных колебаний, которые происходят за 2π секунд и равна ω = 2πvили ω = $frac<2pi>$ , где
ω ― циклическая частота [рад/с];
Гармонические колебания ― колебания, в которых физические величины изменяются по закону синуса или косинуса. Кинематическое уравнение гармонических колебаний имеет вид:
ω ― циклическая частота [рад/с];
φ0 ― начальная фаза колебаний, [рад];
Смещение (x) ― это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать ее от положения равновесия.
Амплитуда колебаний (A) ― максимальное отклонение колеблющейся величины от положения равновесия, т. е. максимальное смещение равно амплитуде колебаний xmax = A.
Начальная фаза колебаний (φ0) определяет смещение в начальный момент времени, выраженное в радианах.
Фаза колебаний (φ) или полная фаза колебаний, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебаний равна φ = ωt + φ0, где
φ ― полная фаза колебаний [рад];
φ0 ― начальная фаза колебаний, [рад];
ω ― циклическая частота [рад/с];
Пример анализа гармонических колебаний точки
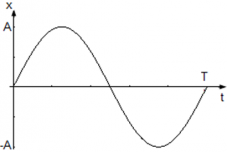
Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид x(t) = Asin(ωt), где
ω ― циклическая частота [рад/с].
Из уравнения x(t) = Asin(ωt) следует, что начального смещения нет (φ0 = 0) и колебания начинаются из положения равновесия. Смещение x достигает максимального значения xmax и равно амплитуде xmax = A, в тот момент, когда модуль синуса равен единице |sin(ωt)| = 1. Когда x = A фаза колебаний равна φ = $frac<pi> <2>+2pi n$ когда x = –A фаза колебаний принимает значения φ = $frac<3pi> <2>+2pi n$ , где n = 0, 1 , 2, … N.
График колебания координаты точки имеет вид:
Определим уравнение и график колебания скорости. Скорость ― это производная координаты по времени: v = xt‘, где
v ― скорость движения точки [м/с];
Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt‘ = |Asin(ωt)|’t = Acos(ωt).
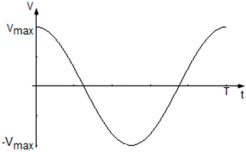
Уравнение скорости точки равно v(t) = Acos(ωt), где
v ― скорость движения точки [м/с];
ω ― циклическая частота [рад/с];
Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно vmax = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.
График колебания скорости точки имеет вид:
Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.
Ускорение ― это производная скорости по времени: a = vt‘, где
a ― ускорение движения точки [м/с2];
v ― скорость движения точки [м/с];
Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt‘ = [Aωcos(ωt)]t‘ = –Aω2sin(ωt).
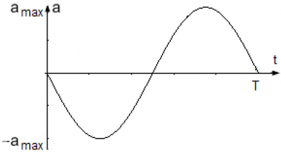
Уравнение ускорения точки равно a(t) = –Aω2sin(ωt), где
a ― ускорение движения точки [м/с2];
ω ― циклическая частота [рад/с];
Модуль ускорения точки максимален, когда |sin(ωt)| = 1 ― тогда же, когда достигает максимума смещение точки. Максимальное ускорение, т. е. амплитуда ускорения точки равна amax = Aω2.
График колебания ускорения точки имеет вид:
Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации. В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную. Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии E = EП + EK, где
E ― полная механическая энергия системы, E = const, [Дж];
EП ― потенциальная энергия системы, изменяющаяся во времени, [Дж];
EK ― кинетическая энергия системы, изменяющаяся во времени, [Дж].
Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).
Потенциальная энергия деформированной пружины равна EП = $frac<2>$ , где
EП ― потенциальная энергия деформированной пружины, [Дж];
k ― коэффициент упругости пружины [Н/м];
x ― деформация пружины (величина ее удлинения или сжатия) [м].
У пружинного маятника деформация пружины ― переменная величина, которая зависит от времени. Кинематическое уравнение движения точки, принадлежащей этому маятнику ― x(t) = Asin(ωt). Следовательно, потенциальную энергию пружинного маятника можно записать как EП = $frac<2>$ = $frac<2>$ = $frac <2>cdot A^2 sin^2 (omega t)$ .
Уравнение потенциальной энергии пружинного маятника EП = $frac <2>cdot A^2 sin^2 (omega t)$ , где
EП ― потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
ω ― циклическая частота [рад/с];
Амплитуда потенциальной энергии пружинного маятника равна EПmax = $frac<2>A^2$ , где
EПmax ― максимальная потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.
График колебаний потенциальной энергии пружинного маятника:
Рассмотрим изменение кинетической энергии маятника. Кинетическая энергия тела равна Eк = $frac<2>$ , где
Eк ― кинетическая энергия тела, [Дж];
v ― скорость движения тела, [м/с].
У тела, которое совершает колебательные движения, скорость ― переменная величина.
Выше было показано, что если уравнение движения точки имеет вид x(t) = Asin(ωt), то уравнение скорости точки v(t) = Aωcos(ωt). Таким образом, кинетическая энергия маятника равна Eк = $frac<2>$ = $frac <2>cdot (Aomegacos(omega t))^2$ = $frac <2>cdot A^2 omega^2 cos^2 (omega t)$ .
Уравнение кинетической энергии маятника Eк = $frac <2>cdot A^2 omega^2 cos^2 (omega t)$ , где
Eк ― кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с];
Амплитуда кинетической энергии маятника равна EКmax = $frac <2>cdot A^2 omega^2$ , где
EКmax ― максимальная кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с].
Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.
График колебаний кинетической энергии маятника:
Математический маятник ― это колебательная система, состоящая из материальной точки, подвешенной на нерастяжимой нити или стержне.
Период колебаний математического маятника равен T = $2pi sqrt<frac>$ , где
l ― длина нити математического маятника [м];
g ― ускорение свободного падения [м/с2].
Период колебаний пружинного маятника равен T = $2pi sqrt<frac>$ , где
Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.
Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.
На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.
http://www.abitur.by/fizika/teoreticheskie-osnovy-fiziki/garmonicheskie-kolebaniya/energiya-garmonicheskix-kolebanij/
http://reshutest.ru/theory/13?theory_id=334
Введём энергию колебания.
Колебательная система движется со скоростью , тогда его кинетическая энергия должна быть равна:
(1)
- где
Вспомним зависимость скорости от времени при гармоническом колебании:
(2)
- где
Подставим (2) в (1) при условии (для упрощения):
=
(3)
Тогда максимальная кинетическая энергия данной системы:
(4)
т.к. максимальное значение .
С другой стороны для пружинного маятника можем записать потенциальную энергию деформации:
(5)
- где
Вспомним зависимость координаты от времени при гармоническом колебании:
(6)
Подставим (5) в (4) при условии (для упрощения):
=
(7)
Тогда максимальная потенциальная энергия данной системы:
(8)
т.к. максимальное значение .
Вывод: задачи школьной физики чаще всего связаны именно с максимальным значением энергии колебания. Её можно рассчитать и как кинетическую энергию в положении равновесия (4), и как потенциальную энергию в точке максимального отклонения (8).
Энергия гармонических колебаний, теория и онлайн калькуляторы
Энергия гармонических колебаний
Рассмотрим превращения энергии, которые происходят при гармонических колебаниях в консервативной системе на примере пружинного маятника.
Потенциальная энергия гармонических колебаний
В процессе механических колебаниях груза на пружине периодически кинетическая энергия ($E_k$) движущегося груза переходит в потенциальную энергию ($E_p$) колебательной системы, состоящей из потенциальной энергии упругодеформированной пружины и потенциальной энергии груза в поле тяжести Земли. Потенциальная энергия пружины при упругой деформации равна:
[E_{p1}=frac{k{left(x+x_0right)}^2}{2}left(1right),]
где $left(x+x_0right)$ — удлинение пружины; $k$ — жесткость пружины.
Потенциальную энергию груза в поле тяжести ($E_{p2}$) найдем как:
[E_{p2}=-mg x+Cleft(2right),]
где $m$ — масса груза, прикрепленного к пружине.
Постоянную $C,$ будем выбирать так, чтобы в положении равновесия полная потенциальная энергия колебательной системы равнялась:
[frac{kx^2_0}{2}+C=0to C=-frac{kx^2_0}{2} left(3right).]
Тогда потенциальная энергия представлена выражением:
[E_p=E_{p1}+E_{p2}=frac{k{left(x+x_0right)}^2}{2}-mg x-frac{kx^2_0}{2}=frac{kx^2}{2}left(4right).]
Кинетическая энергия пружинного маятника
Кинетическая энергия рассматриваемой колебательной системы состоит из энергии движения груза. Используя уравнение смещения груза пружинного маятника при гармонических колебаниях, происходящих по оси X:
[x=A{cos left({omega }_0t+varphi right)(5) }]
найдем уравнение изменения кинетической энергии груза. Для этого найдем скорость движения груза как:
[v=frac{dx}{dt}=-A{omega }_0{sin left({omega }_0t+varphi right)left(6right). }]
В таком случае кинетическая энергия равна:
[E_k=frac{m}{2}A^2{{omega }_0}^2{{sin}^2 left({omega }_0t+varphi right)left(7right). }]
Полная механическая энергия консервативной колебательной системы
Так как пружинный маятник мы считаем консервативной системой, то механическая энергия ее постоянна:
[E=E_k+E_p=const left(8right).]
Проверим справедливость выражения (8),) непосредственным суммированием правых частей выражений (4) и (7): (учитывая (5))
[E=frac{m}{2}A^2{{omega }_0}^2{{sin}^2 left({omega }_0t+varphi right)+ }{frac{kx^2}{2} =frac{m}{2}A^2frac{k}{m}{{sin}^2 left({omega }_0t+varphi right)+frac{k}{2}A^2 }{cos}^2left({omega }_0t+varphi right)=frac{k}{2}A^2=frac{1}{2}m{omega }^2_0A^2(9) },]
где ${{omega }_0}^2=frac{k}{m}$. Формула (9) показывает, что постоянная полная энергия колебательной системы равна потенциальной ее энергии в точках максимального отклонения от положения равновесия (при $x=pm A$). Энергия $E$ равна кинетической энергии при прохождении грузом положения равновесия, скорость груза равна:
[v_x=pm {omega }_0Aleft(10right).]
В ходе взаимных превращений потенциальная и кинетическая энергии гармонически колеблются с одинаковой амплитудой, равной $frac{E}{2}$ в противофазе друг с другом, частота их колебаний равна $2{omega }_0$.
[{E_k =frac{E}{2}left[1-{cos 2({omega }_0t+varphi ) }right]left(11right). }]
[E_p=frac{E}{2}left[1+{cos 2({omega }_0t+varphi ) }right]left(12right).]
Примеры задач на энергию гармонических колебаний
Пример 1
Задание. Что собой представляет фазовая траектория пружинного маятника, при рассмотрении его как гармонического осциллятора?
Решение. Уравнение фазовой траектории — это уравнение закона сохранения энергии:
[frac{kx^2}{2}+frac{mv^2_x}{2}=E=const left(1.1right).]
Разделим обе части выражения (1.1) на $E$ получим:
[frac{x^2}{2{E}/{k}}+frac{v^2_x}{2{E}/{m}}=1left(1.2right).]
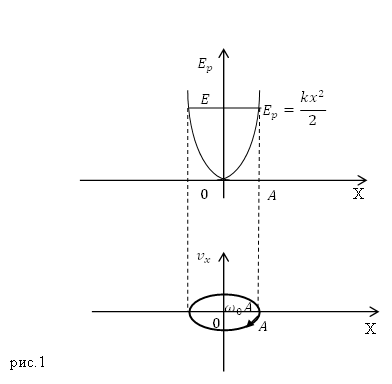
Выражение (1.2) — это уравнение эллипса, полуоси которого равны $sqrt{2{E}/{k}}$ и $sqrt{2{E}/{m}}$.
Фазовую траекторию часто сопоставляют с графиком потенциальной энергии осциллятора. При этом в верхней части рисунка (рис.1) изображают график потенциальной энергии ($E_p(x)$), в нижней части изображают фазовую траекторию, которая соответствует колебаниям со значением полной энергии равной E, указанной на верхнем графике.
Пример 2
Задание. Материальная точка, имеющая массу $m=5cdot {10}^{-2}кг,$ совершает колебания в соответствии с законом: $xleft(tright)={cos (frac{3pi }{2}t)(м) }$. Какова полная энергия этой точки?
Решение. Полная энергия в консервативной колебательной системе величина постоянная и найти ее можно в соответствии с выражением:
[E=frac{1}{2}m{omega }^2_0A^2 left(2.1right).]
Рассматривая уравнение колебаний точки, данное в условии задачи:
[xleft(tright)={cos (frac{3pi }{2}t)(м) },]
имеем: $A=1 м; {omega }_0=frac{3pi }{2}$. Вычислим искомую энергию:
[E=frac{1}{2}cdot 5cdot {10}^{-2}cdot {left(frac{3pi }{2}right)}^21^2approx 0,56 left(Джright).]
Ответ. $E=0,56$ Дж
Читать дальше: гидравлический пресс.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!