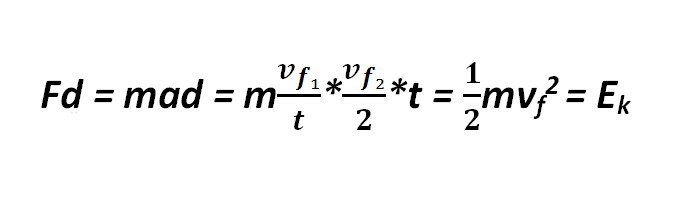Кинетическая энергия вещества

4.4
Средняя оценка: 4.4
Всего получено оценок: 268.
4.4
Средняя оценка: 4.4
Всего получено оценок: 268.
Любое физическое тело представляет собой набор веществ (одного или нескольких), которые состоят из молекул и атомов. Если тело как целое находится в состоянии покоя, то это не значит, что молекулы вещества “замерли” и не двигаются. Такая ситуация возможна только, если температура тела станет равна абсолютному нулю, то есть Tтела = 00К, а при любой температуре, больше нуля, частицы вещества непрерывно, хаотически двигаются с различными скоростями, поэтому полная кинетическая энергия вещества равна сумме кинетических энергий всех частиц.
Чему равна энергия движущейся частицы
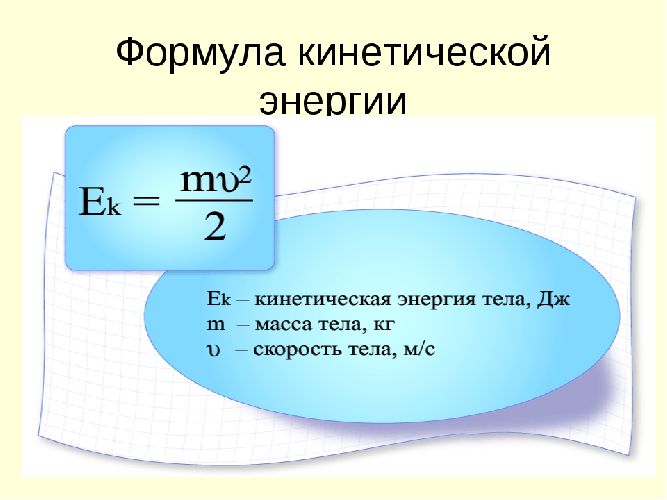
В разделе механики была получена формула для кинетической энергии Ек движущегося со скоростью v тела массой m. Эта формула универсальна и справедлива не только для тел макроскопических размеров, но и для микрочастиц (молекул, атомов, электронов и т.п.):
$ Ек = {m * v^2over 2} $ (1),
Для того чтобы узнать полную кинетическую энергию вещества Епк, необходимо сложить энергии всех частиц:
$ Е^п_к = Е_1+ Е_2 + Е_3 +…. Е_N $ (2),
где N — полное число частиц в веществе.
Понятно, что для вычисления кинетической энергии всего вещества по формуле (2) необходимо знать скорости всех частиц, их массы и общее количество. Но это в принципе нереально хотя бы потому, что в одном моле вещества находится гигантское количество молекул — 6,023*1023 !
Эксперименты показывали, что чем сильнее нагрето вещество, тем быстрее (“энергичнее”) двигаются частицы. Например, исследователи могли это видеть, наблюдая броуновское движение в микроскоп. После изобретения итальянским ученым Галилео Галилеем (1564-1642 г.г.) термометра у физиков появилась возможность проводить измерения величины, названной температурой, которая показывала степень теплового состояния вещества.
Общая кинетическая энергия непрерывного хаотического движения всех частиц входит в состав внутренней энергии вещества, которая кроме кинетической включает в себя:
- Потенциальную энергию частиц, вызванную силами межмолекулярного взаимодействия;
- Энергию электронов в атомах;
- Ядерную энергию.
Что же такое температура?
В молекулярно-кинетической теории теплота рассматривается как одна из форм энергии, а именно — кинетическая энергия атомов и молекул. Чем “горячее” тело, тем с большей скоростью двигаются молекулы вещества и, значит, больше становится их кинетическая энергия. Эта величина, будучи усредненной по всему числу беспорядочно движущихся частиц, и есть температура тела (вещества).
Вместо того, чтобы пытаться вычислить энергию по формуле (2), физиками были получены математические формулы, связавшие кинетическую энергию Епк вещества и температуру T. Использование понятия температуры, которое распространяется на все вещества — газообразные, жидкие и твердые, позволило решить задачу по определению энергии Епк.
Как перейти от температуры к энергии
Для измерения энергии в Международной системе СИ используется единица измерения джоуль (Дж), а температура, как известно, измеряется в градусах. Как количественно связаны эти величины? На примере одноатомного идеального газа попробуем получить формулу, связывающую эти величины.
Напомним, что температура в системе СИ измеряется в градусах Кельвина. Связь температуры в градусах Кельвина и температуры в единицах энергии (Дж) выражается формулой:
$ θ = k * T $ (3),
где: k =1,38*10-23 Дж/К — постоянная Больцмана.
Для идеального газа справедлив закон Клапейрона-Менделеева, выражаемый в виде уравнения состояния:
$ p * V = {mover μ} * R * T $ (4),
где:
p, m и V — давление, масса и объем газа, μ — молярная масса газа,T — температура в градусах по шкале Кельвина, R = 8,3157 джоуль/моль/градус — универсальная газовая постоянная.
В то же время газовая постоянная R равна:
$ R = k * N_a $ (5),
где: k — постоянная Больцмана, Na = 6,023*1023 — число Авогадро, количество молекул в одном моле вещества. Тогда, подставив в уравнение (4) R из уравнения (5), разделив обе части уравнения (4) на объем V и воспользовавшись тем, что:
$ {mover μ} * {Naover V } = n $ — концентрация молекул, получим из формулы (4) выражение для давления в виде:
$ p = n * k * T $ (6).
Для давления одноатомного идеального газа воспользуемся выражением:
$ p = {1over 3} * n * m * v^2_c $ (7),
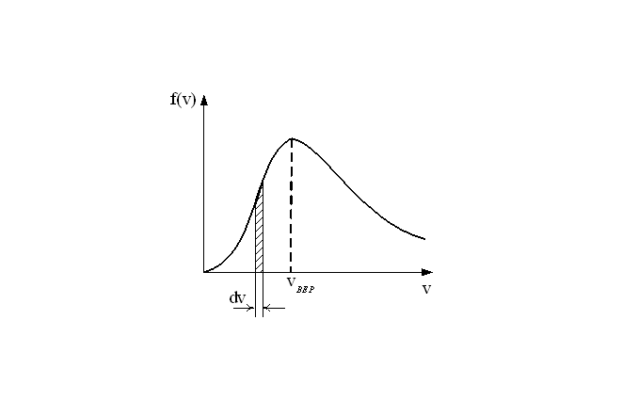
где: v2c — средний квадрат скорости по всем группам молекул. Напомним, что молекулы в газе двигаются с разными скорости. Распределение по скоростям, то есть количество молекул с определенной скоростью, имеет колоколообразный вид, и впервые было получено английским физиком Максвеллом.
Из формул (6), (7) и выражения (1) для кинетической энергии Ек, получим:
$ Ек = { 3 over 2} * k * T $ (8).
Уравнение (8) устанавливает однозначную связь между средней кинетической энергией вещества и его абсолютной температурой.
Если газ будет не одноатомный, то часть энергии уйдет на колебания атомов внутри молекул и на вращение самих молекул. Колебания и вращения тоже обусловлены движением частицы, но выражения для этих составляющих энергии будут несколько иные. Формулы (1) и (7) получены в предположении, что одноатомные частицы двигаются только поступательно.
Что мы узнали?
Итак, мы узнали что кинетическая энергия веществ, представляет собой сумму кинетических энергий всех частиц вещества. Кинетическая энергия движения частиц, усредненная по их числу, определяет температуру вещества. Приведена формула, связывающая среднюю кинетическую энергию вещества с температурой.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.4
Средняя оценка: 4.4
Всего получено оценок: 268.
А какая ваша оценка?
Как найти среднюю кинетическую энергию молекул
Молекула является объектом микромира. Поэтому непосредственное измерение ее кинетической энергии невозможно. Средняя кинетическая энергия является статистическим понятием. Это усредненное значение кинетических энергий всех молекул, входящих в вещество.
Вам понадобится
- — периодическая таблица химических элементов;
- — термометр;
- — калькулятор.
Инструкция
Найдите среднюю кинетическую энергию, используя значение средней скорости молекул вещества. Рассчитайте массу одной молекулы вещества. Для этого определите его молярную массу в килограммах на моль при помощи периодической таблицы химических элементов. Для этого найдите относительные атомные массы всех элементов, входящих в состав молекулы вещества. Они указаны в соответствующих ячейках таблицы. Сложите их, и получите относительную молекулярную массу молекулы. Поделите это число на 1000 и получите молярную массу вещества в килограммах на моль.
Поделите молярную массу на число Авогадро (NA=6,022∙10^23 1/моль) и получите массу одной молекулы вещества m0 в килограммах. Посчитайте среднюю кинетическую энергию молекул, умножив массу одной молекулы m0 на квадрат ее скорости v, а результат поделите на 2 (Ek=m0∙v²/2).
Пример. Рассчитайте среднюю кинетическую скорость молекул азота, если их средняя скорость равна 100 м/с. Молярная масса двухатомной молекулы азота равна 0,028 кг/моль. Найдите массу одной молекулы 0,028/(6,022∙10^23)≈4,6∙10^(-25) кг. Определите среднюю кинетическую энергию молекул Ek= 4,6∙10^(-25)∙100²/2=2,3∙10^(-21) Дж.
Найдите среднюю кинетическую энергию молекул газа через значение температуры. Измерьте эту величину термометром. Если прибор измеряет в градусах Цельсия, переведите значение температуры в Кельвины по абсолютной шкале. Для этого к значению температуры в градусах Цельсия прибавьте число 273. Например, если температура газа 23ºС, то по абсолютной шкале его температура будет равна Т=23+273=296 К.
Определите степень свободы молекулы i. Эта величина для одноатомной молекулы равна 3. Для двухатомной частицы – 5, трехатомной и более – 6. Рассчитайте среднюю кинетическую энергию, умножив степень свободы молекулы на абсолютную температуру газа и постоянную Больцмана (k=1,38∙10^(-23)). Результат поделите на число 2 (Ek=i∙k∙T/2).
Пример. Найдите среднюю кинетическую энергию молекул двухатомного газа при температуре 85ºС. Определите температуру газа по абсолютной шкале Т=85+273=358К. Степень свободы двухатомной молекулы i=5. Произведите расчет Ek=5∙1,38∙10^(-23)∙358/2≈1,24∙10^(-20) Дж.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Виктор Матвеевич Скоков
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Количество независимых переменных, которыми определяется состояние системы, называют числом степеней свободы. Для полной характеристики энергетического состояния движения материальной точки в момент времени t требуется задать три компоненты скорости для того, чтобы определить кинетическую энергию и три координаты, чтобы определить потенциальную энергию, получается всего необходимо шесть переменных. В случае динамического рассмотрения движения материальной точки эти переменные являются зависимыми. Статистическая система, которая состоит из n точек, имеет 6n степеней свободы. Из них 3n степеней свободы — носители кинетической энергии и 3n — носители потенциальной энергии, если система находится в поле внешних сил или частицы взаимодействуют между собой.
Степени свободы
Степени свободы делят на: поступательные, вращательные и колебательные. Три степени свободы материальной точки — поступательные. Система из n материальных точек, между которыми нет жестких связей имеет 3 n степени свободы. Каждая жесткая связь уменьшает число степеней свободы на единицу. Рассмотрим молекулу, состоящую из двух атомов, если считать, что между атомами существует одна жесткая связь, то такая молекула имеет пять степеней свободы, три поступательные и две вращательные. Если связь квазиупругая, то степеней свободы будет шесть, причем из них три поступательные, две вращательные и одна колебательная. Трехатомной нелинейной молекуле с жесткой связью между атомами нужно приписать шесть степеней свободы — три поступательные, три вращательные. Поступательные степен свободы не имеют преимуществ друг перед другом.
Средняя энергия молекулы
Согласно закону равномерного распределения энергии по степеням свободы на каждую степень свободы в среднем приходится одинаковая кинетическая энергия равная $leftlangle {varepsilon }_irightrangle =frac{1}{2}kT$. В таком случае можно сказать, что средняя энергия молекулы $leftlangle {varepsilon } rightrangle$ равна:
где $i=m_{post}+m_{vr}+2m_{kol}$- сумма числа поступательных, вращательных и удвоенного количества колебательных степеней свободы, $k$ — постоянная Больцмана, T- термодинамическая температура. Возникновение коэффициента 2 при подсчёте энергии колебаний объясняется просто: При колебаниях частица имеет как кинетическую, так и потенциальную энергии. Если колебания гармонические, то эти энергии в среднем равны друг другу. Соответственно, $leftlangle {varepsilon }_{kol}rightrangle =kT$.
Закон равномерного распределения энергии по степеням свободы является приближенным, так как получен на основе классической механики и нарушается, если существенными становятся квантовые эффекты.
«Энергия молекул» 👇
Необходимо отметить, что поступательно могут двигаться только молекулы газов.
Из(1) следует, что одноатомные молекулы имеют среднюю кинетическую энергию:
Полную энергию i частицы можно представить:
[{varepsilon }_i=frac{1}{2}m_i{v_i}^2+frac{1}{2}left(J_{i1}{w_{i1}}^2+J_{i2}{w_{i2}}^2+J_{i3}{w_{i3}}^2right)+sumlimits_j{frac{m_{ij}{{eta }_{ij}}^2}{2}}+sumlimits_j{frac{k_{ij}{{xi }_{ij}}^2}{2}}+U_ileft(x_i,y_i,z_iright) left(3right),]
где $U_ileft(x_i,y_i,z_iright)$- потенциальная энергия сложной частицы во внешних полях, ${xi }_{ij}$- отклонение от положения равновесия частицы при колебаниях, ${eta }_{ij}$- скорость колебательных движений частицы, первый индекс обозначает номер сложной частицы, второй определяет номер частицы внутри сложной, $v_i$ — скорость центра масс сложной частицы, $m_i$- масс частицы, $J_1,J_2,J_3$- моменты инерции вращения частицы, $w_1,w_2,w_3$ — угловые скорости вращения частицы относительно ее главных осей. Индекс j принимает столько значений, сколько необходимо, чтобы исчерпать все степени свободы сложной частицы.
Пример 1
Задание: Сравните средние энергии молекул кислорода и азота при одинаковых температурах.
Решение:
Кислород имеет двухатомную молекулу ($O_2)$, предположим, что связь между атомами жесткая, следовательно, молекула кислорода обладает пятью степенями свободы (тремя поступательными и двумя вращательными). Из закона равномерного распределения энергии по степеням свободы имеем средняя энергия молекулы:
[leftlangle varepsilon rightrangle =frac{i}{2}kTto leftlangle {varepsilon }_{O_2}rightrangle =frac{5}{2}kT left(1.1right)]
Азот имеет двухатомную молекулу ($N_2)$, предположим, что связь между атомами жесткая, следовательно, молекула азота также обладает пятью степенями свободы. Соответственно:
[leftlangle {varepsilon }_{N_2}rightrangle =frac{5}{2}kTleft(1.2right).]
Ответ: Средние энергии молекул кислорода и азота при одинаковых температурах одинаковы.
Пример 2
Задание: Водород находится в сосуде при температуре T=300K. Определите среднюю энергию вращательного движения молекул.
Решение:
Основой для решения задачи является закон равномерного распределения энергии по степеням свободы. Из него известно, что на каждую степень свободы приходится в среднем энергия $leftlangle {varepsilon }_irightrangle $, равная:
[leftlangle {varepsilon }_irightrangle =frac{1}{2}kT left(2.1right).]
Следовательно, чтобы решить задачу, осталось определить, сколько вращательных степеней свободы имеет молекула водорода. Для этого вспомним химическую формулу водорода:
[H_2.]
В молекуле имеется два атома, если молекула жесткая, то общее число степеней свободы такой молекулы будет равно пяти. Из них три приходятся на поступательные степени свободы, на вращательные степени свободы остается две степени. Соответственно:
[leftlangle {varepsilon }_{vr}rightrangle =frac{2}{2}kT=kTleft(2.2right)]
Проведем расчет:
[leftlangle {varepsilon }_{vr}rightrangle =1,38cdot {10}^{-23}cdot 300=4,14cdot {10}^{-21}(Дж)]
Ответ: Средняя энергия вращательного движения молекул водорода при заданных условиях равна $4,14cdot {10}^{-21}Дж$.
Пример 3
Задание: Чему равна суммарная средняя кинетическая энергия молекул двухатомного газа, заключенного в объеме 4 л при давлении 1,47 $cdot {10}^5$Па? Молекулы считать жесткими.
Решение:
Жесткие двухатомные молекулы имеют пять степеней свободы. Средняя энергия движения молекулы определяет формула:
[leftlangle varepsilon rightrangle =frac{i}{2}kTto leftlangle varepsilon rightrangle =frac{5}{2}kTleft(3.1right).]
Следовательно кинетическая энергия всех N молекул газа может быть найдена, как:
[leftlangle Erightrangle =frac{5}{2}NkT left(3.2right).]
Из уравнения состояния идеального газа:
[p=nkT, где n=frac{N}{V}to pV=NkTleft(3.3right).]
Подставим в (3.2) уравнение из (3.3), получим:
[leftlangle Erightrangle =frac{5}{2}pV left(3.4right).]
Переведем данные в СИ: V=4 л=4$cdot {10}^{-3}м^3$
Проведем расчет:
[leftlangle Erightrangle =frac{5}{2}1,47 cdot {10}^5cdot 4cdot {10}^{-3}=1470 (Дж)]
Ответ: Суммарная средняя кинетическая энергия молекул двухатомного газа при заданных условиях равна $1470 Дж.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
В природе существует три агрегатных состояния вещества. Об этом мы уже знаем с прошлых шагов 🙃
Наиболее простым для изучения в термодинамике является газ. Его и рассмотрим на примере идеального газа.
Чтобы найти среднюю кинетическую энергию N молекул, находим среднее арифметическое их кинетических энергий.
🚀 Если смешать газы, находящиеся в двух сосудах, через какое-то время установится состояние теплового равновесия. При установлении теплового равновесия между двумя газами, происходит обмен энергией, и средние кинетические энергии частиц газов становятся равны. Но при этом будет равна и температура газов, так как она характеризует интенсивность движения частиц газа.
Можно сделать вывод, что температура является мерой средней кинетической энергии молекул.
Связь между температурой и кинетической энергией устанавливает формула на картинке 👇
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Повседневный опыт показывает, что недвижимые тела можно привести в движение, а движимые остановить. Мы с вами постоянно что-то делаем, мир вокруг суетится, светит солнце… Но откуда у человека, животных, да и у природы в целом берутся силы для выполнения этой работы? Исчезает ли механическое движение бесследно? Начнет ли двигаться одно тело без изменения движения другого? Обо всем этом мы расскажем в нашей статье.
Понятие энергии
Для работы двигателей, которые придают движение автомобилям, тракторам, тепловозам, самолетам, нужно топливо, которое является источником энергии. Электродвигатели придают движение станкам при помощи электроэнергии. За счет энергии воды, падающей с высоты, оборачиваются гидротурбины, соединенные с электрическими машинами, производящими электрический ток. Человеку для того, чтобы существовать и работать, также нужна энергия. Говорят, что для того, дабы выполнять какую-нибудь работу, необходима энергия. Что же такое энергия?
- Наблюдение 1. Поднимем над землей мяч. Пока он пребывает в состоянии спокойствия, механическая работа не выполняется. Отпустим его. Под действием силы тяжести мяч падает на землю с определенной высоты. Во время падения мяча выполняется механическая работа.
- Наблюдение 2. Сомкнем пружину, зафиксируем ее нитью и поставим на пружину гирьку. Подожжем нить, пружина распрямится и поднимет гирьку на некую высоту. Пружина выполнила механическую работу.
- Наблюдение 3. На тележку закрепим стержень с блоком в конце. Через блок перекинем нить, один конец которой намотан на ось тележки, а на другом висит грузик. Отпустим грузик. Под действием силы тяжести он будет опускаться книзу и придаст тележке движение. Грузик выполнил механическую работу.
После анализа всех вышеперечисленных наблюдений можно сделать вывод, что если тело или несколько тел во время взаимодействия выполняют механическую работу, то говорят, что они имеют механическую энергию, либо энергию.
Понятие энергии
Энергия (от греч. слова энергия — деятельность) — это физическая величина, которая характеризирует способность тел выполнять работу. Единицей энергии, а также и работы в системе СИ является один Джоуль (1 Дж). На письме энергия обозначается буквой Е. Из вышеуказанных экспериментов видно, что тело выполняет работу тогда, когда переходит из одного состояния в другое. Энергия тела при этом меняется (уменьшается), а выполненная телом механическая работа равна результату изменения ее механической энергии.
Виды механической энергии. Понятие потенциальной энергии
Различают 2 вида механической энергии: потенциальную и кинетическую. Сейчас подробнее рассмотрим потенциальную энергию.
Потенциальная энергия (ПЭ) — это энергия, определяющаяся взаимным положением тел, которые взаимодействуют, либо частями того самого тела. Поскольку любое тело и земля притягивают друг друга, то есть взаимодействуют, ПЭ тела, поднятого над землей, будет зависеть от высоты поднятия h. Чем выше поднято тело, тем больше его ПЭ. Экспериментально установлено, что ПЭ зависит не только от высоты, на которую оно поднято, но и от массы тела. Если тела были подняты на одинаковую высоту, то тело, имеющее большую массу, будет иметь и большую ПЭ. Формула данной энергии выглядит следующим образом: Eп = mgh, где Eп — это потенциальна энергия, m — масса тела, g = 9,81 Н/кг, h — высота.
Потенциальная энергия пружины
Потенциальной энергией упруго деформированного тела называют физическую величину Eп, которая при изменении скорости поступательного движения под действием сил упругости уменьшается ровно на столько, на сколько растет кинетическая энергия. Пружины (как и другие упруго деформированные тела) имеют такую ПЭ, которая равна половине произведения их жесткости k на квадрат деформации: x = kx2: 2.
Энергия кинетическая: формула и определение
Иногда значение механической работы можно рассматривать без употребления понятий силы и перемещения, акцентировав внимание на том, что работа характеризует изменение энергии тела. Все, что нам может потребоваться, — это масса некоего тела и его начальная и конечная скорости, что приведет нас к кинетической энергии. Кинетическая энергия (КЭ) — это энергия, принадлежащая телу вследствие собственного движения.
Кинетическую энергию имеет ветер, ее используют для придания движения ветряным двигателям. Движимые массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и заставляют их оборачиваться. Вращательное движение при помощи систем передач передается механизмам, выполняющим определенную работу. Движимая вода, оборачивающая турбины электростанции, теряет часть своей КЭ, выполняя работу. Летящий высоко в небе самолет, помимо ПЭ, имеет КЭ. Если тело пребывает в состоянии покоя, то есть его скорость относительно Земли равна нулю, то и его КЭ относительно Земли равна нулю. Экспериментально установлено, что чем больше масса тела и скорость, с которой оно движется, тем больше его КЭ. Формула кинетической энергии поступательного движения в математическом выражении следующая:
Где К — кинетическая энергия, m — масса тела, v — скорость.
Изменение кинетической энергии
Поскольку скорость движения тела является величиной, зависящей от выбора системы отсчета, значение КЭ тела также зависит от ее выбора. Изменение кинетической энергии (ИКЭ) тела происходит вследствие действия на тело внешней силы F. Физическую величину А, которая равна ИКЭ ΔЕк тела вследствие действия на него силы F, называют работой: А = ΔЕк. Если на тело, которое движется со скоростью v1, действует сила F, совпадающая с направлением, то скорость движения тела вырастет за промежуток времени t к некоторому значению v2. При этом ИКЭ равно:
Где m — масса тела; d — пройденный путь тела; Vf1 = (V2 — V1); Vf2 = (V2 + V1); a = F : m. Именно по этой формуле высчитывается, на сколько изменяется энергия кинетическая. Формула также может иметь следующую интерпретацию: ΔЕк = Flcosά, где cosά является углом между векторами силы F и скорости V.
Средняя кинетическая энергия
Кинетическая энергия представляет собой энергию, определяемую скоростью движения разных точек, которые принадлежат этой системе. Однако следует помнить, что необходимо различать 2 энергии, характеризующие разные виды движения: поступательное и вращательное. Средняя кинетическая энергия (СКЭ) при этом является средней разностью между совокупностью энергий всей системы и ее энергией спокойствия, то есть, по сути, ее величина — это средняя величина потенциальной энергии. Формула средней кинетической энергии следующая:
где k — это константа Больцмана; Т — температура. Именно это уравнение является основой молекулярно-кинетической теории.
Средняя кинетическая энергия молекул газа
Многочисленными опытами было установлено, что средняя кинетическая энергия молекул газа в поступательном движении при заданной температуре одна и та же, и не зависит от рода газа. Кроме того, было установлено также, что при нагревании газа на 1 оС СКЭ увеличивается на одно и то же самое значение. Сказать точнее, это значение равно: ΔЕк = 2,07 х 10-23Дж/оС. Для того чтобы вычислить, чему равна средняя кинетическая энергия молекул газа в поступательном движении, необходимо, помимо этой относительной величины, знать еще хотя бы одно абсолютное значение энергии поступательного движения. В физике достаточно точно определены эти значения для широкого спектра температур. К примеру, при температуре t = 500 оС кинетическая энергия поступательного движения молекулы Ек = 1600 х 10-23Дж. Зная 2 величины (ΔЕк и Ек), мы можем как вычислить энергию поступательного движения молекул при заданной температуре, так и решить обратную задачу — определить температуру по заданным значениям энергии.
Напоследок можно сделать вывод, что средняя кинетическая энергия молекул, формула которой приведена выше, зависит только от абсолютной температуры (причем для любого агрегатного состояния веществ).
Закон сохранения полной механической энергии
Изучение движения тел под действием силы тяжести и сил упругости показало, что существует некая физическая величина, которую называют потенциальной энергией Еп; она зависит от координат тела, а ее изменение приравнивается ИКЭ, которая взята с противоположным знаком: ΔЕп = —ΔЕк. Итак, сумма изменений КЭ и ПЭ тела, которые взаимодействуют с гравитационными силами и силами упругости, равна 0: ΔЕп + ΔЕк = 0. Силы, которые зависят только от координат тела, называют консервативными. Силы притяжения и упругости являются консервативными силами. Сумма кинетической и потенциальной энергий тела является полной механической энергией: Еп + Ек = Е.
Этот факт, который был доказан наиболее точными экспериментами,
называют законом сохранения механической энергии. Если тела взаимодействуют силами, которые зависят от скорости относительного движения, механическая энергия в системе взаимодействующих тел не сохраняется. Примером сил такого типа, которые называются неконсервативными, являются силы трения. Если на тело действуют силы трения, то для их преодоления необходимо затратить энергию, то есть ее часть используется на выполнение работы против сил трения. Однако нарушение закона сохранения энергии здесь только мнимое, потому что он является отдельным случаем общего закона сохранения и преобразования энергии. Энергия тел никогда не исчезает и не появляется вновь: она лишь преобразуется из одного вида в другой. Этот закон природы очень важен, он выполняется повсюду. Его еще иногда называют общим законом сохранения и преобразования энергии.
Связь между внутренней энергией тела, кинетической и потенциальной энергиями
Внутренняя энергия (U) тела — это его полная энергия тела за вычетом КЭ тела как целого и его ПЭ во внешнем поле сил. Из этого можно сделать вывод, что внутренняя энергия состоит из КЭ хаотического движения молекул, ПЭ взаимодействия между ними и внутремолекулярной энергии. Внутренняя энергия — это однозначная функция состояния системы, что говорит о следующем: если система находится в данном состоянии, ее внутренняя энергия принимает присущие ему значения, независимо от того, что происходило ранее.
Релятивизм
Когда скорость тела близка к скорости света, кинетическую энергию находят по следующей формуле:
Кинетическая энергия тела, формула которой была написана выше, может также рассчитываться по такому принципу:
Примеры задач по нахождению кинетической энергии
1. Сравните кинетическую энергию шарика массой 9 г, летящего со скоростью 300 м/с, и человека массой 60 кг, бегущего со скоростью 18 км/час.
Итак, что нам дано: m1 = 0,009 кг; V1 = 300 м/с; m2 = 60 кг, V2 = 5 м/с.
Решение:
- Энергия кинетическая (формула): Ек = mv2 : 2.
- Имеем все данные для расчета, а поэтому найдем Ек и для человека, и для шарика.
- Ек1 = (0,009 кг х (300 м/с)2) : 2 = 405 Дж;
- Ек2 = (60 кг х (5 м/с)2) : 2= 750 Дж.
- Ек1 < Ек2.
Ответ: кинетическая энергия шарика меньше, чем человека.
2. Тело с массой 10 кг было поднято на высоту 10 м, после чего его отпустили. Какую КЭ оно будет иметь на высоте 5 м? Сопротивлением воздуха разрешается пренебречь.
Итак, что нам дано: m = 10 кг; h = 10 м; h1 = 5 м; g = 9,81 Н/кг. Ек1 — ?
Решение:
- Тело определенной массы, поднятое на некую высоту, имеет потенциальную энергию: Eп = mgh. Если тело падает, то оно на некоторой высоте h1 будет иметь пот. энергию Eп = mgh1 и кин. энергию Ек1. Чтобы была правильно найдена энергия кинетическая, формула, которая была приведена выше, не поможет, а поэтому решим задачу по нижеследующему алгоритму.
- В этом шаге используем закон сохранения энергии и запишем: Еп1 + Ек1 = Еп.
- Тогда Ек1 = Еп — Еп1 = mgh — mgh1 = mg(h-h1).
- Подставив наши значения в формулу, получим: Ек1 = 10 х 9,81(10-5) = 490,5 Дж.
Ответ: Ек1 = 490,5 Дж.
3. Маховик, имеющий массу m и радиус R, оборачивается вокруг оси, проходящей через его центр. Угловая скорость оборачивания маховика — ω. Дабы остановить маховик, к его ободу прижимают тормозную колодку, действующей на него с силой Fтрения. Сколько оборотов сделает маховик до полной остановки? Учесть, что масса маховика сосредоточена по ободу.
Итак, что нам дано: m; R; ω; Fтрения. N — ?
Решение:
- При решении задачи будем считать обороты маховика подобными оборотам тонкого однородного обруча с радиусом R и массой m, который оборачивается с угловой скоростью ω.
- Кинетическая энергия такого тела равна: Ек = (Jω2) : 2, где J = mR2.
- Маховик остановится при условии, что вся его КЭ истратится на работу по преодолению силы трения Fтрения, возникающей между тормозной колодкой и ободом: Ек = Fтрения*s, где s — это тормозной путь, который равен 2πRN.
- Следовательно, Fтрения*2πRN = (mR2ω2) : 2, откуда N = (mω2R) : (4πFтр).
Ответ: N = (mω2R) : (4πFтр).
В заключение
Энергия — это важнейшая составляющая во всех аспектах жизни, ведь без нее никакие тела не смогли бы выполнять работу, в том числе и человек. Думаем, статья вам внятно дала понять, что собой представляет энергия, а развернутое изложение всех аспектов одной из ее составляющих — кинетической энергии — поможет вам осознать многие процессы, происходящих на нашей планете. А уж о том, как найти кинетическую энергию, вы можете узнать из приведенных выше формул и примеров решения задач.