Алексей Алексеевич Ивахно
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Колебания — это самая общая форма движения динамических систем около положения равновесия. При малых отклонениях от положения равновесия колебания обычно являются гармоническими. В этом заключается их особенная значимость.
Уравнение вида:
$frac{d^2x}{dt^2}+omega^2x=0 (1),$
где $omega^2$ — циклическая частота колебаний; $x$ -расстояние положения равновесия
называют уравнением механических гармонических колебания. Колебания происходят вдоль оси $X$.
Решением уравнения (1) можно считать функции:
$x=Asin (omega t+varphi)$ или
$x=Acos (omega t+varphi_1)$,
где $A$ — амплитуда колебаний.
Систему, которая реализует данные малые колебания, называют линейным или гармоническим осциллятором. Примером гармонического осциллятора может служить
- малое тело, подвешенное на упругую пружину (Пружинный маятник);
- физический маятник (Тело, которое совершает колебания относительно точки (или оси, проходящей через точку тела), не являющейся его центром масс);
- математический маятник; (Малое тело, совершающее колебания на длинном, нерастяжимом, невесомом подвесе).
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 1
Собственными называют колебания системы под воздействием только внутренних сил при отсутствии внешних воздействий.
В полной механической энергии гармонического осциллятора выделяют:
- потенциальную энергию;
- и кинетическую энергию.
Потенциальная энергия
Говорить о потенциальной энергии можно только, если действующие силы потенциальны. Если колебательные движения между двумя точками являются одномерным, то автоматически обеспечивается условие потенциальности и всякую силу, зависящую только от координат, можно считать потенциальной.
Если рассматривается линейный осциллятор, то обычно считают, что потенциальная энергия точки равна нулю в положении равновесия. Считая, что осциллятор заставляет совершать колебания сила упругости;
$F=-kx(2)$
и зная, как связана потенциальная энергия и потенциальная сила, (для одномерного случая: $F=-frac{dU}{dx}$), потенциальную энергию линейного осциллятора определим как:
«Энергия гармонических колебаний» 👇
$U(x)=frac{kx^2}{2}=frac{momega^2x^2}{2}=frac{mA^2omega_0^2}{2}cos^2 (omega t+varphi)= frac{mA^2omega_0^2}{4}(1+cos 2(omega t +varphi)) (3).$
Из формулы (3) видно, что потенциальная энергия при колебаниях изменяется с течением времени, так как изменяется $x$. Частота колебаний потенциальной энергии $2omega$.
Кинетическая энергия.
Кинетическая энергия тела – это энергия движения, она зависит от скорости перемещения материальной точки, задается выражением:
$E_k=frac{mv^2}{2}=frac{mdot{x}^2}{2}=frac{mA^2omega_0^2}{2}sin^2 (omega t+varphi) =frac{mA^2omega_0^2}{4}(1-cos 2(omega t +varphi)) (4).$
Кинетическая энергия является переменной во времени физической величиной. Колебания ее происходят с частотой $2omega$ (эта частота в два раза больше, чем частота колебаний $x$)
Закон сохранения энергии при гармонических колебаниях
Как было отмечено, кинетическая энергия и потенциальная энергия являются переменными во времени величинами, однако, их сумма у гармонического осциллятора, выполняющего свободные колебания, не изменяется:
$frac{mdot{x}^2}{2}+frac{momega^2x^2}{2}=frac{momega^2A^2}{2}=const$.
Полная энергия системы ($E$) не изменяется, поскольку при гармонических колебаниях выполняется закон сохранения механической энергии, так как сила упругости является консервативной.
Закон сохранения энергии позволяет сделать два существенных вывода
Вывод первый. Наибольшая кинетическая энергия осциллятора равна его наибольшей энергии потенциальной энергии.
Данный вывод очевиден, так как потенциальная энергия осциллятора максимальна при смещении точки выполняющей колебания на максимально возможное расстояние, при этом скорость, а соответственно и кинетическая энергия осциллятора равна нулю.
Наибольшую кинетическую энергию колебательная система имеет тогда, когда она проходит положение равновесия ($x=0$), то есть потенциальная энергия равна нулю.
$frac{mV^2}{2}=frac{momega^2A^2}{2}(5),$
где $V$ — максимальная скорость.
Вывод второй. Средняя кинетическая энергия осциллятора равна его средней потенциальной энергии.
Средняя кинетическая энергия.
Пусть параметр $f$ функция времени, тогда средняя ее величина на отрезке времени от $t_1$ до $t_2$ равна:
$f_{sr}=frac{1}{t_2-t_1}int_1^2f(t)dt (6),$
где пределы интегрирования обозначают 1 — время $t_1$; 2 — $t_2$.
Если функцию $f(t)$ изобразить на графике (рис.1), то ее среднее значение будет соответствовать высоте прямоугольника, площадь которого ограничивают функция $f$ и ось $t$ на заданном отрезке времени.
Замечание 1
Площадь под осью $t$ считают отрицательной.
Рисунок 1. График. Автор24 — интернет-биржа студенческих работ
Запишем закон движения осциллятора как:
$x(t)=Acos (omega t+varphi) (7)$,
его скорость равна:
$dot{x}=-Aomegasin (omega t+varphi) (8).$
Выражение для потенциальной энергии представим как:
$U(t) = frac{omega^2A^2}{2}cos^2 (omega t+varphi) (9)$.
Кинетическую энергию представит выражение:
$E_k=frac{omega^2A^2}{2}sin^2 (omega t+varphi) $
Отрезком времени, на котором будем брать среднее, станет период колебаний, вернее одного колебания. Нахождение средних значений кинетической и потенциальной энергии сводят к поиску средних от $cos^2 (omega t+varphi)$ и $sin^2 (omega t+varphi)$:
$(sin^2 (omega t+varphi))_{sr}=frac{1}{T}int_0^T cos^2 (omega t+varphi)dt=frac{1}{T}int_0^Tfrac{1}{2}(1-cos 2(omega t+varphi)dt)=frac{1}{2},$
где $T$ — период колебаний; $omega T=2pi.$
По аналогии получаем:
$sin^2 (omega t+varphi)_sr=frac{1}{2}.$
В результате имеем:
-
средняя по времени потенциальная энергия гармонического колебания за один период равна:
$U_{sr}=frac{momega^2A^2}{4}(10),$
-
средняя по времени кинетическая энергия составила:
$E_{k,sr}=frac{momega^2A^2}{4}(11)$.
Сравнивая (10) и (11) мы видим, что:
$U_{sr}= E_{k,sr}=frac {1}{2}E$,
где $E$ — полная механическая энергия гармонических колебаний.
то есть средняя по времени кинетическая энергия осциллятора равна средней по времени потенциальной энергии.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
тела
совершающего гармонические колебания
Выражение для
потенциальной энергии тела при
гармонических колебаниях следует из
определения потенциальной энергии
или
.
В рассматриваемом случае имеем:
,
а
.
Поэтому
.
Полагая, что в
состоянии равновесия ()
потенциальная энергия тела, совершающего
колебания, равна нулю, имеем:
.
Кинетическая
энергия тела при гармонических колебаниях
определяется скоростью его движения
(
) и определяется величиной:
.
Полная энергия
тела, совершающего гармонические
колебания, равна сумме полученных
выражений для потенциальной и кинетической
энергий:
.
Выражения
представленные выше показывают, что
при колебательном движении кинетическая
энергия преобразуется в потенциальную
и наоборот. При этом полная энергия
колебаний, не зависит от времени
(замкнутая система) и пропорциональна
квадрату амплитуды и квадрату частоты.
3.3. Пружинный, математический, физический и крутильный маятники
Пружинный
маятник
Пружинный
маятник представляет собой систему,
состоящую из пружины и тела, подвешенного
на этой пружине, систему, способную
совершать колебательное движение в
поле действия гравитационных сил или
сил инерции.
Уравнение,
описывающее движение пружинного маятника
в поле тяжести Земли имеет вид (см. рис.
3.1):
Преобразуем
это уравнение к виду:
и,
сделав замену переменных:
,
получим:
.
Как
было показано выше, решением этого
уравнения являются гармонические
колебания
Возвращаясь
к переменной
,
получаем:
или,
с учетом собственной длины пружины
,
имеем:
.
На
рисунке, представленном ниже,
.
Следует отметить,
что в колебательном процессе участвует
не только тело массой,
подвешенное на пружине, но и сама пружина.
Таким образом, возникает вопрос о влиянии
массы пружины ()
на частоту колебаний пружинного маятника.
Заметим, что если тело массой
в полной мере участвует в колебательном
движении, то различные части пружины
имеют различную амплитуду колебаний.
Таким образом, следует ожидать, что в
выражении для частоты колебаний войдет
не вся
,
а только ее часть. Расчеты показывают,
что это действительно так, и в этом
случае выражение для частоты колебаний
пружинного маятника имеет вид:
Математический
маятник
Математический
маятник состоит из подвешенной на
невесомой нерастяжимой нити материальной
точки, которая может совершать
колебательное движение в поле действия
гравитационных сил или в поле действия
сил инерции.
Для того, что бы
реализовать эту модель на практике
должны выполняться следующие условия:
-
размер
тела должен быть много меньше длины
нити
,
-
масса
тела должна быть много больше массы
нити
,
-
происходящее
во время колебаний изменение длины
нити должно быть много меньше длины
самой нити
.
Остановимся на последнем более подробно.
При максимальном
отклонении маятника от состояния
равновесия сила натяжения нити
,
где
— угол максимального отклонения. При
прохождении телом положения равновесия
сила натяжения нити определяется как
силой тяжести, так и центробежной силой
,
где величина центробежной силы может
быть найдена следующим образом. Согласно
закону сохранения энергии запишем
,
откуда
следует:
.
Итак, величина
определяет
значение
,
которое должно быть много меньше
.
Расчет показывает, что это условие
выполняется, когда
.
Из полученного
выражения следует, что подбором амплитуды
колебаний (угла максимального отклонения)
это условие может быть всегда выполнено.
Теперь
рассмотрим движение самого маятника.
Возвращающая сила, действующая вдоль
оси «х» определяется силой натяжения
нити
,
где
,
а
-угол отклонения
.
Воспользуемся законом сохранения
энергии и получим выражение для
центростремительной силы
,
где
соответствует отклонению маятника на
максимальный угол
,
а
.
После
подстановки соответствующих величин
в выражение для
получим:
Если угол отклонения
маятника настолько мал, что
,
то
Сравнивая
это выражение с выражением для силы,
определяющей гармонические колебания,
видим, что частота колебаний математического
маятника
,
а
период колебаний составляет величину:
.
Период
колебаний математического маятника
зависит от его длины и от характеристики
поля, в котором он находится.
Физический
маятник
Физическим
маятником называется твердое тело,
способное совершать колебательное
движение в поле действия гравитационных
сил или сил инерции (см. рис. 3.3).
Ранее было показано,
что законы вращательного движения тела
формально не отличаются от законов
движения материальной точки, с той
разницей, что производится замена
величин
,
,
.
В данном случае
(см. рисунок) момент силы действующий
на физический маятник равен:
.
Если
амплитуда колебаний мала, то и углы
отклонения маятника от состояния
равновесия ()
малы, поэтому
.
В этом случае можем записать:
.
Видим, что
~
и что в рассматриваемом случае роль
коэффициента жесткости играет величина
.
По
аналогии с выражением
можно написать выражение для частоты
колебаний физического маятника в виде:

Замечание.
Если в полученное выражение для частоты
колебания физического маятника подставить
значение момента инерции, соответствующее
материальной точке находящейся на
расстоянии
от точки подвеса (),
то полученное выражение будет
соответствовать частоте колебаний
математического маятника, длиной
.
Сравнивая
формулу для частоты колебаний физического
маятника, с соответствующей формулой
для математического маятника
,
мы видим, что частота колебаний физического
маятника будет равна частоте колебаний
математического, если его длина будет
составлять величину
.
Это,
так называемая, приведенная
длина физического маятника.
Так как
,
где
— момент инерции тела относительно оси,
проходящей через центр инерции
,
выражение для приведенной длины мы
можем записать в виде:
.
Из
этого выражения следует, что периоды
колебаний физического маятника,
подвешенного на параллельных осях,
отстоящих друг от друга на расстояние
равны. В самом деле, отложим на прямой
ОС отрезок
.
Подвесим маятник на ось, проходящую
через точку
.
Тогда приведенная длина будет
,
где
.
Но
.
Подставим это в выражение для
и
получим:

Итак:
приведенные длины, а значит и периоды
(частоты) колебаний физических маятников,
подвешенных на параллельных осях,
отстоящих друг от друга на величину
равную приведенной длине равны.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Введём энергию колебания.
Колебательная система движется со скоростью , тогда его кинетическая энергия должна быть равна:
(1)
- где
Вспомним зависимость скорости от времени при гармоническом колебании:
(2)
- где
Подставим (2) в (1) при условии (для упрощения):
=
(3)
Тогда максимальная кинетическая энергия данной системы:
(4)
т.к. максимальное значение .
С другой стороны для пружинного маятника можем записать потенциальную энергию деформации:
(5)
- где
Вспомним зависимость координаты от времени при гармоническом колебании:
(6)
Подставим (5) в (4) при условии (для упрощения):
=
(7)
Тогда максимальная потенциальная энергия данной системы:
(8)
т.к. максимальное значение .
Вывод: задачи школьной физики чаще всего связаны именно с максимальным значением энергии колебания. Её можно рассчитать и как кинетическую энергию в положении равновесия (4), и как потенциальную энергию в точке максимального отклонения (8).
Энергия гармонических колебаний, теория и онлайн калькуляторы
Энергия гармонических колебаний
Рассмотрим превращения энергии, которые происходят при гармонических колебаниях в консервативной системе на примере пружинного маятника.
Потенциальная энергия гармонических колебаний
В процессе механических колебаниях груза на пружине периодически кинетическая энергия ($E_k$) движущегося груза переходит в потенциальную энергию ($E_p$) колебательной системы, состоящей из потенциальной энергии упругодеформированной пружины и потенциальной энергии груза в поле тяжести Земли. Потенциальная энергия пружины при упругой деформации равна:
[E_{p1}=frac{k{left(x+x_0right)}^2}{2}left(1right),]
где $left(x+x_0right)$ — удлинение пружины; $k$ — жесткость пружины.
Потенциальную энергию груза в поле тяжести ($E_{p2}$) найдем как:
[E_{p2}=-mg x+Cleft(2right),]
где $m$ — масса груза, прикрепленного к пружине.
Постоянную $C,$ будем выбирать так, чтобы в положении равновесия полная потенциальная энергия колебательной системы равнялась:
[frac{kx^2_0}{2}+C=0to C=-frac{kx^2_0}{2} left(3right).]
Тогда потенциальная энергия представлена выражением:
[E_p=E_{p1}+E_{p2}=frac{k{left(x+x_0right)}^2}{2}-mg x-frac{kx^2_0}{2}=frac{kx^2}{2}left(4right).]
Кинетическая энергия пружинного маятника
Кинетическая энергия рассматриваемой колебательной системы состоит из энергии движения груза. Используя уравнение смещения груза пружинного маятника при гармонических колебаниях, происходящих по оси X:
[x=A{cos left({omega }_0t+varphi right)(5) }]
найдем уравнение изменения кинетической энергии груза. Для этого найдем скорость движения груза как:
[v=frac{dx}{dt}=-A{omega }_0{sin left({omega }_0t+varphi right)left(6right). }]
В таком случае кинетическая энергия равна:
[E_k=frac{m}{2}A^2{{omega }_0}^2{{sin}^2 left({omega }_0t+varphi right)left(7right). }]
Полная механическая энергия консервативной колебательной системы
Так как пружинный маятник мы считаем консервативной системой, то механическая энергия ее постоянна:
[E=E_k+E_p=const left(8right).]
Проверим справедливость выражения (8),) непосредственным суммированием правых частей выражений (4) и (7): (учитывая (5))
[E=frac{m}{2}A^2{{omega }_0}^2{{sin}^2 left({omega }_0t+varphi right)+ }{frac{kx^2}{2} =frac{m}{2}A^2frac{k}{m}{{sin}^2 left({omega }_0t+varphi right)+frac{k}{2}A^2 }{cos}^2left({omega }_0t+varphi right)=frac{k}{2}A^2=frac{1}{2}m{omega }^2_0A^2(9) },]
где ${{omega }_0}^2=frac{k}{m}$. Формула (9) показывает, что постоянная полная энергия колебательной системы равна потенциальной ее энергии в точках максимального отклонения от положения равновесия (при $x=pm A$). Энергия $E$ равна кинетической энергии при прохождении грузом положения равновесия, скорость груза равна:
[v_x=pm {omega }_0Aleft(10right).]
В ходе взаимных превращений потенциальная и кинетическая энергии гармонически колеблются с одинаковой амплитудой, равной $frac{E}{2}$ в противофазе друг с другом, частота их колебаний равна $2{omega }_0$.
[{E_k =frac{E}{2}left[1-{cos 2({omega }_0t+varphi ) }right]left(11right). }]
[E_p=frac{E}{2}left[1+{cos 2({omega }_0t+varphi ) }right]left(12right).]
Примеры задач на энергию гармонических колебаний
Пример 1
Задание. Что собой представляет фазовая траектория пружинного маятника, при рассмотрении его как гармонического осциллятора?
Решение. Уравнение фазовой траектории — это уравнение закона сохранения энергии:
[frac{kx^2}{2}+frac{mv^2_x}{2}=E=const left(1.1right).]
Разделим обе части выражения (1.1) на $E$ получим:
[frac{x^2}{2{E}/{k}}+frac{v^2_x}{2{E}/{m}}=1left(1.2right).]
Выражение (1.2) — это уравнение эллипса, полуоси которого равны $sqrt{2{E}/{k}}$ и $sqrt{2{E}/{m}}$.
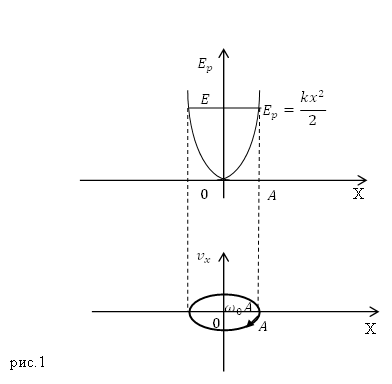
Фазовую траекторию часто сопоставляют с графиком потенциальной энергии осциллятора. При этом в верхней части рисунка (рис.1) изображают график потенциальной энергии ($E_p(x)$), в нижней части изображают фазовую траекторию, которая соответствует колебаниям со значением полной энергии равной E, указанной на верхнем графике.
Пример 2
Задание. Материальная точка, имеющая массу $m=5cdot {10}^{-2}кг,$ совершает колебания в соответствии с законом: $xleft(tright)={cos (frac{3pi }{2}t)(м) }$. Какова полная энергия этой точки?
Решение. Полная энергия в консервативной колебательной системе величина постоянная и найти ее можно в соответствии с выражением:
[E=frac{1}{2}m{omega }^2_0A^2 left(2.1right).]
Рассматривая уравнение колебаний точки, данное в условии задачи:
[xleft(tright)={cos (frac{3pi }{2}t)(м) },]
имеем: $A=1 м; {omega }_0=frac{3pi }{2}$. Вычислим искомую энергию:
[E=frac{1}{2}cdot 5cdot {10}^{-2}cdot {left(frac{3pi }{2}right)}^21^2approx 0,56 left(Джright).]
Ответ. $E=0,56$ Дж
Читать дальше: гидравлический пресс.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Рассмотрим превращения энергии при колебаниях математического маятника.
Выберем систему отсчёта таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
Рис. (1). Схема колебательного движения математического маятника
При колебаниях математического маятника (рис. (1)) изменяется высота (h) грузика относительно положения равновесия и изменяется его скорость (υ).
Причём при максимальных смещениях высота достигает максимального значения
hmax
, а скорость становится равной нулю, в положении равновесия — наоборот: высота тела равна нулю, а скорость достигает максимального значения
vmax
.
Так как высота тела определяет его потенциальную энергию
а скорость — кинетическую энергию
то вместе с изменением высоты и скорости будут изменяться и энергии.
Когда маятник находится в точке, где его смещение от положения равновесия максимально (крайняя левая или крайняя правая точка траектории его движения — точка (A)), то кинетическая энергия маятника равна минимально возможному значению — нулю:
а потенциальная энергия максимальна и равна:
Таким образом, полная механическая энергия маятника в крайних левой и правой точках равна:
Когда маятник находится в какой-либо промежуточной точке между крайней левой или правой точками (точками, где смещение маятника от положения равновесия максимально) и положением равновесия (точка (B)), то его полная механическая энергия (E) равна:
При этом потенциальная и кинетическая энергии принимают некоторые промежуточные значения, большие (0) и меньшие максимального значения:
Когда маятник проходит положение равновесия (точка (O)), то его кинетическая энергия максимальна и равна
а потенциальная энергия принимает нулевое значение
Тогда полная механическая энергия в точке равновесия равна:
Таким образом, можно составить цепочку превращений одного вида энергии в другой при движении математического маятника от крайней левой точки до положения равновесия:
точка (A)
→
точка (B)
→
точка (O),
При движении математического маятника от положения равновесия до крайней правой точки происходит обратное превращение энергии: кинетическая энергия уменьшается от своего максимального значения до нуля, а потенциальная увеличивается от нуля до своего максимального значения.
Обрати внимание!
Полная механическая энергия математического маятника в любой точке траектории его движения постоянна.
Источники:
Рис. 1. Схема колебательного движения математического маятника. . © ЯКласс.