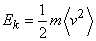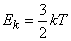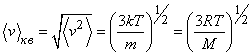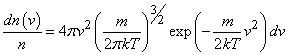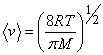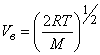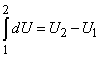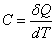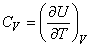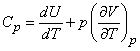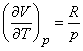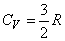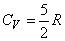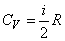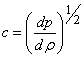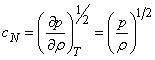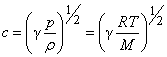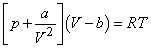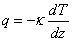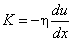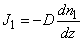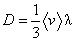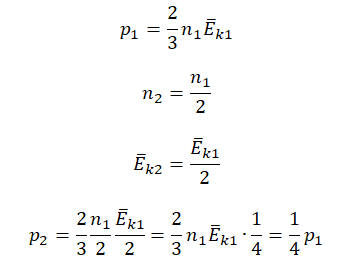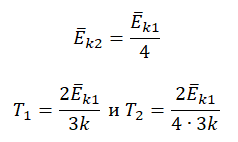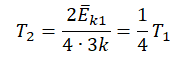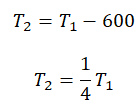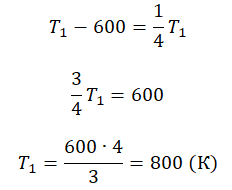Как найти кинетическую энергию теплового движения молекул - Исправление недочетов и поиск решений вместе с Examum.ru

Уравнение состояния идеального газа

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: модель идеального газа, связь между давлением и средней кинетической энергией теплового движения молекул идеального газа, связь температуры газа со средней кинетической энергией его частиц, уравнение , уравнение Менделеева—Клапейрона.

Из трёх агрегатных состояний вещества наиболее простым для изучения является газообразное. В достаточно разреженных газах расстояния между молекулами намного больше размеров самих молекул (тогда как в жидкостях и твёрдых телах молекулы «упакованы» весьма плотно).Поэтому силы взаимодействия между молекулами таких газов очень малы.

Для описания разреженных газов в физике используется модель идеального газа. В рамках этой модели делаются следующие допущения.

1. Пренебрегаем размерами молекул. Иными словами, молекулы газа считаются материальными точками.
2. Пренебрегаем взаимодействием молекул на расстоянии.
3. Соударения молекул друг с другом и со стенками сосуда считаем абсолютно упругими.

Таким образом, идеальный газ — это газ, частицы которого являются не взаимодействующими на расстоянии материальными точками и испытывают абсолютно упругие соударения друг с другом и со стенками сосуда.

Средняя кинетическая энергия частиц газа

Оказывается, что ключевую роль в описании идеального газа играет средняя кинетическая энергия его частиц.

Частицы газа двигаются с разными скоростями. Пусть в газе содержится частиц, скорости которых равны . Масса каждой частицы равна m_0 . Кинетические энергии частиц:

$E_1=frac{displaystyle m_0 v_1^2}{displaystyle 2 vphantom{1^a}}, E_2=frac{displaystyle m_0 v_2^2 }{displaystyle 2 vphantom{1^a}}, ldots,E_N=frac{displaystyle m_0 v_N^2}{displaystyle 2 vphantom{1^a}}.$

Средняя кинетическая энергия частиц газа это среднее арифметическое их кинетических энергий:

$E=frac{displaystyle E_1+E_2+ ldots+E_N}{displaystyle N vphantom{1^a}}= frac{displaystyle 1}{displaystyle N vphantom{1^a}}left ( frac{displaystyle m_0 v_1^2}{displaystyle 2 vphantom{1^a}}+frac{displaystyle m_0 v_2^2}{displaystyle 2 vphantom{1^a}}+ ldots + frac{displaystyle m_0 v_N^2}{displaystyle 2 vphantom{1^a}} right ) =frac{displaystyle m_0}{displaystyle 2 vphantom{1^a}} frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}.$

Последний множитель — это средний квадрат скорости, обозначаемый просто v_2 :

$v_2=frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}.$

Тогда формула для средней кинетической энергии приобретает привычный вид:

$E=frac{displaystyle m_0 v^2}{displaystyle 2 vphantom{1^a}}.$ (1)

Корень из среднего квадрата скорости называется средней квадратической скоростью:

$v=sqrt{ frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}}.$

Основное уравнение МКТ идеального газа

Cвязь между давлением газа и средней кинетической энергией его частиц называется основным уравнением молекулярно-кинетической теории идеального газа. Эта связь выводится из законов механики и имеет вид:

$p= frac{displaystyle 2}{displaystyle 3 vphantom{1^a}} nE.$ (2)

где — концентрация газа (число частиц в единице объёма). С учётом (1) имеем также:

$p= frac{displaystyle 1}{displaystyle 3 vphantom{1^a}} m_0 nv^2.$ (3)

Что такое m_0n ? Произведение массы частицы на число частиц в единице объёма даёт массу единицы объёма, то есть плотность: . Получаем третью разновидность основного уравнения:

$p= frac{displaystyle 1}{displaystyle 3 vphantom{1^a}} rho v^2.$ (4)

Энергия частиц и температура газа

Можно показать, что при установлении теплового равновесия между двумя газами выравниваются средние кинетические энергии их частиц. Но мы знаем, что при этом становятся равны и температуры газов. Следовательно, температура газа — это мера средней кинетической энергии его частиц.

Собственно, ничто не мешает попросту отождествить эти величины и сказать, что температура газа — это средняя кинетическая энергия его молекул. В продвинутых курсах теоретической физики так и поступают. Определённая таким образом температура измеряется в энергетических единицах — джоулях.

Но для практических задач удобнее иметь дело с привычными кельвинами. Связь средней кинетической энергии частиц и абсолютной температуры газа даётся формулой:

$E= frac{displaystyle 3}{displaystyle 2 vphantom{1^a}} kT,$ (5)

где $k=1,38 cdot 10^{-23}$ Дж/К — постоянная Больцмана.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Уравнение состояния идеального газа» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Уравнение состояния идеального газа в форме (p=frac 13nm_0overline {v^2}) или (p=frac 23noverline E) может быть обосновано и методами кинетической теории газов. На основе кинетического подхода сравнительно просто выводится выражение для давления идеального газа в сосуде, которое получается как результат усреднения импульсов молекул, передаваемых стенке сосуда при многочисленных соударениях молекул со стенкой. Величина получаемого при этом давления определяется как

(p=frac 13nmbig (v^2big)),

где (v^2) – среднее значение квадрата скорости молекул, (m) – масса молекулы.

Средняя кинетическая энергия молекул газа (в расчете на одну молекулу) определяется выражением

(E_k=frac 12mbig (v^2big)).

Кинетическая энергия поступательного движения атомов и молекул, усредненная по огромному числу беспорядочно движущихся частиц, является мерилом того, что называется температурой. Если температура T измеряется в градусах Кельвина (К), то связь ее с (E_k) дается соотношением

(E_k=frac 32 kT).

Это соотношение позволяет, в частности, придать более отчетливый физический смысл постоянной Больцмана (k = 1,38·10^{–23}) Дж/K, которая фактически является переводным коэффициентом, определяющим, какая часть джоуля содержится в градусе.

Используя (6) и (7), находим, что (frac 13m v^2 = kT). Подстановка этого соотношения в формулу для энергии приводит к уравнению состояния идеального газа в форме

(p = nkT,) которое уже было получено из уравнения Клапейрона – Менделеева.

Также из уравнений можно определить значение среднеквадратичной скорости молекул:

((v)_{ке}=sqrt{(v^2)}=big (frac {3kT}{m}big )^{frac 12}=big (frac{3RT}Mbig )^{frac 12}).

Расчеты по этой формуле при (T = 273) K дают для молекулярного водорода (v_{кв} = 1838 ) м/с, для азота – (493 ) м/с, для кислорода – (461) м/с и т. д.

Напомним, что газообразное состояние возникает тогда, когда энергия теплового движения молекул вещества превышает энергию их взаимодействия. Молекулы вещества в этом состоянии приобретают прямолинейное поступательное движение, а индивидуальные свойства веществ теряются, и они подчиняются общим для всех газов законам. Газообразные тела не имеют собственной формы и легко изменяют свой объем при воздействии внешних сил или при изменении температуры.

Плотность идеального газа в сосуде – (1,2) кг/м(^3). Если средняя квадратичная скорость молекул газа равна (500) м/с, то газ находится под давлением
Давление кислорода и водорода при одинаковых концентрациях молекул и равных средних квадратичных скоростях их движения находятся в соотношении (М((O_2)) (= 0,032) кг/моль; М((H_2)) (= 0,002) кг/моль)
В вакуумном диоде электроны ускоряются до энергии (140) эВ. Их минимальная скорость у анода лампы равна

(e (= 1,6 ⋅ 10^{-19}) Кл; (m_e) (= 9 ⋅ 10^{-31}) кг; (1) эВ (= 1,6 ⋅ 10^{-19})Дж)
Объем одноатомного газа уменьшили в (2) раза, а среднюю кинетическую энергию молекул увеличили в (3) раза. Определите изменение давления.
Найдите среднюю кинетическую энергию атома аргона, если температура газа равна (117^{circ}C) ((k = 1,38 ⋅ 10^{-23})(frac{Дж}{К})).
Чему равна энергия покоя электрона? ((c = 3 ⋅ 10^8)м/с; (m = 9,1 ⋅ 10^{-31})кг)
Во сколько раз отличаются средние квадратичные скорости молекул диоксида серы и гелия при одинаковой температуре?

(M(_{SO_2}) (= 64 ⋅ 10^{-3})(frac{кг}{моль}); M(_{He}) (= 4 ⋅ 10^{-3})(frac{кг}{моль}))
Во сколько раз изменится среднеквадратичная скорость движения частиц одноатомного идеального газа (υ), если, не меняя его плотности, увеличить давление в (9) раз?
Среднеквадратичная скорость молекул идеального одноатомного газа, заполняющего закрытый сосуд, равна (0,25) км/с. Газ охладили, уменьшив при этом давление на (19%). Как и на сколько изменилась среднеквадратичная скорость молекул этого газа?
Одноатомный газ находится при давлении в (400) кПа. Чему будет равна средняя кинетическая энергия молекул этого газа, если в (1) м(^3) содержится примерно (2·10^{27}) молекул?
Маленькая частичка массой (19,2cdot10^{-12}) кг находится в воздухе. Во сколько раз ее средняя квадратичная скорость будет отличаться от средней квадратичной скорости движения молекул воздуха? (Молярная масса воздуха – (0,029) кг/моль)
Вычислите среднюю квадратичную скорость молекул газа, находящегося под давлением (10) кПа, если его масса равна (3) кг, объем – (16) м(^3).
Можно ли получить температуру ниже или равную абсолютному нулю?
При нагревании ртуть в градуснике расширилась. Что это означает?
Найдите давление углекислого газа в сосуде, если концентрация его молекул равна (2,7 · 10^{20}) м(^{–3}), а среднее значение квадрата их скорости – (3 · 10^4) м(^2)/с(^2). (Масса молекулы углекислого газа равна (7,3 · 10^{–26}) кг)

Источник

Содержание статьи

Идеальный газ.
Средняя кинетическая энергия теплового движения молекул.
Распределение молекул по скоростям.
Внутренняя энергия и теплоемкость идеального газа.
Скорость звука в газе.
Реальные газы.
Процессы переноса в газах.

ГАЗ – одно из агрегатных состояний вещества, в котором составляющие его частицы (атомы, молекулы) находятся на значительных расстояниях друг от друга и находятся в свободном движении. В отличие от жидкости и твердого тела, где молекулы находятся на близких расстояниях и связаны друг с другом значительными по величине силами притяжения и отталкивания, взаимодействие молекул в газе проявляется лишь в короткие моменты их сближения (столкновения). При этом происходит резкое изменение величины и направления скорости движения сталкивающихся частиц.

Название «газ» происходит от греческого слова «haos» и было введено Ван Гельмонтом еще в начале 17 в., оно хорошо отражает истинный характер движения частиц в газе, отличающегося полной беспорядочностью, хаотичностью. В отличие, например, от жидкости газы не образуют свободной поверхности и равномерно заполняют весь доступный им объем.

Газообразное состояние, если причислять к нему и ионизованные газы, является самым распространенным состоянием вещества во Вселенной (атмосферы планет, звезды, туманности, межзвездное вещество и т.д.).

Идеальный газ.

Законы, определяющие свойства и поведение газа, легче всего формулируются для случая так называемого идеального газа или газа относительно низкой плотности. В таком газе среднее расстояние между молекулами предполагается большим по сравнению с радиусом действия межмолекулярных сил. Порядок величины этого среднего расстояния можно определить как 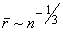, где – n число частиц в единице объема или числовая плотность газа. Если пользоваться приближенной моделью взаимодействия частиц газа, в которой молекулы представляются твердыми упругими шариками диаметром d, то условие идеальности газа записывается как nd³<<1. Характерный размер молекул газа можно в среднем оценить как d = 3·10^–8 см. Это означает, что газ является идеальным, если n << 3·10²² см^–3. Такому условию заведомо отвечает любой газ (например, воздух), находящийся при нормальных условиях (давление p = 1атм, температура T = 273K), поскольку при этих условиях число молекул в одном кубическом сантиметре газа равно 2,69·10¹⁹см^–3 (число Лошмидта). При фиксированном давлении газа условие идеальности удовлетворяется тем лучше, чем выше температура газа, поскольку плотность газа, как это следует из уравнения состояния идеального газа в этом случае обратно пропорциональна его температуре.

Законы идеального газа были в свое время открыты опытным путем. Так еще в 17 в. был установлен закон Бойля – Мариотта

(1) pV = const,

(2) из которого следует, что изменение объема газа V при постоянной температуре T сопровождается таким изменением его давления p, что их произведение остается постоянной величиной.

Если газ находится в условиях, когда постоянным сохраняется его давление, но меняется температура (такие условия можно осуществить, например, поместив газ в сосуд, закрытый подвижным поршнем), то выполняется закон Гей-Люссака

(2) ,

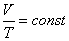
т.е. при фиксированном давлении отношение объема газа к его температуре является постоянным. Оба указанных закона объединяются в универсальное уравнение Клапейрона – Менделеева, которое называется также уравнением состояния идеального газа

(3) pV = nRT.

Здесь n – число молей газа, R = 8,317 Дж/моль·K – универсальная газовая постоянная. Молем любого вещества называется такое его количество, масса которого в граммах равна атомной или молекулярной массе вещества М. В свою очередь, молекулярной массой вещества называется отношение массы молекулы этого вещества к так называемой атомной единице массы (а.е.м.), в качестве которой принимается масса равная 1/12 массы атома ¹²С (изотопа углерода с массовым числом 12) (см. ИЗОТОПЫ). При этом 1 а.е.м. = 1,66·10^–27кг.

Один моль любого вещества содержит одно и то же число молекул, равное числу Авогадро 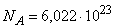моль^–1. Число молей данного количества вещества определяется отношением массы вещества m к его молекулярной массе, т.е. n = m/M .

Используя соотношение n = N/V = nN_A/V, уравнение состояния можно представить в виде, связывающем между собой давление, плотность и температуру

(4) p = nkT,

где вводится величина

k = R/N_A= 1,38·10^–23 Дж/K , которая носит название постоянной Больцмана.

Уравнение состояния в форме (3) или (4) может быть обосновано также методами кинетической теории газов, что позволяет, в частности, придать более отчетливый физический смысл постоянной Больцмана k (см. МОЛЕКУЛЯРНО- КИНЕТИЧЕСКАЯ ТЕОРИЯ).

Из уравнения состояния идеального газа непосредственно следует закон Авогадро: при одинаковых давлениях и температурах в равных объемах любого газа содержится одинаковое число молекул. Из этого закона вытекает и обратное утверждение: различные газы, содержащие одинаковое число молекул, при одинаковых давлениях и температурах занимают одинаковый объем. В частности, при нормальных условиях моль любого газа занимает объем

м³/моль

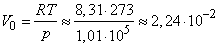
Исходя из этого значения легко определить число Лошмидта

2,69·10²⁵ м^–3= 2,69·10^–19 см^–3

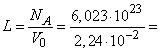
Другой закон, относящийся к смесям идеальных газов, носит название закона Дальтона: давление смеси газов равно сумме парциальных давлений ее компонентов. Парциальным давлением какого либо газа (компонента газовой смеси) называется при этом давление, которое оказывал бы этот газ, если бы он один занимал весь объем, занимаемый смесью.

Средняя кинетическая энергия теплового движения молекул.

Уравнение состояния идеального газа в форме (3) или (4) может быть обосновано и методами кинетической теории газов. На основе кинетического подхода сравнительно просто выводится выражение для давления идеального газа в сосуде, которое получается как результат усреднения импульсов молекул, передаваемых стенке сосуда при многочисленных соударениях молекул со стенкой. Величина получаемого при этом давления определяется как

(5) ,

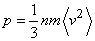
Где бv²с – среднее значение квадрата скорости молекул, m – масса молекулы.

Средняя кинетическая энергия молекул газа (в расчете на одну молекулу) определяется выражением

(6)

Кинетическая энергия поступательного движения атомов и молекул, усредненная по огромному числу беспорядочно движущихся частиц, является мерилом того, что называется температурой. Если температура T измеряется в градусах Кельвина (К), то связь ее с E_k дается соотношением

(7)

Это соотношение позволяет, в частности, придать более отчетливый физический смысл постоянной Больцмана

k = 1,38·10^–23Дж/K, которая фaктически является переводным коэффициентом, определяющим, какая часть джоуля содержится в градусе.

Используя (6) и (7), находим, что (1/3)m бv²с = kT. Подстановка этого соотношения в (5) приводит к уравнению состояния идеального газа в форме

p = nkT, которое уже было получено из уравнения Клапейрона – Менделеева (3).

Из уравнений (6) и (7) можно определить значение средне-квадратичной скорости молекул

(8)

Расчеты по этой формуле при Т = 273К дают для молекулярного водорода бvс_кв = 1838 м/с, для азота – 493 м/с, для кислорода – 461 м/с и т.д.

Распределение молекул по скоростям.

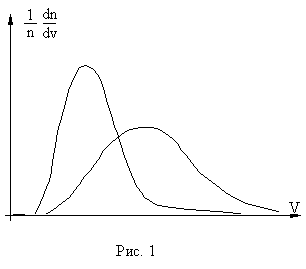
Приведенные выше значения бvс_кв позволяют составить представление о порядке величины среднего значения тепловых скоростей молекул для различных газов. Разумеется, не все молекулы движутся с одинаковыми скоростями. Среди них есть определенная доля молекул с малыми значениями скорости и, наоборот, некоторое число достаточно быстрых молекул. Однако, большая часть молекул обладает скоростями, значения которых группируются относительно наиболее вероятной при данной температуре величины, которая не очень существенно отличается от значений, даваемых формулой (8). Такое распределение молекул по скоростям устанавливается в газе в результате обмена импульсом и энергией при многочисленных столкновениях молекул между собой и со стенками сосуда, Вид этого универсального (не меняющегося во времени) распределения молекул по скоростям, соответствующего состоянию теплового равновесия в газе, был впервые теоретически установлен Максвеллом. С помощью распределения Максвелла определяется относительная доля молекул, абсолютные скорости которых лежат в некотором узком интервале значений dv.

(9)

Вид распределения dn/ndv, описываемого выражением (9), для двух различных температур (T₂ > T₁) представлен на рис.1.

С помощью максвелловского распределения можно вычислить такие важные характеристики газа как средняя, среднеквадратичная и наиболее вероятная скорость теплового движения молекул, рассчитать среднее число столкновений молекул со стенкой сосуда и т.д. Средняя тепловая скорость молекул, например, которая представляет собой фактически средне-арифметическую скорость, определяется при этом формулой

(10)

Наиболее вероятная скорость молекул, соответствующая максимуму кривых, представленных на рис. 1, определена как

(11)

Значения скоростей, определяемых формулами (8), (10) и (11), оказываются близкими по величине. При этом

(12) бvс = 0,93 бvс_кв, n_в= 0,82бvс_кв

Внутренняя энергия и теплоемкость идеального газа.

Чтобы изменить состояние некоторого заданного объема газа (например, нагреть или охладить его), надо либо совершить над ним механическую работу, либо передать ему некоторое количество тепла за счет контакта с другими телами. Количественно эти изменения выражаются с помощью первого начала термодинамики, которое отражает важнейший закон природы: сохранение механической и тепловой энергии тела. Формулировку первого начала для бесконечно малого квазистатического процесса можно представить в виде (см. ТЕРМОДИНАМИКА).

(13) dQ = dU + dA

Здесь dQ – элементарное количество тепла, передаваемое телу, dU – изменение его внутренней энергии,

dA = pdV – элементарная работа, совершаемая газом при изменении его объема (эта работа равна с обратным знаком элементарной работе, совершаемой внешними силами над газом). Обозначение dU соответствует полному дифференциалу от переменной U. Это означает, что приращение внутренней энергии при переходе газа из некоторого состояния 1 в состояние 2 можно представить в виде интеграла

Обозначения dQ и dA означают, что в общем случае интеграл от них нельзя представить в виде разности соответствующих значений в конечном и начальном состоянии газа, поэтому интегрирование (13) по всему процессу приводит к соотношению

Q = U₂ – U₁ + A

Вводится понятие теплоемкости газа как количества тепла, которое нужно сообщить газу, чтобы повысить его температуру на один градус Кельвина. Тогда по определению

Далее под С подразумевается теплоемкость, отнесенная к одному молю газа, или молярная теплоемкость. Внутренняя энергия U также определена для одного моля газа. Если газ нагревается при постоянном объеме (изохорический процесс), т.е. совершаемая газом работа равна нулю, то

(14)

Если состояние газа меняется при постоянном давлении (изобарический процесс), то в соответствии с (13)

(15)

Использование уравнение состояния идеального газа (3) при v = 1 дает

Следовательно, молярные теплоемкости идеального газа при постоянном давлении и при постоянном объеме связаны соотношением

(16) C_p = C_v + R

Внутренняя энергия газа, в общем случае, состоит из кинетической энергии поступательного и вращательного движения молекул, энергии внутреннего (колебательного) движения атомов в молекуле, а также потенциальной энергии взаимодействия молекул. В случае идеального газа вкладом последнего слагаемого в полную энергию можно пренебрегать.

В классической статистической механике доказывается так называемая теорема о равномерном распределении кинетической энергии по степеням свободы молекул, согласно которой на каждую степень свободы молекулы в состоянии теплового равновесия в среднем приходится энергия, равная (1/2)kT.

Для газов, состоящих из одноатомных молекул, (например, инертные газы) средняя кинетическая энергия, приходящаяся на один атом, определена соотношением (7), поскольку она соответствует лишь поступательному движению атомов, (3 степени свободы). В этом случае

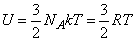
Существенно, что для идеального газа одноатомных молекул внутренняя энергия зависит только от температуры и не зависит от объема.

Для линейных двухатомных молекул число степеней свободы равно пяти (на одну степень свободы меньше, чем для системы двух независимых атомов, поскольку в молекуле эти атомы связаны жесткой связью) Дополнительные две степени свободы описывают вращательное движение молекулы относительно двух взаимно-перпендикулярных осей. При этом

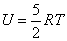
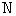
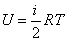
Если атомы в молекуле совершают еще и колебания, то, согласно классической теории, наличие колебательного движения вносит вклад в среднюю энергию молекулы, равный kT (по kT/2, приходящийся на кинетическую и потенциальную энергии колебаний. Тогда в случае молекулы, образованной из атомов,

где i = n_пост + n_вращ + 2n_кол– полное число степеней свободы молекулы. При этом n_пост= 3. Для линейной молекулы n_вращ = 2, n_кол= 3N – 5. Для всех других молекул n_вращ = 3, n_кол= 3N – 6.

Классическая теория, в основном, правильно описывает тепловые явления в газе в некоторых узких интервалах температур, однако температурная зависимость теплоемкости в целом, наблюдаемая в эксперименте, ведет себя далеко не так, как предсказывает классическая теория. Это несоответствие теории и эксперимента было понято только с появлением квантовой теории теплоемкости, основанной на представлении о дискретности вращательных и колебательных уровней молекул. При низких температурах наблюдается только поступательное движение молекул. С ростом температуры все большее число молекул вовлекается во вращательное движение. Если средняя тепловая энергия kT заметно превышает энергию первого вращательного уровня, в молекуле возбуждено уже много вращательных уровней. В этом случае дискретность уровней становится несущественной и теплоемкость равна своему классическому значению. Аналогичная ситуация имеет место и с возбуждением колебательных степеней свободы. Квантовая теория полностью объясняет характер температурной зависимости теплоемкости, ее непрерывный характер, отличающийся постепенным вовлечением в «игру» различных степеней свободы молекул.

Изотермические и адиабатические процессы в газе. Наряду с процессами изменения параметров газа, происходящими при постоянном объеме или при постоянном давлении, возможны изотермические (T = const, внутренняя энергия газа остается неизменной) и адиабатические (без отвода и подвода тепла к газу) процессы. В первом случае все подводимое к газу тепло расходуется на механическую работу, а изменение давления и объема для одного моля газа удовлетворяет условию pV = PT = const. В p—V координатах на плоскости соответствующие зависимости образуют семейство изотерм.

Для адиабатического процесса (dQ = 0) из (13) и (14) следует

C_VdT + pdV = 0

Уравнение состояния идеального газа дает

dT = R^–1(pdV + Vdp).

Используя (16), уравнение адиабатического процесса можно представить в дифференциальной форме

(17) gpdv + Vdp = 0, где g = С_р/C_V– отношение теплоемкостей при постоянном давлении и постоянном объеме, называемое адиабатической постоянной. Дифференциальному соотношению (17) при g = const соответствует уравнение адиабаты pV^g= const

или

(18) TV^{g – 1}= const

Так как g > 1, то из (18) следует, что при адиабатическом сжатии газ нагревается, а при расширении – охлаждается. Это явление находит применение, например, в дизельных двигателях, где горючая смесь воспламеняется за счет адиабатического сжатия.

Скорость звука в газе.

Из гидрогазодинамики известно, что скорость звука в сплошной среде определяется соотношением

В первоначальных теориях (Ньютон) считалось, что давление и плотность связаны обычным уравнением состояния, т.е. p/r = соnst. Это соответствует предположению, что разности температур между сгущениями и разрежениями газа в звуковой волне мгновенно выравниваются, т.е. распространение звука является изотермическим процессом. В этом случае формула Ньютона для скорости звука принимает вид

Эта формула, однако, противоречила эксперименту. Лаплас первым понял, что колебания плотности и связанные с этим колебания температуры в звуковой волне происходят настолько быстро, что для таких процессов теплообмен несущественен и выравнивания температур не происходит. Это означает, что вместо уравнения изотермы надо пользоваться уравнением адиабаты. Тогда выражение для скорости звука принимает вид

(19)

Скорость звука в газе имеет тот же порядок величины, что и средняя тепловая или средне-квадратичная скорости молекул. Это понятно, поскольку возмущения в звуковой волне передаются молекулами, движущимися с тепловыми скоростями. Для молекулярного азота, например, g = 1,4 и скорость звука при T = 273К равна 337 м/с. Средняя тепловая скорость молекул азота бvс при тех же условиях равна 458 м/с.

Реальные газы.

С ростом давления и уменьшением температуры состояние газа начинает все больше отклоняться от идеальности. Эксперимент показал, например, что для азота N₂ при температуре T = 273K и давлении p =100 атм, ошибка в определении объема газа, если пользоваться уравнением состояния (3), может достигать 7%. Это связано с тем, что при таком давлении молекулы газа в среднем удалены друг от друга на расстояние, которое только вдвое больше их собственных размеров, а собственный объем молекул лишь в 20 раз меньше объема газа. При дальнейшем повышении давления становится все более существенным учет влияния на поведение газа как сил межмолекулярного взаимодействия, так и собственного объема молекул.

Пока отклонения от идеальности малы, их можно учесть с помощью так называемого вириального разложения – разложения давления в ряд по степеням плотности молекул в объеме N/V

(20) ,

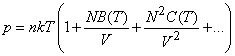
где B(T), C(T) – так называемые вириальные коэффициенты, зависящие от температуры и характеризующие влияние межмолекулярного взаимодействия. Для учета более сильных отклонений предложено много полуэмпирических и эмпирических уравнений состояния реальных газов, из которых наиболее часто используется уравнение Ван-дер-Ваальса.

Уравнение состояния неидеального газа – уравнение Ван-дер-Ваальса записывается для одного моля газа в виде

(21)

В нем учитывается как собственный объем молекул (постоянная b), так и влияние сил притяжения между молекулами (постоянная a). Из этого уравнения вытекает, в частности, существование наблюдаемой на опыте критической температуры и критического состояния. Критическое состояние характеризуется значением T_k и соответствующими ему значениями p_k и V_k. При критической температуре T_k исчезает различие между разными состояниями вещества. Выше этой температуры переход от жидкости к газу либо, наоборот, от газа к жидкости оказывается непрерывным.

Процессы переноса в газах.

Если в газе создается какая-либо неоднородность его параметров (например, разные температуры газа или разные концентрации компонентов газовой смеси в разных частях сосуда), то возникают отклонения состояния газа от равновесия, которые сопровождаются переносом энергии (теплопроводность) или массы компонентов смеси (диффузия) из одной части сосуда в другую. При различии в скоростях перемещения разных слоев газа (например, при течении газа в трубе) возникает поперечный перенос импульса (вязкость). Все эти явления объединяются одним общим названием процессы переноса. При их описании особенно важным оказывается учет характера столкновений молекул в газе. Порядок величины соответствующих коэффициентов переноса (кинетических коэффициентов) и характер зависимости их от основных параметров дается элементарной кинетической теорией газа, основанной на модели молекул в виде твердых упругих шаров и на концепции средней длины свободного пробега молекул. Для переноса энергии в газе принимается

где q – плотность потока энергии (поток тепла), k – коэффициент теплопроводности, dT/dz – градиент температуры в направлении оси z.

Сила вязкого трения, возникающая между двумя слоями в движущемся газе, если имеется поперечное распределение скорости газа u(x), имеет вид

Наконец, если в бинарной газовой смеси молекул с близкой массой компонентов задано распределение плотности одного из компонентов n₁(z), то диффузионный поток молекул компонента в направлении z записывается в виде

Коэффициенты переноса в этих соотношениях: коэффициенты теплопроводности k, вязкости h и самодиффузии D, получаемые методами элементарной кинетической теории, записываются в виде,

(22) , ,

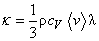
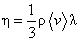
где l – средняя длина свободного пробега молекул, бvс – средняя тепловая скорость молекул. Поскольку 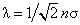, где s – поперечное сечение столкновений молекул. коэффициенты теплопроводности и вязкости не зависят от плотности (или от давления) газа, в то время как коэффициент диффузии D ~ 1/p.

В элементарной теории численные коэффициенты в выражениях (22) оказываются одинаковыми. Точная теория для модели твердых упругих шаров (s = сonst) дает h = 0,5бvс l, k = 2,5(R/M)h,

rD = 1,2h

Более реалистические модели взаимодействия молекул в газе вносят изменения в характер зависимости коэффициентов переноса от температуры, что позволяет обеспечить лучшее совпадение теории с результатами экспериментальных измерений этих коэффициентов.

Владимир Жданов

Источник

Определение

Идеальный газ — газ, удовлетворяющий трем условиям:

Молекулы — материальные точки.
Потенциальная энергия взаимодействия молекул пренебрежительно мала.
Столкновения между молекулами являются абсолютно упругими.

Реальный газ с малой плотностью можно считать идеальным газом.

Измерение температуры

Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.

Обозначение температуры

По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 ^oC).
По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).

Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:

∆t = ∆T

При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:

T = t + 273

Если особо важна точность, следует использовать более точную формулу:

T = t + 273,15

Пример №1. Температура воды равна ^oC. Определить температуру воды в Кельвинах.

T = t + 273 = 2 + 273 = 275 (К)

Основное уравнение МКТ идеального газа

Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).

Основное уравнение МКТ

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

p=23n−Ek

p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.

Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:

p=13m0n−v2

m0— масса одной молекулы газа;

n — концентрация молекул газа;

−v2 — среднее значение квадрата скорости молекул газа.

Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости:

v=√−v2

p=13ρ−v2

ρ — плотность газа

p=nkT

k — постоянная Больцмана (k = 1,38∙10^–3 Дж/кг)

T — температура газа по шкале Кельвина

Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?

Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:

Следствия из основного уравнения МКТ идеального газа

Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):

v=√3kTm0=√3RTM

R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:

R=NAk=8,31 Дж/К·моль

Температура — мера кинетической энергии молекул идеального газа:

−Ek=32kT

T=2−Ek3k

Полная энергия поступательного движения молекул газа определяется формулой:

E=N−Ek

Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?

Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:

Следовательно:

Составим систему уравнений:

Отсюда:

Задание EF19012

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

1.Указать, в каких координатах построен график.

2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

T=2−Ek3

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

pV=νRT

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

νR=p1V1T1=p2V2T2

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

Ответ:

• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.

• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17560

Первоначальное давление газа в сосуде равнялось р₁. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р₂ газа в сосуде стало равным

Ответ:

а) 13p1

б) 2p1

в) 23p1

г) 43p1

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для состояний 1 и 2.

4.Выразить искомую величину.

Решение

Исходные данные:

• Начальное давление: p₀.

• Начальная концентрация молекул: n₁ = 3n.

• Конечная концентрация молекул: n₂ = n.

• Начальная средняя энергия хаотичного движения молекул: E_k1 = E_k.

• Конечная средняя энергия хаотичного движения молекул: E_k2 = 2E_k.

Основное уравнение МКТ:

p=23n−Ek

Составим уравнения для начального и конечного состояний:

p1=23n1−Ek1=233n−Ek=2n−Ek

p2=23n2−Ek2=23n2−Ek=43n−Ek

Отсюда:

n−Ek=p12=3p24

p2=4p16=23p1

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18416

Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Концентрации кислорода и водорода в сосуде равны. Следовательно, n₁ = n₂ = n.

• Давление кислорода вдвое выше давления водорода. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23n−Ek

Применим его для обоих газов и получим:

p1=23n1−Ek1 или 2p=23n−Ek1

p2=23n2−Ek2 или p=23n−Ek2

Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:

−Ek1=3pn

−Ek2=3p2n

Поделим уравнения друг на друга и получим:

−Ek1−Ek2=3pn·2n3p=2

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18824

В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение концентрации молекул аргона к концентрации молекул неона.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.

• Давление аргона в 2 раза больше давления неона. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23n−Ek

Применим его для обоих газов и получим:

p1=23n1−Ek1 или 2p=23n1−Ek

p2=23n2−Ek2 или p=23n2−Ek

Выразим концентрации молекул газа из каждого уравнения:

n1=3p−Ek

n2=3p2−Ek

Поделим уравнения друг на друга и получим:

n1n2=3p−Ek·2−Ek3p=2

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 10.9k

Источник

Молекулярная физика и термодинамика

Напечатано::	Гость
Дата:	суббота, 27 мая 2023, 14:48

1. Введение
2. Уравнение состояния идеального газа
3. Основное уравнение молекулярно-кинетической теории идеальных газов
4. Максвелловский закон распределения молекул по скоростям
5. Средняя длина свободного пробега молекул
6. Явления переноса в газах
7. Теплопроводность газов
8. Внутренне трение в газах
9. Диффузия в газах
10. Соотношение между коэффициентами переноса
11. Понятие о внутренней энергии
12. Число степеней свободы молекул. Внутренняя энергия идеального газа
13. Первое начало термодинамики
14. Работа газа при изменении объема
15. Теплоемкость идеального газа
16. Применение первого начала термодинамики к изопроцессам в газах
17. Адиабатический процесс
18. Круговые процессы
19. Цикл Карно
20. Обратимые и необратимые процессы
21. Второе начало термодинамики
22. Приведенное количество тепла
23. Энтропия
24. Реальные газы. Отклонение свойств реальных газов от идеальности
25. Уравнение Ван-дер-Ваальса
26. Изотермы Ван-дер-Ваальса
27. Критическое состояние вещества.
28. Внутренняя энергия реального газа
29. Эффект Джоуля-Томсона
30. Сжижение газов

1. Введение

Молекулярная
физика — это раздел физики, который рассматривает свойства макроскопических тел
и их агрегатные состояния с точки зрения их молекулярного строения,
взаимодействия и движения молекул. Она изучает явления, происходящие внутри
макроскопических тел.

Основы
молекулярной физики были заложены трудами Ломоносова, Джоуля, Больцмана,
Клаузиуса, Максвелла и других ученых. Благодаря их трудам молекулярная физика
прочно утвердилась в науке. Непосредственным опытным подтверждением
молекулярно-кинетической теории являются процесс диффузии, броуновского
движения, распространения запаха и многие другие явления.

Движение
каждой молекулы в веществе может быть описано законами классической механики.
Однако число молекул в веществе чрезвычайно велико, направления и величины
скоростей молекул совершенно случайны и непрерывно изменяются так, что
становится невозможным охватить уравнениями движения всю совокупность молекул и
сделать какие-либо выводы об их поведении.

Тем не
менее, состояние вещества и его изменение определяется заданием небольшого
числа определенных параметров, как температура, давление, объем, плотность и
т.д., значения которых невозможно указать на основе решений уравнений
классической механики. Дело в том, что свойства огромного числа молекул
подчиняется особым, статистическим закономерностям. Статистическая физика
изучает статистические закономерности, описывающие поведение большой
совокупности объектов. Она основывается на теории вероятностей и позволяет
вычислять средние значения величин, характеризующих движение всей совокупности
молекул (средние скорости молекул, средние кинетические энергии, средние
значения импульса и т. д.) и на этой основе истолковывает свойства вещества,
непосредственно наблюдаемые на опыте (давление, температура и т.д.). В этом
состоит суть молекулярно-кинетического изучения вещества.

Наряду
со статистическим, существует термодинамический метод изучения вещества. В
отличие от статистического метода термодинамический метод не интересуется
строением вещества. Термодинамика изучают условия превращения энергии и
характеризует их с количественной стороны.

В основе
термодинамики лежит небольшое число закономерностей, установленных на основе
большого числа опытных фактов и получивших название начала термодинамики.

У
статистической физики и термодинамики общий предмет изучения – свойства
вещества и происходящие в нем процессы. Подходя к изучению этих свойств с
разных точек зрения, эти методы взаимно дополняют друг друга.

Совокупность
тел, могущих обмениваться энергией между собой и с внешними телами, не
входящими в эту систему, называется термодинамической системой. Одним из
основных понятий термодинамики является понятие состояния системы. Состояние
системы определяется совокупностью значений всех величин, характеризующих
физические свойства системы и называемых термодинамическими параметрами
(температура, давление плотность, теплоемкость, электропроводность и т. д.).
Состояние системы называется стационарным, если значения всех термодинамических
параметров не изменяются во времени. Стационарное состояние называется
равновесным, если его неизменность не обусловлена протеканием каких-либо
процессов во внешних по отношению к данной системе телах.

Исследования показывают, что параметры состояния тел
взаимно связаны и могут быть выражены друг через друга. Поэтому
термодинамическое состояние задается только ограниченным числом параметров
состояния. Такие параметры называются основными параметрами состояния.
Важнейшими параметрами состояния химически однородных систем являются
плотность, объем, давление, температура. И между этими параметрами существует
связь, выражаемая в виде математического уравнения . Уравнение,
связывающее основные параметры состояния, называется уравнением состояния
системы.

2. Уравнение состояния идеального газа

Идеальным
газом называется такой газ, молекулы которого не взаимодействуют между собой на
расстоянии и не имеют собственного объема. Такие молекулы могут быть приняты за
материальные точки. Конечно, молекулы реальных газов не удовлетворяют этому
условию. Однако чем более разрежен газ и чем выше его температура, тем свойства
реального газа становятся близкими к свойствам идеального газа. Свойства таких
газов как водород, кислород, азот и инертные газы при комнатной температуре и
нормальном атмосферном давлении вполне близки к свойствам идеального газа.

Из
сказанного выше ясно, что уравнение состояния идеального газа аналитически
может быть выражено формулой . В этой формуле температура
вещества выражена в абсолютной термодинамической шкале, которая более удобна,
чем широко применяемая на практике стоградусная температурная шкала Цельсия.
Абсолютная температура имеет глубокий физический смысл, как увидим далее, она
определяется средней кинетической энергией теплового движения молекул. С
температурой, выраженной в шкале Цельсия , она связана соотношением

Температуру,
равную 0 К называют абсолютным нулем и ему соответствует .
Температуре соответствует Т=273,
15 К.

Французский физик и инженер Клапейрон (1799-1864), объединив установленные
ранее законы Бойля-Мариотта и Гей-Люссака и Шарля, которые рассматривались в
школе, получил соотношение

,
(2.1)

где В – константа, пропорциональная массе
газа.

В
1811 году итальянский физик и химик Авогадро (1776-1856) установил эакон,
согласно которому один моль любого газа при одинаковом давлении и одинаковой
температуре занимает одинаковый молярный объем . Например, при
нормальных условиях — 0⁰С (273,15К) и нормальном атмосферном
давлении (1,013·10⁵ Па) объем моля любого газа равен 22,4
л/моль=22,4·10^-3 м³/моль. Отсюда видно, что когда масса
газа равна одному молю, константа В уравнении (2.1) будет одинаковой для всех
газов. Таким образом Менделеев (1834-1907) объединил уравнение Клапейрона с
законом Авогадро и получил уравнение (2.1) для моля газа

,
(2.2)

получившее
название уравнения Клапейрона-Менделеева. Постоянная называется
универсальной (или молярной) газовой постоянной. Если в этом уравнении молярный
объем выразим через объем любой массы газа
, где (где М – молярная масса газа), то получим

,
(2.3)

или

,
(2.4)

известные
из школьного курса физики. Полученные выражения представляют уравнение
состояния идеального газа. Единица количества вещества – это моль. Число
частиц, содержащихся в одном моле любого вещества одинаково моль^-1 и называется числом Авогадро.
Уравнение (2.4) можно представлять и в других формах. Выразив в (2.4) массу и
молярную массу газа через массу его одной молекулы и число молекул
и
(— число Авогадро), получим

.
(2.5)

Если
введем постоянную Больцмана , то (2.5) примет
вид

,
(2.6)

Разделив
это уравнение на объем газа, получим

,
(2.7)

где — число молекул в единице
объема (плотность) газа.

3. Основное уравнение молекулярно-кинетической теории идеальных газов

Это уравнение устанавливает связь между давлением и средней
энергией теплового движения молекул. Давление, оказываемое газом на стенки
сосуда, является результатом передачи стенке импульса сталкивающихся с ней
молекул. При расчетах учтем, что движение молекул хаотично, и удары молекул
об стенку являются абсолютно-упругими. Рассмотрим одноатомный газ, занимающий
объем (рис. 1). Выделим на стенке сосуда элементарную
поверхность и вычислим давление, оказываемое на эту
поверхность. При соударении со стенкой молекула
с

Рис.1

массой ,
движущаяся со скоростью перпендикулярно стенке,
передает ей импульс . За время поверхности
стенки достигнут только те молекулы которые заключены в
объеме цилиндра с основанием и высотой .Это
число молекул равно , где — число молекул
в единице объема. Здесь мы упростили рассмотрение движения молекул. На самом
деле молекулы к площадке движутся под разными углами, имея различные скорости.
Для упрощения расчета хаотическое движение молекул по всем направлениям
обычно заменяют движением вдоль трех взаимно перпендикулярных координатных
осей так, что в любой момент времени вдоль каждой из них (например, оси х) движется 1/3 общего числа молекул,
причем одна половина из этого числа, т.е. 1/6 часть молекул, движется вдоль
положительной оси, другая половина – в противоположном направлении. Тогда число
ударов о поверхность за время будет равно /6
При столкновении с поверхностью молекулы передают ей импульс . Воспользовавшись вторым законом Ньютона ,
можем выразить силу давления на поверхность

Давление
газа на стенку выразится в виде

. (2.8)

Молекулы
в сосуде движутся с самыми различными скоростями . Их общее число
. Поэтому вместо скорости в эту
формулу следует подставлять среднюю квадратичную скорость, которая
характеризует всю совокупность молекул

. (2.9)

Поэтому

(2.10)

Здесь —
средняя кинетическая энергия поступательного движения молекул. Тогда уравнение
(2.10) перепишется в виде

.
(2.11)

Таким
образом, давление газа пропорционально средней кинетической энергии теплового движения
молекул газа, заключенных в единице объема. Полученное выражение носит название
основного уравнения молекулярно-кинетической теории газов.

Следствия
из основного уравнения молекулярно-кинетической теории газов

Так как , то получаем

, (2.12)

где —
средняя энергия поступательного движения всех молекул газа.

Отсюда
(2.13)

С
помощью уравнения Клапейрона-Менделеева

легко получаем

откуда

.
(2.14)

Энергия поступательного движения одного моля газа
будет равна

Поделив это уравнение на число Авогадро ,
получаем

Формула

(2.15)

имеет глубокий физический смысл — она выражает,
что термодинамическая температура зависит толь от средней энергии
поступательного движения молекул.

Существенно также, что средняя кинетическая энергия молекул зависит только от температуры
и не зависит от массы молекул. При абсолютно нулевой температуре Т = 0 поступательное движение молекул
прекращается. Подставив

в (2.15),
получаем выражение для среднеквадратичной скорости в виде

(2.16)

Умножая числитель и знаменатель дроби под корнем
на число Авогадро, получим

(2.17)

4. Максвелловский закон распределения молекул по скоростям

Представление
о беспорядочном движении молекул относится не только к направлениям скоростей
молекул, но и к величинам их скоростей. В газах молекулы движутся со
всевозможными скоростями. В них можно найти молекулы, движущиеся с очень малой,
также и с очень большой скоростью. Но большинство молекул движется со
скоростями, близкими, к так называемой, наиболее вероятной скорости. Это
свидетельствует о том, что скорости молекул имеют распределение. В результате
беспорядочных соударений скорости отдельных молекул непрерывно изменяются в
разные интервалы времени скорости одних молекул возрастают, других убывают но,
в целом, распределение скоростей в совокупности молекул носит стационарный
характер. Теоретическую задачу о распределении молекул идеального газа по
скоростям впервые решил английский ученый Максвелл. Он рассматривал газ как
замкнутую систему, содержащую молекул в отсутствие внешних
сил и в состоянии термодинамического равновесия. Вследствие непрерывного
изменения скоростей имеет смысл говорить только о числе молекул, скорости
которых заключены в определенном интервале скорости. Если разбить диапазон
скоростей молекул на интервалы, равные , то на каждый
интервал скорости будет приходиться некоторое число молекул ,
значение которой будет зависеть от того при какой скорости выбран данный
интервал скорости. Относительную долю таких молекул будет пропорциональна
ширине выбранного интервала скорости

Коэффициент
пропорциональности, зависящий от скорости, называется функцией распределения
молекул по скоростям

Из
последней формулы становится очевидным смысл функции распределения: она
выражает долю молекул, скорости которых заключены в единичном интервале
скорости. Применяя статистические методы Максвелл нашел функцию —
закон распределения молекул идеального газа по скоростям

, (2.18)

На рис.
2 представлен график функции (2.18) распределения скоростей молекул в газах.
Эта функция состоит из двух множителей, один из которых возрастает,

Рис. 2

другой убывает
с увеличением скорости, причем убывает быстрее, чем первый множитель.
Произведение этих множителей дает колоколообразную кривую с максимумом при
значении скорости , называемой наиболее вероятной скорости.
Кривая несимметрична относительно. Площадь заштрихованной
полоски, заключенной в интервале скорости от до + выражает
относительное число молекул, скорости которых лежат в этом интервале скоростей.
Вся площадь под кривой равна единице. Значит, функция удовлетворяет
условию нормировки

Этот
интеграл выражает всю площадь, заключенную под кривой функции распределения
молекул по скоростям. С повышением температуры максимум этой кривой смещается в
сторону большей температуры, изменяется и ее форма, растягиваясь в сторону
более высоких температур (рис.3).

Наиболее
вероятная скорость может быть определена из (2.18) решая задачу на экстремум

откуда

.
(2.19)

Рис.3

Из этой
формулы следует, что с повышением температуры максимум кривой распределения
скоростей смещается вправо и кривая растягивается в сторону более высоких
скоростей. Однако площадь, заключенная под кривой остается неизменной. Значение
функции распределения молекул по скоростям заключается в том, что с ее помощью
определяются средние значения величин, характеризующих всю совокупность
молекул. Например, средняя арифметическая скорость определятся как

Подставив
явное выражение из (2.18), получаем

(2.20).

Аналогично
можно найти квадрат среднеквадратичной скорости

. (2.21)

Из
распределения молекул по скоростям можно перейти к их распределению по
кинетическим энергиям . Подставив в (2.18) и , получаем формулу

, (2.22)

с
помощью которой можно определить среднюю кинетическую энергию молекул
идеального газа

. (2.23)

Барометрическая
формула. Распределение Больцмана

При
получении функции распределения Максвелла, предполагалось, что внешние силы на
молекулы газа не действуют и поэтому молекулы распределены по объему равномерно
и давление газа во всех частях его объема одинаково. Если газ находится в
каком-либо силовом поле, распределение его молекул по объему уже не будет
равномерным. В качестве такого распределения рассмотрим распределение давления
и молекул воздуха в поле земного тяготения.

Давление
земной атмосферы обусловлено силой притяжения молекул воздуха к Земле.
Обозначим давление воздуха на высоте через р. Тогда давление на высоте равно
. Причем dh>0 , аdp<0. Отсюда имеем

Или

.
(2.24)

где —
плотность газа. Из уравнения состояния идеального газа имеем

Подставив
плотность в (2..24), получим

или

Откуда,
при , имеем

При .
Потенцируя последнее выражение с учетом значения С, имеем

.
(2.25)

Эту
формулу называют барометрической формулой.

Эту
формулу используем для получения распределения молекул в поле потенциальных
сил. Заменив в (2.25) давление выражением , легко получим

.
(2.26)

На
разных высотах молекулы обладают разной потенциальной энергией.

Отсюда
следует, что распределение молекул по высоте это есть распределение по
потенциальным энергиям.

Больцман
показал, что такое распределение справедливо не только в поле земного
тяготения, но и в любом потенциальном поле. Поэтому такое распределение
получило название распределения Больцмана.

Распределение
Больцмана может быть объединено с распределением Максвелла, приводя к
распределению молекул по полной энергии, согласно которому число молекул,
находящихся в силовом поле, со скоростями от до равно

. (2.27)

В
распределении Больцмана потенциальная энергия частицы может принимать как
непрерывный так и дискретный ряд значений (например, энергии электронов в
атоме). В последнем случае оно имеет вид

где —
число молекул в состоянии с энергией . А – коэффициент пропорциональности (нормирующий множитель),
удовлетворяющий условию

Где —
полное число частиц в рассматриваемой системе. Найдя множитель А и подставив его в формулу распределения,
получим

.
(2.28)

В этом состоит суть квантовой статистики.

5. Средняя длина свободного пробега молекул

При
определении идеального газа мы считали, что молекулы не имеют размеров и могут
рассматриваться как материальные точки. На самом деле, это не так. Они имеют
размеры и при соударениях их центры приближаются друг к другу на некоторое
расстояние. В простейшем случае молекулы рассматриваются как сферические
частицы. Расстояние, на которое сближаются центры двух молекул, называется
эффективным диаметром молекул (рис.4). Величина называется эффективным сечением
молекул.

За
время между двумя последовательными соударениями молекула газа проходит
некоторый путь , который называется длиной свободного
пробега. Длина свободного побега случайная величина. Иногда молекула без
столкновения с другой молекулой проходит значительный путь, иногда этот путь
весьма мал. Вероятность того, что молекула без столкновения проходит путь равна,где
— средний путь, проходимый молекулой без
столкновений, называется средней длиной свободного пробега молекул.

За
одну секунду молекула проходит в среднем путь, равный средней скорости молекул .
Если за одну секунду молекула претерпевает столкновений,
то средняя длина свободного пробега будет равна

(2.29)

Чтобы
подсчитать среднее число столкновений молекул, будем представлять, что все
молекулы, кроме рассматриваемой, неподвижны, движется только рассматриваемая
молекула со скоростью .При своем движении молекула столкнется
со всеми молекулами, центры которых лежат от траектории движения

ее
центра на расстояниях, меньших или равных эффективному диаметру молекулы (рис.
3). Говоря по другому, за единицу времени молекула столкнется со всеми
молекулами, центры которых лежат внутри цилиндра с высотой, равной и

Рис.4

радиусом,
равным (рис.5).
Если — число молекул в единице объема, то среднее число
столкновений будет равно

.
(2.30

Рис.5

На
самом деле, предположение, что в газе движется только одна молекула а все
остальные неподвижны, неверно. Все молекулы движутся и возможность столкновения
двух молекул зависит от их относительной скорости. Поэтому в формулу числа
столкновений вместо средней арифметической скорости должна войти средняя
относительная скорость молекул. Средняя относительная скорость, как показал
Максвелл, равна

т.е.
среднее число столкновений в раз больше

(2.31)

Из
формулы (2.29) находим среднюю длину свободного пробега

.
(2.32)

или

Поскольку
давление газа , то можем получить зависимость от
давления

. (2.33)

Из этой
формулы следует, что

.
(2.34)

Эффективный
диаметр молекул несколько убывает с повышением температуры. Поэтому средняя
длина свободного пробега молекул слегка возрастает с ростом температуры.

Оценим
среднюю длину свободного пробега молекул при нормальных условиях. Примем
эффективный диаметр молекул равным 2·10-10 м,
м^-3
(число Лошмита). Отсюда м.

В
таблице приведены значения молекул воздуха при разных
давлениях и комнатной температуре

	760	1	10^-2	10^-4	10^-6
	6,5·10^-8	5·10^-5	5·10^-3	0,5	50

6. Явления переноса в газах

Под
явлениями переноса понимают явления переноса количества движения (импульса),
энергии и массы вещества из одного слоя вещества в другой слой. Эти явления
выражаются в виде явлений внутреннего трения, теплопроводности и диффузии.
Установлены эмпирические законы для этих явлений:

1.
Сила внутреннего трения

— закон Ньютона. Здесь — коэффициент
внутреннего трения (вязкости), градиент скорости, —
площадь соприкосновения слоев вещества.

2.
Количества тепла, перенесенного за единицу времени

— закон Фурье, коэффициент
теплопроводности, — градиент температуры

3.
Масса вещества, перенесенного за единицу времени

— закон Фика, — коэффициент
диффузии, градиент
концентрации вещества.

7. Теплопроводность газов

Пусть между двумя параллельными стенками, перпендикулярными оси х и имеющими температуры Т₁ и Т₂(Т₁>Т₂) поддерживается постоянная
разность температур. При этом через газ, находящийся между стенками,
установится постоянный поток тепла с градиентом температуры . Рассмотрим поток тепла через площадку ΔS между стенками, на которой температура
газа равна Т. Для расчета
хаотичное движение молекул по всем направлениям заменяем их движением вдоль
трех осей декартовой системы координат. Считаем, что вдоль оси х движется одна треть общего числа
молекул. Из них одна половина движется слева направо другая половина справа
налево. Очевидно, до площадки ΔS достигают без столкновений, (т.е. без
изменения направления движения) только те молекулы, которые отстоят от нее на
расстоянии не далее длины свободного пробега молекул (рис.6). Через площадку ΔS за единицу времени слева направо

Рис.6

и справа
налево проходит одинаковое число молекул, равное . Температура
на поверхности, расположенной на расстоянии от площадки ΔS равна
и на такой же поверхности, расположенной справа
равна . Энергия, которой обладают молекулы на той же
поверхности, расположенной слева равна , и на
поверхности, расположенной справа .

Количество теплоты, переносимое за
единицу времени молекулами, движущимися слева направо и справа налево, равно

Количество
тепла, перенесенного через площадку за единицу времени равно

,
(2.35)

где , — удельная теплоемкость газа при
постоянном объеме, — плотность газа. Из сравнения (2.35) с
эмпирической Фурье находим коэффициент теплопроводности газа

.
(2.36)

Таким
образом, молекулярно-кинетическая теория дает явное выражение зависимости
коэффициента теплопроводности от микроскопических параметров молекул.

8. Внутренне трение в газах

Способ расчета переноса
количества движения аналогичен расчету теплопроводности, поэтому нет
необходимости в его подробном рассмотрении. Количество движения (импульс),
перенесенное слева направо и справа налево через площадку за
время выражаются в виде

откуда
импульс, перенесенный через площадку за время , выражается в
виде

откуда
находим силу внутреннего трения

.
(2.37)

Из
сравнения этой формулы с законом Ньютона, находим коэффициент вязкости газа

или

,
(2.38)

где —
плотность газа.

9. Диффузия в газах

Диффузия
в веществе обуславливается различием числа частиц вдоль заданной оси х. Количество частиц, перенесенных слева
направо и справа налево через площадку за
единицу времени выражается в виде

Количество
частиц, перенесенных через площадку за единицу времени равно

Умножая эту формулу на массу одной частицы и введя концентрацию вещества, находим массу перенесенного вещества

Из
сравнения этой формулы с законом Фика, находим коэффициент диффузии молекул
газа

(2.39)

10. Соотношение между коэффициентами переноса

Теоретически поученные коэффициенты переноса

можно
выражать друг через друга

Подставив
в формулу коэффициента вязкости, получаем

Видим, что коэффициент внутреннего трения газов не
зависит от числа молекул в единице объема, т.е. от давления и плотности газа.
Из формулы следует также, что не зависит от давления и
коэффициент теплопроводности. Это положение становится,
однако, неверным для сильно разреженных газов, при котором длина свободного
пробега молекул больше размеров сосуда, в котором находится газ. В этом случае
молекулы газа летают от одной стенки до другой, не сталкиваясь друг с другом.
Длина свободного пробега молекул становится величиной постоянной, не зависящей
от давления и формула для расчета неверной.

11. Понятие о внутренней энергии

Внутренняя
энергия — это сумма всех видов энергии, заключенных в изолированном теле, т. е.
энергия за исключением кинетической энергии движения и потенциальной энергии в
поле внешних сил. Например, при учете внутренней энергии газа нельзя включать
в нее энергию движения его вместе с сосудом и его потенциальную энергию в поле
земного тяготения.

Внутренняя энергия является однозначной функцией
термодинамического состояния системы. Это значит, что всякий раз, когда система
оказывается в данном состоянии, внутренняя энергия принимает присущее этому
состоянию значение независимо от предшествующего состояния системы. Отсюда
следует, что при переходе системы из одного состояния в другое изменение
внутренней энергии равно разности энергий начального и конечного состояний
системы независимо от процесса, приводящего к этому переходу и не зависит от
пути перехода.

12. Число степеней свободы молекул. Внутренняя энергия идеального газа

При
определении внутренней энергии газа важную роль играет понятие числа степеней
свободы молекул. Под числом степеней свободы системы подразумевается число
независимых координат, полностью определяющих положение системы в пространстве.
В первом приближении молекула газа может быть рассмотрена как материальная
точка, обладающая тремя степенями свободы поступательного движения. Однако,
такое приближение оказывается справедливым только для одноатомных молекул, для
которых можно пренебречь энергией вращательного движения из-за малости ее
момента инерции.

В механике многоатомные молекулы принято рассматривать как
совокупность жестко связанных материальных точек. Например, двухатомная
молекула состоит из двух материальных точек. Такая молекула обладает тремя
степенями свободы поступательного движения (тремя координатами центра масс) и
двумя степенями свободы вращательного движения вокруг двух осей,
перпендикулярных линии связи атомов. Вращение молекулы вокруг третьей оси не
учитывается ввиду чрезвычайной малости энергии вращательного движения вокруг
этой оси. Это значит, что жесткая двухатомная молекула обладает пятью степенями
свободы (. Трехатомная нелинейная молекула имеет шесть
степеней свободы: три поступательные и три вращательные степени свободы вокруг
трех осей симметрии молекулы (рис.7).

Рис. 7

Считать, что связи атомов в молекулах являются жесткими
несправедливо. Поэтому в реальных молекулах следует учитывать также степени
свободы колебательного движения атомов в молекулах. Очевидно, что независимо от
общего числа степеней свободы три степени свободы молекул всегда поступательные
степени свободы. Все три степени свободы равноправны и поэтому естественно
полагать, что на каждую степень свободы поступательного движения приходится
энергия . В классическую статистическую физику Больцман
ввел теорему, согласно которой не только на каждую поступательную степень
свободы, но и на вращательные степени свободы приходится одинаковая энергия . На каждую колебательную степень свободы
приходится энергия , т.е в два раза большая энергия, так как
колеблющаяся частица обладает не только кинетической также и потенциальной
энергией, причем их средние значения одинаковы. С учетом всех степеней свободы
молекулы ее средняя энергия может быть выражена формулой

,
(2.40)

где —
сумма чисел поступательных, вращательных и удвоенного числа колебательных
степеней свободы молекулы

. (2.41)

В
идеальном газе потенциальная энергия взаимодействия молекул равна нулю, поэтому
внутренняя энергия идеального газа складывается только из кинетических энергий
движения. Внутренняя энергия одного моля газа складывается из энергий молекул:

. (2.42)

Внутренняя
энергия любой массы газа

. (2.43)

13. Первое начало термодинамики

Внутренняя энергия тела может изменяться в результате двух
различных процессов – совершения над телом работы и сообщения ему
количества тепла . Совершение работы сопровождается
перемещением внешних тел,
действующих на тело. Например, при работе расширения газа перемещается поршень.
Сообщение телу тепла не связано с перемещением внешних тел. В этом случае
изменение внутренней энергии обусловлено тем, что энергия молекул более
нагретого тела передается молекулам менее нагретого тела. Этот процесс
называется теплопередачей.

Таким образом, приращение внутренней энергии тела может быть
выращено общей формулой

.
(2.44)

Если считать, что не внешние тела совершают работу над данным
телом , а тело само совершает работу А
над внешними телами, т.е. , то выражение (2.44) может быть
переписано в виде

.
(2.45)

Как правило, эту формулу пишут в элементарной форме

.
(2.46)

Представленные
выше уравнения выражают первое начало термодинамики

В последнем выражении является полным
дифференциалом, эта величина не зависит от способа перехода между состояниями,
а и не являются таковыми. Они зависят от вида процесса,
совершаемого над телом, т.е. являются функцией процесса. Поэтому их изменение выражено
не в дифференциальной форме. Если система совершая работу периодически
возвращается в исходное состояние, то изменение ее внутренней энергии =
0 и первое начало термодинамики приводит к выводу . Это означает,
что при любом процессе невозможно получить работу более, чем затраченное
количество теплоты. Периодически действующая машина, которая совершала бы
работу, большую, чем переданная извне энергия – вечный двигатель первого рода –
невозможна.

14. Работа газа при изменении объема

Взаимодействие
газа с соприкасающимися с ним телами можно характеризовать давлением .
Пусть газ заключен в цилиндрический сосуд, закрытый скользящимпоршнем с
площадью (рис.8). Если газ начнет

Рис.8

расширяться, поршень будет
перемещаться и газ над поршнем совершит работу

Где —
сила давления, действующая на поршень, — перемещение
поршня. Но сила давления равна , откуда .Но ,
где — изменение объема газа. Таким образом элементарная
работа расширения выражается формулой

.
(2.47)

Работа,
совершаемая при изменении объема на конечную величину, выражается интегралом

.
(2.48)

Если
давление постоянно,

(2.49)

Из
вышеизложенного следует, что применительно к газам первое начало термодинамики
может быть представлено в виде

. (2.50)

На осях и работы численно равна площади
фигуры, выражающей зависимость давления газа от объема (рис.9 ).

Рис.9

Следует
заметить, графически можно изображать только равновесные процессы, т.е. такие
процессы, которые состоят из непрерывной последовательности равновесных
состояний. При этом считается, что изменение параметров состояния за конечный
промежуток времени бесконечно мал. Все реальные процессы неравновесны. Но при
определенных условиях их неравновесностью можно пренебречь.

15. Теплоемкость идеального газа

Удельная
теплоемкость вещества –это количество теплоты, необходимое для нагревания
единицы массы вещества на 1 К:

(Дж/кг·К).

Молярная
теплоемкость вещества – количество теплоты, необходимое для нагревания 1 моля
вещества на 1 К:

.
(2.51)

Из
сравнения этих формул находим связь между молярной и удельной теплоемкостями
вещества

.
(2.52)

Поскольку
количество теплоты является функцией процесса, то и теплоемкость является
функцией процесса, т. е. зависит от условий передачи тепла и совершения работы.
В случае газов различают теплоемкости газа при постоянном объеме и постоянном
давлении.

Представим
первое начало термодинамики для одного моля газа в виде

. (2.53)

Если
процесс происходит при постоянном объеме (), то из этой
формулы следует

. (2.54)

Согласно
(2.42)

и
отсюда (2.55)

Если
процесс нагревания газа происходит при постоянном давлении то из (2.53) имеем

Первое
слагаемое в этом выражении равно . Дифференцируя уравнение
Клапейрона-Менделеева при , получаем
формулу Майера

(2.56)

Воспользовавшись формулой (2.55) находим
зависимость от числа степеней свободы молекул

(2.57)

Отношение теплоемкостей при постоянном давлении и
постоянном объеме (2.58)

используется при описании некоторых
термодинамических процессов.

Из формул (2.55) и(2.57) следует,
молярные теплоемкости зависят только от числа степеней свободы молекул и не
изменяются с изменением температуры газа. Однако это утверждение весьма
приближенно и относится только к одноатомным газам. Эксперименты показывают,
что степени свободы и теплоемкости двухатомных газов зависят от температуры.
На рис.10 показан ход теплоемкости двухатомного водорода с температурой. При
низких температурах теплоемкость

Рис.10

водорода равна , т е. молекула водорода имеет три степени
свободы и проявляются только поступательные степени свободы. При этих
температурах вращательные степени свободы заморожены. При средних температурах
теплоемкость водорода равна , т е. молекула водорода имеет пять степеней свободы вдобавок к поступательным степеням
свободы и возбуждаются вращательные степени свободы. При высоких температурах
теплоемкость водорода равна. Это свидетельствует о том, что при высоких
температурах вдобавок к поступательным и вращательным степеням свободы
возбуждаются колебательные степени свободы молекул.

Рассмотренный
выше ход теплоемкости с повышением температуры хорошо объясняется квантовой
теорией. Скачки в изменении теплоемкости свидетельствуют о квантовании энергии
вращательного и колебательного движений молекул. Если энергии теплового
движения молекул недостаточно для возбуждения вращательной и колебательной
степеней свободы молекул то они не проявляются в теплоемкости.

16. Применение первого начала термодинамики к изопроцессам в газах

В равновесных процессах изменяются параметры
состояния системы. Состояние газа определяется тремя параметрами, например,
температурой Т, объемом V и давлением р. Однако изучать процессы при изменении всех трех
параметров состояния не удобно. Удобнее изучать изменение состояния,
поддерживая один из параметров состояния, например, объем постоянным, и изучать
связь между оставшимися двумя параметрами. Такие процессы называют
изопроцессами – изохорический , изотермическийи изобарический . 1. Изохорный процесс. На рис.11 показана диаграмма изохорного
процесса на осях р и V. Работа, совершаемая при изохорном
процессе равна нулю

Рис.11

Из первого начала термодинамики следует, что вся
теплота, сообщаемая газу, идет на изменение его внутренней энергии

или

.
(2.59)

2.Изобарный процесс. На рис. 12 показана
диаграмма изобарного процесса на осях р
и V.
Работа, совершаемая при изобарном процессе равна

Рис.12

,
(2.60)

И изображается площадью заштрихованного
прямоугольника (рис. 11тр). Пользуясь уравнением Клапейрона-Менделеева формулу
работы можно выразить через разность температур

.
(2.61)

При
сообщении газу количество теплоты при изобарном процессе

Его внутренняя энергия изменяется на величину

и газ совершает работу

3.Изотермический процесс. На рис.13 показана
диаграмма изобарного процесса на осях р
и V. Из
уравнения Клапейрона-Менделеева следует уравнение изотермического процесса

Рис.13

Работу, совершаемую газом при изотермическом
процессе, находим из выражения (2.48)

(2.62)

При изотермическом процессе внутренняя энергия
газа остается неизменной

И все сообщаемое газу тепло превращается в работу

17. Адиабатический процесс

Адиабатическим процессом
называется процесс происходящий без теплообмена с окружающей средой. Такой
процесс может быть осуществлен в очень теплоизолированных системах и при очень
быстром протекании процесса, при котором не успевает происходить теплообмен между
газом и окружающей средой. Примером адиабатического процесса является
распространение звука, когда из-за большой скорости распространения волны не
успевает происходить теплообмен между волной и средой.

Из первого начала термодинамики
следует, что при адиабатическом процессе и

(2.63)

т. е. работа совершается за счет убыли внутренней
энергии системы. Рассмотрим уравнение адиабатического процесса. Для этого
перепишем это выражение в виде

Продифференцируем уравнение Клапейрона-Менделеева

Исключив из двух выражений температуру, получим

где -называется показателем адиабаты или
коэффициентом Пуассона.

Разделив переменный, получаем

откуда следует

или

. (2.64)

Полученное уравнение называется уравнением
адиабатического процесса. С помощью уравнения Клапейрона-Менделеева уравнение
адиабатического процесса может быть представлены виде

(2.65)

.
(2.66)

На рис.14 показана диаграмма
адиабатического процесса (адиабата). Как

Рис.14

видно из рисунка адиабата более крутая, чем
изотерма. Это объясняется тем, что изменение давления при адиабатическом
расширении вызвано не только изменением объема, но и изменением температуры.

Работу, совершаемую при
адиабатическом процессе, можно найти из выражения (2.63)

Интегрируя это выражение, получим

.
(2.67)

Это выражение можно преобразовать к виду

.
(2.68)

18. Круговые процессы

Круговым процессом или циклом
называется такой процесс, при котором термодинамическая система после ряда
последовательных преобразований вновь возвращается в исходное состояние
(рис.15). Круговые процессы лежат в основе действия всех тепловых двигателей.

Рассмотрим работу при круговом
процессе на диаграмме р и V. Разобьем круговой процесс на два
процесса: процесс расширения 1a2 (работа,
выполненная при расширении равна площади фигуры ) и процесс сжатия 2б1 ( работа сжатия равна
площади фигуры ), причем А₁>А₂. Видно, что работа за цикл А = А₁— А₂ равна
площади цикла. В рассмотренном процессе работа положительна и цикл называется
прямым циклом. Если процесс протекает обратно, то цикл будет обратным циклом и
работа в обратном цикле будет отрицательной.

Рис.15

Применим
первое начало термодинамики к круговому процессу. Система в круговом процессе возвращается в
исходное состояние, поэтому. Значит, количество теплоты, использованное за цикл равно
выполненной работе . В прямом процессе и, значит, газ сам совершает работу за счет
полученного количества теплоты. В обратном процессе работа совершается над
газом и от газа отводится эквивалентное количество теплоты. Первая машина
называется тепловой машиной, вторая – холодильной машиной.

19. Цикл Карно

Французский ученый Сади
Карно(1796-1832) теоретически исследовал наиболее экономичный цикл, состоящий
из двух изотерм и двух адиабат (рис.16 ).

Рис.16

При изотермическом процессе внутренняя энергия
газа не изменяется, поэтому количество теплоты, полученное от нагревателя
равно работе расширения газа из состояния 1 в состояние 2

При адиабатическом расширении 2-3 теплообмен с
окружающей средой отсутствует и работа расширения равна изменению внутренней
энергии газа

Работа, совершенная при изотермическом сжатии 3-4
равна

Работа
адиабатического сжатия 4-1

Работа,
совершаемая при круговом процессе, равна

Нетрудно
доказать, что . В самом деле,

деля
одно уравнение на другое, имеем ,

Отсюда

Очевидно,
в круговом процессе работа, совершаемая газом за цикл, меньше энергии,
полученной от нагревателя. Часть энергии передается холодильнику. Коэффициент
полезного действия цикла равен

. (2.69)

Заменяя и
вышеприведенными выражениями получаем

.
(2.70)

Это есть термический коэффициент полезного действия
идеальной тепловой машины.

20. Обратимые и необратимые процессы

Обратимым
называется такой процесс, который может быть проведен в обратном порядке так,
что система пройдет через те же состояния, что и в прямом процессе, причем при
возвращении в исходное состояние не остаются какие-либо изменения в окружающей
среде. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.

Примером обратимого процесса являются
гармонические колебания, необратимого процесса — затухающие колебания. Процесс
теплопередачи тоже является необратимым процессом. Необратимым процессом
является расширение газа в пустоту. Необратимые процессы протекают только в
одном направлении. Чтобы необратимые процессы могли идти в обратном
направлении, необходим какой-либо компенсирующий процесс. Например, необходимо
периодически восполнять убыль энергии колебаний при затухающих колебаниях, что
обычно осуществляется в часах за счет энергии поднятого груза или сжатой
пружины. Путем совершения работы можно передавать тепло от холодного тела
нагретому телу. Все реальные процессы необратимы

21. Второе начало термодинамики

Как
заметили, работа с трением и теплообмен являются необратимыми процессами. Они
протекают только в одном направлении. Мы определили первое начало термодинамики
как применение закона сохранения энергии к тепловым процессам. Однако этот
закон не позволяет установить направление протекания процессов. Например, от
холодного тела можно взять какое-то количество теплоты и, совершив работу,
передать более нагретому телу. При этом закон сохранения энергии соблюдается.
Как видим, в природе передача тепла от холодного тела к горячему самопроизвольно
не осуществляется, нужно для этого совершить работу. В тепловых машинах от
нагревателя рабочему телу передается количество тепла ,
рабочее тело совершает работу А,
и часть тепла передается холодильнику. Очевидно такая
машина будет тем выгоднее, чем ближе ее коэффициент полезного действия к единице, т.е. чем большая часть полученного от
нагревателя тепла будет превращена в полезную работу, в пределе КПД был бы .
Для такой тепловой машины требовался бы холодильник. Он мог бы работать за счет
охлаждения любых окружающих тел, например, за счет охлаждения океанов. Прибор
такого вида называют вечным двигателем второго рода. Однако все попытки
построить такую машину терпели неудачу.

Обобщая результаты попыток построения такой машины, Кельвин
выдвинул формулировку второго начала термодинамики как принцип невозможности такого кругового процесса,
единственным результатом которого является превращение теплоты, полученной от
нагревателя в эквивалентную ей работу.

Клаузиус сформулировал второе начало термодинамики как
принцип невозможности такого кругового
процесса, единственным результатом которого является передача тепла от
холодного тела к более нагретому. Из формулировки Клаузиуса
следует, что невозможно отобрать теплоту от менее нагретого тела и передать ее
более нагретому телу, не совершив работу. Нетрудно показать, эти формулировки
эквивалентны друг другу. Из отрицания первой формулировки следует отрицание второй
формулировки.

22. Приведенное количество тепла

С
Карно показал, что КПД всех обратимых машин, работающих между одинаковым и
нагревателем и холодильником одинаковы и не зависят от рабочего вещества. КПД
необратимой машины всегда меньше, чем обратимой

Знаки
равенства и неравенства относятся к обратимым и необратимым процессам. Отсюда
имеем

или

Если
считать, что тепло от холодильника получается, а не отдается холодильнику, то

Отношение
Клаузиус назвал приведенным количеством тепла.
Если в теплообмене участвует несколько тел, то

или

23. Энтропия

Сумму
приведенных количеств тепла можно образовать не только для круговых, но и для
любых обратимых переходов из одного состояния в другое. Рассмотрим обратимый
цикл (рис.18). Интеграл представим в
виде

. (2.71)

Учитывая
обратимость, можно записать

Отсюда
видим, интеграл . Независимость интеграла от пути
обратимого перехода между состояниями означает, что этот интеграл выражает
некоторую функцию состояния тела, которую Клаузиус назвал энтропией и обозначил
буквой . Тогда согласно определению

. (размерность)
(2.72)

Каждое состояние тела характеризуется определенным значением
энтропии подобно тому, как оно характеризуется значением внутренней энергии.
Энтропия, как и внутренняя энергия, является полным дифференциалом.

Согласно (2.71) изменение энтропии при обратимом круговом
процессе

(2.73)

Изменение
энтропии при необратимом процессе

Рассмотрим в замкнутой системе
цикл (рис.15),
часть которой, например, необратима, она осуществляется неравновесным процессом, часть обратима (равновесный процесс). Тогда

или

Но интеграл
в правой части неравенства равен изменению энтропии между
состояниями 1 и 2., т.е.

Для малого необратимого процесса

При необратимом процессе энтропия системы
возрастает. Обобщая два процесса, имеем

Знаки
равенства и неравенства относятся к обратимым и необратимым процессам.

Следует
заметить, что полученные выражения изменения энтропии при обратимом и
необратимом процессах относятся только к замкнутым системам, т. е. к системам,
которые не обмениваются теплотой с внешней средой. Если система обменивается
теплотой с внешней средой, то ее энтропия может вести себя каким угодно
образом. Энтропия замкнутой системы может оставаться постоянной (при обратимых
процессах), либо возрастать (при необратимых) процессах, указывая тем самым
равновесность протекания процесса. Используя понятие энтропии, второе начало
термодинамики можно сформулировать как закон возрастания энтропии замкнутой
системы при необратимых процессах: всякий
необратимый процессв в замкнутой системе ведет к возрастанию энтропии системы.

Понятию
энтропии Больцман придал более глубокий статистический смысл. Он ввел понятие
термодинамической вероятности состояния системы – число
микросостояний в системе, осуществляющих данное макросостояние системы.
Термодинамическая вероятность отличается от ее математического определения, она
больше единицы. По Больцману термодинамическая вероятность и энтропия связаны
соотношением

Значит,
энтропия рассматривается как мера вероятности состояния системы. Формула
Больцмана дает статистическое толкование энтропии системы как меры ее
неупрядоченности. Чем больше число микросостояний, тем более неупорядочена
система. Равновесное состояние — это наиболее вероятное состояние и число
микросостояний системы максимальна. Если замкнутая система состоит из
нескольких тел, то энтропия системы равна сумме их энтропий, т. е. энтропия
аддитивна.

Реальные
процессы необратимы. Отсюда можно утверждать, что реальные процессы ведут к
увеличению энтропии. Однако все сказанное выше относится к системам, состоящим
из большого числа частиц. Это утверждение может нарушиться в системах с малым
числом частиц из-за флуктуаций вероятности состояний.

Пусть
система осуществляет равновесный переход из состояния 1 в состояние 2. Тогда на
основании первого начала термодинамики.

Рассмотрим
изменение энтропии идеального газа, используя выражения и

интегрируя,
получим

Изменение
энтропии идеального газа зависит от вида процесса. Например, для
адиабатического процесса и , поэтому ,
при адиабатическом процессе энтропия газа неизменна. При изотермическом
процессе и

При
изохорном процессе

24. Реальные газы. Отклонение свойств реальных газов от идеальности

Уравнением
состояния идеальных газов является уравнение Клапейрона-Менделеева

Однако
реальные газы этому уравнению подчиняются лишь приближенно. Их поведение
следует этому уравнению при низких давлениях и высоких температурах. При
высоких давлениях наблюдаются серьезные отклонения от идеальности. Например,
произведение при р=1000
атм приблизительно в два раза
превышает при давлении р=1
атм.

Отклонение
от идеальности объясняется очень просто. При получении уравнения состояния
идеальных газов считалось, что молекулы не обладают размерами и собственным
объемом и не взаимодействуют между собой на расстоянии. На самом деле, этими
фактами пренебрегать нельзя. Покажем это на расчетах. Радиусы атомов примем
равным 10^-10м. Тогда
объем занятый атомом равен , объем, занятый такими
молекулами при нормальных условиях равен м³<<1 м³. Согласно уравнению
состояния идеального газа, если при неизменной температуре давление увеличить
до 5000 атм, то
объем газа уменьшится в 5000 раз, т.е. плотность газа возрастет 5000 раз и
собственный объем молекул, заключенных в 1м³
составил бы 10^-4·5·10³ ≈ 0,5 м³. Таким образом, на долю самих молекул
приходилась бы половина всего объема газа. Естественно, при таких условиях
закон Бойля–Мариотта будет нарушаться.

Как
замечено, свойства газов зависят от межмолекулярного взаимодействия.
Установлено, силы межмолекулярного взаимодействия действуют на расстояниях не
более 10^-9м и
проявляются как силы притяжения и силы отталкивания. На рис.17 показана
качественная зависимость сил отталкивания и сил
притяжения

рис.17

и
их результирующая . Как видно из рисунка, силы отталкивания
положительные, силы притяжения отрицательные. На расстоянии результирующая
сила равна нулю, т. е. на этом расстоянии силы притяжения и отталкивания
уравновешивают друг друга. При преобладают силы притяжения – отрицательные силы, при —
силы отталкивания — положительные силы. На рис.19 показана зависимость
потенциальной энергии взаимодействия молекул от расстояния.
Очевидно, на больших расстояниях r>> межмолекулярные
силы не действуют и потенциальная энергия взаимодействия равна нулю. При
сближении молекул появляются силы притяжения, которым соответствует
отрицательная по знаку потенциальная энергия взаимодействия молекул. По мере
сближения потенциальная энергия взаимодействия уменьшается, достигая минимума
при . При r<r₀ силы отталкивания
возрастают. Потенциальная энергия взаимодействия становится положительной и
резко возрастает. Критерием различных агрегатных состояний вещества является
соотношение между величинами минимального значения потенциальной энергии взаимодействия
молекул и энергией теплового движения молекул .

Если
<<вещество находится в состоянии
газа. Кинетическая энергия теплового движения молекул не дает молекулам
прицепиться друг к другу и они разлетаются, не образуя молекулярные комплексы.
Если>>, то вещество находится в
твердом состоянии, кинетической энергии теплового движения недостаточно, чтобы
разрывать образовавшиеся связи между молекулами. Если вещество
находится в жидком состоянии, молекулы имеют возможность перемещаться в
пространстве, не расходясь на значительные расстояния.

Таким образом, любое вещество в
зависимости от температуры может находиться в трех агрегатных состояниях.
Температура перехода между состояниями зависит от значения.

25. Уравнение Ван-дер-Ваальса

Для описания состояния реальных газов
было предложено много уравнений . Среди
них наиболее простым и получившим наибольшее распространение является уравнение
Ван-дер-Ваальса. Для получения своего уравнения Ван-дер-Ваальс ввел в уравнение
Клапейрона-Менделеева поправки, учитывающие собственный объем молекул и
межмолекулярные взаимодействия.

Ввиду
наличия собственного объема молекул, объем, предоставленный молекулам для
движения, оказывается меньше объема сосуда, в котором находится газ. Свободный
объем, в котором могут двигаться молекулы одного моля газа, будет равен ,
где — объем, занимаемый самими молекулами. Поправка приблизительно
равен учетверенному собственному объему молекул. Дело в том, что центры двух
молекул не могут приблизиться друг к другу на расстояние меньше, чес
эффективный диаметр молекул . Это значит, что для центров
обеих молекул недоступен сферический объем радиуса .
Такой объем в раз больше собственного объема молекулы
газа На долю одной молекулы приходится объем в два раза меньший, т.е. .

Силы
притяжения между молекулами приводит к появлению дополнительного давления,
которое получило название внутреннего давления Согласно Ван-дер-Ваальсу это
давление пропорционально квадрату числовой плотности молекул, которая, в свою
очередь, обратно пропорциональна объему. Поэтому добавочное давление выражается
в виде . С учетом этих поправок уравнение Ван-дер-Ваальса
для одного моля газа записывается в виде

(2.74)

Для
произвольного количества газа с объемом куравнение
принимает вид

(2.75)

или

.
(2.76)

и называются
поправками Ван-дер-Ваальса.

26. Изотермы Ван-дер-Ваальса

На
рис. 20` показаны изотермы Ван-дер-Ваальса при различных

температурах.
Изотермы имеют различные формы. При высоких температурах

Рис.20

(Т>Т_к)
изотермы реального газа подобны изотермам идеального газа с некоторым
искажением формы. На изотерме, соответствующей температуре Т_к, имеется точка перегиба,
обозначенная буквой К. Эта изотерма называется критической изотермой. Точка
перегиба К называется критической точкой, в этой точке кривая горизонтальна и
производная . Соответствующие этой точке температура Т_к, объем и давление р_к, называются критическими
параметрами, состояние вещества, соответствующее критической точке, называется
критическим состоянием. При температурах ниже критической (Т<Т_к)
изотермы имеют волнообразный участок.

Стремясь
разобраться в характере изотерм при Т<Т_к, приведем уравнение Ван-дер-Ваальса
к общему знаменателю

. (2.77)

При
заданных р и Т это уравнение представляет собой
уравнение третьей степени относительно объема. Оно может иметь три вещественных
корня или один вещественный и два мнимых корня. Первому случают соответствуют
изотермы при низких температурах Т<Т_к, в которых одному значению
давления соответствует три значения объема , а второму –
изотермы при температурах Т>Т_к. На участке 1-2 и 4-6
(рис.23ф ) с уменьшением объема давление растет, это закономерно, на участке же
3-4 с уменьшением объема давление уменьшается. В природе такая зависимость не
встречается. Известно, что при сжатии газа в цилиндре с поршнем при некотором
давлении начинается переход вещества в двухфазное состояние и изотерма
принимает вид кривой 1-2-5-6, на участке 2-5 вещество находится в состоянии
равновесия жидкой и газообразной фаз. Вещество в газообразном состоянии при
температуре ниже критической называется паром, а пар, находящийся в равновесии
с жидкостью — насыщенным паром. Этот вывод был подтвержден опытами ирландского
ученого Эндрюса (1813-1885), который сжимая в цилиндре с поршнем углекислоту
получил при температурах Т<Т_к кривые аналогичные кривой
1-2-5-6 (рис.21).

Рис.21

Уравнение
(2.77) дает возможность определять критические параметры вещества. Подставим
в него критические параметры

При
критической температуре все три корня становятся одинаковыми, поэтому это
уравнение должно иметь вид

или

Поскольку
эти уравнения тождественны, в них должны быть равны и коэффициенты при
одинаковых степенях :

Совместное решение этих уравнений дает

. (2.78)

Если по крайним точкам горизонтальных участков семейства кривых, полученных при
разных температурах, провести линию, то получается колоколообразная кривая
(рис.22), ограничивающая область двухфазных состояний вещества. Эта линия и
критическая изотерма делят диаграмму р—V_m на три области:

Рис.22

под
колоколообразной частью располагается область двухфазных состояний, слева от
нее область жидкого, справа – область пара. Пар от газа отличается тем, что при
изотермическом сжатии он превращается в жидкость. Газ при температуре выше
критической не может быть превращен в жидкость ни при каком давлении.

При
сравнении изотерм Ван-дер-Ваальса с экспериментальными изотермами Эндрюса
видно, что участок 2-5 соответствует двухфазному состоянию вещества. При
некоторых условиях могут быть получены состояния, изображаемые участками
изотерм Ван-дер-Ваальса 2-3 и 4-5. Эти состояния неустойчивы и называются
метастабильными. Участок 2-3 изображает пересыщенный пар, участок 4-5 –перегретую
жидкость. При низких температурах получаются изотермы, которые пересекают ось V_m, переходя в область
отрицательных давлений. Эта область соответствует растянутой жидкости и при
некоторых условиях тоже реализуется (рис23).

Рис.23

27. Критическое состояние вещества.

Понятие о критической температуре впервые ввел Д.И. Менделеев (1861).Эту
температуру он назвал температурой абсолютного кипения жидкости и считал, что
при этой температуре исчезают силы сцепления между молекулами и жидкость
превращается в пар независимо от давления и температуры. Такое понимание вполне
подходит современному представлению о критическом состоянии.

Построим диаграмму зависимости в герметично закрытом сосуде плотности жидкости
и находящегося в равновесии с ней насыщенного пара. В результате расширения
жидкости с повышением температуры ее плотность уменьшается, поэтому кривая ж изогнута вниз. Изменение плотности
насыщенного пара изображается кривой п.
При повышении температуры плотность насыщенного пара возрастает. В некоторой
точке К обе кривые сливается Эта кривая соответствует минимальной плотности
жидкости и максимальной плотности насыщенного пара, следовательно она
представляет такое состояние вещества , при котором теряется всякое различие
между парообразным и жидким состоянием. Переход из жидкого в газообразное
состояние и из газообразного в жидкое состояние происходит непрерывно и теплота
парообразования в этой точке равна нулю. Равно нулю также поверхностное
натяжение жидкости.

В
критической точке кривая зависимости давления вещества от объема горизонтальна,
поэтому случайные изменения объемане приводят к серьезным
изменениям давления, отклонения от среднего значения могут быть
довольно большими. Этим объясняется неоднородность вещества при критической
температуре. Вблизи критической температуры во всем объеме вещества образуются
и вновь распадаются местные сгущения, вследствие которых вещество становится
мутным и непрозрачным. Это явление называется критической
опалесценцией.

Критические температуры большого числа
жидкостей изучены российскими учеными – Авенариусом и его учениками. А.И.
Надеждин в 1885 г. определил, критическую температуру воды (374⁰С).
Столетов занимался сравнением экспериментальных критических параметров с их
теоретическими значениями.

28. Внутренняя энергия реального газа

Внутренняя энергия идеального газа определяется кинетической энергией теплового
движения молекул и для одного моля вещества выражается формулой .
Внутренняя энергия реального газа включает в себя кинетическую энергию
теплового движения молекул и потенциальную энергию их взаимодействия.
Потенциальная энергия реального газа обусловлена только силами притяжения молекул,
обуславливающими внутреннее давление . Поэтому часть внутренней
энергии, обусловленной межмолекулярным взаимодействием, может быть вычислена
как работа, совершаемая по преодолению сил внутреннего давления т.е.

откуда

Знак
минус в этом выражении указывает, что межмолекулярные силы, создающие
внутреннее давление, являются силами притяжения. С учетом обеих составляющих
внутренняя энергия реального газа выражается в виде

она растет тс повышением температуры и увеличением
объема.

Пусть
газ из состояния с объемом расширяется до объема адиабатически
в вакуум без совершения внешней работы. Тогда из выражения получим

Т.е. при
адиабатическом расширении без совершения работы внутренняя энергия газа не
изменяется. Этот равенство формально справедливо и для идеальных и для реальных
газов. Однако физический смысл этого равенства для обоих газов различен. Для
идеального газа равенство означает равенство температур ,
при расширении идеального газа в вакуум его температура не изменяется. В случае
реального газа с учетом

получим

. (2.79)

При расширении V₂>V₁, поэтому Т₁>Т₂. Реальный газ при адиабатическом
расширении в вакуум охлаждается, при сжатии нагревается.

29. Эффект Джоуля-Томсона

При адиабатическом расширении идеального газа с совершением работы он
охлаждается, Работа совершается за счет убыли внутренней энергии. Английские
ученые Джоуль (1818-1889) и Томсон (1824-1907) исследовали изменение
температуры реального газа при адиабатическом расширении. На рис.24 показана
схема их экспериментальной установки. Она состоит из
теплоизолированной

Рис.24

трубки,
внутри которой находится пористая перегородка (дроссель) и два поршня 1 и 2,
которые могут перемещаться без трения. Исследуемый газ сначала находится на
левой стороне от перегородки под давлением р₁,
создаваемым поршнем 1, имеет объем V₁
и температуруТ₁.
Справа поршень вплотную прижат к перегородке. Нажатием на поршень 1 газ через
перегородку перегоняется в правую часть от перегородки, в которой состояние
газа характеризуется давлением р₂,
объемом V₂ и
температурой Т₂.
Давления р₁ и р₂ поддерживаются постоянными.
Такой опыт называют дросселированием газа.

В
зависимости от условий дросселирования газ может охлаждаться Т₂ < Т₁, такое
изменение температуры называется положительным эффектом (<
0), может и нагреваться Т₂ > Т₁,
такое изменение температуры называется отрицательным эффектом (>
0).

Применим к рассматриваемому процессу первое начало термодинамики. Поскольку
процесс происходит без теплообмена с окружаюшей средой, то

. (2.80)

Работа,
совершаемая при расширении газа в правой части положительна и равна,
работа над газом в левой части отрицательна и равна . Полная работа
в процессе равна . Подставив в (2.80),
получаем

. (2.81)

Для
удобства расчетов положим, что количество газа равно одному молю. Пусть V₂>>V₁. Тогда
можно считать,что изменение состояния газа в левой части олисывается уравнением
Ван-дер-Ваальса, а в правой части – уравнением Клапейрона-Менделеева, т.е.

Подставив
эти выражения в (2.81), получим

Преобразуем
третье слагаемое в левой части равенства

С учетом
этого получаем

Знак зависит
от знака выражения в скобках:

если >, то > 0 и эффект
отрицательный,

если >, то < 0 и эффект
положительный.

Уравнение

—=0

связывает
Т₁ и V₁ в одном выражении. На
диаграмме Т₁ ~ V₁ это уравнение описывает
кривую называемую кривой инверсии (рис.25). Область выше этой кривой
соответствует отрицательному эффекту Джоуля-Томсона, ниже кривой –

положительному.

Рис.25

Эффект Джоуля-Томсона обусловлен отклонением свойств реального газа от
идеальности. Для идеального газа , поэтому выражение (2.61)
примет вид

откуда
следует .

Эффект Джоуля-Томсона находит широкое
применение при сжижении газов.

30. Сжижение газов

Превращение
газа в жидкость(сжижение) возможно только при условии, когда температура газа
ниже критической температуры. Такие газы как Сl₂, CО₂, NH₃ удавалось легко
получить в жидком состоянии простым сжатием.. Однако такие газы как О₂,
N₂, H₂, и т.д. такому сжижению не поддавались.
Причину этого объяснил Д.И. Менделеев: сжатие газов производилось при
температуре выше критической. Критические температуры этих газов низки: 154,4;
126,1; 33К соответственно. Их удалось получить в жидком состоянии только при
охлаждении их до температур ниже этих значений. В 1908 нидерландскому ученому
удалось получить жидкий гелий, критическая температура которого равна 5,3К.

Для
сжижения газов применяются два промышленных метода, в основе которых лежит либо
эффект Джоуля-Томсона, либо охлаждение газа заставив его совершить механическую
работу.

В машине
Линде используется эффект Джоля-Томсона. Воздух компрессором К сжимается до
давлений десятков мега Паскаль и охлаждается в холодильнике до температуры ниже
точки инверсии. При дальнейшем расширении газа наблюдается положительный эффект
Джоуля-Томсона. Затем сжатый газ проходит по внутренней трубе теплообменника и
пропускается через дроссель, при этом он сильно расширяется и охлаждается.
Охлажденный воздух вновь засасывается по внешней трубе теплообменника, охлаждая
воздух, текущий по внутренней трубе и так каждая следующая порция воздуха
охлаждается и пропускается через дроссель. При многократном повторении такого
цикла температура воздуха понижается все больше и больше. Через 6-8 часов
такого цикла сжижается и около 5% первоначального воздуха поступает в
дьюаровский сосуд, остальная часть возвращается в теплообменник.

Второй
метод сжижения газов основан на охлаждении газа при совершении работы. Сжатый
газ поступает в поршневую машину (детандер) расширяется, совершая работу по
передвижению поршня за счет своей внутренней энергии и охлаждается.

Академик П.Л. Капица предложил вместо детандера
турбодетандер, то есть воздух направлять в турбину, в котором газ, сжатый всего
лишь до 500 — 600 кПА охлаждается, совершая работу по вращению турбины. Этот
метод был применен П.Л.Капицей для получения жидкого гелия, предварительно
охлажденного лишь до температуры жидкого азота. Современные мощные установки
основаны на действии турбодетандера.

Источник

Уравнение состояния идеального газа

Средняя кинетическая энергия частиц газа

Основное уравнение МКТ идеального газа

Энергия частиц и температура газа

Идеальный газ.

Средняя кинетическая энергия теплового движения молекул.

Распределение молекул по скоростям.

Внутренняя энергия и теплоемкость идеального газа.

Скорость звука в газе.

Реальные газы.

Процессы переноса в газах.

Измерение температуры

Основное уравнение МКТ идеального газа

Следствия из основного уравнения МКТ идеального газа

Молекулярная физика и термодинамика

Оглавление

1. Введение

2. Уравнение состояния идеального газа

3. Основное уравнение молекулярно-кинетической теории идеальных газов

4. Максвелловский закон распределения молекул по скоростям

5. Средняя длина свободного пробега молекул

6. Явления переноса в газах

7. Теплопроводность газов

8. Внутренне трение в газах

9. Диффузия в газах

10. Соотношение между коэффициентами переноса

11. Понятие о внутренней энергии

12. Число степеней свободы молекул. Внутренняя энергия идеального газа

13. Первое начало термодинамики

14. Работа газа при изменении объема

15. Теплоемкость идеального газа

16. Применение первого начала термодинамики к изопроцессам в газах

17. Адиабатический процесс

18. Круговые процессы

19. Цикл Карно

20. Обратимые и необратимые процессы

21. Второе начало термодинамики

22. Приведенное количество тепла

23. Энтропия

24. Реальные газы. Отклонение свойств реальных газов от идеальности

25. Уравнение Ван-дер-Ваальса

26. Изотермы Ван-дер-Ваальса

27. Критическое состояние вещества.

28. Внутренняя энергия реального газа

29. Эффект Джоуля-Томсона

30. Сжижение газов