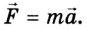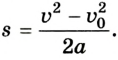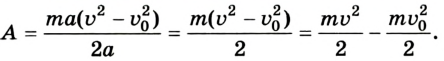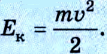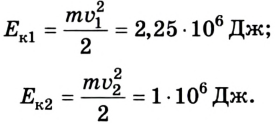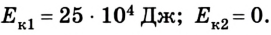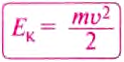Как найти кинетическую энергию в физике формула

Кинетическая энергия тела (Eкин) зависит от массы тела (m) и от скорости его движения (v).

Кинетическая энергия прямо пропорциональна массе тела и квадрату его скорости.

Определяют кинетическую энергию по формуле:

Чтобы рассчитать массу или скорость, формулу преобразуют следующим образом:

С увеличением массы тела в линейной зависимости увеличивается также и его кинетическая энергия. 

Если масса увеличивается в (2) раза, тогда кинетическая энергия увеличивается также в (2) раза.

Зависимость кинетической энергии от массы можно отобразить на данном графике, если принять скорость тела постоянной и равной (2  м/с).

Рис. (1). График, зависимость кинетической энергии от массы

Рис. (2). График, зависимость кинетической энергии от скорости движения

Содержание:

Кинетическая энергия:

Иногда значение работы можно найти, не используя понятия силы и перемещения, на основании характеристики изменения энергии тела.

Рассмотрим тело массой m, на которое действует сила F. Направление действия силы совпадает с направлением перемещения. Работа, которую выполняет эта сила,

A = Fs.
Согласно второму закону механики Ньютона значение силы

Как известно, модуль перемещения равен:

Поэтому

Как известно, выражение 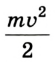 называется кинетической энергией. Следовательно, для расчета работы достаточно определить только массу тела и его начальную и конечную скорости, т. е. знать изменение кинетической энергии тела. Такой метод удобен, поскольку им можно пользоваться даже в случае переменной силы и произвольной траектории.

Физическая величина, описывающая состояние движущегося тела и изменение которой определяет работу, называется кинетической энергией.

Для измерения энергии, как и работы, используется единица джоуль (Дж), названная в честь английского ученого Д. Джоуля.

Кинетической энергией обладает тело, движущееся в данной системе отсчета с определенной скоростью:
Скорость тела, измеренная в разных системах отсчета, будет иметь разное значение, т. е. она является относительной величиной. Поэтому кинетическая энергия тела постоянной массы тоже величина относительная и в разных системах отсчета имеет разное значение.

Рассмотрим, например, два железнодорожных вагона, массы которых составляют по 2 • 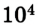кг, движущиеся в одном направлении со скоростями 15 м/с и 10 м/с относительно железнодорожного полотна, причем первый догоняет второго. Их кинетическая энергия соответственно будет:

Если же систему отсчета связать со вторым вагоном, то первый будет двигаться со скоростью 5 м/с , а второй — со скоростью v = 0. В этом случае

Следовательно, при расчетах в разных инерциальных системах отсчета следует учитывать, что кинетическая энергия в случае перехода из одной системы в другую будет изменяться.

Что такое кинетическая энергия

Кинетическая энергия (от греческого слова кинетикос — тот, что приводит в движение) — это энергия, которой тело обладает вследствие собственного движения.

Кинетической энергией обладает ветер, её используют для сообщения движения ветряным двигателям. Движущиеся массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и заставляют их вращаться. На рисунке 175, а изображена ветряная мельница, в которой за счёт энергии ветра мелют зерно. Современные довольно мощные ветряные двигатели (рис. 175, б) используют для того, чтобы вырабатывать электроэнергию, качать из скважин воду и подавать её в водонапорные башни.

Движущаяся вода или нагретый пар, вращая турбины электростанции, теряет часть своей кинетической энергии и выполняет работу. Самолёт, летящий высоко в небе, кроме потенциальной обладает и кинетическуй энергией. Если тело находится в состоянии покоя, т. е. его скорость относительно Земли равна нулю, то и его кинетическая энергия относительно Земли будет равна нулю.

Опытами установлено, что чем больше масса тела и скорость, с которой оно движется, тем больше его кинетическая энергия. Выявленная зависимость математически выражается такой формулой: 

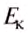
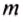
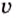
где — кинетическая энергия тела; — масса тела; — скорость движения тела.

Определение кинетической энергии

Наблюдения явлений природы показывают, что работа может выполняться при движении тел. Так, движущийся тепловоз, стыкуясь с вагоном, перемещает его на некоторое расстояние. Выполняется работа и в том случае, когда брошенный камень разбивает лед. Выстреленная из ружья пуля пробивает доску и т. п. Если потенциальной энергией обладают тела, на которые действует сила, то в упомянутых выше случаях работа выполняется потому, что они осуществляли перемещение, двигались.

Какой энергией обладают движущиеся тела

Энергию движущегося тела называют кинетической энергией. 

Кинетическая энергия является физической величиной ее значение можно рассчитывать. Для этого необходимо знать, от каких физических величин она зависит.

Как рассчитывают кинетическую энергию

Поставим желоб под некоторым углом к поверхности стола. На некотором расстоянии от его нижнего конца поставим брусок. На средней части желоба разместим маленький стальной шарик и отпустим его. Скатившись по желобу, шарик ударится о брусок и переместит его на некоторое расстояние. Отметим расстояние, на которое сместился брусок.

Поместим шарик в верхней части желоба и отпустим его. В этом случае, скатившись желобом к основе, шарик приобрел большую скорость, чем раньше. Ударившись в брусок, он переместит его на большее расстояние, чем в предыдущем опыте, соответственно выполнив большую работу.

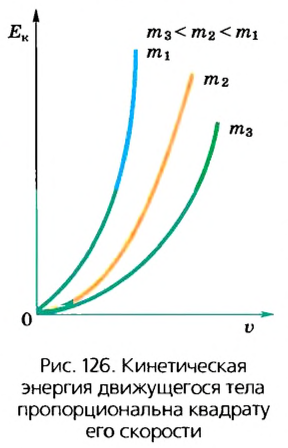
Таким образом, кинетическая энергия тела зависит от его скорости. Эта зависимость нелинейная, что заметно на графике зависимости кинетической энергии тела от его скорости. График имеет вид кривой линии (рис. 126).

Кинетическая энергия тела относительна

Как известно, скорость тела является относительной величиной и зависит от выбора тела отсчета. Поэтому и кинетическая энергия является величиной относительной. Если артиллерийский снаряд, попав в стену, причиняет значительные разрушения, то снаряд, посланный вдогонку сверхзвуковому самолету, не причинит ему существенных повреждений, поскольку скорость снаряда относительно самолета будет небольшой.

Последствия столкновения автомобилей в случае их движения навстречу друг другу будут всегда более ощутимы, чем тогда, когда один автомобиль догоняет другой.

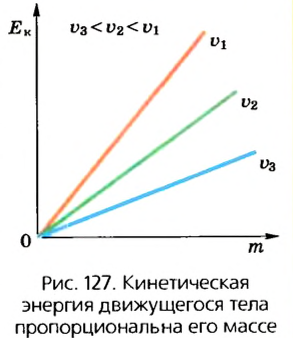
Кинетическая энергия зависит и от массы тела. Если повторим предыдущие опыты с шариком большей массы, то увидим, что перемещения бруска в этом случае будет большим. Эта зависимость линейная, поэтому можно сказать, что кинетическая энергия тела пропорциональна его массе (рис. 127).

Как рассчитать кинетическую энергию

Чтобы рассчитать кинетическую энергию, используют формулу:

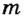
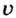
где — масса тела; — скорость тела.

Кинетическая энергия разных физических тел используется для выполнения механической работы. Так, опытные водители автомобилей время от времени отсоединяют двигатель от колес, выключая сцепление, и этим экономят топливо. Работа по преодолению сил трения выполняется за счет кинетической энергии автомобиля. Конструкторы работают над моделью городского автобуса, который начинает движение за счет энергии раскрученного во время стоянки большого маховика. Это дает возможность существенно уменьшить выбросы вредных газов в атмосферу и экономить топливо.

В южных областях Украины, в частности на Крымском полуострове, используют ветряные электростанции, которые работают за счет кинетической энергии потоков воздуха — ветра (рис. 128).

• Заказать решение задач по физике

Кинетическая энергия тела

Рассмотрим движение тела массой т под действием нескольких сил, например движение санок (см. рис. 124). Предположим также, что сила натяжения веревок постоянна, а следовательно, постоянной будет и результирующая сила 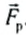. Она совпадает по направлению с перемещением тела или противоположна ему. Эта сила, естественно, вызывает ускорение санок, т. е. изменяет их скорость. Кроме того, она совершает работу. Следовательно, между работой результирующей силы и изменением скорости санок должна существовать связь.

Рассмотрим случай, когда проекция результирующей силы на направление движения положительна, т. е. санки движутся равноускоренно с ускорением а, которое находится из второго закона Ньютона:
    (1)

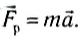
Работа результирующей силы:
A = F_p△r,    (2)
где △r— модуль перемещения тела за некоторый промежуток времени. Подставим выражение (1) в (2). В результате получим:
A = ma△r.    (3)

При равноускоренном одномерном движении модуль перемещения △r и изменение скорости связаны соотношением:
    (4)
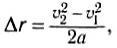
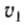
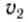
где и — начальная и конечная скорости тела, которое совершило перемещение △r с ускорением а.

Соотношение (3) с учетом (4) примет вид:
    (5) 

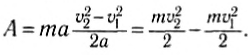
Полученная формула связывает работу результирующей силы, действующей на тело, с изменением величины 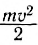. Эта величина называется кинетической энергией тела и обычно обозначается К.
Кинетическая энергия тела — это энергия движения. Она равна половине произведения массы тела на квадрат его скорости:
      (6)

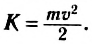
Тогда формула (5) примет вид:
      (7)

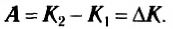
Итак, работа результирующей силы, действующей на тело, равна изменению кинетической энергии тела. Как вы уже знаете, изменение какой-то величины равно разности конечного значения и начального. Из формулы (7) очевидно следует, что кинетическая энергия выражается в тех же единицах, что и работа, т. е. в СИ в джоулях.

Когда результирующая сила действует по направлению движения тела и, следовательно, совершает положительную работу, то K₂>K₁. Это означает, что кинетическая энергия тела увеличивается. Понятно, что, если результирующая сила направлена в сторону, противоположную движению, она совершает отрицательную работу, и кинетическая энергия тела уменьшается. Следует отметить, что, хотя мы получили формулу (7) для частного случая равноускоренного и прямолинейного движения, она справедлива и в случае изменяющейся во времени результирующей силы. Поэтому формулу (7) часто называют теоремой о кинетической энергии.

Итак, любое движущееся тело (рис. 127, 128) обладает кинетической энергией. Поскольку скорость тела зависит от выбора инерциальной системы отсчета, то и кинетическая энергия также зависит от выбора системы отсчета. Очевидно, что, как и работа, кинетическая энергия является скалярной физической величиной. Она не зависит от направления движения тела, а определяется его массой и квадратом скорости.

Главные выводы:

1. Кинетическая энергия тела — это энергия движения. Она равна половине произведения массы тела на квадрат его скорости и зависит от выбора системы отсчета.
2. Изменение кинетической энергии равно работе всех сил, действующих на тело.
3. Кинетическая энергия измеряется в тех же единицах, что и работа.

Одним из важнейших понятий в физике является энергия, то есть способность тела совершать ту или иную работу. Механическая энергия подразделяется на кинетическую и потенциальную. Рассмотрим первый ее вид.

Кинетическая энергия – понятие и определение

Например, движущийся автомобиль способен снести находящееся перед ним препятствие, а падающий камень – оставить вмятину на металлической пластинке.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Кинетическая энергия зависит от скорости движения и массы тела. Она описывается формулой:

(E_k=frac{mnu^2}2)

Единицей измерения кинетической энергии является Джоуль (Дж).

Проведя простые преобразования, легко вывести формулы для вычисления массы тела и скорости движения:

(m=frac{2E_k}{nu^2})

(nu=sqrt{frac{2E_k}m})

Из основной формулы видно: во сколько раз изменяется масса тела, во столько раз изменяется и величина кинетической энергии. Например, если масса будет уменьшена или увеличена в 5 раз, то и величина кинетической энергии станет соответственно меньше или больше в 5 раз.

При увеличении скорости кинетическая энергия увеличивается в квадратичной зависимости. Допустим, скорость движения тела стала в 6 раз больше. Соответственно его кинетическая энергия возросла в 36 раз.

Формула кинетической энергии тела справедлива только для скоростей значительно меньших, чем скорость света. Если же скорость движения приближается к 300 000 км/с, то тут начинает действовать теория относительности, созданная Альбертом Эйнштейном.

Кинетическая энергия зависит от особенностей рассмотрения системы. Если тело принимают как макроскопический объект, то оно будет обладать внутренней энергией. В этом случае кинетическая энергия возникнет только в момент его движения.

Это же тело можно рассматривать и с микроскопической точки зрения. Тепловое движение атомов и молекул обуславливает внутреннюю энергию тела. В то же время средняя кинетическая энергия этого движения пропорциональна абсолютной температуре тела. Коэффициент этой пропорциональной зависимости называется постоянной Больцмана.

Кинетическая энергия атомов и молекул при рассмотрении тела на микроскопическом уровне описывается формулой:

(E_k=frac32kT)

где (k) – это постоянная Больцмана.

Теорема об изменении кинетической энергии

Рассмотрим наиболее простой пример движения, при котором скорость движения и сила, действующая на тело имеют одинаковое направление. Тело совершает перемещение (S), так как сила (F) совершает работу (A). Также она изменяет и скорость движения, придавая телу некоторое ускорение. Это свидетельствует о наличии связи между работой силы и изменением скорости движения.

В данном случае работа силы будет описываться формулой:

A=FS

Запишем второй закон Ньютона в стандартном виде:

F=ma

При условии, что движение является равноускоренным (сила не зависит от координат и времени), работу можно записать так:

A=maS

Вспомним формулу из курса кинематики, связывающую перемещение, ускорение, начальную и конечную скорости движения тела:

(S=frac{nu^2-nu_0^2}{2a})

Подставляем ее в формулу работы:

(A=frac{ma(v^2-v_0^2)}{2a}=frac{mv^2}2-frac{mv_0^2}2)

Полученное равенство показывает, что разность между кинетической энергией в конечной и начальный момент времени равна работе силы. Это позволяет сформулировать теорему об изменении кинетической энергии.

Изменение кинетической энергии тела равна равнодействующей всех сил или работе силы:

(A=E_{k2}-E_{k1})

Таким образом, сила будет совершать отрицательную работу, если она направлена в сторону, противоположную движению тела. В этом случае начальная кинетическая энергия будет больше, чем конечная:

(frac{mv_0^2}2>frac{mv^2}2)

Так как сила имеет противоположное скорости направление, то модуль скорости будет уменьшаться, что и становится причиной уменьшения величины кинетической энергии.

Если же сила будет направлена в сторону движения, то кинетическая энергия будет возрастать:

(frac{mv_0^2}2<frac{mv^2}2)

Фактически теорему об изменении кинетической энергии можно рассматривать как иную формулировку второго закона Ньютона. Поэтому ее использование возможно в различных случаях, например, при рассмотрении действия силы трения, тяжести или упругости.

Примеры решения задач, как найти кинетическую энергию

Рассмотрим примеры решения задач на нахождение кинетической энергии.

Задача 1

Тело, имеющее массу 2 кг движется поступательно со скоростью 36 км/ч. Найдите, какой кинетической энергией оно обладает.

Решение

Прежде чем приступить к вычислению необходимо перевести скорость тела в единицы СИ:

36 км/ч = 10 м/с

Подставим известные значения в формулу кинетической энергии и выполним расчет:

(E_k=frac{2times10^2}2=100;Дж\)

Ответ: кинетическая энергия тела составляет 100 Джоулей.

Задача 2

Груз массой 0,2 кг прикреплен к пружине, которая закреплена горизонтально. Максимальная скорость колебания 3 м/с. Вычислить максимальную кинетическую энергию тела.

Решение

Воспользуемся выражением определения кинетической энергии:

(E_{k_{max}}=frac{mv^2}2)

Выполним вычисление:

(E_{k_{max}}=frac{0.2times3^2}2=0.9;Дж)

Ответ: максимальная кинетическая энергия пружины и груза составляет 0,9 Дж.

Задача 3

Найдите среднюю кинетическую энергию поступательного движения молекулы водорода при температуре Т = 280 К.

Решение

Для решения задачи воспользуемся уравнением, связывающим температуру и энергию:

(E_k=frac32kT)

где k – это постоянная Больцмана

Проведем вычисление:

(E_k=frac{3times1,38times10^{-23}times280}2=579,6times10^{-23};Дж)

Ответ: средняя кинетическая скорость молекулы водорода составляет (579,6times10^{-23};Дж.)

Была ли эта статья полезной?