Содержание:
- Определение и формула кинетической энергии
- Кинетическая энергия материальной точки и тела
- Единицы измерения кинетической энергии
- Теорема Кенига
- Примеры решения задач
Определение и формула кинетической энергии
Определение
Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.
Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.
Встречаются следующие обозначения кинетической энергии: Ek,Wk,T.
Работу, которую производят над телом (A’) можно связать с изменением его кинетической энергии:
$$A^{prime}=E_{k 2}-E_{k 1}(1)$$
Кинетическая энергия материальной точки и тела
Кинетическая энергия материальной точки равна:
$$E_{k}=frac{m v^{2}}{2}=frac{p^{2}}{2 m}=frac{p v}{2}(2)$$
где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной.
Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:
$$E_{k}=frac{1}{2} int_{m} v^{2} d m=frac{1}{2} int_{m} rho v^{2} d V(3)$$
где dm – элементарный участок тела, который можно считать материальной точкой, dV – объем выделенного элементарного участка тела,
v – скорость перемещения рассматриваемого элемента, $rho$ — плотность участка, m–масса всего рассматриваемого тела, V – объем тела.
В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом.
При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:
$$E_{k}=frac{J omega^{2}}{2}=frac{omega^{2}}{2} int_{m} r^{2} d m=frac{L^{2}}{2 J}=frac{L omega}{2}(4)$$
где J – момент инерции тела по отношению к оси вращения, ?–модуль угловой скорости вращения тела,
r – расстояние от элементарного участка тела до оси вращения,
L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение.
Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:
$$E_{k}=frac{bar{L} bar{omega}}{2}(5)$$
$bar{L}$ – момент импульса рассматриваемого тела относительно точки О.
Единицы измерения кинетической энергии
Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:
[Ek]=Дж (джоуль),
в системе СГС –[Ek]= эрг.
При этом: 1 дж= 107 эрг.
Теорема Кенига
Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой,
кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения
системы со скоростью центра масс (vc) и кинетической энергии
(E’k) системы при ее относительном движении к поступательному перемещению системы отсчета.
При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:
$$E_{k}=sum_{i=1}^{n} frac{m_{i} v_{i}^{2}}{2}=frac{m v_{c}^{2}}{2}+E_{k}^{prime}$$
где $mathrm{E}_{k}^{prime}=sum_{i=1}^{n} frac{m_{i} v_{i}^{prime 2}}{2}, v_{i}^{prime}=v_{i}-v_{c}, m=sum_{i=1}^{n} m_{i}$ –суммарная масса системы материальных точек.
Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:
$$E_{k}=frac{m v_{c}^{2}}{2}+frac{J_{c} omega^{2}}{2}(7)$$
где Jc — момент инерции тела по отношению к оси вращения, проходящей через центр масс. В частности, при плоском движении
Jc=const.В общем случае, ось (она называется мгновенной) перемещается в теле, тогда момент инерции является переменным во времени.
Примеры решения задач
Пример
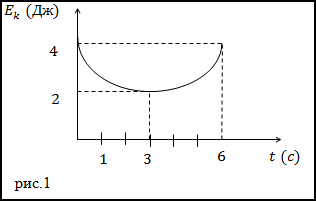
Задание. Какова работа, которая производится над телом за t=3 c (с начала отсчета времени),
при силовом взаимодействии, если изменение кинетической энергии исследуемого тела задано графиком (рис.1)?
Решение. По определению изменение кинетической энергии равно работе (A’),
которая производится над телом при силовом взаимодействии, то есть можно записать, что:
$$A^{prime}=Delta E_{k}(1.1)$$
Исследуя график, приведенный на рис.1 мы видим, что за время t=3 c кинетическая энергия тела изменяется от 4 Дж до 2 Дж, следовательно:
$A^{prime}=2-4=-2$ (Дж)
Ответ. A’=-2 Дж.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Материальная точка движется по окружности, радиус которой равен R. Кинетическая
энергия частицы связана c величиной пути (s), пройденного ей в соответствии с формулой:
$E_{k}=alpha s^{2}(alpha=$const$)$. Какое уравнение связывает силу (F), действующую на точку и путь s?
Решение. В качестве основы для решения задачи используем формулу, определяющую кинетическую энергию материальной точки:
$$E_{k}=frac{m v^{2}}{2}(2.1)$$
Но по условию задачи:
$$E_{k}=alpha s^{2}(2.2)$$
Следовательно, можно приравнять правые части выражений (2.1) и (2.2), и получить:
$$frac{m v^{2}}{2}=alpha s^{2} rightarrow v^{2}=frac{2 alpha s^{2}}{m} rightarrow v=s sqrt{frac{2 alpha}{m}}(2.3)$$
Из второго закона Ньютона нам известно, что сила, действующая на частицу, будет равна:
$$bar{F}=m bar{a}(2.4)$$
где
$$a=sqrt{a_{n}^{2}+a_{tau}^{2}}(2.5)$$
При этом нормальное ускорение частицы (an), перемещающейся по окружности найдем как:
$$a_{n}=frac{v^{2}}{R}=frac{2 alpha s^{2}}{R m}(2.6)$$
Тангенциальную составляющую ускорения (aт)используя определение тангенциального ускорения, определение скорости
($v=frac{d s}{d t}$) и выражение v(s) (2.3) вычислим как:
$$a_{tau}=frac{d v}{d t}=frac{d v}{d s} cdot frac{d s}{d t}=sqrt{frac{2 a}{m}} cdot v=s frac{2 a}{m}(2.7)$$
Используем выражения: (2.5), (2.6), (2.7), окончательно получаем для модуля силы:
$$F=m a=m sqrt{frac{4 alpha^{2} s^{4}}{R^{2} m^{2}}+s^{2} frac{4 alpha^{2}}{m^{2}}}=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$$
Ответ. $F=2 alpha s sqrt{frac{s^{2}}{R^{2}}+1}$
Читать дальше: Формула массы тела.
На чтение 15 мин Просмотров 2.2к.
Навигация
- Кинетическая энергия механической системы
- Энергетические характеристики
- Теорема об изменении кинетической энергии
Кинетическая энергия механической системы
Кинетической энергиейT материальной точки массы m, движущейся со скоростью V, называют величину
T=mV22 . (47)
Кинетической энергией механической системы называют сумму кинетических энергий включенных в эту систему материальных точек:
T=∑nk=1mV2k2 . (48)
В тех случаях, когда масса системы распределена непрерывно, суммирование в выражении (48) заменяют интегрированием по области распределения.
Найдем связь между значениями кинетической энергии механической системы в двух системах отсчета, одна из которых неподвижна, а другая движется поступательно со скоростью →VA . В этом случае скорость →Vkточки в неподвижной координатной системе и относительная скорость →Vrk связаны соотношением
→Vk=→VA+→Vrk .
Тогда вместо (48) получим
T=MV2A2+M→VA→VrC+Tr . (49)
Здесь →VrC=∑mk→VrkM — относительная скорость центра масс; Tr=∑nk=1mk(Vrk)22 — кинетическая энергия механической системы в подвижной системе координат.
Если за начало координат подвижной системы принимается центр масс механической системы С, то выражение (49) упрощается (теорема Кенига):
T=MV2C2+Tr. (50)
Использование выражений (48) и (50) позволяет сформулировать следующие правила вычисления кинетической энергии твердого тела: при поступательном движении тела массой M со скоростью →V
T=MV22 ; (51)
при вращении с угловой скоростью ω вокруг неподвижной оси z тела с моментом инерции Iz
T=Izω22 ; (52)
при плоскопараллельном движении твердого тела с угловой скоростью ω при значении центрального момента инерции ICz относительно оси, перпендикулярной плоскости движения, и значении IPz момента инерции относительно мгновенной оси вращения
T=MV2C2+ICzω22=IPzω22 ; (53)
при сферическом движении с угловой скоростью вращения ω
и значении момента инерции тела Iξотносительно мгновенной оси вращения ξ
T=Iξω22 ; (54)
в общем случае движения твердого тела
T=MV2C2+ICξω22 . (55)
Здесь момент инерции ICξ вычисляется относительно мгновенной оси Cξтакого сферического движения тела, которое оно совершает в системе осей, перемещающихся поступательно вместе с центром масс С.
В качестве примера вычислим кинетическую энергию механической системы, изображенной на рис.28, как сумму кинетических энергий тел ее формирующих. В этом случае
T=Tпост1+Tврбл+Tпост3+Tвр3=P1˙s212g+I2˙ϕ222+P3˙s232g+I3˙ϕ232 .
С учетом уравнений кинематических связей ˙s1=˙ϕ⋅R и ˙s3=˙ϕ3r3 выражение для кинетической энергии рассматриваемой механической системы с двумя степенями свободы может быть записано через любые две переменные, принятые за независимые. Например, если полагать независимыми s1 и s2, то выражение для кинетической энергии примет вид
T=˙s21(P1R2+I)2gR2+˙s223P34g .
Энергетические характеристики
К энергетическим характеристикам силы относят ее мощность, работу и потенциальную энергию.
Мощностью Nсилы →F, точка приложения которой движется со скоростью →V, называют величину
N=→F⋅→V. (56)
Работа силы d‘Aна элементарном интервале времени dtи соответствующем этому промежутку времени элементарному смещению d→rточки приложения определяется по правилу
d‘A=Ndt=→F⋅→Vdt=→F⋅d→r. (57)
Работой A силы на конечном интервале времени [0;t] и соответствующем изменении радиуса – вектора точки приложения этой силы от →r0 до →r называют величину
A=∫t0Ndt=∫→r→r0→Fd→r . (58)
Работа момента пары сил вычисляется аналогично.
Потенциальная энергия Попределена только в тех случаях, когда выражение (57) представляет собой полный дифференциал П:
d‘A=−dП. (59)
При выполнении условия (59) говорят, что сила потенциальна. Сопоставление формул (57) и (59) позволяет записать соотношения, связывающие проекции силы на оси выбранной координатной системы с функцией П:
Fx=−∂П∂x; Fy=−∂П∂y; Fz=−∂П∂z . (60)
Если точка приложения силы переместилась из положения M1(x1;y1;z1) в положение M2(x2;y2;z2), то путем интегрирования (59) можно получить
A12=−∫M2M1dП=П(x1;y1;z1)−П(x2;y2;z2). (61)
Заметим (см. формулы (57), (60) и (61)), что потенциальная энергия определена с точностью до постоянного слагаемого; отмеченная особенность позволяет полагать потенциальную энергию равной нулю в выбираемой нами точке (например, в начале координат). В последнем случае формула (61) принимает вид
A10=−∫M0M1dП=П(x;y;z). (62)
Иными словами – потенциальная энергия равна работе сил по переводу системы из отклоненного положения в начальное.
В том случае, когда для совокупности сил, действующих на механическую систему, можно записать выражение потенциальной энергии П, механическую систему называют консервативной. Такие механические системы обладают важными особенностями – работа действующих сил не зависит от вида траектории и закона движения по ней; работа при движении по замкнутому контуру равна нулю (см. (61)). Из (60) легко получить условия, при выполнении которых существует функция П:
∂Fx∂y=∂Fy∂x ; ∂Fx∂z=∂Fz∂x ; ∂Fz∂y=∂Fy∂z. (63)
В качестве примера вычислим потенциальную энергию для трех частных, но важных для технических приложений, случаев: действуют сила тяжести, центральная сила и сила упругости пружины.
Для силы тяжести →P=→i0+→j0−→kP выполняются критерии (63); тогда, в соответствии с формулами (58) и (62), имеем
П=A10=∫0z(Fxdx+Fydy+Fzdz)=∫0z(−P)dz=Pz. (64)
Для центральной силы →F=F(r)→rr, модуль которой зависит от расстояния rдо начала координат, так же выполняются критерии (63), поэтому
П=A10=∫r0rF(r)→rrd→r=∫r0rF(r)dr . (65)
Силу упругости пружины можно считать центральной силой, направленной к началу координат; в случае прямой пропорциональности между величиной силы Fx и удлинением x пружины имеем Fx=−cx. В этом случае
П=A10=∫0xFxdx=∫0x(−cx)dx=cx22. (66)
При определении энергетических характеристик системы сил суммируют соответствующие характеристики для всех сил, действующих на механическую систему.
Теорема об изменении кинетической энергии
Умножим уравнения (2.5) скалярно на скорость →Vk и сложим.
∑nk=1mkd→Vkdt→Vk=∑nk=1→Fek→Vk+∑nk=1→Fik→Vk=Ne+Ni ,
где Ne и Ni— мощности внешних и внутренних сил, действующих на механическую систему.
Заметим, что если связи между телами, формирующими систему, допускают деформацию (см. пружину жесткостью c2 в примере 21), то точки приложения равных и противоположно направленных внутренних сил →T2 имеют различные скорости, вследствие чего их суммарная мощность не будет равной нулю.
Изменив порядок суммирования и дифференцирования в левой части равенства, ее можно привести к виду
∑nk=1mkd→Vkdt→Vk=ddt∑nk=1mk→V2k2=ddt∑nk=1mkV2k2=dTdt .
Окончательно имеем запись теоремы об изменении кинетической энергии механической системы в дифференциальной форме:
dTdt=Ne+Ni. (67)
— производная по времени от кинетической энергии механической системы равна мощности всех действующих сил.
В дифференциальной форме, основанной на понятии работы силы за элементарный промежуток времени, получим
dT=(Ne+Ni)dt=d‘Ae+d‘Ai. (68)
Интегрируя (68) на интервале времени [0;t], получим интегральную форму записи теоремы об изменении кинетической энергии
T1−T0=Ae+Ai , (69)
где T1=T(t); T0=T(0); Ae=∫t0Nedt; Ai=∫t0Nidt.
В частном случае, когда для совокупности внешних и внутренних сил системы можно записать выражение потенциальной энергии
d‘Ae+d‘Ai=−dП,
вместо (68) имеем соотношение
d(T+П)=0 . (70)
В такой системе выполняется закон сохранения полной механической энергии
T+П=const ,
а сама система называется консервативной.
Загрузить PDF
Загрузить PDF
Существует два вида энергии: потенциальная и кинетическая. Потенциальная энергия — это энергия одного объекта по отношению к другому, которая зависит от их взаимного расположения.[1]
Например, если вы стоите на вершине холма, то ваша потенциальная энергия будет отличаться от той, которой вы обладали бы у подножия этого холма. Кинетическая энергия — это энергия движущегося объекта.[2]
Кинетическая энергия возникает при колебаниях, вращении и поступательном движении (перемещении тела из одного места в другое).[3]
Кинетическую энергию любого объекта легко вычислить, если известны его масса и скорость.[4]
-
1
Запомните формулу для вычисления кинетической энергии. Формула для нахождения кинетической энергии (КЕ) имеет следующий вид: KE = 0,5 x mv2. Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.[5]
- Ответ должен быть выражен в стандартных единицах измерения кинетической энергии, джоулях (Дж). Один джоуль эквивалентен 1 кг * м2/с2.
-
2
Определите массу объекта. Если в исходном условии не дана масса, ее придется определить самостоятельно. Для этого можно взвесить предмет и найти массу в килограммах (кг).
- Настройте весы. Прежде чем взвешивать предмет, необходимо выставить на весах ноль. Это называется тарировкой весов.[6]
- Положите объект на весы. Осторожно положите предмет на весы и запишите его массу в килограммах.
- При необходимости переведите граммы в килограммы. В конечную формулу необходимо подставить значение массы в килограммах.
- Настройте весы. Прежде чем взвешивать предмет, необходимо выставить на весах ноль. Это называется тарировкой весов.[6]
-
3
Найдите скорость объекта. Часто в условии задачи дается скорость объекта. Если скорость не дана, ее можно найти по пройденному расстоянию и затраченному для этого времени.[7]
Скорость измеряется в метрах в секунду (м/с).- Чтобы определить скорость, необходимо расстояние поделить на время: V = d/t. Скорость является векторной величиной, то есть имеет абсолютное значение и направление. Абсолютное значение соответствует величине скорости, а направление указывает на то, куда движется объект.
- Например, скорость объекта может составлять 80 м/с или –80 м/с, в зависимости от направления движения.
- Чтобы вычислить скорость, просто поделите пройденное расстояние на затраченное время.
Реклама
-
1
Запишите формулу. Кинетическая энергия (KE) вычисляется по следующей формуле: KE = 0,5 x mv2. Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.[8]
- Ответ записывается в джоулях (Дж). Это стандартная единица измерения кинетической энергии. Один джоуль эквивалентен 1 кг * м2/с2.
-
2
Подставьте в формулу массу и скорость. Если в условии задачи не дана масса или скорость, необходимо найти их. Предположим, что заданы обе эти величины, и необходимо решить следующую задачу: Найдите кинетическую энергию женщины массой 55 кг, которая бежит со скоростью 3,87 м/с. В условии даны масса и скорость, поэтому их можно сразу подставить в формулу:[9]
- KE = 0,5 x mv2
- KE = 0,5 x 55 x (3,87)2
-
3
Проведите вычисления. После подстановки массы и скорости можно рассчитать кинетическую энергию (KE). Возведите скорость в квадрат и умножьте полученное значение на массу и на 0,5. Помните, что ответ должен получиться в джоулях (Дж).[10]
- KE = 0,5 x 55 x (3,87)2
- KE = 0,5 x 55 x 14,97
- KE = 411,675 Дж
Реклама
-
1
Запишите формулу. Кинетическая энергия (KE) вычисляется по следующей формуле: KE = 0,5 x mv2. Здесь m — масса, которая показывает, как много в данном объекте материи, а v — скорость, то есть мера того, насколько быстро объект меняет свое положение в пространстве.[11]
- Ответ записывается в джоулях (Дж). Это стандартная единица измерения кинетической энергии. Один джоуль эквивалентен 1 кг * м2/с2.
-
2
Подставьте в формулу известные значения. В некоторых задачах дается кинетическая энергия и масса, или кинетическая энергия и скорость. Сначала необходимо подставить в формулу все известные величины.
- Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
- KE = 0,5 x mv2
- 500 Дж = 0,5 x 30 x v2
- Пример 2: чему равна масса предмета, если его кинетическая энергия составляет 100 Дж, и он движется со скоростью 5 м/с?
- KE = 0,5 x mv2
- 100 Дж = 0,5 x m x 52
- Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
-
3
Преобразуйте уравнение, чтобы найти неизвестную величину. Путем алгебраических преобразований перенесите искомую величину по одну, а все известные величины — по другую сторону знака равенства.
- Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
- KE = 0,5 x mv2
- 500 Дж = 0,5 x 30 x v2
- Умножим массу на 0,5: 0,5 x 30 = 15
- Поделим кинетическую энергию на получившееся значение: 500/15 = 33,33
- Извлечем квадратный корень, чтобы найти скорость: 5,77 м/с
- Пример 2: чему равна масса предмета, если его кинетическая энергия составляет 100 Дж, и он движется со скоростью 5 м/с?
- KE = 0,5 x mv2
- 100 Дж = 0,5 x m x 52
- Возведем скорость в квадрат: 52 = 25
- Умножим полученное значение на 0,5: 0,5 x 25 = 12,5
- Поделим кинетическую энергию на эту величину: 100/12,5 = 8 кг
Реклама
- Пример 1: чему равна скорость предмета, если его масса составляет 30 кг и он имеет кинетическую энергию 500 Дж?
Об этой статье
Эту страницу просматривали 29 609 раз.
Была ли эта статья полезной?
Одним из важнейших понятий в физике является энергия, то есть способность тела совершать ту или иную работу. Механическая энергия подразделяется на кинетическую и потенциальную. Рассмотрим первый ее вид.
Кинетическая энергия – понятие и определение
Определение
Кинетическая энергия – это способность движущегося тела совершать определенную работу.
Например, движущийся автомобиль способен снести находящееся перед ним препятствие, а падающий камень – оставить вмятину на металлической пластинке.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Кинетическая энергия зависит от скорости движения и массы тела. Она описывается формулой:
(E_k=frac{mnu^2}2)
Единицей измерения кинетической энергии является Джоуль (Дж).
Проведя простые преобразования, легко вывести формулы для вычисления массы тела и скорости движения:
(m=frac{2E_k}{nu^2})
(nu=sqrt{frac{2E_k}m})
Из основной формулы видно: во сколько раз изменяется масса тела, во столько раз изменяется и величина кинетической энергии. Например, если масса будет уменьшена или увеличена в 5 раз, то и величина кинетической энергии станет соответственно меньше или больше в 5 раз.
При увеличении скорости кинетическая энергия увеличивается в квадратичной зависимости. Допустим, скорость движения тела стала в 6 раз больше. Соответственно его кинетическая энергия возросла в 36 раз.
Формула кинетической энергии тела справедлива только для скоростей значительно меньших, чем скорость света. Если же скорость движения приближается к 300 000 км/с, то тут начинает действовать теория относительности, созданная Альбертом Эйнштейном.
Кинетическая энергия зависит от особенностей рассмотрения системы. Если тело принимают как макроскопический объект, то оно будет обладать внутренней энергией. В этом случае кинетическая энергия возникнет только в момент его движения.
Это же тело можно рассматривать и с микроскопической точки зрения. Тепловое движение атомов и молекул обуславливает внутреннюю энергию тела. В то же время средняя кинетическая энергия этого движения пропорциональна абсолютной температуре тела. Коэффициент этой пропорциональной зависимости называется постоянной Больцмана.
Кинетическая энергия атомов и молекул при рассмотрении тела на микроскопическом уровне описывается формулой:
(E_k=frac32kT)
где (k) – это постоянная Больцмана.
Теорема об изменении кинетической энергии
Рассмотрим наиболее простой пример движения, при котором скорость движения и сила, действующая на тело имеют одинаковое направление. Тело совершает перемещение (S), так как сила (F) совершает работу (A). Также она изменяет и скорость движения, придавая телу некоторое ускорение. Это свидетельствует о наличии связи между работой силы и изменением скорости движения.
В данном случае работа силы будет описываться формулой:
A=FS
Запишем второй закон Ньютона в стандартном виде:
F=ma
При условии, что движение является равноускоренным (сила не зависит от координат и времени), работу можно записать так:
A=maS
Вспомним формулу из курса кинематики, связывающую перемещение, ускорение, начальную и конечную скорости движения тела:
(S=frac{nu^2-nu_0^2}{2a})
Подставляем ее в формулу работы:
(A=frac{ma(v^2-v_0^2)}{2a}=frac{mv^2}2-frac{mv_0^2}2)
Полученное равенство показывает, что разность между кинетической энергией в конечной и начальный момент времени равна работе силы. Это позволяет сформулировать теорему об изменении кинетической энергии.
Изменение кинетической энергии тела равна равнодействующей всех сил или работе силы:
(A=E_{k2}-E_{k1})
Таким образом, сила будет совершать отрицательную работу, если она направлена в сторону, противоположную движению тела. В этом случае начальная кинетическая энергия будет больше, чем конечная:
(frac{mv_0^2}2>frac{mv^2}2)
Так как сила имеет противоположное скорости направление, то модуль скорости будет уменьшаться, что и становится причиной уменьшения величины кинетической энергии.
Если же сила будет направлена в сторону движения, то кинетическая энергия будет возрастать:
(frac{mv_0^2}2<frac{mv^2}2)
Фактически теорему об изменении кинетической энергии можно рассматривать как иную формулировку второго закона Ньютона. Поэтому ее использование возможно в различных случаях, например, при рассмотрении действия силы трения, тяжести или упругости.
Примеры решения задач, как найти кинетическую энергию
Рассмотрим примеры решения задач на нахождение кинетической энергии.
Задача 1
Тело, имеющее массу 2 кг движется поступательно со скоростью 36 км/ч. Найдите, какой кинетической энергией оно обладает.
Решение
Прежде чем приступить к вычислению необходимо перевести скорость тела в единицы СИ:
36 км/ч = 10 м/с
Подставим известные значения в формулу кинетической энергии и выполним расчет:
(E_k=frac{2times10^2}2=100;Дж\)
Ответ: кинетическая энергия тела составляет 100 Джоулей.
Задача 2
Груз массой 0,2 кг прикреплен к пружине, которая закреплена горизонтально. Максимальная скорость колебания 3 м/с. Вычислить максимальную кинетическую энергию тела.
Решение
Воспользуемся выражением определения кинетической энергии:
(E_{k_{max}}=frac{mv^2}2)
Выполним вычисление:
(E_{k_{max}}=frac{0.2times3^2}2=0.9;Дж)
Ответ: максимальная кинетическая энергия пружины и груза составляет 0,9 Дж.
Задача 3
Найдите среднюю кинетическую энергию поступательного движения молекулы водорода при температуре Т = 280 К.
Решение
Для решения задачи воспользуемся уравнением, связывающим температуру и энергию:
(E_k=frac32kT)
где k – это постоянная Больцмана
Проведем вычисление:
(E_k=frac{3times1,38times10^{-23}times280}2=579,6times10^{-23};Дж)
Ответ: средняя кинетическая скорость молекулы водорода составляет (579,6times10^{-23};Дж.)
Данная тема будет посвящена решению задач на расчет
кинетической энергии тела и применение теоремы о кинетической энергии.
Задача 1. Тело массой 10 кг движется вдоль оси Оx
под действием постоянной силы. На рисунке приведен график зависимости проекции
скорости тела на эту ось от времени. Определите кинетическую энергию тела в
момент времени 4 с.
Задача 2. Какую работу совершают силы сопротивления при
остановке автомобиля массой 3 т, движущегося со скоростью 54 км/ч?
Задача 3. На тело массой 2,5 кг действует сила 5 H в течение 3
с. Определите кинетическую энергию тела в этот момент времени, если его
начальная скорость равна нулю.
Задача 4. Тело массой 12 кг ударяется абсолютно неупруго о тело
меньшей массы. Если тело меньшей массы до удара покоилось, а доля потерянной
кинетической энергии после удара составила 14%, то какова масса меньшего тела?
Задача
5. На горизонтальном участке пути
длиной 500 м скорость поезда возрастает с 15 м/с до 20 м/с. Локомотив развивает
постоянную силу тяги 4 ∙ 106 Н. Определите массу поезда, если
коэффициент трения между колесами и рельсами равен 0,07.
«Вам знакомо выражение
«Выше головы не
прыгнешь»?
Это заблуждение.
Человек может все!»
Никола Тесла